统计学基础之摘要统计

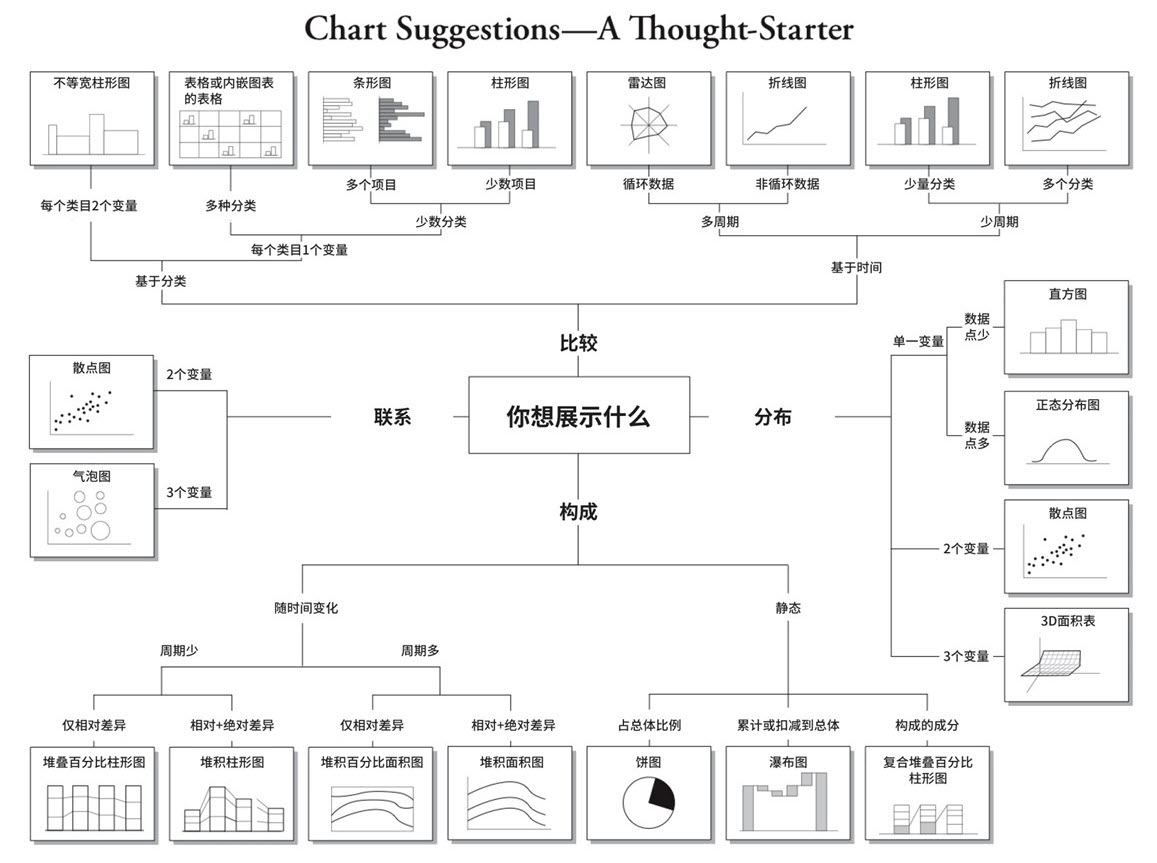
什么是摘要统计？

摘要统计是一种用来描述、概括和呈现数据集特征的统计学工具。它们通常用于数据分析的初步阶段，可以帮助研究者理解数据的基本趋势和模式，但不用于从样本推断总体的结论。摘要统计主要包括两类指标：集中趋势的度量和离散程度的度量。

集中趋势的度量：

• 平均值（Mean）：数据集合中所有数值的总和除以数值的数量。
• 中位数（Median）：将数据集合按数值大小排列后处于中间位置的数值。
• 众数（Mode）：在数据集合中出现次数最多的数值。

离散程度的度量：

• 极差（Range）：数据集中最大值与最小值的差值。
• 四分位数（Quartiles）：将数据分为四等份后，每一份的界限值（主要为Q1, Q2, Q3，分别对应25th, 50th, 75th百分位数）。
• 方差（Variance）：度量数据点与平均值的偏离程度的平方的平均值。
• 标准差（Standard Deviation）：方差的平方根，表示数据的波动大小。
• 变异系数（Coefficient of Variation）：标准差与平均值的比率，用于比较不同单位或平均值差别很大的数据集的离散程度。

摘要统计还包括分布的形状描述，例如偏度（Skewness）和峰度（Kurtosis），它们描述了数据分布的不对称性和尖锐度。

摘要统计通过表格、图形（如直方图、箱线图等）和数值的形式来呈现，使得数据的概况能够快速、直观地被理解。

摘要统计详解

整体与样本

在统计学中，“总体”和“样本”是两个非常重要的概念。

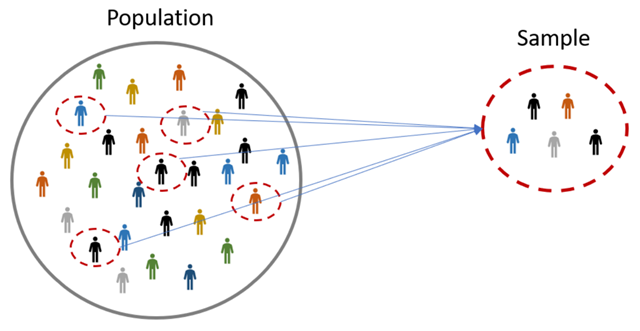
• 总体（Population）：总体是指研究对象的全部情况，可以是所有的人、事、物。例如，如果你想研究中国人的平均身高，那么所有的中国人就构成了你的研究总体。总体的特性通常使用参数（Parameter）来描述。
• 样本（Sample）：样本是从总体中抽取的一部分。在实际研究中，由于时间、金钱、能力等限制，我们通常无法获得关于整个总体的全面信息。所以，我们通常会选择一部分个体作为样本进行研究，然后根据样本的统计结果来推断总体的情况。样本的特性通常使用统计量（Statistic）来描述。

例如，在进行民意调查时，我们无法询问每一位选民，所以我们选择一部分选民作为样本，然后根据他们的回答推测全部选民的观点。一般来说，样本的大小对研究结果的准确性有重要影响——样本越大，样本统计量对总体参数的估计就越准确。

在对样本数据进行描述性统计分析后，我们可以使用推理统计来估计总体参数。推理统计的目的就是根据样本数据推断总体的特性，其中包括点估计、区间估计以及假设检验等。

需要注意的是，样本应该是随机抽取的，这样才能保证样本的代表性，使得我们对样本的观察和分析能够推广到总体。

抽样方法

在数据分析中，根据研究需要和总体的特性，抽样方法可以分为多种类型。每种抽样方法的选择都会影响样本的代表性和研究结果的准确性。以下是一些常用的抽样方法及其特点：

概率抽样方法

概率抽样意味着总体中的每个成员都有机会被选中。它主要用于定量研究。如果要生成代表整个总体的结果，概率抽样技术是最有效的选择。

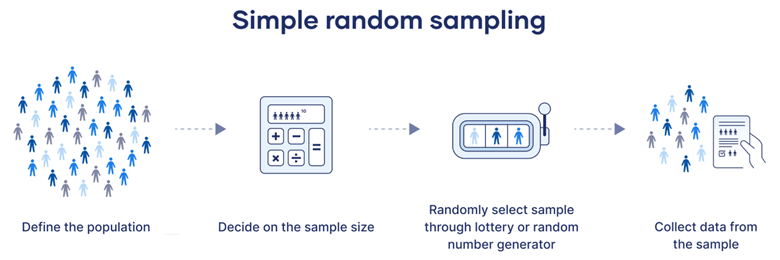
• 简单随机抽样（Simple Random Sampling）：

• • 在这种抽样方法中，每个成员被选中的机会是相等的。可以通过抽签、使用随机数表或计算机生成的随机数来实现。
  • 优点：操作简单，样本代表性好。
  • 缺点：需要能够访问到全部总体名单，对于大型总体可能不切实际。
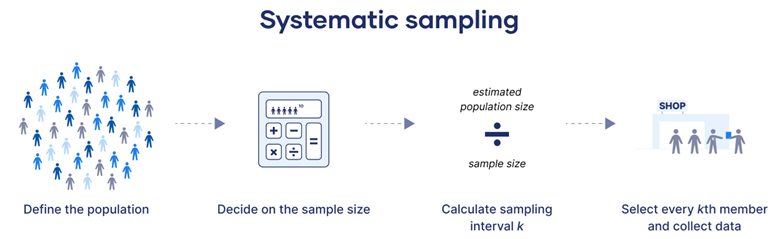
• 系统抽样（Systematic Sampling）：

• • 从总体中按照固定间隔（步长）选择样本，通常会随机选择一个起始点。
  • 优点：操作简便，适用于较大的总体。
  • 缺点：如果总体中有周期性的模式，可能会导致样本的偏差。
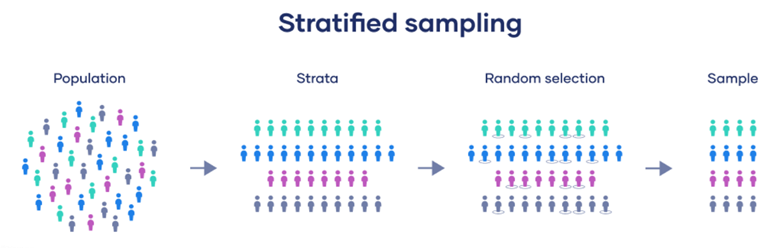
• 分层抽样（Stratified Sampling）：

• • 总体被分成若干互不重叠的子群（层），每个子群内部的成员在某些属性上是相似的，然后从每个子群中进行简单随机抽样。
  • 优点：能够确保各个层中重要的特征在样本中得到充分代表。
  • 缺点：需要对总体进行良好的分层，这需要详细的先验信息。
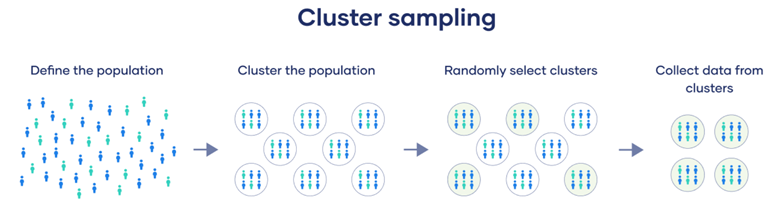
• 簇抽样（Cluster Sampling）：

• • 总体被分成多个簇，簇内的成员在所有属性上的差异较大，类似于小型总体。随机选择一些簇，然后对这些簇进行调查。
  • 优点：减少调查成本，适合地理分布广泛的总体。
  • 缺点：簇内的异质性可能会增加样本误差。
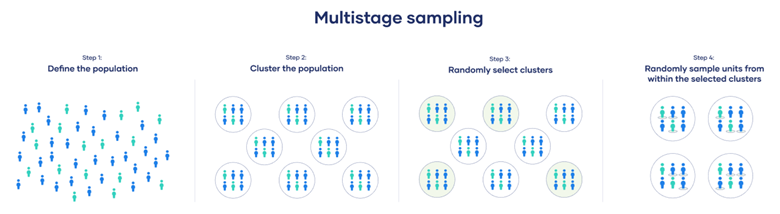
• 多阶段抽样（Multi-stage Sampling）：

• • 结合了分层抽样和簇抽样，是一种分阶段的选择方法，可能在第一阶段进行簇抽样，在第二阶段进行系统抽样或简单随机抽样。
  • 优点：灵活，适合大规模和复杂的总体。
  • 缺点：设计复杂，误差可能会在每个阶段累积。

非概率抽样方法

在非概率样本中，根据非随机标准选择个体，并非每个个体都有机会被纳入。这种类型的样本更容易获得，成本更低，但抽样偏倚的风险更高。这意味着你可以对总体做出的推论比概率样本弱，你的结论可能更有限。如果使用非概率样本，则仍应使其尽可能代表总体。非概率抽样技术通常用于探索性和定性研究。在这些类型的研究中，目的不是检验关于广泛人群的假设，而是对小规模或研究不足的人群形成初步了解。

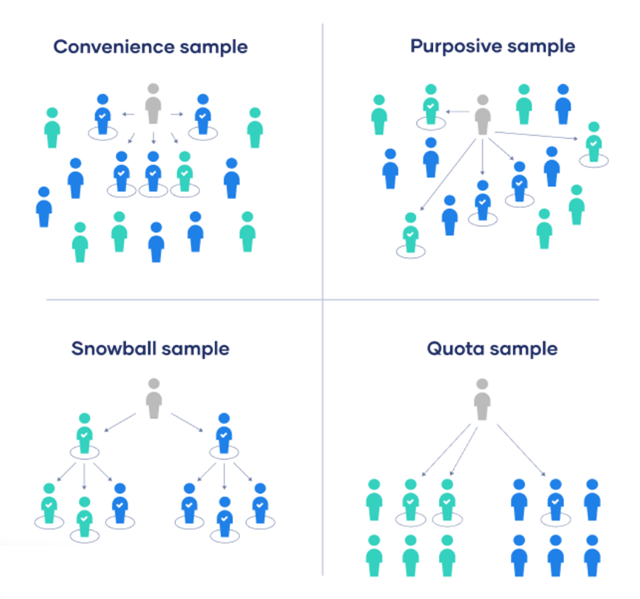
• 方便抽样（Convenience Sampling）：
  • 样本的选择基于方便和可达性，而不是随机性。
  • 优点：操作简单、成本低。
  • 缺点：样本可能不具代表性，可能存在偏差。
• 判断抽样/目的性抽样（Judgmental/Purposive Sampling）：
  • 根据研究者的判断选择特定的个体进行研究。
  • 优点：当需要特定类型的信息时非常有效。
  • 缺点：高度依赖研究者的主观判断，易受偏见影响。
• 雪球抽样（Snowball Sampling）：
  • 在难以接触或识别所有总体成员的情况下使用，通过已有的研究对象推荐其他对象。
  • 优点：适合研究隐秘群体或者网络紧密的群体。
  • 缺点：样本代表性可能有限，可能存在链式推荐的偏差。
• 配额抽样（Quota sampling）
  • 配额抽样依赖于对预定数量或比例的单位进行非随机选择。这称为配额。首先将人口划分为相互排斥的子组（称为分层），然后招募样本单位，直到达到配额。这些单元具有特定的特征，由您在形成地层之前确定。配额抽样的目的是控制样本的组成内容或人员。
  • 优点：配额抽样不需要完整的总体成员列表，因此在成本和时间上比概率抽样方法更为经济高效。
  • 缺点：由于是非概率抽样，配额抽样不能保证样本的统计代表性，抽样误差难以计算，因此结果的推广性受限。

每种抽样方法都有其适用场景和局限性，选择合适的抽样方法取决于研究目的、总体的性质、可用资源等因素。在实际应用中，研究者需要综合考虑各种因素，以获得既经济又有效的样本。

偏差的类型

在统计学和数据分析中，偏差（Bias）是指由于采集、选择、处理或解释数据的方法不当而导致的系统性错误。偏差通常会导致对总体的错误估计。以下是一些常见的偏差类型：

• 选择偏差（Selection Bias）：发生在选择样本过程中，当样本不是随机选择的，导致它不能准确代表总体。
• 测量偏差（Measurement Bias）：当收集数据的工具或过程有缺陷，导致测量结果系统性偏离真实值。
• 抽样偏差（Sampling Bias）：特定类型的选择偏差，发生在抽样方法有缺陷，造成一部分人群被过多或过少地代表。
• 信息偏差（Information Bias）：数据收集或记录过程中的错误，可能是由于记忆错误、误报或误解问题而产生的。
• 混淆偏差（Confounding Bias）：当未考虑或控制混杂变量对结果的影响，导致研究结果不能清晰地反映出暴露因素与结果之间的真实关系。
• 生存者偏差（Survivorship Bias）：当分析的样本只包括“存活”的案例，而未包括在观测期间“死亡”或消失的案例。
• 回归偏差（Regression Bias）：当极端值在随后的测量中倾向于朝向平均值移动，可能会导致数据分析的误解。
• 参与者偏差（Participant Bias）：当参与者知道自己是研究的一部分时，他们的行为可能会因此而改变，这种现象有时被称为“霍桑效应”（Hawthorne Effect）。
• 召回偏差（Recall Bias）：在回顾性研究中，当参与者回忆过去的行为或经历时，可能会不准确或遗忘，尤其是对于时间久远的事件。
• 发布偏差（Publication Bias）：研究结果发表的可能性受到研究结果性质的影响，通常意味着正面或显著的结果更容易被发表。
• 锚定偏差（Anchoring Bias）：当人们在做决策时过度依赖（或“锚定”）于第一个接收到的信息，这可能会影响他们对相关数据的解释。

为了减少偏差的影响，研究者会使用随机抽样、双盲实验、对照组设计、多变量分析等方法来增强研究的有效性和可靠性。

生存者偏差

生存者偏差（Survivorship Bias）是一种逻辑错误，它发生当人们在进行评估或决策时，只关注存活或成功的例子，而忽视了那些失败或消失的例子。这种偏差可以导致误导性的结论，因为它不考虑所有相关的证据，只是基于一个不完整的数据集。

生存者偏差的名称来自于军事历史。在第二次世界大战中，盟军希望通过增加战斗机的装甲来减少飞机被击落的数量。他们分析了返回基地的飞机上弹孔的位置，然后提议增加那些区域的装甲。然而，数学家亚伯拉罕·瓦尔德指出，这种分析忽视了在战斗中丧失的飞机。如果一架飞机没有返回，它就不会被包括在数据中。因此，真正需要额外装甲的实际上是那些在返回的飞机上没有被标记弹孔的部位，因为被击中这些部位的飞机很可能没能存活下来返回基地。瓦尔德的观点逆转了先前的逻辑，从而更有效地提高了飞机的生存率。

生存者偏差的例子

• 公司和投资：投资者在分析某个行业或市场的表现时，可能会只看那些存活下来的公司，而忽视了那些已经失败或被收购的公司，从而高估了投资的平均回报或者某个行业的成功率。
• 个人经历和建议：当人们根据成功人士的经验提出建议时，他们可能会遗漏那些采取了同样行动但失败了的人们。这可能导致”只需努力就能成功”的误导性观点。
• 科学研究和医学：在临床试验和科学研究中，如果只分析那些完成实验的参与者而忽视了那些中途退出的人，可能会导致研究结果存在偏差。

为了避免生存者偏差，重要的是要全面地了解所有的数据，包括那些不成功的、失败的或消失的例子。在分析和决策过程中，应该努力寻找丢失的信息，检查数据是否代表了整个样本，并考虑失败案例对于理解全局有多重要。此外，使用统计分析和逻辑推理来识别和补偿数据中的缺口也是避免生存者偏差的好方法。

总结来说，生存者偏差是一个普遍存在的问题，它可以扭曲我们的认识和判断。通过意识到这种偏差并采取措施来纠正它，我们可以作出更加准确和全面的评估。

参与者偏差

参与者偏差（Participation Bias），也称为自选择偏差（Self-selection Bias），是一种研究设计错误，它发生在研究或调查的参与者并非随机选取，而是基于他们的个人选择决定是否参与。这种偏差可能导致不具代表性的样本，因为选择参与的人可能在某些特征、行为或态度上与不愿意或未能参与的人有所不同。

这种偏差的原因通常与个体自愿参与研究有关。例如，一个健康调查可能吸引那些对健康问题特别关心的人，而这部分人的健康行为可能与一般人群有所不同。由于这种自我选择的原因，样本的数据可能不能准确反映整个目标人群的实际情况。

参与者偏差的例子

• 在线调查：在线调查经常遭受参与者偏差，因为它们通常依赖于受众的自愿参与。那些对调查主题感兴趣或者有时间的人更有可能响应，而这可能并不代表整个人群。
• 健康研究：健康相关的研究，如锻炼或饮食的影响，可能吸引了那些已经有健康生活方式的人，从而影响研究结果。
• 产品反馈：公司征求客户对产品的反馈时，通常只有最满意或最不满意的客户才会去踊跃提供反馈，这可能导致对产品质量的评估存在偏差。

为了减少或避免参与者偏差，研究人员需要采用恰当的策略和研究设计，包括：

• 随机抽样：通过随机选择被研究人群中的成员作为参与者，以确保样本能够代表整个人群。
• 激励措施：提供激励措施（如小礼品、金钱、抽奖）可能鼓励更多人参与，包括那些通常不愿意参与的人。
• 匿名和保密：保证参与者信息的匿名和保密可以提高人们的参与意愿，尤其是当研究涉及敏感主题时。
• 便捷的参与方式：简化参与流程，使人们更容易加入研究，无论是在线还是面对面。
• 广泛宣传：通过不同渠道和方法广泛招募参与者，以避免只吸引特定群体的人。
• 权衡分析：即使采取了上述措施，仍可能存在偏差。因此，研究人员应当对数据进行权衡分析，以了解偏差可能对结果产生的影响，并据此解释研究结果。

通过这些方法，研究人员可以努力确保他们的样本尽可能地代表了整体人群，从而减少由参与者的自我选择带来的偏差。不过，实际中完全消除参与者偏差是非常困难的，通常需要通过后续的统计分析和研究设计来调整和补偿这种偏差。

发布偏差

发布偏差（Publication Bias），有时也称为“抽屉效应”（file drawer effect），是指在科学研究领域中，倾向于只发表那些具有显著性结果的研究，而忽略或未发表那些未能获得显著性结果或与预期结果相悖的研究的现象。这种偏差可能由多个方面造成，包括研究人员、编辑和审稿人的心理倾向，以及学术和商业压力。

发布偏差的原因涉及多个层面，主要包括：

• 研究者偏好：研究者可能更愿意提交和发表那些具有积极结果的研究，因为这样的成果看起来更具“新闻价值”并且更可能被期刊接受。
• 期刊编辑和同行评议：编辑和审稿人可能更倾向于推荐发表那些结果显著、新奇、吸引眼球的研究，而对那些未得到显著结果的研究不太感兴趣。
• 资助和奖励机制：研究资金和学术晋升往往依赖于在高影响力期刊上发表研究成果的数量和质量，这为产生发布偏差提供了激励。

发布偏差对科学研究的影响是多方面的，包括：

• 曲解证据：如果文献中只报道了积极的研究结果，将可能导致对某一领域的理解产生偏见，特别是在进行文献综述或系统评价时。
• 错误的政策和临床决策：医学和公共卫生领域的政策制定者和医疗专业人员依赖于有质量的研究证据来指导实践。如果这些证据受到发布偏差的影响，可能会导致不合适的决策。
• 资源浪费：研究者可能会重复已经进行过但未发表的研究，因为他们无法获得之前失败或不显著结果的信息。

为了减少发布偏差带来的影响，可以采取以下措施：

• 注册临床试验：在临床试验开始之前进行注册，并公开其设计和结果，无论结果如何。
• 鼓励发表所有结果：鼓励研究者发表所有研究结果，包括负面或不显著的结果。
• 开放获取数据：鼓励或要求研究者分享他们的原始数据，以供其他研究人员进行验证和再分析。
• 系统评价和元分析：在进行系统评价和元分析时，尽可能搜索未发表的研究和灰色文献，以获取更全面的研究数据。
• 期刊政策改变：期刊可以改变政策，积极发表那些方法论严谨但结果不显著的研究。

通过这些措施，研究社群可以努力减少发布偏差的影响，提高科学研究的透明度和可复制性，从而增强研究结果的可信度和实用价值。

变量的类型

在统计学和数据分析中，数据可以分为不同的变量类型，每种类型的数据有其特点，需要用适当的方法进行处理和变换。

变量的类型主要有以下几种：

• 定性变量（Qualitative Variable）：也被称为分类变量，这种变量的值表示类别。例如，性别（男、女）、血型（A、B、AB、O）等。定性变量又可以分为以下两种：
  • 名义变量（Nominal Variable）：类别之间没有顺序关系，例如性别、国籍等。
  • 有序变量（Ordinal Variable）：类别之间存在顺序或等级关系，例如教育程度（小学、中学、大学）。
• 定量变量（Quantitative Variable）：这种变量的值表示数量，可以进行数学运算。例如，人的身高、体重等。定量变量又可以分为以下两种：
  • 间隔变量（Interval Variable）：数值之间的差有意义，但没有真正的零点，例如温度（摄氏度或华氏度）。
  • 比例变量（Ratio Variable）：除了数值之间的差有意义外，还有真正的零点，可以进行乘除运算。例如，体重、距离等。

变量的处理与变换

对于数值型变量的处理和变换，主要包括：

• 标准化（Standardization）：转换数据，使其均值为0，标准差为1。
• 归一化（Normalization）：通常是将数据缩放到0和1之间，也可以是其他任何特定的区间。
• 对数转换（Log Transformation）：用于处理具有指数分布的数据，如收入分布，可减少偏态。
• 差分变换（Differencing）：在时间序列数据中用来消除趋势和季节性。

对于分类型变量的处理和变换，可能需要：

• 独热编码（One-Hot Encoding）：将名义变量转换为二进制（0或1）的形式，每个类别都通过一个独立的变量表示。
• 标签编码（Label Encoding）：将类别变量的每个类别映射到一个整数值，但可能引入不必要的数值关系。
• 顺序编码（Ordinal Encoding）：对于序数变量，通过分配一个整数序号来保持类别之间的顺序关系。

在某些情况下，分类型变量也可能需要进行一些进一步的处理，例如：

• 缩减类别水平：如果一个名义变量有很多类别，可以将一些不常见的类别组合成一个“其他”类别。
• 创建派生变量：例如从日期时间变量中提取出年份、月份、星期等。
• 编码交互作用：在模型中包含变量的交互作用，这可能需要对类别变量进行特定的变换。

变量处理和变换的目的是为了使数据更适合于分析，提高模型的准确性和解释性。在实际应用中，选择适当的变量处理和变换策略是一项重要的技能，它取决于数据的特性和分析的目的。

峰度（Kurtosis）和偏度（Skewness）

峰度（Kurtosis）和偏度（Skewness）是描述数据分布形状特征的统计量，它们提供了数据分布形态偏离正态分布的信息。

偏度 (Skewness)

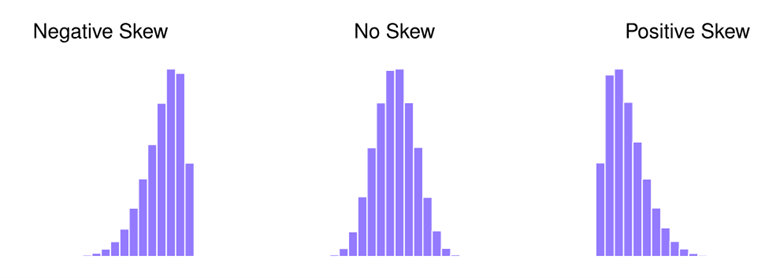
偏度是描述数据分布不对称程度的度量，反映了数据分布的偏斜方向和程度。其值可以是正的、负的或接近零：

• 正偏度（Positive Skew）：当偏度值大于零时，数据分布的尾部向右延伸，即分布的右尾较长，左侧的尾部较短，大部分数据值集中在左侧。这称为右偏或正偏。
• 零偏度（Zero Skew）：当偏度值接近零时，数据分布接近对称，类似于正态分布的形状。
• 负偏度（Negative Skew）：当偏度值小于零时，数据分布的尾部向左延伸，即分布的左尾较长，右侧的尾部较短，大部分数据值集中在右侧。这称为左偏或负偏。

偏度的计算公式如下：

$$ Skewness = \frac{n}{(n-1)(n-2)} \sum (\frac{X_i – \overline{X}}{s})^3 $$

其中 $n$ 是样本大小，$X_i$ 是各个样本点，$\overline{X}$ 是样本均值，$s$ 是样本标准差。

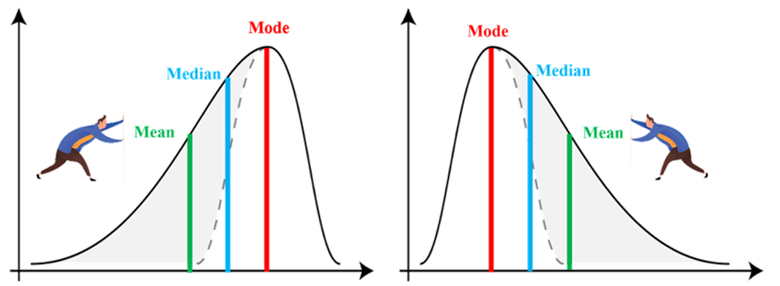
偏度可以揭示大多数值集中在哪里，以及反应了均值、中位数以及众数间的大小关系。

峰度 (Kurtosis)

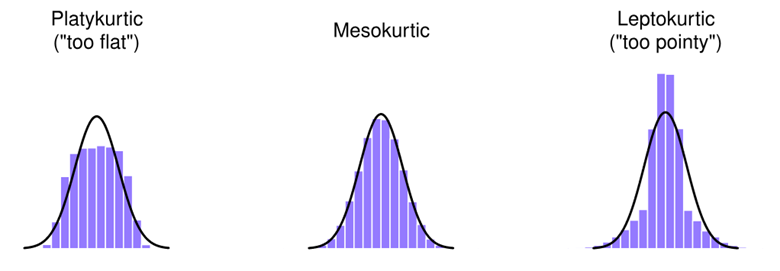
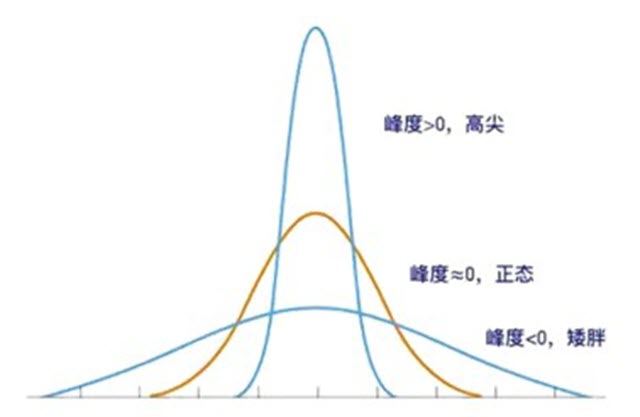
峰度是描述数据分布顶峰厚度和尾部长度的统计量，其值也可以是正的、负的或接近零：

• 正峰度（Positive Kurtosis）：当峰度值大于零时，数据分布比正态分布的峰部更尖锐，尾部更厚或更长，称为高峰度或尖峰型（Leptokurtic）。
• 零峰度（Zero Kurtosis）：当峰度值接近零时，数据分布的峰度接近正态分布，称为中等峰度或正态峰度（Mesokurtic）。
• 负峰度（Negative Kurtosis）：当峰度值小于零时，数据分布的峰部更平坦，尾部更薄或更短，称为低峰度或平顶型（Platykurtic）。

峰度的计算公式如下：

$$ Kurtosis = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum \left(\frac{X_i – \overline{X}}{s}\right)^4 – \frac{3(n-1)^2}{(n-2)(n-3)} $$

其中的参数与偏度公式中的参数相同。

在实际应用中，峰度和偏度常用于金融、品质管理等领域，帮助分析者了解数据的极端值风险、数据的分布特性等。例如，正偏分布可能意味着一项资产的回报存在偶尔的大幅上涨的可能性，高峰度可能意味着极端事件出现的概率比正态分布更高。

平均数（Mean）、中位数（Median）和众数（Mode）

平均数 (Mean)

平均数是所有数据值的总和除以数据数量。它是最常用的集中趋势度量，特别适用于量化数据。

• 特点：平均数受极端值（非常高或非常低的值）的影响较大。
• 适用场景：适用于数据分布比较均匀，没有极端值的情况。
• 注意事项：当数据集中包含极端值时，平均数可能不是一个好的集中趋势度量。

中位数 (Median)

中位数是将数据集按顺序排列后位于中间的数值。如果数据集的数量是偶数，中位数通常是中间两个数值的平均值。

• 特点：中位数不受极端值的影响，因此在存在极端值或偏斜分布的数据集中更有用。
• 适用场景：适用于数据分布不均匀或存在极端值的情况。
• 注意事项：中位数可能不反映数据中的所有特征，尤其是在极端值对分布影响较大时。

众数 (Mode)

众数是数据集中出现次数最多的数值。数据集可能有一个众数、多个众数，或者没有众数。

• 特点：众数是唯一一个用于定性数据（分类数据）的集中趋势度量。
• 适用场景：适用于描述定性数据或寻找数据集中最常见的值。
• 注意事项：众数可能不唯一，有时数据集中没有任何重复的数值，即没有众数。

综合理解

• 当数据分布比较均匀且无极端值时，平均数、中位数和众数可能相近。
• 在偏斜的数据分布中，中位数比平均数更能代表“典型”值。
• 在分析数据时，考虑使用这三种度量的组合，可以更全面地了解数据集的特性。

最后，选择哪种度量取决于数据的性质和分析的目的。平均数适用于量化数据和均匀分布，中位数适用于偏斜分布或存在极端值的情况，众数则适用于定性数据或寻找常见值。在实际分析中，综合考虑这些度量能更全面地理解数据。

不同类型的平均数

在统计学中，有多种不同的平均数概念，它们适用于不同类型的数据和分析情境。最常用的平均数有三种：算术平均数（Arithmetic Mean）、几何平均数（Geometric Mean）和调和平均数（Harmonic Mean）。以下是这三种平均数的定义及其适用场景：

算术平均数（Arithmetic Mean）

定义：所有观测值之和除以观测值的个数。

计算公式：

$$\text{Arithmetic Mean} = \frac{\sum_{i=1}^{n} x_i}{n}$$

其中，\(x_i\) 是每个观测值，\(n\) 是观测值的总数。

适用场景：

• 处理的数据是在同一尺度下测量的，如温度、身高、成绩等。
• 分析的数据没有极端值或者离群值。
• 想要评估数据集中的“典型”值。

几何平均数（Geometric Mean）

定义：所有观测值乘积的n次方根。

计算公式：

$$\text{Geometric Mean} = \left(\prod_{i=1}^{n} x_i \right)^{\frac{1}{n}}$$

其中，\(x_i\) 是每个观测值（必须全部为正数），\(n\) 是观测值的总数。

适用场景：

• 处理的数据是比率或者增长率，如金融投资回报、人口增长率等。
• 数据跨越多个数量级，使用几何平均数可以最小化极端值的影响。
• 分析要求数据的乘积意义，比如串联增长率。

调和平均数（Harmonic Mean）

定义：观测值数量除以各观测值倒数之和。

计算公式：

$$\text{Harmonic Mean} = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}}$$

其中，\(x_i\) 是每个观测值（必须全部为正数），\(n\) 是观测值的总数。

适用场景：

• 数据以速率出现，例如平均速度。
• 当数据是不同大小的数据集的”倒数”时，如计算平均密度。
• 在金融分析中评估股票的平均市盈率。

除了这三种基本的平均数，还有一些其他类型的平均数，如加权平均数（Weighted Mean），它在每个数值上赋予不同的权重，更适用于权重并不相等的情况；以及截断平均数（Trimmed Mean），它排除了一定比例的最高和最低值，适合处理有极端值的数据集。

选择何种平均数的方法取决于数据的特点和分析的目的。通常，算术平均数是最常见和最简单的平均数，但在特定情况下使用几何平均数或调和平均数可能更合适。

四分位数、最大值、最小值和异常值

理解四分位数、最大值、最小值和异常值，我们可以把它们想象成是数据分布的关键标记，它们一起提供了数据集的一个全面概览，包括数据的分散程度、范围以及潜在的异常点。

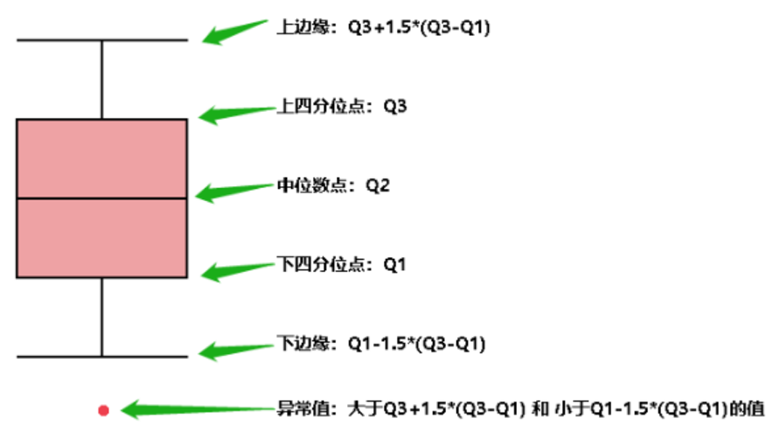
四分位数 (Quartiles)

四分位数将数据分为四等份，每份代表整体的25%。具体来说：

• 第一四分位数（Q1）：在所有数据中排名在25%位置的值，也就是所有数据从小到大排列后，位于1/4位置的数。它把所有数据分为了两部分，较小的25%和剩下的75%。
• 第二四分位数（Q2）：即中位数，排在50%位置的值。它将数据集二等分，等于或小于这个值的数据占一半，等于或大于这个值的数据也占一半。
• 第三四分位数（Q3）：排在75%位置的值，也就是所有数据从小到大排列后，位于3/4位置的数。它将数据分为较大的25%和较小的75%两部分。

最大值和最小值 (Maximum and Minimum)

• 最小值：数据集中最小的数值，表示数据范围的下限。
• 最大值：数据集中最大的数值，表示数据范围的上限。

最大值和最小值共同定义了数据的整体范围，即数据的最大波动区间。

异常值 (Outliers)

异常值是指那些与数据集中其他数值明显不同的数值。它们可能是由于测量误差、数据录入错误或者是真实的极端变异造成的。在四分位数的框架下，异常值通常通过与四分位距（IQR，即Q3与Q1之间的差值）相关的规则来识别。

异常值识别规则：通常，如果一个值大于(Q3 + 1.5 * IQR)或小于(Q1 – 1.5 * IQR)，那么这个值就被认为是异常值。

最大值、最小值和异常值

最大值和最小值通常指的是数据集中的实际观测到的最大和最小数值，它们本身可以是异常值，也可以是非异常值。在数学和统计定义上，最大值和最小值并不自动排除异常值。因此，当你查看一个数据集的最大值和最小值时，这些值可能包含了异常值。

然而，是否应该在分析中包括这些潜在的异常值取决于分析的目的和上下文。如果目的是要理解整个数据集包括所有极端情况，那么应该包括这些最大值和最小值，即使它们是异常值。如果分析是为了识别典型的数据范围并且希望减少异常值的影响，那么你可能会选择忽略这些极端的最大或最小观测值。

在某些情况下，例如生成箱线图时，通常会使用被称为”围栏”（fences）的概念来帮助识别异常值。数据点如果位于(Q1 – 1.5 \times IQR)以下或(Q3 + 1.5 \times IQR)以上，它们可能会被标记为异常值。在这种情况下，”围栏”内的最大值和最小值（不含标记为异常值的数据点）有时被称为”非异常值的最大值”和”非异常值的最小值”。这些值提供了一个没有极端异常值影响的数据范围。

方差、标准差与Z得分

方差、标准差和Z得分是统计学中描述数据分布和测量数据离散度的重要概念。

方差 (Variance)

方差是衡量数据点相对于其均值（平均值）分散程度的统计量。它的计算是基于数据点与均值之间差异的平方。

计算公式: 假设有一组数据$X = {x_1, x_2, …, x_n}$，其均值为 $\bar{x}$。方差 (s^2) 计算方法如下：

$$s^2 = \frac{\sum_{i=1}^n (x_i – \bar{x})^2}{n – 1}$$

其中 (n) 是样本大小，(n – 1) 称为自由度，用于无偏估计。

在实际应用中，如果你在计算整体数据的方差（即总体方差），分母会是 (n) 而不是 (n – 1)。

标准差 (Standard Deviation)

标准差是方差的平方根，提供了一个与原始数据同单位的离散度量，使其更易于解释。

计算公式:

$$s = \sqrt{\frac{\sum_{i=1}^n (x_i – \bar{x})^2}{n – 1}}$$

标准差反映了数据点相对于均值的平均距离。一个较大的标准差意味着数据点分散得较远离均值，一个较小的标准差意味着它们更接近均值。

Z得分 (Z-Score)

Z得分（或标准分数）是一个度量，表示一个数据点相对于平均值的位置，用标准差的数量来表示。

计算公式:

$$z = \frac{x – \bar{x}}{s}$$

其中 (x) 是单个数据点，(\bar{x}) 是均值，(s) 是标准差。

一个数据点的Z得分告诉我们该点距离平均值有多少个标准差。如果一个数据点的Z得分：

• 等于0，它就在均值上。
• 大于0，它就在均值的右侧，即高于平均值。
• 小于0，它就在均值的左侧，即低于平均值。

Z得分也常用于标准化数据，以便在不同的数据集之间进行比较。此外，它在概率统计和假设检验中非常有用，因为它允许我们计算数据点落在标准正态分布的哪个部分。

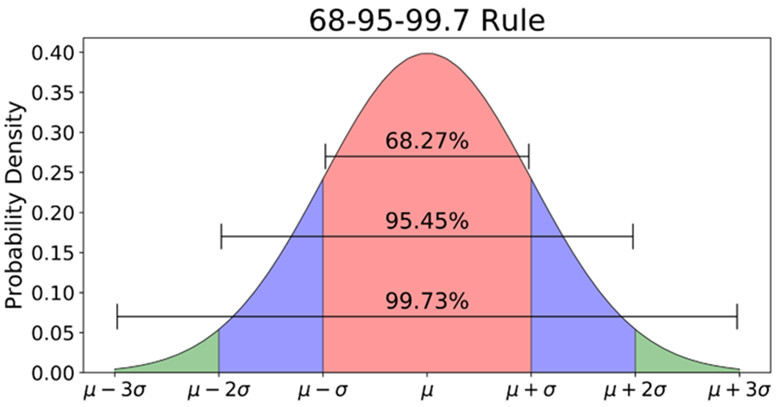
综上所述，方差和标准差是描述数据离散程度的度量，而Z得分是描述单个数据点相对于平均值的相对位置的度量。这些度量在数据分析中是非常基础且重要的工具。

使用Pandas进行摘要统计

使用Pandas进行一般统计

将常用统计整合到一个函数：

def status(x) : 
 return pd.Series([x.count(),x.min(),x.idxmin(),x.quantile(.25),x.median(),
   x.quantile(.75),x.mean(),x.max(),x.idxmax(),x.mad(),x.var(),
   x.std(),x.skew(),x.kurt()],index=['总数','最小值','最小值位置','25%分位数',
   '中位数','75%分位数','均值','最大值','最大值位数','平均绝对偏差','方差','标准差','偏度','峰度'])

使用方法如下：df.apply(status)

异常值的识别

上面的统计方法中驾驶员的最大值与最小值没有排除异常值。可以通过统计四分位的方式实现。

import pandas as pd

# 假设这是你的数据
data = pd.Series([1, 2, 5, 6, 7, 10, 15, 20, 50])

# 计算Q1和Q3以及IQR
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1

# 计算异常值的边界
lower_fence = Q1 - 1.5 * IQR
upper_fence = Q3 + 1.5 * IQR

# 确定异常值
outliers = data[(data < lower_fence) | (data > upper_fence)]

# 确定非异常值的最大值和最小值
non_outlier_max = data[(data >= lower_fence) & (data <= upper_fence)].max()
non_outlier_min = data[(data >= lower_fence) & (data <= upper_fence)].min()

print(f"异常值: {outliers.values}")
print(f"非异常值的最大值: {non_outlier_max}")
print(f"非异常值的最小值: {non_outlier_min}"

Python统计众数

在Python中，你可以使用statistics模块来计算众数，该模块提供了一个名为mode的函数。如果你的数据集中有一个或多个最频繁出现的值，mode函数将返回其中一个。

在使用mode函数之前，请确保你的Python环境中已经安装了statistics模块。这个模块是Python标准库的一部分，因此通常无需额外安装。

下面是一个如何使用statistics.mode函数计算众数的示例：

import statistics

# 示例数据
data = [1, 2, 2, 3, 4, 4, 4, 5, 5, 5]

# 计算众数
mode_value = statistics.mode(data)

print(f"众数是: {mode_value}")

如果数据集中存在多个众数，使用mode函数将抛出一个StatisticsError，因为它设计为只返回单一的众数。

如果你想要找到所有的众数（对于存在多个众数的情况），你可以使用collections模块中的Counter类来帮助你。

以下是一个示例：

from collections import Counter

# 示例数据
data = [1, 2, 2, 3, 4, 4, 4, 5, 5, 5]

# 使用Counter计算每个值的出现次数
counter = Counter(data)

# 找出最高频率
max_count = max(counter.values())

# 找到所有频率等于最高频率的值
modes = [k for k, v in counter.items() if v == max_count]

print(f"众数是: {modes}")

这段代码首先创建了一个对象来计算数据中每个值的出现次数。然后，它找出最大的出现次数，并找到所有出现次数等于这个最大次数的值，它们就是数据集的众数。在这个例子中，如果存在超过一个的众数，modes将会包含它们。

摘要统计与可视化

常见的可视化图形有：

• 柱状图（Bar Charts）：适用于比较不同类别的数据量或者比率。每个柱子的高度代表了数据的数量或者比例。
• 饼图（Pie Charts）：适用于展示各类别在整体中所占的比例，每个扇形的大小代表了其在总体中的占比。
• 直方图（Histograms）：适用于展示数据的分布情况。每个柱子表示一定范围内的数据的数量。
• 箱形图（Box Plots）：适用于展示数据的五数概括（最小值、第一四分位数（Q1）、中位数、第三四分位数（Q3）、最大值），以及可能存在的异常值。
• 散点图（Scatter Plots）：适用于展示两个连续变量之间的关系。
• 折线图（Line Graphs）：适用于展示数据随时间的变化趋势。
• 热力图（Heat Maps）：适用于展示大量数据的分布情况和密度，比如地理热力图。
• 小提琴图（Violin Plots）：结合了箱形图和密度图的特点，不仅可以显示数据的分布情况，还可以展示数据的密度。

以下是一些是一些使用建议：