我们测得一些数据,要对数据进行分析的时候,会发现数据有一些问题使得我们不能满足我们以前分析方法的一些要求(正态分布、平稳性)为了满足经典线性模型的正态性假设,常常需要使用数值变换,使其转换后的数据接近正态,比如数据是非单峰分布的,或者各种混合分布,我们就需要进行一些转化。
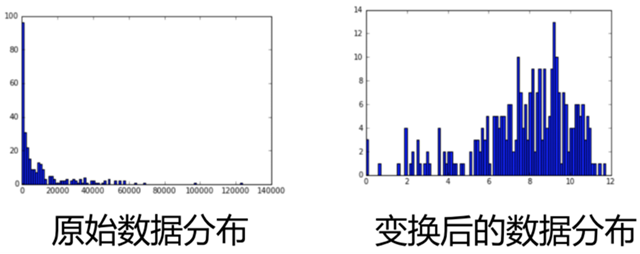
为什么需要做数据变换?
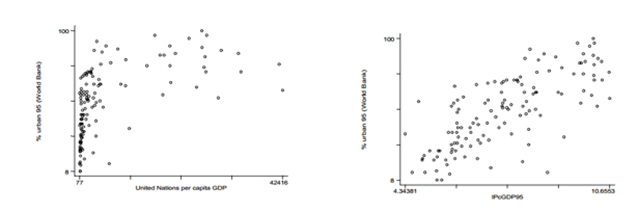
从直观上讲,是为了更便捷的发现数据之间的关系(可以理解为更好的数据可视化)。举个栗子,下图的左图是各国人均GDP和城市人口数量的关系,可以发现人均GDP是严重左偏的,并且可以预知在回归方程中存在明显的异方差性,但如果对GDP进行对数变换后,可以发现较明显的线性关系。为什么呢?因为我们度量相关性时使用的Pearson相关系数检验的是变量间的线性关系,只有两变量服从不相关的二元正态分布时,Pearson相关系数才会服从标准的t-分布,但如果变量间的关系是非线性的,则两个不独立的变量之间的Pearson相关系数也可以为0.
所以,数据变换后可以更便捷的进行统计推断(t检验、ANOVA或者线性回归分析)。例如通常构造估计量的置信区间时是使用样本均值加减两倍标准差的方式,而这就要求样本均值的分布是渐近正态分布,如果数据呈现出明显的偏度,则此时使用上述统计推断方式就是不适用的;另外,最经典的例子就是回归分析中的异方差性,误差项的方差随着自变量的变化而变化,如果直接进行回归估计残差的方差会随着自变量的变化而变化,如果对变量进行适当变换,此时残差服从同一个正态分布。
在统计学中,常用的数值变换方式包括以下几种:
- 对数变换:对数变换可以将数据从指数分布或长尾分布转换为近似正态分布,同时还可以处理数据中的异常值。
- 平方根变换:平方根变换可以将偏态分布的数据转换为近似正态分布,同时还可以降低异常值的影响。
- Box-Cox变换:Box-Cox变换是一种幂函数变换,可以将非正态分布的数据转换为正态分布,从而提高统计分析的准确性。
- 归一化变换:归一化变换可以将数据按照一定比例缩放到特定的范围内,通常是[0,1]或[-1,1]之间。
- 标准化变换:标准化变换可以将数据按照均值为0、标准差为1的标准正态分布进行转换,使得数据具有可比性和可解释性。
- 非线性变换:非线性变换可以通过对数据进行复杂的函数变换,将数据转换为更为合适的分布形式,如指数分布、正态分布等。
需要注意的是,不同的数据变换方法适用于不同的数据分布情况。在实际应用中,需要结合具体的数据特征和分析目的,选择合适的数据变换方式。同时,需要注意数据变换可能会导致原始数据的信息丢失或变形,因此需要谨慎选择和使用。
对数变换
对数变换是统计学中常用的一种数据变换方法,可以将数据从指数分布或长尾分布转换为近似正态分布,同时还可以处理数据中的异常值。
对数变换的基本思想是将数据取对数,由于对数函数是单调递增的,所以对数变换不会改变数据的顺序关系。在对数变换之后,数据的分布形态会变得更加对称,尤其是对于右偏或长尾分布的数据,对数变换可以将数据的分布形态向左移动,使得数据更加集中在均值附近。
对数变换的公式为:y’=log(y)
其中,y为原始数据,y’为变换后的数据。需要注意的是,由于对数函数的定义域为正实数,因此对数变换只适用于正数数据,对于含有零或负值的数据需要进行其他处理,例如加上一个常数或者使用其他数据转换方法。
对数变换有以下几个优点:
- 可以将指数分布或长尾分布转换为近似正态分布,提高统计分析的准确性。
- 对于含有异常值的数据,对数变换可以使得异常值的影响减小,从而提高数据的鲁棒性。
- 对数变换具有可逆性,变换后的数据可以通过指数运算还原到原始数据。
需要注意的是,对数变换可能会导致一些信息的损失或变形,例如在变换后,数据的单位会发生变化,因此需要在实际应用中进行谨慎使用。此外,对数变换还可能导致某些数据出现负数或者零值,因此需要进行适当的处理。
对数变换(log transformation)是特殊的一种数据变换方式,它可以将一类我们理论上未解决的模型问题转化为已经解决的问题。我将说两类比较有代表性的模型。
理论上:随着自变量的增加,因变量的方差也增大的模型。
先给个很经典的例子,如分析美国每月电力生产数。
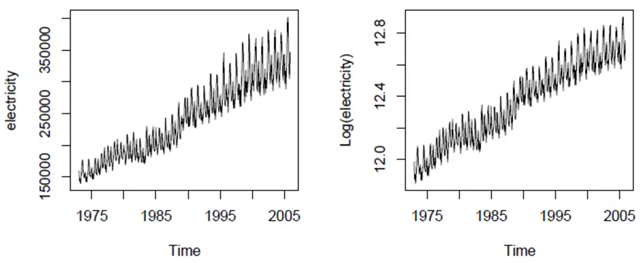
左边是正常数据,可以看到随着时间推进,电力生产也变得方差越来越大,即越来越不稳定。这种情况下常有的分析假设经常就不会满足(误差服从独立同分布的正态分布,时间序列要求平稳)。这必然导致我们寻求一种方式让数据尽量满足假设,让方差恒定,即让波动相对稳定。而这种目的可以通过对数转换做到。
理论上,我们将这类问题抽象成这种模型,即分布的标准差与其均值线性相关。
即:$\sqrt{Var(Z_t)}=\mu_t\times\sigma$,其中$E(Z_t)=\mu_t$
由定义可推:$Z_t=\mu_t(1+\frac{Z_t-\mu_t}{\mu_t})$,利用log函数的性质:$\log(1+x)\approx x$(当x足够小)
那么$\log(Z_t)\approx\log(\mu_t)+\frac{Z_t-\mu_t}{\mu_t}$
那么很容易就知道$E(\log(Z_t))\approx\log(\mu_t)$和$Var(\log(Z_t))\approx\sigma^2$
所以对数变换能够很好地将随着自变量的增加,因变量的方差也增大的模型转化为我们熟知的问题。
经验上:研究数据的增长率分布存在一定规律的模型。
再给个例子:实际研究中,某一研究对象自身性质难以研究,但其增长率是服从一定分布。例如说:$Z_t=(1+X_t)\times Z_{t-1}$,其中$X_t$是每年增长率(不很大)。
我们可以考虑对数变换:$\log(Z_{t-1})=\log(\frac{Z_t}{Z_{t-1}})=\log(1+X_t)\approx X_t$
这样,我们又可以将研究数据的增长率分布存在一定规律的模型转化为我们熟知的问题。
平方根变换
平方根变换是一种常用的数据变换方法,可以将偏态分布的数据转换为近似正态分布,同时还可以降低异常值的影响。
平方根变换的基本思想是将数据取平方根,由于平方根函数是单调递增的,所以平方根变换不会改变数据的顺序关系。在平方根变换之后,数据的分布形态会变得更加对称,尤其是对于右偏或长尾分布的数据,平方根变换可以将数据的分布形态向左移动,使得数据更加集中在均值附近。
平方根变换的公式为:y’=sqrt(y)
其中,y为原始数据,y’为变换后的数据。需要注意的是,由于平方根函数的定义域为非负实数,因此平方根变换只适用于非负数
平方根变换常用于:
- 使服从Poission分布的计数资料或轻度偏态资料正态化,可用平方根变换使其正态化。
- 当各样本的方差与均数呈正相关时,可使资料达到方差齐性。
Box-Cox变换
Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性。
 Box-Cox变换的基本思想是通过对数据进行一定的变换,使得变换后的数据更加符合正态分布的特征。这种变换是一种幂函数变换,其公式如下:
Box-Cox变换的基本思想是通过对数据进行一定的变换,使得变换后的数据更加符合正态分布的特征。这种变换是一种幂函数变换,其公式如下:
y(lambda) = (y^lambda – 1)/lambda, lambda != 0
其中,y是原始数据,lambda是变换参数。通过不同的lambda值,可以得到不同的Box-Cox变换结果。当lambda为1时,Box-Cox变换即为对数变换。当lambda为0时,Box-Cox变换变为一个特殊的极限情况,即数据变换为y^lambda – 1,这时候需要特殊处理。
在实际应用中,通常使用最大似然估计法来估计Box-Cox变换的参数lambda。对于不同的数据集,lambda的值可以取不同的数值,一般来说,lambda的取值范围为-5到5之间。
需要注意的是,Box-Cox变换只适用于正数数据,对于含有零或负值的数据需要进行其他处理,例如加上一个常数或者使用其他数据转换方法。同时,在进行Box-Cox变换时,需要保证变换后的数据具有实际意义,并且变换后的数据不会丢失原始数据的信息。
box-cox变换的目标有两个:
- 一是变换后,可以一定程度上减小不可观测的误差和预测变量的相关性。主要操作是对因变量转换,使得变换后的因变量于回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。
- 二是用这个变换来使得因变量获得一些性质,比如在时间序列分析中的平稳性,或者使得因变量分布为正态分布。
Cox变换的主要特点是引入一个参数lambda,通过数据本身估计该参数进而确定应采取的数据变换形式,Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性,又不丢失信息,后经过一定的推广和改进,扩展了其应用范围。
BoxCox变换的核心参数是lambda(λ),其范围从-5到5。所以我们主要目的在于通过一定的方法,选择除最佳的lambda值。
$$y(\lambda)=\begin{cases}\frac{y^\lambda-1}{\lambda},&\text{if}\lambda\neq0\\\log y,&\text{if}\lambda=0\end{cases}$$
以上y值需要非负数才行,若对阵有负数的数据集,则公式如下:
$$y(\lambda)=\begin{cases}\frac{(y+\lambda_2)^{\lambda_1}-1}{\lambda_1},&\text{if}\lambda_1\neq0\\\log(y+\lambda_2),&\text{if}\lambda_1=0.\end{cases}$$
平时我们想让一个非正态的数据变成正态,一次个想到可能就是取log(即对数转化),可能还有倒数转化,平方根转化等等。而Box-Cox变换是多种变换的统称,当取不同lambda值时,其对应的就是不同的转化方式:

Python的使用:
1)非负性
Python中,Box-Cox的y>0,否则会报错,即:ValueError: Data must be positive.所以对于y<0的情况,可以给y加上一个常数C进行调整,即得如下所示: $$y^{(\lambda)}=\begin{cases}\frac{(y+c)^\lambda-1}{\lambda},&\text{if}\lambda\neq0\\\log(\mathrm{y}+\mathrm{c}),&\text{if}\lambda=0\end{cases}$$ 2)正向Box-Cox使用
首先该变换均在scipy模块之下,主要有以下两个地方:
from scipy.stats import boxcox #1 from scipy.special import boxcox #2
区别在于,1中包含了box-cox中的lambda计算(即不需要给函数boxcox输入参数lmbda,boxcox返回值中就有lambda),所以其格式为:
y, lambda = boxcox(x, lmbda=None, alpha=None)
lambda的计算方法一般为最大似然估计方法和Bayes方法。
而2中不包含lambda的计算,所以其函数参数必填的为数据data和lambda。
y = boxcox(x1, x2, *args, **kwargs)
3)逆向Box-Cox变换
通常我们在Box-cox变换之后,将预处理后的数据投入到模型中进行训练,如果变换处理的是标签,那么还需要对测试集的预测值进行反Box-Cox变换,Python实现如下:
from scipy.special import inv_boxcox y = inv_boxcox(x1, lambda)
其中x为需要进行反Box-Cox变换的数据,lamda为训练集Box-Cox时使用的lambda,一般即为上文中stats.boxcox()返回的第二个参数。需要注意:如果在训练集Box-Cox变换时使用了C常数进行了自变量的非零处理,那么还需要再反变换之后减去这个C常数。
归一化与标准化变换
参考链接:数据缩放:标准化和归一化
非线性变换
我们可以总结这个非线性转换的步骤,即先通过Φ(x)将x空间的点转换成z空间的点,而在z空间上得到一个线性的假设,再恢复到原来的x空间中得到一个二次的假设(这个反运算的过程不一定存在)。
其实这个特征转换是非常重要的,比如在手写数字分类的案例中,我们将原始的像素的特征数据转换到更加具体的、具有物理意义的特征上去,进而进行分类的求解。这个例子其实就是在新的特征空间中做线性分类,而对于原始的像素空间里其实是一个非线性的假设。
Yeo-Johnson变换
Yeo-Johnson变换是一种数据转换方法,旨在将非正态分布的数据转换为接近正态分布,提升统计模型(如线性回归)的假设满足性。它是对Box-Cox变换的扩展,支持处理包含零和负数的数据,适用性更广。
数学公式
Yeo-Johnson的变换公式根据输入值y的正负分情况处理,并引入参数$\lambda$控制变换形式:
$$\psi(y,\lambda)=\begin{cases}\frac{(y+1)^\lambda-1}{\lambda}&\text{if}y\geq0,\lambda\neq0\\\ln(y+1)&\text{if}y\geq0,\lambda=0\\\frac{-(1-y)^{2-\lambda}-1}{2-\lambda}&\text{if}y<0,\lambda\neq2\\-\ln(1-y)&\text{if}y<0,\lambda=2\end{cases}$$ 非负值处理($y\geq0$):
- 类似Box-Cox,但对y 加1避免零值问题。
- 例如,$\lambda=0$ 时退化为对数变换: $\ln(y+1)$ 。
负值处理($y<0$):
- 通过调整$\lambda$ 范围(通常 $\lambda<2$ )灵活处理负数。
- $\lambda=2$时退化为对数变换: $-\ln(1-y)$ 。
参数估计($\lambda$的确定)
通过优化方法寻找使变换后数据最接近正态分布的$\lambda$:
- 最大似然估计(MLE):假设变换后数据服从正态分布,最大化对数似然函数。
- 网格搜索在预设范围内(如 $-5\leq\lambda\leq5$)寻找最小化偏态或残差平方和的 $\lambda$。
应用场景
- 回归模型:满足误差正态性假设,提升线性模型效果。
- 特征工程:处理机器学习中的偏态特征(如长尾分布)。
- 数据可视化:使数据更易分析(如Q-Q图更接近直线)。
与Box-Cox的区别
| 特性 | Box-Cox | Yeo-Johnson |
| 数据范围要求 | 仅正数( y>0 ) | 所有实数(含负数和零) |
| 公式复杂度 | 单一公式 | 分情况处理正负值 |
| 适用性 | 受限 | 更广泛 |
| 参数范围 | $\lambda\in\mathbb{R}$ | $\lambda\in\mathbb{R}$ |
实现步骤(Python示例)
使用scikit-learn的PowerTransformer:
from sklearn.preprocessing import PowerTransformer
# 创建转换器,指定Yeo-Johnson
pt = PowerTransformer(method='yeo-johnson', standardize=False)
# 拟合数据并转换
data = [[-1], [0.5], [10], [2]]
transformed_data = pt.fit_transform(data)
# 查看最佳lambda值
lambda_ = pt.lambdas_[0]
print(f"Optimal λ: {lambda_:.2f}")
# 逆变换
original_data = pt.inverse_transform(transformed_data)
优缺点
- 优点:
- 支持全实数域,适用性广。
- 提升模型性能(如降低异方差性)。
- 缺点:
- 需估计 $\lambda$,计算成本较高。
- 变换后数据可解释性降低。
- 逆变换需保存参数,增加复杂度。
注意事项
- 验证效果:变换后使用统计检验(如Shapiro-Wilk)或Q-Q图检查正态性。
- 避免过拟合:在训练集上拟合 $\lambda$,再应用到测试集。
- 解释性:若业务指标需逆变换,确保保留 $\lambda$ 值。
Yeo-Johnson通过分情况处理和引入灵活参数 $\lambda$,成为处理非正态数据的强有力工具,尤其在数据包含零或负数时替代Box-Cox。正确应用可显著提升模型性能,但需权衡计算成本与结果可解释性。



