数据缩放简介
使用单一指标对某事物进行评价并不合理,因此需要多指标综合评价方法。多指标综合评价方法,就是把描述某事物不同方面的多个指标综合起来得到一个综合指标,并通过它评价、比较该事物。由于性质不同,不同评价指标通常具有不同的量纲和数量级。当各指标相差很大时,如果直接使用原始指标值计算综合指标,就会突出数值较大的指标在分析中的作用、削弱数值较小的指标在分析中的作用。为消除各评价指标间量纲和数量级的差异、保证结果的可靠性,就需要对各指标的原始数据进行特征缩放。
数据缩放,在统计学中的意思是,通过一定的数学变换方式,将原始数据按照一定的比例进行转换,将数据放到一个小的特定区间内,比如0~1或者-1~1。目的是消除不同样本之间特性、数量级等特征属性的差异,转化为一个无量纲的相对数值,结果的各个样本特征量数值都处于同一数量级上。
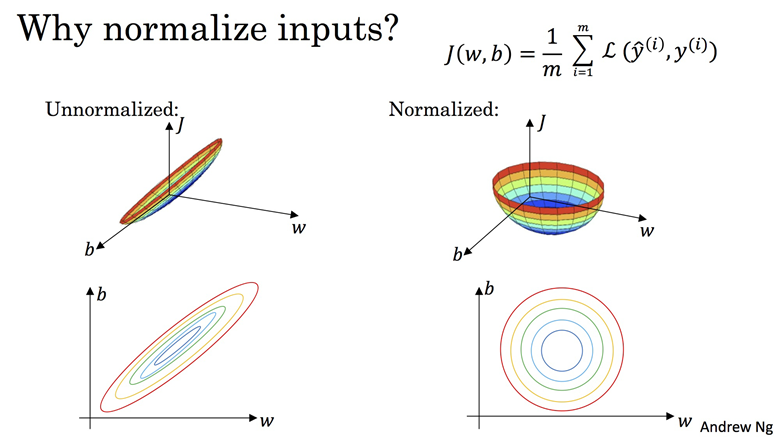
- 基于梯度下降的算法(Gradient Descent Based Algorithms):在基于梯度下降进行优化的算法中,需要进行特征缩放,比如线性回归、逻辑回归、神经网络等。因为计算梯度时会使用特征的值,如果各特征的的取值范围差异很大,不同特征对应梯度的值就会差异很大。为保证平滑走到最优点、按相同速率更新各特征的权重,需要进行特征放缩。通过特征放缩,可以使数值范围变小,进而加速梯度下降。
- 基于距离的算法(Distance-Based Algorithms):在基于距离进行优化的算法中,需要进行特征缩放,比如K近邻、K-Means、SVM、PCA等。因为这些算法是基于数据点的特征值计算它们的距离,距离越小则两者越相似。
- 基于树的算法(Tree-Based Algorithms):基于树的算法对特征(features)的数值范围并不敏感,比如决策树。决策树仅基于单个feature拆分节点,并不受其它feature的影响。
- 线性判别分析、朴素贝叶斯等算法:这两个算法处理了特征数量级差异大的问题,因此不需要进行特征缩放。
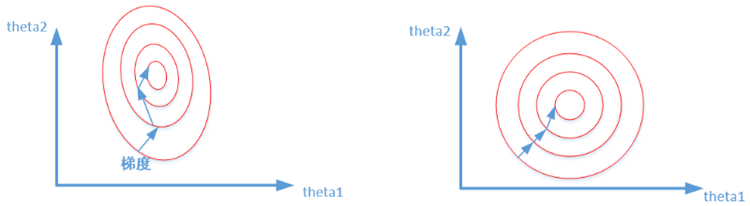
左图为标准化之前,右图为标准化之后,可以看到标准化可以让模型少走很多弯路,从而加快收敛速度,这一点也很容易想象,毕竟个位数与千位数、个位数与个位数之间的”距离”差距还是很大的。
数据缩放主要分为两种:指标一致化、无量纲化:
指标一致化
目的是解决数据性质不同的问题,也就是说涉及到多个不同的统计量时,有的指标数值越大越符合预期(如:生存率),也要一些指标数值越小越符合预期(如:死亡率)。可以看出这两种数据的”方向”是不同的。这时,如果要综合考量两种数据,就要先统一数据方向,一般方法有两种:
- 对原始数据取倒数(下单频率与下单次数)
- 定义不同指标中数值上限,然后依次减去每个指标中的原始数据(比如死亡率与生存率)
无量纲化
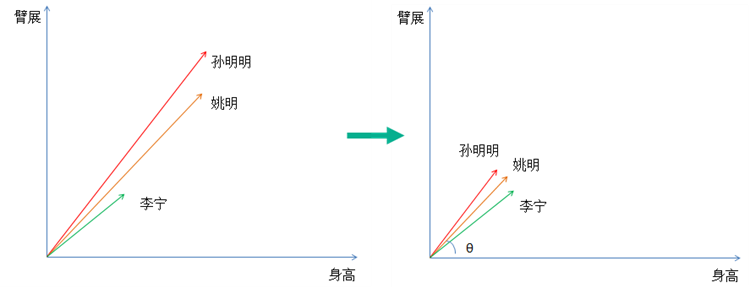
这个是我们经常用到的,目的是解决数据之间的可比性问题,比如有的指标/样本中数据范围在1-100,另一个指标/样本中数据在1-10000,这个范围就是量纲。通过去掉这个的影响,真正突出数据的差别,有点绝对值变为相对值的感觉。可以用的方法有:
Min-Max归一化(Min-Max Normalization)
Min-Max归一化又称为极差法,最简单处理量纲问题的方法,它是将数据集中某一列数值缩放到0和1之间。它的计算方法是:
$${x}’=\frac{x-x_{min}}{x_{max}-x_{min}}$$
该方法是对原始数据的线性变换。min-max标准化方法保留了原始数据之间的相互关系,但是如果标准化后,新输入的数据超过了原始数据的取值范围,即不在原始区间$[x_{min},x_{max}]$中,则会产生越界错误。因此这种方法适用于原始数据的取值范围已经确定的情况。
最大绝对值法(MaxAbs)
最大值绝对值法(MaxAbs)根据最大值的绝对值进行标准化。计算公式为:
$${x}’=\frac{x}{x_{max}}$$
MaxAbs方法跟Max-Min用法类似,也是将数据落入一定区间,但该方法的数据区间为[-1,1]。MaxAbs也具有不破坏原有数据分布结构的特点,因此也可以用于稀疏数据。
均值归一化(Mean Normalization)
与Min-Max归一化类似,区别是使用平均值$\mu$替代分子中的最佳值,公式如下:
$${x}’=\frac{x-\mu}{x_{max}-x_{min}}$$
该方法把数据调到[-1,1],平均值为0。适合一些假设数据中心为0(zero centric data)的算法,比如主成分分析(PCA)。
log函数转化
Log函数也可用于归一化。结果落到[0,1]区间上,具体公式为:
$${x}’=\frac{\log x}{\log x_{max}}$$
该方法适用于以指数分布的数据。其他很多的文章,介绍的时候都是都取以10为底的log值,实际使用中可以根据具体的分布情况确定底数。此方法同样仅限于$x_{max}$已知的产品。
atan函数转换
反正切函数也可以实现数据的归一化:
$${x}’=\frac{atan(x)*2}{\pi}$$
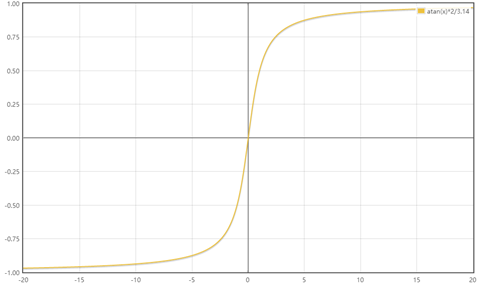
使用这个方法需要注意的是如果想映射的区间为[0,1],则数据都应该大于等于0,小于0的数据将被映射到[-1,0]区间上。
Sigmoid函数转换
Sigmoid函数是一个具有S形曲线的函数,是良好的阈值函数,在(0,0.5)处中心对称,在(0,0.5)附近有比较大的斜率,而当数据趋向于正无穷和负无穷的时候,映射出来的值就会无限趋向于1和0。
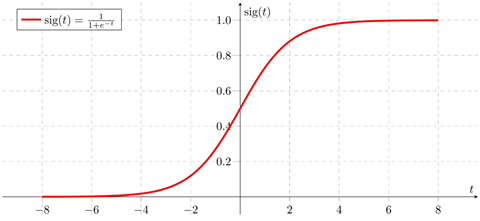
$${x}’=\frac{1}{1+{e}^{-x}}$$
Decimal scaling
这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性A的取值中的最大绝对值。结果落到[-1,1]区间上计算方法为:
$$x^*=\frac{x}{10^j}$$
其中,j是满足条件$\max(|x^*|)\leq1$的最小整数。该方法会对原始数据做出改变,因此需要保存所使用的标准化方法的参数,以便对数据进行恢复。
Z标准化:实现中心化和正态分布
z-score标准化也叫标准差标准化,代表的是分值偏离均值的程度,经过处理的数据符合标准正态分布,即均值为0,标准差为1。其转化函数为
$${x}’=\frac{x-\mu}{\sigma}$$
该方法假设数据是正态分布,但这个要求并不十分严格,如果数据是正态分布则该技术会更有效。当我们使用的算法假设数据是正态分布时,可以使用Standardization,比如线性回归、逻辑回归、线性判别分析。因为Standardization使数据平均值为0,也可以在一些假设数据中心为0 (zero centric data)的算法中使用,比如主成分分析(PCA)。
标准化的缩放处理和每一个样本点都有关系,因为均值和标准差是数据集整体的,与归一化相比,标准化更加注重数据集中样本的分布状况。由于具有一定的样本个数,所以出现少量的异常点对于平均值和标准差的影响较小,因此标准化的结果也不会具有很大的偏差。但是Z-Score方法是一种中心化方法,会改变原有数据的分布结构,不适合用于对稀疏数据做处理。在很多时候,数据集会存在稀疏性特征,表现为标准差小、并有很多元素的值为0,最常见的稀疏数据集是用来做协同过滤的数据集,绝大部分的数据都是0,仅有少部分数据为1。对稀疏数据做标准化,不能采用中心化的方式,否则会破坏稀疏数据的结构。
修改型z-score标准化
将标准分公式中的均值改为中位数,将标准差改为绝对偏差。
$${x}’=\frac{x-x_{median}}{d}$$
中位数是指将所有数据进行排序,取中间的那个值,如数据量是偶数,则取中间两个数据的平均值。
d为所有样本数据的绝对偏差,其计算公式为:
$$d=\frac{1}{N}\sum_{1}^{n}|x_i-x_{median}|$$
RobustScaler
有些时候,数据中会存在离群点(异常值)。这时如果我们使用z-score标准化就会导致数据很容易失去离群特征。这时我们就可以使用RobustScaler方法,它对于数据中心化和数据的缩放健壮性有着更强的参数调节能力。公式为:
$${x}’=\frac{x-x_{median}}{{IQR}}$$
RobustScaler函数使用对异常值鲁棒的统计信息来缩放特征。这个标量去除中值,并根据分位数范围(默认为IQR即四分位数范围)对数据进行缩放。IQR是第1个四分位数(第25分位数)和第3个四分位数(第75分位数)之间的范围。通过计算训练集中样本的相关统计量,对每个特征分别进行定心和缩放。然后将中值和四分位范围存储起来,使用“变换”方法用于以后的数据。
标准化、归一化的区别
标准化、归一化这两个概念总是被混用,以至于有时以为这是同一个概念,既然容易混淆就一定存在共性:它们都是对某个特征(或者说某一列/某个样本)的数据进行缩放(scaling)。
二者差异:归一化Normalization受离群点影响大;标准化Standardization是重新创建一个新的数据分布,因此受离群点影响小
- 如果数据集小而稳定,可以选择归一化
- 如果数据集中含有噪声和异常值,可以选择标准化,标准化更加适合嘈杂的大数据集。
Scikit-Learn中标准化和归一化方法
sklearn.preprocessing提供了许多方便的用于做数据预处理工具,在数据标准化方面,sklearn.preprocessing提供了几种scaler进行不同种类的数据标准化操作:
- StandardScaler
- MinMaxScaler
- MaxAbsScaler
- RobustScaler
在sklearn工具包中的preprocessing类中,每种预处理的方法,一般来说都有三种方法,包括:
- .fit(): 用于计算训练集train_x的均值、方差、最大值、最小值等训练集固有的属性。
- .transform(): 用于在fit()的基础上对指定的数据集(训练集、测试集、验证机)进行标准化、降维、归一化等变换。
- .fit_transform():整合fit()和transform(),同时实现属性学习和变换,该函数仅仅为了简化操作。
所以,一般的操作流程如下:
### 标准步骤 # 1. 设置某种预处理方法 scaler = method() # 2. 使用训练数据来获取训练集的固有属性 scaler.fit(x_train) # 3. 应用到训练集、测试集和验证集 x_train_scaled = scaler.transform(x_train) x_test_scaled = scaler.transform(x_test) x_val_scaled = scaler.transform(x_val) ### 第一种简化方法 # 其中第1.2步可以简化为: scaler = method().fit(X_train) ### 第二种简化方法 # 为了简化操作,可以将第以上操作简化为: # 1. 设置某种预处理方法 scaler = method() # 2. 使用训练数据来获取训练集的固有属性,并应用到训练集 x_train_scaled = scaler.fit_transform(x_train) # 3. 应用到训练集、测试集和验证集 x_test_scaled = scaler.transform(x_test) x_val_scaled = scaler.transform(x_val)
实际使用时通常会和Pandas一起使用,具体如下:
import pandas as pd
from sklearn.preprocessing import StandardScaler
df = pd.read_excel("rfm.xlsx")
ss = StandardScaler()
scale_features = ['r', 'f', 'm']
df[scale_features] = ss.fit_transform(df[scale_features])
对于skleran中不存在的归一化方法,可以在使用时自定义方法,比如:
cols = list(df) # 可以改成自己需要的列的名字
for item in cols:
max_tmp = np.max(np.array(df[item]))
min_tmp = np.min(np.array(df[item]))
if (max_tmp != min_tmp):
df[item] = df[item].apply(lambda x: (x - min_tmp)/(max_tmp - min_tmp))
参考链接:




写得很好~~~,看了很多篇博文,感谢博主。。
感谢博主~~~很适合复习