主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA,下面我们就对PCA的原理做一个总结。
首先考虑一个问题:对于正交属性空间中的样本点,如何用一个超平面(直线的高维推广)对所有样本进行恰当的表达?
可以想到,若存在这样的超平面,那么它大概具有这样的性质:
最近重构性:样本点到这个超平面的距离都足够近,即下图中所有红线(即投影造成的损失)加起来最小。
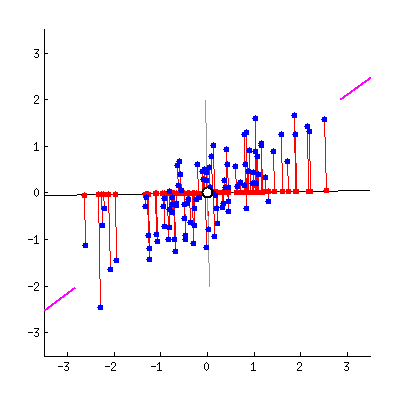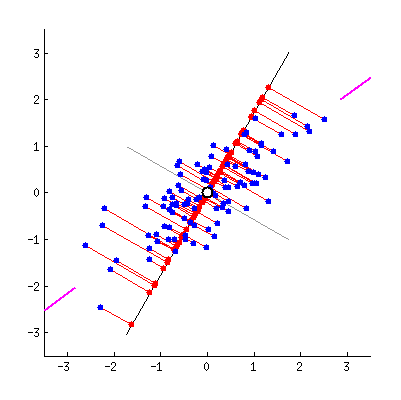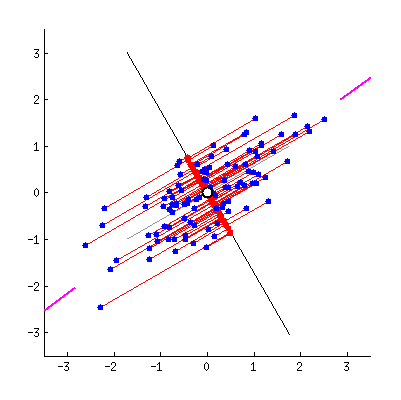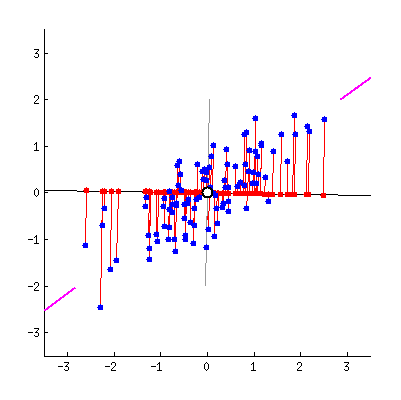
最大可分性:样本点在这个超平面上的投影能尽可能地分开,即下图中红线所示,需最大化投影点的方差。
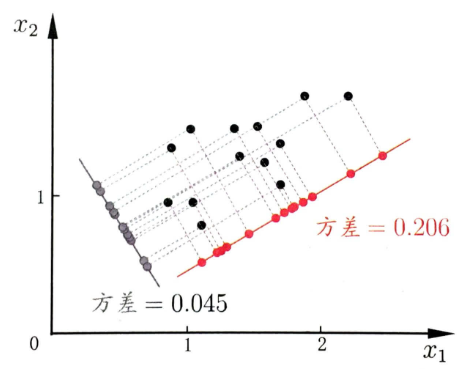
基于最近重构性和最大可分性能分别得到主成分分析的两种等价推到,我们这里主要考虑最大可分性,并且一步一步推到出最终PCA。
问题描述
下表是某些学生的语文、数学、物理、化学成绩统计:
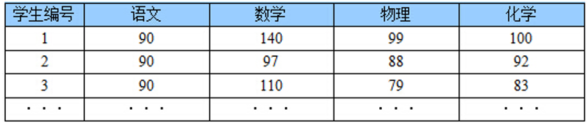
首先,假设这些科目成绩不相关,也就是说某一科目考多少分与其他科目没有关系。那么一眼就能看出来,数学、物理、化学这三门课的成绩构成了这组数据的主成分(很显然,数学作为第一主成分,因为数学成绩拉的最开)。为什么一眼能看出来?因为坐标轴选对了!下面再看一组学生的数学、物理、化学、语文、历史、英语成绩统计,还能不能一眼看出来:
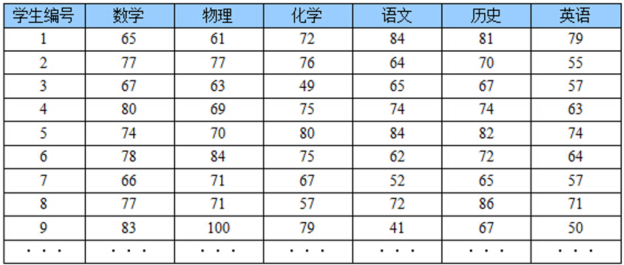
数据太多法直接看出这组数据的主成分,因为在坐标系下这组数据分布的很散乱。究其原因,是因为无法拨开遮住肉眼的迷雾~如果把这些数据在相应的空间中表示出来,也许你就能换一个观察角度找出主成分。如图所示:
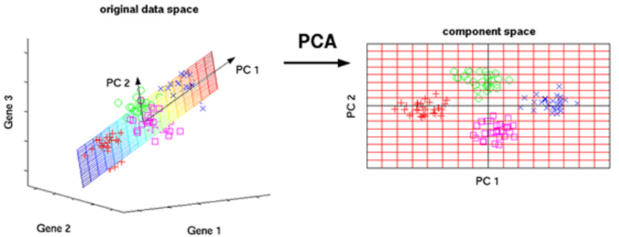
对于更高维的数据,能想象其分布吗?就算能描述分布,如何精确地找到这些主成分的轴?如何衡量提取的主成分到底占了整个数据的多少信息?所以,我们就要用到主成分分析的处理方法。
数据降维
为了说明什么是数据的主成分,先从数据降维说起。数据降维是怎么回事儿?假设三维空间中有一系列点,这些点分布在一个过原点的斜面上,如果你用自然坐标系x,y,z这三个轴来表示这组数据的话,需要使用三个维度,而事实上,这些点的分布仅仅是在一个二维的平面上,那么,问题出在哪里?如果你再仔细想想,能不能把x,y,z坐标系旋转一下,使数据所在平面与x,y平面重合?这就对了!如果把旋转后的坐标系记为x’,y’,z’,那么这组数据的表示只用x’和y’两个维度表示即可!当然了,如果想恢复原来的表示方式,那就得把这两个坐标之间的变换矩阵存下来。这样就能把数据维度降下来了!但是,我们要看到这个过程的本质,如果把这些数据按行或者按列排成一个矩阵,那么这个矩阵的秩就是2!这些数据之间是有相关性的,这些数据构成的过原点的向量的最大线性无关组包含2个向量,这就是为什么一开始就假设平面过原点的原因!那么如果平面不过原点呢?这就是数据中心化的缘故!将坐标原点平移到数据中心,这样原本不相关的数据在这个新坐标系中就有相关性了!有趣的是,三点一定共面,也就是说三维空间中任意三点中心化后都是线性相关的,一般来讲n维空间中的n个点一定能在一个n-1维子空间中分析!
上一段文字中,认为把数据降维后并没有丢弃任何东西,因为这些数据在平面以外的第三个维度的分量都为0。现在,假设这些数据在z’轴有一个很小的抖动,那么我们仍然用上述的二维表示这些数据,理由是我们可以认为这两个轴的信息是数据的主成分,而这些信息对于我们的分析已经足够了,z’轴上的抖动很有可能是噪声,也就是说本来这组数据是有相关性的,噪声的引入,导致了数据不完全相关,但是,这些数据在z’轴上的分布与原点构成的夹角非常小,也就是说在z’轴上有很大的相关性,综合这些考虑,就可以认为数据在x’,y’ 轴上的投影构成了数据的主成分!
特征选择的问题,其实就是要剔除的特征主要是和类标签无关的特征。而这里的特征很多是和类标签有关的,但里面存在噪声或者冗余。在这种情况下,需要一种特征降维的方法来减少特征数,减少噪音和冗余,减少过度拟合的可能性。PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主成分,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。
PCA 计算实例
现在假设有一组数据如下:
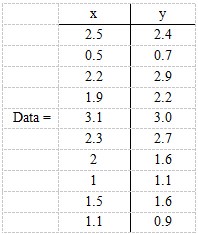
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。
第一步,分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,那么一个样例减去均值后即为(0.69,0.49),得到:
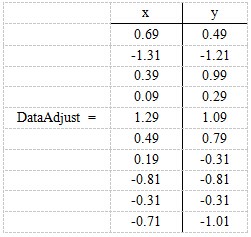
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是:
$$C=\begin{pmatrix}cov(x,x)&cov(x,y)&cov(x,z)\\cov(y,x)&cov(y,y)&cov(y,z)\\cov(z,x)&cov(z,y)&cov(z,z)\end{pmatrix}$$
这里只有x和y,求解得:
$$cov=\begin{pmatrix}.616555556&.615444444\\.615444444&.716555556\end{pmatrix}$$
对角线上分别是x和y的方差,非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增,另一个也增;小于0表示一个增,一个减。如果x和y是统计独立的,那么二者之间的协方差就是0;但是协方差是0,并不能说明x和y是独立的。协方差绝对值越大,两者对彼此的影响越大,反之越小。协方差是没有单位的量,因此,如果同样的两个变量所采用的量纲发生变化,它们的协方差也会产生树枝上的变化。
第三步,求协方差的特征值和特征向量,得到:
$$eigenvalue=\begin{pmatrix}.490833989\\1.28402771\end{pmatrix}$$
$$eigenvalue=\begin{pmatrix}-.735178656&-.677873399\\.677873399&-.735178656\end{pmatrix}$$
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。这里特征值只有两个,我们选择其中最大的那个,这里是1.28402771,对应的特征向量是(-0.677873399, -0.735178656)T。
第五步,将样本点投影到选取的特征向量上。假设样例数为 m,特征数为 n,减去均值后的样本矩阵为 DataAdjust(m*n),协方差矩阵是 n*n,选取的 k 个特征向量组成的矩阵为 EigenVectors(n*k)。那么投影后的数据 FinalData 为:
FinalData(10*1) = DataAdjust(10*2 矩阵) x 特征向量(-0.677873399, -0.735178656)^T
得到的结果是:
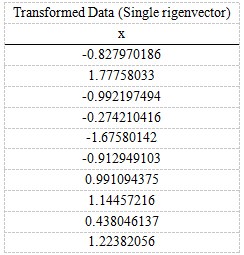
这样,就将原始样例的 n 维特征变成了 k 维,这 k 维就是原始特征在 k 维上的投影。上面的数据可以认为是 2 个特征融合为一个新的特征叫做 LS 特征,该特征基本上代表了这两个特征。上述过程如下图描述:
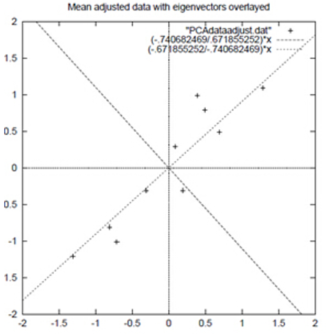
正号表示预处理后的样本点,斜着的两条线就分别是正交的特征向量(由于协方差矩阵是对称的,因此其特征向量正交),最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。整个 PCA 过程貌似及其简单,就是求协方差的特征值和特征向量,然后做数据转换。但是有没有觉得很神奇,为什么求协方差的特征向量就是最理想的 k 维向量?其背后隐藏的意义是什么?整个 PCA 的意义是什么?
PCA 算法原理
在具体给出 PCA 算法之前,先回顾下线性代数中的相关知识,首先,需要强调一点,下面所说的向量,在没有特殊说明下,都指的是列向量。
向量的内积和投影
两个维数相同的向量的内积被定义为:
$$(a_1,a_2,…,a_n)\cdot(b_1,b_2,…,b_n)^T=a_1b_1+a_2b_2+…+a_nb_n$$
接下来,看下内积的几何意义,假设 A,B 是两个 n 维向量,为了简单起见我们假设 A 和 B 均为二维向量,则 $A=(x_1,y_1),B=(x_2,y_2)$。则在二维平面上 A 和 B 可以用两条发自原点的有向线段表示,如下图:
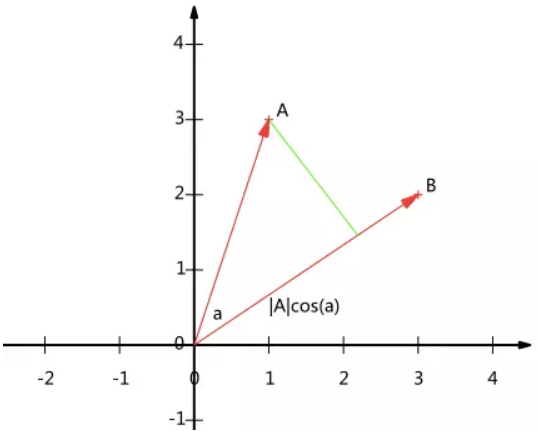
我们从 A 点向 B 所在直线引一条垂线。我们知道垂线与 B 的交点叫做 A 在 B 上的投影,再设 A 与 B 的夹角是 a,则投影的矢量长度为:$|A|cos(a)$,其中 $|A|=\sqrt{x_1^2+y_1^2}$ 是向量 A 的模,也就是 A 线段的标量长度。
我们知道,内积还可表示为 $A\cdot B=|A||B|cos(a)$,也就是说,A 与 B 的内积等于 A 到 B 的投影长度乘以 B 的模。所以,设向量 B 的模为 1,则 A 与 B 的内积值等于 A 向 B 所在直线投影的矢量长度。
基与基变换
我们知道,一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一个有向线段。例如下面这个向量:
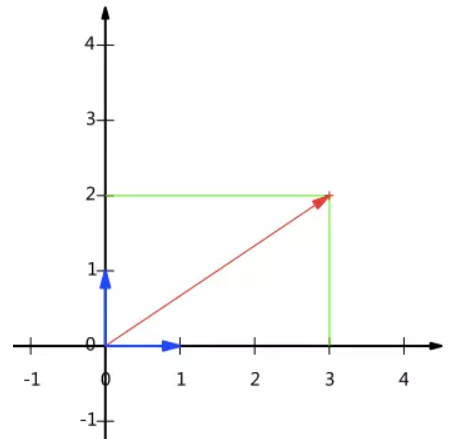
图中的那个向量,我们可以表示为 (3,2),其中 3 表示的是向量在 X 轴的投影值为 3,2 表示的是在 Y 轴的投影值为 2。也就是说我们其实隐式引入了一个定义:以 x 轴和 y 轴上正方向长度为 1 的向量为标准。那么一个向量 (3,2) 实际是说在 x 轴投影为 3 而 y 轴的投影为 2。注意投影是一个矢量,所以可以为负。所以,向量 (x,y) 实际上表示线性组合:
$$x(1,0)^\mathsf{T}+y(0,1)^\mathsf{T}$$
此处的 (1,0),(0,1) 叫做二维空间中的一组基。也是一组正交基。我们之所以默认选择 (1,0) 和 (0,1) 为基,当然是比较方便,因为它们分别是 x 和 y 轴正方向上的单位向量,因此就使得二维平面上点坐标和向量一一对应,非常方便。但实际上任何两个线性无关的二维向量都可以成为一组基,所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的向量。例如,(1,1) 和 (-1,1) 也可以成为一组基。一般来说,我们希望基的模是 1,因为从内积的意义可以看到,如果基的模是 1,那么就可以方便的用向量点乘基而直接获得其在新基上的坐标.实际上,对应任何一个向量我们总可以找到其同方向上模为 1 的向量,只要让两个分量分别除以模就好了。例如,上面的基可以变为:
$$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$$
$$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$$
现在,我们想获得 (3,2) 在新基上的坐标,即在两个方向上的投影矢量值,那么根据内积的几何意义,我们只要分别计算 (3,2) 和两个基的内积,不难得到新的坐标为:$(\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}})$。下图给出了新的基以及 (3,2) 在新基上坐标值的示意图:
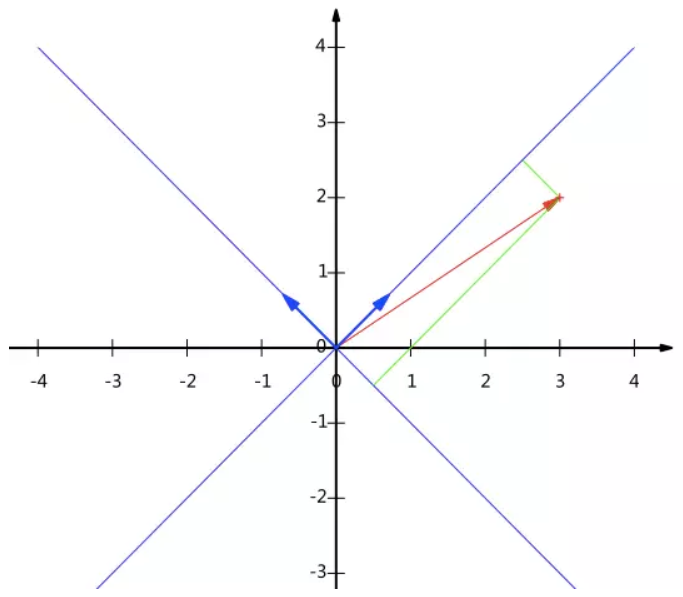
另外这里要注意的是,我们列举的例子中基是正交的(即内积为 0,或直观说相互垂直),但可以成为一组基的唯一要求就是线性无关,非正交的基也是可以的。不过因为正交基有较好的性质,所以一般使用的基都是正交的。
基变换的矩阵表示
通过前面的描述,我们知道,将 (3,2) 变换为新基上的坐标,就是用 (3,2) 去和新的一组基中的每一个去做内积运算。我们可以用矩阵相乘的形式简洁的表示这个变换:
$$\begin{pmatrix}1/\sqrt{2}&1/\sqrt{2}\\-1/\sqrt{2}&1/\sqrt{2}\end{pmatrix}\begin{pmatrix}3\\2\end{pmatrix}=\begin{pmatrix}5/\sqrt{2}\\-1/\sqrt{2}\end{pmatrix}$$
推广到多个向量,假设有 m 个向量,只要将二维向量按列排成一个两行 m 列矩阵,然后用“基矩阵”乘以这个矩阵,就得到了所有这些向量在新基下的值。例如 (1,1),(2,2),(3,3),想变换到刚才那组基上,则可以这样表示:
$$\begin{pmatrix}1/\sqrt{2}&1/\sqrt{2}\\-1/\sqrt{2}&1/\sqrt{2}\end{pmatrix}\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}=\begin{pmatrix}2/\sqrt{2}&4/\sqrt{2}&6/\sqrt{2}\\0&0&0\end{pmatrix}$$
由此我们可以可以看到,基变换可以表示为矩阵相乘。
一般的,如果我们有 M 个 N 维向量,想将其变换为由 R 个 N 维向量表示的新空间中,那么首先将 R 个基按行组成矩阵 A,然后将向量按列组成矩阵 B,那么两矩阵的乘积 AB 就是变换结果,其中 AB 的第 m 列为 A 中第 m 列变换后的结果。数学表示为:
$$\begin{pmatrix}p_1&p_2&\cdots&p_M\end{pmatrix}^\mathsf{T}\begin{pmatrix}a_1&a_2&\cdots&a_M\end{pmatrix}=\begin{pmatrix}p_1a_1&p_1a_2&\cdots&p_1a_M\\p_2a_1&p_2a_2&\cdots&p_2a_M\\\vdots&\vdots&\ddots&\vdots\\p_Ra_1&p_Ra_2&\cdots&p_Ra_M\end{pmatrix}$$
如果 R 小于 N 时,这就是将一 N 维数据变换到更低维度的空间去,因此这种矩阵相乘的表示也可以表示降维变换。两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
优化目标通过上面我们知道,通过选择不同的一组基,可以将同一组数据给出不同的表示,而且如果一组基中基的数量少于向量本身的维数,则可以达到降维的效果。那么,接下来我们的问题就是如何找到一组最优的基,也就是说,如果我们有一组N维向量,现在要将它降到K维(K小于N),那么,我们该如何选择K个基才能最大程度的保留原始N维向量的信息。下面,以一个具体例子来展开,假设我们的数据有5条记录,如下:
$$\begin{pmatrix}1&1&2&4&2\\1&3&3&4&4\end{pmatrix}$$
每一列为一条数据,一行为一个字段,也就是一个特征。
首先,为了后续处理方便,我们将数据进行均值归零化,也就是将每个字段内(也就是每一行)所有值都减去字段的均值,处理以后,新的数据每个字段的均值都为0。变换后的数据如下:
$$\begin{pmatrix}-1&-1&0&2&0\\-2&0&0&1&1\end{pmatrix}$$
在坐标系中的分布如下:
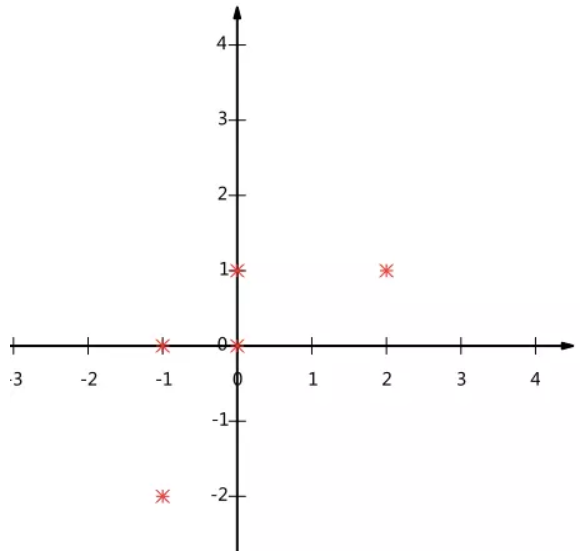
现在,我们要将这些数据降到一维,但是有要尽可能的保留原始的信息。如何去处理呢?通过上面的讨论我们知道,这个问题实际上是要在二维平面中选择一个方向,将所有的数据否投影到这个方向所在的直线上,那么,如何选择这个方向(或者说基)才能更多的保留的原始信息呢?一种直观的看法是:我们希望使投影后的数值尽可能分散以上图为例,可以看出如果向x轴投影,那么最左边的两个点会重叠在一起,中间的两个点也会重叠在一起,于是本身四个各不相同的二维点投影后只剩下两个不同的值了,这是一种严重的信息丢失,同理,如果向y轴投影最上面的两个点和分布在x轴上的两个点也会重叠。所以看来x和y轴都不是最好的投影选择。我们直观目测,如果向通过第一象限和第三象限的斜线投影,则五个点在投影后还是可以区分的。下面,我们通过具体的数学方法来表述下这个问题。
方差
如何选择一个方向或者基才是最优的?我们将所有的点分别向两条直线做投影,基于前面PCA最大可分思想,我们要找的方向是降维后损失最小,可以理解为投影后的数据尽可能的分开,那么这种分散程度可以用数学上的方差来表示,方差越大数据越分散。方差公式如下:
$$Var(a)=\frac{1}{m}\sum_{i=1}^m{(a_i-\mu)^2}$$
由于上面我们已经对每个字段进行均值归零化,所以:
$$Var(a)=\frac{1}{m}\sum_{i=1}^{m}a_i^2$$
所以,上述我们的问题被表述为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大协方差
对于上面二维降成一维的问题来说,找到那个使得方差最大的方向就可以了。不过对于更高维,还有一个问题需要解决。考虑三维降到二维问题。与之前相同,首先我们希望找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而我们选择第二个投影方向。
如果我们还是单纯只选择方差最大的方向,很明显,这个方向与第一个方向应该是“几乎重合在一起”,显然这样的维度是没有用的,因此,应该有其他约束条件。从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。
数学上可以用两个字段的协方差表示其相关性:
$$Cov(a,b)=\frac{1}{m}\sum_{i=1}^{m}(a_i-\mu)(b_i-\mu)$$
由于已经让每个字段均值为0,则:
$$Cov(a,b)=\frac{1}{m}\sum_{i=1}^{m}a_ib_i$$
可以看到,在字段均值为0的情况下,两个字段的协方差简洁的表示为其内积除以元素数m。当协方差为0时,表示两个字段完全独立。为了让协方差为0,我们选择第二个基时只能在与第一个基正交的方向上选择(正交的化,内积为0,正好和协方差为0相对应)。因此最终选择的两个方向一定是正交的。至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
协方差矩阵
我们看到,最终要达到的目的与字段内方差及字段间协方差有密切关系。因此我们希望能将两者统一表示,仔细观察发现,两者均可以表示为内积的形式,而内积又与矩阵相乘密切相关。于是我们来了灵感:
假设我们只有a和b两个字段,那么我们将它们按行组成矩阵X:
$$X=\begin{pmatrix}a_1&a_2&\cdots&a_m\\b_1&b_2&\cdots&b_m\end{pmatrix}$$
然后我们用X乘以X的转置,并乘上系数1/m:
$$\frac{1}{m}XX^T=\begin{pmatrix}\frac{1}{m}\sum_{i=1}^{m}a_i^2&\frac{1}{m}\sum_{i=1}^{m}a_ib_i\\\frac{1}{m}\sum_{i=1}^{m}a_ib_i&\frac{1}{m}\sum_{i=1}^{m}b_i^2\end{pmatrix}$$
这个矩阵对角线上的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。两者被统一到了一个矩阵的。这就是两个字段间的协方差矩阵。
根据矩阵相乘的运算法则,这个结论很容易被推广到一般情况:设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设$C=\frac{1}{m}XX^\mathsf{T}$,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
协方差矩阵对角化
根据上述推导,我们发现要达到优化目前,等价于将协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列,这样我们就达到了优化目的,这样说可能还不是很明晰,我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系:
设原始数据矩阵X对应的协方差矩阵为C,P是一组基(每个基都是一个列向量)组成的矩阵,设$Y=P^TX$,则Y为X对P所包含的那组基做基变换后的数据。设Y的协方差矩阵为D,则有:
$$\begin{array}{lll}D&=&\frac{1}{m}YY^\mathsf{T}\\&=&\frac{1}{m}(P^TX)(P^TX)^\mathsf{T}\\&=&\frac{1}{m}P^TXX^\mathsf{T}P\\&=&P^T(\frac{1}{m}XX^\mathsf{T})P\\&=&P^TCP\end{array}$$
我们要找的P不是别的,而是能让原始协方差矩阵对角化的P。换句话说,优化目标变成了寻找一个矩阵P,满足$P^\mathsf{T}CP$是一个对角矩阵,并且对角元素按从大到小依次排列,那么P的前K列就是要寻找的基,用P的前K列组成的矩阵的转置乘以X就使得X从N维降到了K维并满足上述优化条件。
上文知道,协方差矩阵C是一个是实对称矩阵,在线性代数上,实对称矩阵有一系列非常好的性质:
- 实对称矩阵的特征值都为实数
- 实对称矩阵的所有特征向量正交
- 设特征值重数为r,则必然存在r个线性无关的特征向量对应于,因此可以将这r个特征向量单位正交化
由上面两条可知,一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为$e_1,e_2,\cdots,e_n$,我们将其按列组成矩阵:
$$E=\begin{pmatrix}e_1&e_2&\cdots&e_n\end{pmatrix}$$
则对协方差矩阵C有如下结论:
$$E^\mathsf{T}CE=\Lambda=\begin{pmatrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{pmatrix}$$
其中$\Lambda$为对角矩阵,其对角元素为各特征向量对应的特征值。
到此,我们就已经找到了我们需要的矩阵P=E。P是协方差矩阵的特征向量单位化后按列排列出的矩阵,其中每一列都是C的一个特征向量。如果设P按照$\Lambda$中特征值的从大到小,将特征向量从左到右排列,则用P的前K行组成的矩阵的装置乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y。
PCA 算法流程
设有m条n维数据。
- 将原始数据按列组成n行m列矩阵X
- 将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 求出协方差矩阵$C=\frac{1}{m}XX^\mathsf{T}$
- 求出协方差矩阵的特征值及对应的特征向量
- 将特征向量按对应特征值大小从左到右按列排列成矩阵,取前k列组成矩阵P
- $Y=P^TX$即为降维到k维后的数据
代码实现:
import numpy as np
## X:需要降维的原始数据 topNfeat:需要降到的维数
def PCA(X, topNfeat=9999999):
# 1.原始数据默认都是每一行为一个样本数据,每一列为一个特征,
# 所以进行转置,让每一列代表一个样本数据
X = X.T
# 2.将数据的每一行(代表一个属性字段)进行零均值化
meanValues = np.mean(X, axis=1) # 计算每一行的均值
meanValues = np.mat(meanValues).T # 将一个向量转换成n*1的矩阵
meanRemoved = X - meanValues # 均值归零
# 3.求出协方差矩阵
covMat = np.cov(meanRemoved) # cov计算协方差时除的是(样本个数-1),也就是自由度
# covMat = meanRemoved @ meanRemoved.T / (meanRemoved.shape[1])
print("协方差矩阵:\n", covMat)
# 4求出协方差矩阵的特征值及对应的特征向量
eigVals, eigVects = np.linalg.eig(covMat) # eigVals:特征值 eigVects:特征向量
print("特征值\n", eigVals)
print("特征向量\n", eigVects)
# 5将特征向量按对应特征值大小从左到右按列排列成矩阵,取前k列组成矩阵
# argsort函数返回的是数组值从小到大的索引值,参数中加个-号,变为从大到小
eigValInd = np.argsort(-eigVals)
eigValInd = eigValInd[0:topNfeat] # 取出前topNfeat个最大的特征值所对应的索引
redEigVects = eigVects[:, eigValInd] # redEigVects即为需要的变换矩阵,即P
print("变换矩阵:\n", redEigVects)
# 6 Y=P^TX即为降维到k维后的数据
X_PCA = redEigVects.T @ X
return X_PCA
PCA(X, topNfeat=1)
PCA 算法总结
这里对PCA算法做一个总结。作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点,出现了很多PCA的变种,比如为解决非线性降维的KPCA,还有解决内存限制的增量PCA方法IncrementalPCA,以及解决稀疏数据降维的PCA方法SparsePCA等。
PCA算法的主要优点有:
- 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
- 各主成分之间正交,可消除原始数据成分间的相互影响的因素。
- 计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
- 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
用scikit-learn进行主成分分析
在scikit-learn中,与PCA相关的类都在sklearn.decomposition包中。最常用的PCA类就是sklearn.decomposition.PCA,我们下面主要也会讲解基于这个类的使用的方法。
sklearn.decomposition.PCA参数介绍
PCA类基本不需要调参,一般来说,我们只需要指定我们需要降维到的维度,或者我们希望降维后的主成分的方差和占原始维度所有特征方差和的比例阈值就可以了。现在我们对sklearn.decomposition.PCA的主要参数做一个介绍:
- n_components:这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。当然,我们也可以指定主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的数。当然,我们还可以将参数设置为”mle”,此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值,即不输入n_components,此时n_components=min(样本数,特征数)。
- whiten:判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
- svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’,‘full’,‘arpack’,‘randomized’}。randomized一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
除了这些输入参数外,有两个PCA类的成员值得关注。第一个是explained_variance_,它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分。第二个是explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分。
PCA代码实例
首先我们生成随机数据并可视化:
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D %matplotlib inline from sklearn.datasets.samples_generator import make_blobs # X为样本特征,Y为样本簇类别,共1000个样本,每个样本3个特征,共4个簇 X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3,3],[0,0,0],[1,1,1],[2,2,2]], cluster_std=[0.2,0.1,0.2,0.2], random_state=9) fig = plt.figure() ax = Axes3D(fig, rect=[0,0,1,1], elev=30, azim=20) plt.scatter(X[:,0], X[:,1], X[:,2], marker='o')
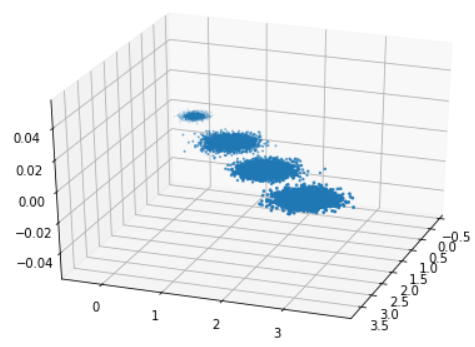
先不降维,只对数据进行投影,看看投影后的三个维度的方差分布,代码如下:
from sklearn.decomposition import PCA pca = PCA(n_components=3) pca.fit(X) print(pca.explained_variance_ratio_) print(pca.explained_variance_)
输出如下:
[0.98318212 0.00850037 0.00831751] [3.78483785 0.03272285 0.03201892]
可以看出投影后三个特征维度的方差比例大约为98.3%:0.8%:0.8%。投影后第一个特征占了绝大多数的主成分比例。现在我们来进行降维,从三维降到2维,代码如下:
pca = PCA(n_components=2) pca.fit(X) print(pca.explained_variance_ratio_) print(pca.explained_variance_)
输出如下:
[0.98318212 0.00850037] [3.78483785 0.03272285]
这个结果其实可以预料,因为上面三个投影后的特征维度的方差分别为:[3.78483785 0.03272285 0.03201892],投影到二维后选择的肯定是前两个特征,而抛弃第三个特征。为了有个直观的认识,我们看看此时转化后的数据分布,代码如下:
X_new = pca.transform(X) plt.scatter(X_new[:,0], X_new[:,1], marker='o') plt.show()
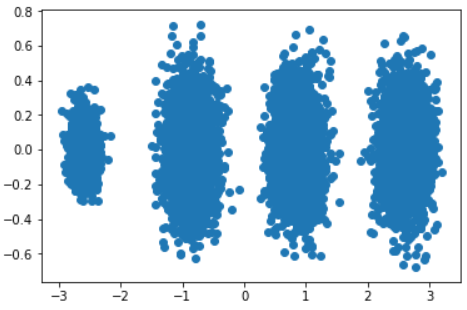
可见降维后的数据依然可以很清楚的看到我们之前三维图中的4个簇。现在我们看看不直接指定降维的维度,而指定降维后的主成分方差和比例。
pca = PCA(n_components=0.95) pca.fit(X) print(pca.explained_variance_ratio_) print(pca.explained_variance_) print(pca.n_components_)
我们指定了主成分至少占95%,输出如下:
[0.98318212] [3.78483785] 1
可见只有第一个投影特征被保留。这也很好理解,我们的第一个主成分占投影特征的方差比例高达98%。只选择这一个特征维度便可以满足95%的阈值。我们现在选择阈值99%看看,代码如下:
pca = PCA(n_components=0.99) pca.fit(X) print(pca.explained_variance_ratio_) print(pca.explained_variance_) print(pca.n_components_)
此时的输出如下:
[0.98318212 0.00850037] [3.78483785 0.03272285] 2
这个结果也很好理解,因为我们第一个主成分占了98.3%的方差比例,第二个主成分占了0.8%的方差比例,两者一起可以满足我们的阈值。最后我们看看让MLE算法自己选择降维维度的效果,代码如下:
pca = PCA(n_components='mle', svd_solver='full') pca.fit(X) print(pca.explained_variance_ratio_) print(pca.explained_variance_) print(pca.n_components_)
输出结果如下:
[0.98318212] [3.78483785] 1
可见由于我们的数据的第一个投影特征的方差占比高达98.3%,MLE算法只保留了我们的第一个特征。
备注:在pca = PCA(n_components=’mle’)(MLE即极大似然估计)时报错
TypeError: ‘>=’ not supported between instances of ‘str’ and ‘int’
通过查看help(PCA)发现,当n_components==’mle’时,需要和参数svd_solver一起使用,且svd_solver需要选择full参数,即pca = PCA(n_components=’mle’, svd_solver=’full’)才可执行成功。
除了PCA类以外,最常用的PCA相关类还有:
- KernelPCA类,它主要用于非线性数据的降维,需要用到核技巧。因此在使用的时候需要选择合适的核函数并对核函数的参数进行调参。
- IncrementalPCA类,它主要是为了解决单机内存限制的。有时候我们的样本量可能是上百万,维度可能也是上千,直接去拟合数据可能会让内存爆掉,此时我们可以用IncrementalPCA类来解决这个问题。IncrementalPCA先将数据分成多个batch,然后对每个batch依次递增调用partial_fit函数,这样一步步的得到最终的样本最优降维。
- SparsePCA和MiniBatchSparsePCA。他们和上面讲到的PCA类的区别主要是使用了L1的正则化,这样可以将很多非主要成分的影响度降为0,这样在PCA降维的时候我们仅仅需要对那些相对比较主要的成分进行PCA降维,避免了一些噪声之类的因素对我们PCA降维的影响。SparsePCA和MiniBatchSparsePCA之间的区别则是MiniBatchSparsePCA通过使用一部分样本特征和给定的迭代次数来进行PCA降维,以解决在大样本时特征分解过慢的问题,当然,代价就是PCA降维的精确度可能会降低。使用SparsePCA和MiniBatchSparsePCA需要对L1正则化参数进行调参。
参考链接: