文章内容如有错误或排版问题,请提交反馈,非常感谢!
香农-范诺编码简介
香农-范诺编码(Shannon-Fano Coding)是一种经典的无损数据压缩算法,由克劳德·香农(Claude Shannon)和罗伯特·范诺(Robert Fano)于1948年左右独立提出。这是第一种基于信息熵理论的压缩算法,比著名的哈夫曼编码出现得更早。
核心思想与原理
香农-范诺编码的核心思想是通过递归划分概率空间来实现压缩:
- 信息熵概念:香农信息论证明,字符$s_i$的理想码长应为$\log_2(1/p_i)$,其中$/p_i$是字符出现概率
- 概率空间划分:将字符集按概率降序排列,不断将其分割为两个概率和尽可能相等的子集
- 二进制分配:每个分割点分配二进制位:
左子集 → 添加0
右子集 → 添加1
- 前缀编码:最终生成的是前缀码(无前缀冲突),无需分隔符即可解码
算法步骤详解
假设有5个字符:A(0.38), B(0.18), C(0.17), D(0.15), E(0.12)
步骤1:概率排序
| 字符 | 概率 |
| A | 0.38 |
| B | 0.18 |
| C | 0.17 |
| D | 0.15 |
| E | 0.12 |
步骤2:递归分割概率空间
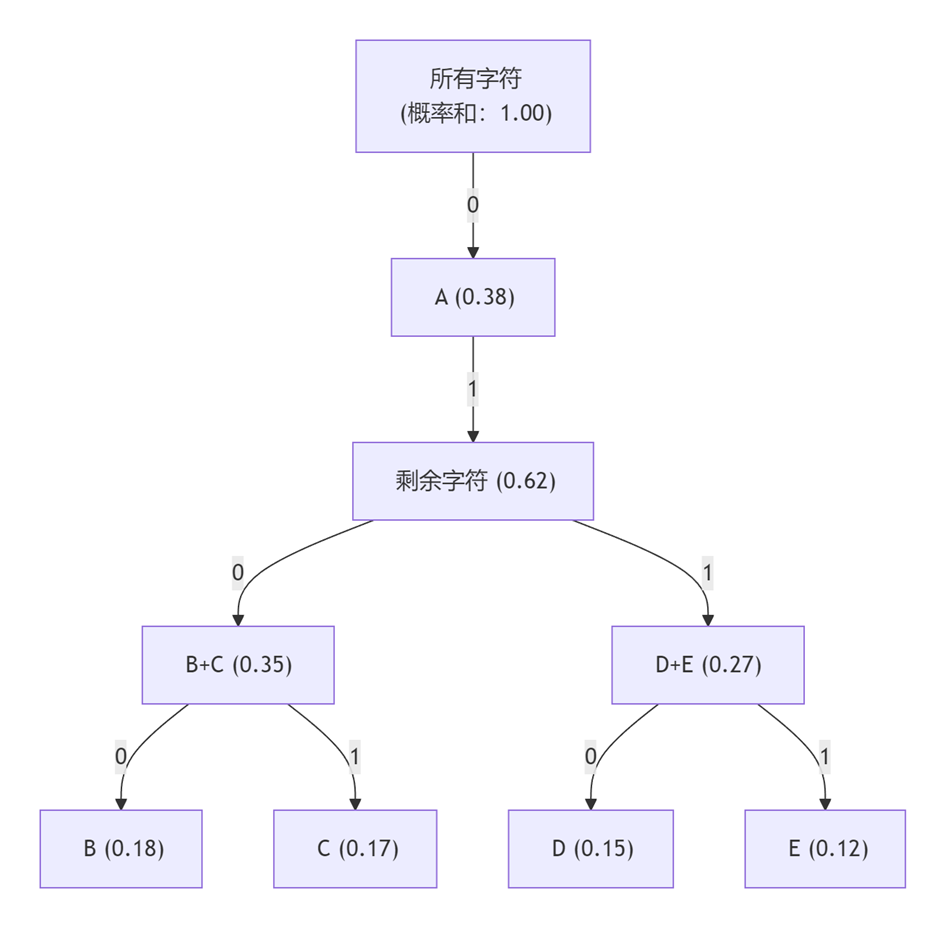
步骤3:生成编码
- 第一次分割:左子集=A添加0,右子集添加1
- 第二次分割:右子集中左=B+C添加0,右=D+E添加1
- 第三次分割:
- B添加0→ 完整编码=10
- C添加1→ 完整编码=11
- 第四次分割:
- D添加0→ 完整编码=10
- E添加1→ 完整编码=111
最终编码表:
| 字符 | 概率 | 编码 | 理想码长 | 实际码长 |
| A | 0.38 | 0 | 1.39 | 1 |
| B | 0.18 | 100 | 2.47 | 3 |
| C | 0.17 | 101 | 2.56 | 3 |
| D | 0.15 | 110 | 2.74 | 3 |
| E | 0.12 | 111 | 3.06 | 3 |
关键特点
- 计算复杂度:
- 时间:$O(n\log n)$(主要来自排序操作)
- 空间:$O(n)$
- 压缩效率:
- 平均码长:$\sum p_il_i \approx 2.19$比特/符号
- 信息熵:$H = -\sum p_i\log _2 p_i \approx 2.17$比特/符号
- 冗余度:约02比特/符号
- 最优分割问题:通过贪心算法找局部最优分割,但不保证全局最优:
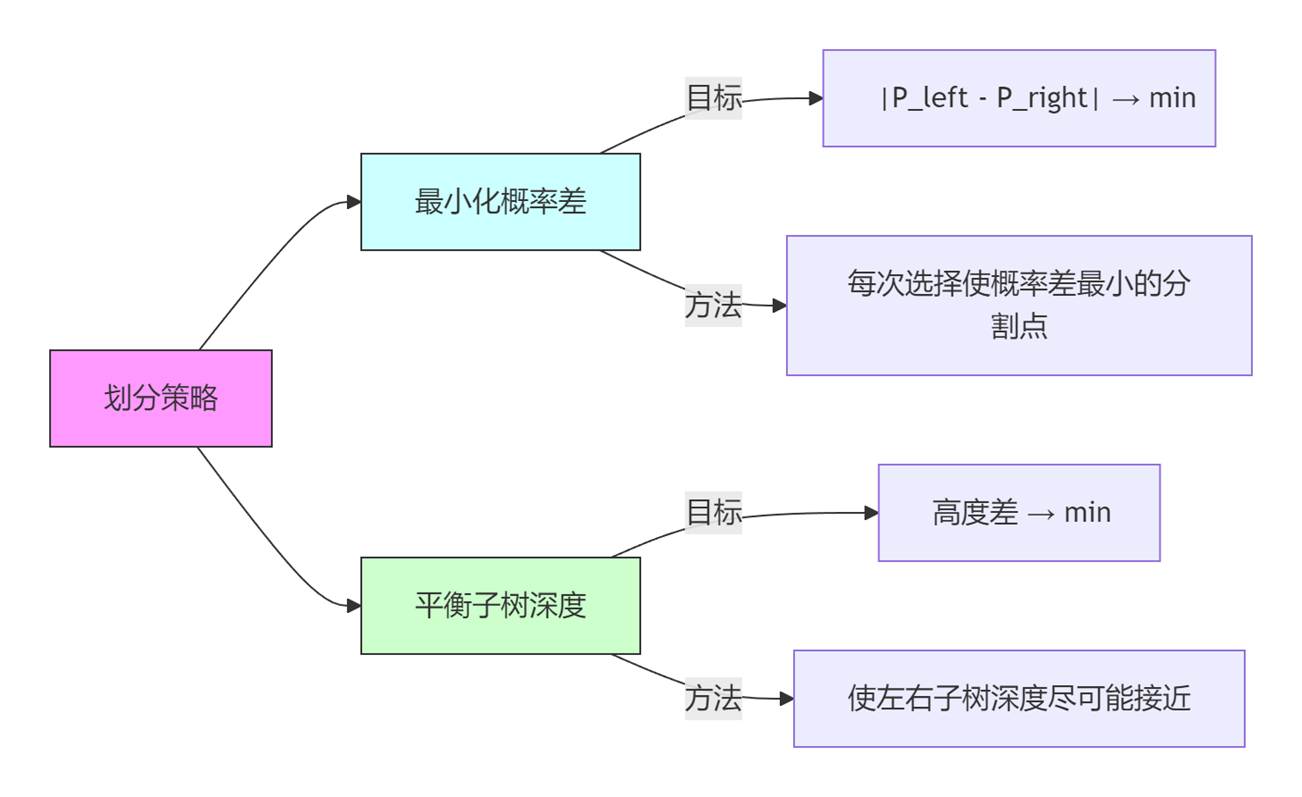
与哈夫曼编码对比
| 特性 | 香农-范诺编码 | 哈夫曼编码 |
| 提出时间 | 1948年 | 1952年 |
| 构建方向 | 自顶向下(递归分割) | 自底向上(节点合并) |
| 最优性保证 | 近似最优(接近熵但非最优) | 严格最优(最小平均码长) |
| 码长分布 | 有时长于哈夫曼编码 | 总是最短平均码长 |
| 复杂度 | $O(n\log n)$ | $O(n\log n)$ |
| 前缀码性质 | 满足 | 满足 |
| 编码唯一性 | 不唯一(取决于分割顺序) | 不唯一(相同概率时) |
| 典型应用 | GZIP(早期版本)、多媒体压缩 | ZIP、JPEG、MP3等主流压缩 |
实际应用
- UNIX压缩工具:早期compact命令使用香农-范诺变体
- 图像压缩:TIFF格式可选香农-范诺压缩,医疗图像传输标准DICOM。
- 通信协议:25分组无线电协议的数据压缩
- 音频编码:SHORTEN无损音频压缩算法(在FLAC出现前)
历史意义与局限性
历史贡献:
- 首个基于信息论的压缩算法
- 证明可实现无损压缩接近香农熵
- 推动哈夫曼等后续算法的发展
局限性:
- 非最优性:存在压缩率更高的算法
- 分割依赖:编码结果受分割顺序影响
- 冗余问题:部分情况下码长超过熵值
- 实现复杂性:相比哈夫曼实现较复杂
八、现代演变
- 自适应变体:根据输入流动态更新概率模型
- 分组编码:将字符组合成”超字符”提高压缩率
- 与LZ结合:在DEFLATE等算法中作为熵编码阶段
虽然哈夫曼编码在实际应用中更受欢迎,但香农-范诺编码作为信息论的第一个实际应用,仍然在压缩算法发展史上占有重要地位。它展示了如何利用信息熵实现高效数据压缩的核心思想,为后续所有熵编码算法奠定了基础。
香农-范诺编码Python实现
import math
from collections import Counter
class ShannonFanoNode:
def __init__(self, char=None, prob=0):
self.char = char # 字符
self.prob = prob # 概率
self.code = "" # 二进制编码
self.left = None # 左子节点
self.right = None # 右子节点
def calculate_probabilities(text):
"""计算字符概率分布"""
counter = Counter(text)
total = len(text)
return [(char, count/total) for char, count in counter.items()]
def find_optimal_split(items):
"""寻找最佳分割点"""
total = sum(prob for _, prob in items)
min_diff = float('inf')
split_idx = 1
left_sum = 0
for i in range(1, len(items)):
left_sum += items[i-1][1]
right_sum = total - left_sum
diff = abs(left_sum - right_sum)
if diff < min_diff:
min_diff = diff
split_idx = i
return split_idx
def build_shannon_fano_tree(items):
"""递归构建香农-范诺树"""
# 基本情况:单个节点
if len(items) == 1:
char, prob = items[0]
return ShannonFanoNode(char, prob)
# 按概率降序排序
sorted_items = sorted(items, key=lambda x: x[1], reverse=True)
# 寻找最佳分割点
split_index = find_optimal_split(sorted_items)
left_items = sorted_items[:split_index]
right_items = sorted_items[split_index:]
# 创建父节点
node = ShannonFanoNode()
# 递归构建子树
node.left = build_shannon_fano_tree(left_items)
node.right = build_shannon_fano_tree(right_items)
# 更新子树编码
if node.left:
if isinstance(node.left, list):
for child in node.left:
child.code = '0' + child.code
else:
node.left.code = '0' + node.left.code
if node.right:
if isinstance(node.right, list):
for child in node.right:
child.code = '1' + child.code
else:
node.right.code = '1' + node.right.code
return [node.left, node.right] if isinstance(node.left, ShannonFanoNode) else node
def generate_codes(node, code_dict, prefix=""):
"""生成字符编码字典"""
if node.char is not None:
node.code = prefix
code_dict[node.char] = prefix
else:
if node.left:
generate_codes(node.left, code_dict, prefix + '0')
if node.right:
generate_codes(node.right, code_dict, prefix + '1')
def shannon_fano_encode(text):
"""香农-范诺编码主函数"""
if not text:
return "", {}
# 计算概率分布
prob_dist = calculate_probabilities(text)
# 构建编码树
root = build_shannon_fano_tree(prob_dist)
# 生成编码字典
code_dict = {}
if isinstance(root, list):
for node in root:
generate_codes(node, code_dict)
else:
generate_codes(root, code_dict)
# 编码文本
encoded = ''.join(code_dict[char] for char in text)
return encoded, code_dict
def shannon_fano_decode(encoded, code_dict):
"""香农-范诺解码"""
reverse_dict = {code: char for char, code in code_dict.items()}
decoded = []
current_code = ""
for bit in encoded:
current_code += bit
if current_code in reverse_dict:
decoded.append(reverse_dict[current_code])
current_code = ""
return ''.join(decoded)
# 测试示例
if __name__ == "__main__":
text = "ABRACADABRA"
print(f"原始文本: {text}")
encoded, code_dict = shannon_fano_encode(text)
print(f"编码结果: {encoded}")
print("编码表:")
for char, code in sorted(code_dict.items()):
print(f" {char}: {code}")
decoded = shannon_fano_decode(encoded, code_dict)
print(f"解码结果: {decoded}")
print(f"原始长度: {len(text)*8} bits")
print(f"编码长度: {len(encoded)} bits")
print(f"压缩率: {1 - len(encoded)/(len(text)*8):.1%}")