数据结构之链表

链表简介

链表（Linked List）是一种基础的数据结构，是由一系列节点（Node）组成的集合。每个节点包括两部分：一部分是数据，另一部分是指向下一个节点的引用（在双向链表中，还有指向前一个节点的引用）。

这是链表（LinkedList）与数组（Array）的主要区别。数组是一种线性数据结构，它的元素在内存中是连续存放的，而链表的元素可以在内存中任意分布。

链表的设计使得各个节点可以分散存储在内存各处，它们的内存地址无须连续。

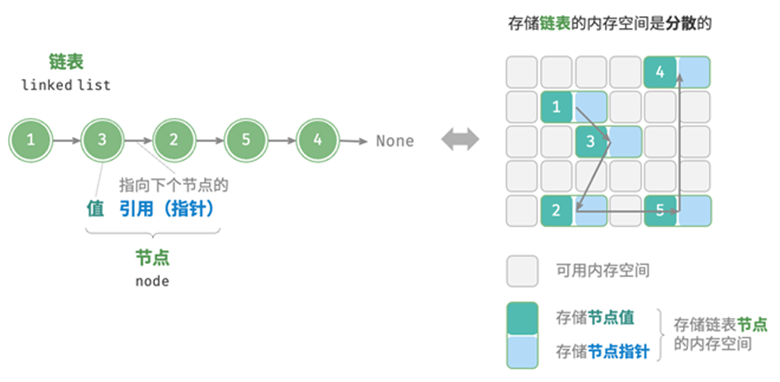
内存空间是所有程序的公共资源，在一个复杂的系统运行环境下，空闲的内存空间可能散落在内存各处。我们知道，存储数组的内存空间必须是连续的，而当数组非常大时，内存可能无法提供如此大的连续空间。此时链表的灵活性优势就体现出来了。

链表的特性：

• 动态大小：链表的大小可以动态调整，与数组不同，数组在创建时需要指定大小，如果超出，需要重新创建并复制数据。
• 高效的插入和删除：链表在插入和删除元素时，只需要改变相关节点的引用，操作时间为O(1)。而数组需要移动元素，时间复杂度为O(n)。
• 内存利用率高：链表不需要连续的内存空间，可以更有效地利用内存。
• 顺序访问：链表需要从头部（有时是尾部，如果是双向链表）开始访问，不能像数组一样直接通过索引访问。

以下是与数组的比较：

• 存储分配：数组在创建时需要预先分配内存空间，而链表可以根据需要动态分配内存。
• 内存利用：数组必须有连续的内存空间，链表可以利用内存中的任何零散空间。
• 访问速度：数组可以通过索引直接访问，访问速度快；链表必须从头部或尾部开始访问，速度较慢。
• 插入和删除：链表可以在任何位置进行快速的插入和删除操作；数组进行插入和删除操作时，需要移动大量元素。
• 空间消耗：链表的每一个节点都需要额外的存储空间来存储一个指向下一个节点的指针，所以空间利用率相对较低。

链表的类型

链表主要可以分为以下几种类型：

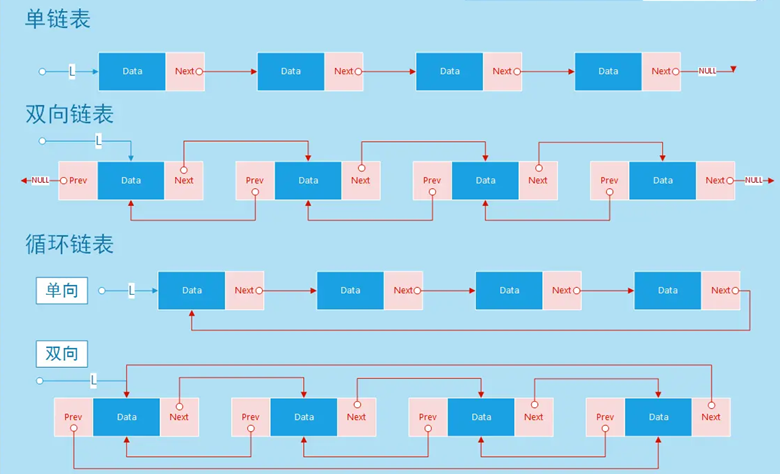
• 单向链表 (Singly Linked List)：单链表是最简单的链表形式。在单链表中，每个节点包含数据和一个指向下一个节点的指针。最后一个节点指向一个空（NULL）值，表示链表的结尾。
• 双向链表 (Doubly Linked List)：在双链表中，每个节点包含数据，一个指向下一个节点的指针，和一个指向前一个节点的指针。这种结构使得在链表中向前和向后移动都非常方便。
• 单向循环链表 (Circular Linked List)：在循环链表中，最后一个节点不是指向空（NULL）值，而是指向链表的头节点，形成一个闭环。
• 双向循环链表 (Doubly Circular Linked List)：双向循环链表是双链表和循环链表的结合。在这种链表中，最后一个节点的下一个节点是头节点，而头节点的前一个节点是尾节点，形成一个双向的闭环。

每种链表类型都有其特定的应用，理解它们的差异和用途对于正确和高效地使用链表非常重要。

单向链表

单向链表（Singly Linked List）是一种链表数据结构，其中每个节点包含数据元素和一个指向下一个节点的引用。链表的头节点用来表示链表的起始点，而尾节点的下一个节点通常为空（nil）。

单链表实现图示：

文字解析：

• Data 数据 + Next 指针，组成一个单链表的内存结构 ；
• 第一个内存结构称为 链头，最后一个内存结构称为 链尾；
• 链尾的 Next 指针设置为 NULL [指向空]；
• 单链表的遍历方向单一【只能从链头一直遍历到链尾】

特点和属性：

• 每个节点包含两个部分：数据元素和指向下一个节点的引用。
• 节点之间的连接是单向的，只能从头节点开始遍历链表。
• 插入和删除节点操作在单向链表中非常高效，因为只需更新指针，而不需要移动大量元素。
• 链表的大小可以动态增长或缩小，不需要提前指定大小。

单向链表通常用于需要频繁插入和删除操作的情况，因为这些操作相对容易实现。然而，访问链表中的特定元素需要从头节点开始遍历，效率较低。

单向链表的C语言实现：

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点
typedef struct node {
    int data;
    struct node *next;
} Node;

// 创建新的节点
Node *create_node(int data) {
    Node *new_node = (Node *) malloc(sizeof(Node));
    if (new_node == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    new_node->data = data;
    new_node->next = NULL;
    return new_node;
}

// 插入节点到链表
void insert_node_at_head(Node **head, int data) {
    Node *new_node = create_node(data);
    new_node->next = *head;
    *head = new_node;
}

// 插入节点到链表的尾部
void insert_node_at_end(Node **head, int data) {
    Node *new_node = create_node(data);

    if (*head == NULL) {
        *head = new_node;
        return;
    }

    Node *last = *head;
    while (last->next != NULL) {
        last = last->next;
    }

    last->next = new_node;
}

// 删除节点
void delete_node(Node **head, int key) {
    Node *temp = *head, *prev;

    if (temp != NULL && temp->data == key) {
        *head = temp->next;
        free(temp);
        return;
    }

    while (temp != NULL && temp->data != key) {
        prev = temp;
        temp = temp->next;
    }

    if (temp == NULL) return;

    prev->next = temp->next;
    free(temp);
}

// 搜索节点
Node *search_node(Node *head, int key) {
    Node *current = head;

    while (current != NULL) {
        if (current->data == key) {
            return current;
        }
        current = current->next;
    }
    return NULL;
}

// 显示链表
void display_list(Node *n) {
    while (n != NULL) {
        printf(" %d ", n->data);
        n = n->next;
    }
}

// 反转链表
void reverse_list(Node **head) {
    Node *prev = NULL;
    Node *current = *head;
    Node *next = NULL;

    while (current != NULL) {
        next = current->next;
        current->next = prev;
        prev = current;
        current = next;
    }
    *head = prev;
}

// 释放链表
void free_list(Node **head) {
    Node *current = *head;
    Node *next;
    while (current != NULL) {
        next = current->next;
        free(current);
        current = next;
    }
    *head = NULL;
}

int main() {
    Node *head = NULL;

    insert_node_at_head(&head, 0);
    insert_node_at_head(&head, 1);
    insert_node_at_head(&head, 2);
    insert_node_at_head(&head, 3);
    insert_node_at_end(&head, -1);
    insert_node_at_end(&head, -2);
    insert_node_at_end(&head, -3);
    printf("Linked list is: ");
    display_list(head);

    delete_node(&head, 0);
    printf("\nLinked list after deletion of 5: ");
    display_list(head);

    reverse_list(&head);
    printf("\nLinked list after reverse: ");
    display_list(head);

    Node *item = search_node(head, 1);
    printf("\nSearch for 1 in the linked-list: %s", item ? "Found" : "Not found");

    free_list(&head);

    return 0;
}

双向链表

双向链表（Doubly Linked List）是一种链表数据结构，其中每个节点包含数据元素、一个指向下一个节点的引用和一个指向前一个节点的引用。相对于单向链表，双向链表提供了更多的灵活性，因为它可以在前向和后向两个方向上遍历链表。

双向链表实现图示：

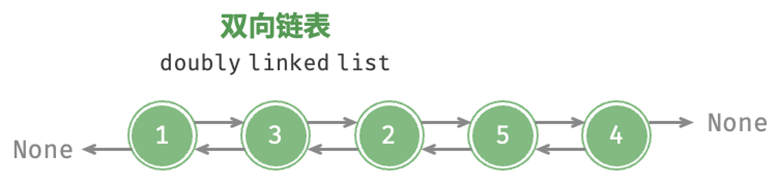
文字解析：

• Data 数据 + Next 指针 + Prev 指针，组成一个双向链表的内存结构；
• 第一个内存结构称为 链头，最后一个内存结构称为 链尾；
• 链头的 Prev 指针设置为 NULL， 链尾的 Next 指针设置为 NULL；
• Prev 指向的内存结构称为 前驱， Next 指向的内存结构称为 后继；
• 双向链表的遍历是双向的，即如果把从链头的 Next 一直到链尾的[NULL] 遍历方向定义为正向，那么从链尾的 Prev 一直到链头 [NULL ]遍历方向就是反向；

特点和属性：

• 每个节点包含三个部分：数据元素、指向下一个节点的引用（通常称为next），和指向前一个节点的引用（通常称为prev）。
• 节点之间的连接是双向的，可以从头节点向后遍历，也可以从尾节点向前遍历。
• 插入和删除节点操作在双向链表中仍然高效，因为只需更新相邻节点的引用。
• 链表的大小可以动态增长或缩小，不需要提前指定大小。

双向链表通常用于需要前向和后向遍历的情况，或者在需要频繁插入和删除节点的情况下。相对于单向链表，双向链表提供了更多的灵活性，但也需要额外的空间来存储前向引用。

双向链表的C语言实现：

#include <stdio.h>
#include <stdlib.h>

// 定义双向链表节点
typedef struct node {
    int data;
    struct node *prev;
    struct node *next;
} Node;

// 创建新的节点
Node *create_node(int data) {
    Node *new_node = (Node *) malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    new_node->data = data;
    new_node->prev = NULL;
    new_node->next = NULL;
    return new_node;
}

// 插入节点到链表的头部
void insert_node_at_head(Node **head, int data) {
    Node *new_node = create_node(data);
    if (*head == NULL) {
        *head = new_node;
        return;
    }
    (*head)->prev = new_node;
    new_node->next = *head;
    *head = new_node;
}

// 插入节点到链表的尾部
void insert_node_at_end(Node **head, int data) {
    Node *new_node = create_node(data);
    if (*head == NULL) {
        *head = new_node;
        return;
    }
    Node *last = *head;
    while (last->next != NULL) {
        last = last->next;
    }
    last->next = new_node;
    new_node->prev = last;
}

// 删除节点
void delete_node(Node **head, int key) {
    Node *temp = *head;
    while (temp != NULL && temp->data != key) {
        temp = temp->next;
    }
    if (temp == NULL) {
        printf("Element not found in the list.\n");
        return;
    }
    if (temp->prev != NULL) {
        temp->prev->next = temp->next;
    }
    if (temp->next != NULL) {
        temp->next->prev = temp->prev;
    }
    if (temp == *head) {
        *head = temp->next;
    }
    free(temp);
}

// 显示链表
void display_list(Node *n) {
    while (n != NULL) {
        printf(" %d ", n->data);
        n = n->next;
    }
}

// 反转链表
void reverse_list(Node **head) {
    Node *temp = NULL;
    Node *current = *head;

    while (current != NULL) {
        temp = current->prev;
        current->prev = current->next;
        current->next = temp;
        current = current->prev;
    }

    if (temp != NULL)
        *head = temp->prev;
}

// 搜索节点
Node *search_node(Node *head, int key) {
    Node *current = head;
    while (current != NULL) {
        if (current->data == key) {
            return current;
        }
        current = current->next;
    }
    return NULL;
}

// 释放链表
void free_list(Node **head) {
    Node *current = *head;
    Node *next;

    while (current != NULL) {
        next = current->next;
        free(current);
        current = next;
    }

    *head = NULL;
}

int main() {
    Node *head = NULL;

    insert_node_at_head(&head, 1);
    insert_node_at_head(&head, 2);
    insert_node_at_head(&head, 3);
    insert_node_at_end(&head, 4);
    insert_node_at_end(&head, 5);
    printf("Doubly linked list is: ");
    display_list(head);

    delete_node(&head, 2);
    printf("\nDoubly linked list after deletion of 2: ");
    display_list(head);

    reverse_list(&head);
    printf("\nDoubly linked list after reversing: ");
    display_list(head);

    Node *item = search_node(head, 3);
    printf("\nSearch for 3 in the linked-list: %s", item ? "Found" : "Not found");

    free_list(&head);

    return 0;
}

循环链表

• 单向循环链表 [Circular Linked List] : 由各个内存结构通过一个指针 Next 链接在一起组成，每一个内存结构都存在后继内存结构，内存结构由数据域和 Next 指针域组成。
• 双向循环链表 [Double Circular Linked List] : 由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成，每一个内存结构都存在前驱内存结构和后继内存结构，内存结构由数据域、Prev 指针域和 Next 指针域组成。

循环链表的单向与双向实现图示：

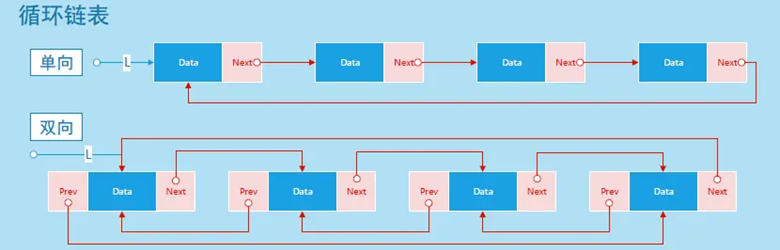
文字解析：

• 循环链表分为单向、双向两种；
• 单向的实现就是在单链表的基础上，把链尾的 Next 指针直接指向链头，形成一个闭环；
• 双向的实现就是在双向链表的基础上，把链尾的 Next 指针指向链头，再把链头的 Prev 指针指向链尾，形成一个闭环；
• 循环链表没有链头和链尾的说法，因为是闭环的，所以每一个内存结构都可以充当链头和链尾；

单向循环链表的C语言实现，包括插入、删除和显示操作：

#include <stdio.h>
#include <stdlib.h>

// 定义单向循环链表节点
typedef struct node {
    int data;
    struct node *next;
} Node;

// 创建新的节点
Node *create_node(int data) {
    Node *new_node = (Node *)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    new_node->data = data;
    new_node->next = new_node; // Point to itself as it is a circular list
    return new_node;
}

// 插入节点到链表的头部
void insert_node_at_head(Node **head, int data) {
    Node *new_node = create_node(data);
    if (*head == NULL) {
        *head = new_node;
        return;
    }
    Node *last = *head;
    while (last->next != *head) {
        last = last->next;
    }
    new_node->next = *head;
    last->next = new_node;  
    *head = new_node;
}

// 删除节点
void delete_node(Node **head, int key) {
    if (*head == NULL) {
        printf("List is empty.\n");
        return;
    }
    Node *temp = *head, *prev;
    if ((*head)->data == key) {
        Node *last = *head;
        while (last->next != *head) {
            last = last->next;
        }
        *head = (*head)->next;
        last->next = *head;
        free(temp);
        return;
    }
    while (temp->next != *head && temp->data != key) {
        prev = temp;
        temp = temp->next;
    }
    if (temp->data != key) {
        printf("Element not found in the list.\n");
        return;
    }
    prev->next = temp->next;
    free(temp);
}

// 显示链表
void display_list(Node *head) {
    if (head == NULL) {
        printf("List is empty.\n");
        return;
    }
    Node *temp = head;
    do {
        printf(" %d ", temp->data);
        temp = temp->next;
    } while (temp != head);
}

int main() {
    Node *head = NULL;

    insert_node_at_head(&head, 1);
    insert_node_at_head(&head, 2);
    insert_node_at_head(&head, 3);

    printf("Circular linked list is: ");
    display_list(head);

    delete_node(&head, 2);

    printf("\nCircular linked list after deletion of 2: ");
    display_list(head);

    return 0;
}

双向循环链表的C语言实现：

#include <stdio.h>
#include <stdlib.h>

// 定义双向循环链表节点
typedef struct node {
    int data;
    struct node *prev;
    struct node *next;
} Node;

// 创建新的节点
Node *create_node(int data) {
    Node *new_node = (Node *)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    new_node->data = data;
    new_node->prev = new_node; // Point to itself as it is a circular list
    new_node->next = new_node; // Point to itself as it is a circular list
    return new_node;
}

// 插入节点到链表的头部
void insert_node_at_head(Node **head, int data) {
    Node *new_node = create_node(data);
    if (*head == NULL) {
        *head = new_node;
        return;
    }
    (*head)->prev->next = new_node;
    new_node->prev = (*head)->prev;
    new_node->next = *head;
    (*head)->prev = new_node;
    *head = new_node;
}

// 删除节点
void delete_node(Node **head, int key) {
    if (*head == NULL) {
        printf("List is empty.\n");
        return;
    }
    Node *temp = *head;
    do {
        if (temp->data == key) {
            temp->prev->next = temp->next;
            temp->next->prev = temp->prev;
            if (*head == temp) {
                *head = (*head)->next;
            }
            free(temp);
            return;
        }
        temp = temp->next;
    } while (temp != *head);
    printf("Element not found in the list.\n");
}

// 显示链表
void display_list(Node *head) {
    if (head == NULL) {
        printf("List is empty.\n");
        return;
    }
    Node *temp = head;
    do {
        printf(" %d ", temp->data);
        temp = temp->next;
    } while (temp != head);
}

int main() {
    Node *head = NULL;

    insert_node_at_head(&head, 1);
    insert_node_at_head(&head, 2);
    insert_node_at_head(&head, 3);

    printf("Circular doubly linked list is: ");
    display_list(head);

    delete_node(&head, 2);

    printf("\nCircular doubly linked list after deletion of 2: ");
    display_list(head);

    return 0;
}

带头链表

带头链表（Head Linked List），也称为带头节点链表或哨兵节点链表，是一种链表数据结构，其中链表的头部包含一个额外的节点，通常称为头节点（Head Node）或哨兵节点（Sentinel Node）。这个额外的节点不包含实际数据，它的主要目的是简化链表操作，确保链表不为空，并在插入和删除节点时提供一致性。

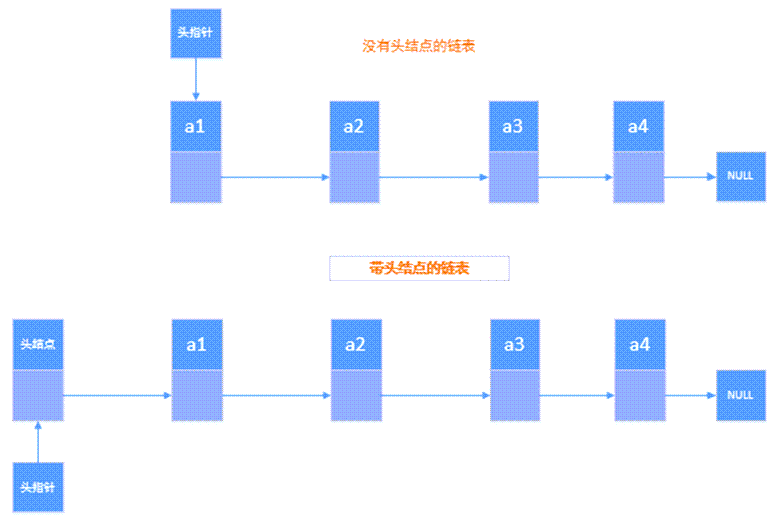
特点和属性：

• 链表的头节点包含两个部分：指向链表的第一个实际节点的引用和通常为空的数据元素。
• 链表的头节点使链表操作更简单，因为不需要特殊处理空链表的情况。
• 带头链表可以用于各种链表问题，包括单向链表、双向链表、循环链表等不同类型的链表。
• 带头链表通常用于简化链表操作，因为它确保链表不为空，即使链表没有实际数据节点时，头节点也存在。这减少了对特殊情况的处理。

带头结点的链表的C语言实现：

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点
typedef struct node {
    int data;
    struct node *next;
} Node;

// 创建带头结点的链表
Node *create_list() {
    Node *head = (Node *)malloc(sizeof(Node));  // 创建头结点
    if (head == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    head->next = NULL;  // 头结点的next指针设为NULL
    return head;
}

// 在链表尾部插入节点
void insert_node_at_end(Node *head, int data) {
    Node *new_node = (Node *)malloc(sizeof(Node));  // 创建新节点
    if (new_node == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    new_node->data = data;  // 设定新节点数据
    new_node->next = NULL;  // 新节点的next指针设为NULL

    Node *temp = head;  // 从头结点开始寻找
    while (temp->next != NULL) {
        temp = temp->next;  // 直到找到最后一个节点
    }
    temp->next = new_node;  // 将最后一个节点的next指针设为新节点
}

// 打印链表
void print_list(Node *head) {
    Node *temp = head->next;  // 从头结点的下一个节点（也就是第一个数据节点）开始
    while (temp != NULL) {
        printf("%d ", temp->data);
        temp = temp->next;
    }
    printf("\n");
}

int main() {
    Node *head = create_list();  // 创建一个带头结点的链表

    insert_node_at_end(head, 1);
    insert_node_at_end(head, 2);
    insert_node_at_end(head, 3);

    print_list(head);  // 打印链表

    return 0;
}

跳表

跳表（Skip List）是一种高级数据结构，用于加速元素的查找操作，类似于平衡树，但实现更加简单。跳表通过层级结构在链表中添加索引层，从而在查找元素时可以跳过部分元素，提高查找效率。跳表通常用于需要快速查找和插入的数据结构，尤其在有序数据集上表现出色。

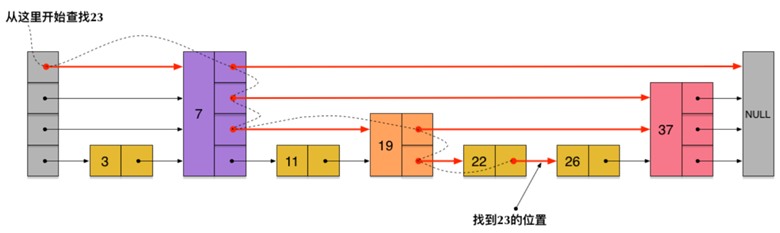
特点和属性：

• 层级结构： 跳表包含多个层级，每个层级是一个有序链表，其中底层链表包含所有元素。
• 索引节点： 在每个层级，跳表添加了一些额外的节点，称为索引节点，以加速查找。
• 快速查找： 查找元素时，跳表可以从顶层开始，根据元素值向右移动，然后下降到下一个层级继续查找。
• 高效插入和删除： 插入和删除元素时，跳表可以利用索引节点快速定位插入或删除位置。
• 平均查找时间： 在平均情况下，跳表的查找时间复杂度为O(log n)，其中n是元素数量。
• 可变高度： 跳表的高度可以根据需要调整，以适应元素的动态插入和删除。

跳表是一种强大的数据结构，适用于需要高效查找和插入操作的场景，例如数据库索引、缓存实现等。它在链表的基础上添加了多级索引，每级索引都是链表的一部分，搜索的效率达到了平均时间复杂度为O(logn)。以下是一个C语言实现的跳表：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// 跳表节点的最大层数
#define MAX_LEVEL 6

// 跳表节点结构体
typedef struct Node {
    int key;
    int value;
    struct Node* forward[MAX_LEVEL + 1];
} Node;

// 跳表结构体
typedef struct SkipList {
    Node* header;
    int level;
} SkipList;

Node* createNode(int level, int key, int value) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->key = key;
    newNode->value = value;
    for (int i = 0; i <= level; i++) {
        newNode->forward[i] = NULL;
    }
    return newNode;
}

SkipList* createSkipList() {
    SkipList* skiplist = (SkipList*)malloc(sizeof(SkipList));
    skiplist->header = createNode(MAX_LEVEL, 0, 0);
    skiplist->level = 1;
    return skiplist;
}

int randomLevel() {
    int level = 1;
    while (rand() < RAND_MAX / 2 && level < MAX_LEVEL) {
        level++;
    }
    return level;
}

void insert(SkipList* skiplist, int key, int value) {
    Node* update[MAX_LEVEL + 1];
    Node* x = skiplist->header;
    for (int i = skiplist->level; i >= 1; i--) {
        while (x->forward[i] != NULL && x->forward[i]->key < key) {
            x = x->forward[i];
        }
        update[i] = x;
    }
    int level = randomLevel();
    if (level > skiplist->level) {
        for (int i = skiplist->level + 1; i <= level; i++) {
            update[i] = skiplist->header;
        }
        skiplist->level = level;
    }
    x = createNode(level, key, value);
    for (int i = level; i >= 1; i--) {
        x->forward[i] = update[i]->forward[i];
        update[i]->forward[i] = x;
    }
}

int search(SkipList* skiplist, int key) {
    Node* x = skiplist->header;
    for (int i = skiplist->level; i >= 1; i--) {
        while (x->forward[i] != NULL && x->forward[i]->key < key) {
            x = x->forward[i];
        }
    }
    x = x->forward[1];
    if (x != NULL && x->key == key) {
        return x->value;
    } else {
        return -1;
    }
}

void display(SkipList* skiplist) {
    for (int i = 1; i <= skiplist->level; i++) {
        Node* x = skiplist->header->forward[i];
        printf("Level %d: ", i);
        while (x != NULL) {
            printf("(%d,%d) ", x->key, x->value);
            x = x->forward[i];
        }
        printf("\n");
    }
}

int main() {
    srand(time(NULL));
    SkipList* skiplist = createSkipList();
    for (int i = 1; i <= 15; i++) {
        insert(skiplist, i, i * 2);
    }
    display(skiplist);
    for (int i = 1; i <= 15; i++) {
        int value = search(skiplist, i);
        printf("Key: %d, Value: %d\n", i, value);
    }
    return 0;
}

链表的遍历

链表的遍历是链表操作中的一个基本技能，在实际编程中，我们需要知道如何遍历链表。下面介绍两种常见的遍历方法：迭代和递归。

迭代方式遍历链表

这种方式最常见，我们使用一个指针从头节点开始，依次访问每一个节点，直到遍历完所有的节点。

以下是使用C语言实现迭代方式遍历链表的代码：

#include <stdio.h>
#include <stdlib.h>

// 定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

// 迭代方式遍历链表
void printList(struct Node* node) {
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}

// 添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

// 主函数
int main()
{
    struct Node* head = NULL;
    for(int i = 5; i > 0; i--) {
        push(&head, i);
    }
    printList(head);
    return 0;
}

递归方式遍历链表

递归方式的基本思想是，我们首先处理当前节点，然后递归处理剩余的节点。

以下是使用C语言实现递归方式遍历链表的代码：

#include <stdio.h>
#include <stdlib.h>

// 定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

// 递归方式遍历链表
void printList(struct Node* node) {
    if (node == NULL) return;
    printf("%d ", node->data);
    printList(node->next);
}

// 添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

// 主函数
int main()
{
    struct Node* head = NULL;
    for(int i = 5; i > 0; i--) {
        push(&head, i);
    }
    printList(head);
    return 0;
}

链表的排序

在链表中进行排序是一个常见的问题，可以使用多种排序算法来解决，例如插入排序、归并排序等。

归并排序

归并排序是一种分治算法。对于链表，它首先将链表一分为二，然后对每一半进行排序，最后再把这两半进行合并。以下是一个简单的链表归并排序的C语言实现：

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int data;
    struct Node* next;
};

// 合并两个已排序的链表
struct Node* SortedMerge(struct Node* a, struct Node* b) {
    struct Node* result = NULL;
    if (a == NULL)
        return b;
    else if (b == NULL)
        return a;

    if (a->data <= b->data) {
        result = a;
        result->next = SortedMerge(a->next, b);
    } else {
        result = b;
        result->next = SortedMerge(a, b->next);
    }
    return result;
}

// 划分函数
void FrontBackSplit(struct Node* source,
                    struct Node** frontRef, struct Node** backRef) {
    struct Node* fast;
    struct Node* slow;
    if (source == NULL || source->next == NULL) {
        *frontRef = source;
        *backRef = NULL;
    } else {
        slow = source;
        fast = source->next;
        while (fast != NULL) {
            fast = fast->next;
            if (fast != NULL) {
                slow = slow->next;
                fast = fast->next;
            }
        }
        *frontRef = source;
        *backRef = slow->next;
        slow->next = NULL;
    }
}

// 主函数实现归并排序
void MergeSort(struct Node** headRef) {
    struct Node* head = *headRef;
    struct Node* a;
    struct Node* b;
    if ((head == NULL) || (head->next == NULL)) {
        return;
    }
    FrontBackSplit(head, &a, &b);
    MergeSort(&a);
    MergeSort(&b);
    *headRef = SortedMerge(a, b);
}

void printList(struct Node* node) {
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}

void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

int main() {
    struct Node* res = NULL;
    struct Node* a = NULL;
    push(&a, 15);
    push(&a, 10);
    push(&a, 5);
    push(&a, 20);
    push(&a, 3);
    push(&a, 2);
    MergeSort(&a);
    printf("Sorted Linked List is: \n");
    printList(a);
    return 0;
}

在这个代码中，MergeSort()是主函数，它接受一个链表的头指针的引用，并将链表排序。FrontBackSplit()和SortedMerge()是两个辅助函数，前者用于将链表一分为二，后者用于合并两个已排序的链表。

插入排序

插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。以下是链表插入排序的C语言实现：

#include <stdio.h>
#include <stdlib.h>

// 节点数据结构
struct Node {
    int data;
    struct Node* next;
};

// 节点插入函数
void sortedInsert(struct Node** head_ref, struct Node* new_node) {
    struct Node* current;
    /* 如果链表为空，或者新节点的值小于链表的第一个节点的值 */
    if (*head_ref == NULL || (*head_ref)->data >= new_node->data) {
        new_node->next = *head_ref;
        *head_ref = new_node;
    } else {
        /* 找到一个位置使得新节点的值大于位置前一个节点的值，但小于位置节点的值 */
        current = *head_ref;
        while (current->next != NULL && current->next->data < new_node->data) {
            current = current->next;
        }
        new_node->next = current->next;
        current->next = new_node;
    }
}

// 插入排序函数
void insertionSort(struct Node** head_ref) {
    struct Node* sorted = NULL;
    struct Node* current = *head_ref;
    while (current != NULL) {
        struct Node* next = current->next;
        sortedInsert(&sorted, current);
        current = next;
    }
    *head_ref = sorted;
}

// 打印链表函数
void printList(struct Node* head) {
    while (head != NULL) {
        printf("%d ", head->data);
        head = head->next;
    }
}

// 构造新节点函数
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

// 主函数
int main() {
    struct Node* a = NULL;
    push(&a, 5);
    push(&a, 20);
    push(&a, 4);
    push(&a, 3);
    push(&a, 30);
    printf("Linked List before sorting \n");
    printList(a);
    insertionSort(&a);
    printf("\nLinked List after sorting \n");
    printList(a);
    return 0;
}

在这个代码中，首先创建了一个待排序的链表，然后调用insertionSort()函数进行排序。排序函数通过反复调用sortedInsert()函数，将原链表中的每个节点按照正确的顺序插入到新链表中。最后，打印出排序后的链表。

链表的反转

反转链表是数据结构中的常见问题，下面给出反转单链表和双链表的方法。

反转单链表

为了反转单链表，我们需要维护三个指针，一个指向当前节点，一个指向前一个节点，一个指向下一个节点。

以下是使用C语言实现反转单链表的代码：

#include <stdio.h>
#include <stdlib.h>

// 定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

// 反转单链表
void reverse(struct Node** head_ref) {
    struct Node* prev   = NULL;
    struct Node* current = *head_ref;
    struct Node* next;
    while (current != NULL) {
        next  = current->next;
        current->next = prev;  
        prev = current;
        current = next;
    }
    *head_ref = prev;
}

// 添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data  = new_data;
    new_node->next = (*head_ref);  
    (*head_ref)    = new_node;
}

// 主函数
int main() {
    struct Node* head = NULL;
    for(int i = 5; i > 0; i--) {
        push(&head, i);
    }
    reverse(&head);
    // 遍历打印链表
    // ...
    return 0;
}

反转双链表

对于双链表，我们只需要遍历一次链表，然后交换每个节点的前后指针即可。

以下是使用C语言实现反转双链表的代码：

#include <stdio.h>
#include <stdlib.h>

// 定义双链表的节点
struct Node {
    int data;
    struct Node* next;
    struct Node* prev;
};

// 反转双链表
void reverse(struct Node** head_ref) {
    struct Node* temp = NULL;
    struct Node* current = *head_ref;
    while (current !=  NULL) {
       temp = current->prev;
       current->prev = current->next;
       current->next = temp;               
       current = current->prev;
    }     
    if(temp != NULL )
        *head_ref = temp->prev;
}

// 添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data  = new_data;
    new_node->next = (*head_ref); 
    new_node->prev = NULL; 
    if((*head_ref) != NULL)  (*head_ref)->prev = new_node;
    (*head_ref)    = new_node;
}

// 主函数
int main() {
    struct Node* head = NULL;
    for(int i = 5; i > 0; i--) {
        push(&head, i);
    }
    reverse(&head);
    // 遍历打印链表
    // ...
    return 0;
}

在这些代码中，reverse()函数用来反转链表。在主函数中，我们创建了一个链表，然后调用reverse()函数来反转链表。

链表的合并

链表合并是另一种常见的操作，通常涉及将两个已排序的链表合并成一个新的有序链表。以下是使用C语言实现的一个简单示例：

#include <stdio.h>
#include <stdlib.h>

struct Node {
    int data;
    struct Node* next;
};

struct Node* sortedMerge(struct Node* a, struct Node* b) {
    struct Node* result = NULL;
    // 基本的递归处理
    if (a == NULL)
        return b;
    else if (b == NULL)
        return a;

    if (a->data <= b->data) {
        result = a;
        result->next = sortedMerge(a->next, b);
    } else {
        result = b;
        result->next = sortedMerge(a, b->next);
    }
    return result;
}

void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

void printList(struct Node* node) {
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}

int main() {
    struct Node* res = NULL;
    struct Node* a = NULL;
    struct Node* b = NULL;

    push(&a, 15);
    push(&a, 10);
    push(&a, 5);

    push(&b, 20);
    push(&b, 3);
    push(&b, 2);

    res = sortedMerge(a, b);

    printf("Merged Linked List is: \n");
    printList(res);

    return 0;
}

在这个代码中，sortedMerge()函数是关键，它通过递归的方式合并两个已排序的链表。push()函数用来向链表添加新的元素，printList()函数用来打印链表。在main()函数中，创建了两个已排序的链表，然后调用sortedMerge()函数进行合并，并打印出合并后的结果。

链表中的问题解决

寻找链表的中间节点

为了找到链表的中间节点，我们可以使用两个指针，一个快指针和一个慢指针。快指针每次移动两个节点，而慢指针每次移动一个节点。当快指针到达链表的末尾时，慢指针将指向链表的中间节点。

以下是使用C语言实现此策略的代码：

#include <stdio.h>
#include <stdlib.h>

//定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

void printMiddle(struct Node* head) {
    struct Node* slow_ptr = head;
    struct Node* fast_ptr = head;

    if (head != NULL) {
        while (fast_ptr != NULL && fast_ptr->next != NULL) {
            fast_ptr = fast_ptr->next->next;
            slow_ptr = slow_ptr->next;
        }
        printf("The middle element is [%d]\n", slow_ptr->data);
    }
}

//添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

//主函数
int main() {
    struct Node* head = NULL;
    int i;
    for (i = 5; i > 0; i--) {
        push(&head, i);
    }
    printMiddle(head);
    return 0;
}

在这段代码中，printMiddle()函数用来找到并打印链表的中间元素。我们在主函数中创建了一个包含5个元素的链表，然后调用printMiddle()函数来找出中间的元素。

检测链表是否有环

为了检测链表是否有环，我们可以使用一个快指针和一个慢指针。如果链表中存在环，那么快指针最终将追上慢指针；如果链表没有环，快指针将到达链表的末尾。

以下是使用C语言实现此策略的代码：

#include <stdio.h>
#include <stdlib.h>

//定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

//检测链表是否有环
int hasCycle(struct Node* head) {
    struct Node* slow_ptr = head;
    struct Node* fast_ptr = head;
    while(slow_ptr && fast_ptr && fast_ptr->next) {
        slow_ptr = slow_ptr->next;
        fast_ptr = fast_ptr->next->next;
        if(slow_ptr == fast_ptr){
            return 1; //存在环
        }
    }
    return 0; //不存在环
}

//添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

//主函数
int main() {
    struct Node* head = NULL;
    push(&head, 1);
    push(&head, 2);
    push(&head, 3);
    push(&head, 4);
    push(&head, 5);

    // 创建环
    head->next->next->next->next = head;

    if(hasCycle(head)) {
        printf("Loop found\n");
    } else {
        printf("No Loop\n");
    }

    return 0;
}

在这段代码中，hasCycle()函数用来检测链表是否有环。在主函数中，我们创建了一个链表并添加了一个环，然后调用hasCycle()函数来检测链表是否存在环。

寻找环的入口点

在确定链表中存在环之后，我们可以找到环的入口点。为了做到这一点，我们可以使用两个指针。当快慢指针在环内相遇后，我们可以将其中一个指针移到链表的头部，然后以相同的速度移动这两个指针。当它们再次相遇时，相遇的点就是环的入口。

以下是使用C语言实现此策略的代码：

#include <stdio.h>
#include <stdlib.h>

// 定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

// 寻找环的入口
struct Node* detectCycle(struct Node* head) {
    struct Node *slow = head, *fast = head;
    while(fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast) {
            slow = head;
            while(slow != fast) {
                slow = slow->next;
                fast = fast->next;
            }
            return slow;
        }
    }
    return NULL;
}

// 添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

// 主函数
int main() {
    struct Node* head = NULL;
    struct Node* entrance = NULL;
    push(&head, 1);
    push(&head, 2);
    push(&head, 3);
    push(&head, 4);
    push(&head, 5);

    // 创建环
    head->next->next->next->next = head;

    entrance = detectCycle(head);

    if(entrance != NULL) {
        printf("Cycle entrance is %d\n", entrance->data);
    } else {
        printf("No Cycle\n");
    }

    return 0;
}

在这段代码中，detectCycle()函数用来寻找链表环的入口。在主函数中，我们创建了一个链表并添加了一个环，然后调用detectCycle()函数来找出环的入口节点。

寻找链表的倒数第k个节点

可以使用两个指针，首先将一个指针向前移动k个节点，然后同时移动这两个指针，当前面的指针到达链表的末尾时，后面的指针就是链表的倒数第k个节点。

为了找到链表的倒数第k个节点，我们可以使用两个指针，两个指针之间的距离保持为k。首先，我们将第一个指针移动k个节点；然后，我们同时移动两个指针，当第一个指针到达链表的末尾时，第二个指针将指向链表的倒数第k个节点。

以下是使用C语言实现此策略的代码：

#include <stdio.h>
#include <stdlib.h>

//定义链表的节点
struct Node {
    int data;
    struct Node* next;
};

//找到链表的倒数第k个节点
struct Node* findKthToLast(struct Node* head, int k) {
    struct Node* first = head;
    struct Node* second = head;
    for(int i = 0; i < k; i++) {
        if(first == NULL) return NULL; // 如果k大于链表的长度
        first = first->next;
    }
    while(first != NULL) {
        first = first->next;
        second = second->next;
    }
    return second;
}

//添加新节点到链表头部
void push(struct Node** head_ref, int new_data) {
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}

//主函数
int main() {
    struct Node* head = NULL;
    struct Node* kth;
    for(int i = 5; i > 0; i--) {
        push(&head, i);
    }
    kth = findKthToLast(head, 2); // 找到倒数第2个节点
    if(kth != NULL)
        printf("The value of 2nd to the last node is %d\n", kth->data);
    else
        printf("The value is not found\n");
    return 0;
}

在这段代码中，findKthToLast()函数用来找到链表的倒数第k个节点。我们在主函数中创建了一个含有5个元素的链表，然后调用findKthToLast()函数来找出倒数第2个元素。

链表的应用

链表是一种非常重要的数据结构，在实际问题中有广泛的应用。以下是一些常见的应用案例：

• 动态内存分配：链表在动态内存分配中被广泛使用，它可以帮助我们以非连续的方式存储数据。
• 执行操作系统进程：在操作系统中，链表被用于执行进程。操作系统需要保持对进程的跟踪，因此它使用链表来存储和操作这些进程。
• 图形模型：在计算机图形学中，链表被用于存储和操作像素。此外，它还被用于实现多边形网格模型和边界表示法。
• 散列表：散列表是一种常见的数据结构，它通过哈希函数将键映射到存储桶。在处理哈希冲突时，链表被用于存储在同一哈希桶中的所有元素。
• 多项式运算：链表在计算机科学中的另一个重要应用是在表示和处理多项式。我们可以使用链表来存储多项式的系数和指数，然后使用链表来执行多项式的运算，如加法和乘法。
• 网页浏览器历史：链表被用于实现浏览器的前进和后退功能，每个节点都存储一个访问过的网页记录。

这只是链表在实际问题中应用的一部分例子，它在许多其他场景中也同样有着广泛的应用。由于链表的灵活性和动态性，我们可以根据需要在程序运行时创建和修改链表，这使得它在解决许多实际问题中显得非常有用。