C语言学习之数组

在C语言中，数组是由相同类型的数据元素构成的数据结构。这些元素在内存中连续存放，每个元素都可以通过索引（数组下标）进行访问。

下面是在学习和使用数组时需要注意的一些重要知识点：

• 数组的声明：C语言中的数组必须在声明时指定其大小，并且此大小必须是常量表达式。
• 数组的初始化：可以在声明数组时立即初始化它。初始化数组的元素数量可以少于数组的大小，这样，剩余的元素将自动初始化为0。如果初始化的元素数量大于声明的数组大小，编译器会报错。
• 数组的索引：数组索引从0开始，这是一个在新手中常见的错误源。如果尝试访问超出数组大小的索引，C语言不会报错，但会导致未定义的行为。
• 数组的大小：C语言不提供直接获取数组大小的函数。通常我们可以通过 sizeof(array)/sizeof(array[0]) 来计算数组长度。
• 多维数组：C语言支持多维数组。对于二维数组，可以看作是数组的数组，例如，可以用来表示矩阵。
• 数组和指针：在C语言中，数组名实际上是指向数组第一个元素的指针。但是，必须注意数组名不是变量，不能对其进行赋值操作。
• 数组作为函数参数：当数组作为函数参数时，实际上传递的是指向数组第一个元素的指针，而不是整个数组。因此，函数中不能通过 sizeof 操作符获取数组的大小。

以上就是C语言中关于数组的一些重要知识点，理解和掌握这些，对于学习和使用C语言将非常有帮助。

C语言数组简介

C 语言支持数组数据结构，它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据，但它往往被认为是一系列相同类型的变量。

数组是类型相同的数据元素的集合，是C语言中的一种构造数据类型，这些元素会顺序地储存在内存的某段区域。

数组的特点

• 数组是一种引用类型数据，存放在内存中。
• 数组当中存放多个数据（元素），类型必须统一。（如果定义的是int类型，那么里面的所有元素都必须是int类型）
• 数组的长度在运行当中不允许改变。（定义的数组元素个数在运行的过程当中不允许改变）

数组的声明并不是声明一个个单独的变量，比如 varName0、varName1、…、varName99，而是声明一个数组变量，比如 varName，然后使用 varName[0]、varName[1]、…、varName[98] 来代表一个个单独的变量。所有的数组都是由连续的内存位置组成。最低的地址对应第一个元素，最高的地址对应最后一个元素。

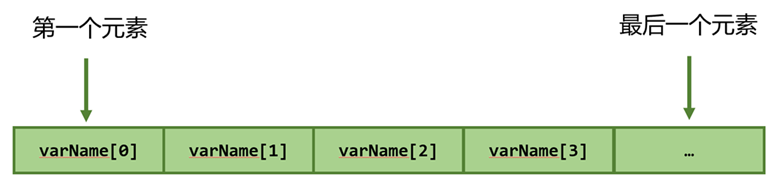
数组中的特定元素可以通过索引访问，第一个索引值为 0。(C 语言还允许我们使用指针来处理数组，这使得对数组的操作更加灵活和高效。)

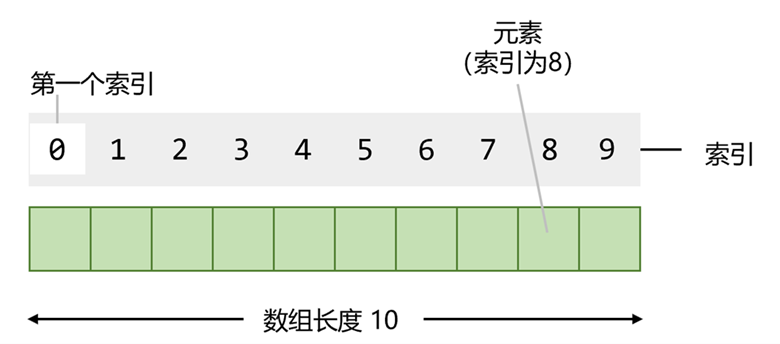
数组是一种基本的数据结构，用于在单一名称下存储固定大小的相同类型数据元素序列。它们在程序设计中广泛使用，尤其是在C语言等低级编程语言中。以下是数组的一些主要优缺点：

优点

• 随机访问：数组提供了快速访问任何位置的元素的能力，因为它们允许通过索引直接访问。这使得访问速度非常快，时间复杂度为O(1)。
• 高效的内存利用：由于数组在内存中是连续存放的，因此可以高效利用缓存，减少访问时间。
• 简单易用：数组的概念非常简单，使用它们来存储和访问数据很直观，对于初学者来说很容易理解和实现。
• 适合于固定大小的数据结构：对于已知数量的元素，数组是一个非常好的选择。
• 基础构建块：数组是许多其他复杂数据结构（如堆、哈希表等）的基础，是学习这些高级结构的基石。

缺点

• 固定大小：一旦创建，数组的大小就固定了，不能动态增加或减少元素。这限制了它的使用，尤其是在不确定数据集大小的场合。
• 内存浪费或不足：如果预留的空间没有完全用完，会造成内存浪费；如果数据过多，超出了预先分配的空间，则无法再添加新的元素，除非创建一个更大的数组并将原数据复制过去，这个过程中会有性能损失。
• 不提供直接的元素插入和删除操作：在数组中插入或删除元素通常需要移动其余的元素以维护连续的存储，这可能是一个高成本的操作，特别是对于大型数组。
• 缺乏灵活性：与一些动态数据结构（如链表、动态数组等）相比，数组在处理大小不确定的数据集时显得不够灵活。

综上所述，数组在特定情况下非常有用，特别是当数据集的大小事先已知且不需要动态变化时。然而，对于需要高度动态数据操作的场景，可能需要考虑使用其他数据结构，如链表、栈、队列或动态数组等，它们提供了更大的灵活性和动态内存管理能力。

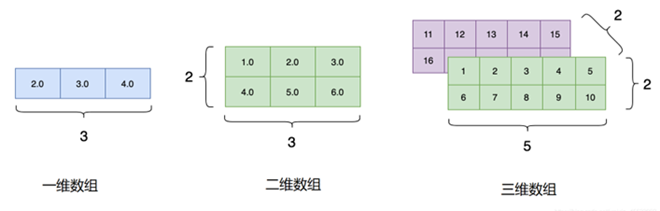
一维数组

声明数组

数组和普通的变量一样，在 C语言中必须先定义（称作声明数组）才能使用。

数组的声明和变量的定义是一样的，需要指定数据类型，并取一个唯一的名字（数组名），不同之处在于，数组名后紧跟方括号[],并且在方括号里面给出该数组所包含元素的总数（也称为数组大小）

在 C 中要声明一个数组，需要指定元素的类型和元素的数量，如下所示：

type arrayName[arraySize];

这叫做一维数组。arraySize 必须是一个大于零的整数常量，type 可以是任意有效的 C 数据类型。例如，要声明一个类型为 double 的包含 10 个元素的数组 balance，声明语句如下：

double balance[10];

现在 balance 是一个可用的数组，可以容纳 10 个类型为 double 的数字。

初始化数组

一维数组静态初始化

前面讲过一种数组初始化方式，定义数组时，使用初始化列表进行初始化。例如：

int a[3]={1,2,3};

这种方式被称为静态初始化，定义数组的同时完成初始化。

一维数组动态初始化

除了静态初始化，C 语言还提供了另外一种初始化数组的方式，例如：

int a[3]; //定义数组，但未初始化
a[0] =1; //初始化 a[0]
a[1] =2; //初始化 a[1]
a[2] =3; //初始化 a[2]

这种方式被称为动态初始化，先定义数组，然后分别对每个元素进行初始化。

一维数组部分初始化

数组部分初始化指的是只对数组一部分元素进行初始化，例如：

int a[5]={1,2,3};

在[ ]中指定数组长度为 5，但{ }中只对前 3 个元素初始化，系统会自动将剩下的元素初始化为 0。

数组一次性赋值为 0

在 C 语言中，如果想给数组全部赋值为 0，一般写法为：

int a[5]={0,0,0,0,0};

除了这种传统的写法，还可以写成：

int a[5]={0};

系统会将剩下的数组元素都赋值为 0，这种写法比较简洁。其实这种由“一维数组部分初始化”演变来的。

定义数组时，不指定数组长度

在 C 语言中，对数组进行静态初始化时，可以不指定数组长度，编译器会根据初始化列表计算出数组长度，例如：

int a[5]={1,2,3,4,5};

可以写为：

int a[ ]={1,2,3,4,5};

[]中虽然没有指定数组长度，但系统会根据{ }中数据的个数确定数组 a 长度为 5。

访问数组元素

数组的元素指的就是数组里面单个的数据。数组实际上是由多个变量排列而成的，因而数组的元素也就是组成数组的单个变量。

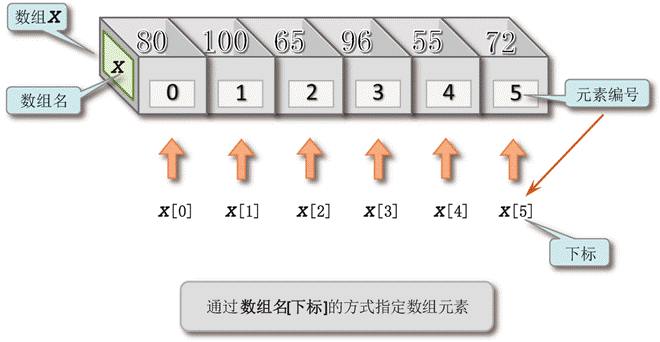
在 C语言中，用数组名 [下标]的方式来指定数组中的某个元素，这里的下标指的就是如图中数组 X 当中的元素编号，C语言的元素编号是从 0 开始的自然数序列号。如要获得数组 X 中的数据 100，就可以用 X[1] 来表示，读作“X 下标 1”或“X1”。对数组当中某个数据的获取和使用我们称为数组数据的引用。

比如图 2 中的数组 X，其中：

• X[0] 表示存储在 X 数组中下标（元素编号）为 0 的元素（即第 1 个数据 80）；
• X[1] 表示存储在 X 数组中下标（元素编号）为 1 的元素（即第 2 个数据 100）；
• X[2] 表示存储在 X 数组中下标（元素编号）为 2 的元素（即第 3 个数据 65）；
• X[3] 表示存储在 X 数组中下标（元素编号）为 3 的元素（即第 4 个数据 96）；
• ……

获取数组长度

C语言并没有直接提供获取数组长度的函数。通常我们可以通过 sizeof(array)/sizeof(array[0]) 来计算数组长度。例如：

#include <stdio.h>

int main() {
    int array[] = {1, 2, 3, 4, 5};
    int length = sizeof(array) / sizeof(array[0]);

    printf("数组长度为: %d\n", length);

    return 0;
}

也可以使用宏定义：

#include <stdio.h>

#define LENGTH(array) (sizeof(array) / sizeof(array[0]))

int main() {
    int array[] = {1, 2, 3, 4, 5};
    int length = LENGTH(array);

    printf("数组长度为: %d\n", length);

    return 0;
}

一维数组的遍历

在C语言中，遍历一维数组可以使用for循环。下面是一个基本的示例：

#include <stdio.h>

int main() {
    int nums[] = {1, 2, 3, 4, 5};  // 定义一个一维数组
    int size = sizeof(nums) / sizeof(nums[0]); // 计算数组的长度

    for (int i = 0; i < size; i++) {  // 遍历数组
        printf("%d\n", nums[i]);  // 打印当前元素
    }

    return 0;
}

在这个例子中，sizeof(nums) / sizeof(nums[0])是用来计算数组长度的一种常用方法，它的含义是“数组总字节大小/数组中单个元素的字节大小”，结果就是数组的长度。然后使用for循环遍历数组中的每一个元素。

二维数组与多维数组

C语言支持多维数组。最常见的是二维数组，它可以看作是数组的数组。二维数组通常用于存储表格数据。

例如，可以这样声明一个二维数组：

int twoD_arr[2][3];

二维数组的引用

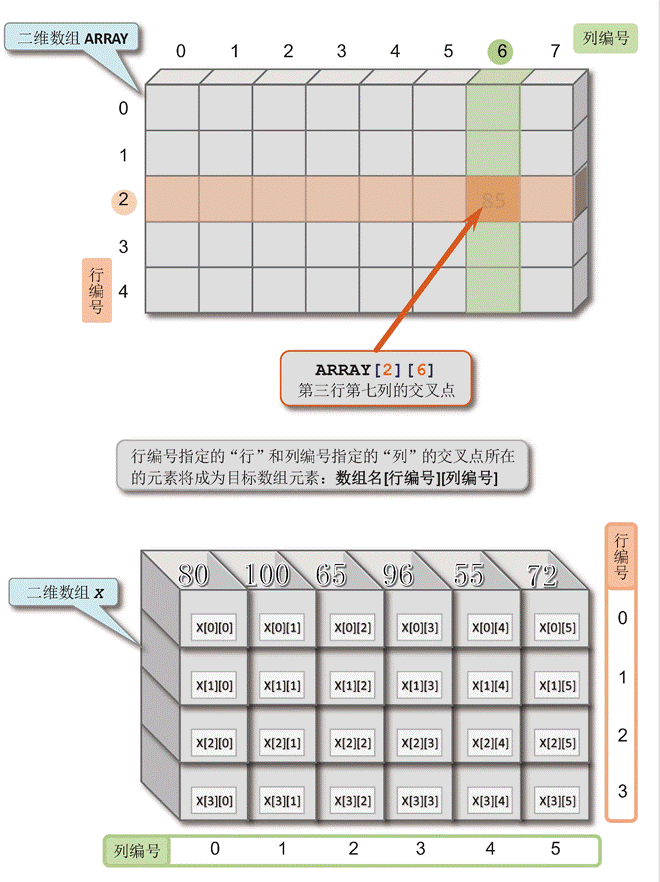
二维数组用两个下标来指定和引用数组元素，第一个下标表示元素所在的行编号，第二个下标表示元素所在的列编号。在“行”和“列”的交叉处所在的元素就是指定的数组元素。

为了访问二维数组中的某一个特定元素（引用），我们利用数组名和元素行编号与列编号的组合来指定具体的数组元素：数组名[行编号][列编号]

譬如，把二维数组 ARRAY 中行编号为 2，列编号为 6 的特定数组元素表示为：ARRAY [2] [6]

C语言中，二维数组的行编号和列编号都是从 0 开始的自然数序列号。因而 ARRAY [2] [6] 中的行编号 2 表示ARRAY数组的第 3 行，列编号 6 表示 ARRAY 数组的第 7 列（见图 4），这样 ARRAY [2] [6] 则为 ARRAY 数组的第 3 行第 7 列交叉位置的数组元素。

二维数组的创建

二维数组在一维数组的基础上加入了 行 和 列 的概念，创建的语法如下：

type_t arr_name [const_line][const_column];

• type_t 是指数组的元素类型
• arr_name 是数组的名字
• const_line数组每行的元素个数
• const_column数组每列的元素个数

二维数组的初始化

二维数组在初始化时可以省略行，但不能省略列，整形二维数组如果没完全初始化，则会自动初始化为 0；

代码示例：

int main()
{
  int arr1[3][4] = {1,2,3,4};
  int arr2[3][4] = {{1,2},{4,5}};
  int arr3[][4] = {{2,3},{4,5}};
  return 0;
}

二维数组的长度

在C语言中，获取二维数组的行数和列数可以通过sizeof运算符来实现。对于二维数组int nums[2][3]，获取行数和列数的方法如下：

int rows = sizeof(nums) / sizeof(nums[0]);     // 获取行数
int cols = sizeof(nums[0]) / sizeof(nums[0][0]); // 获取列数

• sizeof(nums)获取的是整个数组的大小（以字节为单位）。
• sizeof(nums[0])获取的是数组中第一行（也就是一个子数组）的大小（以字节为单位）。
• sizeof(nums[0][0])获取的是数组中一个元素的大小（以字节为单位）。

通过整个数组的大小除以一个子数组的大小，就可以得到行数；通过一个子数组的大小除以一个元素的大小，就可以得到列数。

注意：这种方法只适用于在定义数组的同一作用域内获取数组的长度。如果你将数组作为函数的参数进行传递，那么这种方法就不能用了，因为传递的实际上是一个指向数组的指针，这时候需要在参数中显式地指定数组的大小。

二维数组的遍历

在C语言中，遍历二维数组需要使用两层for循环，一层用于遍历行，另一层用于遍历列。下面是一个基本示例：

#include <stdio.h>

int main() {
    int nums[2][3] = {{1, 2, 3}, {4, 5, 6}};  // 定义一个二维数组

    // 使用嵌套的for循环遍历数组
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 3; j++) {
            printf("%d ", nums[i][j]);  // 打印当前元素
        }
        printf("\n"); // 每遍历完一行后换行
    }

    return 0;
}

数组与字符串

在 C 语言中，字符串应用的非常广泛，但是却没有字符串类型。为了解决这个问题，C语言使用字符数组来存储字符串。

字符串与字符串结束标志

在 C 语言中没有专门定义字符串类型，通常使用字符数组来存储字符串。由于字符串也采用字符数组进行存储，为了区分普通字符数组和字符串，C 语言规定以字符’\0’作为字符串结束标志。例如：

char c[ ]={‘h’,’e’,’l’,’l’,’o’};

以上字符数组中没有’\0’表示是普通的字符数组。

char c[ ]= {‘h’,’e’,’l’,’l’,’o’,’
char c[ ]= {‘h’,’e’,’l’,’l’,’o’,’\0’};
’};

以上字符数组以字符’\0’结束表示是字符串。

分析程序中内存的分布，思考为什么需要’\0’作为结束标志。

除了以上初始化方式，也可以采用字符串对字符数组进行初始化，例如：

char c[ ]=“hello”;

使用字符串方式进行赋值时，系统会自动在字符串末尾添加’\0’。

通过对比可以发现，使用字符串初始化更加简洁、而且无需指定字符数组长度，系统会自动计算字符串长度并且添加’\0’。

’\0’注意事项

在 C 语言中，采用’\0’作为字符串结束标志，当系统读取到’\0’时，认为字符串结束，’\0’之后的内容将不再读取。因此，通常将’\0’添加在字符串末尾，保证字符串完整输出。

不过需要注意的是，’\0’其实可以添加在字符串任意位置上，例如：

char c[ ]={'h','e','
char c[ ]={'h','e','\0','l','l','o','\0'};
','l','l','o','
char c[ ]={'h','e','\0','l','l','o','\0'};
'};

或

char c[ ]=”he
char c[ ]=”he\0llo”;
llo”;

在字符串中‘\0’可以省略单引号，直接写为\0。

下面通过例子了解一下’\0’的作用。

#include<stdio.h>
int main()
{
    char chs1[ ]={'h','e','
#include<stdio.h>
int main()
{
char chs1[ ]={'h','e','\0','l','l','o','\0'};
char chs2[ ]="he\0llo";
printf("%s\n",chs1);
printf("%s\n",chs2);
getchar();
return 0;
}
//输出结果
//he
//he
','l','l','o','
#include<stdio.h>
int main()
{
char chs1[ ]={'h','e','\0','l','l','o','\0'};
char chs2[ ]="he\0llo";
printf("%s\n",chs1);
printf("%s\n",chs2);
getchar();
return 0;
}
//输出结果
//he
//he
'};
    char chs2[ ]="he
#include<stdio.h>
int main()
{
char chs1[ ]={'h','e','\0','l','l','o','\0'};
char chs2[ ]="he\0llo";
printf("%s\n",chs1);
printf("%s\n",chs2);
getchar();
return 0;
}
//输出结果
//he
//he
llo";
    printf("%s\n",chs1);
    printf("%s\n",chs2);
    getchar();
    return 0;
}
//输出结果
//he
//he

以%s 格式分别输出字符串，可以看到只输出了”he”。这是因为当系统读取到’e’后面的’\0’时，就认为字符串结束了，后面的内容不再读取，因此只输出”he”。

像 printf 等函数处理字符串的时候通常都是“不见\0 不死心”，因此使用字符串的时候一定不要忘了结尾的\0。

下面的代码：

#include<stdio.h>

int main() {
    char c1[] = {'a', 'b'};
    printf("%s", c1);
    getchar();
    return 0;
}

可能就会输出：

//ab帑¬煀

因为 c1 没有以’\0’结尾，printf 就一直读，读到了其他的内存空间。

sizeof

由于字符串底层采用字符数组进行存储，因此计算字符串长度，等价于计算字符串转化为字符数组后字符数组的长度，例如：

char c[ ]="hello";

上述代码，经过编译后，会转化为以下字符数组形式：

char c[ ]={'h','e','l','l','o','
char c[ ]={'h','e','l','l','o','\0'};
'};

前面讲过数组长度计算方式对于计算字符串长度同样适用，例如：

int length=sizoef(c)/sizeof(c[0]);

下面通过例子来了解一下。

#include<stdio.h>
int main()
{
    char c1[ ]={'h','e','l','l','o','
#include<stdio.h>
int main()
{
char c1[ ]={'h','e','l','l','o','\0'};
char c2[ ]="hello";
int length1=sizeof(c1)/sizeof(c1[0]);
int length2=sizeof(c2)/sizeof(c2[0]);
printf("%d\n",length1);
printf("%d\n",length2);
getchar();
return 0;
}
/* 运行结果
6
6
*/
'};
    char c2[ ]="hello";
    int length1=sizeof(c1)/sizeof(c1[0]);
    int length2=sizeof(c2)/sizeof(c2[0]);
    printf("%d\n",length1);
    printf("%d\n",length2);
    getchar();
    return 0;
}

/* 运行结果
6
6
*/

strlen

在 C 语言中，字符串有效长度指的是字符串中’\0’之前的字符个数，不包括’\0’。例如：

char c1[ ]={'h','e','l','l','o','
char c1[ ]={'h','e','l','l','o','\0'};
'};

c1 字符串有效长度为 5，不包括最后的’\0’。

char c2[ ]="hello";

c2 字符串有效长度为 5，不包括系统自动添加的’\0’。

在实际开发中，为了快速计算字符串有效长度，可以使用 C 语言标准库提供的 strlen 函数。

#include<stdio.h>
#include<string.h>

int main() {
    char c1[] = {'h', 'e', 'l', 'l', 'o', '
#include<stdio.h>
#include<string.h>
int main() {
char c1[] = {'h', 'e', 'l', 'l', 'o', '\0'};
char c2[] = "hello";
int length1 = strlen(c1);
int length2 = strlen(c2);
printf("%d\n", length1);
printf("%d\n", length2);
getchar();
return 0;
}
/* 运行结果
5
5
*/
'};
    char c2[] = "hello";
    int length1 = strlen(c1);
    int length2 = strlen(c2);
    printf("%d\n", length1);
    printf("%d\n", length2);
    getchar();
    return 0;
}
/* 运行结果
5
5
*/

需要注意的是，strlen 函数内部只会计算字符串中’\0’之前的字符个数，’\0’及之后的字符将被忽略。例如：

char c1[ ]="he
char c1[ ]="he\0llo";
llo";

c1 有效字符串长度为 2，只包含\0 之前的字符个数。

下面通过例子来了解一下

#include<stdio.h>
#include<string.h>

int main()
{
    char c1[ ]="he
#include<stdio.h>
#include<string.h>
int main()
{
char c1[ ]="he\0llo";
int len=strlen(c1);
printf("%d\n",len);
getchar();
return 0;
}
/* 运行结果
2
*/
llo";
    int len=strlen(c1);
    printf("%d\n",len);
    getchar();
    return 0;
}

/* 运行结果
2
*/

中文字符串长度

在C语言中，中文字符的长度取决于其编码方式。现在主要使用的编码方式是UTF-8编码和GB2312编码。

• UTF-8编码: 在UTF-8编码中，中文字符通常使用3个字节表示。UTF-8是一种可变长度的编码方式，英文字符使用1个字节，欧洲的一些其他字符使用2个字节，大多数中文字符使用3个字节，某些特殊字符使用4个字节。
• GB2312编码: 在GB2312编码中，中文字符使用2个字节表示。GB2312编码是中国大陆在较早时期广泛使用的一种编码方式，它包含了汉字和一些英文字符及符号。

在处理中文字符时，需要注意的是C语言的标准库函数（例如strlen）通常无法正确处理中文字符。例如，使用strlen函数计算一个中文字符串的长度时，返回的结果可能并不是你期望的那样。这是因为这些函数是按照字节处理字符串的，而不是按照字符，对于它们来说，一个中文字符可能就是两个或者三个字节长的字符串。

#include<stdio.h>

int main() {
    char c1[] = "标点符";
    int size1 = sizeof(c1);
    printf("size1=%d\n", size1);
    getchar();
    return 0;
}

如果需要处理中文字符，可能需要使用一些特殊的库，如iconv或者C++的std::wstring等，或者使用支持Unicode的语言，如Java、Python等。

iconv 库是一个用于实现字符集转换的库，在处理多语言文本，特别是需要计算特定编码下字符长度时非常有用。如果你希望使用 iconv 来计算中文字符的长度，实际操作中更多的是通过转换编码来计算特定编码下的字节数，而不是直接计算”字符”的长度，因为在不同编码下，字符长度的概念会有所不同。

下面是一个使用 iconv 来转换字符编码并计算转换后的字节数（可以间接看作特定编码下的字符长度）的示例：

首先，确保你的系统安装了iconv。在Linux系统上，通常iconv已经预装；如果没有，可以通过包管理器安装。

以下是一个简单的示例代码，展示如何使用 iconv 将一个UTF-8编码的字符串转换成GB2312编码，并计算转换后（即GB2312编码下）的字节数。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iconv.h>

size_t convert_charset(char *from_charset, char *to_charset, char *inbuf, size_t inlen, char *outbuf, size_t outlen) {
    iconv_t cd;
    char **pin = &inbuf;
    char **pout = &outbuf;

    cd = iconv_open(to_charset, from_charset);
    if (cd == (iconv_t)-1) {
        perror("iconv_open");
        return 0;
    }
    memset(outbuf, 0, outlen);
    if (iconv(cd, pin, &inlen, pout, &outlen) == (size_t)-1) {
        perror("iconv");
        return 0;
    }
    iconv_close(cd);
    return outlen;
}

int main() {
    char *in_utf8 = "中文字符";  // UTF-8编码的字符串
    char out_gb2312[32];  // 准备足够大的缓冲区存储转换后的字符串
    size_t inlen = strlen(in_utf8);
    size_t outlen = sizeof(out_gb2312);

    // 将 UTF-8 编码的字符串转换为 GB2312 编码
    size_t result = convert_charset("UTF-8", "GB2312", in_utf8, inlen, out_gb2312, outlen);

    if (result > 0) {
        printf("转换后的GB2312编码字节数: %zu\n", sizeof(out_gb2312) - result);
    } else {
        printf("转换失败\n");
    }

    return 0;
}

这段代码首先定义了一个convert_charset函数，用于执行实际的编码转换操作，然后在main函数中调用这个函数将一个UTF-8编码的中文字符串转换为GB2312编码，并打印转换后的字节数。

注意：

• 这个示例假设你的输入字符串是有效的UTF-8编码，并且你希望将其转换为GB2312编码。在实际应用中，你可能需要根据实际情况调整这些参数。
• iconv函数的使用可能因系统而异，确保检查你的系统文档以获取更详细的信息。

字符串元素遍历

在 C 语言中，字符串本质上就是以’\0’结尾的字符数组。同理，字符数组也可以使用 for循环进行遍历。

由于字符’\0’是控制字符，无法在控制台中显示。但是为了让读者感受到字符串末尾确实有’\0’的存在，以下代码中，分别使用%d、%c 格式输出数组元素

示例代码如下：

#include<stdio.h>

int main() {
    char c[] = "hello";
    int i;
    int length = sizeof(c) / sizeof(c[0]); //计算字符串长度
    for (i = 0; i < length; i++) {
        printf("%c ", c[i]);
        printf("%d\n", c[i]); //输出字符 ASCII 码
    }
    getchar();
    return 0;
}

运行结果如下：

h 104
e 101
l 108
l 108
o 111
  0

char* 方式引用字符串

在 C 语言中，字符串存储的方式只有一种，采用字符数组格式进行存储。但是引用的方式却有两种，除了前面介绍的字符数组方式，还可以定义 char*类型的变量进行引用。例如：

char *string = "biaodianfu";

以上代码表示，定义 char*类型变量 string，并使用字符串进行初始化。这涉及到后续讲的“指针”的问题。

#include<stdio.h>

int main() {
    char *string = "hello";
    printf("%s", string);
    getchar();
    return 0;
}

但是注意用 char*方式引用字符串的时候不能用 sizeof 算字符串的长度。

数组名与指针

C语言数组名

在C语言中，数组名代表的是数组第一个元素的地址。举个例子，如果你有一个数组int arr[10];，那么表达式arr在大多数上下文中会被视为指向数组首元素的指针（类型为int*）。这意味着arr和&arr[0]在功能上是等价的，都表示数组第一个元素的地址。

使用数组名

使用数组名时，可以通过下标访问数组中的元素。例如，arr[0]访问第一个元素，arr[1]访问第二个元素，以此类推。数组下标实际上是基于数组名这个地址进行的偏移计算。例如，arr[i]在内部等价于*(arr + i)。

数组名的特殊情况

虽然数组名大多数时候被视为指向其首元素的指针，但是有两种情况下数组名的行为和普通指针不完全相同：

• sizeof运算符：当使用sizeof(arr)时，它返回的是整个数组的大小（以字节为单位），而不是指针的大小。比如int arr[10];，在32位系统上，sizeof(arr)的值是40（因为整型通常是4字节，数组有10个元素），而不是指针的大小（32位系统上通常是4字节，64位系统上通常是8字节）。
• &运算符：当对数组名使用&运算符，如&arr，得到的是数组的地址，但类型并不是int*，而是数组类型的指针，即int (*)[10]。这表示指向含有10个整数的数组的指针。

一维数组的本质

当我们使用int score［5］={1,2,3,4,5}；，就是创建了一个名为score的变量，变量类型为int ［5］。

变量类型会决定这个变量在内存中开辟多少空间，此处变量类型为int［5］，顾名思义，就是在内存中开辟5个int类型大小的空间。然后依次在五个空间内存入1.2.3.4.5五个数据。

接下来我们依次打印五个数组元素的地址：

#include<stdio.h>

int main() {
    int arr[5] = {1, 2, 3, 4, 5};
    printf("%p\n", &arr[0]);
    printf("%p\n", &arr[1]);
    printf("%p\n", &arr[2]);
    printf("%p\n", &arr[3]);
    printf("%p\n", &arr[4]);
}
//
//输出：
//0000003493bffdd0
//0000003493bffdd4
//0000003493bffdd8
//0000003493bffddc
//0000003493bffde0

可以发现，每个元素相比于上一个元素地址大四个字节，可是这种变量是在栈区开辟的空间，栈区内存是从高低使用的，难道不应该每个元素的地址相比于上一个元素小四个字节吗？

我们在创建一维数组时，就已经确定了这个变量需要开辟的总空间的大小，整个数组作为一个变量相较于其它数据而言是在低地址的。而在数组内部，c语言规定下标从小到大，数组元素地址也是从小到大的，为什么要这样设计呢？

因为数组的访问本质上是指针对地址的访问。

#include<stdio.h>

int main() {
    int arr[5] = {1, 2, 3, 4, 5};
    printf("%p\n", arr);
    printf("%p\n", &arr);
    printf("%p\n", &arr[0]);
}
//
//输出：
//000000028dfff7d0
//000000028dfff7d0
//000000028dfff7d0

此案例中，三者地址相同，说明&arr，与arr本身都是首个元素的地址。

#include<stdio.h>

int main() {
    int arr[5] = {1, 2, 3, 4, 5};
    int a = arr[4];
    int b = *(arr + 4);
    printf("a=%d\n", a);
    printf("b=%d\n", b);
}
//
//输出：
//a=5
//b=5

此例子说明，arr［4］本质上就是对从arr地址开始，偏移量为4的地址进行访问。而当偏移量为正数，偏移后地址是变大的，也就是说在内存中要保证后面的元素地址比前面的元素大，才能用指针偏移量来访问。

为什么数组下标要从0开始？当我们访问第一个元素，arr［0］本质上来说就是*（arr+0），也就是访问arr地址本身，即第一个元素的地址。如果下标从1开始，那在那么在利用指针访问时就要对所有数据-1，反而麻烦，于是一开始就规定下标从0开始，后续直接利用下标作为偏移量就行了。

二维数组的本质

一维数组的本质是通过首元素地址与偏移量来访问一个地址。二维数组也是通过首元素的地址与偏移量来访问的，但是一个数组元素只有一个地址，相比于首元素的偏移量也是确定的，为何需要两个偏移量？

我们尝试输出一个二维数组的所有元素地址：

#include<stdio.h>

int main() {
    int arr[3][5] = {0};
    int i = 0;
    int j = 0;
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 5; j++) {
            printf("&arr[%d][%d] = %p\n", i, j, &arr[i][j]);
        }
    }
    return 0;
}
//输出：
//&arr[0][0] = 0000001719fffad0
//&arr[0][1] = 0000001719fffad4
//&arr[0][2] = 0000001719fffad8
//&arr[0][3] = 0000001719fffadc
//&arr[0][4] = 0000001719fffae0
//&arr[1][0] = 0000001719fffae4
//&arr[1][1] = 0000001719fffae8
//&arr[1][2] = 0000001719fffaec
//&arr[1][3] = 0000001719fffaf0
//&arr[1][4] = 0000001719fffaf4
//&arr[2][0] = 0000001719fffaf8
//&arr[2][1] = 0000001719fffafc
//&arr[2][2] = 0000001719fffb00
//&arr[2][3] = 0000001719fffb04
//&arr[2][4] = 0000001719fffb08

可以发现，每两个元素之间的差值都是4字节，也就是一个int的内存大小。说明二维数组并非我们想象中那样是一个平面，而是一个连续的地址：

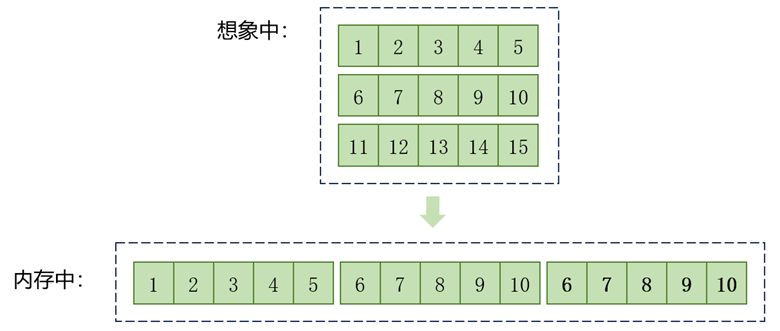
其实二维数组分为两层数组，外层数组用于存放一维数组；内层数组用于存放元素。也许有点难以理解这句话，那我们拿例子来分析：

#include<stdio.h>

int main() {
    int arr1[5] = {1, 2, 3, 4, 5};
    int arr2[5] = {6, 7, 8, 9, 10};
    int arr3[5] = {11, 12, 13, 14, 15};
    int *arr[3] = {arr1, arr2, arr3};

    int i, j;
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 5; j++) { printf("%d ", arr[i][j]); };
        printf("\n");
    }
}
//输出：
//1 2 3 4 5
//6 7 8 9 10
//11 12 13 14 15

在此处,我们有三个基本的数组，每个数组存放5个元素。而在下方有一个存放了三个数组的数组。可以发现，通过利用外层数组名arr来访问，可以正常得到每个元素。那么这样的数组形式是如何访问到每个元素的呢？

首先和大家理清几个概念：

• 外层数组也是数组，但是外层数组的元素是数组
• 外层数组的数组名arr本质上也是一个指针，与一维数组相同
• 对（arr+i）指针解引用，得到的是外层数组的第i-1个元素，但是此元素是一个数组，数组名本质上是指针，所以*（arr+i）得到的是一个指针

如果你理解了以上三点，说明你对数组和指针掌握的还不错。我们是用arr[][]来访问二维数组的，我们在讲解一维数组本质的时候提到过:

arr[i] == *(arr+i)

那么在此连续使用两个[]，其实就是解引用了两次。

arr[i][j] == *(*(arr+i)+j)

那么为什么一维数组解引用一次就得到了目标值，二维数组要解引用两次？我们在理清概念时提起过，外层数组的变量是指针，*（arr + i）得到的是一个指针。对于这样一个指针，我们任然可以使用偏移量j与解引用操作符去访问，*（p+j），将此处的p指针替换为*（arr+i）， 那么我们最后的表达式就是刚才的表达式了。

再用代码证明一次：

#include<stdio.h>

int main() {
    int arr[3][5] = {{1,  2,  3,  4,  5},
                     {6,  7,  8,  9,  10},
                     {11, 12, 13, 14, 15}};
    int i, j;
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 5; j++) { printf("%d ", *(*(arr + i) + j)); };
        printf("\n");
    }
}
//输出：
//1 2 3 4 5
//6 7 8 9 10
//11 12 13 14 15

可以看到，我们确实通过这样的一个表达式访问到了这个二维数组的元素。

在一开始创建了一个行为3，列为5的数组，可以将此二维数组拆成三个一维数组，每个数组有5个元素，5个元素的大小是20字节。

在上述指针的加减法中，arr+1偏移了20个字节的地址，arr+2偏移了40个字节的地址。可以发现，刚好分别就是1个数组的大小与两个数组的大小。这就可以说明，此处的arr是一个指针且指针类型是数组指针。

arr[i][j] == *(*(arr+i)+j)

数组作为函数参数

在C语言中，数组可以作为函数的参数传递，但实际上传递的是数组的首元素的地址，即数组的指针。这意味着在函数内部，你不能直接获取到原始数组的大小（因为你只有一个指向数组首元素的指针）。这里是一些处理数组作为函数参数的基本示例和注意事项。

传递数组给函数

#include <stdio.h>

void printArray(int arr[], int size) {
    for(int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    int myArray[] = {1, 2, 3, 4, 5};
    int size = sizeof(myArray) / sizeof(myArray[0]);
    printArray(myArray, size);
    return 0;
}

修改数组元素的函数

#include <stdio.h>

void doubleValues(int arr[], int size) {
    for(int i = 0; i < size; i++) {
        arr[i] *= 2;
    }
}

int main() {
    int myArray[] = {1, 2, 3, 4, 5};
    int size = sizeof(myArray) / sizeof(myArray[0]);
    doubleValues(myArray, size);

    for(int i = 0; i < size; i++) {
        printf("%d ", myArray[i]);
    }
    printf("\n");
    return 0;
}

注意事项：

• 传递数组的指针： 在C语言中，当数组作为参数传递给函数时，实际上传递的是指向数组首元素的指针。因此，函数接收参数时可以使用指针的语法（如int *arr）或数组的语法（如int arr[]）。无论哪种方式，函数内部对数组元素的更改都会反映在原始数组上。
• 指定数组大小： 由于函数只接收到数组的指针，而不是整个数组，所以必须另外提供数组的大小信息，以便函数知道可以安全访问数组的哪些部分。
• 返回数组：C语言函数不能直接返回一个数组，但可以返回指向数组（通常是动态分配的数组）的指针。

通过将数组作为函数参数传递，可以在C语言中实现数据的有效处理和修改。然而，始终要小心处理指针和数组的大小，以避免内存泄漏或越界访问等问题。

数组作为函数返回

在C语言中，函数不能直接返回一个数组，但它可以返回一个指向数组的指针。有几种方式可以让函数有效地“返回”一个数组。以下是一些常见的方法：

静态数组

函数可以返回一个指向静态数组的指针。由于静态数组在函数调用结束后仍然存在，因此可以安全地返回。但是，每次函数调用都会返回同一个数组，所以这种方法并不适合所有情况。

int* get_array() {
    static int arr[3] = {1, 2, 3};
    return arr;
}

动态分配

函数可以创建一个动态分配的数组（使用malloc或calloc）并返回指向它的指针。这可以工作得很好，但需要记住在函数外部释放内存，以防止内存泄漏。

int* get_array() {
    int* arr = malloc(3 * sizeof(int));
    arr[0] = 1;
    arr[1] = 2;
    arr[2] = 3;
    return arr;
}

通过函数参数返回

另一种方式是将目标数组作为一个参数传递给函数，让函数直接在这个数组中填充数据。

void fill_array(int* arr, int n) {
    for (int i = 0; i < n; i++) {
        arr[i] = i;
    }
}

在上面的例子中，你需要提前知道数组的大小并在函数外部分配足够的空间。在任何情况下，都需要特别注意内存管理以防止内存泄漏或越界访问。

数组的复制

由于数组名是指针，所以复制数组不能简单地复制数组名。

int* a;
int b[3] = {1, 2, 3};

a = b;

上面的写法，结果不是将数组b复制给数组a，而是让a和b指向同一个数组。

以下是两种常见的方法来复制数组：

方法一：逐元素复制

对于基本数据类型的数组（如int、float等），你可以通过循环逐个复制数组的每个元素。例如，复制一个整数数组：

#include <stdio.h>

int main() {
    int source[] = {1, 2, 3, 4, 5};
    int destination[5];
    int i;

    // 数组长度
    int length = sizeof(source)/sizeof(source[0]);

    // 逐元素复制
    for(i = 0; i < length; i++) {
        destination[i] = source[i];
    }

    // 打印复制后的数组
    for(i = 0; i < length; i++) {
        printf("%d ", destination[i]);
    }

    return 0;
}

方法二：使用memcpy

memcpy函数是C标准库中的一部分，定义在string.h头文件中，可以用来复制内存区域，非常适合用来复制数组。使用memcpy时，需要注意源和目标内存区域不要重叠，对于重叠的内存区域复制应使用memmove。

#include <stdio.h>
#include <string.h>

int main() {
    int source[] = {1, 2, 3, 4, 5};
    int destination[5];

    // 计算数组的字节大小
    size_t bytes = sizeof(source);

    // 使用memcpy进行复制
    memcpy(destination, source, bytes);

    // 打印复制后的数组
    for(int i = 0; i < sizeof(source)/sizeof(source[0]); i++) {
        printf("%d ", destination[i]);
    }

    return 0;
}

注意事项

• 当使用逐元素复制方法时，你有机会在复制过程中修改或检查每个元素。
• 使用memcpy时，复制的是字节流，这意味着对于非基本数据类型的数组（例如结构体数组），只要结构体内部没有指针，memcpy也是安全的。如果数组元素包含指针，复制指针值可能不会按期望工作，因为指针指向的是相同的内存地址。
• 对于大型数组，使用memcpy通常比逐元素复制更高效，因为memcpy的实现可能针对特定平台进行了优化。

变长数组与柔性数组

变长数组

在C99标准之前，C语言在创建数组的时候，数组大小的指定只能使用常量、常量表达式，或者如果我们初始化数据的话，可以省略数组大小。比如以下三种方式，得到的数组都是固定的大小。

int arr1[10];
int arr2[3+5];
int arr3[] = {1,2,3};

这样的语法限制，让我们创建数组就不够灵活，有时候数组大了浪费空间，有时候数组又小了不够用。

C99中给一个变长数组（variable-length array，简称 VLA）的新特性，允许我们可以使用变量指定数组大小。以代码为例：

int n = a+b;
int arr[n];

上面示例中，数组arr 就是变长数组，因为它的长度取决于变量n 的值，编译器没法事先确定，只有运行时才能知道n 是多少。变长数组的根本特征，就是数组长度只有运行时才能确定，所以变长数组不能初始化。它的好处是程序员不必在开发时，随意为数组指定一个估计的长度，程序可以在运行时为数组分配精确的长度。变长数组的意思是数组的大小是可以使用变量来指定的，在程序运行的时候，根据变量的大小来指定数组的元素个数，而不是说数组的大小是可变的。数组的大小一旦确定就不能再变化了。

柔性数组

柔性数组的定义

柔性数组也是在C99标准后才出现的，它是指：对于动态内存中的结构体的最后一个成员，可以放一个长度可以改变的数组。

柔性数组的创建与使用

//方法1
struct st{
    int a;
    int arr[];//柔性数组成员
}
//方法2
struct st{
    int a;
    int arr[0];//柔性数组成员
}

根据定义可知，柔性数组必须是结构体的最后一个成员。在上述开辟过程中，我们都在结构体末尾放了一个数组，此数组的[]内部没有值或者值为0。这就是柔性数组的基本语法，若数组不是最后一个成员，或者数组[]内有0以外的值，最后创建的都不是柔性数组。注意：部分编译器只支持其中一种写法。

柔性数组有以下特性：

• 柔性数组成员前至少有一个其它成员
• sizeof计算结构体的大小时，不计入柔性数组成员
• 柔性数组的长度变化由malloc与realloc决定，在第一次使用malloc开辟内存时，必须大于结构体其它成员占用内总和，多出来的内存分配给柔性数组。

为了理解这些特性以及柔性数组的长度变化，我们来分析一串代码：

struct st
{
    int a;
    int arr[];//柔性数组成员
};

int main()
{
    struct st* p = (struct st*)malloc(sizeof(struct st) + 10 * sizeof(int));
    //为结构体开辟空间，并为柔性数组开辟空间存放10个元素
    if (p == NULL)//检查开辟空间是否成功
    {
        perror("malloc");
        return 1;
    }
    //为柔性数组的元素赋值
    int i = 0;
    p->a = 100;

    for (i = 0; i < 10; i++)
    {
        p->arr[i] = i;
    }
    //感觉数组长度不够，增长数组：
    struct st* ptr = realloc(p, sizeof(struct st) + 15 * sizeof(int));
    //增加5个元素的空间
    if (ptr == NULL)//检查开辟空间是否成功
    {
        perror("realloc");
        return 1;
    }
    else
    {
        p = ptr;
        ptr = NULL;
    }
    //对后续开辟的5个空间赋值
    for (i = 10; i < 15; i++)
    {
        p->arr[i] = i;
    }

    //释放空间
    free(p);
    p = NULL;
    return 0;
}

柔性数组开辟：

struct st* p = (struct st*)malloc(sizeof(struct st) + 10 * sizeof(int));

一开始我们创建了一个结构体，在利用动态内存开辟了属于结构体本身的空间后，追加了10个int类型的大小，用于存放柔性数组的元素。此处也利用了sizeof不计算柔性数组的特性，避免程序员自己计算结构体的大小，追加的空间也更加直观。

柔性数组增长：

struct st* ptr = realloc(p, sizeof(struct st) + 15 * sizeof(int));

上述代码在开辟了10个元素的空间后，仍需要空间放其它元素，于是使用realloc开辟了额外的五个空间，这就是柔性数组的长度变化。

可以发现，柔性数组的本质就是动态内存管理，利用malloc与realloc来操作内存，变化数组长度。相比于变长数组，通过变量赋值以后就变成了定长数组，柔性数组其实才是真正意义上的“变长”。

一维数组的排序

在C语言中，对一维数组进行排序的常用方法是使用冒泡排序、插入排序或快速排序等排序算法。

冒泡排序

冒泡排序（Bubble Sort）是一种简单的排序算法，它通过重复地遍历待排序的数列，比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

算法步骤

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个。
• 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

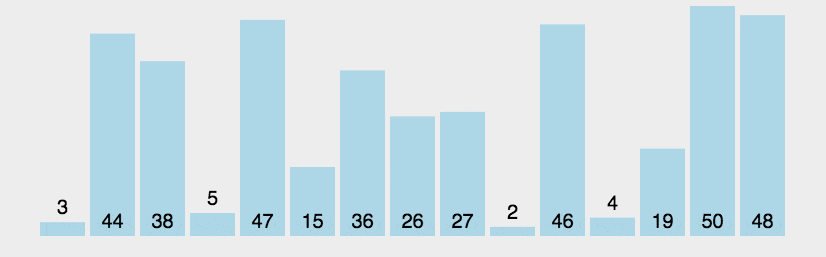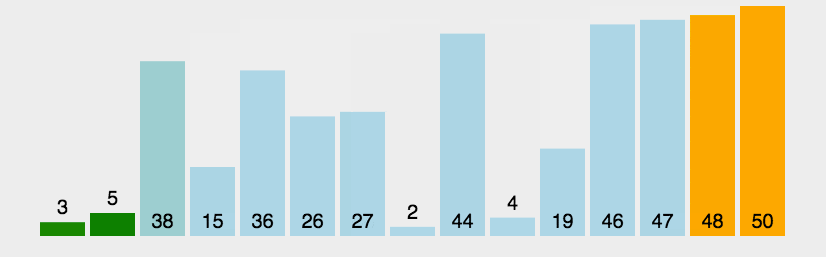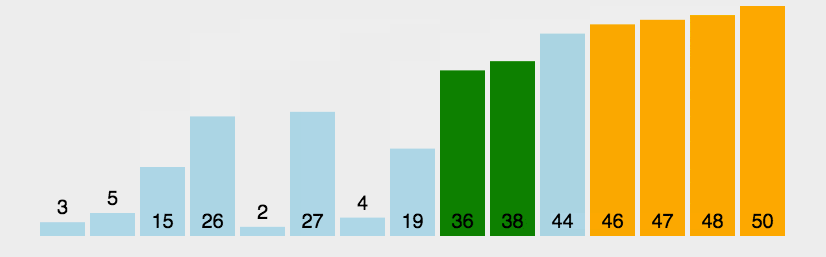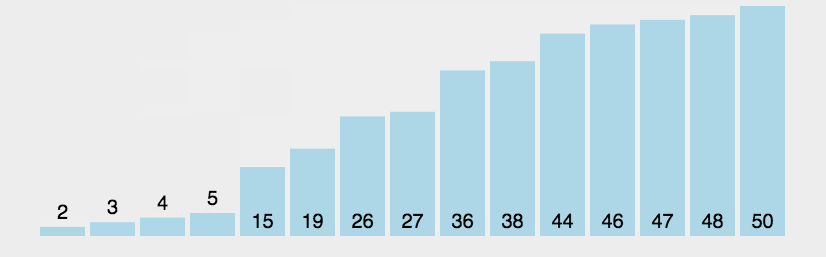
实现示例

以下是冒泡排序的一个简单C语言实现示例，该示例将数组按照升序排序：

#include <stdio.h>

void bubbleSort(int arr[], int n) {
    int i, j, temp;
    for (i = 0; i < n-1; i++) {
        // 最后i个是已经排好的，不需要再次比较
        for (j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                // 交换两个元素
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    bubbleSort(arr, n);
    printf("Sorted array: \n");
    for (int i=0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

特点

• 简单易懂：冒泡排序是最简单的排序算法之一，适合初学者理解和实现。
• 性能：对于小型数据集，冒泡排序可以工作良好。但对于较大的数据集，由于其平均和最坏情况下的时间复杂度均为O(n^2)，效率较低。
• 稳定性：冒泡排序是稳定的排序算法，相同值的元素在排序后不会改变其相对顺序。
• 空间效率：冒泡排序是原地排序，它不需要额外的存储空间，空间复杂度为O(1)。

尽管冒泡排序不适合大规模数据的排序，但它在教学和理解基本排序原理方面仍然非常有价值。

插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法。它的工作方式是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

算法步骤

• 从第一个元素开始，该元素可以认为已经被排序。
• 取出下一个元素，在已经排序的元素序列中从后向前扫描。
• 如果该元素（已排序）大于新元素，将该元素移到下一位置。
• 重复步骤3，直到找到已排序的元素小于或等于新元素的位置。
• 将新元素插入到该位置后。
• 重复步骤2~5。

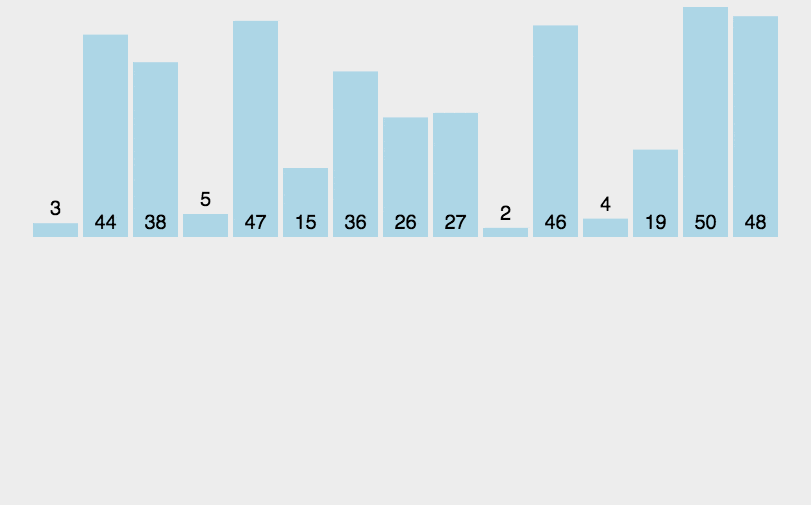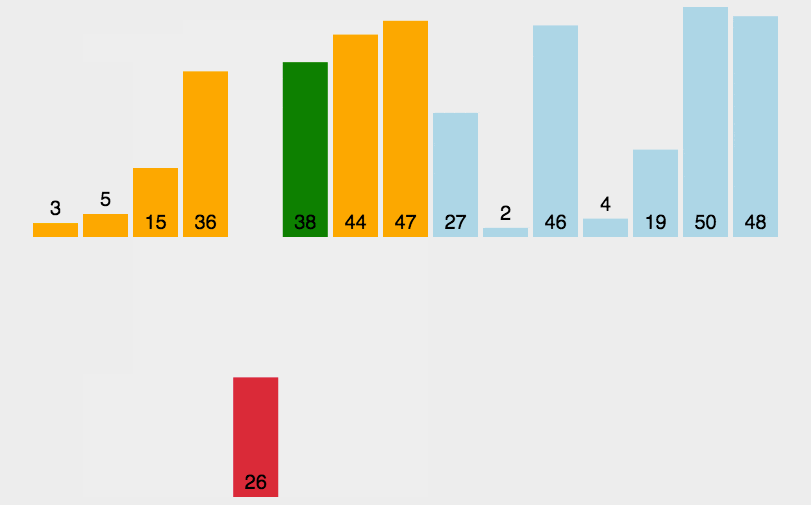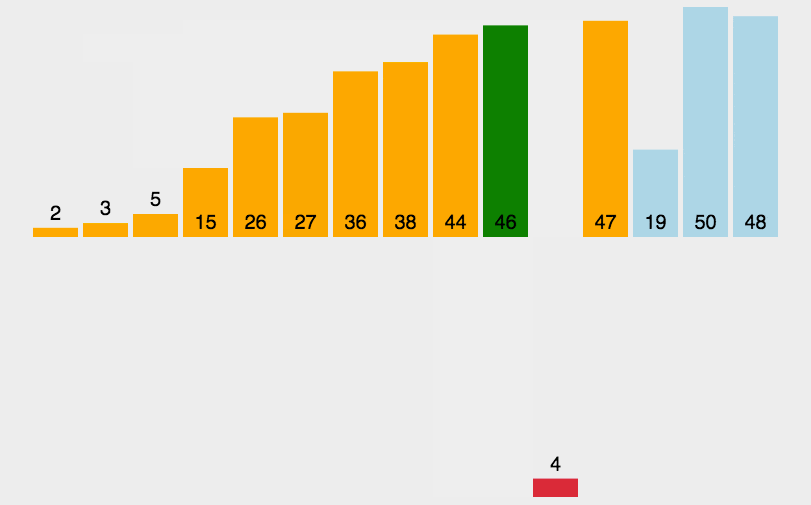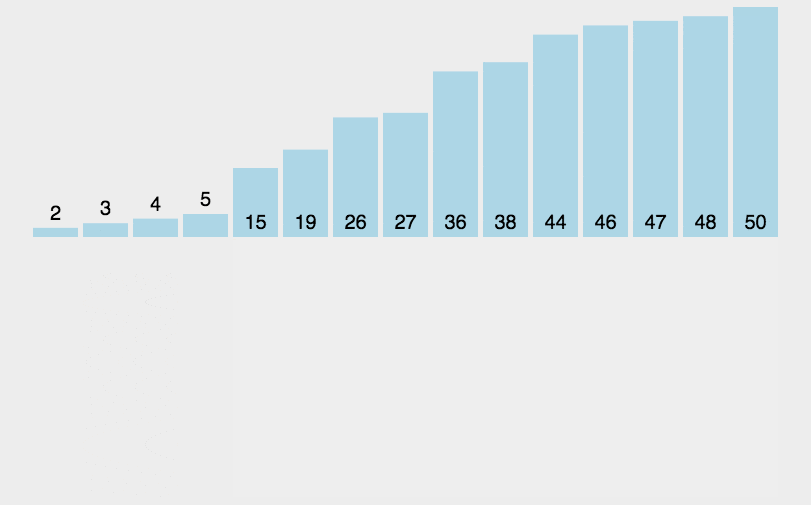
实现示例

以下是插入排序的一个C语言实现示例，该示例将数组按照升序排序：

#include <stdio.h>

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;

        /* 将arr[i]插入到已排序的序列arr[0...i-1]中的正确位置 */
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

int main() {
    int arr[] = {12, 11, 13, 5, 6};
    int n = sizeof(arr)/sizeof(arr[0]);
    insertionSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

特点

• 简单易懂：插入排序算法简单，适合于小规模数据的排序。
• 高效于小规模数据：对于小规模数据集，插入排序比冒泡排序和选择排序性能要好。
• 稳定性：插入排序是稳定的排序算法，相同值的元素在排序后不会改变其相对顺序。
• 适用场景：插入排序适合部分已排序的数据集和小规模数据集。在这些情况下，插入排序可以提供接近线性时间的性能。
• 空间效率：插入排序是原地排序，不需要额外的存储空间，空间复杂度为O(1)。

插入排序虽然在处理大规模数据集时效率不高（时间复杂度为O(n^2)），但其简单易实现、空间高效以及对小规模或部分有序数据集高效的特性使其在特定情况下非常有用。

快速排序

快速排序（Quick Sort）是由C. A. R. Hoare在1960年提出的一种高效的排序算法。它使用分治法（Divide and Conquer）策略来把一个序列分为两个子序列。快速排序在平均状况下的时间复杂度为O(n log n)，且其性能通常比其他O(n log n)复杂度的排序算法更优，因此它是实际应用中非常常见和受欢迎的排序算法。

算法步骤

快速排序的基本步骤如下：

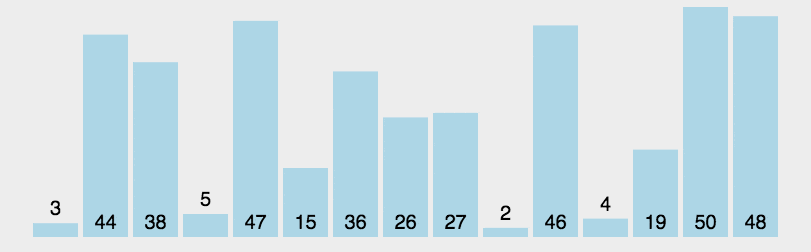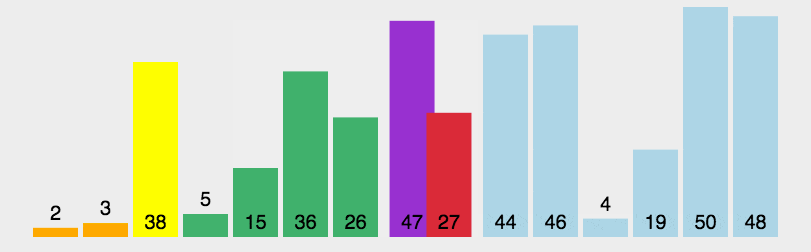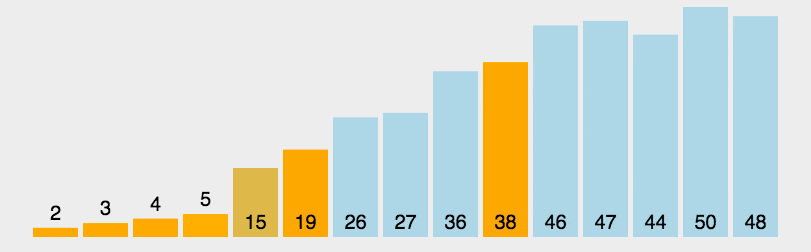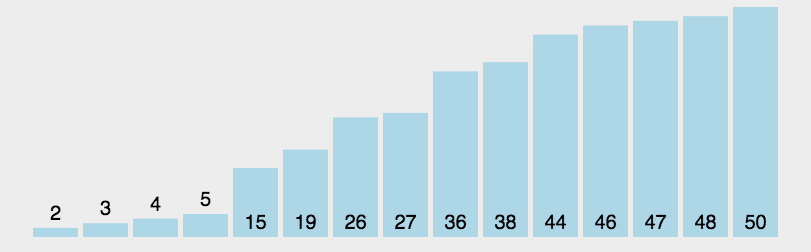
• 选择基准值：从数列中挑出一个元素，称为”基准”（pivot）。
• 分区操作：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
• 递归排序子序列：递归地（recursive）将小于基准值元素的子序列和大于基准值元素的子序列排序。

实现示例

以下是快速排序的一个C语言实现示例：

#include <stdio.h>

// 函数来交换两个元素
void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}

/* 该函数取最后一个元素作为基准，将基准元素放到它正确的位置上，所有比基准小的元素放在左边，比基准大的放在右边 */
int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);

    for (int j = low; j <= high- 1; j++) {
        // 如果当前元素小于或等于pivot，则交换
        if (arr[j] <= pivot) {
            i++;
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

/* arr[] --> 排序数组，
low --> 起始索引，
high --> 结束索引 */
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        /* pi是分区后的索引，arr[pi]现在放在正确的位置 */
        int pi = partition(arr, low, high);

        // 分别对前半部分和后半部分进行递归排序
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    int arr[] = {10, 7, 8, 9, 1, 5};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

特点

• 效率高：快速排序在大多数情况下是非常高效的，平均时间复杂度为O(n log n)。
• 原地排序：快速排序是原地排序，不需要额外的存储空间。
• 不稳定排序：相等元素的相对次序可能会在排序过程中改变，因此快速排序是不稳定的排序算法。
• 适用范围广：适用于大多数需要排序的情况，尤其是数据量大的情况。

快速排序的主要缺点是它的最坏情况性能较差，即O(n^2)。但通过随机选择基准或者“三数取中”等策略，可以有效减少这种最坏情况的发生概率。

数组的应用示例

打印直角状杨辉三角

杨辉三角是二项式系数在三角形阵列中的一种几何排列，在统计和代数中有许多应用。

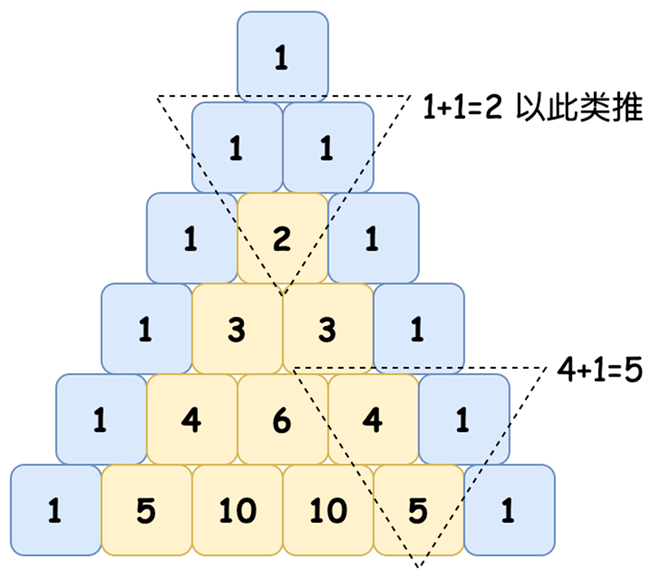
在C语言中，可以使用二维数组来实现打印直角杨辉三角。之所以采用二维数组，是因为杨辉三角的每一个数都是由它上方的两个数相加而来的。

下面是一个实现打印直角杨辉三角的C语言代码示例：

#include <stdio.h>

#define N 10

int main() {
    int arr[N][N]; // 创建二维数组
    int i, j;

    // 初始化数组的第一列和主对角线上的元素为1
    for (i = 0; i < N; i++) {
        arr[i][0] = 1;
        arr[i][i] = 1;
    }

    // 计算杨辉三角其他位置上的元素值
    for (i = 2; i < N; i++) {
        for (j = 1; j < i; j++) {
            arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
        }
    }

    // 打印杨辉三角
    for (i = 0; i < N; i++) {
        for (j = 0; j <= i; j++) {
            printf("%d ", arr[i][j]);
        }
        printf("\n");
    }

    return 0;
}

在这个代码中，N是你想打印的杨辉三角的行数。这个程序首先初始化了二维数组的第一列和主对角线上的元素为1，然后通过两个嵌套的for循环来计算并打印出杨辉三角。

注意，这个代码打印出来的是一个直角杨辉三角。如果你想得到一个等腰杨辉三角，还需要进行额外的格式化输出工作。

筛数法求素数

筛法求素数是一种有效的寻找素数的算法，最著名的筛法是埃拉托斯特尼筛法（Sieve of Eratosthenes）。

以下是一个用C语言和数组实现的筛法求素数的示例：

#include <stdio.h>
#define N 100  // 找出100以内的所有素数

int main() {
    int i, j, a[N+1];
    // 初始化数组，假设所有的数都是素数，用1表示
    for(i = 2; i <= N; i++) {
        a[i] = 1;
    }
    // 筛法求素数
    for(i = 2; i <= N; i++) {
        if(a[i] == 1) {  // 如果i是素数，则将i的倍数标记为非素数，即用0表示
            for(j = i+i; j <= N; j+=i) {
                a[j] = 0;
            }
        }
    }
    // 输出素数
    printf("Prime numbers under %d are:\n", N);
    for(i = 2; i <= N; i++) {
        if(a[i] == 1) {
            printf("%d ", i);
        }
    }
    printf("\n");
    return 0;
}

在这个程序中，首先创建一个布尔数组a[N+1]，并将所有的数组元素初始化为1，表示所有的数都是素数。然后从2开始，将数组中所有2的倍数标记为0，表示这些数不是素数。然后对于下一个还未被标记为0的数即3，再将数组中所有3的倍数标记为0，以此类推，直到遍历到N。最后，输出所有仍然被标记为1的数，这些数就是素数。

这个程序的时间复杂度为O(N log log N)，是一种非常高效的寻找小范围内素数的方法。

约瑟夫问题

约瑟夫问题是一个著名的逻辑问题。这个问题是说，有n个人围成一圈，从第一个人开始报数，报到m的人退出，然后从下一个人再开始报数并按同样的规则退出，直到所有人都退出，求各退出人的原序号。

以下是一个用C语言和数组实现的解决约瑟夫问题的示例：

#include <stdio.h>
#define N 41  //总人数
#define M 3   //每次报数的数目

int main() {
    int a[N+1], i, j, k = 0;
    // 初始化数组，数组下标即为原序号
    for(i = 1; i <= N; i++) {
        a[i] = 1;
    }
    // 模拟报数和退出过程
    for(i = 1; i <= N; i++) {
        for(j = 1; j <= N; j++) {
            if(a[j] == 1) {
                k++;
                if(k == M) {  // 如果报数到M，则退出
                    a[j] = 0;
                    printf("%d ", j);
                    k = 0;
                }
            }
        }
    }
    printf("\n");
    return 0;
}

在这个程序中，首先创建了一个大小为N+1的整数数组a，并将所有的数组元素初始化为1，表示所有的人都在圈内。然后进行一个双层循环，外层循环表示总共需要退出N次，内层循环遍历数组，模拟每次报数和退出的过程。如果某个人退出，则将其数组元素值设置为0，表示这个人已经退出。

这个程序的时间复杂度为O(n^2)，当人数非常大时，这个算法会比较慢。如果要提高效率，可以使用链表或者其他数据结构来代替数组。