什么是 PU Learning?
PU Learning 的全称是 Positive-Unlabeled Learning,即正例-无标记学习。它是一种在半监督学习范畴内的特殊机器学习设定。
与传统的监督学习(数据有明确的“正例”和“负例”标签)不同,PU Learning 处理的数据集只包含两类样本:
- 正例:明确知道属于目标类别的样本。例如:已经确认购买过产品的客户、被医生确诊患病的病人、被人工审核确定的垃圾邮件。
- 无标记样本:不知道属于正例还是负例的样本。这个集合是未标记样本的混合体,其中既包含尚未被发现的正例,也包含真正的负例。例如:网站的所有访问者(其中既有潜在客户也有非客户)、所有接受筛查的病人(其中既有患者也有健康人)、邮箱里的所有邮件(其中既有垃圾邮件也有正常邮件)。
核心思想: 从已知的正例和一个混合的未标记集合中,学习一个分类器,以便将来能够准确区分新的正例和负例。
入门级概念实例
这些实例有助于直观理解PU Learning要解决的问题。
实例1:寻找稀有矿石
- 场景:你是一位地质学家,在一个特定区域发现了一些黄金矿脉(正例)。整个山区有成千上万个勘探点(未标记样本)。你的任务是找出其他可能含有黄金的勘探点。
- 问题:你不能把没有黄金的勘探点都标记为“负例”,因为可能只是你还没找到而已。如果你把一个尚未发现的富矿点错误地标记为“无矿”并用来训练模型,模型就会学会忽略真正的信号。
- PU方法:你可以利用已知的黄金矿脉的地质特征(如土壤成分、磁场强度),从所有勘探点中找出那些地质特征与已知矿脉截然不同的点,这些点可以作为“可靠负例”(比如一片普通的石灰岩地带)。然后,利用这些正例和可靠负例训练模型,再去预测剩余的勘探点。
实例2:推荐系统
- 场景:在一个电商平台,用户点击或购买了的商品是明确的正例。
- 问题:那些用户看到但没有点击的商品不是真正的负例。用户可能因为没看到、暂时不需要、或者将来会购买而没有点击。如果简单地将未点击商品作为负例,模型会认为用户不喜欢的商品范围被夸大,从而推荐过于保守。
- PU方法:将未点击的商品视为未标记样本。通过PU学习,模型可以学会从曝光未点击的商品中区分出用户真正不喜欢的(负例)和可能感兴趣的(隐藏正例)。
为什么 PU Learning 具有挑战性?(核心问题)
直接使用标准分类方法会遇到严重问题:
- 标签偏差:如果你简单地把所有“无标记样本”都当作“负例”来训练一个分类器,会导致严重的问题。因为无标记样本中实际上包含了很多隐藏的正例,把这些隐藏的正例当作负例来学习,会“教坏”模型,导致学到的决策边界完全错误。
- 数据分布失真:标准的分类器通常假设训练数据中的正负分布是真实分布的无偏采样。但在PU学习中,训练集的“负例”集实际上是真实世界数据的一个有偏采样(它缺失了那些隐藏在无标记集合中的正例),这破坏了传统算法的基本假设。
PU Learning 的典型应用场景
PU Learning 在现实世界中极其有用,因为获取完整的负例标签通常非常困难或成本高昂。
- 信息检索与推荐系统:
- 正例:用户点击、购买、长时间浏览的物品。
- 无标记样本:用户看到但未交互的所有其他物品。
- 目标:从无标记样本中找出用户可能喜欢的物品(隐藏正例)进行推荐。
- 异常检测:
- 正例:已确认的欺诈交易、网络攻击、设备故障。
- 无标记样本:绝大部分的正常运行数据。
- 目标:因为“正常”行为千变万化,很难穷举定义,而异常是罕见的。PU学习非常适合从大量正常数据中找出罕见的异常模式。
- 生物信息学:
- 正例:已知与某种疾病相关的基因。
- 无标记样本:人类基因组中其他所有基因(其中大部分是无关的,但可能包含尚未被发现的相关基因)。
- 目标:预测新的致病基因。
- 医疗诊断:
- 正例:通过金标准(如活检)确诊的患者。
- 无标记样本:所有接受筛查但未被确诊的人群(其中包含假阴性和健康人)。
PU Learning 的主要方法论
研究人员提出了多种思路来解决PU学习问题,主要可以归结为三大类:
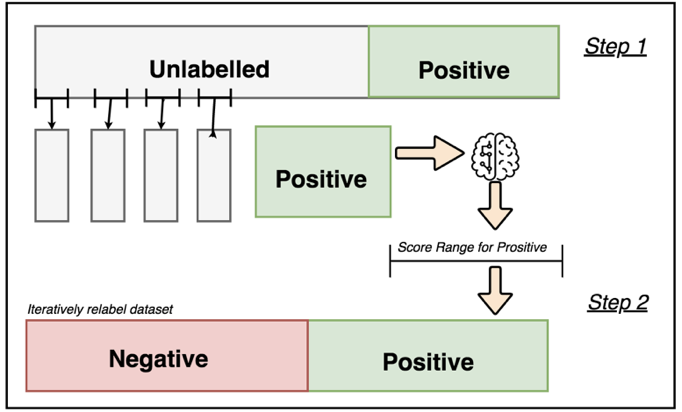
方法一:两步策略
这是最直观和流行的方法。它承认未标记数据是混合的,并尝试从中识别出可靠的负例。
第一步:识别可靠负例
- 利用已知的正例和未标记数据,通过某种技术找出那些“很可能”是负例的样本。
- 常用技术:
- 间谍法:从已知正例中随机抽取一小部分(如10%),把他们“伪装”成未标记样本,放入未标记集合中,这部分样本称为“间谍”。
- 然后使用一种学习算法(如朴素贝叶斯、SVM)在剩下的正例(90%)和整个未标记集合(包含间谍)上进行训练。由于间谍本质是正例,但被算法当作未标记数据处理,那些被分类器判断为“非常不像间谍”的未标记样本,就有很高概率是可靠的负例。
- 其他方法:使用聚类(如k-means)或异常检测算法(如Isolation Forest)来寻找与已知正例分布差异很大的未标记样本作为可靠负例。
第二步:迭代学习
- 一旦找到了一组可靠的负例,问题就转变为了一个更“干净”的有监督学习问题:已知正例 + 可靠负例。
- 可以用任何分类算法(如逻辑回归、决策树、SVM等)在这个数据集上训练一个初始分类器。
- 然后用这个分类器对剩下的未标记数据进行预测,将预测为负例且置信度高的样本加入负例集合。
- 不断迭代这个过程,逐步扩充训练集,直到模型收敛。
方法二:类别先验修正法
这种方法的核心思想是:对标准分类算法的损失函数进行修正,以补偿缺失的负例标签。
- 核心洞察:一个未标记样本的期望损失,可以看作是它作为正例的损失和它作为负例的损失的加权平均,权重就是它是正例的概率。
- 关键步骤:
- 估计类别先验:即估计未标记数据中正例的比例 π = P(y=1)。这是一个具有挑战性但可解决的问题,有专门的估计算法。
- 修正损失函数:基于估计出的 π,对标准二分类损失函数进行数学修正。使得算法在只有正例和未标记样本的情况下,能优化出与拥有完整标签时相近的模型参数。
- 优点:这种方法通常更理论化、更优雅,可以直接利用很多现有的高效算法,只需修改其损失函数即可。
方法三:概率输出法
这种方法将未标记样本视为带有噪声的、概率形式的标签。
- 核心思想:假设每个未标记样本 x属于正例的概率是 P(y=1 | x),属于负例的概率是 1 – P(y=1 | x)。在模型训练过程中,将这些概率权重考虑到目标函数中。
- 常用算法:期望最大化算法(Expectation-Maximization, EM) 经常被用于这种框架。
- E步:基于当前模型参数,计算每个未标记样本属于正例和负例的“期望”概率。
- M步:利用已知正例和带有概率权重的未标记样本,更新模型参数,最大化似然函数。
- 重复E步和M步直到收敛。
Pulearn库使用详解
pulearn 是一个专门用于 正例-无标记学习 的 Python 库,它提供了多种算法来处理仅包含正例(P)和大量未标记(U)样本的分类问题。下面这个表格概括了它的核心组件和实用信息,可以帮助你快速了解其全貌。pulearn 库主要实现了三种主流的PU学习策略,你可以根据具体问题和数据特点进行选择。
Elkanoto 方法
Elkanoto 方法是PU学习中最经典和实用的方法之一,由Charles Elkan和Keith Noto在2008年的论文《Learning classifiers from only positive and unlabeled data》中提出。它巧妙地利用概率估计来解决仅有正例和未标记样本下的分类问题。
方法核心:两步估计与概率校正
Elkanoto方法的核心思想是,未标记样本集中的正例比例,可以通过一个训练出的分类器来估计,进而校正概率估计。其关键步骤和公式如下:
- 可靠负例的识别与分类器训练
- 首先,从原始正例集(P)中随机选取一个子集作为“间谍”正例,混入未标记集(U)中。剩余的P集和整个U集(含间谍)用于训练一个分类器,该分类器的目标是区分“明确的正例”和“未标记数据”。
- 此时,分类器学习到的实际是样本被标记为正例的概率,即 P(s=1 | x, y=1)。这里的s=1表示样本被标记为正例。由于“间谍”正例本质是已知正例,分类器对U中样本的判断,有助于发现那些与已知正例差异巨大的可靠负例。
- 概率校正与最终分类器构建
- 训练第二个分类器来估计真正的类别概率 P(y=1 | x)。关键的一步是进行概率校正。Elkanoto方法证明,存在以下关系:P(y=1 | x) = P(s=1 | x) / c。其中,c = P(s=1 | y=1, x),可以近似为第一个分类器在整个原始正例集(P)上预测概率的平均值。这个 c就是正例被标记出来的概率。
算法步骤与实现
在pulearn库中,ElkanotoPuClassifier封装了这一流程。
- 输入:标记的正例集 P,未标记集 U,一个基础分类器(如SVM、逻辑回归)。
- 步骤:
- 从 P中随机选取一个比例(由 hold_out_ratio参数控制)作为“间谍”正例,与 U混合。
- 用剩余的 P和混合后的 U训练第一个分类器,得到每个样本 x的 P(s=1 | x)。
- 计算先验概率 c,通常取第一个分类器对整个原始正例集(P) 预测概率的平均值。
- 用所有标记数据(原始P作为正例,从U中识别出的可靠负例)训练第二个分类器。在预测时,将其输出的概率除以 c进行校正,得到 P(y=1 | x)。但为了避免校正后概率大于1,通常取 min(1, P(s=1 | x) / c)。
关键参数与注意事项
使用Elkanoto方法时,有几个关键点需要特别注意:
- hold_out_ratio参数:这个参数控制了从原始正例集中抽取多大比例作为“间谍”正例。它直接影响先验概率 c估计的准确性。比例过小,c的估计可能不可靠;比例过大,则会减少用于训练第一个分类器的正例数量。通常需要通过实验(如网格搜索)来调整。
- 基础分类器的选择:所选的基础分类器(如SVM、逻辑回归等)需要能够输出概率估计。算法的性能在很大程度上依赖于这个基础分类器的表现。
- 先验概率 c的稳定性:c的估计至关重要。在实践中,可能会采用多次随机选取“间谍”正例并取平均值等策略来提高 c的稳定性。
优势与局限性
了解Elkanoto方法的优缺点,有助于你在实际应用中做出合适的选择。
优势:
- 理论坚实:方法有概率论基础,逻辑清晰。
- 实现相对简单:pulearn等库使其易于应用。
- 无需
- 效果良好:在许多场景下,特别是当正例和未标记样本中的正例有相似特征时,效果不错。
局限性:
- 对参数敏感:hold_out_ratio等参数的选择对结果影响较大。
- 依赖基础分类器:第一个分类器的性能直接影响整个流程。
- “间谍”样本的假设:方法假设混入U的“间谍”正例与U中隐藏的正例具有相似分布,如果此假设不成立,会影响效果。
- 计算成本:需要训练两个分类器。
代码实例
# 第一步:导入必要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score, precision_score, roc_auc_score, accuracy_score, f1_score
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
import xgboost as xgb
# Plotly 相关库
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import plotly.express as px
import plotly.io as pio
# 设置Plotly默认主题
pio.templates.default = "plotly_white"
# # 第二步:加载和探索数据
# print("=== 步骤1: 数据加载与探索 ===")
# url = "http://archive.ics.uci.edu/ml/machine-learning-databases/00267/data_banknote_authentication.txt"
# data = pd.read_csv(url, header=None)
data = pd.read_csv("data/data_banknote_authentication.txt",header=None)
# 分配列名
data.columns = ['F1','F2','F3','F4','Target']
# 打印数据基本信息
print("数据形状:", data.shape)
print("\n前5行数据:")
print(data.head())
print("\n目标变量分布:")
print(data['Target'].value_counts())
print("\n数据描述性统计:")
print(data.describe())
# 第三步:创建基线模型(全监督学习)
print("\n=== 步骤2: 创建基线模型(全监督学习)===")
# 定义特征和目标
features = ['F1','F2','F3','F4']
# 划分训练集和测试集
x_data = data[features]
y_data = data['Target']
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.2, random_state=7)
# 训练XGBoost分类器作为基线
model = xgb.XGBClassifier(random_state=42)
model.fit(x_train, y_train)
# 定义评估函数
def evaluate_results(y_test, y_predict, y_prob=None):
print('分类结果:')
f1 = f1_score(y_test, y_predict)
print("f1: %.2f%%" % (f1 * 100.0))
roc = roc_auc_score(y_test, y_predict)
print("ROC AUC: %.2f%%" % (roc * 100.0))
rec = recall_score(y_test, y_predict, average='binary')
print("召回率: %.2f%%" % (rec * 100.0))
prc = precision_score(y_test, y_predict, average='binary')
print("精确率: %.2f%%" % (prc * 100.0))
acc = accuracy_score(y_test, y_predict)
print("准确率: %.2f%%" % (acc * 100.0))
if y_prob is not None:
roc_auc_prob = roc_auc_score(y_test, y_prob)
print("ROC AUC (概率): %.2f%%" % (roc_auc_prob * 100.0))
print("-" * 50)
return {'f1': f1, 'roc_auc': roc, 'recall': rec, 'precision': prc, 'accuracy': acc}
# 在测试集上评估基线模型
print("基线模型性能 (全监督学习):")
y_predict_baseline = model.predict(x_test)
y_prob_baseline = model.predict_proba(x_test)[:, 1]
baseline_metrics = evaluate_results(y_test, y_predict_baseline, y_prob_baseline)
# 第四步:创建PU学习场景
print("\n=== 步骤3: 创建PU学习场景 ===")
# 创建数据副本用于PU学习
mod_data = data.copy()
# 提取正例的索引(Target=1)
index_pos = mod_data[mod_data['Target']==1].sample(frac=0.25, random_state=42).index
# 创建PU_Target列,初始化为"Unlabeled"
mod_data['PU_Target'] = "Unlabeled"
# 仅标记25%的正例为"Positive"(其余保持为"Unlabeled")
mod_data.loc[index_pos,'PU_Target'] = 'Positive'
# 打印Target和PU_Target的交叉表
print("Target和PU_Target的交叉表:")
print(pd.crosstab(mod_data['Target'], mod_data['PU_Target'], margins=True))
print("\n我们的目标是从1220个未标记样本中识别出458个隐藏的正例")
# 第五步:实现PU估计器(Elkanoto方法)
print("\n=== 步骤4: 实现PU估计器(Elkanoto方法)===")
def fit_PU_estimator_AM(X, y, hold_out_ratio, estimator):
"""
实现Elkanoto方法的PU估计器
参数:
- X: 特征数据
- y: 标签 (1=Positive, 0=Unlabeled)
- hold_out_ratio: 保留的正例比例
- estimator: 基础分类器
"""
# 提取标记为正例的样本
X_labeled_pos = X[y == 1]
# 随机保留一部分正例作为验证集
X_hold_out = X_labeled_pos.sample(frac=hold_out_ratio, random_state=42)
# 提取非保留样本的索引
idx_non_hold = list(set(X.index) - set(X_hold_out.index))
# 从X和y中移除保留的样本
X_non_hold = X.loc[idx_non_hold]
y_non_hold = y.loc[idx_non_hold]
# 在非保留样本上训练估计器
estimator.fit(X_non_hold, y_non_hold)
# 使用估计器预测保留的正例集,估计P(s=1|y=1)
hold_out_predictions = estimator.predict_proba(X_hold_out)[:, 1]
# 计算平均概率
prob_s1y1 = hold_out_predictions.mean()
return estimator, prob_s1y1
def predict_PU_prob_AM(X, estimator, prob_s1y1):
"""
使用训练好的PU估计器进行预测
参数:
- X: 特征数据
- estimator: 训练好的估计器
- prob_s1y1: P(s=1|y=1)的估计值
"""
predicted_s = estimator.predict_proba(X)[:, 1] # P(s=1|X)
return predicted_s / prob_s1y1 # P(y=1|X) = P(s=1|X) / P(s=1|y=1)
# 准备PU学习的数据
y_pu = mod_data['PU_Target'].map({'Unlabeled': 0, 'Positive': 1}).astype('int')
# 第六步:执行PU学习
print("\n=== 步骤5: 执行PU学习 ===")
# 初始化变量
predicted = np.zeros(len(mod_data))
learning_iterations = 101 # 减少迭代次数以加快演示速度
# 执行多次迭代学习
report = []
for index in range(learning_iterations):
# 每次迭代使用不同的保留样本,因此pu_estimator和probs1y1会不同
pu_estimator, probs1y1 = fit_PU_estimator_AM(
X=mod_data[features],
y=y_pu,
hold_out_ratio=0.25,
estimator=xgb.XGBClassifier(random_state=index) # 每次使用不同的随机种子
)
predicted_index = predict_PU_prob_AM(mod_data[features], pu_estimator, probs1y1)
# 由于预测的概率可能不在[0,1]范围内,进行缩放
predicted_index_scaled = MinMaxScaler().fit_transform(
predicted_index.reshape(-1, 1)
).reshape(-1)
predicted += predicted_index_scaled
# 每20次迭代打印一次进度
if index % 20 == 0:
print(f'学习迭代: {index}/{learning_iterations} => P(s=1|y=1)={probs1y1:.4f}')
# 计算平均概率
mod_data['y_pos_pred_proba'] = predicted / learning_iterations
# 第七步:分析PU学习结果
print("\n=== 步骤6: 分析PU学习结果 ===")
# 查看不同组的预测概率中位数
prob_comparison = pd.pivot_table(
mod_data,
index='Target',
columns='PU_Target',
values='y_pos_pred_proba',
aggfunc='median'
)
print("不同组的预测概率中位数:")
print(prob_comparison)
# 第八步:评估PU学习性能
print("\n=== 步骤7: 评估PU学习性能 ===")
# 在不同阈值下评估性能
thresholds = np.linspace(0.1, 0.9, 50)
performance_report = []
for thre in thresholds:
y_pred_pu = (mod_data['y_pos_pred_proba'] > thre).astype(int)
p = precision_score(mod_data['Target'], y_pred_pu)
r = recall_score(mod_data['Target'], y_pred_pu)
f = f1_score(mod_data['Target'], y_pred_pu)
a = accuracy_score(mod_data['Target'], y_pred_pu)
performance_report.append([thre, p, r, f, a])
performance_df = pd.DataFrame(
performance_report,
columns=['threshold', 'precision', 'recall', 'f1', 'accuracy']
)
# 找到最佳F1分数对应的阈值
best_f1_idx = performance_df['f1'].idxmax()
best_threshold = performance_df.loc[best_f1_idx, 'threshold']
best_f1 = performance_df.loc[best_f1_idx, 'f1']
print(f"最佳阈值: {best_threshold:.4f}, 最佳F1分数: {best_f1:.4f}")
# 使用最佳阈值进行最终预测
y_pred_pu_best = (mod_data['y_pos_pred_proba'] > best_threshold).astype(int)
print("PU学习模型性能 (使用最佳阈值):")
pu_metrics = evaluate_results(mod_data['Target'], y_pred_pu_best, mod_data['y_pos_pred_proba'])
# 第九步:使用Plotly可视化结果
print("\n=== 步骤8: 使用Plotly可视化结果 ===")
# 1. 特征分布图
feature_fig = make_subplots(
rows=2, cols=2,
subplot_titles=[f'特征 {feature} 分布' for feature in features]
)
for i, feature in enumerate(features):
row = i // 2 + 1
col = i % 2 + 1
# 正例分布
pos_data = data[data['Target'] == 1][feature]
feature_fig.add_trace(
go.Histogram(x=pos_data, name='正例', opacity=0.7, marker_color='red'),
row=row, col=col
)
# 负例分布
neg_data = data[data['Target'] == 0][feature]
feature_fig.add_trace(
go.Histogram(x=neg_data, name='负例', opacity=0.7, marker_color='blue'),
row=row, col=col
)
feature_fig.update_layout(
title_text="特征分布 by Target",
height=600,
showlegend=True
)
feature_fig.show()
# 2. PU学习预测概率分布
pu_prob_fig = go.Figure()
# 标记为正例的样本概率分布
positive_data = mod_data[mod_data['PU_Target'] == 'Positive']['y_pos_pred_proba']
pu_prob_fig.add_trace(go.Histogram(
x=positive_data,
name='标记正例',
opacity=0.7,
marker_color='red'
))
# 未标记样本的概率分布
unlabeled_data = mod_data[mod_data['PU_Target'] == 'Unlabeled']['y_pos_pred_proba']
pu_prob_fig.add_trace(go.Histogram(
x=unlabeled_data,
name='未标记样本',
opacity=0.7,
marker_color='blue'
))
pu_prob_fig.update_layout(
title='PU学习预测概率分布',
xaxis_title='预测概率',
yaxis_title='频数',
bargap=0.1,
height=400
)
pu_prob_fig.show()
# 3. 性能指标随阈值变化
metrics_fig = go.Figure()
metrics_fig.add_trace(go.Scatter(
x=performance_df['threshold'],
y=performance_df['precision'],
mode='lines',
name='精确率',
line=dict(width=3)
))
metrics_fig.add_trace(go.Scatter(
x=performance_df['threshold'],
y=performance_df['recall'],
mode='lines',
name='召回率',
line=dict(width=3)
))
metrics_fig.add_trace(go.Scatter(
x=performance_df['threshold'],
y=performance_df['f1'],
mode='lines',
name='F1分数',
line=dict(width=3)
))
# 添加最佳阈值标记
metrics_fig.add_vline(
x=best_threshold,
line_width=2,
line_dash="dash",
line_color="red",
annotation_text=f"最佳阈值: {best_threshold:.3f}"
)
metrics_fig.update_layout(
title='性能指标随阈值变化',
xaxis_title='阈值',
yaxis_title='分数',
height=500
)
metrics_fig.show()
# 4. 方法比较
methods = ['基线模型 (全监督)', 'PU学习模型']
f1_scores = [baseline_metrics['f1'], pu_metrics['f1']]
recall_scores = [baseline_metrics['recall'], pu_metrics['recall']]
precision_scores = [baseline_metrics['precision'], pu_metrics['precision']]
comparison_fig = go.Figure(data=[
go.Bar(name='F1分数', x=methods, y=f1_scores, marker_color='lightblue'),
go.Bar(name='召回率', x=methods, y=recall_scores, marker_color='lightgreen'),
go.Bar(name='精确率', x=methods, y=precision_scores, marker_color='lightsalmon')
])
comparison_fig.update_layout(
title='方法比较',
xaxis_title='方法',
yaxis_title='分数',
barmode='group',
height=500
)
comparison_fig.show()
# 5. 隐藏正例识别情况
true_positives = mod_data[(mod_data['Target'] == 1) & (mod_data['PU_Target'] == 'Unlabeled')]
identified_positives = true_positives[true_positives['y_pos_pred_proba'] > best_threshold]
identification_rate = len(identified_positives)/len(true_positives)*100
# 创建识别情况饼图
identification_fig = go.Figure(data=[go.Pie(
labels=['被正确识别的隐藏正例', '未被识别的隐藏正例'],
values=[len(identified_positives), len(true_positives) - len(identified_positives)],
marker_colors=['lightgreen', 'lightcoral']
)])
identification_fig.update_layout(
title=f'隐藏正例识别情况 (识别率: {identification_rate:.2f}%)',
height=400
)
identification_fig.show()
# 第十步:总结与洞察
print("\n=== 步骤10: 总结与洞察 ===")
print("PU学习关键洞察:")
print("1. PU学习仅使用部分标记的正例和大量未标记样本进行训练")
print("2. 通过迭代估计P(s=1|y=1),我们可以估计P(y=1|X) = P(s=1|X) / P(s=1|y=1)")
print("3. 在这个例子中,我们成功从1220个未标记样本中识别出了隐藏的正例")
print("4. PU学习在真实场景中非常有用,当获取负例标签困难或成本高时")
print(f"\n性能比较总结:")
print(f"基线模型 (全监督) F1分数: {baseline_metrics['f1']:.4f}")
print(f"PU学习模型 F1分数: {pu_metrics['f1']:.4f}")
print(f"\n隐藏的正例识别情况:")
print(f"总隐藏正例数: {len(true_positives)}")
print(f"被正确识别的隐藏正例数: {len(identified_positives)}")
print(f"隐藏正例识别率: {identification_rate:.2f}%")
加权 Elkanoto 方法
加权 Elkanoto 方法是经典 Elkanoto PU 学习方法的重要改进版本,它通过引入样本权重来优化学习过程,特别是在处理类别不平衡和噪声数据时表现更好。
方法背景与动机
经典 Elkanoto 方法的局限性
经典的 Elkanoto 方法虽然理论基础坚实,但在实际应用中存在一些局限性:
- 对噪声敏感:所有样本被平等对待,噪声样本会影响模型性能
- 类别不平衡问题:当正例数量远少于未标记样本时,模型容易偏向负例
- 样本重要性差异:不同样本对模型学习的贡献度不同
加权方法的优势
加权 Elkanoto 方法通过为不同样本分配不同权重来解决上述问题:
- 降低噪声影响:为可能的噪声样本分配较低权重
- 处理类别不平衡:通过权重调整平衡正例和未标记样本的影响
- 关注困难样本:为分类边界附近的样本分配更高权重
方法原理与数学基础
核心思想
加权 Elkanoto 方法的核心思想是:不同的训练样本应该对损失函数有不同的贡献。通过为样本分配权重,模型可以更关注那些对学习决策边界更重要的样本。
数学公式
在经典 Elkanoto 方法中,关键的概率关系为:P(y=1|x) = P(s=1|x) / P(s=1|y=1)
在加权版本中,我们引入权重向量 w,其中每个样本 对应一个权重 。
加权的损失函数可以表示为:L(w) = Σ w_i * L(f(x_i), y_i)
其中 是基础损失函数(如交叉熵损失),是分类器。
算法步骤详解
权重分配策略
加权 Elkanoto 方法的关键在于如何为样本分配权重。常见的策略包括:
基于置信度的权重
# 基于模型预测置信度分配权重
def confidence_based_weights(predictions, alpha=0.5):
"""
基于预测置信度分配权重
predictions: 模型预测概率
alpha: 平滑参数
"""
confidence = np.abs(predictions - 0.5) * 2 # 转换为[0,1]区间
weights = alpha + (1 - alpha) * confidence
return weights
基于距离的权重
def distance_based_weights(X, positive_centroid, beta=1.0):
"""
基于与正例中心的距离分配权重
positive_centroid: 正例样本的中心点
beta: 距离缩放参数
"""
distances = np.linalg.norm(X - positive_centroid, axis=1)
max_distance = np.max(distances)
weights = 1 - (distances / max_distance) * beta
return np.clip(weights, 0.1, 1.0) # 确保权重在合理范围内
加权 Elkanoto 算法流程
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array
class WeightedElkanotoPUClassifier(BaseEstimator, ClassifierMixin):
"""
加权 Elkanoto PU 分类器实现
"""
def __init__(self, base_estimator=None, hold_out_ratio=0.3,
weight_strategy='confidence', n_iter=10, random_state=42):
self.base_estimator = base_estimator
self.hold_out_ratio = hold_out_ratio
self.weight_strategy = weight_strategy
self.n_iter = n_iter
self.random_state = random_state
self.prob_s1y1_ = None
self.estimator_ = None
self.weights_ = None
def _calculate_weights(self, X, y, predictions=None):
"""计算样本权重"""
if self.weight_strategy == 'uniform':
# 均匀权重(退化为经典Elkanoto)
return np.ones(len(X))
elif self.weight_strategy == 'confidence':
# 基于置信度的权重
if predictions is None:
return np.ones(len(X))
return confidence_based_weights(predictions)
elif self.weight_strategy == 'distance':
# 基于距离的权重
positive_indices = np.where(y == 1)[0]
if len(positive_indices) == 0:
return np.ones(len(X))
positive_centroid = np.mean(X[positive_indices], axis=0)
return distance_based_weights(X, positive_centroid)
else:
raise ValueError(f"未知的权重策略: {self.weight_strategy}")
def fit(self, X, y):
"""训练加权PU分类器"""
X, y = check_X_y(X, y)
np.random.seed(self.random_state)
# 分离正例和未标记样本
positive_indices = np.where(y == 1)[0]
unlabeled_indices = np.where(y == 0)[0]
if len(positive_indices) == 0:
raise ValueError("训练数据中必须包含正例样本")
# 迭代优化过程
best_estimator = None
best_prob_s1y1 = 0
best_weights = None
min_loss = float('inf')
for iteration in range(self.n_iter):
# 1. 随机选择保留的正例样本
n_hold_out = max(1, int(len(positive_indices) * self.hold_out_ratio))
hold_out_positives = np.random.choice(
positive_indices, size=n_hold_out, replace=False
)
# 训练样本:剩余正例 + 所有未标记样本
train_indices = np.setdiff1d(
np.arange(len(X)),
hold_out_positives
)
X_train = X[train_indices]
y_train = y[train_indices]
# 2. 初始训练(第一轮使用均匀权重)
if iteration == 0:
sample_weights = np.ones(len(X_train))
else:
# 使用上一轮的预测计算权重
predictions = self.estimator_.predict_proba(X_train)[:, 1]
sample_weights = self._calculate_weights(X_train, y_train, predictions)
# 训练基础分类器
estimator = clone(self.base_estimator)
estimator.fit(X_train, y_train, sample_weight=sample_weights)
# 3. 估计 P(s=1|y=1)
X_hold_out = X[hold_out_positives]
hold_out_probs = estimator.predict_proba(X_hold_out)[:, 1]
prob_s1y1 = np.mean(hold_out_probs)
# 4. 计算损失(加权交叉熵)
train_probs = estimator.predict_proba(X_train)[:, 1]
loss = -np.mean(sample_weights * (
y_train * np.log(train_probs + 1e-10) +
(1 - y_train) * np.log(1 - train_probs + 1e-10)
))
# 5. 选择最佳模型
if loss < min_loss:
min_loss = loss
best_estimator = estimator
best_prob_s1y1 = prob_s1y1
best_weights = sample_weights
self.estimator_ = best_estimator
self.prob_s1y1_ = best_prob_s1y1
self.weights_ = best_weights
return self
def predict_proba(self, X):
"""预测概率"""
X = check_array(X)
prob_s1x = self.estimator_.predict_proba(X)[:, 1]
prob_y1x = prob_s1x / self.prob_s1y1_
# 确保概率在[0,1]范围内
prob_y1x = np.clip(prob_y1x, 0, 1)
prob_y0x = 1 - prob_y1x
return np.vstack([prob_y0x, prob_y1x]).T
def predict(self, X, threshold=0.5):
"""预测类别"""
proba = self.predict_proba(X)
return (proba[:, 1] > threshold).astype(int)
权重策略比较
均匀权重 (Uniform Weighting)
- 策略:所有样本权重相等
- 效果:等价于经典 Elkanoto 方法
- 适用场景:数据相对干净,噪声较少
置信度权重 (Confidence-based Weighting)
def advanced_confidence_weights(predictions, y, alpha=0.3, beta=2.0):
"""
高级置信度权重策略
alpha: 基础权重
beta: 置信度放大系数
"""
# 基础置信度
base_confidence = np.abs(predictions - 0.5) * 2
# 为正例和预测困难的样本分配更高权重
difficulty_weights = 1 + beta * (1 - base_confidence)
# 结合基础权重
weights = alpha + (1 - alpha) * base_confidence * difficulty_weights
# 为正例样本额外加权
positive_mask = (y == 1)
weights[positive_mask] *= 1.5 # 正例权重提升50%
return np.clip(weights, 0.1, 3.0) # 限制权重范围
距离权重 (Distance-based Weighting)
def mahalanobis_distance_weights(X, y, positive_indices):
"""
基于马氏距离的权重分配
"""
from scipy.spatial.distance import mahalanobis
from sklearn.covariance import LedoitWolf
if len(positive_indices) < 2:
return np.ones(len(X))
# 计算正例的均值和协方差
X_positive = X[positive_indices]
centroid = np.mean(X_positive, axis=0)
# 使用Ledoit-Wolf估计器计算稳健的协方差矩阵
cov_estimator = LedoitWolf().fit(X_positive)
cov_matrix = cov_estimator.covariance_
try:
# 计算马氏距离
inv_cov = np.linalg.pinv(cov_matrix)
distances = np.array([mahalanobis(x, centroid, inv_cov)
for x in X])
# 将距离转换为权重(距离越小,权重越大)
max_dist = np.max(distances)
weights = 1 - (distances / max_dist)
except np.linalg.LinAlgError:
# 如果协方差矩阵奇异,使用欧氏距离
distances = np.linalg.norm(X - centroid, axis=1)
max_dist = np.max(distances)
weights = 1 - (distances / max_dist)
return np.clip(weights, 0.1, 1.0)
实际应用示例
完整的使用示例
import numpy as np
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_curve, average_precision_score
import plotly.graph_objects as go
from plotly.subplots import make_subplots
# 生成示例数据
def create_pu_data(n_samples=1000, positive_ratio=0.3, labeled_ratio=0.4, noise_ratio=0.1):
"""创建带有噪声的PU学习数据"""
X, y_true = make_classification(
n_samples=n_samples,
n_features=20,
n_informative=10,
n_redundant=5,
n_clusters_per_class=1,
flip_y=noise_ratio, # 添加标签噪声
random_state=42
)
# 创建PU标签
y_pu = np.zeros_like(y_true)
positive_indices = np.where(y_true == 1)[0]
# 随机选择一部分正例作为标记的正例
n_labeled = int(len(positive_indices) * labeled_ratio)
labeled_indices = np.random.choice(positive_indices, n_labeled, replace=False)
y_pu[labeled_indices] = 1
# 添加特征噪声(模拟测量误差)
noise_mask = np.random.random(len(X)) < 0.1 # 10%的样本添加特征噪声
X_noisy = X.copy()
X_noisy[noise_mask] += np.random.normal(0, 0.5, X[noise_mask].shape)
return X_noisy, y_true, y_pu
# 比较不同权重策略
def compare_weight_strategies():
"""比较不同权重策略的性能"""
X, y_true, y_pu = create_pu_data()
# 划分训练测试集
X_train, X_test, y_pu_train, y_pu_test = train_test_split(
X, y_pu, test_size=0.3, random_state=42, stratify=y_pu
)
_, _, _, y_true_test = train_test_split(
X, y_true, test_size=0.3, random_state=42, stratify=y_pu
)
strategies = ['uniform', 'confidence', 'distance']
results = {}
for strategy in strategies:
print(f"\n=== 测试权重策略: {strategy} ===")
# 创建加权Elkanoto分类器
base_rf = RandomForestClassifier(n_estimators=100, random_state=42)
pu_classifier = WeightedElkanotoPUClassifier(
base_estimator=base_rf,
hold_out_ratio=0.3,
weight_strategy=strategy,
n_iter=5,
random_state=42
)
# 训练模型
pu_classifier.fit(X_train, y_pu_train)
# 预测
y_prob = pu_classifier.predict_proba(X_test)[:, 1]
y_pred = (y_prob > 0.5).astype(int)
# 评估
ap_score = average_precision_score(y_true_test, y_prob)
precision, recall, _ = precision_recall_curve(y_true_test, y_prob)
results[strategy] = {
'ap_score': ap_score,
'precision': precision,
'recall': recall,
'prob_s1y1': pu_classifier.prob_s1y1_,
'classifier': pu_classifier
}
print(f"P(s=1|y=1)估计值: {pu_classifier.prob_s1y1_:.4f}")
print(f"平均精度 (AP): {ap_score:.4f}")
return results, y_true_test
# 可视化比较结果
def plot_comparison(results, y_true):
"""可视化不同权重策略的比较结果"""
fig = make_subplots(
rows=2, cols=2,
subplot_titles=(
'精确率-召回率曲线比较',
'平均精度比较',
'P(s=1|y=1)估计值比较',
'权重分布示例'
)
)
# 1. 精确率-召回率曲线
for strategy, result in results.items():
fig.add_trace(
go.Scatter(
x=result['recall'],
y=result['precision'],
mode='lines',
name=f'{strategy} (AP={result["ap_score"]:.3f})',
line=dict(width=3)
),
row=1, col=1
)
# 2. 平均精度比较
strategies = list(results.keys())
ap_scores = [results[s]['ap_score'] for s in strategies]
fig.add_trace(
go.Bar(x=strategies, y=ap_scores,
marker_color=['blue', 'red', 'green']),
row=1, col=2
)
# 3. P(s=1|y=1)估计值比较
prob_s1y1_values = [results[s]['prob_s1y1'] for s in strategies]
fig.add_trace(
go.Bar(x=strategies, y=prob_s1y1_values,
marker_color=['lightblue', 'lightcoral', 'lightgreen']),
row=2, col=1
)
# 更新布局
fig.update_layout(
height=800,
title_text="加权Elkanoto方法不同权重策略比较",
showlegend=True
)
fig.update_xaxes(title_text="召回率", row=1, col=1)
fig.update_yaxes(title_text="精确率", row=1, col=1)
fig.update_xaxes(title_text="策略", row=1, col=2)
fig.update_yaxes(title_text="平均精度", row=1, col=2)
fig.update_xaxes(title_text="策略", row=2, col=1)
fig.update_yaxes(title_text="P(s=1|y=1)估计值", row=2, col=1)
fig.show()
# 运行比较
results, y_true_test = compare_weight_strategies()
plot_comparison(results, y_true_test)
方法优势与适用场景
主要优势
- 鲁棒性更强:对噪声和异常值的敏感性降低
- 处理不平衡数据:通过权重调整有效处理类别不平衡
- 收敛更快:关注重要样本,加速模型收敛
- 灵活性高:支持多种权重策略,适应不同场景
适用场景
- 高噪声数据:当训练数据包含较多标签噪声时
- 严重类别不平衡:正例数量远少于未标记样本时
- 异质数据:不同样本群体具有不同特征分布时
- 在线学习:需要逐步更新权重的场景
参数调优建议
# 关键参数调优建议
optimal_params = {
'hold_out_ratio': [0.2, 0.3, 0.4], # 保留比例
'weight_strategy': ['uniform', 'confidence', 'distance'],
'n_iter': [5, 10, 15], # 迭代次数
}
# 对于不同数据规模的建议
size_recommendations = {
'small_dataset': {'n_iter': 5, 'hold_out_ratio': 0.2},
'medium_dataset': {'n_iter': 10, 'hold_out_ratio': 0.3},
'large_dataset': {'n_iter': 15, 'hold_out_ratio': 0.4},
}
基于 Bagging 的PU学习
基于 Bagging 的 PU 学习是一种集成学习方法,它通过组合多个弱分类器来提高 PU 学习任务的性能。这种方法特别适合处理 PU 学习中的不确定性和噪声问题。
方法背景与动机
PU 学习的挑战
PU 学习面临两个主要挑战:
- 标签不确定性:未标记样本中既包含正例也包含负例
- 样本选择偏差:标记的正例可能不是所有正例的代表性样本
Bagging 的优势
Bagging(Bootstrap Aggregating)通过以下方式应对这些挑战:
- 减少方差:通过组合多个模型降低过拟合风险
- 处理不确定性:多个模型的不同视角可以更好地处理标签不确定性
- 增强鲁棒性:对噪声和异常值更加稳健
方法原理与理论基础
核心思想
基于 Bagging 的 PU 学习方法的核心思想是:通过多次自助采样创建多个训练子集,在每个子集上训练一个基分类器,然后通过投票或平均来集成这些分类器的预测结果。
数学基础
对于给定的 PU 数据集$D = (X_P, X_U)$,其中$X_P$是标记的正例,是$X_U$未标记样本。
Bagging PU 学习的目标是学习一个函数$f: X \rightarrow [0,1]$,使得:$f(x) = \frac{1}{B} \sum_{b=1}^{B} f_b(x)$
其中$B$是基分类器的数量,$f_b$是第$b$个基分类器。
算法流程详解
基本 Bagging PU 算法
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin, clone
from sklearn.utils import resample
from sklearn.utils.validation import check_X_y, check_array
class BaggingPUClassifier(BaseEstimator, ClassifierMixin):
"""
基于 Bagging 的 PU 分类器
"""
def __init__(self, base_estimator=None, n_estimators=10,
max_samples=1.0, max_features=1.0,
bootstrap=True, random_state=None):
self.base_estimator = base_estimator
self.n_estimators = n_estimators
self.max_samples = max_samples
self.max_features = max_features
self.bootstrap = bootstrap
self.random_state = random_state
self.estimators_ = []
self.feature_indices_ = []
def _create_training_set(self, X, y, random_state):
"""
创建 PU 学习的训练集
关键:从未标记样本中抽取样本作为负例
"""
# 分离正例和未标记样本
positive_indices = np.where(y == 1)[0]
unlabeled_indices = np.where(y == 0)[0]
# 正例采样
n_pos_samples = len(positive_indices)
if self.bootstrap:
pos_sample_indices = resample(
positive_indices,
n_samples=n_pos_samples,
replace=True,
random_state=random_state
)
else:
pos_sample_indices = positive_indices
# 从未标记样本中抽取负例
n_neg_samples = int(len(pos_sample_indices) * self.max_samples)
neg_sample_indices = resample(
unlabeled_indices,
n_samples=n_neg_samples,
replace=True,
random_state=random_state
)
# 合并正例和负例样本索引
sample_indices = np.concatenate([pos_sample_indices, neg_sample_indices])
# 特征采样
n_features = X.shape[1]
n_selected_features = int(n_features * self.max_features)
feature_indices = np.random.choice(
n_features,
size=n_selected_features,
replace=False
)
return sample_indices, feature_indices
def fit(self, X, y):
"""
训练 Bagging PU 分类器
"""
X, y = check_X_y(X, y)
np.random.seed(self.random_state)
self.estimators_ = []
self.feature_indices_ = []
for i in range(self.n_estimators):
# 创建随机种子(确保可重复性)
random_state = np.random.RandomState(self.random_state + i) if self.random_state else None
# 创建训练子集
sample_indices, feature_indices = self._create_training_set(X, y, random_state)
# 提取子集数据
X_subset = X[sample_indices][:, feature_indices]
y_subset = y[sample_indices]
# 创建并训练基分类器
estimator = clone(self.base_estimator)
estimator.fit(X_subset, y_subset)
# 保存模型和特征索引
self.estimators_.append(estimator)
self.feature_indices_.append(feature_indices)
return self
def predict_proba(self, X):
"""
预测概率
"""
X = check_array(X)
n_samples = X.shape[0]
# 收集所有基分类器的预测
all_probas = []
for estimator, feature_indices in zip(self.estimators_, self.feature_indices_):
X_sub = X[:, feature_indices]
probas = estimator.predict_proba(X_sub)
all_probas.append(probas)
# 平均概率
avg_proba = np.mean(all_probas, axis=0)
return avg_proba
def predict(self, X, threshold=0.5):
"""
预测类别
"""
proba = self.predict_proba(X)
return (proba[:, 1] > threshold).astype(int)
改进的 Bagging PU 算法
class ImprovedBaggingPUClassifier(BaggingPUClassifier):
"""
改进的 Bagging PU 分类器
添加了权重和置信度评估
"""
def __init__(self, base_estimator=None, n_estimators=10,
max_samples=1.0, max_features=1.0,
bootstrap=True, random_state=None,
confidence_threshold=0.7, use_weighting=True):
super().__init__(base_estimator, n_estimators, max_samples,
max_features, bootstrap, random_state)
self.confidence_threshold = confidence_threshold
self.use_weighting = use_weighting
self.estimator_weights_ = []
def fit(self, X, y):
"""
训练改进的 Bagging PU 分类器
"""
X, y = check_X_y(X, y)
np.random.seed(self.random_state)
self.estimators_ = []
self.feature_indices_ = []
self.estimator_weights_ = []
for i in range(self.n_estimators):
random_state = np.random.RandomState(self.random_state + i) if self.random_state else None
# 创建训练子集
sample_indices, feature_indices = self._create_training_set(X, y, random_state)
X_subset = X[sample_indices][:, feature_indices]
y_subset = y[sample_indices]
# 训练基分类器
estimator = clone(self.base_estimator)
estimator.fit(X_subset, y_subset)
# 计算基分类器的权重(基于在标记数据上的性能)
if self.use_weighting:
# 使用标记的正例评估性能
labeled_pos_indices = np.where(y == 1)[0]
if len(labeled_pos_indices) > 0:
X_labeled_pos = X[labeled_pos_indices][:, feature_indices]
y_labeled_pos = y[labeled_pos_indices]
# 计算在标记正例上的准确率作为权重
accuracy = estimator.score(X_labeled_pos, y_labeled_pos)
weight = max(0.1, accuracy) # 确保权重不为0
else:
weight = 1.0
else:
weight = 1.0
# 保存模型、特征索引和权重
self.estimators_.append(estimator)
self.feature_indices_.append(feature_indices)
self.estimator_weights_.append(weight)
return self
def predict_proba(self, X):
"""
加权平均概率预测
"""
X = check_array(X)
n_samples = X.shape[0]
# 收集所有基分类器的预测
all_probas = []
for i, (estimator, feature_indices) in enumerate(zip(self.estimators_, self.feature_indices_)):
X_sub = X[:, feature_indices]
probas = estimator.predict_proba(X_sub)
# 应用权重
if self.use_weighting:
weight = self.estimator_weights_[i]
# 对概率进行加权
weighted_probas = probas * weight
all_probas.append(weighted_probas)
else:
all_probas.append(probas)
# 加权平均概率
if self.use_weighting:
total_weight = sum(self.estimator_weights_)
avg_proba = np.sum(all_probas, axis=0) / total_weight
else:
avg_proba = np.mean(all_probas, axis=0)
return avg_proba
def predict_with_confidence(self, X):
"""
返回预测结果和置信度
"""
proba = self.predict_proba(X)
predictions = (proba[:, 1] > 0.5).astype(int)
# 计算置信度(基于概率与决策边界的距离)
confidence = np.abs(proba[:, 1] - 0.5) * 2
return predictions, confidence
def get_estimator_performance(self):
"""
获取各个基分类器的性能评估
"""
performances = []
for i, weight in enumerate(self.estimator_weights_):
performances.append({
'estimator_index': i,
'weight': weight,
'n_features': len(self.feature_indices_[i])
})
return performances
关键技术与优化策略
样本采样策略
def advanced_sampling_strategy(X, y, sampling_method='balanced',
positive_weight=1.5, random_state=None):
"""
高级采样策略
"""
positive_indices = np.where(y == 1)[0]
unlabeled_indices = np.where(y == 0)[0]
if sampling_method == 'balanced':
# 平衡采样:正例和负例数量相等
n_pos = len(positive_indices)
n_neg = min(len(unlabeled_indices), n_pos)
elif sampling_method == 'weighted':
# 加权采样:为正例分配更高权重
n_pos = len(positive_indices)
n_neg = int(n_pos * positive_weight)
elif sampling_method == 'proportional':
# 比例采样:根据数据集大小确定采样比例
total_size = len(positive_indices) + len(unlabeled_indices)
pos_ratio = len(positive_indices) / total_size
n_pos = len(positive_indices)
n_neg = int(n_pos * (1 - pos_ratio) / pos_ratio)
# 执行采样
pos_samples = resample(
positive_indices,
n_samples=n_pos,
replace=True,
random_state=random_state
)
neg_samples = resample(
unlabeled_indices,
n_samples=min(n_neg, len(unlabeled_indices)),
replace=True,
random_state=random_state
)
return np.concatenate([pos_samples, neg_samples])
# 集成到 Bagging PU 分类器中
class AdvancedBaggingPUClassifier(ImprovedBaggingPUClassifier):
def __init__(self, base_estimator=None, n_estimators=10,
sampling_method='balanced', positive_weight=1.5, **kwargs):
super().__init__(base_estimator, n_estimators, **kwargs)
self.sampling_method = sampling_method
self.positive_weight = positive_weight
def _create_training_set(self, X, y, random_state):
positive_indices = np.where(y == 1)[0]
unlabeled_indices = np.where(y == 0)[0]
# 使用高级采样策略
sample_indices = advanced_sampling_strategy(
X, y, self.sampling_method, self.positive_weight, random_state
)
# 特征采样
n_features = X.shape[1]
n_selected_features = int(n_features * self.max_features)
feature_indices = np.random.choice(
n_features,
size=n_selected_features,
replace=False,
random_state=random_state
)
return sample_indices, feature_indices
多样性增强技术
def enhance_diversity(estimators, feature_indices, X, y):
"""
增强基分类器多样性的技术
"""
diversities = []
for i in range(len(estimators)):
# 计算与其他分类器的预测差异
diversity_score = 0
for j in range(len(estimators)):
if i != j:
# 使用标记数据计算预测差异
labeled_indices = np.where(y == 1)[0]
if len(labeled_indices) > 0:
X_labeled = X[labeled_indices]
pred_i = estimators[i].predict(X_labeled[:, feature_indices[i]])
pred_j = estimators[j].predict(X_labeled[:, feature_indices[j]])
disagreement = np.mean(pred_i != pred_j)
diversity_score += disagreement
diversities.append(diversity_score / (len(estimators) - 1))
return diversities
class DiversityEnhancedBaggingPU(AdvancedBaggingPUClassifier):
"""
多样性增强的 Bagging PU 分类器
"""
def __init__(self, base_estimator=None, n_estimators=10,
diversity_weight=0.3, **kwargs):
super().__init__(base_estimator, n_estimators, **kwargs)
self.diversity_weight = diversity_weight
def fit(self, X, y):
# 首先进行标准训练
super().fit(X, y)
# 计算多样性并调整权重
diversities = enhance_diversity(self.estimators_, self.feature_indices_, X, y)
# 结合准确率和多样性调整权重
for i in range(len(self.estimators_)):
accuracy_based_weight = self.estimator_weights_[i]
diversity_based_weight = diversities[i]
# 组合权重
combined_weight = (1 - self.diversity_weight) * accuracy_based_weight + \
self.diversity_weight * diversity_based_weight
self.estimator_weights_[i] = combined_weight
return self
实际应用与评估
完整应用示例
import numpy as np
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_curve, average_precision_score, classification_report
import plotly.graph_objects as go
from plotly.subplots import make_subplots
def demonstrate_bagging_pu():
"""
演示基于 Bagging 的 PU 学习
"""
# 1. 生成 PU 数据
print("=== 生成 PU 数据 ===")
X, y_true = make_classification(
n_samples=2000, n_features=20, n_informative=10,
n_redundant=5, n_clusters_per_class=1,
flip_y=0.05, random_state=42
)
# 创建 PU 标签(仅标记部分正例)
y_pu = np.zeros_like(y_true)
positive_indices = np.where(y_true == 1)[0]
labeled_ratio = 0.3 # 仅标记30%的正例
n_labeled = int(len(positive_indices) * labeled_ratio)
labeled_indices = np.random.choice(positive_indices, n_labeled, replace=False)
y_pu[labeled_indices] = 1
print(f"数据统计:")
print(f"- 总样本数: {len(y_true)}")
print(f"- 真实正例数: {sum(y_true)}")
print(f"- 标记的正例数: {sum(y_pu)}")
print(f"- 未标记样本中的隐藏正例数: {sum(y_true) - sum(y_pu)}")
# 2. 划分训练测试集
X_train, X_test, y_pu_train, y_pu_test = train_test_split(
X, y_pu, test_size=0.3, random_state=42, stratify=y_pu
)
_, _, _, y_true_test = train_test_split(
X, y_true, test_size=0.3, random_state=42, stratify=y_pu
)
# 3. 比较不同方法
print("\n=== 方法比较 ===")
# 方法1: 标准分类器(错误地将未标记样本视为负例)
print("\n--- 方法1: 标准分类器(朴素方法) ---")
naive_rf = RandomForestClassifier(n_estimators=100, random_state=42)
naive_rf.fit(X_train, y_pu_train)
y_pred_naive = naive_rf.predict(X_test)
y_prob_naive = naive_rf.predict_proba(X_test)[:, 1]
ap_naive = average_precision_score(y_true_test, y_prob_naive)
print(f"平均精度 (AP): {ap_naive:.4f}")
# 方法2: 基本 Bagging PU
print("\n--- 方法2: 基本 Bagging PU ---")
base_svm = SVC(C=1.0, kernel='rbf', probability=True, random_state=42)
bagging_pu_basic = BaggingPUClassifier(
base_estimator=base_svm,
n_estimators=20,
max_samples=0.8,
max_features=0.8,
random_state=42
)
bagging_pu_basic.fit(X_train, y_pu_train)
y_prob_basic = bagging_pu_basic.predict_proba(X_test)[:, 1]
ap_basic = average_precision_score(y_true_test, y_prob_basic)
print(f"平均精度 (AP): {ap_basic:.4f}")
# 方法3: 改进的 Bagging PU
print("\n--- 方法3: 改进的 Bagging PU ---")
bagging_pu_improved = ImprovedBaggingPUClassifier(
base_estimator=RandomForestClassifier(n_estimators=50, random_state=42),
n_estimators=30,
max_samples=0.8,
max_features=0.7,
use_weighting=True,
random_state=42
)
bagging_pu_improved.fit(X_train, y_pu_train)
y_prob_improved = bagging_pu_improved.predict_proba(X_test)[:, 1]
ap_improved = average_precision_score(y_true_test, y_prob_improved)
print(f"平均精度 (AP): {ap_improved:.4f}")
# 方法4: 多样性增强的 Bagging PU
print("\n--- 方法4: 多样性增强的 Bagging PU ---")
bagging_pu_diverse = DiversityEnhancedBaggingPU(
base_estimator=RandomForestClassifier(n_estimators=50, random_state=42),
n_estimators=30,
sampling_method='balanced',
diversity_weight=0.3,
random_state=42
)
bagging_pu_diverse.fit(X_train, y_pu_train)
y_prob_diverse = bagging_pu_diverse.predict_proba(X_test)[:, 1]
ap_diverse = average_precision_score(y_true_test, y_prob_diverse)
print(f"平均精度 (AP): {ap_diverse:.4f}")
# 4. 可视化比较结果
print("\n=== 结果可视化 ===")
visualize_comparison(
y_true_test,
[y_prob_naive, y_prob_basic, y_prob_improved, y_prob_diverse],
['朴素方法', '基本BaggingPU', '改进BaggingPU', '多样性BaggingPU'],
[ap_naive, ap_basic, ap_improved, ap_diverse]
)
return {
'naive': {'prob': y_prob_naive, 'ap': ap_naive},
'basic': {'prob': y_prob_basic, 'ap': ap_basic},
'improved': {'prob': y_prob_improved, 'ap': ap_improved},
'diverse': {'prob': y_prob_diverse, 'ap': ap_diverse},
'y_true': y_true_test
}
def visualize_comparison(y_true, probabilities, method_names, ap_scores):
"""
可视化比较结果
"""
fig = make_subplots(
rows=2, cols=2,
subplot_titles=(
'精确率-召回率曲线比较',
'平均精度比较',
'基分类器权重分布',
'预测概率分布'
)
)
# 1. 精确率-召回率曲线
colors = ['red', 'blue', 'green', 'purple']
for i, (y_prob, name, color) in enumerate(zip(probabilities, method_names, colors)):
precision, recall, _ = precision_recall_curve(y_true, y_prob)
fig.add_trace(
go.Scatter(x=recall, y=precision, mode='lines',
name=f'{name} (AP={ap_scores[i]:.3f})',
line=dict(color=color, width=2)),
row=1, col=1
)
# 2. 平均精度比较
fig.add_trace(
go.Bar(x=method_names, y=ap_scores,
marker_color=colors,
text=[f'{score:.3f}' for score in ap_scores],
textposition='auto'),
row=1, col=2
)
# 3. 预测概率分布(以多样性方法为例)
y_prob_diverse = probabilities[3]
fig.add_trace(
go.Histogram(x=y_prob_diverse, nbinsx=30, name='预测概率分布',
marker_color='lightblue', opacity=0.7),
row=2, col=1
)
# 添加决策阈值线
fig.add_vline(x=0.5, line_dash="dash", line_color="red", row=2, col=1)
# 4. 方法性能提升百分比
improvement = [(ap_scores[i] - ap_scores[0]) / ap_scores[0] * 100
for i in range(1, len(ap_scores))]
fig.add_trace(
go.Bar(x=method_names[1:], y=improvement,
marker_color=colors[1:],
text=[f'{imp:.1f}%' for imp in improvement],
textposition='auto'),
row=2, col=2
)
fig.update_layout(
height=800,
title_text="基于Bagging的PU学习方法比较",
showlegend=True
)
fig.update_xaxes(title_text="召回率", row=1, col=1)
fig.update_yaxes(title_text="精确率", row=1, col=1)
fig.update_xaxes(title_text="方法", row=1, col=2)
fig.update_yaxes(title_text="平均精度", row=1, col=2)
fig.update_xaxes(title_text="预测概率", row=2, col=1)
fig.update_yaxes(title_text="频数", row=2, col=1)
fig.update_xaxes(title_text="方法", row=2, col=2)
fig.update_yaxes(title_text="相对于朴素方法的提升 (%)", row=2, col=2)
fig.show()
# 运行演示
results = demonstrate_bagging_pu()
参数调优与模型选择
def parameter_tuning_example():
"""
参数调优示例
"""
# 生成数据
X, y_true = make_classification(n_samples=1500, n_features=15, random_state=42)
y_pu = create_pu_labels(y_true, labeled_ratio=0.3)
# 参数网格
param_grid = {
'n_estimators': [10, 20, 30, 50],
'max_samples': [0.5, 0.7, 0.8, 1.0],
'max_features': [0.5, 0.7, 0.8, 1.0],
'sampling_method': ['balanced', 'weighted', 'proportional']
}
best_score = 0
best_params = {}
# 简化的网格搜索(实际中应使用交叉验证)
for n_est in param_grid['n_estimators']:
for max_samp in param_grid['max_samples']:
for max_feat in param_grid['max_features']:
for samp_method in param_grid['sampling_method']:
# 创建分类器
classifier = AdvancedBaggingPUClassifier(
base_estimator=RandomForestClassifier(n_estimators=50),
n_estimators=n_est,
max_samples=max_samp,
max_features=max_feat,
sampling_method=samp_method,
random_state=42
)
# 训练和评估(简化版)
X_train, X_test, y_pu_train, y_pu_test = train_test_split(
X, y_pu, test_size=0.3, random_state=42
)
_, _, _, y_true_test = train_test_split(
X, y_true, test_size=0.3, random_state=42
)
classifier.fit(X_train, y_pu_train)
y_prob = classifier.predict_proba(X_test)[:, 1]
ap_score = average_precision_score(y_true_test, y_prob)
if ap_score > best_score:
best_score = ap_score
best_params = {
'n_estimators': n_est,
'max_samples': max_samp,
'max_features': max_feat,
'sampling_method': samp_method
}
print(f"最佳参数: {best_params}")
print(f"最佳平均精度: {best_score:.4f}")
return best_params, best_score
def create_pu_labels(y_true, labeled_ratio=0.3):
"""
创建PU标签
"""
y_pu = np.zeros_like(y_true)
positive_indices = np.where(y_true == 1)[0]
n_labeled = int(len(positive_indices) * labeled_ratio)
labeled_indices = np.random.choice(positive_indices, n_labeled, replace=False)
y_pu[labeled_indices] = 1
return y_pu
实际应用场景与最佳实践
适用场景
基于 Bagging 的 PU 学习特别适用于以下场景:
- 高噪声数据:当未标记样本中包含大量噪声时
- 小样本正例:当标记的正例数量有限时
- 数据异质性:当正例样本来自不同分布时
- 稳定性要求高:当需要稳定可靠的预测时
最佳实践建议
class PracticalBaggingPUGuide:
"""
实际应用指南
"""
@staticmethod
def recommend_parameters(data_size, positive_ratio, problem_type):
"""
根据问题特性推荐参数
"""
recommendations = {}
if data_size < 1000:
recommendations.update({
'n_estimators': 10,
'max_samples': 0.9,
'max_features': 0.8
})
elif data_size < 10000:
recommendations.update({
'n_estimators': 20,
'max_samples': 0.8,
'max_features': 0.7
})
else:
recommendations.update({
'n_estimators': 30,
'max_samples': 0.7,
'max_features': 0.6
})
if positive_ratio < 0.1:
recommendations['sampling_method'] = 'weighted'
recommendations['positive_weight'] = 2.0
else:
recommendations['sampling_method'] = 'balanced'
if problem_type == 'high_noise':
recommendations.update({
'n_estimators': 50,
'use_weighting': True,
'diversity_weight': 0.4
})
return recommendations
@staticmethod
def select_base_estimator(problem_characteristics):
"""
根据问题特性选择基分类器
"""
if problem_characteristics['n_features'] > 100:
# 高维数据:使用线性模型或特征选择能力强的模型
from sklearn.linear_model import LogisticRegression
return LogisticRegression(penalty='l1', solver='liblinear')
elif problem_characteristics['n_samples'] < 1000:
# 小样本:使用简单模型避免过拟合
from sklearn.svm import SVC
return SVC(kernel='linear', probability=True)
else:
# 一般情况:使用随机森林
from sklearn.ensemble import RandomForestClassifier
return RandomForestClassifier(n_estimators=100)
@staticmethod
def evaluate_model_robustness(classifier, X, y, n_trials=10):
"""
评估模型鲁棒性
"""
ap_scores = []
for i in range(n_trials):
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=i
)
# 重新训练(使用不同的随机种子)
trial_classifier = clone(classifier)
trial_classifier.set_params(random_state=i)
trial_classifier.fit(X_train, y_train)
# 评估
y_prob = trial_classifier.predict_proba(X_test)[:, 1]
ap_score = average_precision_score(y_test, y_prob)
ap_scores.append(ap_score)
robustness_score = 1 - (np.std(ap_scores) / np.mean(ap_scores))
return {
'mean_ap': np.mean(ap_scores),
'std_ap': np.std(ap_scores),
'robustness': robustness_score
}
参考链接: