随着机器学习等技术的发展,智能化营销已经渗透到各行各业。商家可以通过多种渠道触达消费者,比如淘宝上商家可以圈定他想要的目标人群,进行广告推送,为店铺拉新,也可以通过短信或旺旺这些渠道定向发放优惠券。对很多公司而言,进入到了精细化运营的存量时代,如何找准对营销更敏感的客群,促成营销推广的效率的最大化,成为企业营销过程中的最大挑战。
增益模型(Uplift Model)产生背景
在的广告营销上,小型企业通常会向其所有客户的邮箱、手机发送促销邮件或短信。对这一操作没有投入太多思考的主要原因是因为小企业的用户数量少并且这类活动不太耗费成本。但是,在大型企业的情况中,事情就变得复杂了,因为测量广告的影响变成一种必要。大多数运营经理在营销时主要两种做法:
- 凭经验:广告战役经理根据他的经验采取一些主观安排来选择目标群体。
- 运用响应模型(Response Model):响应模型会根据用户数据告诉你用户采取预期行为的倾向(比如,哪些用户更有可能购买某一类产品)。
常用的点击率预测模型,称为响应模型(response model),即预测用户看到商品后点击的概率。在智能营销的发放优惠券场景下也可以使用这种模型,即用户看到优惠券后购买商品的概率。
通常,公司会使用决策树或类似的分类模型,用历史数据来将用户分类成“高购买倾向”和“低购买倾向”,每个用户获得一个“倾向分数”来指代他购买某类产品的倾向性。然后针对“高购买倾向”的人群推送广告。这里的“高购买倾向”指的是,该潜在用户的各类行为数据和已经购买的老用户的行为数据非常相似,因而我们推断这个潜在用户很可能会购买产品。但这些人,是否是因为我们推送的广告而购买产品的呢?分类模型并不能告诉你答案。这也是倾向模型的局限所在:只能找到对产品“高购买倾向”的人,而不能识别出“对广告更有反应的人”,因而无法对广告的效果做因果归因。
无论是红包还是广告,我们都称为营销的干预手段,其背后都是有成本的。营销的目标就是在成本有限的情况下最大化营销的总产出,关键的一点是我们能否准确找到真正能被营销打动的用户,我们称他们为营销敏感人群,可以通过下面的图进行简单的解释:

比如,我们对人群做四象限的划分,横纵坐标分别是用户在有干预和无干预情况下的购买状况。如上图,左上角人群的购买状况在干预后发生了正向变化,如果我们不对这类人群进行干预,那他有可能是不购买的,但是干预之后的购买概率有极大提升,所以这类人群是我们真正想要触达的用户,即营销敏感人群。而其他人群比如第 2 类和第 3 类,在干预前后的购买状况没有变化,所以预算花费可能是浪费。右下角是一类比较特殊的人群,虽然其在干预前后的状态有跳变,但这种跳变不是我们希望看到的,因为确实有一些人群对营销是反感的,所以对这类人群我们应该极力避免触达。Uplift Model 正是为了识别我们想要的营销敏感人群。
Uplift Model 和 Response Model 之所以有差异,主要在于两个模型的预测目标不一样:
- Response Model 的目标是估计用户看过广告之后转化的概率,这本身是一个相关性,但这个相关性会导致我们没有办法区分出自然转化人群。
- Uplift Model 是估计用户因为广告而购买的概率,这是一个因果推断的问题,帮助我们锁定对营销敏感的人群。所以 Uplift Model 是整个智能营销中非常关键的技术,预知每个用户的营销敏感程度,从而帮助我们制定营销策略,促成整个营销的效用最大化。
用数学的方式来解释,设G表示某种干预策略(如是否推送广告),$\boldsymbol{X}$表示用户特征,$Y = 1 $表示用户输出的正向结果(如下单或点击):
- Reponse model:$P(Y = 1 | \boldsymbol{X})$,看过广告之后购买的概率
- Uplift model:$P(Y = 1 | \boldsymbol{X}, G)$,因为广告而购买的概率
增益模型(Uplift Model)应用场景
应用场景
- 精准营销:识别“ Persuadables”(仅因干预而转化的用户),避免对“Sure Things”(无论如何都会购买)和“Lost Causes”(无论如何不购买)浪费资源。
- 动态定价:预测价格调整对用户购买意愿的边际影响。
- 医疗个性化:为患者选择最有效的治疗方案。
- 客户留存:定向干预高流失风险且对干预敏感的用户。
行业实际应用案例
Netflix 的个性化推荐
- 目标: 仅对受推荐影响的用户展示内容,避免打扰“自然转化”用户。
- 方法:
- 构建 Uplift 模型识别“Persuadables”用户。
- 特征:用户观影历史、页面停留时间、设备类型。
金融风控中的催收策略优化
- 场景: 识别对催收电话敏感的用户,降低坏账率。
- 技术:
- 使用S-Learner 建模,特征包括还款历史、联系方式有效性。
- 结果:减少无效催收成本 30%+。
游戏用户留存干预
- 案例: 某手游公司通过 Uplift 模型定向发放免费道具。
- 策略:
- 对“可能流失但受道具激励”的用户(Sleeping Dogs)进行干预。
- 使用Two-Model Approach(T-Learner)预测干预效果。
零售动态定价
- 目标: 预测价格调整对销量的边际影响。
- 方法:
- 基于 A/B 测试数据训练 Uplift 模型。
- 特征:商品类别、用户价格敏感度、促销历史。
增益模型(Uplift Model)的原理
增益模型(Uplift Model)是一种基于因果推断的机器学习方法,其核心目标是量化某个干预(如广告推送、促销活动、医疗治疗)对个体行为或结果的因果效应。它的核心思想是:回答“干预是否真正改变了结果”这一问题,而不仅仅是预测结果本身。
增益模型与传统预测模型的区别在于:
- 传统模型:预测个体在干预下的结果(如“用户看到广告后是否会购买”)。
- 增益模型:预测干预对个体的因果效应,即干预带来的增量变化(如“用户因为看到广告而购买的概率提升值”)。
核心思想:因果推断与反事实框架
增益模型的原理建立在反事实(Counterfactual)推理的基础上。对于每个个体,我们需要同时观测两种潜在结果:
- 干预组结果(Treatment Group):个体接受干预后的结果$Y^T$。
- 对照组结果(Control Group):个体未接受干预时的结果$Y^C$。
个体处理效应(ITE,Individual Treatment Effect)定义为两者的差值:
$$\text{ITE} = Y^T – Y^C$$
然而,现实中我们只能观测到其中一个结果(要么在干预组,要么在对照组),无法同时观测两者的真实值。因此,增益模型的目标是通过建模估计这种反事实差异。
核心公式与建模目标
增益模型的数学本质是估计条件平均处理效应(CATE,Conditional Average Treatment Effect):
$$\text{CATE}(X) = E[Y^T – Y^C \mid X]$$
其中 X 是用户的特征变量。通过建模 $\text{CATE}(X)$ ,我们可以预测干预对不同特征个体的因果效应。
核心方法:基于条件独立假设
增益模型依赖以下假设:
- 随机化实验数据:用户被随机分配到实验组(接受干预)和对照组(未接受干预),确保两组特征分布一致。
- 条件独立假设(CIA):在控制特征X 后,干预分配 T 与潜在结果无关,即 $T \perp (Y(1), Y(0)) \mid X$。
目标:通过建模实验组和对照组的差异,学习条件平均处理效应(CATE):$\tau(x) = E[Y(1) – Y(0) \mid X = x]$
增益模型的有效性依赖于以下因果推断假设:
- 无混淆性(Unconfoundedness):所有影响干预分配和结果的混杂变量均已观测并包含在X 中。
- 重叠性(Overlap):每个个体均有概率被分配到干预组或对照组(即$0 < P(T=1 \mid X) < 1$ )。
- 稳定单元处理值假设(SUTVA):个体的结果不受其他个体是否接受干预的影响(无干扰效应)。
Uplift常见建模方法
基础方法
双模型法(Two-Model Approach)
双模型法是Uplift建模中最基础、最直观的方法之一,核心思想是通过分别建模实验组(接受干预)和对照组(未接受干预)的响应概率,计算个体层面的增量效应(Uplift)。
核心原理
- 目标:估计干预措施对个体的因果效应(即$\text{Uplift} = Y(1) – Y(0)$ ,其中Y(1) 和 Y(0) 为潜在结果)。
- 假设:
- 实验组和对照组的特征分布相似(无选择偏差)。
- 忽略未观测混杂因素(如未记录的变量影响干预分配)。
建模步骤
- 数据划分:
- 将数据分为实验组(T=1)和对照组(T=0)。
- 确保两组样本的特征分布尽量一致(可通过倾向得分匹配或随机实验设计保证)。
- 模型训练:
- 实验组模型$M_1$:使用实验组数据训练,预测个体在接受干预时的响应概率$P(Y=1|T=1, X)$ 。
- 对照组模型$M_0$:使用对照组数据训练,预测个体未接受干预时的响应概率$P(Y=1|T=0, X)$。
- 常用模型:逻辑回归、随机森林、梯度提升树(GBDT)等。
- Uplift计算:
- 对每个样本X ,计算其Uplift值为两模型预测结果的差值:$\text{Uplift}(X) = M_1(X) – M_0(X)$
- 结果解释:
- $\text{Uplift} > 0$ :干预对该个体有正向效果(敏感人群)。
- $\text{Uplift} \leq 0$ :干预无效或负向效果(不敏感或反感人群)。
优缺点分析
优点
- 简单易实现:直接复用传统分类模型,无需复杂框架。
- 可解释性:结果可分解为实验组和对照组的预测贡献。
- 适用性广:适用于任何可预测二元响应的场景(如转化率、购买率等)。
缺点
- 误差累积:两个模型的预测误差会叠加,导致Uplift估计偏差。例如:若$M_1$高估,$M_0$低估,Uplift会被显著放大。
- 忽略交互效应:未显式建模处理变量(T)与特征(X)的交互关系。
- 依赖数据均衡性:实验组/对照组样本量差异大时,模型性能可能下降。
改进方法
- 模型校准(Calibration):对$M_1$和$M_0$的输出进行概率校准(如Platt Scaling或Isotonic Regression),减少预测偏差。
- 联合训练(Shared Representation):在神经网络中共享底层特征表示层,仅在上层分叉处理实验组和对照组(类似TARNet),减少特征学习差异。
- 集成学习:使用Bagging或Boosting集成多个双模型,降低方差。例如:对实验组和对照组分别做Bootstrap采样,训练多个模型取平均。
- 倾向得分调整:若数据存在选择偏差,可引入倾向得分P(T=1|X) 对样本加权,缓解分布差异。
适用场景
- 随机对照试验(RCT)数据:实验组和对照组通过随机分配,特征分布天然一致。
- 快速验证需求:需快速验证Uplift模型效果,作为基线方法。
- 资源有限场景:缺少复杂建模工具或计算资源时的替代方案。
代码实现框架(Python示例)
from sklearn.ensemble import RandomForestClassifier from sklearn.calibration import CalibratedClassifierCV # 实验组和对照组数据 X_treatment = treatment_data.drop(columns=['T', 'Y']) y_treatment = treatment_data['Y'] X_control = control_data.drop(columns=['T', 'Y']) y_control = control_data['Y'] # 训练实验组模型(校准概率) model_treatment = CalibratedClassifierCV(RandomForestClassifier()) model_treatment.fit(X_treatment, y_treatment) # 训练对照组模型 model_control = CalibratedClassifierCV(RandomForestClassifier()) model_control.fit(X_control, y_control) # 计算Uplift值 uplift_scores = model_treatment.predict_proba(X_all)[:, 1] - model_control.predict_proba(X_all)[:, 1]
标签转换法(Class Transformation)
标签转换法(Class Transformation)是Uplift建模中一种巧妙的方法,通过重新定义目标变量,将因果效应估计问题转换为传统分类任务。其核心思想是通过构造特殊标签,让模型直接学习干预的增量效应。
核心原理
- 目标:直接建模干预的因果效应,避免双模型法的误差累积问题。
- 核心假设:
- 实验组(T=1)和对照组(T=0)的数据分布相似(可通过随机实验或倾向得分调整保证)。
- 干预的个体效应(ITE)可以通过特征X 的线性或非线性组合表达。
具体方法
Transformed Outcome(TO)方法(Zheng标签法)
- 标签定义:构造新标签Z,将Uplift问题转换为二分类任务:$Z = Y \times (2T – 1)$
- 当T=1且Y=1 时,Z=1(干预有效)。
- 当T=0且Y=0 时,Z=1(未干预且未转化,说明干预可能有效)。
- 其他情况下Z=-1 或0 。
- 训练目标:训练一个分类模型,预测 P(Z=1|X) ,该概率直接反映干预的增量效应。
- 数学推导:新标签的期望值与Uplift的关系:$\mathbb{E}[Z|X] = \mathbb{E}[Y(1) – Y(0)|X] = \text{Uplift}(X)$
因此,模型预测值 $\hat{P}(Z=1|X)$ 即为Uplift的无偏估计。
改进:逆概率加权(IPW)
若实验组和对照组分布不均衡,需引入倾向得分 $\pi(X) = P(T=1|X)$ ,对样本加权:$Z_{\text{weighted}} = Z \times( \frac{T}{\pi(X)} + \frac{1-T}{1-\pi(X)})$
通过加权消除选择偏差,提升模型鲁棒性。
优缺点分析
优点
- 单模型建模:避免双模型法的误差累积,简化训练流程。
- 直接优化目标:标签构造使模型直接学习Uplift值,理论无偏。
- 灵活性:兼容任意分类模型(如逻辑回归、XGBoost、神经网络)。
缺点
- 依赖数据均衡性:
- 实验组/对照组样本量差异大时,需通过IPW或重采样调整。
- 若倾向得分$\pi(X)$估计不准确,加权可能引入偏差。
- 信息损失:将连续Uplift值转换为离散标签(如1/-1),可能丢失部分信息。
- 假设强约束:要求实验组和对照组的特征分布重叠性高(即共同支撑域足够大)。
改进方法
- 连续标签转换:构造连续标签$Z = Y \times (2T-1)$,使用回归模型预测Uplift。
- 分位数分组:将样本按Uplift预测值分位,对高/低敏感人群单独建模。
- 集成学习:结合多个标签转换模型(如Bagging或Stacking),减少方差。
适用场景
- 随机对照试验(RCT)数据:实验组和对照组通过随机分配,满足分布一致性假设。
- 高维特征场景:深度学习模型中,标签转换法可避免双模型法的特征对齐问题。
- 快速迭代需求:需快速验证Uplift模型效果,且业务方接受非直观结果解释。
代码实现示例(Python)
import numpy as np from sklearn.linear_model import LogisticRegression # 构造转换后的标签 Z data['Z'] = data['Y'] * (2 * data['T'] - 1) # 若实验组/对照组不均衡,添加IPW权重 propensity_model = LogisticRegression().fit(X, data['T']) data['propensity_score'] = propensity_model.predict_proba(X)[:, 1] data['weight'] = data['T'] / data['propensity_score'] + (1 - data['T']) / (1 - data['propensity_score']) data['Z_weighted'] = data['Z'] * data['weight'] # 训练模型(以逻辑回归为例) model = LogisticRegression() model.fit(X, data['Z_weighted']) # 预测Uplift值(需校准到[-1, 1]区间) uplift_scores = model.predict_proba(X)[:, 1] * 2 - 1
树模型与集成方法
Uplift决策树
Uplift决策树是一种专门用于估计个体处理效应(ITE)的树模型,通过递归分割数据,最大化不同节点中处理组和对照组的响应差异。其核心目标是将人群划分为对干预敏感、不敏感或反感等子群,从而优化干预策略。
与普通决策树的区别
- 目标差异:
- 普通决策树:预测目标变量(分类或回归)。
- Uplift决策树:估计处理效应(Uplift),即干预带来的增量效果$\tau(X) = Y(1) – Y(0)$ 。
- 分裂标准:
- 普通决策树:信息增益、基尼系数、均方误差等。
- Uplift决策树:基于处理效应异质性的指标(如KL散度、欧氏距离、Qini系数)。
核心假设
- 无未观测混杂:所有影响处理分配和结果的变量均被观测。
- 处理分配随机性或可调整性:通过随机实验或倾向得分匹配保证处理组和对照组的可比性。
算法细节
分裂标准:
- KL散度(Kullback-Leibler Divergence):衡量处理组和对照组在节点内的分布差异。最大化KL散度以找到最区分处理效应的分裂。$\text{KL}(P \| Q) = \sum_i P(i) \log \frac{P(i)}{Q(i)}$
- P :处理组的响应分布。
- Q :对照组的响应分布。
- 欧氏距离(Euclidean Distance):直接计算处理组和对照组响应均值的差异:$D = ( \mu_T – \mu_C)^2$
- $\mu_T$ :处理组的平均响应。
- $\mu_C$ :对照组的平均响应。
- 卡方散度(Chi-Square Divergence):检验处理组和对照组分布的独立性:$\chi^2 = \sum \frac{(O_{T,i} – E_{T,i})^2}{E_{T,i}} + \frac{(O_{C,i} – E_{C,i})^2}{E_{C,i}}$
- O : 观测频数, E : 期望频数。
- Qini系数:衡量模型排序能力,通过累积增益曲线下面积(AUUC)优化分裂。
树构建流程:
- 初始化:从根节点开始,包含全部样本。
- 特征选择:对每个特征和分割点,计算分裂标准(如KL散度)。
- 最佳分裂:选择最大化分裂标准的特征和分割点。
- 递归分割:对子节点重复上述步骤,直到满足停止条件(如最小样本量、深度限制)。
- 叶节点处理效应:叶节点的Uplift值为处理组和对照组响应均值之差:$\tau_{\text{leaf}} = \bar{Y}_T – \bar{Y}_C$
防止过拟合策略:
- 预剪枝:设置最小节点样本量、最大深度、最小增益阈值。
- 后剪枝:基于交叉验证的复杂度剪枝(CCP)。
- 正则化:在分裂标准中加入惩罚项(如节点样本量的倒数)。
评估指标
- AUUC(Area Under the Uplift Curve)
- 定义:将样本按预测Uplift降序排序,计算累积增益曲线下面积。
- 解释:AUUC越高,模型区分敏感人群的能力越强。
- Qini系数
- 公式:$Q = \sum_{i=1}^n (Y_{T,i} – Y_{C,i}) \cdot \mathbb{I}(\text{rank}_i \leq k)$,$\text{rank}_i$ :样本按预测Uplift的排名。
- 优势:直观反映模型在Top-K人群中的增益效果。
- 提升图(Uplift Lift Chart)
- 绘制:将样本分位数与累积Uplift值对比,验证模型排序一致性。
优缺点分析
优点
- 可解释性:树结构清晰展示特征对处理效应的影响路径。
- 非参数性:无需假设处理效应与特征的函数形式。
- 自动特征交互:通过树分裂捕捉变量间的交互效应。
缺点
- 高方差:对数据扰动敏感,需通过剪枝和集成缓解。
- 局部最优:贪心算法可能导致次优分裂。
- 处理连续特征:需手动分箱或动态分割,可能损失信息。
代码实现(Python示例)
from causalml.inference.tree import UpliftTreeClassifier
from causalml.metrics import auuc_score
# 数据准备(X为特征,T为处理变量,y为结果)
uplift_model = UpliftTreeClassifier(
max_depth=5,
min_samples_leaf=100,
criterion='KL' # 可选'KL', 'ED', 'Chi'
)
uplift_model.fit(X, T, y)
# 预测Uplift值
uplift_scores = uplift_model.predict(X)
# 评估AUUC
auuc = auuc_score(y, uplift_scores, T)
因果森林(Causal Forest)
因果森林(Causal Forest)是因果推断领域的一种集成学习方法,基于随机森林(Random Forest)框架,专门用于估计个体处理效应(Individual Treatment Effect, ITE)或条件平均处理效应(Conditional Average Treatment Effect, CATE)。其核心思想是通过构建多棵决策树,捕捉特征与干预效应之间的复杂关系,并对处理效应进行无偏估计。
核心原理
与随机森林的异同:
- 相同点:
- 基于Bootstrap聚合(Bagging)和随机子空间(Random Subspace)构建多棵树。
- 通过投票或平均提高模型的稳定性和泛化能力。
- 不同点:
- 目标不同:随机森林预测结果变量,因果森林估计处理效应(CATE)。
- 分裂标准:因果森林的分裂规则最大化处理效应的异质性。
- Honesty原则:因果森林强制将数据分为训练集和估计集,防止过拟合。
核心假设:
- 无未观测混杂(Unconfoundedness):所有影响处理分配和结果的变量均被观测。
- 重叠性(Overlap):每个个体均有概率被分配到处理组和对照组。
- 处理效应异质性:处理效应随特征变化而不同。
算法细节
算法步骤
- 数据拆分:
- 将数据分为两个子集:一部分用于训练树结构(训练集),另一部分用于估计叶节点的处理效应(估计集)。
- Honesty原则:确保训练和估计使用不同数据,避免过拟合。
- 单棵树构建:
- Bootstrap采样:从数据中有放回地抽取样本。
- 递归分裂:在每个节点选择特征和分割点,最大化子节点间处理效应的异质性。
- 分裂标准:基于CATE的方差减少或KL散度。
$$\Delta = \text{Var}(CATE_{\text{parent}}) – ( \frac{n_{\text{left}}}{n_{\text{parent}}} \text{Var}(CATE_{\text{left}}) + \frac{n_{\text{right}}}{n_{\text{parent}}} \text{Var}(CATE_{\text{right}}))$$
- 停止条件:节点样本量小于阈值或处理效应异质性不显著。
- 叶节点处理效应估计:
- 使用估计集数据计算叶节点内处理组和对照组的平均结果差异:
$$\hat{\tau}(x) = \frac{1}{n_{T,\text{leaf}}} \sum_{i \in T_{\text{leaf}}} Y_i – \frac{1}{n_{C,\text{leaf}}} \sum_{i \in C_{\text{leaf}}} Y_i$$
- 集成多棵树:
- 对每个样本的CATE取所有树的预测均值:%\hat{\tau}_{\text{forest}}(x) = \frac{1}{B} \sum_{b=1}^B \hat{\tau}_b(x)$
- B :树的棵数。
改进技术:
- 倾向得分加权:若数据非随机分配,引入倾向得分调整样本权重。
- 局部中心化(Local Centering):对结果变量和处理变量进行残差化处理,减少偏差。
- 正交随机森林(Orthogonal Forest):结合双重机器学习(Double ML)消除混杂因素影响。
优缺点分析
优点
- 非参数性:无需假设处理效应与特征的函数形式,适应复杂非线性关系。
- 高鲁棒性:通过集成学习和Honesty原则降低方差与过拟合风险。
- 统计一致性:在大样本下,估计结果收敛于真实CATE。
- 处理高维数据:随机子空间法自动筛选重要特征。
缺点
- 计算复杂度高:需构建多棵树并维护两个数据子集,计算开销大。
- 可解释性低:相比单棵树,森林的黑箱性质更强。
- 数据要求严格:需保证处理组和对照组的样本量均衡及特征重叠。
评估方法
- 基于Honesty的交叉验证:利用估计集数据计算均方误差(MSE)或平均处理效应误差(ATE Error)。
- 残差诊断:检验残差是否与特征无关,验证模型的无偏性。
- 协变量平衡测试:检查处理后特征在叶节点内的分布是否平衡。
代码实现(Python示例)
from econml.grf import CausalForest
import numpy as np
# 数据准备:X为特征,T为处理变量(0/1),Y为结果
# 假设处理变量T已通过随机实验或倾向得分调整
# 初始化因果森林模型
cf = CausalForest(
n_estimators=1000,
max_depth=10,
min_samples_split=10,
honest=True # 启用Honesty原则
)
# 拟合模型
cf.fit(X, T, Y)
# 预测CATE
cate_estimates = cf.predict(X)
# 评估ATE(平均处理效应)
ate = np.mean(cate_estimates)
print(f"Estimated ATE: {ate:.4f}")
元学习器(Meta-Learners)
S-Learner(Single Learner)
S-Learner(Single Learner)是因果推断中用于估计个体处理效应(ITE)或条件平均处理效应(CATE)的一种单模型方法。其核心思想是将处理变量作为特征输入模型,通过预测不同处理状态下的潜在结果差异来量化因果效应。
基本思路
- 单模型建模:将处理变量T(通常为二元变量,0或1)与协变量X合并为输入特征,训练一个统一的模型$\mu(X, T)$预测结果变量Y 。
- 处理效应估计:对每个样本,分别计算T=1 和 T=0 时的预测结果,差值即为处理效应:$\hat{\tau}(x) = \mu(x, 1) – \mu(x, 0)$
核心假设
- 无未观测混杂(Unconfoundedness):所有影响处理分配和结果的变量均被观测。
- 重叠性(Overlap):每个个体均有概率被分配到处理组和对照组(即$0 < P(T=1|X=x) < 1$)。
- 模型灵活性:模型需足够复杂以捕捉T 与 X 的交互效应。
算法步骤
- 数据准备:
- 输入数据:协变量X 、处理变量T 、结果变量Y 。
- 构造特征:将T 作为特征与X 合并,形成新特征空间[X, T] 。
- 模型训练:
- 选择模型(如线性回归、随机森林、神经网络等),拟合Y 与 [X, T] 的关系:$\mu(X, T) = \mathbb{E}[Y | X, T]$
- 处理效应预测:
- 对每个样本x ,分别计算 T=1 和 T=0 时的预测值:$\hat{Y}(1) = \mu(x, 1), \quad \hat{Y}(0) = \mu(x, 0)$
- 计算个体处理效应:$\hat{\tau}(x) = \hat{Y}(1) – \hat{Y}(0)$
优缺点分析
优点
- 模型简单:仅需训练单一模型,计算成本低,易于实现。
- 自然捕捉交互效应:将T 作为特征,模型可自动学习处理变量与协变量的交互作用。
- 适用性广:兼容任意预测模型(线性/非线性),灵活性高。
缺点
- 处理效应稀释:若处理变量T 对结果影响较小,模型可能难以有效区分处理效应。
- 偏向主要群体:当处理组和对照组样本量差异大时,模型可能偏向预测主要群体的结果。
- 模型误设风险:若模型未正确建模T 与X 的交互,会导致处理效应估计偏差。
改进策略
- 倾向得分调整:对非随机数据,引入倾向得分$\pi(X) = P(T=1|X)$作为权重或额外特征,缓解选择偏差。
- 交互项显式编码:在线性模型中手动添加$T \times X$交互项,确保处理效应异质性被建模。
- 模型正则化:使用L1/L2正则化防止过拟合,提升模型泛化能力。
适用场景
- 随机对照试验(RCT)数据:处理组和对照组分布均衡,满足无混杂假设。
- 高维特征与小样本:单模型减少参数数量,降低过拟合风险。
- 明确交互效应:处理变量与某些协变量存在已知的交互作用,需模型自动捕捉。
代码实现(Python示例)
import numpy as np from sklearn.ensemble import GradientBoostingRegressor # 构造数据集:X为特征,T为处理变量,Y为结果 # 假设数据已预处理(标准化、缺失值填充等) # 合并T作为特征 X_train = np.hstack([X, T.reshape(-1, 1)]) # 训练S-Learner模型 model = GradientBoostingRegressor() model.fit(X_train, Y) # 预测潜在结果 X_t1 = np.hstack([X, np.ones((X.shape[0], 1))]) # T=1 X_t0 = np.hstack([X, np.zeros((X.shape[0], 1))]) # T=0 Y_hat1 = model.predict(X_t1) Y_hat0 = model.predict(X_t0) # 计算CATE cate = Y_hat1 - Y_hat0
T-Learner(Two Learner)
T-Learner(Two Learner)是因果推断中用于估计个体处理效应(ITE)或条件平均处理效应(CATE)的一种双模型方法。其核心思想是分别对处理组和对照组训练两个独立的预测模型,通过对比两个模型的预测结果差异来量化因果效应。
基本思路
- 双模型建模:
- 在处理组(T=1)和对照组(T=0)上分别训练模型$\mu_1(X)$和$\mu_0(X)$,预测潜在结果Y(1)和Y(0)。
- 处理效应为两模型的预测差值:$\hat{\tau}(x) = \mu_1(x) – \mu_0(x)$
核心假设
- 无未观测混杂(Unconfoundedness):所有影响处理分配和结果的变量均被观测。
- 重叠性(Overlap):每个个体均有概率被分配到处理组和对照组(即$0 < P(T=1|X=x) < 1$)。
- 模型独立性:处理组和对照组的模型需独立捕捉各自群体的特征与结果关系。
算法步骤
- 数据分割:将数据分为处理组(T=1 )和对照组( T=0 )两个子集。
- 模型训练:
- 处理组模型:用处理组数据训练\mu_1(X) ,预测 Y(1) 。
- 对照组模型:用对照组数据训练\mu_0(X) ,预测 Y(0) 。
- 处理效应预测:
- 对每个样本x ,分别用 \mu_1(x) 和 \mu_0(x) 预测其潜在结果:$\hat{Y}(1) = \mu_1(x), \quad \hat{Y}(0) = \mu_0(x)$
- 计算个体处理效应:$\hat{\tau}(x) = \hat{Y}(1) – \hat{Y}(0)$
优缺点分析
优点
- 灵活捕捉异质性:处理组和对照组模型独立训练,可更好适应两群体的特征差异(如非线性关系、交互效应)。
- 避免处理效应稀释:与S-Learner不同,T-Learner直接建模两群体的差异,避免处理变量被其他特征主导。
- 兼容复杂模型:可针对处理组和对照组分别选择最优模型(如处理组用神经网络,对照组用随机森林)。
缺点
- 样本利用率低:数据被分割为两部分,单个模型训练样本减少,可能导致过拟合(尤其是小数据场景)。
- 模型不一致性风险:若处理组和对照组模型结构差异大(如一个线性、一个非线性),预测结果可能不可比。
- 处理组-对照组样本量失衡:当两群体样本量差异大时,小样本群体的模型预测准确性下降,影响处理效应估计。
改进策略
- 倾向得分加权:对非随机数据,引入倾向得分$\pi(X)$调整样本权重,缓解选择偏差。
- 模型正则化:对处理组和对照组模型施加相同的正则化约束(如L2正则化),提升预测一致性。
- 集成学习:对每个群体使用集成方法(如随机森林)提升小样本下的模型鲁棒性。
适用场景
- 处理组和对照组差异显著:两群体的特征分布或结果响应模式差异较大(如营销中高价值用户与普通用户)。
- 大样本数据:处理组和对照组均有足够样本支持独立建模。
- 需要高精度处理效应估计:如医疗领域需精准评估不同患者亚群的治疗效果差异。
实际案例
- 案例:保险业个性化定价策略
- 目标:识别对“保费折扣”敏感的用户,优化折扣投放策略。
- 步骤:
- 随机对部分用户提供保费折扣(处理组),其余为对照组。
- 使用T-Learner:
- 处理组模型:用处理组数据训练GBDT模型,预测折扣下的续保率Y(1) 。
- 对照组模型:用对照组数据训练GBDT模型,预测无折扣的续保率Y(0) 。
- 计算每个用户的CATE(续保率提升幅度),优先对CATE前10%的用户发放折扣。
- 效果:续保率提升8%,折扣成本减少20%。
代码实现(Python示例)
import numpy as np from sklearn.ensemble import GradientBoostingRegressor # 假设数据已加载:X为特征,T为处理变量(0/1),Y为结果 # 分割处理组和对照组数据 X_t1 = X[T == 1] # 处理组特征 Y_t1 = Y[T == 1] # 处理组结果 X_t0 = X[T == 0] # 对照组特征 Y_t0 = Y[T == 0] # 对照组结果 # 训练处理组和对照组模型 model_t1 = GradientBoostingRegressor() model_t0 = GradientBoostingRegressor() model_t1.fit(X_t1, Y_t1) model_t0.fit(X_t0, Y_t0) # 预测所有样本的潜在结果 Y_hat1 = model_t1.predict(X) # 假设所有样本接受处理 Y_hat0 = model_t0.predict(X) # 假设所有样本未接受处理 # 计算CATE cate = Y_hat1 - Y_hat0
X-Learner(Cross-Learner)
X-Learner(Cross-Learner)是因果推断中一种结合双模型框架与元学习(Meta-Learning)的方法,旨在更高效地估计条件平均处理效应(CATE)。其核心思想是通过交叉预测(Cross-Prediction)和残差学习(Residual Learning),利用处理组和对照组的信息互补性,提升小样本或非随机数据下的处理效应估计精度。
基本思路
- 三步交叉学习:
- 基础模型:类似T-Learner,先分别对处理组和对照组训练两个模型,预测潜在结果。
- 反事实预测与残差计算:利用交叉预测生成反事实结果,并计算残差(实际结果与预测结果的差异)。
- 元学习器建模:以残差为新的目标变量,训练元模型直接估计处理效应。
- 核心公式:
- 处理组模型\mu_1(X) 和对照组模型 \mu_0(X) 预测潜在结果:$\hat{Y}_1 = \mu_1(X), \quad \hat{Y}_0 = \mu_0(X)$
- 反事实预测:
- 处理组的反事实对照结果:$\tilde{Y}_0 = \mu_0(X_{T=1})$
- 对照组的反事实处理结果:$\tilde{Y}_1 = \mu_1(X_{T=0})$
- 残差计算:
- 处理组残差:$D_1 = Y_{T=1} – \tilde{Y}_0$
- 对照组残差:$D_0 = \tilde{Y}_1 – Y_{T=0}$
- 元模型训练:
- 处理效应估计:$\tau_1(X) = D_1 , \tau_0(X) = D_0$
- 元模型$g(X)$综合$\tau_1$和$\tau_0$的加权平均:$\hat{\tau}(x) = g(x) = \pi(x) \tau_0(x) + (1-\pi(x)) \tau_1(x)$
- $\pi(x) $:倾向得分(处理概率),用于加权不同群体的残差信息。
核心假设
- 无未观测混杂:所有混淆变量均被观测。
- 模型灵活性:基础模型需准确预测潜在结果,元模型需捕捉处理效应异质性。
- 倾向得分可估计:需可靠估计P(T=1|X) (尤其非随机数据)。
算法步骤
- 基础模型训练:
- 处理组模型$\mu_1(X)$:用处理组数据$(X_{T=1}, Y_{T=1})$训练。
- 对照组模型$\mu_0(X)$:用对照组数据$(X_{T=0}, Y_{T=0})$训练。
- 交叉预测与残差生成:
- 对处理组样本,用$\mu_0(X_{T=1})$预测反事实对照结果$\tilde{Y}_0$,计算残差$D_1 = Y_{T=1} – \tilde{Y}_0$。
- 对对照组样本,用$\mu_1(X_{T=0})$预测反事实处理结果$\tilde{Y}_1$,计算残差$D_0 = \tilde{Y}_1 – Y_{T=0}$。
- 元模型训练:
- 处理组元模型$\tau_1(X)$:用处理组数据$(X_{T=1}, D_1)$训练。
- 对照组元模型$\tau_0(X)$:用对照组数据$(X_{T=0}, D_0)$训练。
- 倾向得分估计$\pi(X)$:通过逻辑回归或机器学习模型预测$P(T=1|X)$。
- 加权集成处理效应:
- 最终CATE估计:$\hat{\tau}(x) = \pi(x) \cdot \tau_0(x) + (1-\pi(x)) \cdot \tau_1(x)$
- 倾向得分作用:在非随机数据中,高倾向得分样本更可能属于处理组,因此更信任对照组元模型的估计。
优缺点分析
优点
- 高效利用小样本:通过交叉预测,同时利用处理组和对照组的数据训练元模型,缓解样本不足问题。
- 适应非随机数据:倾向得分加权可校正选择偏差,提升非随机实验中的估计无偏性。
- 鲁棒的异质性捕捉:元模型直接建模处理效应,而非潜在结果,更聚焦于效应异质性。
缺点
- 计算复杂度高:需训练四个模型(2个基础模型 + 2个元模型 + 倾向得分模型),计算成本显著增加。
- 依赖倾向得分精度:若倾向得分估计不准确,加权集成可能引入偏差。
- 模型链式误差累积:基础模型的预测误差会传递到元模型,影响最终CATE估计。
改进策略
- 双重机器学习(Double ML):对基础模型和倾向得分模型进行正交化处理,消除混杂变量影响。
- 集成学习增强鲁棒性:用随机森林或梯度提升树替代线性模型作为元模型,提升非线性效应捕捉能力。
- 半参数化建模:结合参数化倾向得分和非参数元模型,平衡灵活性与可解释性。
适用场景
- 观测性数据(非随机实验):存在选择偏差时,倾向得分加权可校正估计。
- 处理组-对照组样本量失衡:小样本群体通过交叉预测补充信息。
- 复杂处理效应异质性:元模型直接学习效应差异,适应非线性、高维交互场景。
代码实现(Python示例)
import numpy as np from sklearn.ensemble import RandomForestRegressor from sklearn.linear_model import LogisticRegression # 假设数据已加载:X为特征,T为处理变量(0/1),Y为结果 # 第一步:训练基础模型 # 处理组模型 model_t1 = RandomForestRegressor() model_t1.fit(X[T == 1], Y[T == 1]) # 对照组模型 model_t0 = RandomForestRegressor() model_t0.fit(X[T == 0], Y[T == 0]) # 第二步:交叉预测与残差计算 # 处理组的反事实对照结果预测 D1 = Y[T == 1] - model_t0.predict(X[T == 1]) # 对照组的反事实处理结果预测 D0 = model_t1.predict(X[T == 0]) - Y[T == 0] # 第三步:训练元模型 # 处理组元模型 meta_model_t1 = RandomForestRegressor() meta_model_t1.fit(X[T == 1], D1) # 对照组元模型 meta_model_t0 = RandomForestRegressor() meta_model_t0.fit(X[T == 0], D0) # 倾向得分估计 propensity_model = LogisticRegression() propensity_model.fit(X, T) pi = propensity_model.predict_proba(X)[:, 1] # 第四步:加权集成CATE tau_1 = meta_model_t1.predict(X) tau_0 = meta_model_t0.predict(X) cate = pi * tau_0 + (1 - pi) * tau_1
R-Learner(Robust-Learner)
R-Learner(Robust-Learner)是因果推断中一种基于**双重机器学习(Double Machine Learning)和正交化(Orthogonalization)**的方法,旨在通过分离倾向得分建模与结果建模,提升处理效应估计的鲁棒性。其核心思想是通过残差学习消除混杂变量影响,从而在模型误设或高维特征下仍能保持无偏估计。
基本思路
- 双重去偏(Debiasing):
- 第一阶段:分别估计倾向得分$\pi(X) = P(T=1|X)$和结果模型$\mu_0(X) = \mathbb{E}[Y|T=0,X]$、$\mu_1(X) = \mathbb{E}[Y|T=1,X]$。
- 第二阶段:通过残差正交化,消除混杂变量对处理效应估计的干扰。
- 结果残差:$\tilde{Y} = Y – \mu_T(X)$(其中$\mu_T(X)4是处理状态对应的结果预测)。
- 处理残差:$\tilde{T} = T – \pi(X4。
- 处理效应估计:通过回归$\tilde{Y}$对$\tilde{T}$的条件均值,直接估计CATE:$\hat{\tau}(x) = \frac{\mathbb{E}[\tilde{Y} \cdot \tilde{T} | X=x]}{\mathbb{E}[\tilde{T}^2 | X=x]}$
核心假设
- 无未观测混杂:所有影响处理分配和结果的变量均被观测。
- Neyman正交性:估计方程对倾向得分和结果模型的误设具有鲁棒性(通过正交化实现)。
- 交叉拟合(Cross-fitting):避免过拟合,提升泛化能力。
算法步骤
- 数据分割:将数据随机分为K 折(通常K=5),每次用K-1折训练模型,剩余1折预测。
- 第一阶段建模:
- 倾向得分模型:用机器学习模型(如逻辑回归、随机森林)估计$\hat{\pi}(X)$。
- 结果模型:分别对处理组和对照组训练模型$\hat{\mu}_1(X)$和$\hat{\mu}_0(X)$。
- 残差计算:
- 结果残差:$\tilde{Y}_i = Y_i – ( T_i \hat{\mu}_1(X_i) + (1-T_i) \hat{\mu}_0(X_i))$
- 处理残差:$\tilde{T}_i = T_i – \hat{\pi}(X_i)$
- 第二阶段处理效应估计:
- 通过加权回归或非参数模型(如核回归、梯度提升树)拟合:$\hat{\tau}(x) = \arg\min_{\tau} \sum_{i=1}^n ( \tilde{Y}_i – \tau(x) \tilde{T}_i)^2$
- 最终CATE为$\hat{\tau}(x)$。
优缺点分析
优点
- 对模型误设鲁棒:正交化使估计量对倾向得分和结果模型的误设具有双鲁棒性(只要两者中一个正确即可)。
- 适应高维数据:可结合Lasso、随机森林等高维模型处理大量特征。
- 无偏性保障:在交叉拟合下,即使使用黑箱模型,仍能保证渐近无偏性。
缺点
- 计算复杂度高:需多次训练模型(交叉拟合)和残差计算,耗时较长。
- 小样本表现不稳定:数据量不足时,残差估计可能波动较大。
- 依赖交叉拟合实现:未正确应用交叉拟合时,可能导致过拟合。
改进策略
- 高效交叉拟合:使用并行计算加速多折模型训练。
- 正则化增强:对倾向得分和结果模型施加L1/L2正则化,防止过拟合。
- 半参数扩展:结合参数化处理效应模型与非参数正交化,提升可解释性。
适用场景
- 高维混杂变量:特征维度高(如基因数据、用户行为数据),需正则化模型。
- 观测性研究(非随机数据):存在复杂选择偏差,需双重去偏。
- 模型鲁棒性要求高:无法确保倾向得分或结果模型完全正确时。
代码实现(Python示例)
import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression, Lasso
from sklearn.ensemble import GradientBoostingRegressor
from econml.dml import LinearDML
# 假设数据已加载:X为特征,T为处理变量(连续或二元),Y为结果
# 使用EconML库实现R-Learner(基于LinearDML)
model = LinearDML(
model_y=GradientBoostingRegressor(), # 结果模型
model_t=LogisticRegression(), # 倾向得分模型(若T为二元)
discrete_treatment=True, # 处理变量是否为离散
cv=5 # 交叉拟合折数
)
model.fit(Y, T, X=X)
# 估计CATE
cate = model.effect(X)
# 自定义实现(简化版)
kf = KFold(n_splits=5)
cate_estimates = []
for train_idx, test_idx in kf.split(X):
X_train, X_test = X[train_idx], X[test_idx]
T_train, T_test = T[train_idx], T[test_idx]
Y_train, Y_test = Y[train_idx], Y[test_idx]
# 训练倾向得分模型
ps_model = LogisticRegression().fit(X_train, T_train)
pi_hat = ps_model.predict_proba(X_test)[:, 1]
# 训练结果模型
y_model = Lasso().fit(X_train, Y_train)
mu_hat = y_model.predict(X_test)
# 计算残差
Y_tilde = Y_test - mu_hat
T_tilde = T_test - pi_hat
# 拟合CATE模型
tau_model = GradientBoostingRegressor().fit(X_test, Y_tilde / T_tilde)
cate_estimates.append(tau_model.predict(X_test))
# 合并交叉拟合结果
cate = np.concatenate(cate_estimates)
深度学习与高级方法
DragonNet
DragonNet是一种结合深度学习与因果推断的方法,旨在通过端到端的神经网络架构同时建模倾向得分(Propensity Score)和潜在结果(Potential Outcomes),以提升处理效应估计的准确性和鲁棒性。其核心设计通过共享表示层和任务特定层,有效捕捉混杂变量的复杂影响,适用于高维数据和非线性场景。
基本思路
- 联合建模:DragonNet通过单一神经网络同时学习倾向得分和潜在结果,利用共享隐藏层提取混杂变量的共同特征,减少偏差。
- 共享表示层:提取输入特征X 的高阶表示$\Phi(X)$。
- 任务特定层:
- 倾向得分头:预测处理概率$\pi(X) = P(T=1|X)$。
- 结果预测头:分别预测处理组和对照组的潜在结果$\mu_1(X)$和$\mu_0(X)$。
- 损失函数:结合倾向得分损失(交叉熵)和结果预测损失(均方误差),并引入正则化项平衡两者:$\mathcal{L} = \mathcal{L}_{\text{propensity}} + \alpha \mathcal{L}_{\text{outcome}} + \lambda \|\theta\|^2$。其中,$\alpha$为任务权重,$\lambda$为正则化系数。
核心假设
- 无未观测混杂:所有影响处理分配和结果的变量均被观测。
- 表示学习有效性:共享层能有效捕捉混杂变量的高阶交互和非线性关系。
- 平衡表示:通过倾向得分调整,使处理组和对照组的特征分布在共享层中对齐。
算法步骤
- 输入数据:特征X,处理变量$T \in \{0,1\}$,结果Y 。
- 共享表示层:通过多层感知机(MLP)或卷积层提取特征表示$\Phi(X)$ 。
- 任务特定层:
- 倾向得分头:基于$\Phi(X)$预测$\pi(X)$。
- 结果预测头:
- 若T=1,预测$\mu_1(X)$;若T=0 ,预测$\mu_0(X)$。
- 可选扩展:预测反事实结果(如用$\Phi(X)$同时预测$\mu_1(X)$和$\mu_0(X)$)。
- 联合训练:同时优化倾向得分损失和结果损失,通过梯度下降更新参数。
- 处理效应估计:个体处理效应(ITE)为:$\hat{\tau}(x) = \hat{\mu}_1(x) – \hat{\mu}_0(x)$
优缺点分析
优点
- 高维数据处理能力:神经网络自动捕捉复杂特征交互,适合图像、文本等高维数据。
- 表示平衡:共享层促进处理组和对照组的特征分布对齐,缓解选择偏差。
- 端到端学习:联合训练倾向得分和结果模型,减少分阶段建模的误差累积。
缺点
- 计算复杂度高:大规模神经网络训练需较高算力,调参难度大。
- 小样本表现差:数据量不足时,共享层易过拟合,导致倾向得分和结果预测不准确。
- 解释性弱:黑箱模型难以直观解释处理效应异质性来源。
改进策略
- 半监督学习:利用未标注数据增强共享层表示学习。
- 对抗训练:引入判别器网络,强制处理组和对照组的特征分布在共享层中不可区分。
- 多任务正则化:在损失函数中加入处理组和对照组预测结果的一致性约束。
适用场景
- 高维或非结构化数据:如医疗影像、用户行为序列、基因组数据等。
- 非线性混杂关系:传统线性模型无法捕捉复杂因果机制时。
- 观测性研究:存在隐式选择偏差,需通过表示学习平衡群体分布。
代码实现(PyTorch示例)
import torch
import torch.nn as nn
import torch.optim as optim
class DragonNet(nn.Module):
def __init__(self, input_dim):
super(DragonNet, self).__init__()
# 共享表示层
self.shared_layer = nn.Sequential(
nn.Linear(input_dim, 256),
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU()
)
# 倾向得分头
self.propensity_head = nn.Sequential(
nn.Linear(64, 1),
nn.Sigmoid()
)
# 结果预测头
self.outcome_head = nn.ModuleDict({
'1': nn.Linear(64, 1), # 处理组结果
'0': nn.Linear(64, 1) # 对照组结果
})
def forward(self, x):
phi = self.shared_layer(x)
propensity = self.propensity_head(phi)
y1 = self.outcome_head['1'](phi)
y0 = self.outcome_head['0'](phi)
return propensity, y1, y0
# 训练过程
model = DragonNet(input_dim=100)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion_propensity = nn.BCELoss()
criterion_outcome = nn.MSELoss()
for epoch in range(100):
for X, T, Y in dataloader:
propensity_pred, y1_pred, y0_pred = model(X)
# 计算损失
loss_propensity = criterion_propensity(propensity_pred, T)
# 根据实际处理状态选择预测结果
outcome_pred = torch.where(T == 1, y1_pred, y0_pred)
loss_outcome = criterion_outcome(outcome_pred, Y)
# 总损失(α=0.5)
total_loss = loss_propensity + 0.5 * loss_outcome
# 反向传播
optimizer.zero_grad()
total_loss.backward()
optimizer.step()
# 估计ITE
propensity, y1, y0 = model(X_test)
ite = y1 - y0
CEVAE(Causal Effect VAE)
CEVAE(因果效应变分自编码器)是一种基于变分推断和深度生成模型的因果推断方法,专为存在未观测混杂变量的场景设计。它通过隐变量建模和反事实生成,直接估计个体处理效应(ITE),尤其适用于高维观测数据与复杂因果关系的场景。
基本思路
- 隐变量建模:假设存在潜在变量Z同时影响处理变量T和结果Y,即使部分混杂变量未被观测,CEVAE通过变分自编码器(VAE)推断Z的分布,从而校正混杂偏差。
- 生成过程:
- 处理分配:$T \sim P(T|Z)$
- 结果生成:$Y \sim P(Y|T, Z)$
- 特征生成:$X \sim P(X|Z)$(观测特征由潜在变量生成)
- 推断目标:通过最大化观测数据的变分下界(ELBO),同时学习潜在变量Z的分布和因果机制,估计反事实结果Y(1)和Y(0)。
核心假设
- 隐变量存在性:存在潜在变量Z能够解释所有混杂效应。
- 可忽略性(Ignorability):给定Z,处理分配T与潜在结果独立,即$T \perp Y(1), Y(0) | Z$。
- 生成模型有效性:VAE能够准确建模Z、T、Y、X的联合分布。
算法步骤
- 编码器网络(推断模型):输入观测数据X、T、Y,输出潜在变量Z的后验分布参数(均值$\mu_z$和方差$\sigma_z^2$)。
$$q_\phi(Z|X,T,Y) = \mathcal{N}(\mu_z, \sigma_z^2)$$
- 解码器网络(生成模型):从Z生成处理变量T、结果Y、观测特征X:
$$p_\theta(T|Z), \quad p_\theta(Y|T,Z), \quad p_\theta(X|Z)$$
- 目标函数(ELBO):最大化观测数据的对数似然下界:$\mathcal{L}(\theta, \phi) = \mathbb{E}_{q_\phi(Z|X,T,Y)}[\log p_\theta(X,T,Y,Z)] – \text{KL}(q_\phi(Z|X,T,Y) \| p(Z))$
- KL散度项:约束潜在变量分布接近先验p(Z)(通常为标准正态分布)。
- 反事实预测:
- 对每个样本i ,从$q_\phi(Z|X_i,T_i,Y_i)$采样$Z_i$。
- 生成反事实结果:$\hat{Y}_i(1) = \mathbb{E}[p_\theta(Y|T=1,Z_i)], \quad \hat{Y}_i(0) = \mathbb{E}[p_\theta(Y|T=0,Z_i)]$
- 个体处理效应(ITE)估计:$\hat{\tau}_i = \hat{Y}_i(1) – \hat{Y}_i(0)$
优缺点分析
优点
- 处理未观测混杂:通过隐变量Z捕捉未观测的混杂因素,提升因果效应估计的无偏性。
- 高维数据适应:VAE天然适合处理图像、文本等高维或非结构化数据。
- 反事实生成能力:直接生成潜在结果,支持个性化决策。
缺点
- 模型假设严格:若隐变量Z未能完全捕捉混杂因素,估计结果仍有偏差。
- 计算复杂度高:需要训练深度生成模型,对算力和数据量要求较高。
- 解释性差:隐变量Z的含义不明确,难以验证模型合理性。
改进策略
- 对抗训练:引入判别器网络确保Z与T 独立(增强可忽略性假设)。
- 半监督扩展:利用未标注数据提升隐变量表示的泛化性。
- 结构化因果先验:在VAE中嵌入因果图结构,引导隐变量学习方向。
适用场景
- 存在未观测混杂的观察性数据:如医疗记录中未记录的遗传因素、经济研究中未观测的个体偏好。
- 高维特征与非线性关系:如基因组数据、用户行为日志、传感器时序数据。
- 需要反事实预测的任务:个性化治疗推荐、动态定价、政策干预模拟。
代码实现(PyTorch示例)
import torch
import torch.nn as nn
import torch.optim as optim
import torch.distributions as dist
class CEVAE(nn.Module):
def __init__(self, x_dim, z_dim):
super(CEVAE, self).__init__()
# 编码器
self.encoder = nn.Sequential(
nn.Linear(x_dim + 1 + 1, 256), # X + T + Y
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 2 * z_dim) # 输出μ_z和logσ_z^2
)
# 解码器
self.decoder_t = nn.Sequential(
nn.Linear(z_dim, 1),
nn.Sigmoid()
)
self.decoder_y = nn.Sequential(
nn.Linear(z_dim + 1, 1) # Z + T
)
self.decoder_x = nn.Sequential(
nn.Linear(z_dim, x_dim)
)
def encode(self, x, t, y):
inputs = torch.cat([x, t, y], dim=1)
h = self.encoder(inputs)
mu_z, logvar_z = torch.chunk(h, 2, dim=1)
return mu_z, logvar_z
def decode(self, z, t):
# 生成T、Y、X
t_pred = self.decoder_t(z)
y_input = torch.cat([z, t], dim=1)
y_pred = self.decoder_y(y_input)
x_recon = self.decoder_x(z)
return t_pred, y_pred, x_recon
def forward(self, x, t, y):
# 变分推断
mu_z, logvar_z = self.encode(x, t, y)
z = dist.Normal(mu_z, torch.exp(0.5*logvar_z)).rsample()
t_pred, y_pred, x_recon = self.decode(z, t)
return z, mu_z, logvar_z, t_pred, y_pred, x_recon
# 训练过程
model = CEVAE(x_dim=100, z_dim=10)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
for epoch in range(100):
for X, T, Y in dataloader:
# 前向传播
z, mu_z, logvar_z, t_pred, y_pred, x_recon = model(X, T, Y)
# 计算损失
recon_loss = nn.MSELoss()(x_recon, X) # 特征重建损失
t_loss = nn.BCELoss()(t_pred, T) # 处理变量损失
y_loss = nn.MSELoss()(y_pred, Y) # 结果变量损失
kl_loss = -0.5 * torch.sum(1 + logvar_z - mu_z.pow(2) - logvar_z.exp()) # KL散度
total_loss = recon_loss + t_loss + y_loss + 0.1 * kl_loss
# 反向传播
optimizer.zero_grad()
total_loss.backward()
optimizer.step()
# 反事实预测
def predict_ite(model, x):
# 编码观测数据
mu_z, logvar_z = model.encode(x, t=torch.zeros_like(T), y=model.decoder_y(torch.cat([z, t], dim=1)))
z_samples = dist.Normal(mu_z, torch.exp(0.5*logvar_z)).sample()
# 生成反事实结果
y1 = model.decoder_y(torch.cat([z_samples, torch.ones_like(T)], dim=1))
y0 = model.decoder_y(torch.cat([z_samples, torch.zeros_like(T)], dim=1))
return y1 - y0
生成对抗网络(GANITE)
GANITE是一种基于生成对抗网络(GAN)的因果推断方法,旨在通过对抗训练生成反事实结果,从而估计个体处理效应(ITE)。其核心创新在于结合生成模型与对抗学习,解决观测数据中反事实结果的缺失问题,尤其适用于高维特征和非线性因果关系的场景。
基本思路
- 反事实生成:每个个体仅能观测到一种处理下的结果(如接受治疗或未接受治疗),GANITE通过生成器模拟缺失的反事实结果,构建完整的潜在结果分布。
- 对抗训练:
- 生成器(Generator):输入观测数据(特征X、处理T、结果Y),生成反事实结果$\hat{Y}(1-T)$。
- 判别器(Discriminator):区分生成的反事实结果与真实观测结果,迫使生成器提高生成质量。
- 处理效应估计:基于生成的反事实结果,直接计算个体处理效应$\hat{\tau}(x) = \hat{Y}(1|x) – \hat{Y}(0|x)$。
网络结构
- 生成器G :
- 输入:X、T、Y。
- 输出:反事实结果$\hat{Y}(1-T)$。
- 目标:最小化生成结果与真实潜在结果之间的差异(若可知),同时欺骗判别器。
- 判别器D :
- 输入:X、T、Y或$\hat{Y}(1-T)$。
- 输出:判断输入结果是否为真实观测值。
- 目标:准确区分真实结果与生成结果。
- 推断器I (可选):
- 输入:X。
- 输出:估计处理效应$\hat{\tau}(x)$。
- 目标:最小化处理效应估计误差。
损失函数
- 对抗损失:$\mathcal{L}_{\text{adv}} = \mathbb{E}[\log D(X, T, Y)] + \mathbb{E}[\log (1 – D(X, 1-T, \hat{Y}(1-T)))]$
- 结果重构损失(若部分反事实结果已知):$\mathcal{L}_{\text{recon}} = \mathbb{E} \left[ \| Y(1-T) – \hat{Y}(1-T) \|^2 \right]$
- 处理效应一致性损失:$\mathcal{L}_{\text{consist}} = \mathbb{E} \left[ \| \hat{\tau}(X) – (\hat{Y}(1) – \hat{Y}(0)) \|^2 \right]$
- 总损失:$\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{adv}} + \alpha \mathcal{L}_{\text{recon}} + \beta \mathcal{L}_{\text{consist}}$。其中,$\alpha$和$\beta$为超参数。
算法步骤
- 数据预处理:标准化特征X,处理变量T编码为二元变量(0/1),结果Y归一化。
- 生成器训练:
- 输入(X, T, Y),生成反事实结果$\hat{Y}(1-T)$。
- 优化目标:最小化对抗损失和重构损失。
- 判别器训练:
- 输入真实数据(X, T, Y)和生成数据$(X, 1-T, \hat{Y}(1-T))$。
- 优化目标:最大化对真实和生成数据的区分能力。
- 推断器训练(若存在):
- 输入X,输出处理效应$\hat{\tau}(X)$。
- 优化目标:最小化处理效应估计误差(需部分已知ITE或通过生成结果计算)。
- 交替训练:
- 交替更新生成器、判别器和推断器,直至收敛。
优缺点分析
优点
- 反事实生成能力:直接生成缺失的反事实结果,支持复杂非线性关系建模。
- 高维数据处理:GAN的生成能力适合图像、文本等高维或非结构化数据。
- 对抗平衡:判别器迫使生成器生成与真实数据分布一致的反事实结果,缓解选择偏差。
缺点
- 训练不稳定:GAN的经典问题(如模式坍塌、梯度消失)可能导致生成结果质量波动。
- 计算复杂度高:需要同时训练多个网络,对算力和调参要求较高。
- 依赖生成质量:若生成器未能准确模拟反事实分布,处理效应估计将严重偏差。
改进策略
- Wasserstein GAN(WGAN):使用Wasserstein距离替代JS散度,提升训练稳定性。
- 条件生成对抗网络(CGAN):在生成器和判别器中显式加入处理变量T 的条件信息,增强生成可控性。
- 协变量平衡:在损失函数中引入处理组和对照组特征分布的相似性约束(如MMD损失)。
适用场景
- 观测性研究中的反事实预测:如医疗领域评估未采用的治疗方案效果,或金融领域评估未实施的策略影响。
- 高维或非结构化数据:如医疗影像、用户行为序列、时间序列数据。
- 个性化决策支持:需要针对个体生成反事实结果以制定最优策略的场景。
代码实现(PyTorch示例)
import torch
import torch.nn as nn
import torch.optim as optim
class Generator(nn.Module):
def __init__(self, input_dim):
super(Generator, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_dim + 1 + 1, 256), # X + T + Y
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 1) # 生成反事实Y(1-T)
)
def forward(self, x, t, y):
inputs = torch.cat([x, t, y], dim=1)
return self.net(inputs)
class Discriminator(nn.Module):
def __init__(self, input_dim):
super(Discriminator, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_dim + 1 + 1, 128), # X + T + Y
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 1),
nn.Sigmoid()
)
def forward(self, x, t, y):
inputs = torch.cat([x, t, y], dim=1)
return self.net(inputs)
# 初始化模型
gen = Generator(input_dim=100)
disc = Discriminator(input_dim=100)
optimizer_G = optim.Adam(gen.parameters(), lr=1e-4)
optimizer_D = optim.Adam(disc.parameters(), lr=1e-4)
criterion = nn.BCELoss()
# 训练循环
for epoch in range(1000):
for X, T, Y in dataloader:
# 生成反事实结果
T_cf = 1 - T
Y_cf = gen(X, T, Y)
# 训练判别器
real_labels = torch.ones(X.size(0), 1)
fake_labels = torch.zeros(X.size(0), 1)
# 真实数据损失
real_output = disc(X, T, Y)
d_loss_real = criterion(real_output, real_labels)
# 生成数据损失
fake_output = disc(X, T_cf, Y_cf.detach())
d_loss_fake = criterion(fake_output, fake_labels)
d_loss = d_loss_real + d_loss_fake
optimizer_D.zero_grad()
d_loss.backward()
optimizer_D.step()
# 训练生成器
validity = disc(X, T_cf, Y_cf)
g_loss = criterion(validity, real_labels) # 欺骗判别器
optimizer_G.zero_grad()
g_loss.backward()
optimizer_G.step()
# 处理效应估计
def estimate_ite(gen, X):
Y1 = gen(X, T=torch.ones(X.size(0), 1), Y=torch.zeros(X.size(0), 1))
Y0 = gen(X, T=torch.zeros(X.size(0), 1), Y=torch.zeros(X.size(0), 1))
return Y1 - Y0
双网络结构(TARNet/CFR)
TARNet(Treatment-Agnostic Representation Network)和CFR(Counterfactual Regression)是两种基于神经网络的双分支因果推断方法,通过共享表示层和正则化策略解决选择偏差和混杂因素问题,尤其适用于存在处理异质性的高维数据场景。
核心原理
TARNet:治疗无关的表示网络
- 基本思想:
- 共享表示层:通过神经网络提取输入特征X 的公共表示$\Phi(X)$,消除混杂变量对处理分配的影响。
- 双分支预测头:在共享层后分别构建处理组(T=1)和对照组(T=0)的潜在结果预测分支。
- 损失函数:仅基于观测到的结果进行训练,即处理组分支仅用T=1样本,对照组分支仅用T=0 样本。
- 模型结构:$\begin{aligned} \Phi(X) &= \text{SharedMLP}(X) \\ \hat{Y}_1 &= \text{MLP}_1(\Phi(X)) \quad (\text{处理组分支}) \\ \hat{Y}_0 &= \text{MLP}_0(\Phi(X)) \quad (\text{对照组分支}) \end{aligned}$
- 处理效应估计:$\hat{\tau}(x) = \hat{Y}_1(x) – \hat{Y}_0(x)$
CFR:反事实回归
- 核心改进:
- 平衡表示正则化:在TARNet基础上,通过正则化项强制处理组和对照组的表示分布$\Phi(X|T=1)$和$\Phi(X|T=0)$对齐,缓解选择偏差。
- 常用正则化方法:
- MMD(最大均值差异):衡量两组表示分布的距离。
- Wasserstein距离:通过最优传输理论平衡分布。
- 损失函数:$\mathcal{L} = \mathcal{L}_{\text{outcome}} + \alpha \cdot \mathcal{L}_{\text{balance}}$
- 结果损失:$\mathcal{L}_{\text{outcome}} = \frac{1}{n} \sum_{i=1}^n ( \hat{Y}_t(x_i) – Y_i )^2 \quad (t=T_i)$
- 平衡损失(以MMD为例):$\mathcal{L}_{\text{balance}} = \text{MMD}^2 ( \{\Phi(x_i)\}_{T_i=1}, \{\Phi(x_j)\}_{T_j=0})$
算法步骤
- 输入数据:特征X,处理变量$T \in \{0,1\}$,结果Y。
- 共享表示层:使用多层感知机(MLP)提取特征表示$\Phi(X)$。
- 双分支预测:
- 处理组分支:基于$\Phi(X)$预测$\hat{Y}_1$。
- 对照组分支:基于$\Phi(X)$预测$\hat{Y}_0$。
- 平衡正则化(仅CFR):计算处理组和对照组表示的分布差异(如MMD),作为正则化项加入损失函数。
- 联合优化:同时最小化结果预测误差和分布差异,更新网络参数。
- 处理效应估计:
- 对每个样本x,计算$\hat{\tau}(x) = \hat{Y}_1(x) – \hat{Y}_0(x)$。
优缺点分析
优点
- 处理异质性建模:双分支结构允许处理组和对照组独立学习非线性效应,适应处理异质性。
- 平衡表示(CFR):强制处理组和对照组在表示空间中对齐,有效减少选择偏差。
- 计算效率:网络结构简单,训练速度快于GAN或VAE类方法。
缺点
- 无显式反事实生成:无法生成反事实结果,仅依赖双分支预测潜在结果。
- 正则化敏感性(CFR):平衡项的权重$\alpha$需精细调参,否则易导致欠拟合或过拟合。
- 依赖观测数据分布:若处理组和对照组样本量严重不均衡,平衡效果可能受限。
改进策略
- 动态权重调整:根据样本量自动调整平衡项的权重$\alpha$。
- 深度平衡网络:引入对抗训练(如CFR-WASS,使用Wasserstein距离替代MMD)。
- 多任务学习:联合预测处理倾向得分(类似DragonNet),增强表示学习。
适用场景
- 观测性数据中的因果效应估计:如医疗研究中评估药物对不同患者的异质性疗效。
- 高维特征和复杂非线性关系:如基因表达数据、用户行为特征、图像嵌入表示。
- 需要快速部署的场景:相比GANITE和CEVAE,TARNet/CFR训练速度更快。
代码实现(PyTorch示例)
import torch
import torch.nn as nn
import torch.optim as optim
class TARNet(nn.Module):
def __init__(self, input_dim, hidden_dim=64):
super(TARNet, self).__init__()
# 共享表示层
self.shared = nn.Sequential(
nn.Linear(input_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU()
)
# 处理组分支
self.treat_branch = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, 1)
)
# 对照组分支
self.control_branch = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, 1)
)
def forward(self, x):
phi = self.shared(x)
y1 = self.treat_branch(phi)
y0 = self.control_branch(phi)
return y1, y0
class CFR(nn.Module):
def __init__(self, input_dim, alpha=0.5):
super(CFR, self).__init__()
self.tarnet = TARNet(input_dim)
self.alpha = alpha
def mmd_loss(self, phi, t):
# 计算处理组和对照组表示的MMD距离
phi_t1 = phi[t.squeeze() == 1]
phi_t0 = phi[t.squeeze() == 0]
if phi_t1.shape[0] == 0 or phi_t0.shape[0] == 0:
return torch.tensor(0.0)
# MMD计算(简化版)
mean_t1 = phi_t1.mean(dim=0)
mean_t0 = phi_t0.mean(dim=0)
return torch.norm(mean_t1 - mean_t0, p=2) ** 2
def forward(self, x, t, y):
y1_pred, y0_pred = self.tarnet(x)
# 选择实际处理对应的预测
y_pred = torch.where(t == 1, y1_pred, y0_pred)
# 计算损失
outcome_loss = nn.MSELoss()(y_pred, y)
phi = self.tarnet.shared(x)
balance_loss = self.mmd_loss(phi, t)
total_loss = outcome_loss + self.alpha * balance_loss
return total_loss
# 训练过程
model = CFR(input_dim=50, alpha=0.5)
optimizer = optim.Adam(model.parameters(), lr=0.001)
for epoch in range(100):
for X, T, Y in dataloader:
loss = model(X, T, Y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 估计ITE
y1, y0 = model.tarnet(X_test)
ite = y1 - y0
匹配方法(Propensity Score Matching)
倾向评分匹配(PSM)是一种基于观测数据的因果推断方法,通过构建处理组和对照组的可比样本来减少混杂偏差,估计平均处理效应(如ATE、ATT)。其核心思想是利用倾向评分(Propensity Score)平衡协变量分布,模拟随机对照试验(RCT)的组间均衡性。
基本概念
- 倾向评分(Propensity Score):定义为给定协变量 X 下个体接受处理 T=1 的条件概率:$e(X) = P(T=1 | X)$.通过逻辑回归、随机森林等模型估计。
- 可忽略性假设(Ignorability):给定X,潜在结果与处理分配独立,即$Y(1), Y(0) \perp T | X$。
- 重叠性假设(Overlap):处理组和对照组的倾向评分分布存在重叠区域,即$0 < e(X) < 1$。
匹配目标
通过匹配处理组和对照组中倾向评分相近的个体,构造近似平衡的样本,使得组间差异仅由处理效应引起,而非协变量差异。
算法步骤
- 估计倾向评分:
- 使用逻辑回归、GBM或神经网络建模e(X) 。
- 示例(逻辑回归):$\log ( \frac{e(X)}{1 – e(X)}) = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p$
- 选择匹配方法:
- 最近邻匹配(Nearest Neighbor):为每个处理组个体寻找倾向评分最接近的对照组个体。
- 卡尺匹配(Caliper Matching):仅匹配倾向评分差异小于预定阈值(如1倍标准差)的个体。
- 分层匹配(Stratification):将倾向评分分为若干层,在各层内计算效应后加权平均。
- 核匹配(Kernel Matching):使用核函数(如高斯核)对对照组个体进行加权。
- 评估匹配质量:
- 标准化差异(Standardized Difference):$d = \frac{|\bar{X}_{\text{treat}} – \bar{X}_{\text{control}}|}{\sqrt{(s_{\text{treat}}^2 + s_{\text{control}}^2)/2}}$,通常要求d < 0.1。
- 可视化检查:绘制匹配前后协变量分布的直方图或QQ图。
- 效应估计:
- 平均处理效应(ATE):$\hat{\tau}_{\text{ATE}} = \frac{1}{N} \sum_{i=1}^N ( Y_i(1) – Y_i(0))$
- 处理组平均效应(ATT):$\hat{\tau}_{\text{ATT}} = \frac{1}{N_{\text{treat}}} \sum_{i \in \text{treat}} ( Y_i – \frac{1}{M} \sum_{j \in \text{control}(i)} Y_j)$,其中M 为每个处理组个体匹配的对照个体数。
优缺点分析
优点
- 直观易解释:通过协变量平衡模拟RCT,结果易于理解。
- 灵活性强:支持多种匹配算法和效应估计方法。
- 低计算成本:相比机器学习模型,PSM计算效率高。
缺点
- 依赖模型假设:
- 倾向评分模型误设(如非线性关系未捕捉)导致匹配失效。
- 无法处理未观测混杂变量(违反可忽略性假设)。
- 信息损失:卡尺匹配可能丢弃大量样本,降低统计功效。
- 方差-偏差权衡:过度匹配(精确匹配)减少偏差但增加方差,反之亦然。
改进策略
- 增强倾向评分估计:使用GBM、LASSO或深度学习模型捕捉非线性关系和交互效应。
- 双重稳健估计(Doubly Robust Estimation):结合倾向评分和结果模型,任一模型正确即可保证无偏估计。
- 熵平衡(Entropy Balancing):直接优化协变量平衡权重,避免倾向评分建模。
- 协变量平衡倾向评分(CBPS):在倾向评分估计中直接约束协变量平衡。
适用场景
- 观察性研究中的因果效应估计:如评估政策干预、药物治疗效果等。
- 低维至中维协变量:协变量维度较高时需结合降维技术(如PCA)。
- 探索性分析:作为基线方法快速验证处理效应方向。
代码实现(Python示例)
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import NearestNeighbors
# 生成模拟数据
np.random.seed(42)
n = 1000
X = np.random.normal(size=(n, 5)) # 5个协变量
true_ps = 1 / (1 + np.exp(-(X[:, 0] + 0.5*X[:, 1] - 0.3*X[:, 2])))
T = np.random.binomial(1, true_ps)
Y = 50 + 10*T + 2*X[:, 0] + 3*X[:, 1] + np.random.normal(scale=5, size=n)
# 步骤1:估计倾向评分(逻辑回归)
ps_model = LogisticRegression()
ps_model.fit(X, T)
ps = ps_model.predict_proba(X)[:, 1]
# 步骤2:卡尺匹配(最近邻1:1)
treat_indices = np.where(T == 1)[0]
control_indices = np.where(T == 0)[0]
# 计算卡尺(0.2倍标准差)
caliper = 0.2 * np.std(ps)
matched_control = []
for i in treat_indices:
# 计算处理个体i与所有对照的倾向评分差异
diffs = np.abs(ps[i] - ps[control_indices])
# 筛选差异小于卡尺的候选
candidates = control_indices[diffs <= caliper]
if len(candidates) > 0:
# 选择差异最小的一个
nearest = candidates[np.argmin(diffs[diffs <= caliper])]
matched_control.append(nearest)
control_indices = control_indices[control_indices != nearest] # 避免重复匹配
# 构造匹配后的数据集
matched_treat = treat_indices[:len(matched_control)]
matched_data = pd.DataFrame({
'Y_treat': Y[matched_treat],
'Y_control': Y[matched_control]
})
# 步骤3:计算ATT
ATT = np.mean(matched_data['Y_treat'] - matched_data['Y_control'])
print(f"Estimated ATT: {ATT:.2f}")
Uplift方法对比表
基础方法
| 方法 | 核心优势 | 核心局限 | 适用场景 |
| 双模型法 | 简单快速,易实现 | 忽略处理变量与特征交互,误差累积 | 基线验证,样本量充足且处理效应独立 |
| 标签转换法 (TO) | 避免双模型误差累积,计算高效 | 依赖样本均衡性,仅支持二元处理 | 均衡实验设计,需快速建模 |
树模型与集成方法
| 方法 | 核心优势 | 核心局限 | 适用场景 |
| Uplift决策树 | 可解释性强,直接优化Uplift增益 | 过拟合风险高,对高维数据敏感 | 中小数据集,需直观展示因果异质性 |
| 因果森林 | 捕捉复杂异质性,支持非线性效应 | 依赖倾向得分准确性,计算成本较高 | 大规模数据,处理效应异质性复杂场景 |
元学习器
| 方法 | 核心优势 | 核心局限 | 适用场景 |
| S-Learner | 单模型轻量,资源占用低 | 处理效应易被特征淹没(交互弱时失效) | 处理变量与特征强交互,样本量有限 |
| T-Learner | 允许两组模型独立优化 | 误差累积,忽略处理与特征交互 | 实验组/对照组分布差异显著但交互弱 |
| X-Learner | 适合非均衡数据,反事实修正鲁棒 | 依赖基模型预测能力,误差传递风险 | 实验组样本稀缺,需修正反事实估计 |
| R-Learner | 双重鲁棒性,适合高维混杂因素 | 需同时准确建模倾向得分和结果模型 | 观察性数据,存在高维混杂变量 |
深度学习与高级方法
| 方法 | 核心优势 | 核心局限 | 适用场景 |
| DragonNet | 端到端联合建模结果和倾向得分 | 需平衡任务损失权重,调参复杂 | 需同时利用深度表示和倾向得分的场景 |
| CEVAE | 建模潜在变量解决未观测混杂 | 依赖潜在变量分布假设,计算复杂 | 存在未观测混杂的观察性数据 |
| GANITE | 生成反事实结果,灵活处理复杂分布 | 训练不稳定,需大量数据和算力 | 研究性质项目,反事实生成需求场景 |
| TARNet/CFR | 高维非线性数据建模,表示学习对齐分布 | 计算成本高,需复杂调参 | 图像、文本等高维特征因果推断 |
其他方法
| 方法 | 核心优势 | 核心局限 | 适用场景 |
| 倾向评分匹配 (PSM) | 直观易解释,快速验证ATE | 无法估计ITE,依赖倾向得分准确性 | 观察性数据快速评估ATE,需严格重叠性检验 |
实践建议
- 数据量小/特征简单:优先选择Uplift决策树或S-Learner。
- 非均衡数据:X-Learner或PSM(倾向得分匹配)。
- 高维数据/复杂交互:因果森林或R-Learner。
- 未观测混杂:CEVAE或DragonNet(需验证假设)。
- 深度特征(如图像):TARNet/CFR或GANITE(研究场景)。
- 工业快速落地:因果森林或R-Learner(平衡效果与效率)。
Uplift常见评估指标
核心评估指标
Qini系数(Qini Coefficient)
Qini系数是Uplift模型评估中最核心的指标之一,用于衡量模型对用户处理效应(Uplift)的排序能力。它的核心思想是:通过模型预测的Uplift值对用户进行排序,评估前k%用户的实际增益是否显著高于随机策略。
Qini系数的定义与计算
- 数学定义:Qini系数是Qini曲线(累积增益曲线)与随机模型基线曲线之间的面积差(Area Between Curves, ABC)。
- Qini曲线:按模型预测的Uplift值降序排列用户后,前k%用户的累积增益。
- 随机基线:假设无模型干预时,随机选择用户的累积增益(线性增长)。
- 计算公式:设样本总数为 N,处理组和对照组的响应数分别为$Y_t$和$Y_c$,则:
- 累积增益(前k个样本的实际增益):$\text{Gain}(k) = ( \frac{Y_t(k)}{N_t(k)} – \frac{Y_c(k)}{N_c(k)}) \times k$,其中$N_t(k)$和$N_c(k)$为前k个样本中处理组和对照组的数量。
- Qini系数:$\text{Qini} = \sum_{k=1}^N \text{Gain}(k) – \frac{1}{2} \times \text{Gain}(N)$(积分形式为Qini曲线下面积减去随机基线下面积)
- 计算步骤:
- Step 1:按模型预测的Uplift值从高到低对用户排序。
- Step 2:依次计算前10%、20%、…、100%用户的累积增益。
- Step 3:绘制Qini曲线(X轴为样本比例,Y轴为累积增益)。
- Step 4:计算Qini曲线与随机直线之间的面积差(Qini系数)。
Qini曲线与Qini系数的可视化
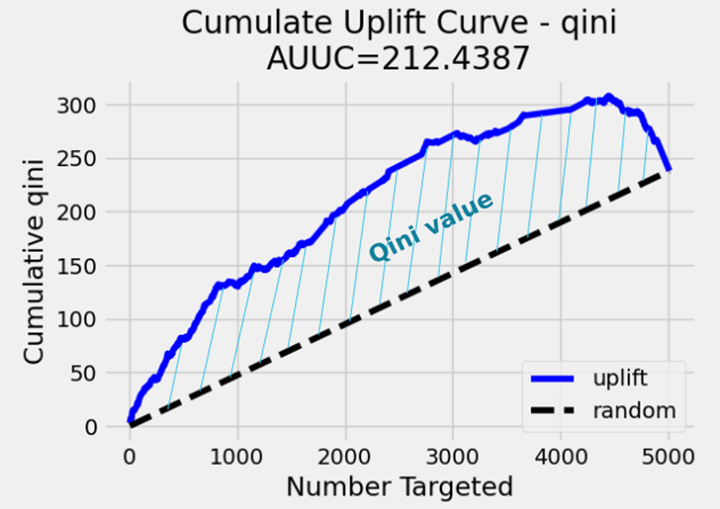
- Qini曲线示例:
- 理想模型:曲线快速上升至峰值后趋于平缓(模型精准识别高Uplift用户)。
- 随机模型:斜率为常数的直线(无排序能力)。
- 反向模型:曲线低于随机基线(模型排序完全错误)。
- Qini系数的取值范围:
- 最大值:当模型完美排序时,Qini系数趋近于理论最大增益(如所有高Uplift用户均被排在前面)。
- 负值:模型排序效果差于随机策略。
Qini系数的核心作用
- 评估排序能力:回答业务问题:“模型是否能将高Uplift用户排在前面?”
- 高Qini系数:模型能有效区分高/低价值用户,指导资源优先分配。
- 低Qini系数:模型排序能力差,可能需调整特征或算法。
- 对比模型性能:通过比较不同模型的Qini系数,选择最优模型。
- 例如:模型A的Qini系数为45,模型B为0.32 → 模型A更优。
- 指导业务决策:
- 确定干预阈值:根据Qini曲线的拐点,选择最佳用户覆盖比例(如触达前30%用户)。
- 估算ROI:结合增益值计算投入产出比。
Qini系数的优缺点
| 优点 | 缺点 |
| 直观反映模型的排序能力 | 对处理组/对照组样本量不均衡敏感 |
| 支持跨模型对比(如与传统响应模型对比) | 无法直接反映个体Uplift预测的准确性 |
| 适用于业务场景(如营销资源分配) | 需依赖处理组和对照组的观测数据 |
Qini系数的改进与注意事项
- 样本不均衡的修正:
- IPW加权(逆概率加权):对处理组和对照组样本进行加权,平衡样本分布。
- 标准化增益:将增益值除以随机基线的最大增益,消除样本量影响。
- 验证数据要求:
- 随机实验数据:处理组和对照组的用户需随机分配,避免选择偏差。
- 重叠性(Overlap):所有用户均有概率被分配到处理组和对照组。
- 与其他指标的联合使用:
- AUUC(Area Under Uplift Curve):更关注相对增益,减少对随机基线的依赖。
- 分位数响应提升:验证Top 10%用户的真实增益是否显著。
Qini系数的Python实现
import numpy as np
import pandas as pd
from sklearn.metrics import auc
def calculate_qini(y_true, uplift, treatment):
# 按Uplift降序排序
df = pd.DataFrame({'y': y_true, 'uplift': uplift, 'treatment': treatment})
df = df.sort_values(by='uplift', ascending=False).reset_index(drop=True)
# 累积计算处理组和对照组的响应数与样本数
n = len(df)
cum_treat = df['treatment'].cumsum()
cum_control = (1 - df['treatment']).cumsum()
cum_y_treat = (df['y'] * df['treatment']).cumsum()
cum_y_control = (df['y'] * (1 - df['treatment'])).cumsum()
# 计算每个点的增益(避免除零)
gain = (cum_y_treat / np.where(cum_treat == 0, 1e-6, cum_treat)) - \
(cum_y_control / np.where(cum_control == 0, 1e-6, cum_control))
gain = gain * np.arange(1, n+1) # 累积增益乘以样本数
# 计算Qini曲线和随机基线
x = np.arange(n) / n
perfect_gain = gain.max() * x # 完美模型的增益(理论值)
random_gain = gain.iloc[-1] * x
# 计算Qini系数(面积差)
qini_area = auc(x, gain) - auc(x, random_gain)
normalized_qini = qini_area / auc(x, perfect_gain - random_gain)
return normalized_qini
# 示例数据
np.random.seed(42)
n_samples = 1000
uplift = np.random.randn(n_samples) # 模型预测的Uplift值
treatment = np.random.randint(0, 2, n_samples) # 处理组标签(0/1)
y_true = (0.3 * uplift + 0.1 * np.random.randn(n_samples) > 0).astype(int) # 模拟真实响应
print(f"Qini系数: {calculate_qini(y_true, uplift, treatment):.4f}")
AUUC(Area Under the Uplift Curve)
AUUC(Uplift曲线下面积)是评估Uplift模型排序能力的关键指标,直接反映模型对不同用户处理效应(Uplift)的区分能力。与Qini系数类似,AUUC通过累积增益曲线衡量模型性能,但更关注实际增益的绝对面积而非与随机基线的差值。
AUUC的定义与计算
- 数学定义:AUUC是Uplift曲线(累积增益曲线)下方的面积,反映模型在不同分位点下的累积增益总和。
- Uplift曲线:按模型预测的Uplift值降序排列用户后,前k%用户的累积增益。
- 随机基线:AUUC通常不直接减去随机基线,因此其值可能随样本量变化,需结合业务场景解读。
- 计算公式:
- 单个分位点增益(前k个样本的实际增益):$\text{Uplift}(k) = \frac{Y_t(k)}{N_t(k)} – \frac{Y_c(k)}{N_c(k)}$,其中$Y_t(k)$和$Y_c(k)$是前k个样本中处理组和对照组的响应数,$N_t(k)$和$N_c(k)$是样本数。
- AUUC:对全部k值(通常为1到N)的Uplift增益积分:$\text{AUUC} = \sum_{k=1}^N \text{Uplift}(k)$,实际计算中常通过梯形法则(Trapezoidal Rule)近似曲线下面积。
- 计算步骤:
- Step 1:按模型预测的Uplift值从高到低对用户排序。
- Step 2:依次计算前10%、20%、…、100%用户的Uplift增益。
- Step 3:绘制Uplift曲线(X轴为样本比例,Y轴为累积增益)。
- Step 4:计算曲线下面积(AUUC)。
Uplift曲线与AUUC的可视化
- Uplift曲线示例:
- 理想模型:曲线快速上升至峰值后趋于平缓(模型精准识别高Uplift用户)。
- 随机模型:水平线或缓慢上升(无区分能力)。
- 反向模型:曲线下降(模型排序错误,高Uplift用户被排在后部)。
- AUUC的取值特点:
- 正值:模型排序效果优于随机策略。
- 负值:模型排序效果差于随机策略。
- 最大值:当模型完美排序时,AUUC趋近于理论最大增益。
AUUC的核心作用
- 评估模型排序能力:
- 回答业务问题:“模型是否将高Uplift用户排在前部?”
- 高AUUC:模型能有效区分用户敏感度,指导资源分配。
- 低AUUC:模型无法区分用户,需优化特征或算法。
- 对比模型性能:
- 直接比较不同模型的AUUC值,无需依赖随机基线。
- 例如:模型A的AUUC为25,模型B为0.18 → 模型A更优。
- 业务决策支持:
- 确定干预范围:根据曲线拐点选择最佳用户覆盖比例(如触达前20%用户)。
- 估算总增益:AUUC值近似等于模型带来的总增益(需结合样本量)。
AUUC的优缺点
| 优点 | 缺点 |
| 直接反映模型的绝对增益能力 | 值受样本量和响应率影响,难以跨数据集对比 |
| 无需计算随机基线,计算更简单 | 对处理组/对照组样本量不均衡敏感 |
| 直观展示模型在不同分位点的效果 | 无法区分模型是否优于随机策略(需结合曲线观察) |
AUUC与Qini系数的对比
| 指标 | 计算目标 | 基线处理 | 适用场景 |
| AUUC | 累积增益的绝对面积 | 不减去随机基线 | 需直接对比模型绝对增益的场景 |
| Qini系数 | 模型与随机基线的增益面积差 | 需减去随机基线 | 需标准化评估模型超越随机策略的能力 |
AUUC的改进与注意事项
- 样本不均衡的修正:
- 标准化AUUC:将AUUC除以完美模型的AUUC,得到相对值(类似AUC的归一化)。
- IPW加权:对处理组和对照组样本进行逆概率加权,平衡样本分布。
- 验证数据要求:
- 随机实验数据:处理组和对照组需随机分配,避免选择偏差。
- 重叠性(Overlap):所有用户均有概率被分配到处理组和对照组。
- 与其他指标联合使用:
- Qini系数:结合两者评估模型排序能力和超越随机策略的程度。
- 分位数响应提升:验证Top 10%用户的真实增益是否符合预期。
AUUC的Python实现
import numpy as np
import pandas as pd
from sklearn.metrics import auc
def calculate_auuc(y_true, uplift, treatment):
# 按Uplift降序排序
df = pd.DataFrame({'y': y_true, 'uplift': uplift, 'treatment': treatment})
df = df.sort_values(by='uplift', ascending=False).reset_index(drop=True)
# 累积计算处理组和对照组的响应数与样本数
n = len(df)
cum_treat = df['treatment'].cumsum()
cum_control = (1 - df['treatment']).cumsum()
cum_y_treat = (df['y'] * df['treatment']).cumsum()
cum_y_control = (df['y'] * (1 - df['treatment'])).cumsum()
# 计算每个点的Uplift增益(避免除零)
uplift_gain = (cum_y_treat / np.where(cum_treat == 0, 1e-6, cum_treat)) - \
(cum_y_control / np.where(cum_control == 0, 1e-6, cum_control))
# 计算AUUC(梯形法则积分)
x = np.arange(n) / n
auuc = auc(x, uplift_gain)
return auuc
# 示例数据
np.random.seed(42)
n_samples = 1000
uplift = np.random.randn(n_samples) # 模型预测的Uplift值
treatment = np.random.randint(0, 2, n_samples) # 处理组标签(0/1)
y_true = (0.3 * uplift + 0.1 * np.random.randn(n_samples) > 0).astype(int) # 模拟真实响应
print(f"AUUC: {calculate_auuc(y_true, uplift, treatment):.4f}")
增益图(Uplift Curve)
增益图(Uplift Curve)是评估Uplift模型排序能力的核心可视化工具,通过展示模型在不同分位点下的累积增益,直观反映模型对用户处理效应(Uplift)的区分能力。它不仅能对比模型与随机策略的效果差异,还能指导业务决策(如确定干预用户比例)。
增益图的定义与构成
- 核心思想:
- 按模型预测的Uplift值对用户降序排列,从前到后依次选择前k%的用户,计算其实际增益(即处理组与对照组的响应率差异)。
- 通过绘制累积增益随用户比例的变化曲线,直观展示模型的排序能力。
- 图形构成:
- 横轴(X轴):用户比例(0%到100%),表示按Uplift值排序后累计触达的用户范围。
- 纵轴(Y轴):累积增益(Cumulative Uplift),即前k%用户的平均处理效应(ATE)乘以用户数。
- 关键曲线:
- 模型曲线:实际Uplift模型的累积增益曲线。
- 随机基线:随机选择用户时的理论增益(线性增长或无增益)。
- 完美曲线:假设模型完美排序时的理论最大增益(先快速上升后平缓)。
- 示例图:
- 理想模型:曲线陡峭上升至峰值后平缓(高Uplift用户集中在前部)。
- 随机模型:线性增长或无明显趋势(无区分能力)。
- 反向模型:曲线低于随机基线(模型排序错误)。
增益图的绘制步骤
- 数据准备:
- 输入数据:用户真实响应标签(y_true)、模型预测的Uplift值(uplift_score)、处理组标签(treatment)。
- 数据要求:处理组和对照组需满足随机分配(RCT数据)或满足条件独立假设。
- 排序与累积计算:
- Step 1:按模型预测的Uplift值对用户降序排列。
- Step 2:依次计算前k%(k=1,2,…,100)用户的累积增益:$\text{Uplift}(k) = \left( \frac{Y_t(k)}{N_t(k)} – \frac{Y_c(k)}{N_c(k)} \right) \times k$,其中:
- $Y_t(k)$和$Y_c(k)$:前k个用户中处理组和对照组的响应数。
- $N_t(k)$和$N_c(k)$:前k个用户中处理组和对照组的样本数。
- 绘制曲线:
- 连接所有分位点的累积增益值,形成增益图。
- 添加参考线:
- 随机基线:$\text{Uplift}(k) = \text{整体ATE} \times k$。
- 完美曲线:假设前k%用户的Uplift值为真实最大值时的理论曲线。
增益图的解读方法
- 模型效果判断:
- 曲线高于随机基线:模型有效,排序能力优于随机策略。
- 曲线接近完美曲线:模型接近理想性能。
- 曲线低于随机基线:模型排序错误,需重新训练或调整。
- 关键分位点分析:
- 峰值点:曲线达到最大增益时对应的用户比例(如30%),表示最优干预范围。
- 拐点:曲线斜率显著下降的位置,指导资源分配(如仅触达拐点前的用户)。
- 业务指标估算:
- 总增益:曲线下面积(AUUC)近似等于模型带来的总增益。
- ROI计算:结合增益值和成本(如营销费用)估算投入产出比。
增益图的核心应用场景
- 模型对比:
- 对比不同模型(如Meta-Learner vs.双模型)的增益图,选择排序能力最优的模型。
- 示例:模型A的曲线始终高于模型B → 模型A更优。
- 资源分配决策:
- 确定干预比例:根据峰值或拐点选择最佳用户覆盖范围(如仅触达前20%用户)。
- 预算约束优化:在有限预算下,选择增益斜率最大的区间优先投放资源。
- 业务效果验证:
- 离线评估:验证模型对历史数据的增益是否符合预期。
- 在线实验:对比增益图预测的增益与实际A/B测试结果的一致性。
增益图的优缺点
| 优点 | 缺点 |
| 直观展示模型对不同用户群的区分能力 | 对处理组/对照组样本量不均衡敏感 |
| 直接关联业务指标(如转化率、ROI) | 需结合数值指标(如AUUC)量化模型性能 |
| 支持多模型对比与阈值选择 | 依赖数据质量(如随机分配和处理效应稳定性) |
增益图的Python实现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def plot_uplift_curve(y_true, uplift_score, treatment):
# 按Uplift降序排序
df = pd.DataFrame({'y': y_true, 'uplift': uplift_score, 'treatment': treatment})
df = df.sort_values(by='uplift', ascending=False).reset_index(drop=True)
# 计算累积增益
n = len(df)
x = np.arange(1, n+1) / n # 用户比例(0~1)
uplift_gain = []
for k in range(1, n+1):
sub_df = df.head(k)
y_t = sub_df[sub_df['treatment'] == 1]['y'].sum()
n_t = sub_df['treatment'].sum()
y_c = sub_df[sub_df['treatment'] == 0]['y'].sum()
n_c = k - n_t
uplift = (y_t / max(n_t, 1e-6)) - (y_c / max(n_c, 1e-6))
uplift_gain.append(uplift * k) # 累积增益
# 计算随机基线和完美曲线(示例)
overall_ate = (df[df['treatment']==1]['y'].mean() - df[df['treatment']==0]['y'].mean())
random_gain = [overall_ate * k for k in range(1, n+1)]
perfect_gain = np.sort(uplift_gain)[::-1] # 降序排列(理论最大值)
# 绘制增益图
plt.figure(figsize=(10, 6))
plt.plot(x, uplift_gain, label='Model', color='#1f77b4')
plt.plot(x, random_gain, label='Random', linestyle='--', color='#ff7f0e')
plt.plot(x, perfect_gain, label='Perfect', linestyle=':', color='#2ca02c')
plt.xlabel('Proportion of Population Targeted', fontsize=12)
plt.ylabel('Cumulative Uplift', fontsize=12)
plt.title('Uplift Curve', fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
# 示例数据
np.random.seed(42)
n_samples = 1000
uplift_score = np.random.randn(n_samples) # 模型预测的Uplift值
treatment = np.random.randint(0, 2, n_samples) # 处理组标签(0/1)
y_true = (0.3 * uplift_score + 0.1 * np.random.randn(n_samples) > 0).astype(int)
plot_uplift_curve(y_true, uplift_score, treatment)
注意事项
- 样本均衡性:
- 处理组与对照组样本量差异大时,需标准化增益值(如使用权重或比率)。
- 避免因样本不均衡导致曲线扭曲。
- 数据质量:
- 确保处理组和对照组用户特征分布一致(可通过协变量平衡检验)。
- 使用RCT数据或因果推断方法消除混杂偏差。
- 业务解读:
- 结合业务场景理解增益值(如转化率提升1%可能对应百万收入)。
- 避免过度依赖离线指标,需通过A/B测试验证实际效果。
ATE估计误差(ATE Estimation Error)
平均处理效应(Average Treatment Effect, ATE)是因果推断中的核心指标,用于衡量处理(Treatment)对结果变量的平均影响。然而,实际估计ATE时,由于数据局限性和方法缺陷,常会引入ATE估计误差,即估计值与真实值之间的偏差。
ATE与ATE估计误差的定义
- ATE的数学定义:ATE表示处理组(Treated Group)与对照组(Control Group)的潜在结果均值之差:$\text{ATE} = \mathbb{E}[Y(1) – Y(0)]$。其中,Y(1)和Y(0)分别是个体接受处理和不接受处理的潜在结果。
- ATE估计误差:通过观测数据得到的ATE估计值$\hat{\text{ATE}}$与真实ATE之间的差异:$\text{误差} = \hat{\text{ATE}} – \text{ATE}$,误差由偏差(Bias)和方差(Variance)共同构成,总误差可通过均方误差(MSE)衡量:$\text{MSE} = \text{Bias}^2 + \text{Variance}$
ATE估计误差的来源
| 误差来源 | 描述 | 示例 |
| 1. 选择偏差(Selection Bias) | 处理组与对照组存在系统性差异,导致无法直接比较结果。 | 在观测数据中,健康意识强的人更可能接种疫苗(处理组),其本身患病风险较低,导致疫苗效果被高估。 |
| 2. 混淆变量(Confounding) | 未观测的变量同时影响处理分配和结果,导致因果效应估计失真。 | 收入水平影响用户是否收到优惠券(处理)和购买行为(结果),若未控制收入,优惠券效果的ATE估计会有偏差。 |
| 3. 模型误设(Model Misspecification) | 统计模型未正确捕捉处理效应与协变量的关系。 | 使用线性回归估计非线性效应,或忽略处理与协变量的交互作用。 |
| 4. 测量误差(Measurement Error) | 处理变量或结果变量的测量不准确。 | 用户是否点击广告(处理)的记录存在遗漏,或销售额(结果)的统计存在误差。 |
| 5. 非依从性(Non-compliance) | 实验设计中部分个体未按分配接受处理(如拒绝治疗或交叉使用对照组处理)。 | 随机试验中,部分患者未服用药物(处理组非依从),而部分对照组患者自行购买药物(对照组污染)。 |
| 6. 样本量不足(Small Sample) | 小样本下估计量的方差较大,导致估计不稳定。 | 在小规模临床试验中,ATE估计值可能因偶然性偏离真实值。 |
ATE估计误差的影响
- 业务决策误导:
- 高估处理效应可能导致过度投资无效策略(如推广对转化率无实际提升的广告)。
- 低估处理效应可能错失高回报机会(如放弃真正有效的治疗方案)。
- 模型评估失真:Uplift模型依赖准确的ATE估计来评估性能(如Qini系数和AUUC)。若ATE估计误差大,模型排序能力的评估结果不可靠。
- 因果结论无效:存在严重偏差时,统计显著性(如p值)可能无法反映真实因果效应,导致错误结论。
减少ATE估计误差的方法
- 随机对照试验(RCT):
- 通过随机分配处理,消除选择偏差和混淆变量的影响。
- 局限性:成本高,且可能存在非依从性或外部效度问题。
- 倾向得分匹配(Propensity Score Matching, PSM):
- 根据协变量计算倾向得分(处理概率),为处理组样本匹配相似的对照组样本,减少选择偏差。
- 公式:$\hat{\text{ATE}} = \frac{1}{N} \sum_{i=1}^N [ \frac{T_i Y_i}{\hat{e}(X_i)} – \frac{(1-T_i) Y_i}{1-\hat{e}(X_i)}]$,其中$\hat{e}(X_i)$为倾向得分。
- 双重稳健估计(Doubly Robust Estimation):
- 结合倾向得分模型和结果回归模型,只要其中之一正确,即可得到无偏估计。
- 公式:$\hat{\text{ATE}} = \frac{1}{N} \sum_{i=1}^N [ \hat{\mu}_1(X_i) – \hat{\mu}_0(X_i)]$,其中$\hat{\mu}_1(X_i)$和$\hat{\mu}_0(X_i)$为处理组和对照组的预测结果。
- 工具变量(Instrumental Variables, IV):
- 使用与处理变量相关但独立于结果的变量(工具变量),解决非依从性或未观测混淆问题。
- 示例:在药物效果评估中,使用“医生处方偏好”作为工具变量。
- 增大样本量:减少估计量的方差,提高估计精度。
- 敏感性分析(Sensitivity Analysis):评估未观测混淆变量对估计结果的影响程度,判断结论的稳健性。
ATE估计误差的评估方法
- 置信区间与假设检验:通过Bootstrap或渐近分布计算置信区间,判断估计值的统计显著性。
- 均方误差(MSE)分解:$\text{MSE} = \mathbb{E}[(\hat{\text{ATE}} – \text{ATE})^2] = \text{Bias}^2 + \text{Variance}$
- Bias:估计值的系统性偏离。
- Variance:估计量的波动性。
- 交叉验证(Cross-Validation):将数据分为训练集和验证集,评估ATE估计在不同子样本中的稳定性。
分位数响应提升(Quantile Uplift)
分位数响应提升(Quantile Uplift)是评估Uplift模型在用户群体不同分位点(如前10%、20%、…、100%)上处理效应(Uplift)表现的重要方法。它通过将用户按模型预测的Uplift值分桶,观察各分位区间内的实际提升效果,帮助识别模型在不同用户子群体中的性能差异,优化资源分配策略。
分位数响应提升的定义与目的
- 核心思想:
- 按模型预测的Uplift值将用户降序排列,划分为若干分位区间(如十分位)。
- 计算每个分位区间内处理组与对照组的响应率差异,作为该分位的实际Uplift值。
- 直观展示模型在不同分位区间的预测准确性和增益分布。
- 解决的问题:
- 模型局部性能验证:验证高预测Uplift的用户是否真实存在高处理效应。
- 资源分配优化:确定哪些分位用户对干预最敏感,优先触达。
- 模型偏差检测:识别模型在特定分位区间(如中低分位)的表现异常。
- 与增益图的区别:
- 增益图:展示累积增益(前k%用户的整体提升效果)。
- 分位数响应提升:展示各独立分位区间的离散提升效果,更细粒度分析模型能力。
分位数响应提升的计算方法
- 步骤说明:
- Step 1:按模型预测的Uplift值对用户降序排列。
- Step 2:将用户划分为N个等分区间(如10个分位)。
- Step 3:在每个分位区间内,计算处理组和对照组的响应率差异:$\text{Uplift}_q = \frac{Y_t(q)}{N_t(q)} – \frac{Y_c(q)}{N_c(q)}$,其中:
- q 表示第q个分位区间(如第1分位为前10%用户)。
- $Y_t(q)$和$Y_c(q)$是该分位内处理组和对照组的响应数。
- $N_t(q)$和$N_c(q)$是该分位的处理组和对照组样本数。
- 分位划分示例(以10分位为例):
| 分位区间 | 用户比例 | Uplift值范围 |
| 第1分位 | 前10%用户 | 预测Uplift最高区间 |
| 第2分位 | 10%-20%用户 | 次高区间 |
| … | … | … |
| 第10分位 | 后10%用户 | 预测Uplift最低或负向区间 |
- 注意事项:
- 样本均衡:确保每个分位区间的处理组和对照组样本量足够(否则需合并分位或加权)。
- 随机基线:计算随机策略下的分位Uplift值(各分位Uplift应接近整体ATE)。
分位数响应提升的可视化与解读
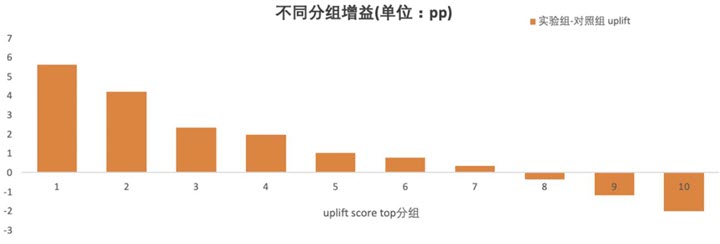
- 可视化方法:
- 柱状图:横轴为分位区间,纵轴为Uplift值,对比模型与随机基线的表现。
- 折线图:展示分位Uplift值的变化趋势,观察高分位是否显著高于低分位。
- 热力图:结合分位和用户特征,分析高Uplift分位的用户画像。
- 示例图:理想模型:高分位Uplift显著高于低分位,且随分位下降Uplift递减。
- 无效模型:各分位Uplift接近随机基线(无区分能力)。
- 反向模型:低分位Uplift高于高分位(排序错误)。
- 关键结论:
- 模型有效性:若前10%分位的Uplift远高于其他分位,模型具备精准识别高敏感用户的能力。
- 业务决策:根据分位Uplift的衰减点(如第5分位后Uplift趋近于零),确定最优干预范围。
- 模型诊断:若中间分位Uplift异常波动,可能提示模型过拟合或特征选择问题。
分位数响应提升的核心应用
- 模型性能对比:
- 对比不同模型在各分位的Uplift值,选择高分位区分能力强的模型。
- 示例:模型A的第1分位Uplift为8%,模型B为5% → 模型A更优。
- 用户分层策略:
- 高价值用户聚焦:对前1-2个分位用户投入更多资源(如定制化营销)。
- 负向效应规避:避免触达Uplift为负的分位用户(如后10%用户)。
- 因果效应异质性分析:
- 探究不同分位用户的处理效应差异,辅助业务理解驱动因素。
- 示例:前10%用户对折扣敏感,中间用户对赠品敏感,尾部用户无响应。
- 模型校准:
- 验证预测Uplift值与实际Uplift值的单调性,校准模型输出。
分位数响应提升的优缺点
| 优点 | 缺点 |
| 直观展示模型在不同分位的局部性能 | 分位划分的粒度影响结论(需业务经验选择) |
| 指导精细化用户分层和资源分配 | 对样本量要求高,小样本下分位结果不稳定 |
| 帮助识别模型偏差和过拟合 | 未考虑分位间的累积效应(需结合增益图) |
Python实现示例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def calculate_quantile_uplift(y_true, uplift, treatment, n_quantiles=10):
# 按Uplift降序排序
df = pd.DataFrame({'y': y_true, 'uplift': uplift, 'treatment': treatment})
df = df.sort_values(by='uplift', ascending=False).reset_index(drop=True)
# 划分分位区间
df['quantile'] = pd.qcut(df.index, n_quantiles, labels=False, duplicates='drop')
quantile_stats = []
for q in range(n_quantiles):
sub_df = df[df['quantile'] == q]
if len(sub_df) == 0:
continue
y_t = sub_df[sub_df['treatment'] == 1]['y'].sum()
n_t = sub_df['treatment'].sum()
y_c = sub_df[sub_df['treatment'] == 0]['y'].sum()
n_c = len(sub_df) - n_t
uplift_q = (y_t / max(n_t, 1)) - (y_c / max(n_c, 1))
quantile_stats.append({'quantile': q+1, 'uplift': uplift_q})
return pd.DataFrame(quantile_stats)
# 示例数据
np.random.seed(42)
n_samples = 5000
uplift = np.random.randn(n_samples) # 模型预测的Uplift值
treatment = np.random.randint(0, 2, n_samples) # 处理组标签(0/1)
y_true = (0.3 * uplift + 0.1 * np.random.randn(n_samples) > 0).astype(int) # 模拟真实响应
# 计算分位数响应提升
quantile_uplift = calculate_quantile_uplift(y_true, uplift, treatment, n_quantiles=10)
# 绘制柱状图
plt.figure(figsize=(10, 6))
plt.bar(quantile_uplift['quantile'], quantile_uplift['uplift'], color='#1f77b4')
plt.axhline(y=quantile_uplift['uplift'].mean(), color='red', linestyle='--', label='Random Baseline')
plt.xlabel('Quantile', fontsize=12)
plt.ylabel('Uplift', fontsize=12)
plt.title('Quantile Uplift Analysis', fontsize=14)
plt.legend()
plt.grid(axis='y')
plt.show()
欧米伽系数(Omega Coefficient)
欧米伽系数(Omega Coefficient)是用于评估Uplift模型性能的指标之一,衡量模型在不同用户分位区间上处理效应(Uplift)排序能力的稳健性和区分度。它通过对比模型增益与随机策略的增益差异,综合反映模型在整体用户群体中的有效性。
Omega系数的定义与核心思想
- 基本定义:Omega系数是Uplift模型的增益曲线(Uplift Curve)与随机基线(Random Baseline)之间的标准化面积差,反映模型相较于随机策略的增益提升比例。其取值范围通常为0, 1,值越高表示模型排序能力越强。
- 核心思想:
- 若模型能准确识别高敏感用户(High-Uplift Users),其增益曲线会快速上升并显著高于随机基线,Omega系数趋近于1。
- 若模型无区分能力(如随机排序),Omega系数趋近于0。
- 若模型排序错误(如将低Uplift用户排在前列),Omega系数可能为负。
- 与Qini系数的区别:
- Qini系数:基于增益曲线下面积(AUUC)减去随机基线面积,再除以完美模型面积,强调模型与理想情况的差距。
- Omega系数:直接标准化模型与随机基线的增益差异,更关注模型相对于随机策略的改进幅度。
Omega系数的计算方法
- 公式推导:$\text{Omega} = \frac{\text{AUUC} – \text{AUUC}_{\text{random}}}{\text{AUUC}_{\text{perfect}} – \text{AUUC}_{\text{random}}}$,其中:
- AUUC(Area Under the Uplift Curve):模型增益曲线下面积。
- AUUC_random:随机基线增益曲线下面积(通常为线性增长)。
- AUUC_perfect:完美模型增益曲线下面积(假设前k%用户的Uplift均为最大值)。
- 计算步骤:
- Step 1:按模型预测的Uplift值对用户降序排列。
- Step 2:绘制增益曲线,计算AUUC(积分或累加)。
- Step 3:计算随机基线和完美模型的AUUC。
- Step 4:代入公式计算Omega系数。
- 示例:
- 假设AUUC=0.6,AUUC_random=0.3,AUUC_perfect=0.9,则Omega=(0.6-0.3)/(0.9-0.3)=0.5。
- 表示模型增益相比随机策略提升了50%的可能最大增益。
Omega系数的应用场景
- 模型对比:
- 对比不同模型(如Meta-Learner vs.树模型)的Omega系数,选择排序能力最优的模型。
- 示例:模型A的Omega=0.7,模型B=0.5 → 模型A更优。
- 阈值选择:
- 结合Omega系数与增益曲线拐点,确定最佳用户干预比例(如Omega最高时对应的分位点)。
- 业务效果预估:
- Omega系数越高,模型对高价值用户的识别能力越强,可预期更高的投资回报率(ROI)。
Omega系数的优缺点
| 优点 | 缺点 |
| 标准化指标,便于跨模型和跨场景比较 | 对数据质量敏感(需处理组/对照组均衡) |
| 直接关联业务收益(增益提升比例) | 依赖完美模型的假设,实际场景中完美模型难定义 |
| 对模型局部排序能力敏感 | 计算复杂度较高(需积分或累加计算) |
Python实现示例
import numpy as np
import pandas as pd
def calculate_omega(y_true, uplift, treatment):
# 按Uplift降序排序
df = pd.DataFrame({'y': y_true, 'uplift': uplift, 'treatment': treatment})
df = df.sort_values(by='uplift', ascending=False).reset_index(drop=True)
# 计算增益曲线AUUC
n = len(df)
uplift_gain = []
for k in range(1, n+1):
sub_df = df.head(k)
y_t = sub_df[sub_df['treatment'] == 1]['y'].sum()
n_t = sub_df['treatment'].sum()
y_c = sub_df[sub_df['treatment'] == 0]['y'].sum()
n_c = k - n_t
uplift = (y_t / max(n_t, 1e-6)) - (y_c / max(n_c, 1e-6))
uplift_gain.append(uplift * k)
auuc = np.trapz(uplift_gain, dx=1/n) # 积分计算AUUC
# 计算随机基线AUUC
overall_ate = (df[df['treatment']==1]['y'].mean() - df[df['treatment']==0]['y'].mean())
random_gain = [overall_ate * k for k in range(1, n+1)]
auuc_random = np.trapz(random_gain, dx=1/n)
# 计算完美模型AUUC(假设前k%用户的Uplift均为最大值)
perfect_gain = sorted(uplift_gain, reverse=True)
auuc_perfect = np.trapz(perfect_gain, dx=1/n)
# 计算Omega系数
omega = (auuc - auuc_random) / (auuc_perfect - auuc_random)
return omega
# 示例数据
np.random.seed(42)
n_samples = 1000
uplift = np.random.randn(n_samples) # 模型预测的Uplift值
treatment = np.random.randint(0, 2, n_samples) # 处理组标签(0/1)
y_true = (0.3 * uplift + 0.1 * np.random.randn(n_samples) > 0).astype(int) # 模拟真实响应
omega = calculate_omega(y_true, uplift, treatment)
print(f"Omega Coefficient: {omega:.3f}")
实验验证指标
增量响应率(Incremental Response Rate, IRR)
增量响应率(Incremental Response Rate, IRR)是评估干预策略(如营销活动、产品改版、优惠券发放等)对目标用户群体响应率(如点击、购买、留存)净提升效果的核心指标。它通过对比处理组(受干预)与对照组(未受干预)的响应率差异,量化策略带来的实际因果效应。
IRR的定义与核心公式
- 基本定义:IRR表示干预策略对用户响应率的净提升,即处理组的响应率与对照组的响应率之差:$\text{IRR} = \frac{Y_t}{N_t} – \frac{Y_c}{N_c}$,其中:
- $Y_t $和$Y_c$:处理组和对照组的响应人数(如点击广告的用户数)。
- $N_t $和$N_c$:处理组和对照组的样本总量。
- 与ATE的关系:
- IRR是平均处理效应(ATE)在二元响应场景下的具体表现形式,即:$\text{IRR} = \mathbb{E}[Y(1) – Y(0)] = \text{ATE}$
- 区别:IRR通常用于业务场景中计算实际观测的增益效果,而ATE更强调潜在结果的期望差异。
- 与Uplift的关系:
- Uplift模型预测的个体处理效应(ITE)期望值即为IRR。
- 在用户分群分析中,IRR可视为特定群体(如高价值用户)的局部ATE。
IRR的应用场景
- 策略效果评估:衡量营销活动、产品功能迭代等策略的真实增益(如广告点击率提升2%)。示例:某电商发放优惠券后,处理组购买率为15%,对照组为10% → IRR=5%。
- 资源分配决策:对比不同策略的IRR,优先实施高IRR的干预(如策略A的IRR=8% vs 策略B=3%)。
- 用户分群优化:计算不同用户群体的IRR,筛选对干预敏感的子群体(如新用户IRR=10%,老用户IRR=1%)。
- 模型效果验证:验证Uplift模型预测的增益是否与实际IRR一致,评估模型准确性。
IRR的计算步骤与注意事项
- 标准计算步骤:
- Step 1:随机划分处理组(接受干预)和对照组(不接受干预)。
- Step 2:收集两组的响应数据(如是否购买)。
- Step 3:分别计算处理组和对照组的响应率。
- Step 4:计算IRR = 处理组响应率 – 对照组响应率。
- 关键注意事项:
- 随机化:确保处理组和对照组用户特征分布一致,避免选择偏差。
- 样本量均衡:对照组和处理组样本量差异过大会导致估计误差。
- 时间窗口:响应率需在相同时间窗口内统计(如活动开始后7天)。
- 稀释效应:排除自然波动(如季节性因素)对IRR的影响。
- 统计显著性检验:
- 使用Z检验或卡方检验判断IRR是否显著非零:$Z = \frac{\text{IRR}}{\sqrt{\frac{p_t(1-p_t)}{N_t} + \frac{p_c(1-p_c)}{N_c}}}$,其中$p_t = Y_t/N_t$,$p_c = Y_c/N_c$。
IRR的优缺点
| 优点 | 缺点 |
| 直观易懂,直接关联业务效果 | 依赖随机实验,观测数据中易受混淆变量影响 |
| 计算简单,无需复杂模型 | 仅反映平均增益,无法识别个体异质性 |
| 支持A/B测试快速验证策略有效性 | 对样本量敏感,小样本下误差较大 |
IRR的优化方法
- 提升IRR的策略:
- 精准定向:通过Uplift模型筛选高敏感用户(如预测IRR>5%的用户)。
- 动态干预:根据用户实时行为调整干预策略(如购物车放弃时触发优惠券)。
- 组合策略:叠加互补干预(如折扣+限时提醒)提升综合增益。
- 降低误差的方法:
- 增大样本量:减少随机波动的影响,提高统计功效。
- 分层抽样:按用户特征(如地域、活跃度)分层随机分组,确保组间均衡。
- 双重差分法(DID):在观测数据中控制时间趋势和固有差异,校正IRR。
成本效益比(ROI)
成本效益比(Return on Investment, ROI)是衡量投资或项目经济效益的核心指标,反映投入成本与获得收益之间的比例关系。它广泛应用于商业决策、市场营销、工程投资等领域,帮助评估资源投入的可行性和效率。
ROI的定义与核心公式
- 基本定义:ROI表示每单位成本产生的净收益,通常以百分比或比率形式表示。其核心公式为:$\text{ROI} = \frac{\text{净收益}}{\text{总成本}} \times 100\%$或$\text{ROI} = \frac{\text{总收益} – \text{总成本}}{\text{总成本}} \times 100\%$
- 关键概念:
- 净收益:总收益减去总成本(包括直接成本和间接成本)。
- 总成本:包括资金、时间、人力、设备等所有投入。
- 时间范围:ROI需明确计算周期(如年度、项目周期)。
- 示例:
- 某广告活动总成本为10万元,带来销售额30万元,净收益为20万元 → ROI = 20/10 × 100% = 200%。
- 某投资项目投入50万元,最终回报80万元 → ROI = (80-50)/50 × 100% = 60%。
ROI的应用场景
- 投资决策:
- 对比不同项目的ROI,优先选择高回报率的方案。
- 示例:项目A的ROI=50%,项目B的ROI=25% → 优先投资项目A。
- 营销效果评估:
- 计算广告、促销活动的ROI,优化预算分配。
- 示例:搜索引擎广告ROI=150%,社交媒体广告ROI=80% → 增加搜索引擎广告预算。
- 产品开发:
- 评估新产品研发的预期收益与成本风险。
- 示例:开发成本100万元,预期年收益200万元 → ROI=100%,支持立项。
- 运营效率分析:
- 分析流程优化、自动化工具引入的ROI。
- 示例:采购自动化系统成本50万元,年节省人力成本80万元 → ROI=60%。
ROI的变种与扩展
- 年化ROI:将非年度周期的收益折算为年收益率,便于跨周期比较:$\text{年化ROI} = \left(1 + \frac{\text{净收益}}{\text{总成本}}\right)^{\frac{12}{\text{月份数}}} – 1$,示例:6个月获得60%回报 → 年化ROI = (1+0.6)^(12/6) -1 = 140%。
- 增量ROI(边际ROI):衡量追加投入的边际效益:$\text{增量ROI} = \frac{\text{新增收益} – \text{新增成本}}{\text{新增成本}} \times 100\%$,示例:追加广告费10万元,新增销售额15万元 → 增量ROI=(15-10)/10×100%=50%。
- 风险调整后ROI:结合风险因素(如概率、波动率)修正预期收益:$\text{调整后ROI} = \text{预期ROI} \times (1 – \text{风险损失率})$,示例:预期ROI=80%,但存在20%风险损失概率 → 调整后ROI=80%×0.8=64%。
ROI计算的注意事项
- 成本与收益的界定:
- 显性成本:直接支出(如广告费、设备采购)。
- 隐性成本:机会成本、时间成本、品牌风险等。
- 长期收益:需考虑未来现金流的贴现(如使用NPV)。
- 时间价值的影响:
- ROI未考虑资金的时间价值,长期项目需结合净现值(NPV)或内部收益率(IRR)分析。
- 示例:投资100万元,5年后回报150万元 → 简单ROI=50%,但贴现后实际收益可能为负。
- 数据准确性:
- 避免估算偏差(如高估收益、低估成本)。
- 使用历史数据、A/B测试或市场调研提高预测精度。
- 行业基准对比:
- 参考行业平均ROI(如电商行业广告ROI约200-300%),评估自身表现。
ROI的优缺点
| 优点 | 缺点 |
| 简单直观,快速评估项目可行性 | 忽略资金的时间价值(需结合NPV/IRR) |
| 支持跨项目、跨行业对比 | 无法反映风险大小(如高ROI伴随高风险) |
| 指导资源分配和优先级排序 | 依赖准确的成本收益数据,估算偏差影响大 |
ROI与其他指标的关系
| 指标 | 定义 | 与ROI的区别 |
| NPV(净现值) | 未来现金流贴现后的净收益 | 考虑时间价值,适合长期项目评估 |
| IRR(内部收益率) | 使NPV=0的贴现率 | 反映投资效率,与ROI互补 |
| ROAS(广告支出回报率) | 广告收益与支出的比率 | ROAS=收益/成本,ROI=净收益/成本 |
指标对比与适用场景
| 指标 | 核心作用 | 数据要求 | 适用阶段 |
| Qini系数 | 评估模型排序能力 | 处理组/对照组观测数据 | 离线评估 |
| AUUC | 衡量相对增益累积效果 | 处理组/对照组观测数据 | 离线评估 |
| 增益图 | 可视化模型分位效果 | 处理组/对照组观测数据 | 离线评估 |
| ATE误差 | 验证全局效应估计准确性 | 真实ATE(仿真或RCT数据) | 离线验证 |
| 分位数提升 | 聚焦关键用户组效果 | 处理组/对照组观测数据 | 离线/在线分析 |
| 欧米伽系数 | 仿真环境下个体效应准确性 | 真实ITE(仅仿真数据) | 离线验证 |
| IRR/ROI | 验证实际业务收益 | A/B测试结果 | 在线实验 |
注意事项
- 离线评估局限性:
- 依赖处理组/对照组数据质量(需满足SUTVA、可忽略性假设)。
- 无法完全替代在线实验验证。
- 指标选择原则:
- 业务目标导向:如ROI优先选择成本效益比。
- 数据可用性:真实ITE不可得时,优先Qini/AUUC。
- 合成数据验证:
- 使用半合成数据(如添加已知处理效应)辅助评估模型可靠性。
Uplift学习资料
开源项目与工具库
- CausalML
- GitHub链接:https://github.com/uber/causalml
- 简介:Uber开源的因果推断库,支持Uplift Modeling(Meta-Learners、因果森林等)、实验分析等功能,提供完整文档和示例代码。
- 适用场景:广告效果评估、用户干预策略优化。
- EconML
- GitHub链接:https://github.com/microsoft/EconML
- 简介:微软开发的因果机器学习库,集成双重机器学习(Double ML)、DR Learner等方法,适合复杂因果效应估计。
- 适用场景:经济学、政策评估、医疗效果分析。
- DoWhy
- GitHub链接:https://github.com/py-why/dowhy
- 简介:基于Python的因果推断框架,提供因果图建模、假设检验和效应估计功能。
- 适用场景:因果关系的发现与验证。
- UpliftPythonToolbox
- GitHub链接:https://github.com/duketemon/pyuplift
- 简介:轻量化的Uplift Modeling工具库,支持多种模型(如Uplift Tree、S-Learner)。
公开数据集
- Criteo Uplift Dataset
- 下载链接:Criteo Uplift Modelling (kaggle.com)
- 简介:Criteo发布的广告干预实验数据集,包含用户特征、处理组/对照组标签及转化行为,适合Uplift建模。
- Hillstrom Email Campaign Dataset
- 下载链接:Kevin Hillstrom MineThatData E-MailAnalytics (kaggle.com)
- 简介:电商邮件营销数据集,包含用户是否收到邮件、历史购买行为等字段,适合入门级Uplift建模练习。
参考链接:



您好!文中的公式没有被渲染。