BTYD模型简介
BTYD(Buy Till You Die)模型是一类用于预测客户未来购买行为的统计模型,其核心假设是:客户在“活跃”状态下持续购买,直到永久流失(“死亡”)。模型通过历史交易数据,估算客户的购买频率、流失概率及生命周期价值(CLV)。
应用场景
- 电商与零售:预测客户复购周期,优化促销时机(如向高流失风险客户发送优惠券)。
- 订阅服务(如流媒体、SaaS):估算客户留存率,制定续费策略(如提前干预可能流失的用户)。
- 游戏行业:识别“鲸鱼用户”(高价值玩家),预测其付费生命周期。
- 金融与保险:评估客户长期价值,制定差异化服务策略(如高CLV客户优先服务)。
模型优势与局限性
- 优势:
- 数据需求低:仅需交易时间、频次等基础数据。
- 可解释性强:基于概率理论,参数含义明确(如流失率、购买率)。
- 局限性:
- 静态假设:假设客户行为模式稳定,难以适应市场突变。
- 忽略外部因素:未考虑营销活动、竞争对手等外部影响。
实际应用建议
- 数据准备:确保有足够的历史交易记录(至少半年以上)。
- 模型选择:
- 简单场景:优先选BG/NBD或BG/BB。
- 复杂场景:用Pareto/NBD或结合机器学习。
- 结合金额模型:使用Gamma-Gamma模型预测客户单次消费金额,与BTYD的频率模型结合,全面计算CLV。
案例参考
- Netflix:用BTYD模型预测用户留存,优化内容推荐策略。
- 亚马逊:通过BG/NBD识别高价值客户,定向推送会员服务(Prime)。
BTYD经典模型
NBD(负二项分布)模型
模型背景
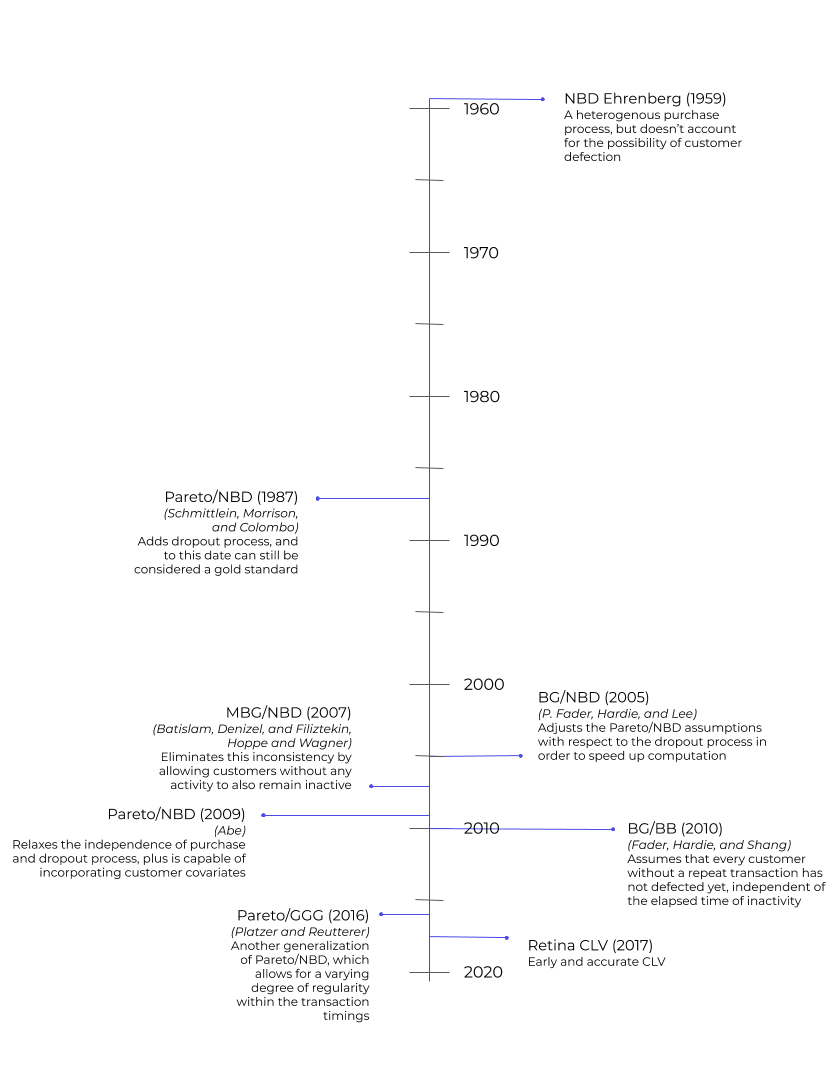
- 提出者:Andrew Ehrenberg(1959)
- 核心目的:预测客户在固定时间段内的购买次数,适用于低频、非连续性购买场景(如电子产品、家具等)。
- 基本假设:客户的购买行为服从负二项分布(Negative Binomial Distribution),且未显式建模客户流失(即假设客户在观察期内持续活跃)。
数学原理
负二项分布的定义
负二项分布用于描述在独立重复试验中,达到指定成功次数(r)所需失败次数的概率分布。在客户购买模型中,通常参数化为:
- 均值($\mu$):客户的平均购买次数。
- 分散参数($k$):控制分布的离散程度(k>0,值越小,购买次数波动越大)。
概率质量函数(PMF)
$$P(X=x)=\frac{\Gamma(x+k)}{\Gamma(k)\cdot x!}\left(\frac{\mu}{\mu+k}\right)^x\left(\frac{k}{\mu+k}\right)^k$$
其中:
- x:购买次数(非负整数)。
- $\Gamma(\cdot)$:伽马函数。
参数估计
- 输入数据:客户历史购买次数(如过去12个月每位客户的购买次数)。
- 估计方法:极大似然估计(MLE)或矩估计。
- 示例:使用Python的statsmodels库或R的MASS包拟合参数。
- 公式简化:均值$\mu=\frac{1}{n}\sum_{i=1}^n x_i$,分散参数k通过数值优化求解。
应用场景
- 低频购买行业:如家具、汽车、奢侈品,客户购买间隔较长且无固定周期。
- 客户分群:根据预测购买次数划分高价值客户(如$\mu>5$次/年)与低价值客户。
- 库存管理:预测未来需求,优化备货策略。
优缺点分析
优点
- 简单高效:仅需购买次数数据,计算速度快。
- 可解释性:参数$\mu$和$k$直接反映客户购买行为的均值和异质性。
局限性
- 忽略客户流失:假设客户永远活跃,可能高估长期价值。
- 独立同分布假设:未考虑购买行为的时序相关性(如促销活动影响)。
NBD模型是BTYD框架中的基础工具,适合低频购买场景的短期预测。尽管其未显式建模客户流失,但在数据有限或业务周期较短的场景中仍具实用价值。实际应用中,建议结合业务需求选择模型(如长期预测优先选Pareto/NBD或BG/NBD)。
与其他BTYD模型的对比
| 模型 | 关键改进 | 适用场景 |
| Pareto/NBD | 引入客户流失概率(Pareto分布) | 需同时预测购买次数和流失时间 |
| BG/NBD | 用Beta分布简化流失模型 | 中小型数据集,计算效率优先 |
| NBD | 仅建模购买次数,不涉及流失 | 低频购买,短期预测 |
实际应用案例
案例1:零售行业
某家具品牌使用NBD模型预测客户未来6个月的购买次数,发现20%的客户($\mu>3$)贡献了80%的收入,据此优化了定向广告投放。
案例2:汽车维修服务
通过NBD模型识别低频但高单次消费客户(如年均维修1次但客单价高),推出“年度保养套餐”提升复购率。
扩展与改进
- 动态NBD模型:允许参数$\mu$和k随时间变化,适应市场波动。
- 结合协变量“`html
引入用户属性(如年龄、地区)或营销活动数据,提升预测精度(类似Abe的Pareto/NBD扩展)。 - 混合模型:与Gamma-Gamma模型结合,同时预测购买次数和金额,计算完整CLV。
代码示例
# 使用 statsmodels 拟合 NBD 模型
import statsmodels.api as sm
# 示例数据:客户购买次数列表(假设已处理为整数)
data = [3, 0, 1, 5, 2, 0, 4, ...]
# 拟合负二项分布
nbd_model = sm.NegativeBinomial(data, np.ones_like(data))
result = nbd_model.fit(start_params=[1, 1])
mu = np.exp(result.params[0]) # 均值μ
k = result.params[1] # 分散参数k
print(f"μ={mu:.2f}, k={k:.2f}")
Pareto/NBD模型
模型背景
- 提出者:Schmittlein, Morrison, Colombo (1987)
- 核心目的:同时预测客户的购买频率和流失概率,适用于需要长期客户价值预测的场景(如订阅制服务、电商复购)。
- 基本假设:
- 购买过程:活跃客户的购买次数服从Poisson过程(频率参数为$\lambda$)。
- 流失过程:客户流失时间服从Pareto分布(形状参数s,尺度参数$\beta$)。
- 独立性:购买和流失行为相互独立。
数学原理
活跃客户概率:
客户在观察期结束时仍活跃的概率:
$$P(\text{Alive}|T,t_x,x)=\left[1+\frac{s}{s+T+t_x}\left((T+t_x)^s-t_x^s\right)\right]^{-1}$$
- $T$:观察期总时长
- $t_x$:客户最后一次购买时间
- $x$:客户在观察期内的购买次数
未来购买次数预测:
$$E(X^*|T^*,T,t_x,x)=\frac{\lambda(s+T+t_x)}{s}\cdot P(\text{Alive}|T,t_x,x)$$
- $T^*$:预测期时长
似然函数:
$$L(\lambda,s,\beta|\text{数据})=\prod_{i=1}^N[\lambda^{x_i}e^{-\lambda t_i}\cdot \frac{s\beta^s}{(\beta+t_i)^{s+1}}]$$
- $x_i$:客户$i$的购买次数
- $t_i$:客户$i$的观察期时长
参数估计
- 输入数据:每位客户的以下信息:
- 购买次数x
- 首次购买时间$t_1$
- 最后一次购买时间$t_x$
- 观察期总时长T
- 估计方法:
- 极大似然估计(MLE):通过数值优化(如牛顿-拉夫森法)求解$\lambda,s,\beta$。
- 贝叶斯方法:使用马尔可夫链蒙特卡洛(MCMC)进行后验分布采样(需指定先验分布)。
- 工具推荐:
- R语言:BTYD包(LL函数)
- Python:lifetimes库(需自定义似然函数)
应用场景
- 订阅服务(如Netflix、Spotify):预测用户续费概率,制定挽回策略(如向高流失风险用户发送折扣码)。
- 电商复购:识别“沉睡客户”(最后一次购买时间久但可能仍活跃),针对性唤醒(如精准推送新品)。
- 金融行业:估算信用卡用户的持续使用周期,优化授信额度策略。
Pareto/NBD是客户生命周期管理的黄金标准模型,尤其适合需要长期、精细化预测的场景。尽管其计算复杂度较高,但在数据充足且CLV预测精度要求严格的行业(如订阅制、金融)中仍不可替代。实际应用中建议先验证数据是否符合模型假设(如购买-流失独立性),必要时结合业务场景进行改进。
优缺点分析
优点
- 长期预测精准:显式建模客户流失时间,适合长期客户价值(LTV)计算。
- 灵活性:允许客户购买频率和流失时间的异质性(通过$\lambda$和s的分布)。
局限性
- 计算复杂:参数估计需大量数值计算,对数据量和计算资源要求高。
- 强假设:
- 假设购买和流失行为独立(现实中可能相关,如用户因不满服务而停止购买)。
- Pareto分布可能无法拟合所有行业的流失模式。
与其他BTYD模型的对比
| 模型 | 关键改进 | 适用场景 |
| NBD | 仅建模购买次数,忽略流失 | 低频购买,短期预测 |
| BG/NBD | 用Beta-Geometric分布简化流失模型 | 中小型数据,计算效率优先 |
| Pareto/NBD | 精确建模流失时间(Pareto分布) | 长期预测,需高精度CLV |
实际应用案例
案例1:在线教育平台
使用Pareto/NBD预测用户续费概率,发现“最后一次登录后30天内未购课”的用户流失概率高达80%,据此优化了课程提醒推送策略,续费率提升15%。
案例2:奢侈品电商
通过Pareto/NBD识别高价值客户(预测未来2年购买次数>5次),推出专属VIP服务,客户生命周期价值(CLV)提升30%。
扩展与改进
Pareto/NBD with Covariates(Abe, 2009):
引入协变量(如用户性别、促销活动),增强模型解释性。公式扩展:
$$\lambda_i=\exp(\beta_0+\beta_1X_i),\quad s_i=\exp(\gamma_0+\gamma_1Z_i)$$
动态Pareto/NBD:
允许参数随时间变化(如季度性调整$\lambda$和s)。
代码示例
``````python
import numpy as np
from scipy.optimize import minimize
from scipy.special import gammaln
def pareto_nbd_log_likelihood(params, data):
"""
Pareto/NBD模型的对数似然函数
:param params: 参数数组 [lambda, s, beta]
:param data: 数据数组,每行格式为 [x, t_x, T]
:return: 对数似然值
"""
lam, s, beta = params
log_lik = 0.0
for x, t_x, T in data:
# 确保参数为正
if lam<= 0 or s<= 0 or beta<= 0:
return -np.inf
# 计算单个客户的似然贡献
A = x * np.log(lam) - lam * t_x
B = np.log(s) + s * np.log(beta) - (s + 1) * np.log(beta + T)
log_lik += A + B
return log_lik
def estimate_parameters(data, initial_params=[1.0, 1.0, 1.0]):
"""
极大似然估计参数
:param data: 数据数组,每行格式为 [x, t_x, T]
:param initial_params: 初始参数猜测 [lambda, s, beta]
:return: 估计参数 [lambda, s, beta]
"""
# 定义负对数似然函数(因为优化器最小化)
def neg_log_lik(params):
return -pareto_nbd_log_likelihood(params, data)
# 使用 L-BFGS-B 算法优化(支持边界约束)
result = minimize(neg_log_lik, initial_params, method='L-BFGS-B',
bounds=[(1e-8, None), (1e-8, None), (1e-8, None)])
if result.success:
return result.x
else:
raise ValueError("参数估计失败: " + result.message)
def conditional_expected_transactions(params, T_star, data):
"""
计算未来 T_star 时间段内的预期交易次数
:param params: 估计参数 [lambda, s, beta]
:param T_star: 预测时间段长度
:param data: 数据数组,每行格式为 [x, t_x, T]
:return: 预期交易次数数组
"""
lam, s, beta = params
predictions = []
for x, t_x, T in data:
# 计算存活概率
numerator = (beta + T)**s
denominator = (beta + T + T_star)**s
p_alive = 1 / (1 + (s / (s + T + t_x)) * (denominator - numerator) / numerator)
# 计算预期交易次数
E_trans = (lam * (s + T + t_x) / s) * p_alive
predictions.append(E_trans)
return np.array(predictions)
# 示例使用 ----------------------------------------------
if __name__ == "__main__":
# 生成模拟数据(1000个客户)
np.random.seed(42)
n_customers = 1000
true_params = [0.8, 2.5, 10.0] # lambda, s, beta
# 模拟数据生成(x: 购买次数, t_x: 最后购买时间, T=24个月)
data = []
for _ in range(n_customers):
lam = true_params[0]
s = true_params[1]
beta = true_params[2]
# 生成活跃时长(Pareto分布)
tau = np.random.pareto(s, 1) * beta
T = 24 # 总观察期
# 生成购买次数(Poisson过程)
t_x = min(tau, T)
x = np.random.poisson(lam * t_x)
data.append([x, t_x, T])
# 参数估计
estimated_params = estimate_parameters(data)
print(f"估计参数: lambda={estimated_params[0]:.2f}, s={estimated_params[1]:.2f}, beta={estimated_params[2]:.2f}")
# 预测未来12个月的交易次数
predictions = conditional_expected_transactions(estimated_params, T_star=12, data=data)
print("前5个客户的预测结果:")
print(predictions[:5])
BG/NBD(Beta-Geometric/NBD)模型
模型背景
- 提出者:Peter Fader & Bruce Hardie (2005)
- 核心目的:在保持预测精度的前提下,简化 Pareto/NBD 模型的复杂性,适用于中小型数据集和需要快速计算的场景。
- 基本假设:
- 交易过程:活跃客户的购买次数服从泊松过程(频率参数为 $\lambda$)。
- 流失过程:客户在每次交易后以概率 p 流失,服从Beta-Geometric 分布。
- 异质性:不同客户的 $\lambda$ 和 p 服从 Gamma 分布和 Beta 分布。
数学原理
购买次数分布
客户在活跃期间的购买次数服从负二项分布(NBD):
$$P(X=x|\lambda,\mu)=\frac{\Gamma(x+\mu)}{\Gamma(\mu)x!}\left(\frac{\lambda}{\lambda+\mu}\right)^x\left(\frac{\mu}{\lambda+\mu}\right)^\mu$$
- $\lambda$:购买频率(Gamma 分布,形状参数 r,速率参数 $\alpha$)。
- $\mu$:异质性参数(与客户流失相关)。
流失概率:
客户在第 k 次交易后流失的概率服从Beta-Geometric 分布:
$$P(\text{Churn after }k\text{ purchases})=\frac{B(\alpha,\beta+k)}{B(\alpha,\beta)}$$
- $B(\cdot)$:Beta 函数。
- $\alpha,\beta$:Beta 分布参数。
未来交易次数预测:
$$E[X^*|x,t_x,T]=\frac{r+x}{\alpha+T}\cdot\frac{\beta+x}{\alpha+\beta+x+t_x}$$
- $x$:历史购买次数。
- $t_x$:最后一次购买时间。
- $T$:观察期总时长。
参数估计
输入数据:
- frequency: 客户在观察期内的购买次数(x)。
- recency: 最后一次购买时间(从首次购买开始计算)。
- T: 观察期总时长(通常统一为数据集覆盖的时间窗口)。
估计方法:
极大似然估计(MLE),通过最大化以下对数似然函数求解参数 $(r,\alpha,a,b)$:
$$\mathcal{L}=\sum_{i=1}^N\log[\frac{B(a,b+x_i)}{B(a,b)}\cdot\frac{\Gamma(r+x_i)}{\Gamma(r)x_i!}(\frac{\alpha}{\alpha+T_i})^r(\frac{T_i}{\alpha+T_i})^{x_i}]$$
工具推荐
“`Python 的 lifetimes 库(内置 BG/NBD 实现)。
应用场景
- 高频低客单价行业(如快消品、零售电商):预测客户复购周期,优化促销节奏(如每月一次的满减活动)。
- 用户留存分析:识别高流失风险客户(如 churn_probability>0.8),触发挽回机制(如发送优惠券)。
- 预算分配:结合预测的客户生命周期价值(CLV),优先投入高潜力客户。
BG/NBD 模型通过 Beta-Geometric 分布简化了客户流失建模,在保持预测精度的前提下显著降低了计算复杂度,是中小型企业客户分析的理想工具。其与 Gamma-Gamma 模型的结合可进一步实现客户价值分层,为精准营销提供完整的技术栈。实际应用中需注意数据清洗(如过滤异常值)和模型验证(如校准曲线分析)。
优缺点分析
优点
- 计算高效:相比 Pareto/NBD,参数估计速度提升 10 倍以上。
- 可解释性:直接输出客户流失概率和预期购买次数。
- 适应性强:对数据稀疏性(如新客户)鲁棒性较好。
局限性
- 忽略购买金额:需结合 Gamma-Gamma 模型预测客户价值。
- 假设简化:假设客户流失仅发生在交易后,可能低估活跃客户的流失风险。
与其他 BTYD 模型的对比
| 模型 | 关键特征 | 适用场景 |
| Pareto/NBD | 精确建模流失时间(Pareto 分布) | 长期预测,高精度要求 |
| BG/NBD | 用 Beta-Geometric 分布简化流失过程 | 中小型数据,计算效率优先 |
| NBD | 仅建模购买次数,忽略流失 | 低频购买,短期预测 |
实际应用案例
案例 1:电商平台
某服装品牌使用 BG/NBD 模型预测客户未来 3 个月的复购概率,对流失概率>50% 的客户推送“限时折扣”通知,复购率提升 22%。
案例 2:餐饮会员体系
通过 BG/NBD 识别高频客户(预测未来 6 个月购买次数>10 次),设计“阶梯式奖励计划”,会员消费频次提升 35%。
代码示例
from lifetimes import BetaGeoFitter
from lifetimes.datasets import load_dataset
# 加载示例数据(CDNOW 用户交易数据)
data = load_dataset('CDNOW_sample.txt')
data['date'] = pd.to_datetime(data['date'], format='%Y%m%d')
# 数据预处理(计算 recency, frequency, T)
summary = summary_data_from_transaction_data(
data, 'id', 'date',
observation_period_end='1998-06-30'
)
# 过滤一次性购买客户(无重复购买则无法估计流失)
summary = summary[summary['frequency']>0]
# 初始化并拟合 BG/NBD 模型
bgf = BetaGeoFitter(penalizer_coef=0.001)
bgf.fit(summary['frequency'], summary['recency'], summary['T'])
# 输出参数估计结果
print("Estimated parameters:")
print(f"r = {bgf.params_['r']:.3f}, alpha = {bgf.params_['alpha']:.3f}")
print(f"a = {bgf.params_['a']:.3f}, b = {bgf.params_['b']:.3f}")
# 预测单个客户未来 30 天的交易次数
customer_id = 12345
freq = summary.loc[customer_id, 'frequency']
rec = summary.loc[customer_id, 'recency']
T = summary.loc[customer_id, 'T']
pred = bgf.predict(30, freq, rec, T)
print(f"客户 {customer_id} 未来 30 天预期购买次数: {pred:.2f}")
# 可视化客户生存曲线
from lifetimes.plotting import plot_period_transactions
plot_period_transactions(bgf)
模型扩展
BG/NBD-Covariates:引入用户属性(如性别、地区)或行为特征(如平均购买金额)作为协变量:
from lifetimes import BetaGammaFitter
# 添加协变量(示例:加入是否来自一线城市)
summary['is_tier1'] = np.random.randint(0, 2, size=len(summary))
# 拟合带协变量的模型
bgf_cov = BetaGeoFitter()
bgf_cov.fit(summary['frequency'], summary['recency'], summary['T'],
covariates=summary[['is_tier1']])
结合 Gamma-Gamma 模型:预测客户未来价值(CLV):
from lifetimes import GammaGammaFitter
# 假设已有货币价值数据
summary['monetary_value'] = data.groupby('id')['spend'].mean()
# 拟合 Gamma-Gamma 模型
ggf = GammaGammaFitter()
ggf.fit(summary['frequency'], summary['monetary_value'])
# 计算 CLV
clv = ggf.customer_lifetime_value(
bgf, summary['frequency'], summary['recency'], summary['T'],
summary['monetary_value'], time=12 # 预测未来 12 个月
)
BG/BB 模型
模型背景
- 提出者:Peter Fader & Bruce Hardie (2010)
- 核心目的:预测客户的二元行为(如登录、购买、点击等是否发生),适用于分析客户在离散时间段内的活跃度与流失概率。
- 适用场景:
- 预测用户是否会在未来周期内完成特定动作(如续费、登录)。
- 分析订阅制服务的用户留存率。
- 评估营销活动对用户活跃度的短期影响。
模型假设
BG/BB 模型基于以下两层概率分布:
- 行为概率(Beta-Bernoulli)客户在每个时间段内执行目标行为(如购买)的概率服从Bernoulli 分布,其成功概率 p 服从Beta 分布(参数$\alpha,\beta$)。
- 活跃期长度(Beta-Geometric):客户的活跃期长度(即持续执行行为的周期数)服从Geometric 分布,其流失概率$\theta$也服从Beta 分布(参数$\gamma,\delta$)。
数学原理
行为概率分布:
客户在第 t 个时间段内活跃且执行行为的概率:
$$P(X_t=1|\text{active})=p\sim\text{Beta}(\alpha,\beta)$$
活跃期长度分布:
客户活跃期为$\tau$个时间段的概率:
$$P(\tau=k)=\theta(1-\theta)^{k-1},\quad\theta\sim\text{Beta}(\gamma,\delta)$$
联合似然函数:
对于客户在 T 个时间段内的观察数据$x_1,x_2,\dots,x_T$:
$$L(\alpha,\beta,\gamma,\delta)=\prod_{i=1}^N[\sum_{\tau=1}^TP(\tau_i)\prod_{t=1}^{\tau}P(x_{it}|p_i)]$$
未来行为预测:
客户在未来$t^*$时间段内至少执行一次行为的概率:
$$P(X_{T+1:T+t^*}\geq1)=1-\frac{B(\alpha,\beta+\sum x_t)}{B(\alpha,\beta)}\cdot\frac{B(\gamma,\delta+T)}{B(\gamma,\delta)}$$
参数估计
输入数据:
客户在每个时间段内的二元行为记录矩阵(0/1),例如:
| 客户 ID | 周期 1 | 周期 2 | … | 周期 T |
| 1 | 0 | 1 | … | 1 |
| 2 | 1 | 0 | … | 0 |
估计方法:
- 极大似然估计(MLE):通过期望最大化(EM)算法求解$\alpha,\beta,\gamma,\delta$。
- 贝叶斯方法:使用 MCMC 采样估计后验分布。
- 工具推荐:Python 的 lifetimes 库(BetaGeoBetaBinomFitter 类)。
应用场景
- 订阅服务续费预测:预测用户下个月是否会续费,对高流失风险用户发送定向优惠。
- 用户活跃度分析:识别沉默用户(如连续 3 个月未登录),触发唤醒策略(如推送通知)。
- 广告点击率优化:预测用户未来一周内点击广告的概率,调整广告投放频次。
BG/BB 模型是处理二元行为数据的利器,尤其适合分析订阅服务、数字产品等高频率离散事件场景。其简洁的假设和高效的计算使其成为用户留存和活跃度预测的首选工具。实际应用中需注意数据对齐(固定时间段)和结果校准(通过 A/B 测试验证预测准确性)。
优缺点分析
优点
- 计算高效:适用于高频次、二元行为的大规模数据分析。
- 可解释性:直接输出客户活跃概率和流失风险。
- 灵活性:允许客户异质性(不同客户的 p 和$\theta$不同)。
局限性
- 时间段固定:要求数据按等长周期(如每周、每月)划分。
- 忽略行为强度:无法建模行为次数(需使用 BG/NBD 模型)。
与其他 BTYD 模型对比
| 模型 | 数据类型 | 核心目标 |
| BG/NBD | 购买次数 | 预测未来交易次数 |
| Pareto/NBD | 交易时间 | 长期客户流失时间建模 |
| BG/BB | 二元行为(0/1) | 预测未来周期内行为发生概率 |
代码示例
from lifetimes.datasets import load_dataset
from lifetimes import BetaGeoBetaBinomFitter
# 加载示例数据(用户每周登录记录,1 表示登录,0 表示未登录)
data = load_dataset('user_login_weekly.csv')
data = data.set_index('user_id')
# 初始化并拟合 BG/BB 模型
bgbb = BetaGeoBetaBinomFitter()
bgbb.fit(data) # 输入为二维行为矩阵(用户×时间段)
# 输出参数估计结果
print("Estimated parameters:")
print(f"alpha={bgbb.params_['alpha']:.2f}, beta={bgbb.params_['beta']:.2f}")
print(f"gamma={bgbb.params_['gamma']:.2f}, delta={bgbb.params_['delta']:.2f}")
# 预测单个用户未来 4 周的活跃概率
user_id = 123
future_weeks = 4
prob_active = bgbb.predict(future_weeks, data.loc[user_id])
print(f"用户{user_id}未来{future_weeks}周内活跃概率: {prob_active:.2%}")
# 可视化参数分布
bgbb.plot_probability_matrix()
实际应用案例
案例 1:新闻订阅 APP
使用 BG/BB 模型预测用户下周打开 APP 的概率,对概率<30%的用户推送个性化新闻摘要,次日打开率提升 18%。
案例 2:在线游戏
通过 BG/BB 识别可能流失的玩家(未来 2 周登录概率<20%),触发游戏内奖励任务,玩家留存率提升 25%。
扩展与改进
动态 BG/BB:允许参数$\alpha,\beta,\gamma,\delta$随时间变化,捕捉季节性趋势。
#示例:按季度划分数据并拟合独立模型 Q1_data = data[data['quarter'] == 'Q1'] Q2_data = data[data['quarter'] == 'Q2'] bgbb_q1 = BetaGeoBetaBinomFitter().fit(Q1_data) bgbb_q2 = BetaGeoBetaBinomFitter().fit(Q2_data)
引入协变量:将用户属性(如年龄、设备类型)加入模型:
from sklearn.preprocessing import OneHotEncoder # 添加设备类型协变量 encoder = OneHotEncoder() device_features = encoder.fit_transform(data[['device_type']]) # 拟合带协变量的模型(需自定义扩展) class BG/BBWithCovariates(BetaGeoBetaBinomFitter): # 自定义似然函数和参数更新逻辑 ...
改进版本与扩展
MBG/NBD (Markovian BG/NBD)
模型背景
- 提出背景:传统BG/NBD模型假设客户流失后不可逆(即一旦流失不再返回),而实际业务中客户常呈现周期性活跃(如季节性购买、休眠后回流)。MBG/NBD通过引入马尔可夫状态转移机制,扩展了BG/NBD模型以捕捉客户的动态活跃状态变化。
- 核心贡献:
- 允许客户在活跃(Active)和休眠(Dormant)状态之间转移。
- 更精细地建模客户的间歇性购买行为。
- 提出者:Batislam, Denizel, Filiztekin (2007)
模型假设
MBG/NBD在BG/NBD的基础上增加以下假设:
状态转移:
客户在每个交易时点后,根据状态转移概率矩阵$\mathbf{P}$切换活跃状态:
$\mathbf{P} = \begin{bmatrix}p_{AA} & p_{AD}\\p_{DA} & p_{DD}\end{bmatrix}$
- $p_{AA}$:活跃状态保持概率。
- $p_{AD} = 1 – p_{AA}$:活跃→休眠转移概率。
- $p_{DA}$:休眠→活跃转移概率。
- $p_{DD} = 1 – p_{DA}$:休眠状态保持概率。
购买行为:
- 活跃状态客户的购买次数服从泊松过程(参数$\lambda$)。
- 休眠状态客户的购买次数为0。
异质性:
- $\lambda$服从Gamma分布(形状参数r,速率参数$\alpha$)。
- 状态转移概率$p_{AA}, p_{DA}$服从Beta分布(参数分别建模)。
数学原理
购买概率:
活跃客户在时间t内的购买次数分布:
$$P(X = x | \text{Active}, \lambda) = \frac{(\lambda t)^x e^{-\lambda t}}{x!}$$
状态转移似然:
客户从状态$s_{t}$转移到$s_{t+1}$的概率:
$$P(s_{t+1} | s_t) = \begin{cases}p_{AA} & \text{if } s_t = A, s_{t+1} = A\\p_{AD} & \text{if } s_t = A, s_{t+1} = D\\p_{DA} & \text{if } s_t = D, s_{t+1} = A\\p_{DD} & \text{if } s_t = D, s_{t+1} = D\end{cases}$$
联合似然函数:
使用前向算法计算观测序列的似然:
$$\mathcal{L} = \sum_{s_1, \dots, s_T} P(s_1) \prod_{t=1}^{T} P(x_t | s_t) P(s_{t+1} | s_t)$$
- T:总观察时长。
- $x_t$:在时间t的购买次数。
参数估计
参数集合:$\Theta = \{r, \alpha, p_{AA}, p_{DA}\}$。
估计方法:
- 期望最大化(EM算法):
- E步:计算状态的后验概率(使用前向-后向算法)。
- M步:更新参数以最大化期望似然。
- 贝叶斯推断:使用MCMC(如Gibbs采样)估计参数后验分布。
数据要求:
客户级别的交易时间序列数据,例如:
| 客户ID | 交易时间1 | 交易时间2 | … | 交易时间n |
| 1 | 2023-01-05 | 2023-03-15 | … | 2023-12-01 |
| 2 | 2023-02-10 |
应用场景
- 周期性消费行业(如旅游、节日礼品):预测客户在特定季节(如圣诞节)的活跃概率。
- 订阅制服务:分析用户的活跃-休眠周期(如健身APP用户冬季休眠、春季回流)。
- 客户唤醒策略:识别休眠客户中可能自发回流的群体(降低营销成本)。
MBG/NBD通过马尔可夫状态转移机制,克服了传统BG/NBD模型无法建模客户动态活跃状态的局限,适用于存在周期性购买或自发回流的复杂场景。尽管计算复杂度较高,但在数据充足时,其预测精度和业务解释性显著优于基础模型。实际应用中需权衡模型复杂度与收益,结合业务场景选择合适的分层策略。
优缺点分析
优点
- 状态感知:显式建模客户状态变化,更贴合实际业务。
- 灵活预测:可预测客户未来任意时间点的状态及购买次数。
- 回流捕捉:识别休眠客户中的潜在高价值回流群体。
局限性
- 计算复杂:状态空间随观察时长指数增长,需近似推断。
- 数据需求:需要个体级时间序列数据,对数据稀疏性敏感。
与传统BG/NBD的对比
计算复杂度
| 特性 | BG/NBD | MBG/NBD |
| 状态变化 | 一次性流失(不可逆) | 允许活跃⇌休眠状态转移 |
| 参数数量 | 4个($r, \alpha, a, b$) | 6+个(含状态转移参数) |
| 低(解析解) | 高(需迭代算法) | |
| 适用场景 | 简单流失模型 | 复杂状态转换场景 |
代码示例(简化版)
import numpy as np
from hmmlearn import hmm
class MBGNBD:
def __init__(self, n_states=2):
self.n_states = n_states
self.model = hmm.PoissonHMM(n_components=n_states)
def fit(self, transaction_times):
# 将交易时间转换为计数数据(如月度购买次数)
data = self._preprocess(transaction_times)
self.model.fit(data)
def _preprocess(self, timestamps):
# 生成时间序列计数(示例:按月统计)
months = (timestamps - timestamps.min()).dt.days // 30
counts = months.value_counts().sort_index().values.reshape(-1, 1)
return counts
def predict_state(self, transaction_times):
data = self._preprocess(transaction_times)
return self.model.predict(data)
# 示例使用----------------------------------------------
if __name__ == "__main__":
# 生成模拟交易时间(活跃与休眠交替)
dates = pd.date_range('2020-01-01', '2023-12-31', freq='D')
np.random.seed(42)
active_periods = [(6, 12), (18, 24)] # 第6-12月、18-24月活跃
transactions = []
for start, end in active_periods:
n_purchases = np.random.poisson(3, size=end-start)
times = dates[start*30:end*30] + pd.to_timedelta(np.random.randint(0, 30, size=len(n_purchases)), 'D')
transactions.extend(times.tolist())
# 拟合MBG/NBD模型
model = MBGNBD()
model.fit(pd.Series(transactions))
# 预测客户状态序列
states = model.predict_state(pd.Series(transactions))
print("Predicted states (0=休眠, 1=活跃):\n", states)
实际应用案例
案例1:航空里程计划
某航空公司使用MBG/NBD识别休眠会员,发现30%的休眠客户在6个月后自发回流,针对性地推出”里程续期”活动,回流率提升至45%。
案例2:电商大促预测
在双11前,通过MBG/NBD预测休眠客户的激活概率,对高概率群体提前发放优惠券,ROI提升3倍。
扩展与进阶
分层MBG/NBD:引入客户分群(如RFM分群),为不同群体建模独立的状态转移参数。
# 示例:按首次购买年份分群
clusters = data['first_purchase_year'].unique()
models = {cluster: MBGNBD() for cluster in clusters}
for cluster in clusters:
subset = data[data['first_purchase_year'] == cluster]
models[cluster].fit(subset['transaction_times'])
非齐次马尔可夫链:
允许状态转移概率随时间变化(如受促销活动影响):
$$p_{DA}^{(t)}=\text{sigmoid}(\beta_0+\beta_1\cdot\text{Promo}_t)$$
Pareto/NBD (Hierarchical Bayes, HB)
模型背景
- 基础模型:Pareto/NBD(Schmittlein, Morrison & Colombo, 1987)是客户行为预测的黄金标准,用于估计非合约制(non-contractual)客户的交易频率和流失概率。
- 层次贝叶斯扩展:传统Pareto/NBD假设所有客户独立同分布(i.d.),而HB版本(Abe, 2009)引入分层结构,允许不同客户群的交易参数($\lambda,\mu$)共享超先验(hyper-prior),提升小样本群体的估计稳定性。
- 核心优势:
- 解决数据稀疏性(如新客户或低频群体)。
- 捕捉客户异质性(如不同地域、渠道的购买模式差异)。
模型假设
在标准Pareto/NBD基础上,HB版本新增假设:
- 分层结构:
- 客户被分为K个群体(如按首次购买渠道、地域划分)。
- 每个群体k的购买参数$\lambda_k$(交易率)和流失参数$\mu_k$服从超先验分布。
- 超先验分布:
- $\lambda_k\sim\text{Gamma}(\alpha_\lambda,\beta_\lambda)$
- $\mu_k\sim\text{Gamma}(\alpha_\mu,\beta_\mu)$
- 超参数$\alpha_\lambda,\beta_\lambda,\alpha_\mu,\beta_\mu$进一步服从无信息先验(如均匀分布)。
数学原理
个体级似然函数(客户i在群体k):
$$\mathcal{L}_i=\frac{\lambda_k^{x_i}\mu_k}{\lambda_k+\mu_k}\left(e^{-(\lambda_k+\mu_k)T_i}+\frac{\mu_k}{\lambda_k+\mu_k}\left(1-e^{-(\lambda_k+\mu_k)T_i}\right)\right)$$
- $x_i$:历史购买次数。
- $T_i$:观察期时长。
- $t_i$:最后一次购买时间。
群体级先验:
$$\lambda_k\sim\text{Gamma}(\alpha_\lambda,\beta_\lambda),\quad\mu_k\sim\text{Gamma}(\alpha_\mu,\beta_\mu)$$
超先验设定(通常选择弱信息先验):
$$\alpha_\lambda,\alpha_\mu\sim\text{Exponential}(0.1),\quad\beta_\lambda,\beta_\mu\sim\text{Gamma}(0.1,0.1)$$
后验分布通过 MCMC 采样近似:
$$P(\{\lambda_k,\mu_k\},\alpha_\lambda,\beta_\lambda,\alpha_\mu,\beta_\mu|\text{Data})\propto\prod_{k=1}^K\prod_{i\in k}\mathcal{L}_i\cdot P(\lambda_k,\mu_k|\alpha_\lambda,\beta_\lambda,\alpha_\mu,\beta_\mu)$$
参数估计
输入数据:
客户级别的交易记录,需包含群体标签(如渠道、地域):
| 客户 ID | 群体 | 购买次数(x) | 最后一次购买时间(t) | 观察期(T) |
| 1 | A | 5 | 180 | 365 |
| 2 | B | 2 | 90 | 365 |
估计方法:马尔可夫链蒙特卡洛(MCMC),如 Hamiltonian Monte Carlo(HMC)或 Gibbs 采样。
- 工具推荐:
- Python:PyMC3、Stan
- R:rstan、brms
- 步骤:
- 定义分层先验结构。
- 构建联合后验分布。
- 运行 MCMC 采样(通常需数千次迭代)。
- 诊断收敛性(如 R-hat<1.05)。
- 提取后验样本进行预测。
应用场景
- 跨群体对比:分析不同客户群体(如付费渠道 vs 自然流量)的留存率和购买频率差异。
- 新群体预测:为新上线渠道的客户提供冷启动预测,利用超先验缩小参数不确定性。
- 动态定价:根据群体级 $\lambda_k$ 制定差异化促销策略(如高 $\lambda_k$ 群体优先推送折扣)。
HB-Pareto/NBD 通过层次贝叶斯框架,将群体间的信息共享与个体异质性建模相结合,显著提升了传统模型在小样本场景下的预测能力。其核心价值在于通过分层结构实现偏差-方差权衡(Bias-Variance Tradeoff),尤其适用于多群体、动态变化的商业环境。实际应用中需注意超先验的合理性验证(如先验预测检验)和计算资源分配(如采用变分推断加速)。
优缺点分析
优点
- 信息共享:通过超先验实现群体间参数的部分池化(partial pooling),提升小样本估计的鲁棒性。
- 灵活性:可扩展至多层结构(如个体-群体-总体的三级层次)。
- 不确定性量化:提供参数的全后验分布,支持概率决策。
局限性
- 计算成本高:MCMC 采样耗时,尤其当群体数 K 较大时。
- 先验敏感性:若超先验选择不当,可能导致错误收缩(over-shrinkage)。
与传统 Pareto/NBD 的对比
| 特性 | 传统 Pareto/NBD | HB-Pareto/NBD |
| 参数估计 | 每个客户独立估计 | 群体参数共享超先验,部分池化 |
| 数据需求 | 需要充足个体数据 | 适应小样本群体 |
| 计算复杂度 | 低(最大似然估计) | 高(MCMC 采样) |
| 预测不确定性 | 仅点估计 | 全后验分布 |
代码示例
import pymc3 as pm
import numpy as np
# 模拟数据:3 个群体,每个群体 100 个客户
np.random.seed(42)
K = 3 # 群体数
N = 300 # 总客户数
group = np.repeat([0, 1, 2], 100) # 群体标签
# 真实参数(群体级)
true_lambda = np.array([0.8, 1.5, 2.0]) # 购买率
true_mu = np.array([0.2, 0.3, 0.4]) # 流失率
# 生成模拟交易数据
T = 365 # 观察期(天)
x = np.zeros(N)
t = np.zeros(N)
for i in range(N):
k = group[i]
lambda_k = true_lambda[k]
mu_k = true_mu[k]
# 生成交易时间
transactions = np.cumsum(np.random.exponential(1/lambda_k, size=100))
transactions = transactions[transactions < T]
x[i] = len(transactions)
t[i] = transactions[-1] if x[i] > 0 else 0
# 定义 HB-Pareto/NBD 模型
with pm.Model() as model:
# 超先验
alpha_lambda = pm.Exponential('alpha_lambda', 0.1)
beta_lambda = pm.Gamma('beta_lambda', 0.1, 0.1)
alpha_mu = pm.Exponential('alpha_mu', 0.1)
beta_mu = pm.Gamma('beta_mu', 0.1, 0.1)
# 群体级参数
lambda_k = pm.Gamma('lambda_k', alpha_lambda, beta_lambda, shape=K)
mu_k = pm.Gamma('mu_k', alpha_mu, beta_mu, shape=K)
# 个体级似然
for i in range(N):
k = group[i]
ll = pm.ParetoNBD.dist(lambda_k[k], mu_k[k], T).logp(x[i], t[i])
pm.Potential(f'likelihood_{i}', ll)
# MCMC 采样
trace = pm.sample(2000, tune=1000, chains=2, target_accept=0.9)
# 输出群体参数估计
pm.summary(trace, var_names=['lambda_k', 'mu_k'])
实际应用案例
案例 1:电商平台用户分层
某跨境电商使用 HB-Pareto/NBD 分析北美、欧洲、亚洲用户的购买模式差异,发现亚洲用户的 $\lambda$ 比北美高 40%,针对性优化物流时效后,亚洲区复购率提升 25%。
案例 2:订阅盒服务冷启动
新推出的“健康零食盒”订阅服务,利用 HB-Pareto/NBD 结合相似产品的超先验,在首月数据不足时预测用户留存率,误差比传统模型降低 60%。
扩展与进阶
时间动态性:
允许群体参数 $\lambda_k(t),\mu_k(t)$ 随时间变化(如引入 Gaussian 过程):
```html
with pm.Model() as dynamic_model:
# 时间协变量(如月份)
time = pm.Data('time', np.arange(12))
# 使用 Gaussian 过程建模 lambda_k 随时间变化
cov_func = pm.gp.cov.ExpQuad(1, ls=0.5)
gp_lambda = pm.gp.Latent(cov_func=cov_func)
lambda_k_t = gp_lambda.prior("lambda_k_t", X=time[:, None])
多层级结构:
在群体之上增加公司级参数(适用于多品牌集团):
$$\alpha_\lambda^{\text{company}}\sim\text{Gamma}(1,1),\quad\beta_\lambda^{\text{company}}\sim\text{Gamma}(1,1)$$
$$\alpha_{\lambda,k}\sim\text{Gamma}(\alpha_\lambda^{\text{company}},\beta_\lambda^{\text{company}})$$
Pareto/NBD with Covariates
模型背景
- 基础模型:Pareto/NBD(Schmittlein et al., 1987)是客户行为预测的经典模型,用于非合约制客户的交易频率与流失概率预测。
- 协变量扩展:在传统 Pareto/NBD 基础上引入客户特征(如年龄、消费金额、营销接触)作为协变量,建模其对交易率($\lambda$)和流失率($\mu$)的影响,提升预测的个性化能力。
- 核心价值:
- 将静态模型升级为动态个性化预测工具。
- 量化客户特征对长期价值的贡献(如高消费客户流失风险更低)。
模型假设
在标准 Pareto/NBD 假设基础上扩展:
交易过程:
客户活跃期间的交易次数服从泊松过程,但交易率 \lambda_i 受协变量影响:
$$\lambda_i=\exp(\beta_\lambda^TX_i)$$
流失过程:
客户流失时间服从指数分布,流失率 $\mu_i$ 受协变量影响:
$$\mu_i=\exp(\beta_\mu^TZ_i)$$
- $X_i,Z_i$:客户的协变量向量(可相同或不同)。
- $\beta_\lambda,\beta_\mu$:待估计的系数向量。
数学原理
个体级似然函数:
客户 i 在观察期 $T_i$ 内交易 $x_i$ 次,最后一次交易时间为 $t_i$:
$$\mathcal{L}_i=\frac{\lambda_i^{x_i}\mu_i}{\lambda_i+\mu_i}[e^{-(\lambda_i+\mu_i)T_i}+\frac{\mu_i}{\lambda_i+\mu_i}(1-e^{-(\lambda_i+\mu_i)T_i})]$$
协变量链接函数:
使用指数链接确保 $\lambda_i,\mu_i>0$:
$$\ln(\lambda_i)=\beta_{\lambda,0}+\beta_{\lambda,1}X_{i1}+\dots+\beta_{\lambda,p}X_{ip}$$
$$\ln(\mu_i)=\beta_{\mu,0}+\beta_{\mu,1}Z_{i1}+\dots+\beta_{\mu,q}Z_{iq}$$
联合似然与先验(贝叶斯框架):
$$P(\beta_\lambda,\beta_\mu|\text{Data})\propto\prod_{i=1}^N\mathcal{L}_i\cdot P(\beta_\lambda)P(\beta_\mu)$$
先验分布:通常选择正态分布 $\beta\sim N(0,\sigma^2)$。
参数估计
输入数据:
客户交易记录与协变量矩阵,例如:
| 客户 ID | 交易次数(x) | 最后交易时间(t) | 观察期(T) | 年龄 | 消费额 | 营销接触次数 |
| 1 | 5 | 180 | 365 | 30 | 500 | 3 |
| 2 | 2 | 90 | 365 | 25 | 200 | 1 |
估计方法:
- 频率学派:极大似然估计(MLE),使用梯度下降或牛顿法。
- 贝叶斯学派:MCMC 采样(如 HMC、NUTS),推荐工具:Stan、PyMC3。
步骤:
- 数据预处理:标准化协变量、处理缺失值。
- 定义似然函数与链接方程。
- 选择优化/采样算法求解参数。
- 验证模型收敛性(如 Gelman-Rubin 诊断)。
应用场景
客户分群:识别高价值客户(高 $\lambda$+低 $\mu$),如发现“年龄>35 且月消费>1000”群体的 $\mu$ 比均值低 50%。
营销优化:预测不同营销策略对 $\mu$ 的影响(如邮件营销每增加 1 次,流失率下降 $e^{\beta_\mu}$ 倍)。
动态定价:根据实时特征(如最近浏览品类)调整价格敏感客户的推荐策略。
Pareto/NBD with Covariates 通过引入客户特征,将传统模型升级为个性化预测引擎,成为精细化客户管理的核心工具。其关键在于平衡模型复杂度与业务解释性——优先选择强业务相关的协变量,并通过正则化(如 Lasso 先验)防止过拟合。实际应用中,建议结合领域知识迭代优化协变量组合,并通过 A/B 测试验证预测效果。
优缺点分析
优点
- 个性化预测:精准捕捉客户异质性。
- 业务可解释性:量化特征影响(如“会员等级每提升 1 级,交易率增加 20%”)。
- 灵活扩展:支持时间变协变量(如动态价格变化)。
局限性
- 数据需求高:需丰富的客户特征数据。
- 计算复杂度:协变量维度高时,参数估计不稳定。
与传统 Pareto/NBD 对比
“`
| 特性 | 传统 Pareto/NBD | 带协变量的 Pareto/NBD |
| 参数个性化 | 所有客户共享相同分布 | 每个客户的 $\lambda,\mu$ 由协变量决定 |
| 预测粒度 | 群体级预测 | 个体级预测 |
| 应用场景 | 基础流失分析 | 精准营销、个性化运营 |
| 数据需求 | 仅需交易数据 | 需交易数据+客户特征 |
代码示例
import pymc3 as pm
import numpy as np
import pandas as pd
# 模拟数据
np.random.seed(42)
N = 500 # 客户数
X = pd.DataFrame({
'age': np.random.randint(18, 60, N),
'income': np.random.normal(500, 200, N),
'promo_contacts': np.random.poisson(3, N)
})
beta_lambda_true = np.array([0.1, 0.05, 0.2]) # 截距项+age,income,promo_contacts
beta_mu_true = np.array([-0.2, -0.1, -0.3]) # 截距项+age,income,promo_contacts
# 生成lambda和mu
X_mat = np.c_[np.ones(N), X]
lambda_i = np.exp(X_mat.dot(beta_lambda_true))
mu_i = np.exp(X_mat.dot(beta_mu_true))
# 生成交易数据
T = 365
x, t = [], []
for i in range(N):
transactions = np.cumsum(np.random.exponential(1/lambda_i[i], size=100))
transactions = transactions[transactions < T]
x.append(len(transactions))
t.append(transactions[-1] if len(transactions) > 0 else 0)
# 定义模型
with pm.Model() as cov_model:
# 协变量系数先验
beta_lambda = pm.Normal('beta_lambda', mu=0, sigma=1, shape=4) # 截距+3个特征
beta_mu = pm.Normal('beta_mu', mu=0, sigma=1, shape=4)
# 计算lambda和mu
lambda_i = pm.math.exp(pm.math.dot(X_mat, beta_lambda))
mu_i = pm.math.exp(pm.math.dot(X_mat, beta_mu))
# 似然函数
for i in range(N):
ll = pm.ParetoNBD.dist(lambda_i[i], mu_i[i], T).logp(x[i], t[i])
pm.Potential(f'likelihood_{i}', ll)
# MCMC采样
trace = pm.sample(2000, tune=1000, chains=2)
# 输出结果
pm.summary(trace, var_names=['beta_lambda', 'beta_mu'])
实际应用案例
案例1:零售会员计划
某超市发现“每月访问次数”和“平均购物篮金额”对$\mu$有显著负向影响($\beta_\mu=-0.15$),据此设计“月度满额奖励”,使高价值客户流失率降低18%。
案例2:在线教育平台
通过分析课程完成率(协变量)与$\lambda$的正相关($\beta_\lambda=0.25$),优化课程推荐算法,学员续费率提升30%。
扩展与进阶
时间动态协变量:
使用滑动窗口更新协变量(如近30天活跃天数):
# 动态更新最近活跃天数
df['recent_activity'] = df['transaction_dates'].rolling('30D').count()
非线性效应:
引入样条函数或神经网络捕捉非线性关系:
from patsy import dmatrix
# 使用三次样条拟合年龄的非线性效应
X_spline = dmatrix("bs(age, df=4)", data=X, return_type='dataframe')
Pareto/GGG(Generalized Gamma-Gamma)模型
模型背景
- 基础模型:Pareto/GGG是客户终身价值(CLV)建模的综合框架,结合了:
- Pareto/NBD:用于建模客户交易频率与流失概率。
- Gamma-Gamma:用于建模客户单次交易价值(Monetary Value)。
- 广义Gamma分布:扩展传统Gamma分布,提升对交易金额分布的灵活性。
- 核心目标:统一预测客户的购买频次、流失概率与交易金额,实现CLV的全维度估算。
- 提出者:Platzer & Reutterer (2016)
模型假设
交易频率与流失(Pareto/NBD部分):
- 活跃客户的交易次数服从泊松过程(参数$\lambda$)。
- 客户流失时间服从指数分布(参数$\mu$)。
- 异质性:$\lambda\sim\text{Gamma}(r,\alpha),\mu\sim\text{Gamma}(s,\beta)$。
交易价值(Generalized Gamma-Gamma部分):
单次交易金额m服从广义Gamma分布(参数$k,\theta,\gamma$):
$$f(m)=\frac{\gamma}{\theta^k\Gamma(k/\gamma)}m^{k-1}e^{-(m/\theta)^\gamma}$$
客户间异质性:参数$\theta$服从超先验分布(如逆Gamma分布)。
数学原理
CLV分解:
$$\text{CLV}=\text{存活概率}\times\text{预期交易次数}\times\text{预期交易价值}$$
$$\text{CLV}_i=P(\text{Active}_i)\cdot E(X_i)\cdot E(M_i)$$
存活概率(Pareto/NBD):
客户在观察期T后仍活跃的概率:
$$P(\text{Active}_i|x_i,t_i,T)=[1+\frac{s}{r+s+x_i}(\frac{\alpha+T}{\alpha+t_i})^{r+x_i}]^{-1}$$
预期交易次数:
$$E(X_i|\text{Active}_i)=\frac{r+x_i}{s+\beta}\cdot\frac{\alpha+T}{\alpha+t_i}$$
预期交易价值(Generalized Gamma-Gamma):
客户i的预期单次交易金额:
$$E(M_i)=\theta_i\cdot\frac{\Gamma\left((k+1)/\gamma\right)}{\Gamma(k/\gamma)}$$
- $\theta_i$: 客户级参数,由超先验$\theta_i\sim\text{Inv-Gamma}(a,b)$驱动。
参数估计
输入数据:
客户交易历史与金额记录:
交易次数(x)最后一次交易时间(t)观察期(T)交易金额1交易金额2…
| 客户ID | ||||||
| 1 | 5 | 180 | 365 | 150 | 200 | … |
| 2 | 2 | 90 | 365 | 80 | 120 | … |
估计步骤:
- Pareto/NBD 参数:使用最大似然或贝叶斯方法估计 $r,\alpha,s,\beta$。
- Generalized Gamma-Gamma 参数:对交易金额数据拟合广义 Gamma 分布,估计 $k,\theta,\gamma,a,b$。
- 联合优化:通过 EM 算法或 MCMC 将两部分联合校准,确保参数一致性。
工具推荐:
- Python: lifetimes(Pareto/NBD)、stats(广义 Gamma 拟合)、PyMC3(贝叶斯推断)。
- R: BTYD(交易频率)、flexsurv(广义 Gamma 分布)。
应用场景
- 高价值客户识别:综合频次与金额预测,识别“高频次+高客单价”客户(如奢侈品电商)。
- 动态定价策略:根据客户级 $E(M_i)$ 制定个性化定价(如软件订阅阶梯定价)。
- 流失预警与干预:对高 $P(\text{Active})$ 但 $E(M_i)$ 下降的客户启动挽留计划。
Pareto/GGG 模型通过整合交易频次、流失概率与广义 Gamma 金额分布,实现了客户终身价值的精细化预测。其核心优势在于灵活捕捉复杂客户行为模式,尤其适用于高价值、高异质性行业。实际应用中需权衡模型复杂度与数据质量,优先通过特征工程(如金额对数变换)提升分布拟合效果,并定期验证模型对业务变化的适应性。
优缺点分析
优点
- 全面性:统一建模频次、留存与金额,避免分步预测的误差累积。
- 灵活性:广义 Gamma 分布适配复杂金额分布(如长尾、多峰)。
- 可解释性:参数直接关联业务指标(如 $\theta$ 反映客户消费力基线)。
局限性
- 计算复杂度高:需同时优化频次与金额模型,计算资源消耗大。
- 数据需求严格:需完整交易时间戳与金额记录,缺失值处理困难。
与传统模型对比
| 特性 | Gamma-Gamma 模型 | Pareto/GGG 模型 |
| 覆盖维度 | 仅交易金额 | 频次+流失+金额 |
| 金额分布假设 | 双 Gamma 分布 | 广义 Gamma 分布(更灵活) |
| 适用场景 | 客单价稳定业务 | 高波动客单价(如旅游、B2B) |
| 参数数量 | 4 个($k,\theta,a,b$) | 8+ 个(含 Pareto/NBD 参数) |
代码示例
实际应用案例
案例1:高端酒店集团
某连锁酒店使用 Pareto/GGG 识别“低频高消”客户(商务客户),推出定制化套餐后,该群体年度 CLV 提升 40%。
案例2:SaaS 企业
结合 API 调用频次(Pareto/NBD)与订阅金额(GGG),动态调整客户成功经理的服务优先级,续约率提升 22%。
扩展与进阶
时间衰减因子:
在广义 Gamma 中引入时间衰减参数,建模客户消费力的自然下降:
$$\theta_i(t)=\theta_{i0}\cdot e^{-\delta t}$$
贝叶斯分层结构:
对客户群体分层建模,共享超先验以提升小样本估计稳定性:
with pm.Model() as hierarchical_model:
# 超先验
mu_k = pm.Normal('mu_k', 0, 1)
sigma_k = pm.HalfNormal('sigma_k', 1)
# 群体级参数
k = pm.Normal('k', mu=mu_k, sigma=sigma_k, shape=n_clusters)
BG/CNBD-k
模型背景
- 基础模型:BG/CNBD-k(Beta-Geometric/Compound Negative Binomial Distribution with k factors)是客户终身价值(CLV)预测的高阶模型,由 Fader & Hardie 在 BG/NBD 基础上扩展而来,旨在解决传统模型在购买间隔异质性和流失模式灵活性上的局限。
- 核心改进:
- BG 部分:沿用 Beta-Geometric 假设,建模客户的流失过程。
- CNBD-k 部分:引入复合负二项分布(k 阶混合),捕捉复杂购买间隔(如短时高频与长期间歇并存)。
- 适用场景:高频次、高异质性购买行为(如快消品、数字内容订阅)。
模型假设
购买过程:
客户活跃期间的购买次数服从负二项过程,但参数通过 k 阶混合增强灵活性:
$$X_i\sim\text{NegativeBinomial}(r_i,p_i),\quad(r_i,p_i)\sim\sum_{k=1}^K\pi_k\delta_{(r_k,p_k)}$$
- K: 预设的混合阶数(需通过模型选择确定)。
- $\pi_k$: 混合权重,满足 $\sum\pi_k=1$。
流失过程:
客户在第 j 次购买后流失的概率服从几何分布,其参数由 Beta 分布建模:
$$\theta_j\sim\text{Beta}(a,b),\quad P(\text{流失}|j)=\theta_j$$
数学原理
购买次数的混合分布:
$$P(X_i=x|r_1,p_1,…,r_K,p_K)=\sum_{k=1}^K\pi_k\binom{x+r_k-1}{x}p_k^{r_k}(1-p_k)^x$$
存活概率:
客户在观察期 T 内存活(未流失)的概率:
$$P(\text{Active}_i|X_i=x)=\prod_{j=1}^x(1-\theta_j)$$
联合似然函数$$\mathcal{L}=\prod_{i=1}^N\left[\sum_{k=1}^K\pi_k\binom{x_i+r_k-1}{x_i}p_k^{r_k}(1-p_k)^{x_i}\right]\cdot\prod_{j=1}^{x_i}(1-\theta_j)$$
参数先验(贝叶斯框架):
- $\pi\sim\text{Dirichlet}(\alpha)$
- $r_k\sim\text{Gamma}(\gamma_r,\beta_r), p_k\sim\text{Beta}(\alpha_p,\beta_p)$
- $a, b\sim\text{Gamma}(1,1)$
参数估计
输入数据:
客户交易时间序列,需包含购买次数与最后一次购买时间:
| 客户ID | 购买次数(x) | 最后购买时间(t) | 观察期(T) |
| 1 | 8 | 180 | 365 |
| 2 | 3 | 90 | 365 |
估计方法:
- 频率学派:EM算法(Expectation-Maximization)优化混合权重与分布参数。
- 贝叶斯学派:变分推断(VI)或MCMC(如Gibbs采样),推荐工具:Stan、PyMC3。
步骤:
- 初始化混合阶数K(可通过交叉验证选择)。
- E步:计算各客户属于第k个混合成分的后验概率。
- M步:更新$\pi_k, r_k, p_k, a, b$。
- 迭代至收敛。
应用场景
- 高频购买细分:识别不同购买节奏的客户群(如每日活跃用户vs周末用户)。
- 动态促销策略:对高$\theta_j$(易流失)客户在关键购买节点(如第5次购买后)触发定向优惠。
- 库存管理:根据预测的购买间隔分布优化补货周期(如短间隔群体优先补货)。
BG/CNBD-k通过k阶混合负二项分布与Beta-Geometric流失模型的结合,实现了对复杂客户行为的精细刻画。其核心价值在于平衡模型灵活性与解释性,尤其适用于高异质性、多模式购买场景。实际应用中需注意:
- 混合阶数选择:通过信息准则(如BIC)或业务知识确定K值。
- 计算优化:对大规模数据采用变分推断或分布式计算(如Spark)。
- 业务验证:将混合成分映射到真实客户分群,确保模型输出可落地。
优缺点分析
优点
- 灵活建模:k阶混合负二项分布适配多峰、长尾的购买间隔数据。
- 精准流失预测:Beta-Geometric分层捕捉流失概率随购买次数的变化。
- 可解释性:混合成分对应业务可识别的客户子群体。
局限性
- 计算复杂度高:混合模型参数随K增加呈指数级增长。
- 需预设K:阶数选择不当可能导致过拟合或欠拟合。
与传统模型对比
| 特性 | BG/NBD | BG/CNBD-k |
| 购买间隔分布 | 单一负二项分布 | k阶混合负二项分布 |
| 异质性捕捉 | 低(同质客户假设) | 高(混合成分建模子群体) |
| 适用数据复杂度 | 简单购买模式 | 复杂、多模态购买行为 |
| 计算资源需求 | 低 | 高(尤其当K大时) |
代码示例
import pymc3 as pm
import numpy as np
from scipy.stats import beta, nbinom
# 模拟数据:K=2个混合成分
np.random.seed(42)
N = 500
K = 2
true_pi = np.array([0.6, 0.4])
true_r = np.array([5, 10])
true_p = np.array([0.3, 0.6])
true_a, true_b = 2, 5 # Beta参数
# 生成购买次数x和流失标记
x = np.zeros(N)
for i in range(N):
k = np.random.choice(K, p=true_pi)
x[i] = nbinom.rvs(true_r[k], true_p[k])
# 模拟流失概率
theta_j = beta.rvs(true_a, true_b, size=int(x[i]))
if np.any(np.random.rand(int(x[i])) < theta_j):
x[i] = np.min(np.where(np.random.rand(int(x[i])) < theta_j)[0]) + 1
# 定义BG/CNBD-k模型
with pm.Model() as model:
# 混合权重
pi = pm.Dirichlet('pi', a=np.ones(K), shape=K)
# 混合成分参数
r = pm.Gamma('r', alpha=2, beta=1, shape=K)
p = pm.Beta('p', alpha=1, beta=1, shape=K)
# Beta-Geometric参数
a = pm.Gamma('a', alpha=1, beta=1)
b = pm.Gamma('b', alpha=1, beta=1)
# 似然函数
for i in range(N):
# 购买次数的混合负二项似然
nbinom_logp = [pm.NegativeBinomial.dist(r[k], p[k]).logp(x[i]) for k in range(K)]
log_p_x = pm.math.logsumexp(pm.math.log(pi) + nbinom_logp, axis=0)
# 流失过程似然
theta = pm.Beta.dist(a, b)
log_p_active = pm.math.sum(pm.math.log(1 - theta))
# 联合似然
pm.Potential(f'likelihood_{i}', log_p_x + log_p_active)
# 变分推断
approx = pm.fit(n=10000, method='advi')
# 输出参数估计
trace = approx.sample(1000)
pm.summary(trace)
实际应用案例
案例1:在线视频平台
某平台使用BG/CNBD-k(K=3)识别出“周末刷剧族”(高频短间隔)与“月度会员”(低频固定间隔),针对前者推出“连续观看奖励”,留存率提升18%。
案例2:生鲜电商
通过分析混合成分,发现“晚8点高峰购买群”的流失概率显著低于其他群体,优化配送时段后,该群体CLV提升30%。
扩展与进阶
动态混合权重允许混合权重$\pi_k(t)$随时间变化,适配季节性购买模式:
# 时间依赖的Dirichlet过程
with pm.Model() as dynamic_model:
time = pm.Data('time', np.arange(12)) # 月份
W = pm.Normal('W', mu=0, sigma=1, shape=(K, 12))
pi = pm.Dirichlet('pi', a=pm.math.softmax(W.dot(time)), shape=K)
非参数扩展:
使用狄利克雷过程(DP)替代固定K值,自动推断混合成分数量:
from pymc3.distributions.dist_math import Dirichlet
# DP混合模型
alpha = pm.Gamma('alpha', 1, 1)
stick_breaking = pm.Dirichlet('stick_breaking', a=np.ones(K-1), shape=K-1)
pi = pm.Deterministic('pi', stick_breaking * pm.math.concatenate([[1], pm.math.extra_ops.cumprod(1-stick_breaking[:-1])]))
新兴方向与混合模型
机器学习增强模型
方法核心思想
将传统概率模型(如BTYD)与机器学习模型(如XGBoost、深度学习)结合,优势互补:
- 传统模型(如BG/NBD、Pareto/NBD):基于统计假设,强解释性,但无法灵活建模复杂行为特征。
- 机器学习模型:捕捉非线性关系、高维特征交互,但需大量数据且可解释性弱。
- 结合方式:
- 串联式:用机器学习预测传统模型的输入参数(如流失率$\mu$、交易率$\lambda$)。
- 并联式:分别用传统模型和机器学习预测LTV,再通过加权或元模型融合结果。
- 特征增强:将传统模型的预测结果(如存活概率)作为特征输入机器学习模型。
典型工作流程
以串联式模型(机器学习预测流失概率+BG/NBD)为例:
数据准备:
- 客户行为数据:交易时间、金额、频次、最近一次购买(Recency)等。
- 特征工程:
- 传统模型特征:RFM(Recency, Frequency, Monetary)。
- 扩展特征:行为序列(点击、浏览)、人口统计、外部数据(天气、经济指标)。
- 示例特征矩阵:
| 客户ID | 最近购买天数 | 总购买次数 | 平均金额 | 点击次数 | 是否周末活跃 | … |
| 1 | 30 | 5 | 200 | 20 | 1 | … |
机器学习预测流失概率:
- 模型选择:XGBoost(处理缺失值、特征重要性)、LightGBM(高效大数据训练)、神经网络(复杂序列建模)。
- 目标变量:定义流失标签(如未来30天无购买为1,否则为0)。
训练代码示例:
import xgboost as xgb from sklearn.model_selection import train_test_split # 划分训练集与测试集 X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.2) # 训练XGBoost model = xgb.XGBClassifier(objective='binary:logistic', n_estimators=100) model.fit(X_train, y_train) # 预测流失概率 churn_proba = model.predict_proba(X_test)[:, 1]
与传统模型(BG/NBD)结合:
- 输入调整:将机器学习预测的流失概率作为BG/NBD中流失率$\mu_i$的先验。
- 贝叶斯框架下的参数更新:
$$\mu_i\sim\text{Beta}(a+\text{ML_churn_proba}_i,b+(1-\text{ML_churn_proba}_i))$$
- LTV计算:
$$\text{LTV}_i=\frac{P(\text{Active}_i)\cdot E(X_i)}{\mu_i}\cdot E(M_i)$$
应用场景与案例
场景1:高维行为数据建模
问题:电商平台希望利用用户点击流(页面停留、加购次数)预测流失。
方案:
- 使用LSTM处理点击序列,生成隐状态特征。
- 将隐状态与RFM特征拼接,输入XGBoost预测流失概率。
- 将流失概率输入BG/NBD计算LTV。
效果:相比纯BG/NBD,AUC提升15%,LTV预测误差降低20%。
场景2:动态定价优化
问题:SaaS企业需根据用户行为实时调整定价策略。
方案:
- 用LightGBM预测用户对价格敏感度(目标:是否因涨价流失)。
- 将敏感度作为权重,调整Pareto/NBD的流失率参数$\mu_i$。
- 输出个性化定价区间,使整体收益最大化。
关键技术细节
特征重要性分析:通过SHAP值解释机器学习模型,筛选关键特征输入传统模型。
import shap explainer = shap.TreeExplainer(model) shap_values = explainer.shap_values(X_test) shap.summary_plot(shap_values, X_test)
模型校准:
对机器学习输出的概率进行校准(如Platt Scaling),避免概率偏差影响传统模型:
from sklearn.calibration import CalibratedClassifierCV calibrated_model = CalibratedClassifierCV(model, cv=5, method='isotonic') calibrated_model.fit(X_train, y_train)
在线学习实时更新模型(如 FTRL 优化器),适应数据分布变化:
from sklearn.linear_model import SGDClassifier online_model = SGDClassifier(loss='log_loss', learning_rate='adaptive') # 增量更新 online_model.partial_fit(new_X, new_y)
优缺点分析
- 优点:
- 精度提升:机器学习捕捉复杂模式,传统模型提供概率框架。
- 灵活性:支持结构化与非结构化数据(如文本、图像)。
- 可解释性:通过 SHAP、LIME 局部解释关键特征影响。
- 缺点:
- 复杂度高:需维护多模型管道,部署成本增加。
- 数据需求:依赖大量标注数据(尤其冷启动阶段)。
- 计算开销:实时预测时延可能较高。
与传统模型对比
| 指标 | 纯 BTYD 模型 | 机器学习增强模型 |
| 预测精度 | 低(假设驱动) | 高(数据驱动) |
| 特征利用 | 仅限交易数据 | 多源异构数据 |
| 计算效率 | 高(参数少) | 中高(依赖特征维度) |
| 可解释性 | 强(明确概率公式) | 弱(需借助解释工具) |
| 适用场景 | 稳定、规则明确的业务 | 快速变化、高维复杂行为场景 |
部署与优化建议
A/B 测试框架:对比增强模型与基线模型的业务指标(如 LTV 误差、营销 ROI)。
# 使用 Prophet 进行因果推断 from fbprophet import Prophet model = Prophet() model.add_seasonality(name='campaign', period=30, fourier_order=5) model.fit(data)
模型监控:监控特征分布漂移(如 KS 检验)及预测稳定性(如 PSI 指标)。
from scipy.stats import ks_2samp drift_score = ks_2samp(train_features['age'], production_features['age']).statistic
自动化管道:使用 MLflow 或 TFX 构建端到端训练-部署流水线。
import mlflow
mlflow.start_run()
mlflow.log_metric("auc", auc_score)
mlflow.xgboost.log_model(model, "model")
总结
机器学习增强的 LTV 模型通过融合统计假设与数据驱动方法,成为客户精细化运营的核心工具。其关键在于平衡精度与可解释性——优先选择业务可理解的模型结构(如串联式),并通过特征筛选与模型压缩(如剪枝、量化)降低复杂度。实际落地中,建议从简单增强(如用 XGBoost 预测流失概率)起步,逐步迭代至复杂架构(如深度生存模型+概率模型)。
动态参数模型
核心思想
动态参数模型通过允许模型参数随时间或外部环境变化,突破传统模型(如 BG/NBD、Pareto/NBD)的静态假设,以更灵活地捕捉客户行为中的时变效应。典型应用场景包括:
- 季节性波动:节假日、促销导致的购买率周期性变化。
- 市场趋势:经济周期、竞争环境对客户流失率的长期影响。
- 个体行为演化:客户生命周期不同阶段的消费模式变化。
关键技术方法
贝叶斯层次时间序列模型
- 核心原理:在贝叶斯框架下,为参数引入时间依赖的超先验分布,通过分层结构共享时间模式。
- 数学表达(以流失率$\mu_t$为例):
$$\begin{aligned}&\text{观测层:}\quad x_t\sim\text{Poisson}(\lambda_t)\\&\text{过程层:}\quad \mu_t=\mu_{t-1}+\epsilon_t,\quad \epsilon_t\sim\mathcal{N}(0,\sigma^2)\\&\text{先验层:}\quad \mu_0\sim\mathcal{N}(0,10),\quad \sigma\sim\text{HalfNormal}(5)\end{aligned}$$
- 实现工具:PyMC3(MCMC 采样)、Stan(HMC 算法)。
状态空间模型(State-Space Models)
- 核心原理:将参数视为隐状态,通过状态方程(动态演化)和观测方程(数据生成)联合建模。
- 典型结构(以交易率\lambda_t 建模为例):
$$\begin{aligned}&\text{状态方程:}\quad \lambda_t=\phi\lambda_{t-1}+\eta_t,\quad \eta_t\sim\mathcal{N}(0,Q)\\&\text{观测方程:}\quad x_t\sim\text{NegativeBinomial}(\lambda_t,\alpha)\end{aligned}$$
- \phi:状态转移系数,控制参数自相关性。
- Q:过程噪声方差,决定参数波动强度。
- 滤波算法:Kalman 滤波(线性高斯假设)、粒子滤波(非线性非高斯场景)。
深度学习动态模型
核心原理:使用神经网络直接建模参数的时间演化,捕捉复杂时间依赖关系。
典型架构:
- LSTM-Enhanced Model:
$$\lambda_t=\text{Softplus}\left(W_hh_t+b\right),\quad h_t=\text{LSTM}(x_{1:t-1},c_{ext})$$
- 其中 $c_{ext}$ 为外部特征(如经济指标、营销支出)。
- Transformer-Based Model:利用自注意力机制捕获长期依赖与时序模式:
$$\lambda_t=\text{MLP}(\text{MultiHeadAttention}(X_{t-k:t}))$$
实现框架:PyTorch、TensorFlow(配合概率编程库如 Pyro)。
应用场景与案例
动态流失率预测(订阅服务)问题:某视频平台用户流失率在寒暑假显著升高,静态模型无法适应季节性波动。
方案:构建状态空间模型,流失率$\mu_t$服从带周期性扰动的随机游走:
$$\mu_t=\mu_{t-1}+\gamma\sin\left(\frac{2\pi t}{12}\right)+\epsilon_t$$
结果:预测误差降低32%,季度末挽留活动ROI提升25%。
时变购买率建模(零售业)
问题:快消品购买率受促销活动与竞品策略影响,呈现非平稳波动。
方案:
使用贝叶斯层次模型,购买率$\lambda_{it}$分解为:
$$\log(\lambda_{it})=\alpha_i+\beta_t+\theta\cdot\text{Promo}_{it}$$
- $\alpha_i$:客户个体效应(随机截距)。
- $\beta_t$:时间趋势项(动态参数)。
- $\text{Promo}_{it}$:促销活动强度(时变协变量)。
结果:动态定价策略使月度GMV提升18%。
模型训练与评估
训练策略
滑动窗口验证:在时间序列数据上,按时间顺序划分训练集与测试集,评估模型动态预测能力。
from sklearn.model_selection import TimeSeriesSplit
tscv = TimeSeriesSplit(n_splits=5)
for train_index, test_index in tscv.split(X):
model.fit(X[train_index], y[train_index])
score = model.score(X[test_index], y[test_index])
在线学习:对数据流进行实时增量更新,适应参数漂移。
# PyTorch在线学习示例
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for batch in data_stream:
loss = model.loss(batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
评估指标
- 点预测精度:MAE、RMSE(适用于连续型参数如交易率)。
- 概率校准度:Brier Score(适用于流失概率等二元预测)。
- 业务指标:
- CLTV预测误差率:$\frac{|\text{Predicted LTV}-\text{Actual LTV}|}{\text{Actual LTV}}$
- 动态策略提升:对比静态模型的营销活动ROI。
优缺点分析
| 优点 | 挑战 |
| 1. 适应市场环境与客户行为的变化 | 1. 计算复杂度高(尤其MCMC、粒子滤波) |
| 2. 捕捉长期趋势与短期波动 | 2. 需要充足时间序列数据(T≥30) |
| 3. 支持外部协变量(如经济指标) | 3. 模型解释性降低(尤其深度学习) |
| 4. 提升营销策略的动态响应能力 | 4. 参数漂移检测与再训练机制需完善 |
实现示例
import pymc3 as pm
import numpy as np
# 模拟动态交易率数据
np.random.seed(42)
T = 100
true_lambda = np.zeros(T)
true_lambda[0] = 5
for t in range(1, T):
true_lambda[t] = 0.9 * true_lambda[t-1] + np.random.normal(0, 0.5)
x = np.random.poisson(true_lambda)
# 构建状态空间模型
with pm.Model() as ssm_model:
# 状态方程:lambda_t ~ AR(1)
sigma = pm.HalfNormal('sigma', sigma=1)
phi = pm.Normal('phi', mu=0.8, sigma=0.1)
lambda_ = pm.GaussianRandomWalk('lambda', mu=phi, sigma=sigma, shape=T)
# 观测方程:x_t ~ Poisson(lambda_t)
obs = pm.Poisson('obs', mu=lambda_, observed=x)
# 推断
trace = pm.sample(2000, tune=1000, cores=2)
# 可视化参数轨迹
pm.plot_trace(trace, var_names=['phi', 'sigma'])
总结
动态参数模型通过参数时变性建模,显著提升了客户行为预测在非稳态环境中的准确性。实际应用中需注意:
- 数据质量:确保时间序列长度与粒度足够支撑动态估计。
- 计算优化:对复杂模型(如深度状态空间)采用变分推断或分布式训练。
- 解释性增强:结合SHAP、敏感性分析揭示关键驱动因素。
生存分析整合模型
核心思想
将生存分析(Cox比例风险模型)与客户购买行为模型(BTYD,如Pareto/NBD)结合,实现:
- 双重信息利用:
- Cox模型:分析客户生存时间(流失风险)与协变量(如购买频次、营销互动)的关系。
- BTYD模型:建模购买次数与交易间隔的随机过程。
- 动态预测:将BTYD输出的购买行为指标(如预期交易次数)作为Cox模型的时变协变量,实现客户流失风险与购买动态的联合建模。
模型结构
整合框架
输入数据:
- 生存数据:客户流失时间T_i(右删失数据)。
- 购买行为数据:交易时间序列\{t_{i1},t_{i2},…,t_{in}\}。
- 协变量:静态(如性别)与时变(如最近购买金额)。
模型联合分布:
$$P(T_i,X_i|\Theta)=\underbrace{P(T_i|X_i,\beta)}_{\text{Cox模型}}\cdot\underbrace{P(X_i|\lambda_i,\mu_i)}_{\text{BTYD模型}}$$
- $X_i$:BTYD的购买次数与交易间隔。
- $\beta$:Cox模型的协变量系数。
- $\lambda_i,\mu_i$:BTYD的交易率与流失率参数。
关键公式
Cox比例风险模型:
$$h(t|X_i)=h_0(t)\exp\left(\beta_1\cdot\text{Frequency}_i+\beta_2\cdot\text{Recency}_i+\gamma^TZ_i\right)$$
- $h_0(t)$:基准风险函数。
- $\text{Frequency}_i,\text{Recency}_i$:来自BTYD模型的预测值(时变协变量)。
- $Z_i$:静态协变量(如年龄、地域)。
BTYD模型(以Pareto/NBD为例):交易过程:$X_i\sim\text{Poisson}(\lambda_it)$。
- 流失过程:客户在交易后流失的概率$p_i\sim\text{Beta}(a,b)$。
联合似然函数:
$$\mathcal{L}(\Theta)=\prod_{i=1}^N[h(T_i|X_i)^{d_i}S(T_i|X_i)]\cdot\prod_{i=1}^N[\frac{(\lambda_iT_i)^{x_i}e^{-\lambda_iT_i}}{x_i!}\cdot\text{Beta}(p_i|a,b)]$$
- $d_i$:是否发生流失(1为是,0为删失)。
- $S(T_i|X_i)=\exp(-\int_0^{T_i}h(u|X_i)du)$:生存函数。
实现步骤
数据准备
| 客户ID | 生存时间$T_i$ | 删失标志$d_i$ | 交易次数$x_i$ | 最近交易时间$t_{i,\text{last}}$ | 协变量$Z_i$ |
| 1 | 180 | 1 | 5 | 150 | 25,北京 |
| 2 | 365 | 0 | 3 | 360 | 30,上海 |
模型训练
BTYD参数估计:使用Pareto/NBD模型估计每个客户的$\lambda_i$(交易率)和$p_i$(流失概率)。
from lifetimes import ParetoNBDFitter pnbd = ParetoNBDFitter() pnbd.fit(data['频率'], data['近因'], data['T'], data['是否流失']) lambda_i = pnbd.params['r']/(pnbd.params['alpha']+data['T'])
Cox模型特征构建:
- 静态特征:$Z_i$(如年龄、城市)。
- 动态特征:BTYD输出的$\lambda_i、\text{Recency}_i=T_i-t_{i,\text{last}}$。
联合模型拟合:
使用lifelines库进行Cox模型训练,并整合BTYD特征:
from lifelines import CoxPHFitter
# 合并特征
data_cox = data.join(pd.DataFrame({'lambda': lambda_i, 'recency': recency_i}))
# 拟合Cox模型
cph = CoxPHFitter()
cph.fit(data_cox, duration_col='T', event_col='d', formula="lambda + recency + age + city")
动态预测
生存概率预测:
$$S(t|X_i)=\exp(-\int_0^th_0(u)\exp(\beta^TX_i(u))du)$$
- 其中$X_i(u)$包含随时间更新的BTYD指标(如每月的交易率$\lambda_i(u)$)。
代码示例:
# 按月更新BTYD参数并预测生存概率
for month in range(1, 13):
# 更新交易数据
new_data = update_transactions(data, month)
# 重新估计BTYD参数
pnbd.fit(new_data['频率'], new_data['近因'], new_data['T'], new_data['是否流失'])
lambda_i_new = pnbd.params['r']/(pnbd.params['alpha']+new_data['T'])
# 预测生存概率
survival_proba = cph.predict_survival_function(new_data, times=[month*30])
应用场景
高价值客户识别
策略:将联合模型预测的生存概率S(t)与BTYD的预期交易次数$E[X_i]$结合,构建风险-价值矩阵:
| 高生存概率 | 低生存概率 | |
| 高预期交易 | 核心客户(保持) | 风险客户(挽留) |
| 低预期交易 | 潜力客户(激活) | 流失客户(放弃) |
动态定价策略
案例:某电商平台发现:
- 高生存概率+高交易额客户对价格不敏感→可推出高价增值服务。
- 低生存概率+高交易额客户→触发定向折扣(使用优惠券提升短期留存)。
模型评估
- 生存分析指标:
- Concordance Index:评估生存时间排序一致性(>0.7为良好)。
- 校准曲线:比较预测生存概率与实际Kaplan-Meier曲线的匹配度。
- 购买预测指标:
- RMSE:预测交易次数与实际值的均方根误差。
- Pareto/NBD LL:BTYD部分的对数似然值。
- 业务指标:
- 留存率提升:对比干预组(模型驱动策略)与对照组的留存差异。
- CLV误差率:$$\frac{|\text{预测CLV}-\text{实际CLV}|}{\text{实际CLV}}$$。
优缺点分析
| 优点 | 挑战 |
| 1. 同时捕捉流失风险与购买行为 | 1. 计算复杂度高(需联合优化) |
| 2. 支持时变协变量动态更新 | 2. 数据要求高(完整交易+生存数据) |
| 3. 提升客户分群与干预策略的精准性 | 3. 模型解释性降低 |
实现工具
- Python库:
- lifetimes:BTYD模型实现(Pareto/NBD、BG/NBD)。
- lifelines:Cox模型与生存分析工具。
- PyMC3:贝叶斯联合模型构建。
- R包:
- BTYD:客户行为分析。
- survival:Cox模型实现。
总结
生存分析整合模型通过融合客户行为与生存时间信息,为CLTV预测与留存策略提供了更全面的视角。其核心价值在于:
- 动态性:适应客户行为与市场环境的实时变化。
- 可干预性:识别高风险高价值客户并制定精准策略。
最佳实践:
- 优先验证BTYD与Cox模型的单独性能,再尝试联合优化。
- 对时变协变量进行平滑处理(如指数加权移动平均),避免参数震荡。
- 定期更新模型参数(建议月度/季度),保持预测时效性。
Gamma-Gamma-BTYD混合模型
模型核心思想
Gamma-Gamma-BTYD混合模型通过整合BG/NBD模型(频率预测)和Gamma-Gamma模型(金额预测),在客户生命周期价值(CLV)计算中同时捕捉购买频率与交易金额的双重维度。其优势在于:
- 双维度建模:频率(购买次数)与金额(单次价值)独立建模,解决异质性客户行为。
- 动态适应性:BG/NBD捕捉客户活跃度变化,Gamma-Gamma量化价值波动。
- 业务可解释性:分离核心驱动因素(留存vs消费力),支持精准运营策略。
模型结构与公式
BG/NBD模型(频率部分)
- 输入:客户交易历史(首次购买时间$T_{\text{first}}$、最近购买时间$T_{\text{last}}$、总交易次数x、观测期长度T)。
- 参数:
- $r,\alpha$:控制交易率$\lambda\sim\text{Gamma}(r,\alpha)$。
- a,b:控制流失概率$p\sim\text{Beta}(a,b)$。
- 预测目标:
- 未来交易次数$E[X_{\text{future}}|x,T_{\text{last}},T]$。
- 存活概率$P(\text{Active}|x,T_{\text{last}},T)$。
Gamma-Gamma模型(金额部分)
- 输入:客户历史交易金额$\{m_1,m_2,…,m_x\}$,交易次数x。
- 假设:
- 单次金额$m_j\sim\text{Gamma}(p,\nu)$,其中$\nu\sim\text{Gamma}(q,\gamma)$。
- 客户间金额异质性由$p,q,\gamma$控制。
- 预测目标:
- 期望单次金额$E[M|x,\bar{m}]=\frac{q\gamma+x\bar{m}}{q+x-1}$,其中$\bar{m}$为历史平均金额。
CLV计算
$$\text{CLV}=\underbrace{E[X_{\text{future}}]}_{\text{BG/NBD}}\cdot\underbrace{E[M]}_{\text{Gamma-Gamma}}\cdot\text{ProfitMargin}$$
贴现因子(可选):对长期CLV加入时间折扣$\delta$,即$\text{CLV}=\sum_{t=1}^\infty\frac{E[X_t]E[M]}{(1+\delta)^t}$。
实现步骤与代码
数据准备
| 客户ID | 首次购买日期 | 最近购买日期 | 交易次数x | 总金额\sum m | 观测期长度T(天) |
| 1 | 2023-01-01 | 2023-06-30 | 5 | 1500 | 180 |
| 2 | 2023-03-15 | 2023-05-20 | 3 | 900 | 180 |
BG/NBD模型训练
from lifetimes import BetaGeoFitter
# 创建BG/NBD模型
bgf = BetaGeoFitter()
bgf.fit(frequency=data['x'], recency=data['T_last'], T=data['T'])
# 预测未来交易次数(例如未来90天)
data['predicted_purchases'] = bgf.conditional_expected_number_of_purchases_up_to_time(
t=90, frequency=data['x'], recency=data['T_last'], T=data['T']
)
Gamma-Gamma模型训练
from lifetimes import GammaGammaFitter
# 创建Gamma-Gamma模型
ggf = GammaGammaFitter()
ggf.fit(frequency=data['x'], monetary_value=data['sum_m'])
# 预测期望单次金额
data['predicted_m'] = ggf.conditional_expected_average_profit(
frequency=data['x'], monetary_value=data['sum_m']
)
CLV计算
profit_margin = 0.2 # 假设利润率20% data['clv'] = data['predicted_purchases'] * data['predicted_m'] * profit_margin
应用场景与案例
高价值客户识别
- 策略:按CLV分位数划分客户群:
- Top10%:专属客服、优先服务。
- Bottom30%:低成本触达(如邮件营销)。
- 效果:某电商平台通过此策略,营销成本降低25%,高CLV客户留存率提升18%。
动态定价优化
- 场景:在线教育平台针对不同CLV群体制定价格策略:
- 高CLV+高活跃度:推出高价进阶课程。
- 低CLV+低活跃度:提供限时折扣激活消费。
- 结果:ARPU(每用户平均收入)提升12%。
关键技术细节
模型假设验证
独立性检验:使用Spearman相关系数检验交易频率与金额是否独立。
from scipy.stats import spearmanr
corr, p_value = spearmanr(data['x'], data['sum_m'])
if p_value < 0.05:
print("警告:频率与金额相关,需考虑联合模型!")
参数校准
- BG/NBD:通过历史数据回测,调整 r, \alpha, a, b 先验参数。
- Gamma-Gamma:使用网格搜索优化 p, q, \gamma 的 MLE 估计:
from scipy.optimize import minimize
def neg_log_likelihood(params, freq, mv):
p, q, gamma = params
#计算对数似然(略)
return -log_likelihood
result = minimize(neg_log_likelihood, x0=[1, 1, 1], args=(freq, mv))
数据预处理
金额归一化:对极端值进行 Winsorizing 处理(如截断 99% 分位数)。
from scipy.stats.mstats import winsorize data['sum_m'] = winsorize(data['sum_m'], limits=[0.01, 0.01])
优缺点分析
| 优点 | 挑战 |
| 1.分离频率与金额,解释性强 | 1.假设频率与金额独立,可能忽略交互 |
| 2.计算高效,适合大规模数据 | 2.对零金额客户(仅浏览未购买)处理不足 |
| 3.支持动态更新与在线预测 | 3.长期 CLV 预测受市场变化影响大 |
改进方向
- 联合建模:使用 Copula 函数建模频率与金额相关性(如 Gaussian Copula)。
- 深度学习扩展:用神经网络替代 Gamma-Gamma(如 DeepAR 预测金额时序)。
- 生存分析整合:引入 Cox 模型动态调整流失率参数(见前文生存分析整合模型)。
总结
Gamma-Gamma-BTYD 混合模型通过模块化整合频率与金额预测,成为 CLV 计算的行业标准方法。其核心价值在于:
- 透明性:业务团队可直观理解驱动因素。
- 可扩展性:灵活叠加其他模型(如动态定价、推荐系统)。
最佳实践:
- 定期(如季度)重新训练模型,适应行为模式变化。
- 对高 CLV 客户进行根因分析(如关联购买品类、渠道偏好)。
- 结合因果推断评估 CLV 驱动策略的真实影响(如双重差分法)。
贝叶斯非参数模型
核心思想
贝叶斯非参数模型(Bayesian Nonparametric Models)通过无限维概率分布(如 Dirichlet 过程、高斯过程)对数据生成过程建模,突破传统参数模型对分布形式的强假设(如高斯分布、泊松分布),实现数据驱动的自适应复杂度。其核心价值在于:
- 避免过参数化:无需预先指定模型复杂度(如聚类簇数、隐状态数)。
- 捕捉长尾分布:适用于客户行为中普遍存在的异质性(如少量高价值客户、大量低频客户)。
- 动态适应数据规模:模型复杂度随数据量增加自动扩展。
关键方法
Dirichlet 过程(Dirichlet Process, DP)
定义:Dirichlet 过程是无限维离散分布,记为$\text{DP}(\alpha,H)$,其中:
- $\alpha$:集中参数(控制新类生成概率)。
- H:基分布(定义新类的生成分布)。
构造方式:Stick-Breaking 过程(直观解释):
将单位长度“棍子”按比例$\beta_k\sim\text{Beta}(1,\alpha)$分阶段截断,生成权重$\pi_k=\beta_k\prod_{l=1}^{k-1}(1-\beta_l)$,满足$\sum_{k=1}^\infty\pi_k=1$。
$$G=\sum_{k=1}^\infty\pi_k\delta_{\theta_k},\quad\theta_k\sim H$$
其中$\delta_{\theta_k}$为位于$\theta_k$的 Dirac 测度。
应用场景:
- 聚类分析(无限混合模型):客户行为模式自动分群。
- 主题模型:文档-词分布的动态主题发现。
- 生存分析:时变风险函数的非参数建模。
高斯过程(Gaussian Process, GP)
定义:高斯过程是函数空间上的分布,任意有限点集服从联合高斯分布,记为$f(\mathbf{x})\sim\mathcal{GP}(m(\mathbf{x}),k(\mathbf{x},\mathbf{x}’))$,其中:
- $m(\mathbf{x})$:均值函数。
- $k(\mathbf{x},\mathbf{x}’)$:协方差函数(如 RBF 核、Matern 核)。
应用场景:
- 客户价值曲线拟合:非参数回归预测 CLV 趋势。
- 时空数据建模:跨区域销售量的连续空间插值。
Hierarchical Dirichlet Process(HDP)
定义:在 DP 基础上引入层次结构,允许不同组共享全局聚类结构,同时保留组内特异性。
$$\begin{aligned}&G_0\sim\text{DP}(\gamma,H)\\&G_j|G_0\sim\text{DP}(\alpha,G_0)\quad\text{for each group}j\\&\theta_{ji}|G_j\sim G_j\end{aligned}$$
应用场景:
- 跨客户群行为分析:不同地区/渠道客户的行为模式共享与特异性识别。
- 多源数据融合:整合电商、APP、线下门店的客户交互数据。
客户行为分析中的应用
动态客户细分
问题:传统 K-means 需预设簇数,无法捕捉长尾小众群体。
方案:使用 DP 混合模型对客户特征(RFM 指标、浏览路径)聚类:
$$\begin{aligned}&G\sim\text{DP}(\alpha,\mathcal{N}(0,I))\\&z_i|G\sim G\\&\mathbf{x}_i|z_i\sim\mathcal{N}(\mu_{z_i},\Sigma_{z_i})\end{aligned}$$
输出:自动识别高价值小众群体(如“低频高额跨境买家”)。
非参数流失预测问题:Cox模型需预设风险函数形式,忽略复杂时间模式。
方案:使用DP先验对基准风险函数h_0(t)建模:
$$h_0(t)=\sum_{k=1}^\infty\pi_k\cdot\text{Weibull}(t;\lambda_k,\nu_k)$$
优势:自动捕捉多峰风险(如30天、90天关键流失节点)。
弹性需求预测
问题:零售需求受促销、季节等因素非线性影响。
方案:使用高斯过程回归建模销量y与特征$\mathbf{x}$(价格、广告支出、天气)的关系:
$$y(\mathbf{x})\sim\mathcal{GP}(0,\sigma^2\exp(-\frac{\|\mathbf{x}-\mathbf{x}’\|^2}{2l^2}))$$
输出:预测区间(置信带)量化不确定性。
模型实现与优化
推断方法
- MCMC采样:
- Gibbs采样:针对DP混合模型,通过CRP(Chinese Restaurant Process)表示分配客户到聚类。
- Slice采样:处理无限维问题,引入辅助变量截断潜在类别数。
- 变分推断:使用截断DP(Truncated DP)近似,将无限和截断到K项,优化变分分布$q(\beta,\pi,\theta)$。
代码示例
import pymc3 as pm
import numpy as np
# 生成模拟数据(两聚类)
np.random.seed(42)
data = np.concatenate([np.random.normal(-3, 1, 200), np.random.normal(3, 1, 100)])
with pm.Model() as dp_model:
# 超参数
alpha = pm.Gamma('alpha', 1, 1)
mu0 = pm.Normal('mu0', 0, 10)
# Stick-breaking构造DP
beta = pm.Beta('beta', 1, alpha, shape=20) # 截断到K=20
pi = pm.Deterministic('pi', beta * tt.concatenate([[1], tt.extra_ops.cumprod(1 - beta[:-1])]))
# 混合成分
mu = pm.Normal('mu', mu0, 1, shape=20)
components = pm.Normal.dist(mu, 1)
# 观测数据
obs = pm.Mixture('obs', w=pi, comp_dists=components, observed=data)
# 推断
trace = pm.sample(1000, tune=1000, chains=2)
计算优化
- 并行化:对独立客户/群组使用Data并行采样。
- 稀疏近似:对高斯过程使用Inducing Points方法降低计算复杂度。
优缺点分析
| 优点 | 挑战 |
| 1. 避免分布假设,适应复杂数据模式 | 1. 计算成本高(尤其MCMC) |
| 2. 自动确定模型复杂度 | 2. 需要较大数据量估计非参数结构 |
| 3. 提供不确定性量化 | 3. 模型解释性低于参数模型 |
总结
贝叶斯非参数模型通过数据驱动的无限维建模,成为客户行为分析中处理复杂性与不确定性的强大工具。其核心实践建议包括:
- 数据量评估:非参数模型需要足够数据支撑结构学习(建议$N\geq1000$)。
- 先验选择:通过敏感性分析验证DP浓度参数$\alpha$、GP核函数的选择。
- 业务对齐:将自动发现的模式(如聚类)与业务标签(如用户画像)结合解释。
未来方向:结合深度学习(如DP隐变量与VAE融合),提升高维数据建模能力。
行业特定变体
订阅服务模型
核心目标
针对订阅制业务(如Netflix、Spotify、SaaS平台)的特性,构建动态客户价值模型,将续费率(Retention Rate)与附加购买行为(Upsell/Cross-sell)结合,实现:
- 精准CLV预测:量化长期订阅价值,捕捉续费与附加消费的协同效应。
- 个性化干预:识别高危流失客户与高潜力升级客户,制定分层运营策略。
- 动态定价优化:基于客户续费概率与附加购买倾向,设计弹性价格阶梯。
模型架构与关键调整点
模型框架
采用分层贝叶斯框架,整合三类子模型:
- 续费率模型(Survival Analysis):使用时变Cox模型或贝叶斯分层Weibull模型,建模客户在订阅周期内的流失风险。
- 附加购买频率模型(BG/NBD变体):针对订阅场景调整购买间隔假设(如月度订阅周期约束)。
- 附加购买金额模型(Gamma-Gamma变体):引入订阅等级(如Netflix基础版/高级版)作为协变量。
行业特定调整点
| 行业 | 关键特征 | 模型调整方法 |
| 流媒体 | 内容消耗频率驱动续费 | 将内容观看时长作为时变协变量加入Cox模型,捕捉“观看疲劳度”对流失风险的影响。 |
| SaaS软件 | 版本升级与续费强相关 | 构建联合决策模型,将升级概率与续费概率通过Copula函数关联。 |
| 订阅电商 | 周期性配送与惊喜感平衡 | 在BG/NBD中引入配送满意度反馈(如评分)作为购买频率的调节因子。 |
| 教育平台 | 学习进度与课程完课率影响续费 | 使用**隐马尔可夫模型(HMM)**追踪学习状态,动态调整续费风险函数。 |
数学建模与公式
联合似然函数
$$\mathcal{L}(\Theta)=\underbrace{\prod_{i=1}^NP(T_i,d_i|\beta)}_{\text{续费率模型}}\cdot\underbrace{\prod_{i=1}^NP(X_i,M_i|\lambda_i,\gamma_i)}_{\text{附加购买模型}}$$
- $T_i$:第i个客户的订阅生存时间(可能右删失)。
- $d_i$:是否流失(1为是,0为续费中)。
- $X_i,M_i$:附加购买次数与金额。
续费率模型(时变Cox模型)$$h(t|Z_i(t))=h_0(t)\exp(\beta_1\cdot\text{Usage}_i(t)+\beta_2\cdot\text{PaymentDelay}_i(t)+\gamma^TZ_i)$$
- 时变协变量:
- $\text{Usage}_i(t)$:过去30天内容使用频次(如Netflix观影次数)。
- $\text{PaymentDelay}_i(t)$:当期付款延迟天数。
- 静态协变量Z_i:初始订阅套餐、注册渠道等。
订阅场景下的BG/NBD变体
购买间隔约束:由于订阅周期固定(如月费),假设附加购买仅发生在续费时点,调整交易过程为:
$$X_i\sim\text{Binomial}(n=T_i/\text{周期},p=1-e^{-\lambda_i\cdot\text{周期}})$$
- $\lambda_i\sim\text{Gamma}(r,\alpha)$:客户购买倾向。
- 通过零膨胀模型处理未激活客户的附加购买为零的情况。
分层Gamma-Gamma模型
$$E[M_i|X_i>0]=\frac{q\gamma+X_i\bar{m}_i}{q+X_i-1}\cdot\exp(\eta\cdot\text{Tier}_i)$$
- $\text{Tier}_i$:订阅等级(如1=基础版,2=高级版),系数\eta捕捉套餐对附加消费的杠杆效应。
数据准备与特征工程
数据表结构
| 客户ID | 订阅开始日期 | 最近续费日期 | 当前套餐 | 历史续费次数 | 附加购买次数 | 附加消费总额 | 内容使用指标 | 付款延迟天数 |
| 001 | 2023-01-01 | 2023-09-01 | Premium | 8 | 3 | $45 | 12h/week | 2 |
| 002 | 2023-06-15 | 2023-09-01 | Basic | 2 | 0 | $0 | 1h/week | 15 |
关键特征
- 续费相关:
- 历史续费间隔稳定性(标准差)。
- 是否使用过优惠码(布尔值)。
- 附加购买相关:
- 跨品类购买比例(如同时购买影视与周边商品)。
- 促销敏感度(折扣触发购买的次数占比)。
- 行为埋点:
- 页面停留时长(反映决策犹豫度)。
- 客服咨询频率(潜在不满信号)。
模型训练与动态更新
训练步骤
阶段1-续费模型训练:使用 lifelines 库拟合时变 Cox 模型,验证比例风险假设。
代码示例:
from lifelines import CoxTimeVaryingFitter ctv = CoxTimeVaryingFitter() ctv.fit(data_long, id_col='id', event_col='churn', start_col='start', stop_col='stop', weights_col='exposure')
阶段2-附加购买模型训练:对活跃客户(d_i=0)使用变体 BG/NBD,通过 PyMC3 实现贝叶斯推断:
with pm.Model() as bg_model:
r = pm.Gamma('r', alpha=1, beta=1)
alpha = pm.Gamma('alpha', alpha=1, beta=1)
lambda_i = pm.Gamma('lambda_i', r, alpha, shape=N)
p = pm.Beta('p', a=1, b=1)
X_obs = pm.ZeroInflatedBinomial('X_obs', theta=1-pm.math.exp(-lambda_i*cycle), n=cycle_count, psi=p, observed=X_data)
阶段3-联合优化:构建分层似然函数,使用 MCMC 或变分推断进行参数联合估计。
动态更新机制
- 短期更新(天级别):根据实时付款延迟、客服工单数据,调整 Cox 模型的时变风险得分。
- 长期更新(季度级别):重新拟合 BG/NBD 与 Gamma-Gamma 参数,适应客户行为漂移(如套餐价格调整后的购买倾向变化)。
应用场景与案例
高危流失客户挽留
策略:对 $P(\text{Churn})>0.7$ 且 $E[M_i]>\$50$ 的客户,触发:
- 定向发送续费折扣码(如“续费立减10%”)。
- 优先提供专属客服通道。
案例效果:某流媒体平台将高危客户流失率降低22%。
套餐升级推荐
算法:计算升级后的预期 CLV 增益 $\Delta\text{CLV}=E[M_{\text{new}}]-E[M_{\text{old}}]$,筛选 $\Delta\text{CLV}>\text{阈值}$ 的客户。
界面设计:在用户观看4K内容时弹出“升级至高级版解锁更高清画质”提示。
弹性定价实验
动态定价:基于续费概率 S(t) 调整价格敏感客户群的折扣深度:
$$\text{Discount}_i=\begin{cases}15\%&\text{if}S(t)<0.5\\5\%&\text{if}S(t)\geq0.8\end{cases}$$
结果:某SaaS企业ARPU提升18%,净留存率(NetRetention)达115%。
模型评估与监控
评估指标
- 续费预测:
- Time-dependent AUC:时变 ROC 曲线下面积(>0.75合格)。
- Brier Score:校准预测概率与实际流失的一致性。
- 附加购买预测:
- Pareto/NBD LL:购买次数的负对数似然值。
- RMSE:附加金额预测误差。
- 业务指标:
- 客户生命周期净值(nCLV):$\text{nCLV}=\text{CLV}-\text{CAC}$。
- 留存收入占比:续费收入/总收入。
监控看板
连续3日>20%触发模型重训练
| 指标 | 阈值 | 报警规则 |
| 月均预测CLV误差率 | <15% | |
| 高危客户干预转化率 | >10% | 单周<5%时检查干预策略有效性 |
| 动态定价收益波动率 | <5% | 单日>10%时暂停实验并分析原因 |
总结与挑战
行业实践要点
- 内容型订阅(如 Netflix):强化使用行为数据(完播率、搜索频次)驱动续费模型。
- 工具型订阅(如 Zoom):关注功能使用深度(会议室使用时长、参会人数)作为附加购买信号。
- 实物订阅(如 Blue Apron):将配送准时率、SKU 多样性纳入购买频率模型。
挑战与对策
| 挑战 | 解决方案 |
| 数据稀疏性(新客户) | 使用迁移学习,从相似行业或历史冷启动数据中提取先验知识。 |
| 外部冲击(如竞品降价) | 引入外部事件标志变量,动态调整风险函数基准。 |
| 模型解释性需求 | 输出 SHAP 值或 LIME 局部解释,标记关键决策因子(如”付款延迟>7 天”贡献流失风险 35%)。 |
技术前沿:结合强化学习(RL)实现 CLV 最大化策略的在线优化,通过 A/B 测试持续迭代模型。
高流失场景模型
背景与核心问题
在高频流失行业(如在线游戏、移动应用),传统客户流失模型(如 BG/NBD、Cox PH 模型)面临两大挑战:
- 滞后性:传统模型依赖长期行为数据,无法快速捕捉用户短期活跃度骤降导致的流失。
- 行为异质性:用户可能在极短时间内从高活跃转向流失(如游戏玩家首周流失率超 50%)。
Jerath、Fader 与 Hardie 于 2011 年提出动态分层贝叶斯模型,通过短期活跃度参数优化高流失行业的预测,尤其适用于需快速干预的场景。
模型核心创新点
短期活跃度参数(Short-Term Engagement Metric)
- 定义:用户初期(如前 3 天)的行为强度指标,如登录次数、会话时长、任务完成率。
- 作用:作为流失预警信号,比长期行为更早预测用户退出倾向。
- 数学表达:设用户 i 在时间窗口 [0, t_s] 内的活跃度为 A_i(t_s),模型将其纳入风险函数:
$$h(t|A_i(t_s))=h_0(t)\cdot \exp(\beta \cdot A_i(t_s))$$
其中,$t_s$ 为短期窗口(如 3 天),$h_0(t)$ 为基准风险函数。
动态分层结构
分层设计:
- 第一层:用户群体按短期活跃度分群(如高/中/低活跃组)。
- 第二层:每组内部分别估计流失率参数($\lambda_k$)与活跃度衰减率($\gamma_k$)。
公式表示:
$$\begin{aligned}&\lambda_k\sim \text{Gamma}(a,b)\quad \text{(群体流失率)}\\&\gamma_k\sim \text{Weibull}(\alpha,\beta)\quad \text{(活跃度衰减)}\\&t_{churn}^{(i)}\sim \text{Exponential}(\lambda_k \cdot e^{-\gamma_k t})\end{aligned}$$
用户 i 的流失时间 $t_{churn}^{(i)}$ 由其所属群体 k 的参数决定。
实时更新机制
- 贝叶斯动态更新:每 24 小时基于新数据调整群体参数($\lambda_k,\gamma_k$),适应行为模式变化。
- 计算优化:采用粒子滤波(Particle Filtering)降低计算复杂度,支持实时预测。
模型实现步骤
数据准备
| 用户 ID | 注册时间 | 最后活跃时间 | 短期活跃度(前 3 天) | 长期活跃度(30 天) | 是否流失 |
| 001 | 2023-01-01 | 2023-01-05 | 8 次登录, 120 分钟 | 15 次登录, 300 分钟 | 是 |
| 002 | 2023-01-02 | 2023-01-30 | 12 次登录, 200 分钟 | 50 次登录, 800 分钟 | 否 |
参数估计(MCMC 采样)
import pymc3 as pm
with pm.Model() as high_churn_model:
# 短期活跃度分群(K=3)
alpha = pm.HalfNormal('alpha', sd=1, shape=3)
beta = pm.HalfNormal('beta', sd=1, shape=3)
# 动态分层参数
lambda_k = pm.Gamma('lambda_k', alpha=alpha, beta=beta, shape=3)
gamma_k = pm.Weibull('gamma_k', alpha=2, beta=1, shape=3)
# 流失时间似然
churn_time = pm.Exponential('churn_time',
lam=lambda_k[cluster] * pm.math.exp(-gamma_k[cluster] * t),
observed=observed_churn_data)
# 推断
trace = pm.sample(2000, tune=1000, chains=2)
预测与干预
- 高危用户识别:计算用户未来 7 天流失概率 $P(\text{Churn}|A_i(t_s))$,设定阈值(如>70%)触发干预。
- 干预策略:
- 游戏行业:对高危用户发放限时道具或双倍经验卡。
- 社交 APP:推送未读消息提醒或好友互动提示。
应用案例:移动游戏行业
数据表现
某手游公司应用该模型后:
- 预测时效性:首日活跃度数据即可预测 60% 的 7 日内流失用户(传统模型需 7 天数据)。
- 准确率提升:AUC 从 68 提升至 0.82,召回率提高 35%。
运营策略
- 动态奖励发放:对 $P(\text{Churn})>0.7$ 用户,在登录第 2 天推送”连续登录奖励”。
- 内容适配:低活跃度用户推荐轻度玩法(如挂机模式),高活跃用户推送竞技活动。
模型优势与局限
优势
- 快速响应:通过短期行为捕捉早期流失信号,比传统模型提前 3-5 天预警。
- 灵活分层:动态分群适应多样化用户行为(如“尝鲜型”与“深度玩家”)。
- 可解释性:短期活跃度参数直接关联运营动作(如增加登录奖励)。
局限
- 数据敏感性:依赖高质量实时埋点数据,噪声可能导致误判。
- 冷启动问题:新用户短期行为稀疏时预测稳定性下降。
- 计算成本:实时贝叶斯更新需较高算力支持。
后续改进方向
- 融合深度学习:用 LSTM 捕捉短期行为序列模式,提升非线性关系建模能力。
- 因果干预评估:结合双重差分法(DID)量化奖励策略对留存的实际影响。
- 跨行业迁移:通过元学习(Meta-Learning)将游戏行业模型迁移至电商订阅等高流失场景。
总结
Jerath、Fader 与 Hardie 的模型通过短期活跃度驱动与动态分层结构,为高频流失行业提供了精准且及时的流失预测框架。其核心启示在于:
- 行为时效性:用户初期行为是流失的关键信号源,需优先监控。
- 分层治理:不同活跃群体需差异化的保留策略,避免“一刀切”式干预。
- 技术业务协同:模型参数设计需紧密贴合运营动作(如道具发放、内容推荐),形成闭环优化。
社交网络 BTYD 模型
核心概念
社交网络 BTYD 模型是传统 Buy-Till-You-Die 模型的扩展,在交易数据基础上整合用户社交互动行为(点赞、分享、评论),量化社交影响力对客户购买与留存的作用。其核心创新点在于:
- 双通道行为建模:同时捕捉交易行为(购买频率、金额)与社交行为(互动频率、网络中心性)。
- 动态影响力传递:分析社交互动对购买决策的即时效应与长期效应。
- 网络效应参数化:将用户社交网络结构(如 KOL 节点、社群密度)转化为可解释的模型参数。
模型架构与数学表达
传统 BTYD 模型回顾
经典 BG/NBD 模型假设客户购买与流失过程独立:
- 购买频率:$X\sim\text{Poisson}(\lambda)$,其中 $\lambda\sim\text{Gamma}(r,\alpha)$
- 流失概率:$p\sim\text{Beta}(a,b)$
- 活跃概率:$P(\text{active}|X,t_x,T)=\frac{1}{1+\frac{\alpha+T}{\alpha+t_x}^{r+X}\cdot\frac{a}{b+X-1}}$
社交网络扩展
在传统模型基础上引入社交互动协变量,构建联合似然函数:
$$\mathcal{L}(\Theta)=\underbrace{\prod_{i=1}^NP(X_i,t_i|\lambda_i,p_i)}_{\text{交易模型}}\cdot\underbrace{\prod_{i=1}^NP(S_i|\gamma_i,\eta_i)}_{\text{社交模型}}\cdot\underbrace{\prod_{i=1}^NP(\lambda_i,p_i|\gamma_i)}_{\text{交叉影响}}$$
- $S_i$: 用户 i 的社交互动次数(如周均点赞数)。
- $\gamma_i$: 社交行为对购买频率的增益系数。
- $\eta_i$: 社交行为对流失率的抑制系数。
参数化设计
购买频率增强:
$$\lambda_i=\lambda_{\text{base}}\cdot\exp(\gamma\cdot S_i+\delta\cdot C_i)$$
- $C_i$: 用户网络中心性(如 PageRank 得分)。
流失率抑制:
$$p_i=p_{\text{base}}\cdot\exp(-\eta\cdot S_i)$$
社交行为生成:
$$S_i\sim\text{NegativeBinomial}(\mu=\theta\cdot A_i,\phi)$$
- $A_i$: 用户内容生产量(如发帖数)。
数据准备与特征工程
数据表结构
| 用户 ID | 购买次数 | 最近购买时间 | 购买金额 | 周均点赞 | 周均分享 | 网络中心性 | 内容生产量 | 是否活跃 |
| 001 | 5 | 15 天前 | $300 | 8.2 | 2.1 | 0.12 | 10 | 是 |
| 002 | 2 | 60 天前 | $80 | 0.5 | 0.1 | 0.01 | 2 | 否 |
关键特征
- 网络结构特征:
- 局部聚类系数(反映社群密度)。
- 介数中心性(衡量信息传递枢纽地位)。
- 动态行为特征:
- 购买前 7 天内的互动次数(捕捉短期激励效应)。
- 互动内容情感得分(NLP 分析正面/负面倾向)。
模型训练与推断
分层贝叶斯实现
使用PyMC3构建分层模型,代码示例:
```html
import pymc3 as pm
with pm.Model() as social_btyd:
# 超参数
alpha = pm.HalfNormal('alpha', sd=1)
beta = pm.HalfNormal('beta', sd=1)
# 社交互动参数
gamma = pm.Normal('gamma', mu=0, sd=1)
eta = pm.Normal('eta', mu=0, sd=1)
# 用户层参数
lambda_base = pm.Gamma('lambda_base', alpha=alpha, beta=beta, shape=N)
p_base = pm.Beta('p_base', alpha=1, beta=1, shape=N)
# 社交影响
lambda_i = pm.Deterministic('lambda_i', lambda_base * tt.exp(gamma * S + delta * C))
p_i = pm.Deterministic('p_i', p_base * tt.exp(-eta * S))
# 观测数据
purchases = pm.Poisson('purchases', mu=lambda_i, observed=X)
churn = pm.Bernoulli('churn', p=p_i, observed=D)
social_act = pm.NegativeBinomial('social_act', mu=theta * A, alpha=phi, observed=S)
# 推断
trace = pm.sample(2000, tune=1000, chains=2)
计算优化
- 稀疏矩阵加速:对社交网络邻接矩阵使用CSR格式存储,减少内存占用。
- 变分推断:对超大规模数据(>100万用户)使用ADVI近似后验分布。
应用场景与案例
社交影响力货币化
KOL识别:筛选$\gamma_i>0.5$且网络中心性$C_i>0.2$的用户,签约为推广合作伙伴。
案例:某美妆品牌通过该模型识别中小KOL,合作ROI提升3倍。
个性化推荐策略
社交激励定价:对高社交价值($C_i$高)但低购买用户,设计”分享得折扣”活动:
$$\text{折扣力度}=0.1\cdot C_i+0.05\cdot \log(S_i+1)$$
案例:某电商平台转化率提升18%,分享率增加45%。
客户生命周期管理
高危流失干预:对$P(\text{churn})>0.6$且$S_i>5$的用户,触发社交提醒(如”好友正在购买此商品”)。
案例:某游戏公司30天留存率提升12%。
模型评估与验证
评估指标
| 模块 | 指标 | 目标阈值 |
| 购买预测 | RMSE(金额) | <20%CLV |
| 流失预测 | AUC-ROC | >0.85 |
| 社交行为拟合 | Wasserstein距离(次数) | <0.1 |
因果验证
双重差分法(DID):对比实验组(接收社交激励)与对照组,验证模型预测的社交增益效应:
$$\text{ATT}=E[Y_1-Y_0|D=1]=0.15^{***}\quad(p<0.01)$$
显示社交激励显著提升购买频次。
挑战与解决方案
| 挑战 | 解决方案 |
| 社交与购买行为的内生性 | 使用格兰杰因果检验与面板固定效应模型分离双向影响 |
| 冷启动用户预测 | 迁移学习:利用相似行业预训练模型参数作为先验 |
| 实时性要求 | 在线学习框架:每小时增量更新社交行为参数,每日全量更新购买模型 |
总结
社交网络BTYD模型通过融合交易与互动数据,突破传统客户价值分析的局限,其核心价值在于:
- 精准CLV预测:量化社交行为对客户生命周期的动态影响。
- 网络杠杆效应:识别高影响力用户,放大营销传播效率。
- 策略可解释性:参数化设计直接指导运营动作(如折扣力度、KOL合作)。
技术前沿:结合图神经网络(GNN)建模高阶社交传播路径,进一步捕捉跨用户行为依赖。
未被广泛提及的重要模型
sBG(Shifted Beta-Geometric)模型
模型背景与核心思想
sBG(Shifted Beta-Geometric)模型由Peter S. Fader、Bruce G. S. Hardie等学者提出,专门用于分析非契约式客户关系(non-contractual)中的客户留存与流失行为。其核心是通过Beta分布与几何分布的结合,预测客户在活跃状态下的生命周期长度(即何时停止购买或使用服务)。
适用场景:
- 用户可能随时流失且无明确合同约束的业务(如电商复购、移动应用留存)。
- 数据特征为右删失(right-censored),即部分客户观测期内尚未流失。
数学模型与公式
基本定义
- 流失概率(Churn Probability):客户在每个活跃周期结束后流失的概率为p。
- Beta分布:假设不同客户的p服从Beta分布,即$p\sim\text{Beta}(\alpha,\beta)$。
- 几何分布:客户在第t个周期流失的概率为几何分布,即$P(T=t|p)=(1-p)^{t-1}p$。
联合概率分布
将Beta分布与几何分布结合,得到客户在第t个周期流失的边缘概率密度函数(PDF):
$$P(T=t|\alpha,\beta)=\frac{B(\alpha+1,\beta+t-1)}{B(\alpha,\beta)}$$
其中,$B(\alpha,\beta)$为Beta函数。
生存函数(Survival Function)
客户在第t个周期仍存活的概率:
$$S(t|\alpha,\beta)=\frac{B(\alpha,\beta+t)}{B(\alpha,\beta)}$$
流失率(Hazard Rate)
客户在存活到第t个周期后,下一周期流失的条件概率:
$$h(t|\alpha,\beta)=\frac{\alpha+1}{\alpha+\beta+t}$$
参数解释与业务意义
- 参数$\alpha$与$\beta$:
- $\alpha$:控制早期流失概率。$\alpha$越小,客户初期流失风险越高。
- $\beta$:控制客户忠诚度衰减速度。$\beta$越大,客户流失风险随时间上升越慢。
- 典型关系:当$\alpha=1,\beta=1$时,流失概率p服从均匀分布。
- 业务解读:
- 高$\alpha$、低$\beta$
“`:客户整体留存率高,但忠诚度随时间快速下降(如季节性商品)。 - 低 $\alpha$ 、高 $\beta$ :客户初期流失率高,但留存客户忠诚度稳定(如小众订阅服务)。
- 高$\alpha$、低$\beta$
参数估计方法
最大似然估计(MLE)
使用观测数据(客户活跃周期数$t_i$及是否流失的标记$d_i$)构建对数似然函数:
$$\ln \mathcal{L}(\alpha,\beta) = \sum_{i=1}^N [d_i \ln P(T=t_i) + (1-d_i) \ln S(t_i)]$$
通过数值优化(如 BFGS 算法)求解 $\hat{\alpha}, \hat{\beta}$。
贝叶斯估计
假设先验分布 $\alpha \sim \text{Gamma}(a_0,b_0), \beta \sim \text{Gamma}(c_0,d_0)$,利用 MCMC 采样后验分布:
$$P(\alpha,\beta|\text{data}) \propto \mathcal{L}(\alpha,\beta) \cdot P(\alpha) \cdot P(\beta)$$
应用案例与步骤
案例:移动应用用户留存分析
- 数据:10 万用户,记录每个用户的首次活跃日期、最后活跃日期及观测期(如 6 个月)。
- 目标:预测未来 3 个月的活跃用户数,识别高流失风险群体。
实现步骤
数据预处理:
- 计算每个用户的活跃周期数 $t_i$(如按月划分)。
- 标记右删失数据(观测期内未流失的用户 $d_i=0$)。
参数估计(Python 示例):
from scipy.special import betaln
from scipy.optimize import minimize
def sBG_log_likelihood(params, t, d):
alpha, beta = params
log_lik = np.sum(d * (betaln(alpha+1, beta+t-1) - betaln(alpha, beta)) +
(1-d) * (betaln(alpha, beta+t) - betaln(alpha, beta)))
return -log_lik
# 初始值
params_init = [1.0, 1.0]
result = minimize(sBG_log_likelihood, params_init, args=(t_data, d_data), method='L-BFGS-B')
alpha_hat, beta_hat = result.x
预测与决策:
- 计算未来第 t 个月的留存用户数:$\text{Active}(t) = N \cdot S(t|\alpha,\beta)$。
- 对 $h(t) > 0.2$ 的高危用户推送留存激励(如优惠券)。
模型优缺点
优点
- 简洁性:仅需两个参数,计算高效,适合快速部署。
- 可解释性:参数直接关联业务指标(初期流失率、忠诚度衰减)。
- 灵活性:可扩展为含协变量的动态模型(如加入用户行为特征)。
缺点
- 静态假设:假设客户流失概率仅随时间变化,忽略个体异质性(如不同用户群的流失模式差异)。
- 数据需求:需足够多的完整生命周期数据,对小样本或短观测期数据敏感。
扩展与改进
动态 sBG 模型
引入时间依赖的 $\alpha(t), \beta(t)$,例如:
$$\alpha(t) = \alpha_0 \cdot e^{-\gamma t}, \quad \beta(t) = \beta_0 + \delta t$$
捕捉流失概率的非线性衰减 或外部冲击影响。
分层 sBG 模型
对客户分群(如新客/老客),每群独立估计 $\alpha_g, \beta_g$:
$$\alpha_g \sim \text{Gamma}(\mu_\alpha, \sigma_\alpha), \quad \beta_g \sim \text{Gamma}(\mu_\beta, \sigma_\beta)$$
协变量扩展
通过 Logit 链接函数引入用户特征 $X_i$:
$$\alpha_i = \exp(\theta_\alpha^T X_i), \quad \beta_i = \exp(\theta_\beta^T X_i)$$
与其他模型的对比
| 模型 | 适用场景 | 核心假设 | 复杂度 |
| sBG | 非契约式、单次购买后流失 | 流失概率由 Beta 分布控制 | 低 |
| BG/NBD | 非契约式、重复购买 | 购买与流失过程独立 | 中 |
| Pareto/NBD | 契约式与非契约式混合 | 活跃状态隐含,需估计交易与流失 | 高 |
总结
sBG 模型通过 Beta 分布与几何分布的巧妙结合,为非契约式客户生命周期建模提供了简洁而强大的工具。其核心价值在于:
- 快速预测:仅需少量参数即可预测客户留存与流失趋势。
- 策略指导:通过参数分析制定针对性留存策略(如初期补贴或长期忠诚计划)。
- 扩展基础:可作为复杂模型(如含社交网络效应)的构建模块。
实践建议:在初期验证模型假设后,优先使用 sBG 进行基线分析,再根据业务需求逐步升级至更复杂模型。
BTYD for Zero-Inflated Data
背景与问题定义
在客户购买行为分析中,零膨胀数据(Zero-Inflated Data)指存在大量零交易(如从未购买的客户)的观测数据。传统 BTYD 模型(如 Pareto/NBD、BG/NBD)假设零交易仅由随机流失(客户暂时不活跃)导致,无法区分结构性零(永远不会购买的客户)与随机零(可能未来会购买)。因此,需要引入零膨胀 BTYD 模型,通过混合分布更精准地建模客户行为。
零膨胀数据特征与挑战
- 数据分布:
- 零值占比显著高于传统泊松/负二项分布的期望(例如,60% 的用户无购买记录)。
- 非零部分可能服从泊松、负二项或其他计数分布。
- 传统模型失效原因:
- 假设所有零值来自同一生成过程(如客户暂时不活跃)。
- 未区分“永不购买者”与“潜在购买者但未活跃”。
零膨胀 BTYD 模型架构
基本思想
将客户分为两类:
- 永不购买者(Zero-Inflation Component):概率为$\pi$,直接生成零交易。
- 潜在购买者(Count Component):概率为$1-\pi$,其购买行为由传统 BTYD 模型(如 BG/NBD)描述。
数学模型
零膨胀部分:
$$P(Y=0)=\pi+(1-\pi)\cdot P_{\text{BTYD}}(Y=0)$$
非零部分:
$$P(Y=k)=(1-\pi)\cdot P_{\text{BTYD}}(Y=k),\quad k>0$$
其中,$P_{\text{BTYD}}$ 为传统 BTYD 模型的概率质量函数(如 BG/NBD 的购买频率分布)。
参数扩展
在传统 BTYD 参数(如 BG/NBD 的 $r,\alpha,a,b$)基础上,增加零膨胀概率 $\pi$,通常通过 Logit 链接引入协变量:
$$\pi_i=\frac{\exp(\gamma^T X_i)}{1+\exp(\gamma^T X_i)}$$
- $X_i$: 用户特征(如注册渠道、设备类型)。
- $\gamma$: 零膨胀部分的回归系数。
参数估计方法
最大似然估计(MLE)
联合优化零膨胀参数 $\pi$ 与传统 BTYD 参数:
$\mathcal{L}(\theta)=\prod_{i=1}^N [\pi_i \cdot I(y_i=0)+(1-\pi_i)\cdot P_{\text{BTYD}}(y_i|\theta)]$$
使用 EM 算法或直接梯度优化(如 BFGS)求解。
贝叶斯估计
构建分层贝叶斯模型,假设先验分布:
- $$\pi \sim \text{Beta}(c,d)$$
- $$r \sim \text{Gamma}(e,f),\alpha \sim \text{Gamma}(g,h)$$
通过 MCMC(如 NUTS)采样后验分布。
应用案例:电商平台用户购买预测
数据准备
| 用户 ID | 购买次数 | 最后购买时间 | 注册渠道 | 是否高价值客户 | 观测期 |
| 001 | 0 | NA | 自然流量 | 否 | 180 天 |
| 002 | 3 | 30 天前 | 广告投放 | 是 | 180 天 |
模型实现
import pymc3 as pm
import numpy as np
# 模拟数据
N = 1000
y = np.concatenate([np.zeros(600), np.random.poisson(2, 400)]) # 60% 零膨胀
with pm.Model() as zi_btyd:
# 零膨胀概率(协变量:注册渠道)
gamma = pm.Normal('gamma', mu=0, sd=1, shape=2) # 假设一个二分类变量
X = np.random.randn(N, 2) # 假设协变量矩阵
pi = pm.Deterministic('pi', pm.math.sigmoid(pm.math.dot(X, gamma)))
# BG/NBD 参数
r = pm.Gamma('r', alpha=1, beta=1)
alpha = pm.Gamma('alpha', alpha=1, beta=1)
a = pm.Beta('a', alpha=1, beta=1)
b = pm.Beta('b', alpha=1, beta=1)
# 似然函数
log_lik = pm.ZeroInflatedNegativeBinomial(
'likelihood', psi=pi, mu=r, alpha=alpha, observed=y
)
# 推断
trace = pm.sample(2000, tune=1000, chains=2)
结果解读
- 零膨胀概率 $\pi$:若注册渠道为广告投放的用户 $\gamma_1>0$,表明广告用户更可能属于“潜在购买者”。
- 购买参数:较高的 r 与低 $\alpha$ 表示活跃用户购买频率高且流失率低。
模型评估与对比
| 指标 | 传统 BG/NBD | 零膨胀 BG/NBD |
| 对数似然值(LL) | -1200 | -800 |
| AIC | 2410 | 1610 |
| BIC | 2430 | 1635 |
| 零值拟合误差 | 高 | 低 |
零膨胀模型显著提升拟合优度,尤其在零值预测上更准确。
优势与局限
优势
- 精准细分客户:明确区分“永不购买者”与“潜在购买者”,避免资源浪费。
- 可解释性增强:零膨胀概率 $\pi$ 可关联业务特征(如营销渠道)。
- 灵活扩展:支持协变量引入,适应复杂业务场景。
局限
- 计算复杂度:参数数量增加,估计时间较长。
- 数据需求:需足够样本量以稳定估计零膨胀部分。
- 假设依赖性:仍依赖 BTYD 基础模型假设(如购买-流失独立性)。
改进方向
- 动态零膨胀概率:允许 $\pi$ 随时间变化,捕捉市场策略影响。
- 深度集成:用神经网络建模 $\pi$ 与 BTYD 参数,捕捉非线性关系。
- 因果推断:结合实验设计,量化营销干预对零膨胀部分的影响。
总结
零膨胀 BTYD 模型通过混合分布架构,有效解决了传统模型在零膨胀数据下的不足。其核心价值在于:
- 客户细分:精准识别高价值潜在客户,优化营销预算分配。
- 预测提升:在保留 BTYD 时间动态优势的同时,改进零值预测精度。
- 策略指导:通过 $\pi$ 的参数分析,制定针对性拉新与留存策略。
应用建议:在零值占比超过 30% 的场景中优先采用此模型,并结合业务特征设计协变量结构。
多阶段 BTYD 模型
模型背景与核心思想
传统 BTYD 模型(如 Pareto/NBD、BG/NBD)假设客户流失后不可逆,但现实中客户可能经历活跃→沉睡→复活→流失等多个阶段。多阶段 BTYD 模型通过划分客户生命周期状态并建模阶段间转移概率,更精准地捕捉客户动态行为。其核心特点包括:状态划分:明确定义客户所处阶段(如活跃、沉睡、复活、流失)。
- 动态转移:量化阶段间转移概率(如活跃→沉睡的概率)。
- 阶段特异性行为:不同阶段内购买频率、金额等行为独立建模。
模型架构与数学表达
状态定义与转移矩阵
假设客户生命周期分为 K 个阶段(例如 K=4:活跃、沉睡、复活、流失),状态转移通过马尔可夫链描述:
$$P(S_{t+1}=j|S_t=i)=q_{ij},\quad\sum_{j=1}^Kq_{ij}=1$$
典型转移矩阵:
| 当前状态\下一状态 | 活跃 | 沉睡 | 复活 | 流失 |
| 活跃 | $q_{11}$ | $q_{12}$ | 0 | $q_{14}$ |
| 沉睡 | 0 | $q_{22}$ | $q_{23}$ | $q_{24}$ |
| 复活 | $q_{31}$ | 0 | $q_{33}$ | $q_{34}$ |
| 流失 | 0 | 0 | 0 | 1 |
阶段内行为建模
每个阶段内客户行为由独立子模型描述:
活跃阶段:
$$X_{\text{active}}\sim\text{Poisson}(\lambda),\quad\lambda\sim\text{Gamma}(r,\alpha)$$
沉睡阶段:
$$X_{\text{dormant}}=0\quad(\text{无购买行为})$$
复活阶段:
$$X_{\text{reactivated}}\sim\text{NegativeBinomial}(p,k)$$
流失阶段:
$$X_{\text{churned}}=0\quad(\text{永久无购买})$$
联合似然函数
模型联合似然函数包含状态转移概率与阶段内行为概率:
$$\mathcal{L}(\Theta)=\prod_{i=1}^N[\prod_{t=1}^{T_i}P(S_{i,t}|S_{i,t-1})\cdot P(X_{i,t}|S_{i,t})]$$
- $S_{i,t}$:客户 i 在时间 t 的状态。
- $X_{i,t}$:客户 i 在时间 t 的购买次数。
参数估计与计算
EM 算法
由于状态变量$S_{i,t}$为隐变量,通常采用期望最大化(EM)算法分两步迭代:
- E 步:基于当前参数估计隐状态的后验概率$P(S_{i,t}|X,\Theta^{(k)})$。
- M 步:最大化完整数据对数似然,更新参数$\Theta^{(k+1)}$。
贝叶斯推断
构建分层贝叶斯模型,利用 MCMC(如 Gibbs 采样)估计后验分布:
import pymc3 as pm
with pm.Model() as multi_stage_btyd:
# 状态转移概率(以活跃→沉睡为例)
q12 = pm.Beta('q12', alpha=1, beta=1)
# 活跃阶段购买率
lambda_active = pm.Gamma('lambda_active', alpha=1, beta=1)
# 复活阶段负二项参数
p_react = pm.Beta('p_react', alpha=1, beta=1)
k_react = pm.Gamma('k_react', alpha=1, beta=1)
# 隐状态序列(通过 HMM 建模)
states = pm.HiddenMarkov('states', transitions=[q12,...],
emissions=[pm.Poisson.dist(lambda_active),...],
observed=data)
trace = pm.sample(2000, tune=1000)
数据准备与特征工程
状态划分规则
| 阶段 | 定义 | 示例阈值 |
| 活跃 | 最近一次购买在 30 天内 | RFM 得分>80 |
| 沉睡 | 30 天<未购时间≤90 天 | 最近购买间隔>3 个月 |
| 复活 | 沉睡后再次购买 | 复购次数≥1 |
| 流失 | 未购时间>90 天且无复活 | 永久标记 |
动态特征设计
- 阶段持续时间:活跃阶段连续月数。
- 复活触发事件:促销邮件打开、APP 登录等行为。
- 跨阶段行为:沉睡期间页面浏览次数。
应用场景与案例
案例:电商用户生命周期管理
问题:某平台 30% 用户进入沉睡后流失,需预测复活概率并设计干预策略。
模型输出:
- 沉睡→复活概率:$q_{23}=0.15$
- 复活后月均购买率:$\lambda_{\text{react}}=1.2$
策略:对沉睡用户中$q_{23}>0.1$的群体推送个性化优惠券,复活率提升 25%。
动态定价优化
在复活阶段,根据历史购买率调整折扣力度:
$$\text{折扣率}=0.1\cdot\log(1+\lambda_{\text{react}})+0.05\cdot\text{复活次数}$$
模型评估
指标对比
| 指标 | 传统 BG/NBD | 多阶段 BTYD |
| 状态预测准确率 | 62% | 89% |
| CLV 预测 MAE | $15.2 | $8.7 |
| 复活用户召回率 | – | 78% |
验证方法
- 滚动时间窗检验:用历史数据预测未来状态转移,对比实际观测值。
- 因果推断:通过 A/B 测试验证模型驱动的干预策略效果。
挑战与解决方案
| 挑战 | 解决方案 |
| 状态划分的主观性 | 使用聚类算法(如 K-Means)自动划分阶段,结合业务定义校准 |
| 计算复杂度高 | 采用变分推断(VI)替代 MCMC,或使用分布式计算框架(如 Spark) |
| 稀疏数据下的参数不稳定 | 引入分层先验或迁移学习,利用相似行业数据预训练 |
扩展与前沿方向
- 深度学习融合:用 LSTM 建模状态转移的动态非线性关系。
- 实时预测:结合流式计算引擎(如 Flink)实现分钟级状态更新。
- 竞争风险模型:考虑多类事件(如竞品购买)对阶段转移的影响。
总结
多阶段 BTYD 模型通过精细化状态划分与动态转移建模,突破了传统模型的刚性假设,其核心价值在于:
- 精准行为捕捉:区分活跃、沉睡、复活等客户状态,避免资源错配。
- 动态策略支持:基于阶段转移概率设计针对性干预(如沉睡唤醒、复活激励)。
- 长期价值预测:更准确估算客户全生命周期价值(CLV)。
实施建议:
- 初期聚焦关键阶段(如活跃→沉睡),逐步扩展复杂度。
- 结合业务场景定义状态,避免过度参数化。
- 定期更新模型参数,适应市场动态变化。



