统计学基础之概率分布

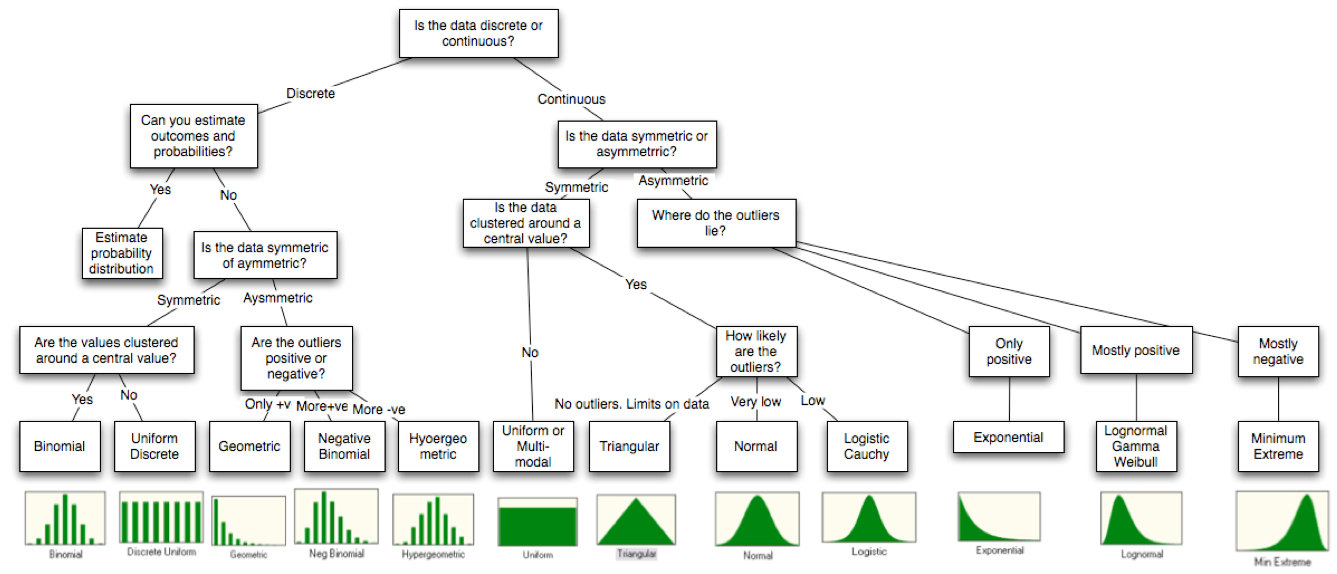
什么是概率分布？

概率分布是数学统计中的一个概念，它描述了一个或多个随机变量在各个可能取值上的概率。这些取值可能是离散的，也可能是连续的。

• 如果是离散的随机变量，我们通常会使用概率质量函数（probability mass function）来描述概率分布。比如，掷一枚公正的骰子，每个面出现的概率都是1/6。
• 如果是连续的随机变量，我们通常会使用概率密度函数（probability density function）来描述概率分布。比如，正态分布（也叫高斯分布）就是一个常见的连续概率分布，其形状呈钟形，可以描述许多自然现象和统计数据。

每个概率分布都有自己的期望值（均值）和方差（表示数据分散程度）。概率分布是概率论和统计学中非常核心的概念，对于进行数据分析、建立统计模型、理解机器学习算法都非常重要。

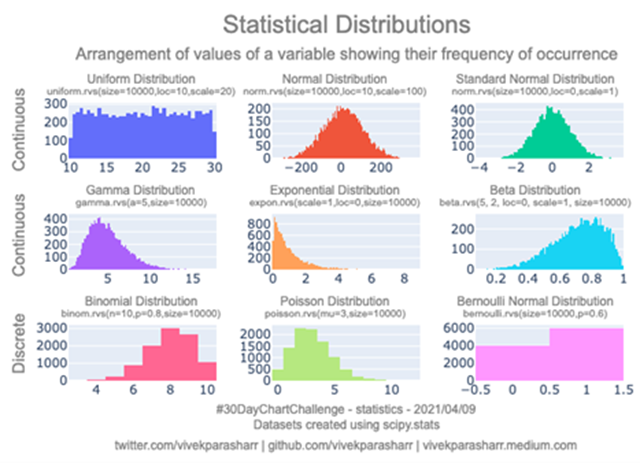
概率分布主要分为两大类：离散概率分布和连续概率分布。

离散概率分布

离散概率分布描述的是离散随机变量的概率分布，即这类随机变量的取值是可数的。常见的离散概率分布包括：

• 伯努利分布（Bernoulli distribution）：随机变量只有两个可能的结果，通常用来描述单次实验成功或失败的情形，例如抛一次硬币。
• 二项分布（Binomial distribution）：描述在固定次数的独立伯努利实验中成功的次数，比如抛十次硬币得到正面的次数。
• 泊松分布（Poisson distribution）：用来描述在一定时间或空间内发生某个事件的次数，当这些事件以固定的平均速率且相互独立地随机发生时。
• 几何分布（Geometric distribution）：描述在一系列独立的伯努利试验中，得到第一个成功所需的试验次数。
• 超几何分布（Hypergeometric distribution）：与二项分布类似，但是在不放回的情况下进行抽样时使用。
• 负二项分布（Negative binomial distribution）：扩展了几何分布，描述在一系列独立的伯努利试验中，得到预定数量的成功所需的试验次数。

连续概率分布

连续概率分布描述的是连续随机变量的概率分布，即这类随机变量的取值是无限不可数的。常见的连续概率分布包括：

• 均匀分布（Uniform distribution）：在区间[a,b]内的每一个数出现的概率是相等的。
• 正态分布（Normal distribution）：也称高斯分布，其概率密度函数呈钟形，是统计学中最著名的概率分布。
• 指数分布（Exponential distribution）：描述了独立随机事件发生的时间间隔。
• 伽马分布（Gamma distribution）：指数分布的一种推广，用于描述多个独立事件发生所需的时间总和。
• 贝塔分布（Beta distribution）：定义在(0,1)区间的随机变量的分布，用于模型概率的概率。
• 卡方分布（Chi-squared distribution）：用于估计一个正态分布的样本方差相对于真实方差的质量。

这些分布各有其特点和适用的场合，了解和识别这些分布在数据分析和统计推断中扮演着重要的角色。

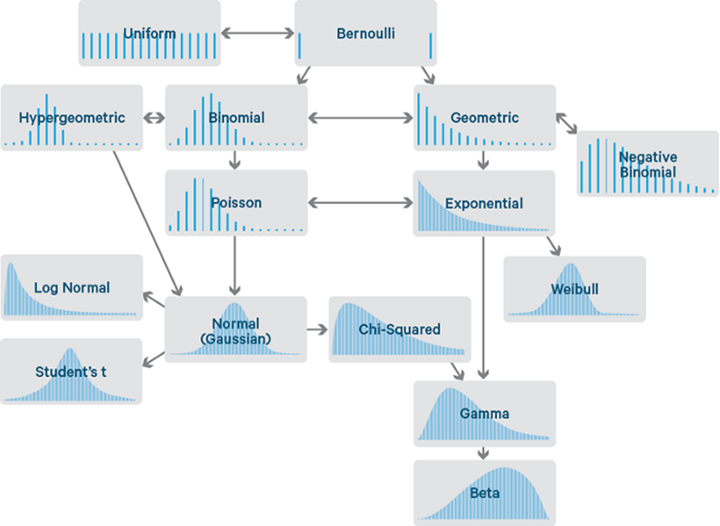
常见离散概率分布简介

伯努利分布（Bernoulli distribution）

伯努利实验（Bernoulli trial）是概率论和统计学中的一个基本概念，它指的是一个只有两个可能结果的单次随机实验。这两个结果通常被称为“成功”和“失败”，其中“成功”的概率是固定的，用(p)表示；相应地，“失败”的概率则是(1-p)。伯努利实验是二项分布的基础，并且是很多其他统计模型的构建块。

伯努利实验的特点：

• 结果只有两种可能：成功或失败。
• 每次实验是独立的，即每次的结果不影响其他实验的结果。
• “成功”的概率p在每次实验中都是相同的。

伯努利分布（Bernoulli distribution）：

伯努利分布（Bernoulli distribution）是描述单次伯努利实验结果的概率分布。如果随机变量(X)服从伯努利分布，那么X只能取两个值：0（代表失败）或1（代表成功）。它的概率质量函数（PMF）可以写为：

$$P(X=x)=\begin{cases}p&\text{if}x=1\\1-p&\text{if}x=0\end{cases}$$

其中p是实验结果为成功的概率。

期望值和方差：

由于伯努利分布非常简单，它的期望值（mean）和方差（variance）也很容易计算。

• 期望值E[X]：成功的概率，即p。
• 方差Var[X]：成功的概率与失败的概率的乘积，即p(1-p)。

示例：

抛一枚硬币就是一个典型的伯努利实验，假设硬币是公平的，那么得到正面（成功，X=1）的概率是0.5，得到反面（失败，X=0）的概率也是0.5。

应用：

伯努利实验及其分布在各种领域都有应用，例如在心理学研究中，一个实验的结果可能是一个受试者答对或答错一个问题；在生物学中，一个植物的种子发芽或不发芽；在质量控制中，一个产品合格或不合格，等等。了解伯努利实验及其分布对于理解更复杂的分布，如二项分布和泊松分布，非常重要，因为这些复杂的分布往往是在多次伯努利实验的基础上定义的。

二项分布（Binomial distribution）

二项分布（Binomial distribution）是一种离散概率分布，用于描述在给定的独立实验次数中成功的次数，其中每次实验成功的概率都是固定的。二项分布的名字来自于二项式定理，因为它的每个随机变量的可能结果的概率可以用二项式系数来表示。

二项分布的特性：

• 组成二项分布的每次实验（或者试验）都是独立的。
• 每次实验的结果只有两种可能：成功或失败。
• 每次实验成功的概率是固定的，记作p。
• 实验会进行固定的n次。

二项分布的概率质量函数（PMF）：

如果随机变量X服从参数为n和p的二项分布，那么X的概率质量函数可以表示为：

$$P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}$$

其中，

• $\binom{n}{k}$是组合数，也就是从n次试验中选出k次成功的所有可能方式的数量，计算公式为$\frac{n!}{k!(n-k)!}$。
• $p^k$是k次成功的概率，
• $(1-p)^{n-k}$是$n-k$次失败的概率。

期望值和方差：

二项分布的这两个参数可以用来计算期望值（平均值）和方差（数据分散程度）。

• 期望值E[X]：实验进行n次时，预期的成功次数。它等于实验次数与单次成功概率的乘积，即np。
• 方差Var[X]：描述成功次数的变异程度。它等于实验次数与单次成功概率与失败概率的乘积，即np(1-p)。

示例：

假设你掷了一个公正的硬币（成功概率(p=0.5)10次，想要知道恰好有3次正面朝上（成功）的概率。这里n=10，k=3，所以概率是：

$$P(X=3)=\binom{10}{3}(0.5)^3(1-0.5)^{10-3}$$

计算上述概率需要计算组合数，然后将其乘以相应概率的幂。

应用：二项分布在现实世界的许多领域都有应用，包括质量控制、医疗试验、生物学测试、投资风险评估等。了解二项分布对于数据分析和统计推断至关重要，因为它提供了一种量化不确定性和变异性的方法。

泊松分布（Poisson distribution）

泊松分布（Poisson distribution）是离散概率分布的一种，命名自法国数学家西莫恩·德尼·泊松。它适用于描述在固定的时间间隔、空间区域或者其他特定条件下，发生某种随机事件的次数的概率分布，而这些事件是相互独立的，并且以恒定的平均速率发生。

泊松分布的特点：

• 描述在一定时间或空间内发生某个事件的次数。
• 事件在不同的时间或空间是独立的。
• 事件发生的平均速率（或平均发生次数）是已知的，并且在观察期内是恒定的。
• 事件在非常短的时间或空间内同时发生两次的概率几乎为零。

泊松分布的概率质量函数（PMF）：

如果随机变量(X)服从参数为$\lambda$（事件的平均发生率）的泊松分布，那么X在实际时间或者空间内发生k次事件的概率可以通过以下概率质量函数计算：

$$P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}$$

其中：

• $\lambda$是单位时间或单位空间内平均发生次数。
• e是自然对数的底数（约等于71828）。
• k是可能观察到的事件数，可以取0,1,2,…

期望值和方差：

泊松分布的期望值和方差相等，都等于$\lambda$：

• 期望值E[X]：$\lambda$
• 方差Var[X]：$\lambda$

示例：

假设某银行的柜台每小时平均接待10位顾客，我们想知道在下一个小时内恰好接待7位顾客的概率。在这里，$\lambda=10$，k=7，所以概率是：

$$P(X=7)=\frac{10^7e^{-10}}{7!}$$

应用：

泊松分布在各个领域都有广泛的应用，例如：

• 电话呼叫中心每小时接到的呼叫数。
• 一段时间内网站的访问次数。
• 某个时间段内公共汽车站的乘客到达数量。
• 放射性物质衰变产生的粒子数。

泊松分布是处理和分析稀有事件的概率分布，尤其在事件的平均发生率已知的情况下非常有用。它也常用于逼近二项分布，特别是在二项分布的试验次数非常大，而成功概率p很小的情况下。

几何分布（Geometric distribution）

几何分布（Geometric distribution）是离散概率分布的一种，用于描述在一系列独立的伯努利试验中，获得第一次成功所需的试验次数。每次试验都只有两个可能的结果：成功或失败，而成功的概率在每次试验中都是相同的。

几何分布的特点：

• 每个试验都是独立的。
• 每次试验的成功概率是相同的，记作p。
• 关心的是进行多少次试验才能得到第一个成功。

存在两种不同的几何分布定义方式，根据定义，随机变量可以取值为：

• 数学定义1：随机变量X表示第一次成功之前失败的次数。在这种情况下，X可以取值(0,1,2,…)。
• 数学定义2：随机变量Y表示得到第一次成功时的试验次数。在这种情况下，Y可以取值(1,2,3,…)。

概率质量函数（PMF）：

对于第一种定义，随机变量X的概率质量函数为：

$$P(X=k)=(1-p)^kp$$

对于第二种定义，随机变量Y的概率质量函数为：

$$P(Y=k)=(1-p)^{k-1}p$$

在这两个公式中：

• k是失败次数（第一种定义）或试验次数（第二种定义）。
• p是每次试验中成功的概率。
• (1-p)是每次试验中失败的概率。

期望值和方差：

对于几何分布，期望值和方差可以分别用以下公式计算：

• 期望值（对于Y）：$E[Y]=\frac{1}{p}$
• 方差（对于Y）：$Var[Y]=\frac{1-p}{p^2}$

示例：

假设你在玩掷硬币游戏，硬币是公平的，所以正面朝上（成功）的概率p是0.5。你想知道，平均需要掷几次硬币才能得到第一次正面朝上。

根据几何分布的期望值公式：($E[Y]=\frac{1}{p}$，在这里p=0.5，所以E[Y]=2。这意味着平均你需要掷两次硬币才能得到第一个正面朝上。

应用：

几何分布在多个领域有应用，包括但不限于：

• 在质量控制中，它可以用来模拟寻找第一个有缺陷的产品所需的检查数量。
• 在生物学研究中，它可以用来估计某种基因突变出现的频率。
• 在市场营销研究中，几何分布可以用来估计顾客购买产品之前的浏览次数。

总的来说，几何分布提供了一种衡量在期望成功率不变的情况下，实现首次成功需要尝试多少次的方法。

超几何分布（Hypergeometric distribution）

超几何分布（Hypergeometric distribution）是一种离散概率分布，它描述了在不进行替换的情况下，从固定大小的总体中抽取一定数量的样本时，成功状态出现的次数。与二项分布相比，超几何分布的特征是抽样时没有替换，这意味着每次抽样的结果都会影响后续抽样的概率。

超几何分布的特点：

• 总体由两种状态组成：成功和失败。
• 从这个总体中不放回地随机抽取一定数量的样本。
• 每次抽取都是独立的，但由于是不放回抽样，后一次抽取的概率受前一次抽取的影响。
• 关心在抽取的样本中观察到成功状态的次数。

超几何分布的参数：

• N：总体大小，即总体中对象的总数。
• K：总体中具有成功状态的对象数。
• n：抽取的样本数量。
• k：在抽取的样本中观察到的成功状态的次数。

概率质量函数（PMF）：

超几何分布的概率质量函数给出了在n个样本中恰好有k个成功的概率，其表达式为：

$$P(X=k)=\frac{{\binom{K}{k}}{\binom{N-K}{n-k}}}{{\binom{N}{n}}}$$

其中：

• $\binom{K}{k}$表示从具有成功状态的K个对象中选择k个的方式数。
• $\binom{N-K}{n-k}$表示从剩余的失败状态的N-K个对象中选择n-k个的方式数。
• $\binom{N}{n}$是从总体中随机抽取n个对象的总方式数。

期望值和方差：

超几何分布的期望值E[X]和方差Var[X]可以用以下公式表示：

• 期望值E[X]：$\frac{nK}{N}$
• 方差Var[X]：$\frac{nK(N-K)(N-n)}{N^2(N-1)}$

示例：

假设你有一个包含20个球的桶，其中有8个白球和12个黑球。如果你不放回地随机抽取5个球，你可能想知道抽到恰好3个白球的概率：

这里N=20，K=8，n=5，k=3，所以概率是：

$$P(X=3)=\frac{{\binom{8}{3}}{\binom{12}{2}}}{{\binom{20}{5}}}$$

这个概率可以通过计算上述组合数并应用超几何分布的PMF公式得到。

应用：

超几何分布在各种领域都有应用，例如：

• 质量控制中，用于描述在没有替换的情况下从生产批次中抽取一定数量的产品并检查它们时，缺陷产品的数量。
• 生态学中，估计种群中特定物种的数量。
• 社会科学调查中，比如在没有完全普查的情况下，从总体群体中随机抽样来估计某个属性的频率。

超几何分布通常适用于样本量不大且无法替换的情况，其准确地反映了每次抽样对于随后抽样结果的影响。

负二项分布（Negative binomial distribution）

负二项分布（Negative binomial distribution），又称为帕斯卡分布（Pascal distribution），是离散概率分布的一种。它描述了在一系列独立的、具有相同成功概率的伯努利试验中，要达到指定数量的成功所需进行的试验次数。

负二项分布的特点：

• 每次试验结果只有两种可能，即成功或失败。
• 试验是独立的，每次成功的概率 p 都是相同的。
• 关心的是进行多少次试验才能达到指定数量的成功，而非第一次成功发生在第几次试验。

负二项分布的参数：

• 成功概率 p：在单次伯努利试验中获得成功的概率。
• 成功次数 r：在停止试验前期望达到的成功次数。

概率质量函数（PMF）：

负二项分布的概率质量函数给出了在获得第 r 次成功之前已经发生了 k 次失败的概率。对于随机变量 X（表示失败次数），其 PMF 表达式为：

$$P(X=k)=\binom{k+r-1}{k}(1-p)^kp^r$$

其中：

• $\binom{k+r-1}{k}$ 是组合数，表示在 k+r-1 个试验中选择 k 个失败的方式数。
• k 是失败的次数。
• r 是成功的次数。
• p 是单次试验中获得成功的概率。

期望值和方差：

对于负二项分布，期望值和方差分别为：

• 期望值 E[X]：$\frac{r(1-p)}{p}$
• 方差 Var[X]：$\frac{r(1-p)}{p^2}$

示例：

考虑一个生物学家观察到一个稀有鸟种的情况。假设每次观察到该鸟种的概率是 0.1。生物学家希望知道，平均而言，在观察到这种鸟三次之前，他会经历多少次没有观察到的情况。

这里，我们有 p=0.1 和 r=3。根据负二项分布的期望值公式，我们计算出平均的失败次数 $E[X]=\frac{r(1-p)}{p}=\frac{3(1-0.1)}{0.1}=27$ 次。

应用：

负二项分布广泛应用于各个领域，包括：

• 生态学：在观察到特定数量的动植物种类之前的观察次数。
• 经济学：在达到一定数目的销售量之前的失败销售次数。
• 医学研究：在获得一定数目的治愈个案之前的试验次数。
• 质量控制：在生产过程中达到一定数量的合格品之前的不合格品数量。

负二项分布通常用于在试验中寻求成功次数时的场景，特别是当成功概率很低或者要求成功次数较多时。它可以看作是几何分布的一种推广，因为几何分布是负二项分布在 r=1 时的特殊情况。

常见连续概率分布简介

均匀分布（Uniform distribution）

均匀分布（Uniform distribution）是最简单的概率分布之一，它描述了所有可能结果在一个区间内均等可能出现的情况。在均匀分布中，每个值在给定的范围内都有相同的概率。这种分布可以是离散的，也可以是连续的。

均匀分布的特点：

• 所有可能结果的概率相等。
• 无论是离散的还是连续的，均匀分布都可以在一个有限的区间内定义。

均匀分布的参数：

对于连续均匀分布，一般需要两个参数来定义：

• a：区间的下限。
• b：区间的上限。

对于离散均匀分布，参数通常是可能结果的数目。

概率密度函数和概率质量函数：

对于连续均匀分布，其概率密度函数（PDF）为：

$$f(x)=\begin{cases}\frac{1}{b-a},&\text{for }a\leq x期望值和方差：

对于连续均匀分布，其期望值和方差分别为：

• 期望值 E[X]：$\frac{a+b}{2}$
• 方差 Var[X]：$\frac{(b-a)^2}{12}$

对于离散均匀分布，其期望值和方差分别为：

• 期望值 E[X]：$\frac{n+1}{2}$
• 方差 Var[X]：$\frac{(n^2-1)}{12}$

应用：

• 在理想情况下，连续均匀分布常用于描述物理现象，如物体在一段时间内的速度或者在一定区间内的位置。
• 在抽奖中，如果每个号码被抽到的概率相同，则可以使用离散均匀分布来模拟抽奖行为。
• 在计算机科学中，生成随机数时通常使用连续均匀分布。
• 在经济学中，如果没有足够的信息推断消费者的偏好，则可能假设消费者对一系列产品的偏好是均匀分布的。

均匀分布的关键特性是所有的事件或值都具有相同的概率，这使得它在需要等概率模型的场景中非常有用。

正态分布（Normal distribution）

正态分布（Normal distribution），也被称为高斯分布（Gaussian distribution），是连续概率分布的一种，其概率密度函数呈”钟形”曲线，即，大部分观察值聚集在平均值附近，离平均值越远的值出现的概率越小。正态分布是统计学和自然科学中最常见的一种分布。

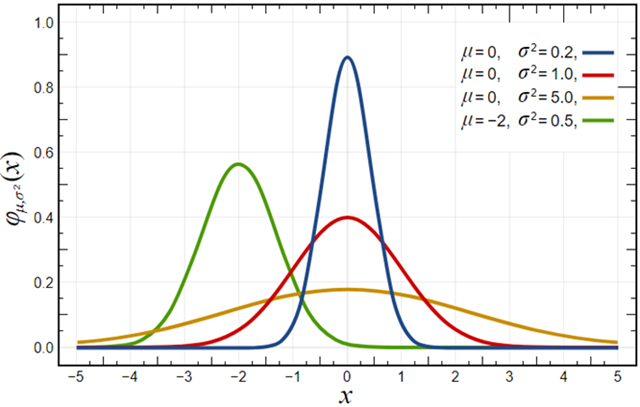
正态分布的特点：

• 形状为对称的钟形曲线，称为正态曲线。
• 分布的平均值、中位数和众数在同一位置。
• 曲线两端永远接近但不会触及横轴（即具有无限的尾部）。

正态分布的参数：

• 均值 $\mu$：分布的中心或平均值，它是分布的对称轴。
• 标准差 $\sigma$：描述分布的数据点偏离均值的程度。标准差越大，分布越分散。

概率密度函数（PDF）：

正态分布的概率密度函数描述了在任意点 (x) 处取得特定值的概率。正态分布的 PDF 表达式为：

$$f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp(-\frac{1}{2}(\frac{x-\mu}{\sigma})^2)$$

其中 $\exp$ 表示指数 e 的幂。

累积分布函数（CDF）：

正态分布的累积分布函数表示随机变量的值小于或等于 (x) 的概率。对于正态分布，CDF 表达式为：

$$F(x)=\frac{1}{2}[1+\text{erf}(\frac{x-\mu}{\sigma\sqrt{2}})]$$

其中 $\text{erf}$ 是误差函数。

期望值和方差：

正态分布的期望值 E[X] 和方差 Var[X] 分别为：

• 期望值 E[X]：$\mu$
• 方差 Var[X]：$\sigma^2$

标准正态分布：

当 $\mu=0$ 且 $\sigma=1$ 时，正态分布成为标准正态分布。标准正态分布的 PDF 为：

$$f(z)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}z^2)$$

任何正态分布都可以通过标准化变换为标准正态分布，这个过程称为正态标准化，使用公式：

$$z=\frac{x-\mu}{\sigma}$$

应用：

正态分布在许多领域都有应用，包括：

• 测量误差的建模。
• 自然现象的描述，如人类的身高和血压。
• 金融市场中资产回报的建模。
• 心理测验评分的分析。

中心极限定理：

正态分布的普遍性可以部分地通过中心极限定理来解释，该定理表明，足够大的样本量下，多个随机变量之和的分布趋于正态分布，无论原始随机变量的分布如何。只要随机变量是独立的，具有有限的均值和方差，这个定理就适用。

正态分布因其数学属性和实际应用的普遍性而成为概率论和统计学中最重要的分布之一。

指数分布（Exponential distribution）

指数分布（Exponential distribution）是连续概率分布的一种，经常用于描述独立随机事件发生的时间间隔。在许多自然和社会现象中，比如放射性物质的衰变、顾客在商店中的等待时间或者机器设备的寿命，指数分布都找到了应用。它的一个关键特征是无记忆性（memorylessness），意味着未来事件的概率不受过去事件的影响。

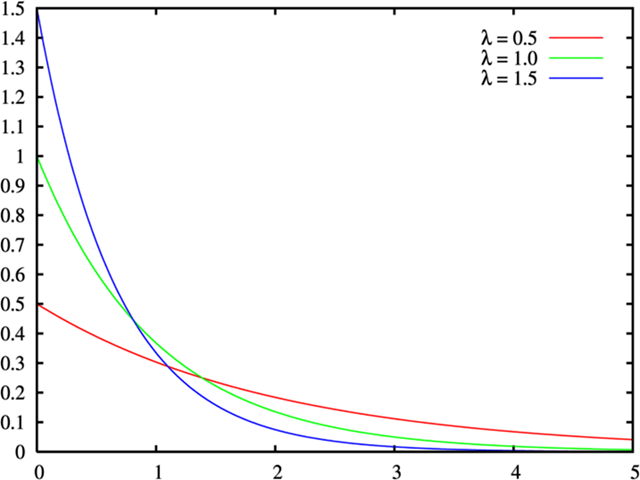
指数分布的特点：

• 无记忆性：已经过去的时间对未来的预测没有影响。
• 描述时间间隔：如上文所述，常用于描述两个连续随机事件之间的时间。

指数分布的参数：

• 率参数（$\lambda$, lambda）：平均每单位时间发生的事件数，$\lambda>0$。

概率密度函数（PDF）：

指数分布的概率密度函数用来描述在连续时间内事件发生的概率分布。对于指数分布，PDF定义为：

$$f(x;\lambda)=\begin{cases}\lambda e^{-\lambda x},&x\geq0\\0,&x<0\end{cases}$$

这里的e是自然对数的底数，约等于2.71828。

累积分布函数（CDF）：

指数分布的累积分布函数描述了随机变量小于或等于某个值的概率。其表达式为：

$$F(x;\lambda)=1-e^{-\lambda x},\text{for}x\geq0$$

期望值和方差：

指数分布的期望值E[X]和方差Var[X]分别为：

• 期望值E[X]：$\frac{1}{\lambda}$
• 方差Var[X]：$\frac{1}{\lambda^2}$

无记忆性：

指数分布的无记忆性指的是过去已经经过的时间对未来事件发生的概率没有影响。具体来说，如果X是指数分布的随机变量，则对于任何正数s和t，都有：

$$P(X>s+t\mid X>s)=P(X>t)$$

这个属性在实际应用中非常重要，比如在网络理论和排队理论中。

应用：

• 放射性衰变：放射性元素衰变的时间间隔通常服从指数分布。
• 服务系统：如呼叫中心中顾客的到达时间、网站上页面请求之间的时间。
• 可靠性工程：如电子设备或机械部件在故障之前的寿命。

关系到其他分布：

• 指数分布是伽马分布的特殊情况，当伽马分布的形状参数k=1时，它就是指数分布。
• 指数分布与泊松分布密切相关，如果事件在单位时间内以固定的平均率$\lambda$随机且独立地发生，则这些事件的时间间隔将遵循指数分布。

指数分布因其简单性和在模型实际情况中的有效性而广泛应用于工程、物理科学、经济学和生物医学等诸多领域。

伽马分布（Gamma distribution）

伽马分布（Gamma distribution）是一种连续概率分布，广泛用于表示一系列事件发生所需的等待时间，特别是当这些事件以恒定的平均速率连续且独立地发生时。它是指数分布的推广，并包括它作为其特殊情况。伽马分布在统计学、工程、生物学、气象学等多个领域有着广泛的应用。

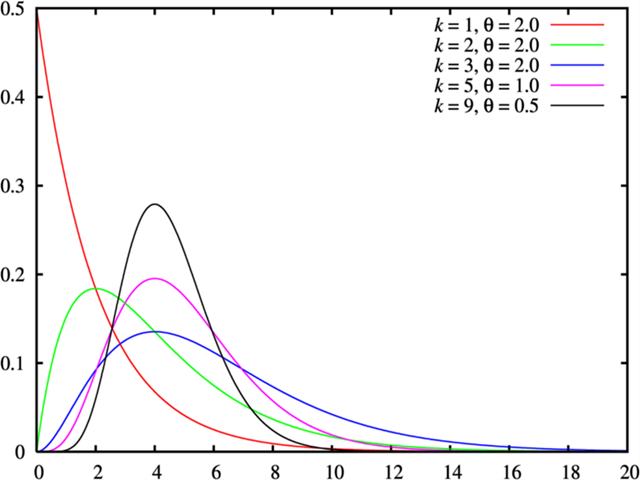
伽马分布的特点：

• 灵活的形状：适用于描述多种类型的现象。
• 仅在正实数上定义：适用于表示等待时间或生命期等。
• 包含其他分布：当形状参数为1时，伽马分布退化为指数分布；当形状参数为正整数时，它与卡方分布相关。

伽马分布的参数：

伽马分布有两个参数：

• 形状参数k或$\alpha$：决定了分布的形状，$k>0$。
• 尺度参数$\theta$或$\beta$）：与事件发生率的倒数相关，$\theta>0$。

概率密度函数（PDF）：

对于x>0和形状参数k、尺度参数$\theta$，伽马分布的概率密度函数为：

$$f(x;k,\theta)=\frac{x^{k-1}e^{-\frac{x}{\theta}}}{\theta^k\Gamma(k)}$$

其中，$\Gamma(k)$是伽马函数，定义为：

$$\Gamma(k)=\int_0^\infty t^{k-1}e^{-t}dt$$

对于正整数k，$\Gamma(k)=(k-1)!$。

累积分布函数（CDF）：

伽马分布的累积分布函数难以表示成闭合形式，但可以通过下列不完全伽马函数来表达：

$$F(x;k,\theta)=\frac{1}{\Gamma(k)}\gamma(k,\frac{x}{\theta})$$

其中，不完全伽马函数$\gamma(k,z)$为：

$$\gamma(k,z)=\int_0^z t^{k-1}e^{-t}dt$$

期望值和方差：

伽马分布的期望值E[X]和方差Var[X]分别为：

• 期望值E[X]：$k\theta$
• 方差Var[X]：$k\theta^2$

应用：

• 等待时间问题：伽马分布可以用来描述某些事件连续发生多次所需的等待时间。
• 可靠性分析：伽马分布可以应用于寿命数据的建模，特别是当物品的寿命是由多个独立因素的累积效应导致时。
• 贝叶斯统计：在贝叶斯推断中，伽马分布常作为某些参数的先验分布，特别是在处理泊松过程或指数分布的参数时。
• 医学研究：如病人的生存时间分析。

伽马分布因其灵活性和数学特性而在理论和应用领域都很重要。通过调整形状和尺度参数，伽马分布能够适应不同的应用场景，提供了一种功能强大的方式来描述和分析等待时间和生命期数据。

贝塔分布（Beta distribution）

贝塔分布（Beta distribution）是定义在区间[0,1]上的一种连续概率分布，它由两个正参数α(alpha)和β(beta)控制。贝塔分布常用于表示一定范围内的概率值的不确定性，它在贝叶斯统计中特别有用，尤其是作为二项式随机变量的先验分布。

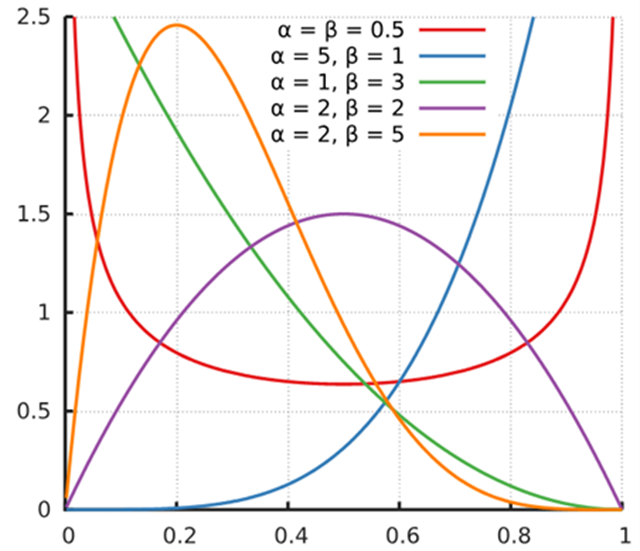
贝塔分布的特点：

• 定义域为[0,1]，适合模拟比例或概率。
• 形状灵活，可以根据参数的不同取值呈现出不同的形态，如均匀分布、J形分布、U形分布等。
• 参数α和β的不同组合可以表示数据的不同信念，从而在贝叶斯推断中作为先验知识。

贝塔分布的参数：

• 形状参数α(alpha)：影响分布靠近0的密度。
• 形状参数β(beta)：影响分布靠近1的密度。

概率密度函数（PDF）：

在区间[0,1]上，对于给定的参数α和β，贝塔分布的概率密度函数为：

$$f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$$

其中，$B(\alpha,\beta)$是贝塔函数，它是伽马函数的一个特例，定义为：

$$B(\alpha,\beta)=\int_0^1t^{\alpha-1}(1-t)^{\beta-1}dt=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$$

累积分布函数（CDF）：

由于贝塔分布的累积分布函数（CDF）没有闭合形式的解析表达式，它通常通过不完全贝塔函数(I_x(\alpha,\beta))来表示：

$$F(x;\alpha,\beta)=\int_0^xf(t;\alpha,\beta)dt=I_x(\alpha,\beta)$$

其中，$I_x(\alpha,\beta)$是规范化不完全贝塔函数。

期望值和方差：

贝塔分布的期望值(E[X])和方差(Var[X])分别为：

• 期望值E[X]：$\frac{\alpha}{\alpha+\beta}$
• 方差Var[X]：$\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$

应用：

• 贝叶斯统计：作为二项分布参数的先验分布或后验分布。
• 机器学习：在某些分类算法的信赖度评估中使用。
• 项目管理：评估项目完成的概率。
• 医学统计：模拟某种治疗效果的不确定性。

贝塔分布的灵活性使其在实际问题中具有广泛的应用，它可以通过调整形状参数来精确地反映出我们对于一个概率值的先验信念。在实际应用中，α和β的选择通常基于具体问题的需求和先验知识。

卡方分布（Chi-squared distribution）

卡方分布（Chi-squared distribution）是统计学中重要的概率分布之一，它是由独立标准正态分布变量的平方和构成。卡方分布在假设检验中尤为重要，特别是在方差分析、卡方检验以及置信区间的计算中。此外，它还与其他多种统计分布有关，如t分布和F分布。

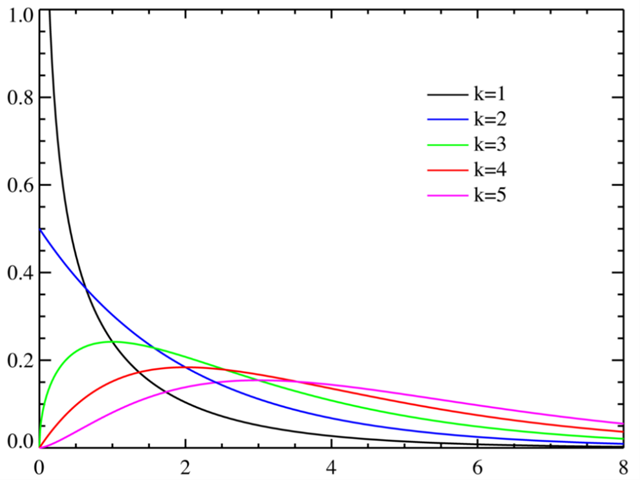
卡方分布的特点：

• 只有一个参数，即自由度df。
• 非负：卡方分布只在正半轴上定义$x\geq0$。
• 右偏：随着自由度的增加，分布逐渐趋于对称。

卡方分布的参数：

• 自由度(df)：通常与样本数量或约束条件的数量相关。

概率密度函数（PDF）：

假设有k个独立的标准正态分布随机变量$Z_1,Z_2,…,Z_k$，则这些随机变量平方和的分布$X=Z_1^2+Z_2^2+…+Z_k^2$服从自由度为k的卡方分布。其概率密度函数为：

$$f(x;k)=\begin{cases}\frac{1}{2^{k/2}\Gamma(k/2)}x^{(k/2)-1}e^{-x/2},&x>0\\0,&x\leq0\end{cases}$$

其中，$\Gamma(k/2)$是伽马函数。

累积分布函数（CDF）：

卡方分布的累积分布函数没有简单的闭合形式，但可以通过特殊的数学软件或查表来获得。

期望值和方差：

卡方分布的期望值E[X]和方差Var[X]分别为：

• 期望值E[X]：k（与自由度相同）
• 方差Var[X]：2k（方差是自由度的两倍）

应用：

• 卡方检验：用于检验分类变量之间是否独立。
• 拟合优度测试：检验一组观察值的一致性与某个特定分布。
• 置信区间的估计和假设检验：在方差分析中估计方差以及测试方差是否相等。
• 在多变量分析中：如计算独立性的卡方距离。

与其他分布的关系：

• 卡方分布是伽马分布的特殊情况，当伽马分布的形状参数k是自由度的一半，尺度参数$\theta$是2时。
• 当自由度为1时，卡方分布也称为标准正态分布的平方。
• 在估计正态分布的方差时，相关的统计量服从卡方分布。
• t分布的平方等于一个卡方分布，该卡方分布的自由度与t分布相同。

卡方分布在统计推断和假设检验中的应用非常广泛，是现代统计分析不可或缺的一部分。

T分布

T分布（也称作学生t分布或者Student’s t-distribution）是概率论和统计学中的一种连续概率分布，由威廉·戈塞特（William Sealy Gosset）于1908年在笔名“学生”（Student）下发表。T分布是用来估计正态总体均值的情况下，当样本量较小且总体方差未知时非常有用的。

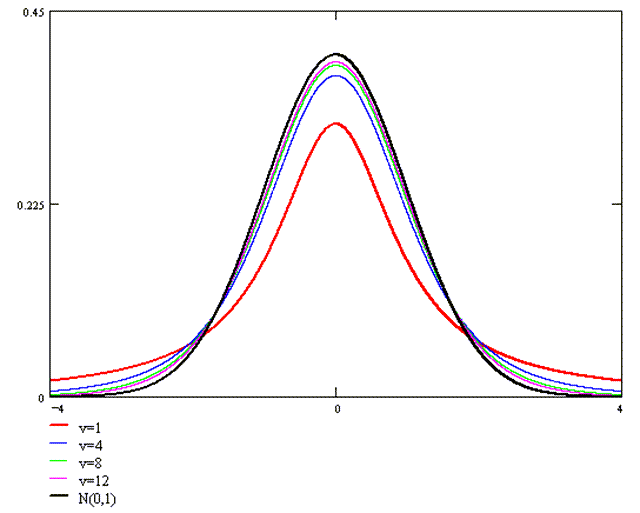
T分布的特点：

• 形状由自由度（df）决定：随着自由度的增加，t分布越来越接近正态分布。
• 对称：与正态分布一样，t分布是关于均值对称的。
• 比正态分布的尾部更厚：这意味着在t分布中，相对于正态分布，出现极端值的可能性更大。

T分布的参数：

• 自由度(df)：通常与样本数量或约束条件的数量相关。，它相关于样本量，通常为样本量减1(n-1)。自由度越大，t分布越接近正态分布。

概率密度函数（PDF）：

对于给定的自由度df，t分布的概率密度函数为：

$$f(t;df)=\frac{\Gamma(\frac{df+1}{2})}{\sqrt{df\pi}\Gamma(\frac{df}{2})}(1+\frac{t^2}{df})^{-\frac{df+1}{2}}$$

其中，$\Gamma(x)$是伽马函数。

累积分布函数（CDF）：

t分布的累积分布函数没有简单的闭合形式，但可以通过特殊的数学软件或查表来获得。

期望值和方差：

• 期望值E[X]：当自由度$\nu>1$时，t分布的期望值为0。
• 方差Var[X]：当自由度$\nu>2$时，t分布的方差为$\frac{\nu}{\nu-2}$。随着自由度的增加，t分布的方差逐渐趋向于1，也就是趋向于标准正态分布的方差。

应用：

• 置信区间：在样本量小且总体标准差未知时，用于构造均值的置信区间。
• 假设检验：用于t检验，比较两组数据的均值差异，或者单样本均值与总体均值的差异。

与其他分布的关系：

• t分布是对正态分布的一种修正，用以适应小样本情况。
• 当自由度趋于无穷大时，t分布趋于标准正态分布。
• t分布和F分布有关，t分布的平方等于自由度为1的F分布。

T分布是统计推断中非常重要的工具，它使得在样本量较小且总体方差未知时，我们仍然可以对总体均值进行推断。在应用T分布时，通常通过查表或使用统计软件来找到相应自由度和概率水平下的t分布的临界值。

F分布

F分布（也称为斯涅德科尔斯克-费希尔分布，Snedecor’s F distribution或Fisher-Snedecor distribution）是统计学中使用的一种连续概率分布，主要用于方差分析（ANOVA）、回归分析以及两个独立估计的方差比较的假设检验中。F分布是两个卡方分布随机变量之比的分布，其中这两个卡方分布随机变量都被它们各自的自由度所除。

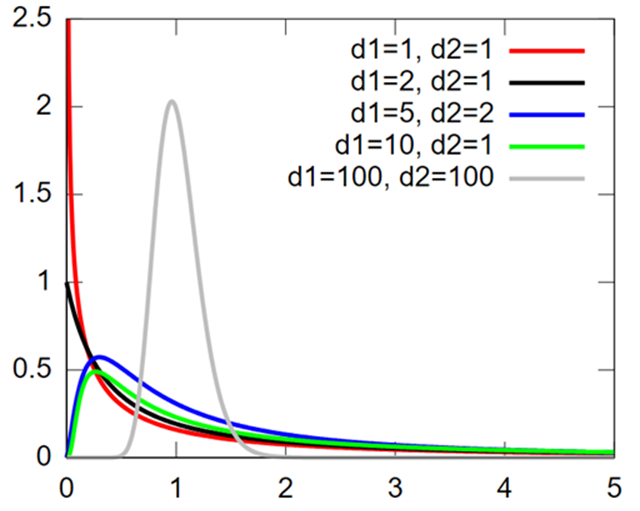
F分布的特点：

• 由两组自由度df1和df2参数化，其中df1对应于分子，df2对应于分母。
• 非负：F分布的取值范围是$[0,\infty)$。
• 非对称性：在自由度固定的情况下，F分布是右偏的。

F分布的参数：

• 自由度df1：分子的自由度，与第一个卡方分布相关。
• 自由度df2：分母的自由度，与第二个卡方分布相关。

概率密度函数（PDF）：

给定自由度df1和df2的情况下，F分布的概率密度函数为：

$$f(x;df1,df2)=\frac{\sqrt{(\frac{df1\cdot x}{df1\cdot x+df2})^{df1}(\frac{df2}{df1\cdot x+df2})^{df2}}}{x\cdot B(\frac{df1}{2},\frac{df2}{2})}$$

其中B表示贝塔函数。

累积分布函数（CDF）：

F分布的累积分布函数没有简单的闭合形式，通常通过数值积分或查表来确定。

期望值和方差：

F分布的期望值E[X]和方差Var[X]分别为：

• 期望值E[X]：当(df2>2)时，$E[X]=\frac{df2}{df2-2}$。
• 方差Var[X]：当(df2>4)时，$Var[X]=\frac{2\cdot df2^2\cdot (df1+df2-2)}{df1\cdot (df2-2)^2\cdot (df2-4)}$。

应用：

• 方差分析（ANOVA）：检验多个群体均值是否存在显著性差异。
• F检验：比较两组方差以检验它们是否显著不同。
• 模型选择：在多重回归分析中，比较模型的复杂度和拟合优度。

与其他分布的关系：

• F分布与t分布和卡方分布密切相关。如果一个随机变量T服从t分布，那么(T^2)将服从F分布。
• F分布可用于推导卡方分布。特别是，如果随机变量F服从自由度为df1和df2的F分布，且df1为1，则(df2\cdot F)将服从自由度为df2的卡方分布。

F分布在统计学的很多领域中都有广泛应用，尤其是在比较两个样本方差或进行方差分析时。在实际应用中，人们通常通过查F分布表或使用统计软件来获得F分布的临界值或概率。

韦伯分布(Weibull distribution)

韦伯分布（Weibull distribution）是一种连续概率分布，广泛用于生存数据分析和可靠性工程中，特别是在描述产品寿命或故障时间方面。

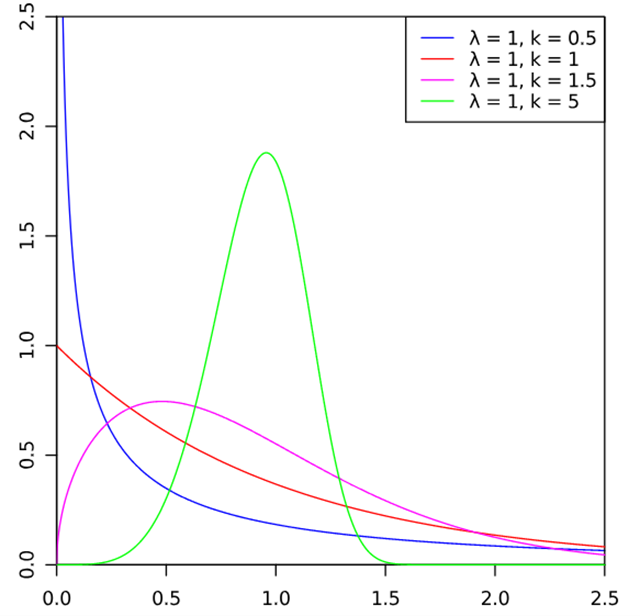
韦伯分布的特点：

• 形状参数和尺度参数可以调整分布的形状，使其能模拟早期故障、随机故障或磨损故障等各种情况。
• 韦伯分布是通过两个参数$\lambda$（scale参数，也称为特征寿命）和k（shape参数，也称为形状参数）来定义的。
• 形状参数k决定了分布的形状：
  • 当k<1时，随着时间的增加，失效率递减，对应于早期失效。
  • 当k=1时，失效率是恒定的，此时韦伯分布简化为指数分布。
  • 当k>1时，随着时间的增加，失效率递增，对应于磨损失效。
• 韦伯分布是右偏的（除非k=1）

韦伯分布的参数：

• 形状参数k：决定分布的形状，可以描述故障率是增加、减少还是保持不变。
• 尺度参数$\lambda$：相当于分布的“尺度”或“范围”，对应于概率密度函数上的延伸程度。

概率密度函数（PDF）：

韦伯分布的概率密度函数为：

$$f(x;k,\lambda)=\frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^k}$$

其中，x是随机变量，$\lambda$是scale参数，k是shape参数。

累积分布函数（CDF）：

韦伯分布的累积分布函数为：

$$F(x;k,\lambda)=1-e^{-(x/\lambda)^k}$$

CDF表示随机变量X小于或等于某个特定值x的概率。

期望值和方差：

韦伯分布的期望值E[X]和方差Var[X]分别为：

• 期望值E[X]：$E[X]=\lambda\Gamma(1+1/k)$。
• 方差Var[X]：$Var[X]=\lambda^2[\Gamma(1+2/k)-(\Gamma(1+1/k))^2]$。

这里，$\Gamma(z)$是伽马函数。

应用：

韦伯分布常用于以下领域：

• 可靠性分析：预测产品、系统或设备的寿命和失效模式。
• 生存分析：估计生物生存时间、病人生存时间等。
• 工业工程：设计产品和预防维护计划时，对部件的失效模式进行建模。
• 天气预报和气象学：模型化风速等气象数据。
• 金融风险管理：对极端市场事件的建模分析。

韦伯分布的灵活性和多样性使其成为分析各类生命周期数据的有力工具。通过适当的参数选择，它可以描述各种不同的失效率趋势。在实践中，经常使用最大似然估计（MLE）来估计韦伯分布的参数。

对数正态分布(Log-normal distribution)

对数正态分布（Log-normal distribution）是一种连续概率分布，如果一个随机变量的对数服从正态分布，那么这个随机变量就服从对数正态分布。

对数正态分布的特点：

• 对数正态分布的形状是右偏的，取值范围为正实数$(0,\infty)$。
• 对数正态分布的模式（最大概率密度的点）和中位数（概率密度函数积分为5的点）都小于均值。

对数正态分布的参数：

• 位置参数$\mu$：对应于正态分布的均值，决定了分布的中心位置。
• 尺度参数$\sigma$：对应于正态分布的标准偏差，决定了分布的宽度和峰度。

概率密度函数（PDF）：

给定位置参数(\mu)和尺度参数(\sigma)的情况下，对数正态分布的概率密度函数为：

$$f(x;\mu,\sigma)=\frac{1}{x\sigma\sqrt{2\pi}}e^{-(\ln x-\mu)^2/(2\sigma^2)}$$

累积分布函数（CDF）：

对数正态分布的累积分布函数没有简单的闭合形式，但可以表示为正态分布的累积分布函数：

$$F(x;\mu,\sigma)=\Phi(\frac{\ln x-\mu}{\sigma})$$

其中$\Phi$是正态分布的累积分布函数。

期望值和方差：

对数正态分布的期望值(E[X])和方差(Var[X])分别为：

• 期望值 E[X]：$E[X]=e^{\mu+\sigma^2/2}$。
• 方差 Var[X]：$Var[X]=(e^{\sigma^2}-1)e^{2\mu+\sigma^2}$。

应用：

对数正态分布在各个领域都有应用，例如：

• 收入分布：经济学中，个人收入往往呈对数正态分布。
• 股票价格：金融领域中，股票价格的长期趋势常被模拟为对数正态分布。
• 生物学：某些生物学特征，如动物大小或生长过程，可能服从对数正态分布。
• 工业工程：产品寿命和某些工艺的响应时间等。

由于对数正态分布是对数变换的结果，这意味着它能够模拟那些不能为负、且可能呈现指数增长的随机过程。在处理具有极端值或者重尾特性的数据时，对数正态分布提供了一种有用的模型选择。

柯西分布 (Cauchy distribution)

柯西分布（Cauchy distribution），也称为洛伦兹分布（Lorentz distribution），是一种连续概率分布。它以奥古斯丁·路易·柯西（Augustin-Louis Cauchy）的名字命名，是一种在数学、物理学和工程学等领域都有应用的分布。

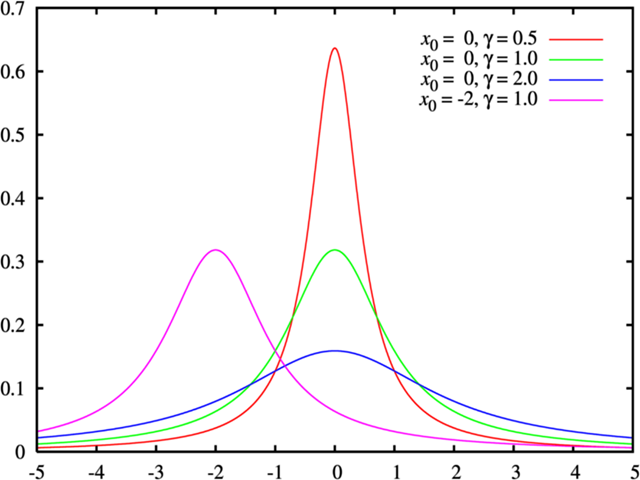
柯西分布的特点：

• 中心峰值非常尖锐，并且在中心附近缓慢递减。
• 具有厚尾特性（heavy-tailed），即尾部的概率比正态分布更高，意味着它更容易产生极端的大值或小值。
• 没有定义好的期望值或方差。

柯西分布的参数：

• 位置参数 $x_0$：它是分布的中位数和众数，确定了分布的中心位置。
• 尺度参数 $\gamma$：它决定了分布的宽度，类似于正态分布的标准偏差，但对于柯西分布来说并不是方差，因为柯西分布的方差是无定义的。

概率密度函数（PDF）：

柯西分布的概率密度函数为：

$$f(x;x_0,\gamma)=\frac{1}{\pi\gamma[1+(\frac{x-x_0}{\gamma})^2]}$$

累积分布函数（CDF）：

柯西分布的累积分布函数可以表示为：

$$F(x;x_0,\gamma)=\frac{1}{\pi}\arctan(\frac{x-x_0}{\gamma})+\frac{1}{2}$$

期望值和方差：

由于柯西分布的厚尾特性，其数学期望和方差都是无定义的。这是因为对于柯西分布，这些积分不收敛：

• 期望值（(E[X])）：无定义。
• 方差（(Var[X])）：无定义。

应用：

• 物理学：在物理学中，柯西分布用于描述共振行为和光谱线宽。
• 信号处理：柯西分布可以用来建模具有某些类型噪声的信号。
• 金融学：在金融学中，柯西分布有时用来模拟资产回报率，它能够捕捉极端事件的发生。

尽管缺乏期望值和方差，柯西分布仍然是一个有用的模型，尤其是在处理对极端值敏感的情况时。然而，在统计分析中处理柯西分布数据需要特别的注意，因为标准的统计量（如均值和标准差）不具有良好的统计性质。在实践中，中位数和四分位数范围（interquartile range, IQR）通常被用作柯西分布的位置和尺度参数的稳健估计。

帕累托分布 (Pareto distribution)

帕累托分布（Pareto distribution）是以意大利经济学家维尔弗雷多·帕累托（Vilfredo Pareto）命名的，它是描述社会、科学、地理和许多其他类型现象的一种重尾分布。最初，帕累托用它来描述财富分布，即在许多经济系统中，少数人掌握了大部分财富。

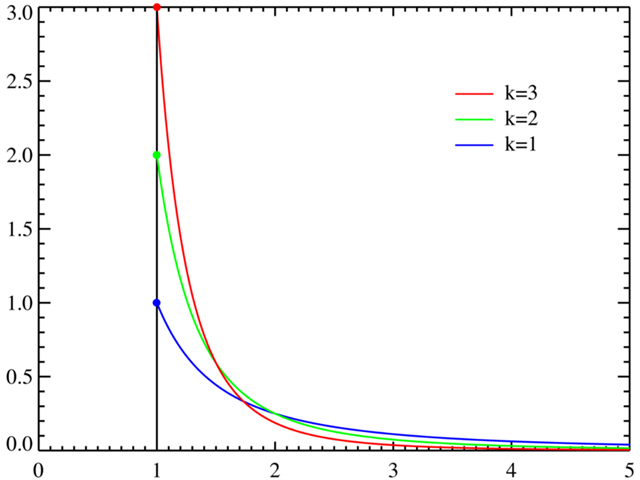
帕累托分布的特点：

• 描述的现象中有少数大事件和多数小事件。
• 重尾特性：这意味着相比于指数分布和正态分布，帕累托分布在其尾部有更大的概率值。这一特性使得帕累托分布能够很好地描述极端事件，如自然灾害的大小、城市人口、公司规模等。
• 其中位数小于平均值（如果平均值存在）。

帕累托分布的参数：

• 形状参数 $\alpha$：又称为尾指数，这个参数决定了尾部的厚度。形状参数越大，尾巴越薄，极端事件出现的概率就越小。
• 尺度参数 $x_m$：又称为最小值参数，是分布的下限，帕累托分布随机变量的可能值不能小于这个值。

概率密度函数（PDF）：

帕累托分布的概率密度函数为：

$$f(x;\alpha,x_m)=\begin{cases}\frac{\alpha x_m^\alpha}{x^{\alpha+1}}&\text{if}x\geq x_m,\\0&\text{if}x期望值（均值）和方差：

帕累托分布的均值（如果存在）和方差分别为：

• 期望值 E[X]：如果 $\alpha>1$，则 $E[X]=\frac{\alpha x_m}{\alpha-1}$；如果 $\alpha\leq1$，则均值不存在（无穷大）。
• 方差 Var[X]：如果 $\alpha>2$，则 $Var[X]=\frac{x_m^2\alpha}{(\alpha-1)^2(\alpha-2)}$；如果 $\alpha\leq2$，则方差不存在（无穷大）。

应用：

• 帕累托分布在经济学、社会学、地理学、科学和工程学中有广泛应用。例如：
• 经济学：描述财富分布，其中少数人拥有大部分财富。
• 保险业：对保险业的大型索赔进行建模。
• 城市科学：城市的人口规模分布往往遵循帕累托法则。
• 文件大小分布：互联网上的文件大小分布。

帕累托分布的一个著名概念是“80/20法则”，它大致描述了在许多情况下，大约80%的效果来自20%的原因。不过实际的比例可能并不精确为80/20，而是更广泛地指出少数因素常常对结果有着显著的

概率分布的主要应用

概率分布在多个学科和应用领域都有广泛的用途。它们用于描述随机变量的行为，并且能够提供关于数据如何分布的洞察。以下是一些主要应用领域：

统计分析：通过对数据集进行拟合，确定最佳的概率分布模型，以进行描述性分析、推断性分析和预测。

• 金融：
  • 风险管理：使用概率分布来评估金融产品的风险，如股票、债券、衍生品等。
  • 定价模型：如使用对数正态分布来估算股票价格在未来的变化。
  • 保险数学：估计保险索赔的概率，以帮助确定保险费率。
• 工程：
  • 可靠性工程：使用概率分布预测系统或组件的故障率和寿命。

  信号处理：分析和处理随机信号，如使用高斯分布对噪声进行建模。

• 物理科学：
  • 量子物理学：粒子位置和动量的概率分布。
  • 统计力学：原子和分子的行为分布。
• 生物学和医学：
  • 流行病学：疾病的发生率和传播模式。
  • 生物信息学：基因序列出现的概率分布。
• 环境科学：
  • 气候模型：模拟降雨量、温度等的变化。
  • 灾害评估：地震、洪水等自然灾害发生的概率分析。
• 心理学和社会科学：
  • 调查分析：分析调查数据，如测量社会态度和行为模式。
  • 决策理论：评估不确定性下的决策，如使用贝叶斯方法。
  • 排队理论：分析和预测顾客流量、服务时间，以管理和优化服务系统。
• 机器学习和数据科学：
  • 概率建模：使用概率分布来建立数据生成的模型。
  • 贝叶斯推断：更新对未知参数的概率分布，根据观测到的数据。
• 制造业：
  • 质量控制：生产过程中产品质量的统计分析。
  • 库存管理：预测产品需求，优化库存量。
• 营销：
  • 消费者行为分析：模拟消费者购买模式和品牌选择。
  • 销售预测：预测产品的销售量和市场趋势。

这些只是概率分布在互联网领域内应用的一些例子。由于互联网数据通常是大规模、高维度且动态的，因此概率分布和统计模型在数据分析和决策过程中起着至关重要的作用。

概率分布在互联网的应用

在互联网领域中，概率分布被用于多种不同的应用，以支持决策制定、预测、用户行为分析等。以下是一些概率分布在互联网上的具体应用实例：

• 用户行为分析：
  • 用户点击网页的行为可以使用泊松分布进行建模。
  • 在线购物中用户花费金额的分布可能会使用伽玛分布或对数正态分布。
• 推荐系统：
  • 概率分布可以用来模拟用户对物品的评分或偏好。
  • 多臂老虎机算法（bandit algorithms），其中使用概率模型来平衡探索和利用之间的关系。
• 网络流量分析：
  • 网络流量到达的模式可以用泊松过程或更复杂的自适应过程建模。
  • 分布式拒绝服务攻击（DDoS）的检测也可能涉及到异常流量模式的识别，这通常是通过比较概率分布实现的。
• 搜索引擎优化（SEO）：
  • 关键词搜索频率可以使用概率分布进行建模，从而帮助优化搜索引擎结果。
• 广告投放和定价：
  • 广告点击率（CTR）往往具有特定的概率分布，这有助于决定广告位置和定价。
  • 预测广告展示和点击的数量，通常使用泊松或负二项分布。
• 信息安全：
  • 检测网络异常行为，如入侵检测，可以依据诸如正态分布异常点的概念。
  • 密码猜测和破解尝试的分布可能会用到概率分布。
• 容量规划和资源分配：
  • 预测服务器负载和客户端请求，以准备适当的资源，以避免过载或浪费。
• 社交媒体分析：
  • 分析用户发布内容的频率或者社交网络中的连接模式。
  • 情感分析，如使用贝叶斯方法，预测用户对产品或服务的情感倾向。
• 云计算和大数据：
  • 云服务中资源的使用模式，如CPU时间或内存使用，常常符合特定的概率分布。
  • 大数据处理中数据抽样和分布式计算。
• 机器学习和人工智能：
  • 生成模型（如生成对抗网络 GANs），通过学习训练数据的分布来生成新的数据点。
  • 贝叶斯网络和概率图模型在理解数据关联和推理中的应用。
• 电子商务：
  • 预测产品的销量和库存管理。
  • 客户生命周期价值（Customer Lifetime Value, CLV）的建模和预测。

这些只是概率分布在互联网领域内应用的一些例子。由于互联网数据通常是大规模、高维度且动态的，因此概率分布和统计模型在数据分析和决策过程中起着至关重要的作用。

概率分布在机器学习中的应用

在机器学习中，概率分布的应用非常广泛，它们用于从数据中学习、进行推断、做出预测，以及评估模型的不确定性。以下是一些概率分布在机器学习中的具体应用：

• 朴素贝叶斯分类器（Naive Bayes Classifier）：使用特定的概率分布（如多项分布、伯努利分布等）来建模特征，并基于贝叶斯定理进行分类。
• 概率图模型（Probabilistic Graphical Models）：例如贝叶斯网络（Bayesian Networks）和马尔可夫随机场（Markov Random Fields），使用概率分布来表示变量之间的关系。
• 隐马尔可夫模型（Hidden Markov Models, HMMs）：对时序数据建模，比如语音识别、自然语言处理中的词性标注等，通过概率分布描述状态转移和观测概率。
• 高斯混合模型（Gaussian Mixture Models, GMMs）：对数据进行聚类分析，每个簇由一个高斯分布表示，并通过期望最大化（EM）算法来估计参数。
• 生成对抗网络（Generative Adversarial Networks, GANs）：使用概率分布来生成新的数据样本，如图像、音乐等，使生成的分布尽可能接近真实数据的分布。
• 回归分析：线性回归中假设误差项符合正态分布，以建立预测模型。泊松回归或负二项回归用于建模计数数据。
• 贝叶斯推断：用于更新对模型参数的概率信念，常常使用贝塔分布、狄利克雷分布、伽马分布作为先验分布。
• 强化学习：在决策过程中使用概率模型来评估行为的预期回报。
• 自然语言处理（NLP）：语言模型，如n-gram模型，通常使用概率分布来建模词序列的出现概率。
• 聚类算法：如K均值（K-means）算法的扩展版本，比如K-medoids或使用概率分布进行软聚类的方法。
• 异常检测：分布的尾部可以用来识别异常值或者离群点。
• 非参数方法：如核密度估计（Kernel Density Estimation, KDE）用于估计未知的概率密度函数。
• 深度学习中的不确定性建模：使用概率分布进行权重和激活函数的正则化，比如变分自编码器（Variational Autoencoders, VAEs）。
• 超参数优化：使用概率分布对模型的超参数进行搜索，比如贝叶斯优化。

概率分布提供了一种统一的语言来描述和处理不确定性，这在机器学习中是一个核心的概念。通过对不同类型的数据和问题使用适当的概率分布及其相关的统计方法，机器学习模型可以更加有效地进行学习和推断。