在潜在语义分析LSA的文章中对LDA有一些简单的介绍，今天的目标是对LDA进行相对深入的了解，大致搞明白其原理。
LDA简介
在机器学习领域中有2个LDA：
- 线性判别分析(Linear Discriminant Analysis)，主要用于降维和分类。
- 隐含狄利克雷分布(Latent Dirichlet Allocation)，在主题模型中占有重要的地位，目前在文本挖掘领域包括文本主题识别、文本分类以及文本相似度计算方面都有应用。
这里主要讲的是隐含狄利克雷分布。
Latent Dirichlet Allocation（文档主题生成模型简称LDA），又名潜在狄利克雷分布，是非监督机器学习技术，用于识别文档集中潜在的主题词信息。它可以将文档集中每篇文档的主题按照概率分布的形式给出。同时它是一种无监督学习算法，在训练时不需要手工标注的训练集，需要的仅仅是文档集以及指定主题的数量k即可。此外LDA的另一个优点则是，对于每一个主题均可找出一些词语来描述它。它也可以被称为一个三层贝叶斯概率模型，其中包含词，主题和文档。它的中心思想是一篇文章的每个词都是通过一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语。它的特点是文档到主题服从多项式分布，主题到词服从多项式分布。
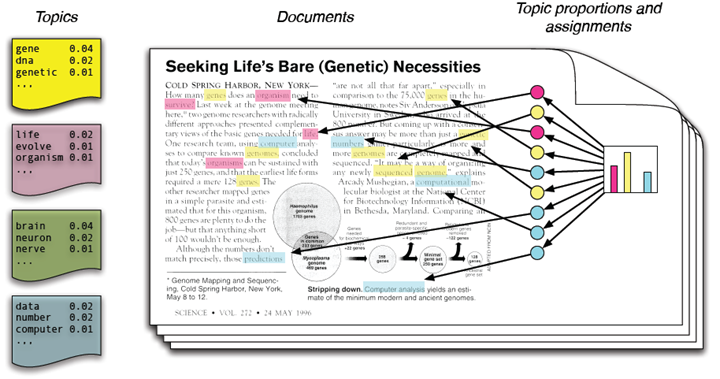
LDA是一种典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。所谓词袋模型，是将一篇文档，我们仅考虑一个词汇是否出现，而不考虑其出现的顺序。在词袋模型中，”我喜欢你”和”你喜欢我”是等价的。与词袋模型相反的一个模型是n-gram，n-gram考虑了词汇出现的先后顺序。有兴趣的读者可以参考其他书籍。
另外，正如Beta分布是二项式分布的共轭先验概率分布，狄利克雷分布作为多项式分布的共轭先验概率分布。因此正如LDA贝叶斯网络结构中所描述的，在LDA模型中一篇文档生成的方式如下:
- 从狄利克雷分布中取样生成文档i的主题分布
- 从主题的多项式分布中取样生成文档i第j个词的主题
- 从狄利克雷分布中取样生成主题的词语分布
- 从词语的多项式分布中采样最终生成词语
何为LDA(Latent Dirichlet Allocation)？简单的说，L(Latent隐含)，主题隐含在文档中；DA(Dirichlet Allocation狄利克雷分布)，文档的主题服从Dirichlet Distribution。
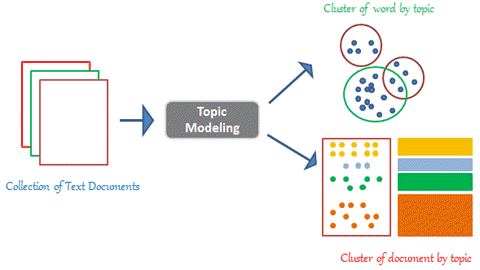
LDA(Latent Dirichlet Allocation)通过建立一种：
- 词袋模型(Bag-of-Word Model)：一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系
- 统计模型(Statistical Model)：经过数理统计法求得各变量之间的函数关系
- 生成概率模型(Generative Probabilistic Model)：认为每一类数据都服从某一种分布，如狄利克雷分布
- 主题模型(Topic Model)：在机器学习和自然语言处理等领域，用来在一系列文档中发现抽象主题的一种统计模型
- 无监督学习模型(Unsupervised Model)：在训练时不需要人工标注的数据集，需要的仅仅是文档集以及指定主题的数量K
来发现文档集(Document Collection/Corpus)中的抽象主题，从而试图解决这类问题。
LDA由Blei, David M., Andrew Y. Ng, and Michael I. Jordan于2003年提出，可以将文档集中每篇文档的主题按照概率分布的形式给出。
LDA原理中的基础概念
为了深入理解LDA主题模型，我们需要了解下列5个部分：
- 一个概念：贝叶斯定理
- 一个函数：Gamma函数
- 五个分布：二项分布<->Beta分布，多项分布<->Dirichlet分布，共轭分布
- 两个模型：PLSA模型，LDA模型
- 两个算法：变分推断之EM算法，Gibbs采样算法(马尔科夫链蒙特卡罗MCMC)
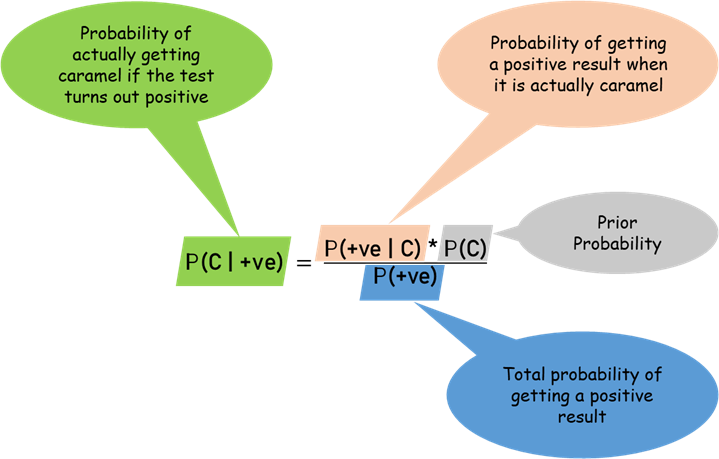
贝叶斯定理Bayes Theorem
$$P(A|B)=\frac{P(A)\times{P(B|A)}}{P(B)}$$
$$\text{posterior}=\text{prior}\times\text{likelihood}$$
- 概率:用于在已知一些参数的情况下，预测接下来的观测所得到的结果。
- likelihood(似然):用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。
- 后验概率=先验概率*似然
- P(A|B):是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
- P(A):是A的先验概率。之所以称为”先验”是因为它不考虑任何B方面的因素。
- P(B|A):是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
- P(B):是B的先验概率。
- P(B|A)P(B):称作标准似然(standardised likelihood)
伽玛函数Gamma Function
Gamma函数的具体形式如下：
$$\Gamma(x)=\int_{0}^{\infty}e^{-u}u^{x-1}du$$
其中，x>0。Gamma函数的图像如下所示：
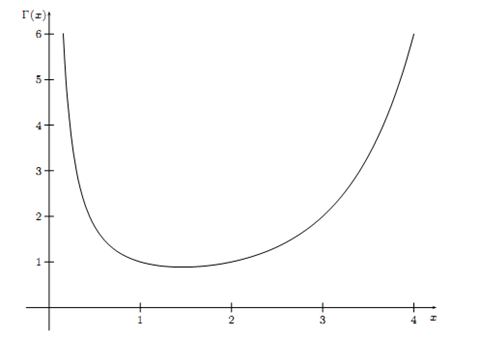
Gamma函数$\Gamma(x)$具有如下的一些性质：
性质1：
$$\Gamma(x+1)=x\Gamma(x)$$
这个性质可以通过分部积分的方法得到证明，证明如下：
$$\begin{matrix}\Gamma(x+1)=\int_{0}^{\infty}e^{-u}u^{x}du\\=\int_{0}^{\infty}-u^{x}de^{-u}\\=-u^xe^{-u}\mid_0^{\infty}-\int_{0}^{\infty}-e^{u}xu^{x-1}du\\=x\int_{0}^{\infty}e^{-u}u^{x-1}du\\=x\Gamma(x)\end{matrix}$$
性质2：
$$\Gamma(1)=1,\;\Gamma(\frac{1}{2})=\sqrt{\pi}$$
性质3：
$$\Gamma(n+1)=n!$$
二项分布Binomial Distribution
二项分布是概率分布里面最简单也是最基本的分布，要理解二项分布，我们首先得定义n次独立重复试验的概念：n次独立重复试验是指在相同的条件下，重复做的n次试验称为n次独立重复试验。
假设对于一个事件A，在一次试验中，其发生的概率为p，那么其不发生的概率为1−p，那么在nn次独立重复试验中事件AA恰好发生kk次的概率为：
$$P_n(k)=C_n^kp^{k}(1-p)^{n-k}$$
在这里，参数k是一个随机变量，便称这样的随机变量k服从二项分布，记为：$k\simB(n,p)$。
可以验证下式成立：
$$\sum_{k=0}^{n}P_n(k)=\sum_{k=0}^{n}C_n^kp^{k}(1-p)^{n-k}=1$$
多项分布Multinomial Distribution
多项式分布是二项分布的一个推广形式，在二项分布中，事件A的取值可能只能是发生或者是没有发生，而在多项式分布中事件A的取值可能有k种，取每一种可能的概率为$p_i$，其中$p_i$满足：
$$\sum_{i=1}^{k}p_i=1$$
多项式分布的概率形式为：：
$$P(x_1,x_2,…,x_k;n,p_1,p_2,…,p_k)=\frac{n!}{x_1!…x_k!}{p_1}^{x_1}…{p_k}^{x_k}$$
贝塔分布 Beta Distribution
Beta函数的具体形式如下：
$$Beta\left(a,b\right)=\int_{0}^{1}x^{a-1}\left(1-x\right)^{b-1}dx$$
其中，a>0,b>0。Beta函数有如下的一个性质：
$$Beta(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$$
上述的关于Beta函数的性质将Beta函数与Gamma函数联系起来，对于该性质的证明如下所示：
$$\begin{matrix}\Gamma(a)\Gamma(b)=\int_{0}^{\infty}e^{-u}u^{a-1}du\cdot\int_{0}^{\infty}e^{-v}v^{b-1}dv\\=\int_{0}^{\infty}\int_{0}^{\infty}e^{-\left(u+v\right)}u^{a-1}v^{b-1}dudv\\\end{matrix}$$
此时，令$z=u+v,t=\frac{u}{u+v}$，上式可转化为：
$$\begin{matrix}\Gamma(a)\Gamma(b)=\int_{0}^{\infty}\int_{0}^{1}e^{-z}(zt)^{a-1}[z(1-t)]^{b-1}zdzdt\\=\int_{0}^{\infty}e^{-z}z^{a-1}zdz\cdot\int_{0}^{1}t^{a-1}(1-t)^{b-1}dt\\=\Gamma(a+b)\cdot\int_{0}^{1}t^{a-1}(1-t)^{b-1}dt\\=\Gamma(a+b)\cdot Beta(a,b)\end{matrix}$$
由此可知：
$$Beta(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$$
狄利克雷分布 Dirichlet Distribution
Dirichlet函数的基本形式为：
$$D(a_1,a_2,\cdots,a_k)=\int\cdots\int x_1^{a_1-1}\cdots x_k^{a_k-1}dx_1\cdots dx_k$$
其中$x_1\cdots x_k\geq0，\sum_{i=1}^{k}x_i=1$。而Dirichlet分布的概率密度函数为：
$$p(x_1,\cdots,x_k)=\frac{1}{D(a_1,\cdots,a_k)}x_1^{a_1}\cdots x_k^{a_k}$$
其中，$0\leq x_1\cdots x_n\leq1$，且$\sum_{i=1}^{k}x_k=1$，$D(a_1,\cdots,a_k)$的形式为：
$$D(a_1,\cdots,a_k)=\frac{\Gamma(a_1)\cdots\Gamma(a_k)}{\Gamma(a_1+\cdots+a_k)}$$
注意到Beta分布是特殊的Dirichlet分布，即k=2时的Dirichlet分布。
共轭分布 Conjugate Distribution
有了如上的贝叶斯定理，对于贝叶斯派而言，有如下的思考方式：先验分布+样本信息⇒后验分布
述的形式定义是贝叶斯派的思维方式，人们对于事物都会存在着最初的认识（先验分布），随着收集到越来越多的样本信息，新观察到的样本信息会不断修正人们对事物的最初的认识，最终得到对事物较为正确的认识（后验分布）。若这样的后验概率$P(\theta\mid x)$和先验概率$P(x)$满足同样的分布，那么先验分布和后验分布被称为共轭分布，同时，先验分布叫做似然函数的共轭先验分布。
有了如上的的共轭先验分布的定义，有如下的两个性质：
1、Beta分布是二项分布的共轭先验分布
$$Beta(p\mid\alpha,\beta )+Count(m_1,m_2)=Beta(p\mid\alpha+m_1,\beta+m_2)$$
对于上式，对于事件A，假设其发生的概率为p，不发生的概率为1-p，发生的次数为$m_1$，不发生的概率为$m_2$，且有$m_1+m_2=n$。则对于参数$m_1$，则有：
$$P(m_1\mid p)=p^{m_1}(1-p)^{n-m_1}=p^{m_1}(1-p)^{m_2}$$
而对于参数p，则是服从参数为$\alpha$和$\beta$的Beta分布：
$$P(p\mid\alpha,\beta)=\frac{p^{a-1}(1-p)^{b-1}}{\int_{0}^{1}p^{a-1}(1-p)^{b-1}dp}$$
已知在贝叶斯定理中有如下的公式成立：
$$P(B\mid A)=\frac{P(A\mid B)P(B)}{P(A)}\propto P(A\mid B)P(B)$$
则对于上述的后验概率，即为：
$$\begin{matrix}P(p\mid m_1)=\frac{P(m_1\mid p)\cdot P(p)}{P(m_1)}\\\propto P(m_1\mid p)\cdot P(p)\\=p^{m_1}(1-p)^{m_2}\cdot\frac{p^{a-1}(1-p)^{b-1}}{\int_{0}^{1}p^{a-1}(1-p)^{b-1}dp}\\\propto p^{m_1}(1-p)^{m_2}\cdot p^{a-1}(1-p)^{b-1}\\=p^{a+m_1-1}(1-p)^{b+m_2-1}\end{matrix}$$
由上可知，Beta分布是二项分布的共轭先验分布。
2、Dirichlet分布是多项式分布的共轭先验分布
$$Dir(\vec{p}\mid\vec{\alpha})+MultCount(\vec{m})=Dir(\vec{p}\mid\vec{\alpha}+\vec{m})$$
我们对上式采用与Beta分布同样的证明方式，对于多项式分布，有下式成立：
$$P(\vec{m}\mid\vec{p})=p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}$$
然而概率$\vec{p}$服从的参数为$\vec{\alpha}$的Dirichlet分布，即：
$$P(\vec{p}\mid\vec{\alpha})=\frac{p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}}{D(\alpha_1,\alpha_2,\cdots,\alpha_k)}$$
由贝叶斯定理可知：
$$\begin{matrix}P(\vec{p}\mid\vec{m})=\frac{P(\vec{m}\mid\vec{p})\cdot P(\vec{p})}{P(\vec{m})}\propto P(\vec{m}\mid\vec{p})\cdot P(\vec{p})\\=p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}\cdot\frac{p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}}{D(\alpha_1,\alpha_2,\cdots,\alpha_k )}\propto p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}\cdot p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}\\=p_1^{m_1+\alpha_1}p_2^{m_2+\alpha_2}\cdots p_k^{m_k+\alpha_k}\end{matrix}$$
由此可知，Dirichlet分布是多项式分布的共轭先验分布。
LDA求解之Gibbs采样算法
Gibbs采样算法求解LDA的思路
首先，回顾LDA的模型图如下：
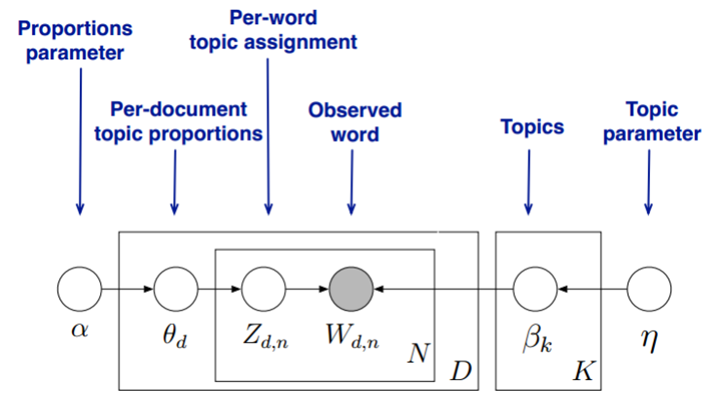在 Gibbs 采样算法求解 LDA 的方法中，我们的 $\alpha, \eta$ 是已知的先验输入，我们的目标是得到各个 $z_{dn}, w_{kn}$ 对应的整体 $\vec z, \vec w$ 的概率分布，即文档主题的分布和主题词的分布。由于我们是采用 Gibbs 采样法，则对于要求的目标分布，我们需要得到对应分布各个特征维度的条件概率分布。
我们的所有文档联合起来形成的词向量 $\vec w$ 是已知的数据，不知道的是语料库主题 $\vec z$ 的分布。假如我们可以先求出 w, z 的联合分布 $p(\vec w, \vec z)$，进而可以求出某一个词 $w_i$ 对应主题特征 $z_i$ 的条件概率分布 $p(z_i=k|\vec w, \vec z_{\neg i})$。其中，$\vec z_{\neg i}$ 代表去掉下标为 i 的词对应的主题后的主题分布。有了条件概率分布 $p(z_i=k|\vec w, \vec z_{\neg i})$，我们就可以进行 Gibbs 采样，最终在 Gibbs 采样收敛后得到第 i 个词的主题。
如果我们通过采样得到了所有词的主题，那么通过统计所有词的主题计数，就可以得到各个主题的词分布。接着统计各个文档对应词的主题计数，就可以得到各个文档的主题分布。
主题和词的联合分布与条件分布的求解
要使用 Gibbs 采样求解 LDA，关键是得到条件概率 $p(z_i=k|\vec w,\vec z_{\neg i})$ 的表达式。那么这一节我们的目标就是求出这个表达式供 Gibbs 采样使用。
首先我们简化下 Dirichlet 分布的表达式,其中 $\triangle(\alpha)$ 是归一化参数：
$$Dirichlet(\vec p|\vec \alpha)=\frac{\Gamma(\sum\limits_{k=1}^K\alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^Kp_k^{\alpha_k-1}=\frac{1}{\triangle(\vec \alpha)}\prod_{k=1}^Kp_k^{\alpha_k-1}$$
现在我们先计算下第 d 个文档的主题的条件分布 $p(\vec z_d|\alpha)$，在上一篇中我们讲到 $\alpha\to\theta_d\to\vec z_d$ 组成了 Dirichlet-multi 共轭,利用这组分布，计算 $p(\vec z_d|\vec \alpha)$ 如下：
$$\begin{align}p(\vec z_d|\vec \alpha) &=\int p(\vec z_d| \vec \theta_d)p(\theta_d| \vec \alpha)d \vec \theta_d\\&=\int \prod_{k=1}^Kp_k^{n_d^{(k)}}Dirichlet(\vec \alpha)d\vec \theta_d\\&=\int \prod_{k=1}^Kp_k^{n_d^{(k)}}\frac{1}{\triangle(\vec \alpha)}\prod_{k=1}^Kp_k^{\alpha_k-1}d\vec \theta_d\\&= \frac{1}{\triangle(\vec \alpha)}\int \prod_{k=1}^Kp_k^{n_d^{(k)}+\alpha_k-1}d\vec \theta_d\\&=\frac{\triangle(\vec n_d+\vec \alpha)}{\triangle(\vec \alpha)}\end{align}$$
其中，在第 d 个文档中，第 k 个主题的词的个数表示为：$n_d^{(k)}$,对应的多项分布的计数可以表示为：
$$\vec n_d=(n_d^{(1)},n_d^{(2)},…n_d^{(K)})$$
有了单一一个文档的主题条件分布，则可以得到所有文档的主题条件分布为：
$$p(\vec z|\vec \alpha)= \prod_{d=1}^Mp(\vec z_d|\vec \alpha)= \prod_{d=1}^M\frac{\triangle(\vec n_d+ \vec \alpha)}{\triangle(\vec \alpha)}$$
同样的方法，可以得到，所有主题对应的词的条件分布 $p(\vec w|\vec z,\vec \eta)$ 为：
$$p(\vec w|\vec z,\vec \eta)=\prod_{k=1}^Kp(\vec w_k|\vec z,\vec \eta)=\prod_{k=1}^K\frac{\triangle(\vec n_k+ \vec \eta)}{\triangle(\vec \eta)}$$
其中，第 k 个主题中，第 v 个词的个数表示为：$n_k^{(v)}$,对应的多项分布的计数可以表示为：
$$\vec n_k=(n_k^{(1)},n_k^{(2)},…n_k^{(V)})$$
最终我们得到主题和词的联合分布 $p(\vec w,\vec z|\vec \alpha, \vec \eta)$ 如下：
$$p(\vec w,\vec z) \propto p(\vec w,\vec z|\vec \alpha, \vec \eta)=p(\vec z|\vec \alpha)p(\vec w|\vec z,\vec \eta)= \prod_{d=1}^M\frac{\triangle(\vec n_d+ \vec \alpha)}{\triangle(\vec \alpha)}\prod_{k=1}^K\frac{\triangle(\vec n_k+ \vec \eta)}{\triangle(\vec \eta)}$$
有了联合分布，现在我们就可以求 Gibbs 采样需要的条件分布 $p(z_i=k|\vec w,\vec z_{\neg i})$ 了。需要注意的是这里的 i 是一个二维下标，对应第 d 篇文档的第 n 个词。
对于下标 i,由于它对应的词 $w_i$ 是可以观察到的，因此我们有：
$$p(z_i=k|\vec w,\vec z_{\neg i})\propto p(z_i=k,w_i=t|\vec w_{\neg i},\vec z_{\neg i})$$
对于 $z_i=k,w_i=t$,它只涉及到第 d 篇文档和第 k 个主题两个 Dirichlet-multi 共轭，即：
$$\vec \alpha\to\vec \theta_d\to\vec z_d$$
$$\vec \eta\to\vec \beta_k\to\vec w_{(k)}$$
其余的 M+K-2 个 Dirichlet-multi 共轭和它们这两个共轭是独立的。如果我们在语料库中去掉 $z_i,w_i$,并不会改变之前的 M+K 个 Dirichlet-multi 共轭结构，只是向量的某些位置的计数会减少，因此对于 $\vec \theta_d,\vec \beta_k$,对应的后验分布为：
$$p(\vec \theta_d|\vec w_{\neg i},\vec z_{\neg i})=Dirichlet(\vec \theta_d|\vec n_{d,\neg i}+\vec \alpha)$$
$$p(\vec \beta_k|\vec w_{\neg i},\vec z_{\neg i})=Dirichlet(\vec \beta_k|\vec n_{k,\neg i}+\vec \eta)$$
现在开始计算 Gibbs 采样需要的条件概率：
$$\begin{align}p(z_i=k|\vec w,\vec z_{\neg i}) & \propto p(z_i=k,w_i=t|\vec w_{\neg i},\vec z_{\neg i})\\&=\int p(z_i=k,w_i=t,\vec \theta_d,\vec \beta_k|\vec w_{\neg i},\vec z_{\neg i})d\vec \theta_d d\vec \beta_k \\&= \int p(z_i=k, \vec \theta_d| \vec w_{\neg i},\vec z_{\neg i})p(w_i=t,\vec \beta_k| \vec w_{\neg i},\vec z_{\neg i})d\vec \theta_d d\vec \beta_k \\&= \int p(z_i=k|\vec \theta_d)p(\vec \theta_d| \vec w_{\neg i},\vec z_{\neg i})p(w_i=t|\vec \beta_k)p(\vec \beta_k|\vec w_{\neg i},\vec z_{\neg i})d\vec \theta_d d\vec \beta_k \\&=\int p(z_i=k|\vec \theta_d)Dirichlet(\vec \theta_d|\vec n_{d,\neg i}+\vec \alpha)d\vec \theta_d*\int p(w_i=t|\vec \beta_k)Dirichlet(\vec \beta_k|\vec n_{k,\neg i}+\vec \eta)d\vec \beta_k\\&=\int \theta_{dk}Dirichlet(\vec \theta_d|\vec n_{d,\neg i}+\vec \alpha)d\vec \theta_d\int \beta_{kt}Dirichlet(\vec \beta_k|\vec n_{k,\neg i}+\vec \eta)d\vec \beta_k\\&=E_{Dirichlet(\theta_d)}(\theta_{dk})E_{Dirichlet(\beta_k)}(\beta_{kt})\end{align}$$
在 LDA 基础里我们讲到了 Dirichlet 分布的期望公式，因此我们有：
$$E_{Dirichlet(\theta_d)}(\theta_{dk})=\frac{n_{d,\neg i}^{k}+\alpha_k}{\sum\limits_{s=1}^Kn_{d,\neg i}^{s}+\alpha_s}$$
$$E_{Dirichlet(\beta_k)}(\beta_{kt})=\frac{n_{k,\neg i}^{t}+\eta_t}{\sum\limits_{f=1}^Vn_{k,\neg i}^{f}+\eta_f}$$
最终我们得到每个词对应主题的 Gibbs 采样的条件概率公式为：$$p(z_i=k|\vec w,\vec z_{\neg i}) =\frac{n_{d,\neg i}^{k}+\alpha_k}{\sum\limits_{s=1}^K n_{d,\neg i}^{s}+\alpha_s} \ \frac{n_{k,\neg i}^{t}+\eta_t}{\sum\limits_{f=1}^V n_{k,\neg i}^{f}+\eta_f}$$
有了这个公式，我们就可以用Gibbs采样去采样所有词的主题，当Gibbs采样收敛后，即得到所有词的采样主题。
利用所有采样得到的词和主题的对应关系，我们就可以得到每个文档词主题的分布$\theta_d$和每个主题中所有词的分布$\beta_k$。
LDA Gibbs采样算法流程总结
LDA Gibbs采样算法流程。
- 选择合适的主题数K, 选择合适的超参数向量$K,\vec \alpha,\vec \eta$
- 对应语料库中每一篇文档的每一个词，随机的赋予一个主题编号z
- 重新扫描语料库，对于每一个词，利用Gibbs采样公式更新它的topic编号，并更新语料中该词的编号。
- 重复第3步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。
- 统计语料库中的各个文档各个词的主题，得到文档主题分布$\theta_d$，统计语料库中各个主题词的分布，得到LDA的主题与词的分布$\beta_k$。
此时我们的模型已定，也就是LDA的各个主题的词分布$\beta_k$已经确定，我们需要得到的是该文档的主题分布。因此在Gibbs采样时，我们的$E_{Dirichlet(\beta_k)}(\beta_{kt})$已经固定，只需要对前半部分$E_{Dirichlet(\theta_d)}(\theta_{dk})$进行采样计算即可。
LDA Gibbs采样算法的预测流程：
- 对应当前文档的每一个词，随机的赋予一个主题编号z
- 重新扫描当前文档，对于每一个词，利用Gibbs采样公式更新它的topic编号。
- 重复第2步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。
- 统计文档中各个词的主题，得到该文档主题分布。
LDA Gibbs采样算法小结
使用Gibbs采样算法训练LDA模型，我们需要先确定三个超参数$K,\vec \alpha,\vec \eta$。其中选择一个合适的K尤其关键, 这个值一般和我们解决问题的目的有关。如果只是简单的语义区分，则较小的K即可，如果是复杂的语义区分，则K需要较大，而且还需要足够的语料。由于Gibbs采样可以很容易的并行化，因此也可以很方便的使用大数据平台来分布式的训练海量文档的LDA模型。
LDA求解之变分推断EM算法
变分推断EM算法求解LDA的思路
变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。首先来看EM算法在这里的使用，我们的模型里面有隐藏变量$\theta,\beta,z$，模型的参数是$\alpha,\eta$。为了求出模型参数和对应的隐藏变量分布，EM算法需要在E步先求出隐藏变量$\theta,\beta,z$的基于条件概率分布的期望，接着在M步极大化这个期望，得到更新的后验模型参数$\alpha,\eta$。
问题是在EM算法的E步，由于$\theta,\beta,z$的耦合，我们难以求出隐藏变量$\theta,\beta,z$的条件概率分布，也难以求出对应的期望，需要“变分推断“来帮忙，这里所谓的变分推断，也就是在隐藏变量存在耦合的情况下，我们通过变分假设，即假设所有的隐藏变量都是通过各自的独立分布形成的，这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布，这样就可以顺利的使用EM算法了。
当进行若干轮的E步和M步的迭代更新之后，我们可以得到合适的近似隐藏变量分布$\theta,\beta,z$和模型后验参数$\alpha,\eta$，进而就得到了我们需要的LDA文档主题分布和主题词分布。
可见要完全理解LDA的变分推断EM算法，需要搞清楚它在E步变分推断的过程和推断完毕后EM算法的过程。
LDA的变分推断思路
要使用EM算法，我们需要求出隐藏变量的条件概率分布如下：
$$p(\theta,\beta,z|w,\alpha,\eta)=\frac{p(\theta,\beta,z, w|\alpha,\eta)}{p(w|\alpha,\eta)}$$
前面讲到由于$\theta,\beta,z$之间的耦合，这个条件概率是没法直接求的，但是如果不求它就不能用EM算法了。怎么办呢，我们引入变分推断，具体是引入基于mean field assumption的变分推断，这个推断假设所有的隐藏变量都是通过各自的独立分布形成的，如下图所示：
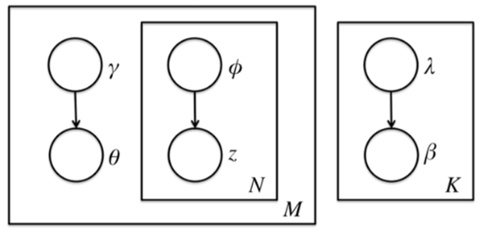我们假设隐藏变量$\theta$是由独立分布$\gamma$形成的，隐藏变量z是由独立分布$\phi$形成的，隐藏变量$\beta$是由独立分布$\lambda$形成的。这样我们得到了三个隐藏变量联合的变分分布q为：
$$\begin{align}q(\beta,z,\theta|\lambda,\phi,\gamma)&=\prod_{k=1}^Kq(\beta_k|\lambda_k)\prod_{d=1}^Mq(\theta_d,z_d|\gamma_d,\phi_d)\\&=\prod_{k=1}^Kq(\beta_k|\lambda_k)\prod_{d=1}^M(q(\theta_d|\gamma_d)\prod_{n=1}^{N_d}q(z_{dn}|\phi_{dn}))\end{align}$$
我们的目标是用$q(\beta,z,\theta|\lambda,\phi,\gamma)$来近似的估计$p(\theta,\beta,z|w,\alpha,\eta)$，也就是说需要这两个分布尽可能的相似，用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离，即：
$$(\lambda^*,\phi^*,\gamma^*)=\underbrace{arg\;min}_{\lambda,\phi,\gamma}D(q(\beta,z,\theta|\lambda,\phi,\gamma)||p(\theta,\beta,z|w,\alpha,\eta))$$
其中$D(q||p)$即为KL散度或KL距离，对应分布q和p的交叉熵。即：
$$D(q||p)=\sum\limits_{x}q(x)log\frac{q(x)}{p(x)}=E_{q(x)}(log\;q(x)-log\;p(x))$$
我们的目的就是找到合适的$\lambda^*,\phi^*,\gamma^*$,然后用$q(\beta,z,\theta|\lambda^*,\phi^*,\gamma^*)$来近似隐藏变量的条件分布$p(\theta,\beta,z|w,\alpha,\eta)$，进而使用EM算法迭代。
这个合适的$\lambda^*,\phi^*,\gamma^*$,也不是那么好求的，怎么办呢？我们先看看我能文档数据的对数似然函数$log(w|\alpha,\eta)$。如下,为了简化表示，我们用$E_q(x)$代替$E_{q(\beta,z,\theta|\lambda,\phi,\gamma)}(x)$，用来表示x对于变分分布$q(\beta,z,\theta|\lambda,\phi,\gamma)$的期望。
$$\begin{align}\log(w|\alpha,\eta)&=\log\int\int\sum\limits_zp(\theta,\beta,z, w|\alpha,\eta)d\theta d\beta\\&=\log\int\int\sum\limits_z\frac{p(\theta,\beta,z, w|\alpha,\eta)q(\beta,z,\theta|\lambda,\phi,\gamma)}{q(\beta,z,\theta|\lambda,\phi,\gamma)}d\theta d\beta \\&=\log\;E_q\frac{p(\theta,\beta,z, w|\alpha,\eta)}{q(\beta,z,\theta|\lambda,\phi,\gamma)}\\&\geq E_q\;\log\frac{p(\theta,\beta,z, w|\alpha,\eta)}{q(\beta,z,\theta|\lambda,\phi,\gamma)}\\&=E_q\;\log{p(\theta,\beta,z, w|\alpha,\eta)}-E_q\;\log{q(\beta,z,\theta|\lambda,\phi,\gamma)}\end{align}$$
其中用到了Jensen不等式：
$$f(E(x))\geq E(f(x))\;\;$$
f(x)为凹函数
我们一般记为：
$$L(\lambda,\phi,\gamma;\alpha,\eta)=E_q\;log{p(\theta,\beta,z, w|\alpha,\eta)}-E_q\;log{q(\beta,z,\theta|\lambda,\phi,\gamma)}$$
由于$L(\lambda,\phi,\gamma;\alpha,\eta)$是我们的对数似然的一个下界，所以这个L一般称为ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度有什么关系呢？注意到：
$$\begin{align}D(q(\beta,z,\theta|\lambda,\phi,\gamma)||p(\theta,\beta,z|w,\alpha,\eta))&=E_q log q(\beta,z,\theta|\lambda,\phi,\gamma)- E_q log p(\theta,\beta,z|w,\alpha,\eta)\\&=E_q log q(\beta,z,\theta|\lambda,\phi,\gamma)- E_q log\frac{p(\theta,\beta,z, w|\alpha,\eta)}{p(w|\alpha,\eta)}\\&=-L(\lambda,\phi,\gamma;\alpha,\eta) + log(w|\alpha,\eta) \end{align}$$
在式中，由于对数似然部分和我们的KL散度无关，可以看做常量，因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数$\lambda,\phi,\gamma$。
极大化ELBO求解变分参数
为了极大化ELBO，我们首先对ELBO函数做一个整理如下：
$$\begin{align}L(\lambda,\phi,\gamma;\alpha,\eta)&=E_q[\log p(\beta|\eta)]+ E_q[\log p(z|\theta)] +E_q[\log p(\theta|\alpha)]\\&+ E_q[\log p(w|z,\beta)]-E_q[\log q(\beta|\lambda)]\\&-E_q[\log q(z|\phi)] -E_q[\log q(\theta|\gamma)] \end{align}$$
可见展开后有7项，现在我们需要对这7项分别做一个展开。为了简化篇幅，这里只对第一项的展开做详细介绍。在介绍第一项的展开前，我们需要了解指数分布族的性质。指数分布族是指下面这样的概率分布：
$$p(x|\theta)=h(x)\exp(\eta(\theta)*T(x)-A(\theta))$$
其中，$A(x)$为归一化因子，主要是保证概率分布累积求和后为1，引入指数分布族主要是它有下面这样的性质：
$$\frac{d}{d\eta(\theta)}A(\theta)=E_{p(x|\theta)}[T(x)]$$
这个证明并不复杂，这里不累述。我们的常见分布比如Gamma分布，Beta分布，Dirichlet分布都是指数分布族。有了这个性质，意味着我们在ELBO里面一大推的期望表达式可以转化为求导来完成，这个技巧大大简化了计算量。
回到我们ELBO第一项的展开如下：
$$\begin{align}E_q[\log p(\beta|\eta)] &= E_q[\log\prod_{k=1}^K(\frac{\Gamma(\sum\limits_{i=1}^V\eta_i)}{\prod_{i=1}^V\Gamma(\eta_i)}\prod_{i=1}^V\beta_{ki}^{\eta_i-1})]\\&=K\log\Gamma(\sum\limits_{i=1}^V\eta_i)-K\sum\limits_{i=1}^V\log\Gamma(\eta_i) +\sum\limits_{k=1}^KE_q[\sum\limits_{i=1}^V(\eta_i-1)\log\beta_{ki}]\end{align}$$
式中的第三项的期望部分，可以用上面讲到的指数分布族的性质，转化为一个求导过程。即：
$$E_q[\sum\limits_{i=1}^V\log\beta_{ki}]=(\log\Gamma(\lambda_{ki})-\log\Gamma(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))^{‘}=\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}})$$
其中：
$$\Psi(x)=\frac{d}{dx}\log\Gamma(x)=\frac{\Gamma^{‘}(x)}{\Gamma(x)}$$
最终，我们得到EBLO第一项的展开式为：
$$\begin{align}E_q[\log p(\beta|\eta)] &= K\log\Gamma(\sum\limits_{i=1}^V\eta_i)-K\sum\limits_{i=1}^V\log\Gamma(\eta_i) +\sum\limits_{k=1}^K\sum\limits_{i=1}^V(\eta_i-1)(\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))\end{align}$$
类似的方法求解其他6项，可以得到ELBO的最终关于变分参数$\lambda,\phi,\gamma$的表达式。其他6项的表达式为：
$$\begin{align}E_q[\log p(z|\theta)]=\sum\limits_{n=1}^N\sum\limits_{k=1}^K\phi_{nk}\Psi(\gamma_{k})-\Psi(\sum\limits_{k^{‘}=1}^K\gamma_{k^{‘}})\end{align}$$
$$\begin{align}E_q[\log p(\theta|\alpha)] &= \log\Gamma(\sum\limits_{k=1}^K\alpha_k)-\sum\limits_{k=1}^K\log\Gamma(\alpha_k) +\sum\limits_{k=1}^K(\alpha_k-1)(\Psi(\gamma_{k})-\Psi(\sum\limits_{k^{‘}=1}^K\gamma_{k^{‘}}))\end{align}$$
$$\begin{align} E_q[\log p(w|z,\beta)] &=\sum\limits_{n=1}^N\sum\limits_{k=1}^K\sum\limits_{i=1}^V\phi_{nk}w_n^i(\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))\end{align}$$
$$\begin{align}E_q[\log q(\beta|\lambda)]=\sum\limits_{k=1}^K(\log\Gamma(\sum\limits_{i=1}^V\lambda_{ki})-\sum\limits_{i=1}^V\log\Gamma(\lambda_{ki}))+\sum\limits_{k=1}^K\sum\limits_{i=1}^V(\lambda_{ki}-1)(\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))\end{align}$$
$$\begin{align}E_q[\log q(z|\phi)]&=\sum\limits_{n=1}^N\sum\limits_{k=1}^K\phi_{nk}\log\phi_{nk}\end{align}$$
$$\begin{align} E_q[\log q(\theta|\gamma)]&= \log\Gamma(\sum\limits_{k=1}^K\gamma_k)-\sum\limits_{k=1}^K\log\Gamma(\gamma_k) + \sum\limits_{k=1}^K(\gamma_k-1)(\Psi(\gamma_{k})-\Psi(\sum\limits_{k^{‘}=1}^K\gamma_{k^{‘}}))\end{align}$$
有了ELBO的具体的关于变分参数λ,ϕ,γ的表达式，我们就可以用EM算法来迭代更新变分参数和模型参数了。
EM算法之E步：获取最优变分参数
有了前面变分推断得到的ELBO函数为基础，我们就可以进行EM算法了。但是和EM算法不同的是这里的E步需要在包含期望的EBLO计算最佳的变分参数。如何求解最佳的变分参数呢？通过对ELBO函数对各个变分参数$\lambda,\phi,\gamma$分别求导并令偏导数为0，可以得到迭代表达式，多次迭代收敛后即为最佳变分参数。
这里就不详细推导了，直接给出各个变分参数的表达式如下：
$$\begin{align}\phi_{nk}&\propto\exp(\sum\limits_{i=1}^Vw_n^i(\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))+\Psi(\gamma_{k})-\Psi(\sum\limits_{k^{‘}=1}^K\gamma_{k^{‘}}))\end{align}$$
其中，$w_n^i=1$当且仅当文档中第n个词为词汇表中第i个词。
$$\begin{align}\gamma_k&=\alpha_k+\sum\limits_{n=1}^N\phi_{nk}\end{align}$$
$$\begin{align}\lambda_{ki}&=\eta_i+\sum\limits_{n=1}^N\phi_{nk}w_n^i\end{align}$$
由于变分参数$\lambda$决定了$\beta$的分布，对于整个语料是共有的，因此我们有：
$$\begin{align}\lambda_{ki}&=\eta_i+ \sum\limits_{d=1}^M\sum\limits_{n=1}^{N_d}\phi_{dnk}w_{dn}^i\end{align}$$
最终我们的E步就是用上式来更新三个变分参数。当我们得到三个变分参数后，不断循环迭代更新，直到这三个变分参数收敛。当变分参数收敛后，下一步就是M步，固定变分参数，更新模型参数$\alpha,\eta$了。
EM算法之M步：更新模型参数
由于我们在E步，已经得到了当前最佳变分参数，现在我们在M步就来固定变分参数，极大化ELBO得到最优的模型参数$\alpha,\eta$。求解最优的模型参数$\alpha,\eta$的方法有很多，梯度下降法，牛顿法都可以。LDA这里一般使用的是牛顿法，即通过求出ELBO对于$\alpha,\eta$的一阶导数和二阶导数的表达式，然后迭代求解$\alpha,\eta$在M步的最优解。
对于$\alpha$,它的一阶导数和二阶导数的表达式为：
$$\nabla_{\alpha_k}L=M(\Psi(\sum\limits_{k^{‘}=1}^K\alpha_{k^{‘}})-\Psi(\alpha_{k}))+\sum\limits_{d=1}^M(\Psi(\gamma_{dk})-\Psi(\sum\limits_{k^{‘}=1}^K\gamma_{dk^{‘}}))$$
$$\nabla_{\alpha_k\alpha_j}L=M(\Psi^{‘}(\sum\limits_{k^{‘}=1}^K\alpha_{k^{‘}})-\delta(k,j)\Psi^{‘}(\alpha_{k}))$$
其中，当且仅当k=j时，$\delta(k,j)=1$,否则$\delta(k,j)=0$。
对于$\eta$,它的一阶导数和二阶导数的表达式为：
$$\nabla_{\eta_i}L=K(\Psi(\sum\limits_{i^{‘}=1}^V\eta_{i^{‘}})-\Psi(\eta_{i}))+\sum\limits_{k=1}^K(\Psi(\lambda_{ki})-\Psi(\sum\limits_{i^{‘}=1}^V\lambda_{ki^{‘}}))$$
$$\nabla_{\eta_i\eta_j}L= K(\Psi^{‘}(\sum\limits_{i^{‘}=1}^V\eta_{i^{‘}})- \delta(i,j)\Psi^{‘}(\eta_{i}))$$
其中，当且仅当i=j时，$\delta(i,j)=1$,否则$\delta(i,j)=0$。
最终牛顿法法迭代公式为：
$$\begin{align}\alpha_{k}=\alpha_k+\frac{\nabla_{\alpha_k}L}{\nabla_{\alpha_k\alpha_j}L}\end{align}$$
$$\begin{align}\eta_{i}=\eta_i+\frac{\nabla_{\eta_i}L}{\nabla_{\eta_i\eta_j}L}\end{align}$$
LDA主题模型实例
使用场景
- 自动推测出文档集中讨论的主题
- 推测出的主题信息可以用于总结和组织文档，也可以用于降低特征和维度
- 文档X在讨论什么？->主题识别
- 文档X和文档Y的相似度是多少？->文本相似度计算
- 如果我对主题Z感兴趣，那么哪篇文档最对我的胃口？->推荐系统
- 其他使用场景
- 情感分析
- 图片目标定位
- 音乐自动谐波分析
- 生物信息学
假设
- 主题相似的文档将使用相似的词组
- 文件定义/建模：
- 文档是潜在主题的概率分布
- 主题是单词的概率分布
文档-主题分布:
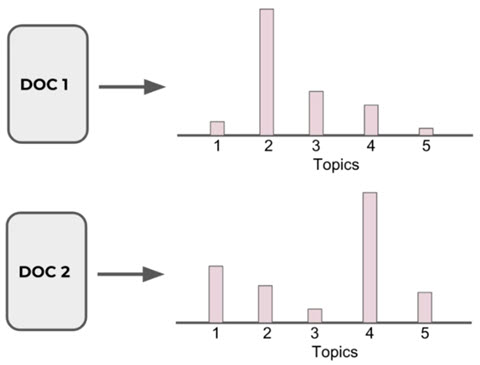
主题-词分布:
LDA认为单词携带了强烈的语义信息，包含相似主题的文档中会出现相似的单词组。
一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成，每个主题都有一个单词的概率分布与之相关联。
LDA模型与别的词袋模型的不同之处就在于，它利用了单词的概率分布而不是单词的出现频率。其他词袋模型可能会考虑文档中出现得最频繁的单词，而LDA使用了一种更全面的方法：考虑主题的单词分布。
盘子表示法Plate Notation
当我们谈论LDA时，经常用盘子表示法来简洁地表达LDA模型参数间的依赖关系。
LDA是一个三层贝叶斯模型，如下图所示，矩形框是”盘子”，代表复制品(replicates)。
- 大盘子代表文档层
- 中盘子代表单词层
- 小盘子代表主题层
根据这些参数指向的位置(落在哪个盘子中)，可以看出一个参数是应用于文档层，还是应用于主题层，还是单词层。
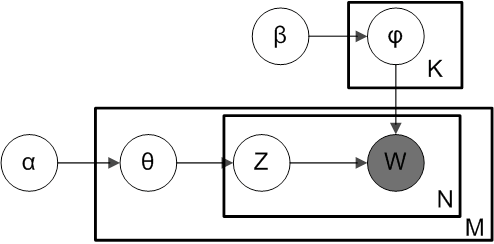
参数：
- M:语料库中文档的数量
- N:文档中单词的数量
- K:语料库中主题的数量
- $\alpha$:每篇文档的主题分布(先验狄利克雷分布)的参数，是一个K维向量，K是主题数量
- 越高，代表每篇文档可能包含更多的主题，而不只是包含一个或者两个特定的主题
- 越低，代表每篇文档包含的主题数越少
- $\theta_i$:文档i的主题分布
- $z_{ij}$:文档i中第j个单词的主题编号，服从多项式分布
- $\beta$:每个主题的单词分布(先验狄利克雷分布)的参数，是一个V维向量，V是文档中单词的数量
- 越高，代表每个主题可能包含更多的单词
- 越低，代表每个主题包含的单词数越少
- $\varphi{z{ij}}$:主题$z_{ij}$的单词分布
- $w_{ij}$:特定的单词，服从多项式分布
生成过程：主题->文档
简单点，一篇文档的生成分为三步：
- 决定文档中单词的数量
- 给文档选择一个主题分布(i.e.20%topicA,30%topicB,50%topicC)
- 生成文档中的单词，通过：
- 首先基于文档的主题分布选一个主题
- 再基于主题的单词分布随机选一个单词
- 重复上面两步，直到单词数量达到一开始设定的上限
举例：我们有一篇文章，它包含4个主题：Arts,Budgets,Children,Education。
如下图所示，每个主题可以被它下面的这些单词描述。
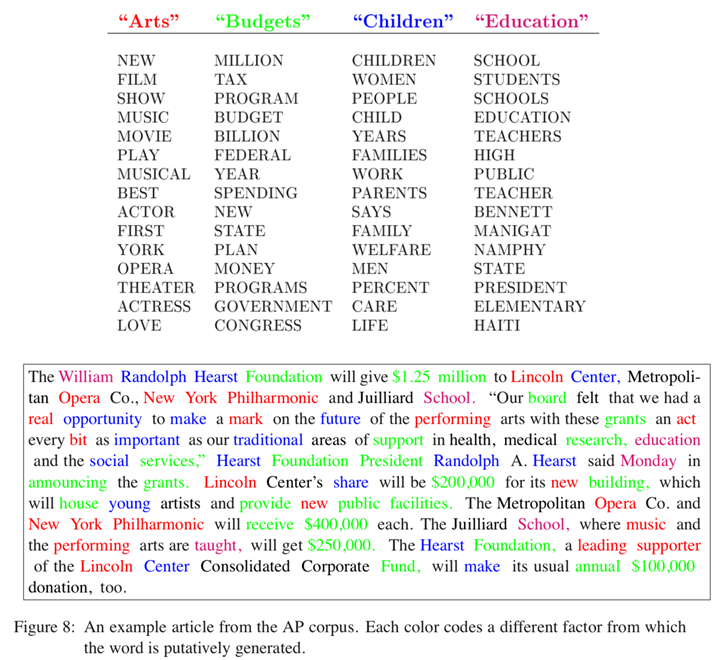
现在我们要写一篇包含这4个主题的文章：
- 设定文档的长度为1000个词
- 假设文档的主题分布是：30%Arts,20%Budgets,30%Children,20%Education
- 首先基于文档的主题分布选一个主题(根据我们的主题分布，1000个词中大约300词来自主题Arts)
- 再基于主题的单词分布随机选一个单词
- 重复上面两步1000次
这就是LDA认为的人类写文章的过程。
在生成过程中文章的语法无关紧要，重要的是单词的分布，也许我们无法阅读生成后的文章，但是我们至少能知道这篇文章的主题是关于什么的。值得注意的是，这个生成过程，从主题开始，不断挑选单词生成文档，它并不是LDA中运行的算法，而它的逆过程才是。
逆过程：文档->主题
假如你有一个语料库/文档集，你希望LDA去学习每篇文档中k个主题的分布，以及每个主题的单词分布。
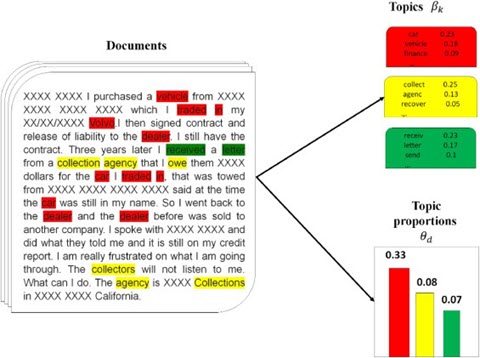
LDA从文档层回溯，去推测哪些主题可能用于生成该文档。
- 随机给每篇文档中的每个单词分配(assign)k个主题中的一个主题
- 对于每篇文档d，更新(重新采样Resample)单词的主题
- 假设除了当前文档之外的所有主题分配是正确的
- 计算两个概率
- 当前文档d中的单词被分配到主题t的概率P(topic t|doc d)
- 所有文档中被分配到主题t的单词中是单词w的概率P(word w|topic t)
- 基于这两个概率的乘积P(topic t|doc d)*P(word w|topic t)分配给单词w一个新的主题
- 不断重复上述步骤，最终达到稳定状态，这时可以认为所有主题的分配是合理的，得到文档的主题分布
根据上文提到的文档生成模型，两个概率的乘积P(topic t|doc d)*P(word w|topic t)就是主题t生成单词w的概率，所以用这个概率重新采样当前单词的主题是说得通的。
这个逆过程就是吉布斯采样。
LDA代码实例
使用数据：https://www.kaggle.com/gauravduttakiit/npr-data
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
npr = pd.read_csv('npr.csv')
print(npr.head())
cv = CountVectorizer(max_df=0.95, min_df=2, stop_words='english')
dtm = cv.fit_transform(npr['Article'])
print(len(cv.get_feature_names()))
LDA = LatentDirichletAllocation(n_components=7, random_state=42)
LDA.fit(dtm)
print(len(LDA.components_))
for i in range(len(LDA.components_)):
print(i, len(LDA.components_[i]))
for index, topic in enumerate(LDA.components_):
print(f'THE TOP 15 WORDS FOR TOPIC #{index}')
print([cv.get_feature_names()[i] for i in topic.argsort()[-15:]])
topic_results = LDA.transform(dtm)
npr['Topic'] = topic_results.argmax(axis=1)
print(npr.head())
总结
文档是主题上的概率分布，主题是单词上的概率分布。
LDA接受的输入是若干文档。她认为每篇文档中的单词是语义相关的。她试图想明白每篇文档是如何创造出来的。我们只需要告诉她有多少个主题需要构造，她就会根据主题的数量在语料库上生成主题和单词的分布。基于她的输出，可以预测新文档的主题分布，计算文档之间的相似度，文本分类。
- Input
- 文档集(Corpus)
- K: the number of topics
- Output
- 主题的单词分布(Topic-Word Distribution)->每个主题在讨论什么
- 文档的主题分布(Doc-Topic Distribution)->每篇文档中包含了哪些主题
优点：
- 对于每一个主题均可找出一些词语来描述它
- 是一个有效的主题建模工具
- 在许多领域已经展示出了很好的结果，比如推荐，文本分类
不足
- 必须事先指定主题的数量K，而这个K的选取是困难的，需要大量的试验来确定
- 假如语料库中有许多关联的主题，狄利克雷主题分布无法捕捉主题间的相关性
参考链接：
