文章内容如有错误或排版问题,请提交反馈,非常感谢!
哈夫曼编码简介
哈夫曼编码(Huffman Coding)是一种基于字符出现频率进行编码的无损数据压缩算法,由大卫·哈夫曼于1952年提出。它的核心思想是:赋予高频字符较短的编码,赋予低频字符较长的编码,从而使整个数据的平均编码长度达到最小。这是一种前缀码(Prefix Code),意味着任何字符的编码都不是另一个字符编码的前缀,这保证了编码的唯一可解码性。

原理与动机
- 传统编码的问题:固定长度编码(如ASCII)简单,但无论字符出现频率如何,都使用相同位数表示。对于包含许多重复字符(高频字符)的文件,这种方式会产生大量冗余。
- 哈夫曼编码的解决方案:利用字符频率的统计信息。通过将短码分配给高频字符,长码分配给低频字符,高频字符的短码节省的空间 > 低频字符的长码额外消耗的空间,从而使总的编码长度(比特数)显著减少。
关键概念
- 前缀码:没有任何一个字符的编码是另一个字符编码的前缀。这是哈夫曼编码能正确解码的关键。例如,假设A=0, B=10, C=110,那么接收到的比特流010110可以唯一解码为A B C,因为没有编码是另一个的前缀。
- 哈夫曼树:是构建哈夫曼编码的核心数据结构。它是一种特殊的二叉树,其中:
- 叶子节点(Leaf Nodes): 代表原始数据中的字符及其频率(或权重)。
- 内部节点(Internal Nodes): 不存储字符本身,其值是它所有子节点频率(权重)值的总和。
- 根节点(Root Node): 树的顶部节点,其值是所有字符频率的总和。
- 编码规则:
- 从根节点到每个叶子节点(代表字符)的路径定义了该字符的哈夫曼编码。
- 向左分支走通常代表’0’。
- 向右分支走通常代表’1’(约定可以互换,但需保持一致)。
构建哈夫曼树和编码的步骤

假设我们有一个源数据,包含字符A, B, C, D, E,频率分别为:A: 15, B: 7, C: 6, D: 6, E: 5 (频率总和为39)。
- 创建叶子节点集合:为每一个唯一的字符创建一个节点,节点值是其频率。把所有节点放入一个最小堆(Min-Heap)(或根据频率排序的列表)。A(15),B(7), C(6), D(6), E(5)
- 循环合并频率最低的两个节点:
- 迭代1: 从堆中弹出两个频率最小的节点:E(5)和C(6)。创建一个新节点N1,它的值是5 + 6 = 11。让E(5)成为N1的左孩子(编码’0’),C(6)成为N1的右孩子(编码’1’)。将N1(11)放回堆中。当前堆:A(15),B(7), D(6), N1(11)
- 迭代2: 弹出最小的两个:D(6)和B(7)。创建新节点N2(6+7=13)。让D(6)为左孩子(’0’),B(7)为右孩子(’1’)。放回N2(13)。当前堆:A(15),N1(11), N2(13)
- 迭代3: 弹出最小的两个:N1(11)和N2(13)。创建新节点N3(11+13=24)。让N1(11)为左孩子(’0’),N2(13)为右孩子(’1’)。放回N3(24)。当前堆:A(15),N3(24)
- 迭代4: 弹出最后两个:A(15)和N3(24)。创建根节点Root(15+24=39)。让A(15)为左孩子(’0’),N3(24)为右孩子(’1’)。
- 生成哈夫曼编码: 从根节点开始,沿着路径到每个字符(叶子节点):
- E: Root(39) -> Right(1) -> N3(24) -> Left(0) -> N1(11) -> Left(0) -> E(5) = 100
- C: Root(39) -> Right(1) -> N3(24) -> Left(0) -> N1(11) -> Right(1) -> C(6) = 101
- D: Root(39) -> Right(1) -> N3(24) -> Right(1) -> N2(13) -> Left(0) -> D(6) = 110
- B: Root(39) -> Right(1) -> N3(24) -> Right(1) -> N2(13) -> Right(1) -> B(7) = 111
- A: Root(39) -> Left(0) -> A(15) = 0
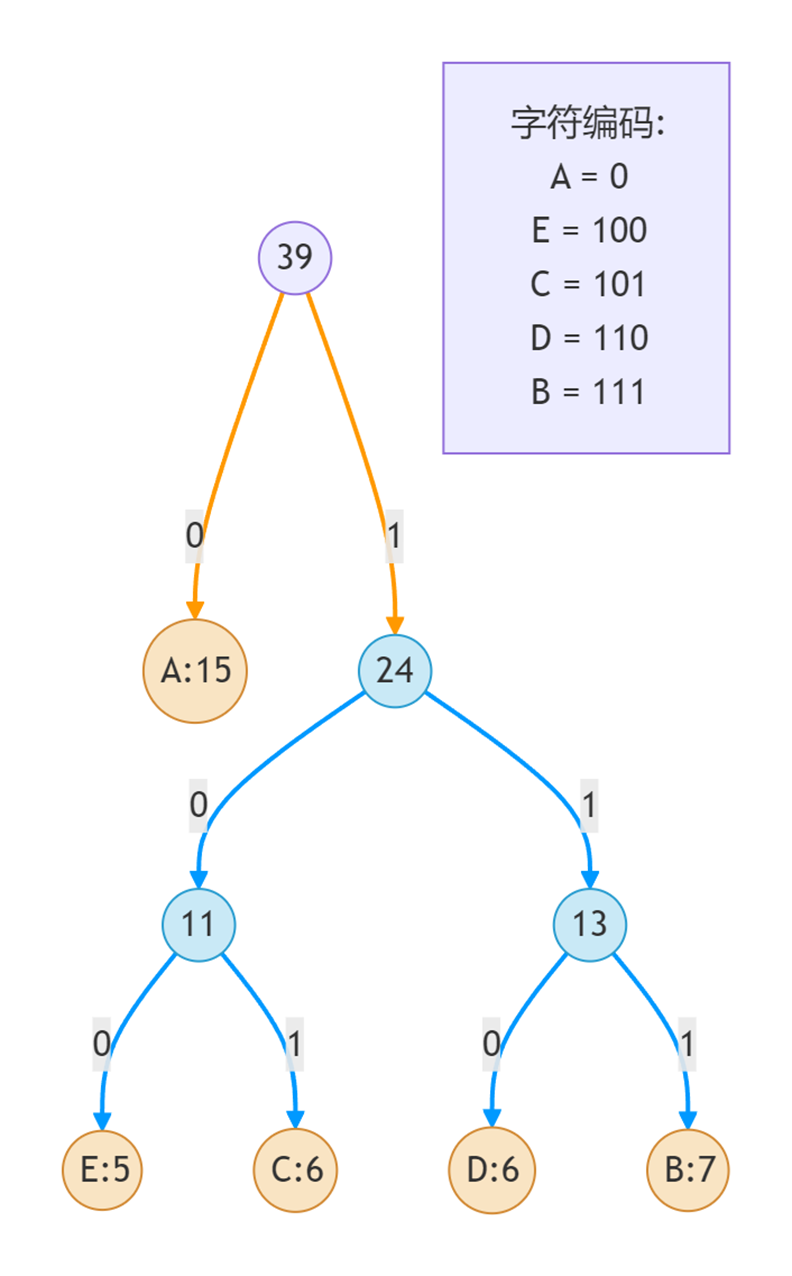
最终编码:
| 字符 | 频率 | 原始 ASCII (8 bits) | 哈夫曼编码 | 编码长度 (bits) | 该字符总比特数 (频率 * 长度) |
| A | 15 | 01000001 | 0 | 1 | 15 * 1 = 15 |
| B | 7 | 01000010 | 111 | 3 | 7 * 3 = 21 |
| C | 6 | 01000011 | 101 | 3 | 6 * 3 = 18 |
| D | 6 | 01000100 | 110 | 3 | 6 * 3 = 18 |
| E | 5 | 01000101 | 100 | 3 | 5 * 3 = 15 |
| 总计 | 39 | 39 * 8 = 312 | 15+21+18+18+15 = 87 |
分析:
- 原始数据比特数:39 个字符 * 8 bits/字符 = 312 bits。
- 哈夫曼编码比特数: 见上表计算 =87 bits。
- 压缩率:(312 – 87) / 312 ≈1% (节省了约72.1%的空间)。
- 平均编码长度:87 / 39 ≈23 bits/字符 (远低于原始8 bits/字符)。
为什么是最优?(理论依据)
哈夫曼编码是一种贪心算法(Greedy Algorithm),并且可以证明它对于给定字符及其频率,能够生成最优的前缀码(即平均编码长度最小)。其最优性基于以下两个性质:
- 贪心选择性质: 每次合并两个频率最小的节点(子树)是局部最优的选择,因为这个合并产生的新节点频率是其子树频率之和,而合并最小频率的两棵树可以最大限度地最小化它们在最终编码长度中的贡献(路径长度 * 频率)。
- 最优子结构性质: 由子树构造出来的哈夫曼树也是最优的。
算法特点
优点:
- 高效的无损压缩:对于偏斜分布的数据(少数字符出现频率非常高),压缩效果显著。
- 简单高效:构建哈夫曼树的时间复杂度为O(n log n),其中n是唯一字符的数量。编码和解码过程(借助树或编码表)非常快 O(1)。
- 前缀码保证:无需分隔符即可唯一解码。
- 自适应变体:存在自适应的哈夫曼编码算法,可以动态调整编码以适应数据流的变化。
缺点:
- 依赖频率统计:压缩前需要扫描整个数据流(或基于样本)以统计频率。对于小文件或不提供频率信息的场景,元数据(哈夫曼树本身)可能会抵消部分压缩收益。
- 频率敏感:压缩率高度依赖字符的实际频率分布。如果字符频率分布均匀,压缩效果会很差。
- 树结构需要存储/传输:为了解码,接收方需要知道哈夫曼树的结构(或等价信息)。这增加了额外的开销。常见的存储方法包括存储字符与其频率(需要再次构建树)或存储树本身的结构(如前序遍历序列)。
- 非通用:为某个数据生成的最优哈夫曼树不一定适用于其他数据。
- 对错误敏感:传输过程中的单个比特错误可能导致解码过程中的一大段数据错误(传播)。
应用
哈夫曼编码是许多主流无损压缩格式和工具的基石之一:
- 文件压缩:如ZIP,GZIP, BZIP2 (与其他技术如LZ77结合)。
- 图像压缩:JPEG(在量化后的DCT系数上使用), PNG (与LZ77结合在DEFLATE中)。GIF。
- 音频/视频压缩:作为熵编码部分用在MP3,AAC, 26x (x=1, 2, 3, 4, 5), MPEG等标准中,对量化后的变换系数或预测残差进行编码。
- 网络传输:HTTP/2的HPACK头部压缩协议中使用了类似哈夫曼的编码。
哈夫曼编码的Python实现
以下是哈夫曼编码的完整Python实现,包含构建哈夫曼树、生成编码表、编码和解码等功能:
import heapq
from collections import defaultdict
import json
class HuffmanNode:
def __init__(self, char=None, freq=0):
self.char = char # 字符(叶子节点)
self.freq = freq # 频率(权重)
self.left = None # 左子节点
self.right = None # 右子节点
# 用于堆排序,按照频率从小到大
def __lt__(self, other):
return self.freq < other.freq
class HuffmanCoding:
def __init__(self):
self.heap = [] # 最小堆
self.codes = {} # 字符到编码的映射
self.reverse_codes = {} # 编码到字符的映射
self.root = None # 哈夫曼树的根节点
def build_frequency_dict(self, text):
"""构建字符频率字典"""
freq_dict = defaultdict(int)
for char in text:
freq_dict[char] += 1
return freq_dict
def build_heap(self, freq_dict):
"""将字符频率字典构建为最小堆"""
for char, freq in freq_dict.items():
node = HuffmanNode(char, freq)
heapq.heappush(self.heap, node)
def merge_nodes(self):
"""合并节点构建哈夫曼树"""
while len(self.heap) > 1:
# 取出频率最小的两个节点
node1 = heapq.heappop(self.heap)
node2 = heapq.heappop(self.heap)
# 创建新节点作为它们的父节点
merged = HuffmanNode(freq=node1.freq + node2.freq)
merged.left = node1
merged.right = node2
# 将新节点加入堆
heapq.heappush(self.heap, merged)
# 堆中最后的节点就是根节点
self.root = heapq.heappop(self.heap)
def build_codes_helper(self, root, current_code):
"""递归构建编码表"""
if root is None:
return
# 找到叶子节点
if root.char is not None:
self.codes[root.char] = current_code
self.reverse_codes[current_code] = root.char
return
# 递归处理左右子树
self.build_codes_helper(root.left, current_code + "0")
self.build_codes_helper(root.right, current_code + "1")
def build_codes(self):
"""构建编码表和反向映射表"""
self.build_codes_helper(self.root, "")
def encode_text(self, text):
"""将文本编码为二进制字符串"""
encoded_text = ""
for char in text:
encoded_text += self.codes[char]
return encoded_text
def decode_text(self, encoded_text):
"""将二进制字符串解码为文本"""
current_code = ""
decoded_text = ""
for bit in encoded_text:
current_code += bit
# 当前编码在映射表中找到对应字符
if current_code in self.reverse_codes:
char = self.reverse_codes[current_code]
decoded_text += char
current_code = ""
return decoded_text
def compress(self, text):
"""压缩文本的完整过程"""
# 特殊情况处理
if text == "":
return "", {}
# 1. 构建频率字典
freq_dict = self.build_frequency_dict(text)
# 2. 构建最小堆
self.build_heap(freq_dict)
# 3. 合并节点构建哈夫曼树
self.merge_nodes()
# 4. 构建编码表
self.build_codes()
# 5. 编码文本
encoded_text = self.encode_text(text)
return encoded_text, freq_dict
def decompress(self, encoded_text, freq_dict):
"""解压缩的完整过程"""
# 特殊情况处理
if encoded_text == "":
return ""
# 1. 使用频率字典重建哈夫曼树
self.build_heap(freq_dict)
self.merge_nodes()
# 2. 构建编码表(反向映射)
self.build_codes()
# 3. 解码文本
decoded_text = self.decode_text(encoded_text)
return decoded_text
# 测试哈夫曼编码
def test_huffman_coding():
print("=== 哈夫曼编码测试 ===")
# 测试用例1:常规情况
text1 = "ABRACADABRA"
print(f"\n原文本: '{text1}'")
huffman = HuffmanCoding()
encoded, freq_dict = huffman.compress(text1)
decoded = huffman.decompress(encoded, freq_dict)
# 输出编码表
print("\n字符编码表:")
for char, code in sorted(huffman.codes.items()):
print(f"'{char}': {code}")
print(f"\n编码结果: {encoded}")
print(f"解码结果: '{decoded}'")
print(f"原始长度: {len(text1) * 8} 位, 编码后长度: {len(encoded)} 位")
compression_ratio = (len(text1) * 8 - len(encoded)) / (len(text1) * 8) * 100
print(f"压缩率: {compression_ratio:.2f}%")
# 验证正确性
assert decoded == text1, "解压缩结果与原始文本不一致!"
# 测试用例2:单个字符重复
text2 = "AAAAA"
print(f"\n原文本: '{text2}'")
huffman = HuffmanCoding()
encoded, freq_dict = huffman.compress(text2)
decoded = huffman.decompress(encoded, freq_dict)
print("\n字符编码表:")
for char, code in sorted(huffman.codes.items()):
print(f"'{char}': {code}")
print(f"\n编码结果: {encoded}")
print(f"解码结果: '{decoded}'")
print(f"原始长度: {len(text2) * 8} 位, 编码后长度: {len(encoded)} 位")
# 验证正确性
assert decoded == text2, "解压缩结果与原始文本不一致!"
# 测试用例3:空文本
text3 = ""
print(f"\n原文本: '{text3}'")
huffman = HuffmanCoding()
encoded, freq_dict = huffman.compress(text3)
decoded = huffman.decompress(encoded, freq_dict)
print(f"编码结果: '{encoded}'")
print(f"解码结果: '{decoded}'")
# 验证正确性
assert decoded == text3, "解压缩结果与原始文本不一致!"
# 测试用例4:复杂文本
text4 = "Huffman coding is a data compression algorithm."
print(f"\n原文本: '{text4}'")
huffman = HuffmanCoding()
encoded, freq_dict = huffman.compress(text4)
decoded = huffman.decompress(encoded, freq_dict)
print(f"\n编码结果: {encoded[:50]}... (只显示前50位)")
print(f"解码结果: '{decoded}'")
print(f"原始长度: {len(text4) * 8} 位, 编码后长度: {len(encoded)} 位")
compression_ratio = (len(text4) * 8 - len(encoded)) / (len(text4) * 8) * 100
print(f"压缩率: {compression_ratio:.2f}%")
# 验证正确性
assert decoded == text4, "解压缩结果与原始文本不一致!"
print("\n所有测试通过!")
if __name__ == "__main__":
test_huffman_coding()
实现说明
关键类与函数
- HuffmanNode: 表示哈夫曼树的节点
- char: 字符(仅叶子节点)
- freq: 字符出现的频率
- left/right: 左右子节点
- HuffmanCoding: 哈夫曼编码的主要类
- build_frequency_dict(): 统计字符频率
- build_heap(): 将字符频率构建为最小堆
- merge_nodes(): 合并节点构建哈夫曼树
- build_codes(): 递归生成编码表
- encode_text(): 编码文本为二进制串
- decode_text(): 解码二进制串为文本
- compress(): 完整的压缩过程
- decompress(): 完整的解压过程
实现步骤
- 压缩过程:
- 统计输入文本中字符的出现频率
- 创建节点对象并加入最小堆
- 循环合并频率最小的两个节点,直至形成完整树
- 从根节点递归遍历树,生成前缀码表
- 使用编码表替换文本中的字符
- 解压过程:
- 使用保存的频率字典重建哈夫曼树
- 递归遍历树重新生成编码表
- 根据编码表逐位解析二进制数据

写得不错,很清晰