引言:聚类的美好承诺与普遍困境
当我们谈论聚类分析时,脑海中往往会浮现这样一个理想场景:将相似的数据对象自动分组,为业务决策提供清晰指导。这种无监督学习方法的吸引力在于其能够探索数据内在结构,而无需预先标记的训练数据。
然而在实际应用中,许多数据科学家和分析师却发现,聚类结果常常令人失望。这种失望感跨越多个领域,在城市分析场景中表现得尤为明显。本文将以城市分析为例,深入探讨聚类算法的普遍局限性,特别是在高维数据环境中的实际挑战。
聚类基础:理想化的数学美感与现实落差
从数学角度看,聚类旨在将数据空间中相互靠近的点归为一类。在二维或三维空间中,这一概念直观易懂——我们很容易用肉眼判断点与点之间的远近关系。
然而在实际业务场景中,数据往往处于高维空间。以城市聚类分析为例,我们可能需要考虑17个甚至更多特征维度:
- 用户行为维度:城市UV、转化率、渠道占比
- 业务运营维度:订单量、间夜量、订单有效率、拒单率
- 市场结构维度:商圈覆盖率、集团产量占比、有产酒店数
- 经济指标维度:ADR、加价率、低星产量占比
维度灾难随之而来:随着特征数量增加,数据点在空间中的分布变得极其稀疏,传统的“距离”概念逐渐失去意义。
低维世界的直观美感 vs 高维空间的复杂现实
理想案例:假设我们只用“城市订单量”和“城市ADR”两个维度对城市进行聚类,结果清晰可见:
- 集群A:高订单量、低ADR(如经济型酒店主导的城市)
- 集群B:低订单量、高ADR(如高端商务城市)
- 集群C:均衡型城市
现实挑战:当我们加入更多维度时,情况变得复杂。以三个城市在四个维度上的表现为例:
| 城市 | 订单量 | ADR | 微信渠道占比 | 拒单率 |
| 城市A | 高 | 中 | 低 | 低 |
| 城市B | 中 | 高 | 高 | 低 |
| 城市C | 高 | 中 | 高 | 高 |
在二维空间中,城市A和C在“订单量-ADR”平面上很接近,但当加入“拒单率”维度后,它们反而变得疏远。这种距离概念的失真在高维数据分析中极为常见,不仅是城市分析特有的问题。
聚类算法的内在局限:通用性问题
类别数量的主观性困境
聚类作为无监督学习方法,最大的挑战之一是需要预先指定聚类数量。常见的“肘部法则”试图通过寻找拐点来确定最优类别数,但这一方法仍存在主观判断成分。
业务现实:数据到底应该分为3类、5类还是7类?这往往取决于业务需求而非数学最优解,这一困境在所有聚类应用中普遍存在。
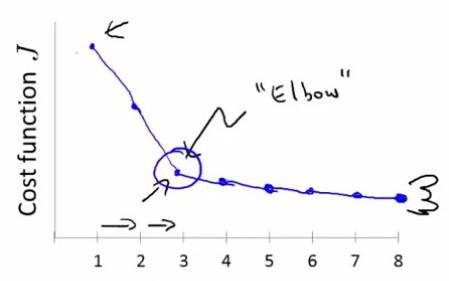
K值的确定困境
业务场景:某连锁酒店集团需要将全国城市分为不同等级,以制定差异化运营策略。
数据分析过程:使用肘部法则确定K值,得到以下SSE(误差平方和)变化曲线:
- K=3 → SSE=1250
- K=4 → SSE=890(下降360)
- K=5 → SSE=650(下降240)
- K=6 → SSE=500(下降150)
- K=7 → SSE=420(下降80)
决策困境:
- 从数学角度看,K=5之后SSE下降幅度明显减缓,似乎K=5是最优解
- 但业务团队认为:一线城市、新一线城市、二线城市、三线城市、四线及以下城市,这种5分类符合市场认知
- 然而在验证时发现,某些经济发达的三线城市与弱二线城市特征相似,被归为同一类,导致资源分配不合理
解决方案:采用轮廓系数结合业务验证的方法,最终确定K=6,将“强势三线”城市单独归类。这种主观性与客观指标的平衡是聚类应用的典型挑战。
算法选择的任意性
不同的聚类算法对相同数据会产生截然不同的结果。K-means、层次聚类、DBSCAN等算法各有偏好,而距离计算方法(欧氏距离、曼哈顿距离等)的选择也直接影响聚类效果。
技术现实:算法选择本身就成了一个需要大量实验和经验的决策过程,这在所有聚类应用中都是常见问题。
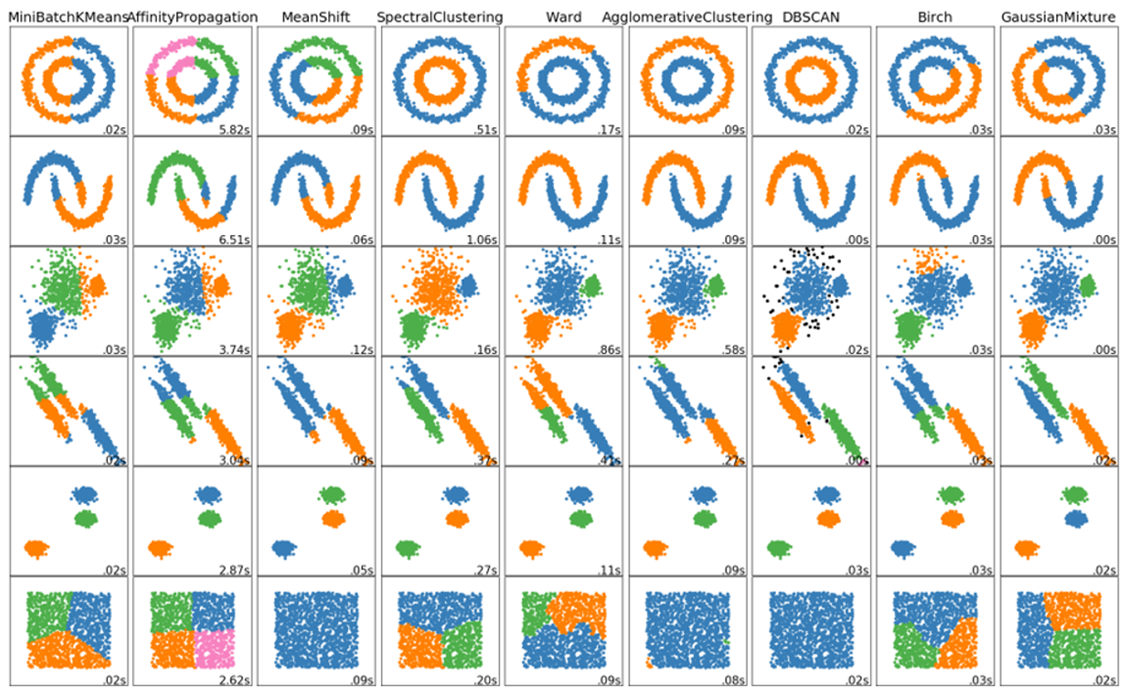
同一数据集,不同算法的对比:
K-means聚类结果(基于欧氏距离):
- 类别1:高订单量、高ADR、低拒单率(8个城市)
- 类别2:中等各项指标(45个城市)
- 类别3:低订单量、低ADR、高拒单率(247个城市)
DBSCAN聚类结果(基于密度):
- 核心城市群:15个高度相似的一二线城市
- 边缘城市群:82个具有部分相似特征的城市
- 噪声点:203个特征各异的城市
业务洞察:K-means强行将所有城市分类,而DBSCAN承认了大多数城市的独特性,这更符合业务现实——不是所有数据点都能被简单归类。算法选择本质上反映了对数据结构的不同假设。
为什么聚类分析常常失效:根本原因分析
问题一:因果关系的普遍混淆
聚类能够识别出特征相似的数据对象,但这些特征未必是影响业务结果的关键因素。例如,两个城市可能在17个维度上都相似,但导致其业务增长的核心因素可能只是其中的2-3个关键指标。
正确思路:应先通过因果分析确定影响业务的核心因素,然后基于这些关键特征进行聚类,而非盲目使用所有可用数据。
因果关系的混淆——聚类中的“根本性陷阱”
这个问题的核心在于:聚类算法发现的是“相关性”(Correlation),而业务决策需要的是“因果性”(Causation)。将两者混淆,是导致聚类结果无法指导业务行动的主要原因。
一个经典的类比:冰淇淋与溺水率
- 数据现象:冰淇淋销量越高,溺水发生率也越高
- 聚类逻辑:基于这两个变量对城市聚类
- 荒谬结论:禁止销售冰淇淋可以降低溺水率?
- 真相:共同因果因素是天气炎热
这个例子清晰地展示了:基于表面相关性的分组,其结论对于干预行动是无效甚至误导的。
在城市分析中的具体体现
假设场景:某OTA平台希望找出“高增长潜力城市”进行重点市场投入。
错误做法(先有蛋):
- 收集所有17个维度的数据
- 直接进行聚类分析
- 得到3个城市类别
- 基于表面相似性分配资源
风险与陷阱:聚类发现的是结果性指标的相似性,而非增长驱动因素的相似性。
正确做法(先有鸡):
- 定义业务目标(果):如“提升城市订单增长率”
- 因果分析识别关键因素(因):如通过回归分析找到核心驱动因素
- 筛选特征进行聚类:仅使用关键驱动因素
- 解读结果并行动:基于因果相似性制定策略
问题二:特征权重的平等假设陷阱
聚类算法默认所有特征权重相等,这在高维数据分析中尤为危险。不重要的特征噪音可能掩盖真正有意义的模式。
特征权重平等的业务案例
- 业务背景:某平台希望识别“高潜力增长型城市”进行重点投入。
- 错误做法:使用全部17个特征进行聚类分析
- 问题展现:城市D和城市E在业务逻辑上非常相似(都是新兴旅游城市,增长快速),但由于无关特征(如商圈覆盖率)的差异,被分到不同类别。
- 根本原因:聚类算法平等对待所有特征,而实际上某些特征对业务目标影响有限。
- 正确做法:
- 与业务专家确定关键增长因素
- 仅使用关键特征进行聚类
- 结果准确率显著提升
问题三:业务解释性的普遍缺失
即使数学上完美的聚类结果,也可能缺乏业务解释性。聚类算法不会告诉我们为什么这些数据被归为一类。
业务解释性挑战的案例
- 案例背景:某次聚类分析得到了一个“异常类别”,包含5个特征迥异的城市:上海、张家界、东莞、西宁、三亚。
- 深入分析发现:这些城市在“三方占比”和“城市加价率”两个指标上异常相似,反映了平台与当地酒店的合作深度。
- 业务价值:这个“意外发现”帮助平台优化了酒店合作策略,但对城市分级本身帮助有限。聚类结果需要额外的业务解读才能产生价值。
改进策略:让聚类真正为业务服务
问题导向的特征工程
不要将所有可用数据都扔给聚类算法。首先明确业务问题,然后基于问题选择相关特征。这一原则适用于所有聚类应用场景。
迭代式分析流程
- 建立“聚类-分析-验证-调整”的迭代流程:
- 初步聚类获得假设
- 深入分析各类别特征
- 业务验证聚类合理性
- 调整特征和参数重新聚类
结合监督学习方法
将聚类与分类、回归等监督学习结合使用。例如,先通过聚类发现模式,再建立预测模型验证这些模式的实际价值。
结论:理性看待聚类的价值
聚类算法是一把有力的数据探索工具,但绝非数据分析的“银弹”。其价值不在于自动给出完美答案,而在于帮助我们发现数据中隐藏的模式和假设。
关键认知转变:聚类应该是分析的起点而非终点。它为我们提供需要进一步验证的假设,而非直接可用的业务结论。
在数据分析中,成功的聚类应用需要数据技术与业务洞察的深度结合。只有理解聚类的普遍局限性,才能更好地发挥其优势,让数据真正为决策服务。城市分析中的挑战只是聚类方法普遍问题的一个具体体现,理解这一本质有助于我们在各种场景中更有效地应用这一工具。