时间序列与平稳性
在数学上,随机过程被定义为一族时间随机变量,即{x(t),t∈T},其中T表示时间t的变动范围。当T={0,±1,±2,…}时,此类随机过程x(t)是离散时间t的随机函数,称为时间序列。时间序列的构成要素有:
- 长期趋势(T)是在较长时期内受某种根本性因素作用而形成的总的变动趋势
- 季节变动(S)是在一年内随着季节的变化而发生的有规律的周期性变动。它是诸如气候条件、生产条件、节假日或人们的风俗习惯等各种因素影响的结果。
- 循环变动(C)是时间序列呈现出得非固定长度的周期性变动。循环波动的周期可能会持续一段时间,但与趋势不同,它不是朝着单一方向的持续变动,而是涨落相同的交替波动。
- 不规则变动(I)是时间序列中除去趋势、季节变动和周期波动之后的随机波动。不规则波动通常总是夹杂在时间序列中,致使时间序列产生一种波浪形或震荡式的变动。只含有随机波动的序列也称为平稳序列。
除非你的时间序列是平稳的,否则不能建立一个时间序列模型。在百度词条中是这样粗略的讲的:平稳时间序列粗略地讲,一个时间序列,如果均值没有系统的变化(无趋势)、方差没有系统变化,且严格消除了周期性变化,就称之是平稳的。
平稳性的判断标准
判断一个序列是不是平稳序列有三个评判标准:
均值
均值,是与时间t无关的常数。下图(左)满足平稳序列的条件,下图(右)很明显具有时间依赖。
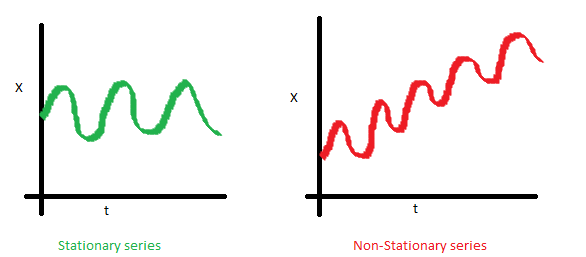
方差
方差,是与时间t无关的常数。这个特性叫做方差齐性。下图显示了什么是方差对齐,什么不是方差对齐。(注意右手边图中的不同分布)
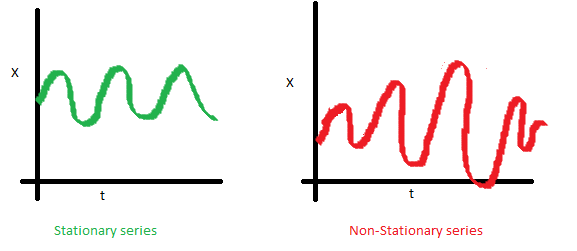
协方差
协方差,只与时期间隔k有关,与时间t无关的常数。如下图(右),可以注意到随着时间的增加,曲线变得越来越近。因此红色序列的协方差并不是恒定的。
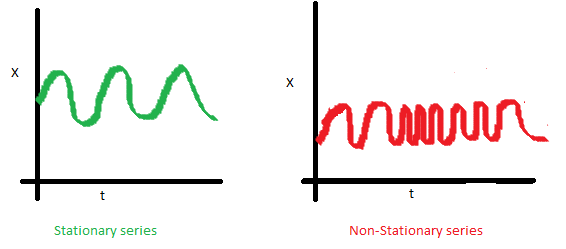
平稳性分类
时间序列的平稳性,和其它随机过程一样,分为严平稳和宽平稳。
严平稳
如果对所有的时刻t,任意正整数k和任意k个正整数$(t_1,t_2,…,t_k)$,$(r_{t1},r_{t2},…,r_{tk})$的联合分布与$(r_{t1+t},r_{t2+t},…,r_{tk+t})$的联合分布相同,我们称时间序列${r_t}$是严平稳的。也就是,$(r_{t1},r_{t2},…,r_{tk})$的联合分布在时间的平移变换下保持不变,这是个很强的条件。
宽平稳
若时间序列$\{r_t\}$满足下面两个条件:$E(r_t)=\mu$,$\mu$是常数$Cov(r_t,r_{t-l})=\gamma_l$,$\gamma_l$只依赖于l则时间序列$\{r_t\}$为弱平稳的。即该序列的均值,$r_t$与$r_{t-l}$的协方差不随时间而改变,l为任意整数。
平稳性检测方法
在数学中,平稳随机过程(Stationary random process)或者严平稳随机过程(Strictly-sense stationary random process),又称狭义平稳过程,是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程:即随机过程的统计特性不随时间的推移而变化。这样,数学期望和方差这些参数也不随时间和位置变化。平稳在理论上有严平稳和宽平稳两种,在实际应用上宽平稳使用较多。宽平稳的数学定义为:对于时间序列$y_t$,若对任意的t,k,m,满足:
$$E(y_t)=E(y_{t+m})$$
$$cov(y_t,y_{t+k})=cov(y_{t+k},y_{t+k+m})$$
则称时间序列$y_t$是宽平稳的。
单位根检验
单位根检验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了。Dickey-Fuller test和Augmented Dickey Fuller test(ADF)可以测试一个自回归模型是否存在单位根(unit root)。
为了保持单位和平均数相似,这里采用了标准差来代替方差:
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries, window=12):
rolmean = timeseries.rolling(window=window, center=False).mean()
rolstd = timeseries.rolling(window=window, center=False).std()
orig = plt.plot(timeseries, color='blue', label='Original') #设置原始图,移动平均图和标准差图的式样
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label='Rolling Std')
plt.legend(loc='best') #使用自动最佳的图例显示位置
plt.title('Rolling Mean & Standard Deviation')
plt.show() #供肉眼观察是否平稳
print('ADF检验结果:')
dftest = adfuller(timeseries, autolag='AIC') #使用减小AIC的办法估算ADF测试所需的滞后数
#将ADF测试结果、显著性概率、所用的滞后数和所用的观测数打印出来
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','Num Lags Used','Num Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)
test_stationarity(ts_week)
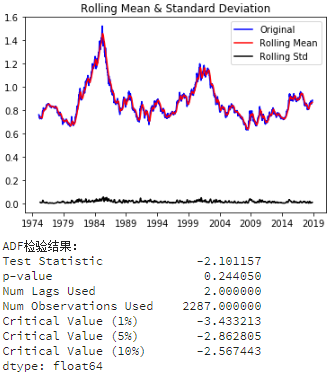
ADF检验测试结果由测试统计量和一些置信区间的临界值组成。如果”测试统计量”少于”临界值”,我们可以拒绝无效假设,并认为序列是稳定的。
- Test Statistic的值如果比Critical Value(5%)小则满足稳定性需求
- p-value越低(理论上需要低于0.05)证明序列越稳定。
白噪声检测
对于纯随机序列,又称白噪声序列,序列的各项数值之间没有任何相关关系,序列在进行完全无序的随机波动,可以终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。
#生成一个伪随机白噪声用于测试 acorr_ljungbox 的可靠性 from statsmodels.stats.diagnostic import acorr_ljungbox #导入白噪声检验函数 from random import gauss whitenoise = pd.Series([gauss(0.0, 1.0) for i in range(1000)]) #创建一个高斯分布的白噪声 print(u'白噪声检验结果为:', acorr_ljungbox(whitenoise, lags=1)) #检验结果:平稳度,p-value。p-value>0.05为白噪声
时间序列转为平稳序列
将时间序列转为平稳序列,常见的方法如:
- Deflation by CPI
- Logarithmic(取对数)
- First Difference(一阶差分)
- Seasonal Difference(季节差分)
- Seasonal Adjustment
总结起来,影响时间序列不稳定的主要有2个因素:
- 趋势 Trend
- 季节性 Seasonality
测试数据:AirPassengers(https://pan.baidu.com/s/1kTyHsSfU9jiQigPO3wYUrQ 提取码:fz48)。这个数据集是1949-1960年每个月国际航空的乘客数量的数据。
加载数据
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
data = pd.read_csv('AirPassengers.csv', parse_dates=['TravelDate'], index_col='TravelDate')
print(data.head())
ts = data['Passengers']
ts.head(10)
plt.plot(ts)
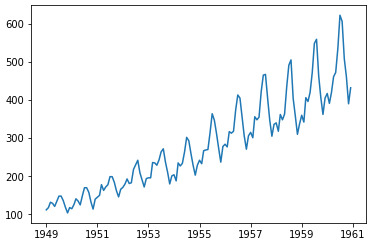
检测稳定性
test_stationarity(ts)
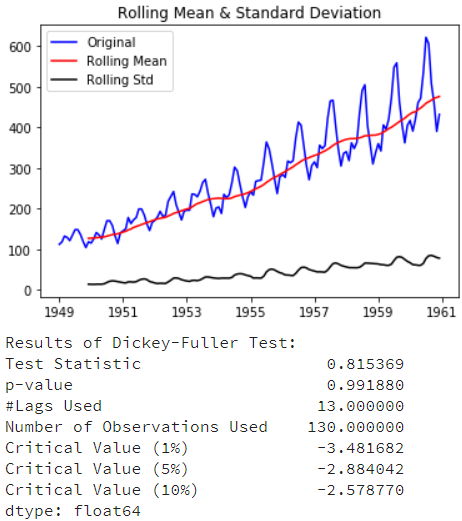
这里这个结果表明这些序列很不稳定,所以接下来考虑如何处理数据,使得序列相对稳定。
消除趋势
消除趋势的第一个方法是转换。在本例中我们可以清楚地看到有一个显著的趋势。我们可以通过变换,惩罚较高值而不是较小值。这可以采用取对数log,平方根,立方跟等。
在《Analysis of Financial Time Series》提到,对原始数据取对数有两个用处:
- 将指数增长转为线性增长
- 可以平稳序列的方差
ts_log = np.log(ts) plt.plot(ts_log)
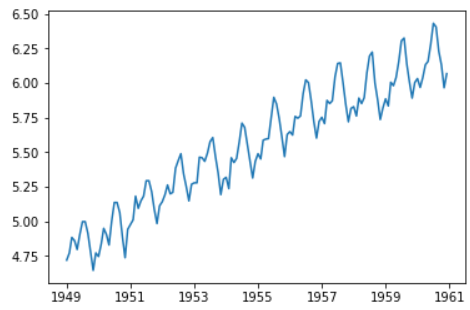
这里我们可以明显看到一个上升的趋势,但是混杂在噪音当中,所以需要去除杂音。这里简单平滑一下数据。平滑的窗口取值12(一年有12个月)。
在这个例子中,很容易看到数据趋势,但是它表现的不是很直观。我们可以使用一些技术来估计或对这个趋势建模,然后将它从序列中删除。常用的方法有:
- 聚合-取一段时间的平均值(月/周平均值)
- 平滑-取滚动平均数
- 多项式回归分析-适合的回归模型
这里主要讨论平滑分方法。平滑是指采取滚动估计,即考虑过去的几个实例:
移动平均数
在这个方法中,根据时间序列的频率采用“K”连续值的平均数。我们可以采用过去一年的平均数,即过去12个月的平均数。
moving_avg = ts_log.rolling(12).mean() plt.plot(ts_log) plt.plot(moving_avg, color='red')
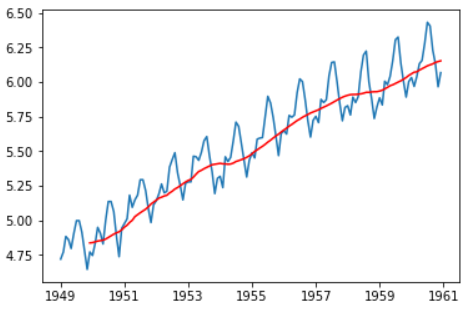
红色表示了滚动平均数。让我们从原始序列中减去这个平均数。注意,从我们采用过去12个月的值开始,滚动平均法还没有对前11个月的值定义:
ts_log_moving_avg_diff = ts_log - moving_avg ts_log_moving_avg_diff.head(12)
TravelDate 1949-01-01 NaN 1949-02-01 NaN 1949-03-01 NaN 1949-04-01 NaN 1949-05-01 NaN 1949-06-01 NaN 1949-07-01 NaN 1949-08-01 NaN 1949-09-01 NaN 1949-10-01 NaN 1949-11-01 NaN 1949-12-01 -0.065494 Name: Passengers, dtype: float64
注意前11个月是NaN值,现在让我们对这11个月排除后测试稳定性。
ts_log_moving_avg_diff.dropna(inplace=True) test_stationarity(ts_log_moving_avg_diff)
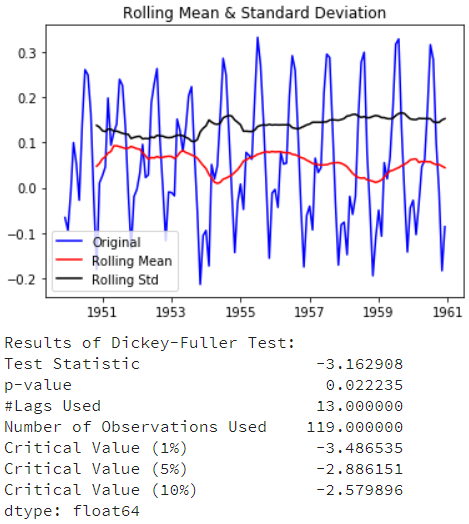
从上面的测试结果看,已经得到了一个稳定的序列。但是,这个方法有一个缺陷:需要先设定平滑的窗口期,实际在应用的时候像股票这样的数据很难去设定窗口期,所以,我们采取“加权移动平均法”可以对最近的值赋予更高的权重。
加权移动平均
指数加权移动平均法是很受欢迎的方法,所有的权重被指定给先前的值连同衰减系数。这可以通过 Pandas 实现:
expwighted_avg = ts_log.ewm(halflife=12).mean() plt.plot(ts_log) plt.plot(expwighted_avg, color='red')
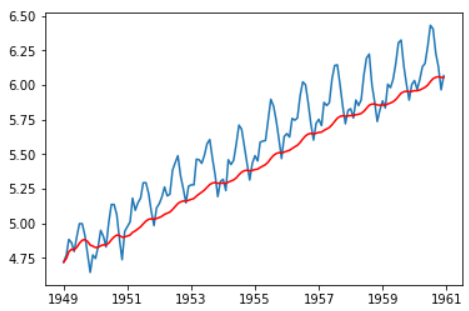
注意,这里使用了参数“halflife”来定义指数衰减量。这只是一个假设,很大程度上取决于业务领域。其他参数,如跨度和质心也可以用来定义衰减。让我们再来检测下新得到的序列的稳定性:
ts_log_ewma_diff = ts_log - expwighted_avg test_stationarity(ts_log_ewma_diff)
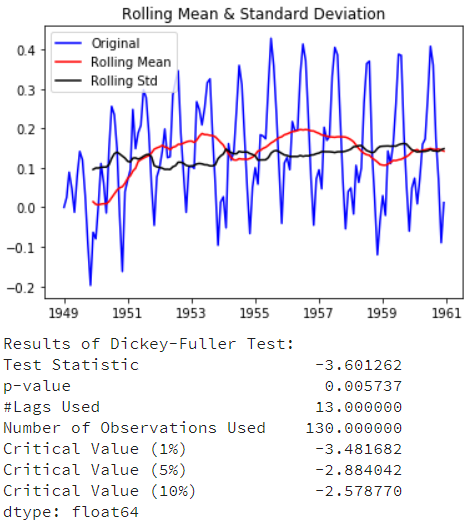
检测结果比移动平均的效果更好(TestStatistic的值比1%的临界值还小),另外不会出现前面11个月数据遗漏问题。
消除季节性
两种消除趋势和季节性的方法:
- 差分:采用一个特定时间差的差值
- 分解:建立有关趋势和季节性的模型和从模型中删除它们
差分
处理趋势和季节性的最常见的方法之一就是差分法。可以使用Pandas来实现差分:
ts_log_diff = ts_log.diff() # ts_log_diff = ts_log - ts_log.shift() plt.plot(ts_log_diff)
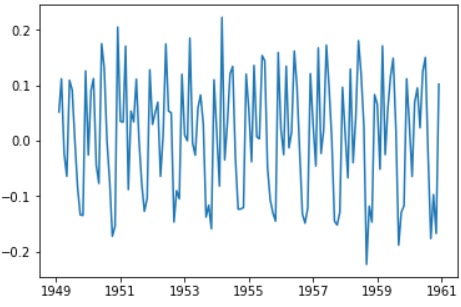
图中可以看出很大程度上减少了趋势。让我们再来检测下:
ts_log_diff.dropna(inplace=True) test_stationarity(ts_log_diff)
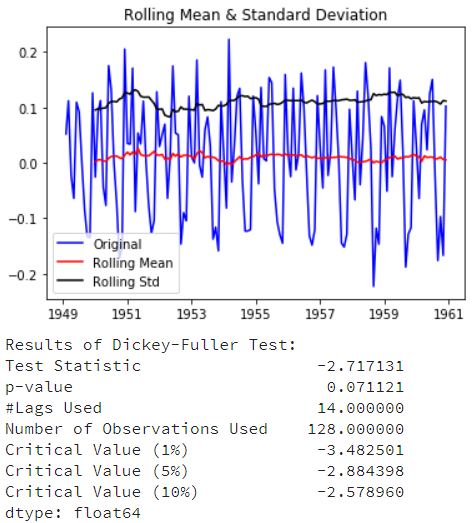
可以看到平均数和标准差随着时间有小的变化。同时,DF检验统计量小于10%的临界值,因此该时间序列在90%的置信区间上是稳定的。我们也可以采取二阶或三阶差分在具体应用中获得更好的结果。
分解
statsmodels.tsa.seasonal.seasonal_decompose可以将时间序列的数据分解为趋势(trend),季节性(seasonality)和残差(residual)三部分:
from statsmodels.tsa.seasonal import seasonal_decompose decomposition = seasonal_decompose(ts_log) trend = decomposition.trend seasonal = decomposition.seasonal residual = decomposition.resid plt.subplot(411) plt.plot(ts_log, label='Original') plt.legend(loc='best') plt.subplot(412) plt.plot(trend, label='Trend') plt.legend(loc='best') plt.subplot(413) plt.plot(seasonal, label='Seasonality') plt.legend(loc='best') plt.subplot(414) plt.plot(residual, label='Residuals') plt.legend(loc='best') plt.tight_layout()
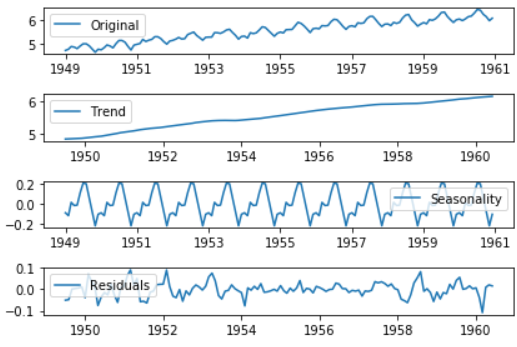
趋势和季节性,还有残差值都被分解出来,然后我们计算残差值的稳定性。
ts_log_decompose = residual ts_log_decompose.dropna(inplace=True) test_stationarity(ts_log_decompose)
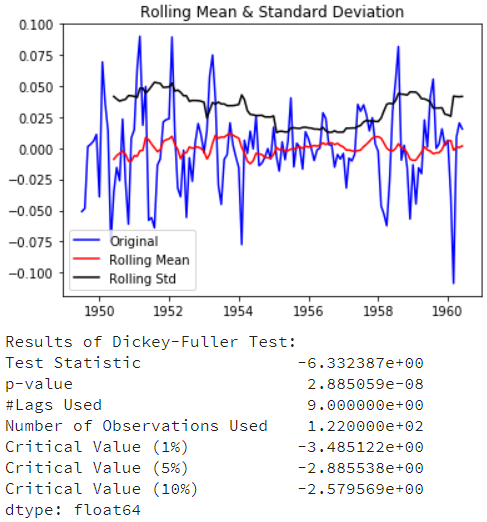
DF测试统计量明显低于1%的临界值,这样时间序列是非常接近稳定。
时间序列建模
相关系数与自相关函数
相关系数
对于两个向量,我们希望定义它们是不是相关。一个很自然的想法,用向量与向量的夹角作为距离的定义,夹角小,就距离小,夹角大,就距离大。我们通常使用余弦公式来计算角度:
$$\cos<\vec{a},\vec{b}>=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$$
对于$\vec{a}\cdot\vec{b}$我们叫做内积,例如:
$$(x_1,y_1)\cdot(x_2,y_2)={x_1}{x_2}+{y_1}{y_2}$$
相关系数的定义公式,X和Y的相关系数为:
$$\rho_{xy}=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$$
根据样本的估计计算公式为:
$$\rho_{xy}=\frac{\sum_{t=1}^{T}(x_t-\bar x)(y_t-\bar y)}{\sqrt{\sum_{t=1}^{T}(x_t-\bar x)^{2}\sum_{t=1}^{T}(y_t-\bar y)^{2}}}=\frac{\overrightarrow{(X-\bar x)}\cdot\overrightarrow{(Y-\bar y)}}{|\overrightarrow{(X-\bar x)}||\overrightarrow{(Y-\bar y)}|}$$
相关系数实际上就是计算了向量空间中两个向量的夹角,协方差是去均值后两个向量的内积。如果两个向量平行,相关系数等于1或者-1,同向的时候是1,反向的时候就是-1。如果两个向量垂直,则夹角的余弦就等于0,说明二者不相关。两个向量夹角越小,相关系数绝对值越接近1,相关性越高。只不过这里计算的时候对向量做了去均值处理,即中心化操作。而不是直接用向量$X$,$Y$计算。
自相关函数(Autocorrelation Function, ACF)
相关系数度量了两个向量的线性相关性,而在平稳时间序列$\{r_t\}$中,我们有时候很想知道,$r_t$与它的过去值$r_{t-i}$的线性相关性。这时候我们把相关系数的概念推广到自相关系数。
$r_t$与$r_{t-l}$的相关系数称为$r_t$的间隔为$l$的自相关系数,通常记为$\rho_l$:
$$\rho_l=\frac{Cov(r_t,r_{t-l})}{\sqrt{Var(r_t)Var(r_{t-l})}}=\frac{Cov(r_t,r_{t-l})}{Var(r_t)}$$
这里用到了弱平稳序列的性质:$$Var(r_t)=Var(r_{t-l})$$
对一个平稳时间序列的样本$\{r_t\}$,$1\le t\le T$,则间隔为$l$的样本自相关系数的估计为:
$$\hat\rho_l=\frac{\sum_{t=l+1}^{T}(r_t-\bar r)(r_{t-l}-\bar r)}{\sum_{t=1}^{T}(r_t-\bar r)^{2}},0\le l\leq T-1$$
则函数$\hat\rho_1,\hat\rho_2,\hat\rho_3…$称为$r_t$的样本自相关函数(ACF)
当自相关函数中所有的值都为0时,我们认为该序列是完全不相关的;因此,我们经常需要检验多个自相关系数是否为0。
混成检验
原假设:
$$H0:\rho_1=…=\rho_m=0$$
备择假设:
$$H1:\exists i\in\{1,…,m\},\rho_i\ne0$$
混成检验统计量:
$$Q(m)=T(T+2)\sum_{l=1}^{m}\frac{\hat{\rho_l}^{2}}{T-l}$$
$Q(m)$渐进服从自由度为$m$的$\chi^2$分布
决策规则:
$$Q(m)>\chi_\alpha^{2},拒绝H_0$$
即,$Q(m)$的值大于自由度为$m$的卡方分布$100(1-\alpha)$分位点时,我们拒绝$H_0$。
大部分软件会给出$Q(m)$的p-value,则当p-value小于等于显著性水平$\alpha$时拒绝H0。
示例:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tushare as ts
pro = ts.pro_api()
df = pro.daily(ts_code='600519.SH', start_date='20180101') #茅台股价
df = df[['trade_date','close']]
df['trade_date'] = pd.to_datetime(df['trade_date'])
data = df.set_index('trade_date')
data['change_pct'] = ''
for i in range(0, len(data['close'])-1):
data.iloc[i, 1] = 100*(data['close'][i+1]-data['close'][i])/data['close'][i] #计算每日收益率(涨跌幅)
data['change_pct'] = data['change_pct'][0:-1]
data['close_diff_1'] = data['close'].diff(1)
data = data[0:-1] #由于changepct值最后一行缺失,因此去除最后一行
data['change_pct'] = data['change_pct'].astype('float64') #使changepct数据类型和其他三列保持一致
data.plot(subplots=True, figsize=(12,12))
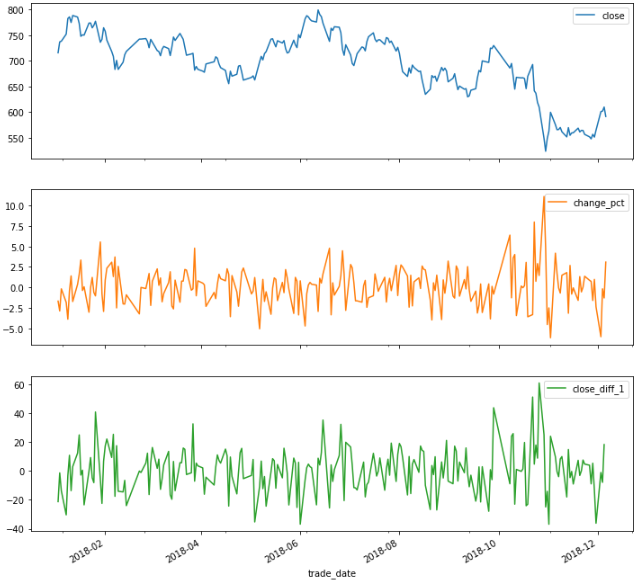
import statsmodels.api as sm
close_data = data['close'] #上证指数每日收盘价
m = 10 #检验10个自相关系数
acf,q,p = sm.tsa.acf(close_data, nlags=m, qstat=True)
#np.r_是按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等,类似于pandas中的concat()。
#np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等,类似于pandas中的merge()。
out = np.c_[range(1,11), acf[1:], q, p]
output = pd.DataFrame(out, columns=['lag','ACF','Q','P-value'])
output = output.set_index('lag')
print(output)
lag ACF Q P-value 1.0 0.963283 212.504727 3.903196e-48 2.0 0.928599 410.863584 6.054892e-90 3.0 0.893812 595.463129 9.703299e-129 4.0 0.858595 766.569712 1.337073e-164 5.0 0.820359 923.482644 2.201222e-197 6.0 0.778788 1065.538402 5.955998e-227 7.0 0.744518 1195.960070 5.278705e-254 8.0 0.712521 1315.960270 8.343090e-279 9.0 0.686764 1427.955165 7.044640e-302 10.0 0.658661 1531.448754 0.000000e+00
我们取显著性水平为0.05,可以看出,所有的p-value都小于0.05;则我们拒绝原假设$H_0$。因此,我们认为该序列是序列相关的。我们再来看看同期的日收益率序列:
change_data = data['change_pct']
m = 10 #检验10个自相关系数
acf,q,p = sm.tsa.acf(change_data, nlags=m, qstat=True) ##计算自相关系数及p-value
out = np.c_[range(1,11), acf[1:], q, p]
output = pd.DataFrame(out, columns=['lag',"AC","Q","P-value"])
output = output.set_index('lag')
print(output)
lag AC Q P-value 1.0 0.010467 0.025092 0.874137 2.0 -0.018733 0.105814 0.948468 3.0 -0.015576 0.161875 0.983496 4.0 -0.023547 0.290575 0.990414 5.0 0.034672 0.570871 0.989298 6.0 -0.133740 4.760213 0.574915 7.0 -0.047866 5.299284 0.623491 8.0 -0.085952 7.045520 0.531729 9.0 0.064843 8.043923 0.529726 10.0 -0.032424 8.294713 0.600074
可以看出,p-value均大于显著性水平0.05。我们选择假设$H_0$,即收益率序列没有显著的相关性。
自相关图与偏相关图详解
数据集:澳大利亚墨尔本10年最低气温 链接:https://pan.baidu.com/s/17sVPK8iI-dlC4W6oGpd-Xg提取码:jtei
import pandas as pd
from matplotlib import pyplot as plt
data = pd.read_csv("daily-minimum-temperatures-in-me.csv", parse_dates=['Date'], index_col='Date')
data.head()
data.plot(figsize=(12, 6))
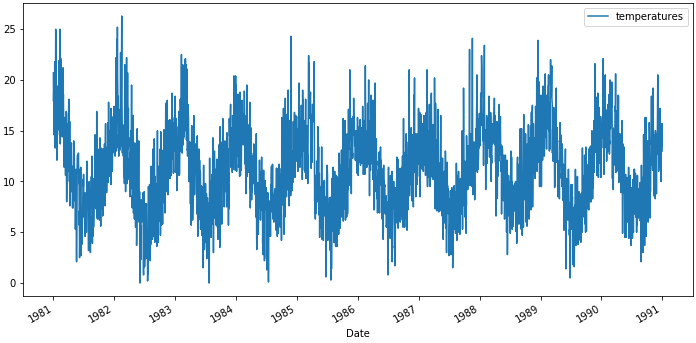
相关与自相关
统计中的相关性说的是两个变量间的相关程度。我们假设如果每个变量都符合正态分布,可以使用皮尔逊相关系数(Pearson correlation coefficient)来统计变量间的相关性。皮尔逊相关系数是-1和1之间的数字分别描述负相关或正相关。值为零表示无相关。
自相关(英语:Autocorrelation),也叫序列相关,是一个信号于其自身在不同时间点的互相关。非正式地来说,它就是两次观察之间的相似度对它们之间的时间差的函数。它是找出重复模式(如被噪声掩盖的周期信号),或识别隐含在信号谐波频率中消失的基频的数学工具。自相关函数在不同的领域,定义不完全等效。在某些领域,自相关函数等同于自协方差。
由于时间序列的相关性与之前的相同系列的值进行了计算,这被称为序列相关或自相关。一个时间序列的自相关系数被称为自相关函数,或简称ACF。这个图被称为相关图或自相关图。
以下是利用statsmodels库中使用plot_acf()函数计算和绘制”每日最低气温”自相关图:
import statsmodels.api as sm sm.graphics.tsa.plot_acf(data) plt.figure(figsize=(12, 6)) plt.show()

这个示例创建了一个2D的平面图,显示沿x轴的延迟值以及y轴上的相关性(-1到1之间)。置信区间被画成圆锥形。默认情况下,置信区间这被设置为95%。
默认情况下,图中显示的是所有的延迟值,这让真实情况掩藏了,我们可以将x轴上的延迟值限制为50,让图更容易看懂。
sm.graphics.tsa.plot_acf(data, lags=50) plt.figure(figsize=(12, 6)) plt.show()
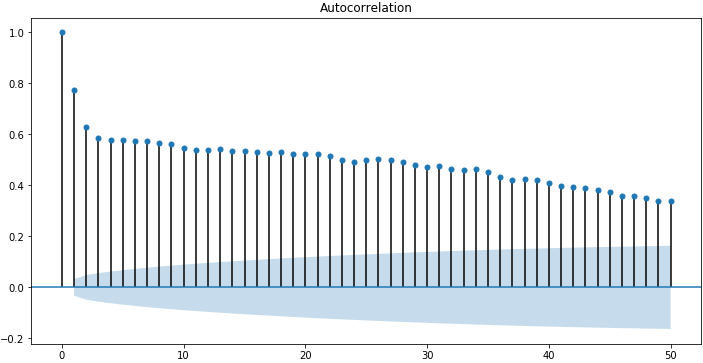
偏自相关函数(PACF)
偏自相关函数用来度量暂时调整所有其他较短滞后的项($y_{t–1},y_{t–2},…,y_{t–k–1}$)之后,时间序列中以k个时间单位($y_{t}$和$y_{t–k}$)分隔的观测值之间的相关。
偏自相关是剔除干扰后时间序列观察与先前时间步长时间序列观察之间关系的总结。在滞后k处的偏自相关是在消除由于较短滞后条件导致的任何相关性的影响之后产生的相关性。一项观察的自相关和在先验时间步上的观测包括直接相关和间接相关。这些间接相关是线性函数观察(这个观察在两个时间步长之间)的相关。偏自相关函数试图移除这些间接相关。
下面的示例使用statsmodels库中的plot_pacf()来计算和绘制最低每日温度数据集里的前50个滞后的偏自相关函数:
sm.graphics.tsa.plot_pacf(data, lags=50) plt.figure(figsize=(12, 6)) plt.show()
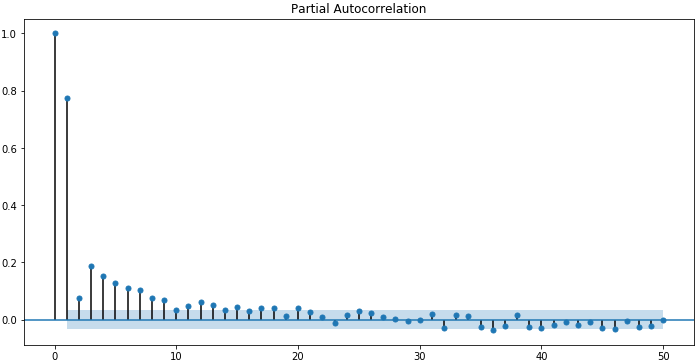
ACF和PACF图的直观认识
时间序列的自相关函数和偏自相关函数的平面图描述了完全不同的情形。我们可以使用ACF和PACF图来探索一些信息。
自回归直观认识(intuition)
考虑由自回归(AR)过程产生的滞后时间为k的时间序列。我们知道,ACF描述了一个观测值与另一个观测值之间的自相关,包括直接和间接的相关性信息。这意味着我们可以预期AR(k)时间序列的ACF强大到(如同使用了)k的滞后,并且这种关系的惯性将继续到之后的滞后值,随着效应被削弱而在某个点上缩小到没有。我们知道,PACF只描述观测值与其滞后(lag)之间的直接关系。这表明,超过k的滞后值(lag value)不会再有相关性。这正是ACF和PACF图对AR(k)过程的预期。
滑动平均直观认识(Moving Average Intuition)
考虑由滑动平均(MA)过程产生的滞后(lag)时间为k的时间序列。请记住,滑动平均过程是先前预测的残留偏差的时间序列的自回归模型。考虑滑动平均模型的另一种方式是根据最近预测的错误修正未来的预测。我们期望MA(k)过程的ACF与最近的lag值之间的关系显示出强烈的相关性,然后急剧下降到低或者无相关性。根据定义,这解释了整个过程是如何产生的。对于PACF,我们预计图会显示与滞后(lag)的关系,以及滞后(lag)之前的相关。再次强调,这正是MAF(k)过程的ACF和PACF图的预期。
自相关和偏自相关用于测量当前序列值和过去序列值之间的相关性,并指示预测将来值时最有用的过去序列值。了解了此内容,您就可以确定ARIMA模型中过程的顺序。更具体来说,
- 自相关函数(ACF)。延迟为k时,这是相距k个时间间隔的序列值之间的相关性。
- 偏自相关函数(PACF)。延迟为k时,这是相距k个时间间隔的序列值之间的相关性,同时考虑了间隔之间的值。
截尾与拖尾是什么鬼?
截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF)。
- 截尾:在大于某个常数k后快速趋于0为k阶截尾
- 拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
自回归移动平均模型(ARMA(p,q))是时间序列中最为重要的模型之一,它主要由两部分组成:AR代表p阶自回归过程,MA代表q阶移动平均过程,其公式如下:
$$z_t=\varphi_{1}z_{t-1}+\varphi_{2}z_{t-2}+…+\varphi_{p}z_{t-p}+\alpha_{t}-\theta_{1}\alpha_{t-1}-…-\theta_{p}\alpha_{t-p}$$
模型的简化形式为:
$$\varphi_{p}(B)z_{t}=\theta_{q}(B)\alpha_(t)$$
其中:
$$\varphi_{p}(B)=1-\varphi_{1}B-\varphi_{2}B^2-…-\varphi_{p}B^p$$
$$\theta_{q}(B)=1-\theta_{1}B-\theta_{2}B^2-…-\theta_{q}B^q$$
依据模型的形式、特性及自相关和偏自相关函数的特征,总结如下:
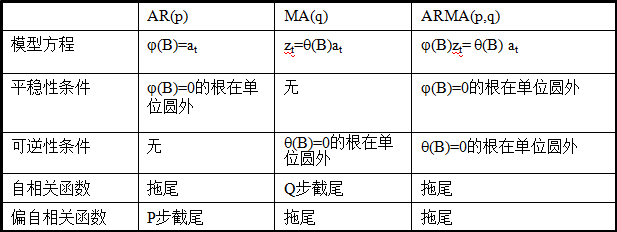
在时间序列中,ARIMA模型是在ARMA模型的基础上多了差分的操作。
白噪声序列与线性时间序列
白噪声序列
随机变量X(t)(t=1,2,3…),如果是由一个不相关的随机变量的序列构成的,即对于所有S不等于T,随机变量$X_t$和$X_s$的协方差为零,则称其为纯随机过程。对于一个纯随机过程来说,若其期望和方差均为常数,则称之为白噪声过程。白噪声过程的样本实称成为白噪声序列,简称白噪声。之所以称为白噪声,是因为他和白光的特性类似,白光的光谱在各个频率上有相同的强度,白噪声的谱密度在各个频率上的值相同。
线性时间序列
时间序列{$r_t$},如果能写成:
$$r_t=\mu+\sum_{i=0}^{\infty}\psi_ia_{t-i}$$
$\mu$为$r_t$的均值,$\psi_0=1,\{a_t\}$为白噪声序列,则我们称$\{r_t\}$为线性序列。其中$a_t$称为在$t$时刻的新息(innovation)或扰动(shock)。
很多时间序列具有线性性,即是线性时间序列,相应的有很多线性时间序列模型,例如接下来要介绍的AR、MA、ARMA,都是线性模型,但并不是所有的金融时间序列都是线性的。对于弱平稳序列,我们利用白噪声的性质很容易得到$r_t$的均值和方差:
$$E(r_t)=\mu,Var(r_t)=\sigma_a^2\sum_{i=0}^{\infty}\psi_i^{2}$$
$\sigma_a^2$为$a_t$的方差。因为$Var(r_t)$一定小于正无穷,因此$\{\psi_i^2\}$必须是收敛序列,因此满足$i\to\infty$时,$\psi_i^2\to0$。即,随着$i$的增大,远处的扰动$a_{t-i}$对$r_t$的影响会逐渐消失。
自回归模型(AutoRegressive,AR)
AR模型的理解
让我们用下面的例子来理解AR模型:一个国家当前的GDP称x(t)取决于去年的GDP,即x(t-1)。一个国家在一个财政年度的GDP取决于前一年建立的制造厂/服务,以及本年度新成立工厂/服务。但是GDP的主要组成部分是前一部分,因此,我们可以把GDP的等式写成:
$$x(t)=\alpha* x(t–1)+error(t)$$
这个方程称为AR公式。公式表示下一个点完全依赖与前面一个点。$\alpha$是我们寻求的系数,以便最小化误差函数。注意,x(t-1)同样依赖x(t-2)。因此,波动在未来会逐渐消退。
例如,假设x(t)是一个城市在某一天出售的果汁瓶的数量。在冬天,很少有供应商购买果汁瓶。突然,在一个特定的日子里,温度上升,果汁的需求猛增到1000个。然而,几天后,气候又变得寒冷起来。但是,知道人们在炎热的日子里已经习惯了喝果汁,在寒冷的日子里仍有50%的人还在喝果汁。接下来的几天,这个比例下降到25%(50%的50%),然后在数天之后逐渐变小。下面的图表说明了AR系列的惯性特性:
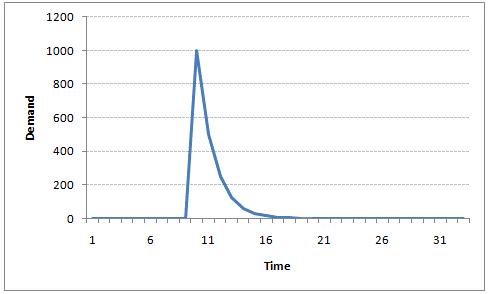
在上节中,我们计算了部分数据端的ACF,看表可知间隔为1时自相关系数是显著的。这说明在$t-1$时刻的数据$r_{t-1}$,在预测$t$时刻$r_t$时可能是有用的!
根据这点我们可以建立下面的模型:
$$r_t=\phi_0+\phi_1r_{t-1}+a_t$$
其中{$a_t$}是白噪声序列,这个模型与简单线性回归模型有相同的形式,这个模型也叫做一阶自回归(AR)模型,简称AR(1)模型。从AR(1)很容易推广到AR(p)模型:
$$r_t=\phi_0+\phi_1r_{t-1}+\cdots+\phi_pr_{t-p}+a_t\qquad(2.0)$$
AR(p)模型的特征根及平稳性检验
我们先假定序列是弱平稳的,则有:
$$E(r_t)=\mu\qquad Var(r_t)=\gamma_0\qquad Cov(r_t,r_{t-j})=\gamma_j$$
其中$\mu$,$\gamma_0$是常数。因为{$a_t$}是白噪声序列,因此有:
$$E(a_t)=0,Var(a_t)=\sigma_a^2$$
所以有:
$$E(r_t)=\phi_0+\phi_1E(r_{t-1})+\phi_2E(r_{t-2})+\cdots+\phi_pE(r_{t-p})$$
根据平稳性的性质,又有$E(r_t)=E(r_{t-1})=…=\mu$,从而:
$$\mu=\phi_0+\phi_1\mu+\phi_2\mu+\cdots+\phi_p\mu\\$$
$$E(r_t)=\mu=\frac{\phi_0}{1-\phi_1-\phi_2-\cdots-\phi_p}\qquad$$
公式中假定分母不为0,我们将下面的方程称为特征方程:
$$1-\phi_1x-\phi_2x^2-\cdots-\phi_px^p=0$$
该方程所有解的倒数称为该模型的特征根,如果所有的特征根的模都小于1,则该AR(p)序列是平稳的。
下面我们就用该方法,检验日收益率序列的平稳性:
change_data = data['change_pct'] #载入收益率序列 change_data = np.array(change_data, dtype=np.float) model = sm.tsa.AR(change_data) results_AR = model.fit() plt.figure(figsize=(12,6)) plt.plot(change_data, 'b', label='changepct') plt.plot(results_AR.fittedvalues, 'r', label='ARmodel') plt.legend()
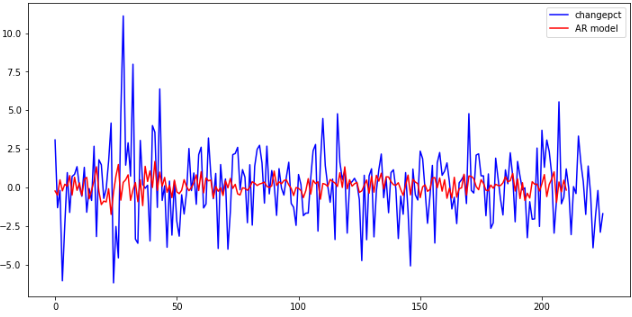
看看模型有多少阶:
print(len(results_AR.roots)) #模型阶数
可以看出,自动生成的AR模型是15阶的。关于阶次的讨论在下节内容,我们画出模型的特征根,来检验平稳性:
r1 = 1
theta = np.linspace(0, 2*np.pi, 360)
x1 = r1*np.cos(theta)
y1 = r1*np.sin(theta)
plt.figure(figsize=(6,6))
plt.plot(x1, y1, 'k') #画单位圆
roots = 1/results_AR.roots #计算results_AR.roots后取倒数
for i in range(len(roots)):
plt.plot(roots[i].real, roots[i].imag, '.r', markersize=8) #画特征根
plt.show()
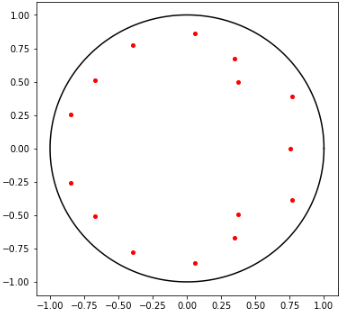
可以看出,所有特征根都在单位圆内,则序列为平稳的。
AR模型的阶数确定
对于线性回归模型的阶数,一般认为随着阶数的升高,会提高模型的精度。但是过高的阶数会造成模型过于复杂。下面介绍两种确定AR模型阶数的方法:偏相关函数(pACF)和信息准则函数(AIC、BIC、HQIC)。
偏相关函数(pACF)首先引入阶数依次升高的AR模型:
$$r_t=\phi_{0,1}+\phi_{1,1}r_{t-1}+\epsilon_{1t}$$
$$r_t=\phi_{0,2}+\phi_{1,2}r_{t-1}+\phi_{2,2}r_{t-2}+\epsilon_{2t}$$
$$r_t=\phi_{0,3}+\phi_{1,3}r_{t-1}+\phi_{2,3}r_{t-2}+\phi_{3,3}r_{t-3}+\epsilon_{3t}$$
$$r_t=\phi_{0,4}+\phi_{1,4}r_{t-1}+\phi_{2,4}r_{t-2}+\phi_{3,4}r_{t-3}+\phi_{4,4}r_{t-4}+\epsilon_{4t}$$
$$\dots\dots\dots\dots$$
等式右边第一项为常数项,最后一项为误差项,$\hat{\phi}_{i,i}$为{rt}的间隔为i的样本偏自相关函数。$\hat{\phi}_{i,i}$表示的是在第i-1行的基础上添加的一个阶数对{rt}的贡献。对于AR模型,当超过某个值p时,偏自相关函数应逐渐趋近于0,这既符合我们的直观认识,也有相应的理论证明可以找到。
对于偏相关函数的介绍,这里不详细展开,重点介绍一个性质:AR(p)序列的样本偏相关函数是p步截尾的。所谓截尾,就是快速收敛应该是快速的降到几乎为0或者在置信区间以内。
下面对2018年茅台股价涨跌幅作出偏自相关函数图,在5%的显著水平下,取置信区间为
$$\frac{2}{\sqrt{n}}=\frac{2}{\sqrt{243}}$$
查看pACF图:
fig = plt.figure(figsize=(12, 6)) ax1 = fig.add_subplot(111) fig = sm.graphics.tsa.plot_pacf(change_data, lags=40, ax=ax1)
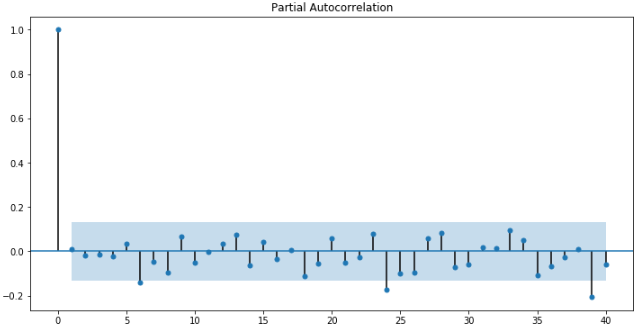
很遗憾,从上图中并不太容易确定一个明显的阶数p。不过确实可以看出,随着时间的增加,偏相关函数逐渐趋近于0。这个结果给了我们两点思路:首先偏相关函数趋近于0,说明运用AR模型模拟该序列是有一定的合理性;其次上图很难确定阶数p或阶数p很大,说明模型可能有MA(滑动平均,将在后面介绍)的部分。它至少给了我们一些感性的认识。
信息准则函数
目前比较常用的信息准则函数包括赤池信息量(AIC),贝叶斯信息量(BIC)和汉南-奎因信息量(HQIC)。他们都基于似然函数L和参数的数量k,其中n表示样本大小。由于Python中有相应的函数,所以公式仅作了解:
$$AIC=-2\lnL+2k$$
$$BIC=-2\lnL+\lnn\cdotk$$
$$HQIC=-2\lnL+\ln(\lnn)\cdotk$$
我们的目标是,选择阶数k使得信息量的值最小。以上这么多可供选择的模型,我们通常采用AIC法则。我们知道:增加自由参数的数目提高了拟合的优良性,AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。
下面我们来测试下3种准则下确定的p,仍然用日收益率序列。为了减少计算量,我们只计算间隔前7个看看效果。
aicList = []
bicList = []
hqicList = []
for i in range(1, 8): #从1阶开始算
order = (i, 0) #使用ARMA模型,其中MA阶数为0,只考虑了AR阶数。
chgdataModel = sm.tsa.ARMA(change_data, order).fit()
aicList.append(chgdataModel.aic)
bicList.append(chgdataModel.bic)
hqicList.append(chgdataModel.hqic)
plt.figure(figsize=(10, 6))
plt.plot(aicList, 'ro--', label='aic value')
plt.plot(bicList, 'bo--', label='bic value')
plt.plot(hqicList, 'ko--', label='hqic value')
plt.legend(loc=0)
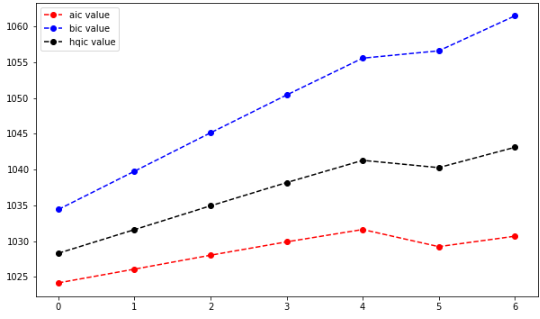
计算信息准则函数的时候,我们发现随着阶数的增加,运算速度越来越慢,所以只取了前7阶,可以看出AIC给出的阶数为0,BIC和HQIC给出的阶数为0。当然,前面提到只用AR模型预测该序列是不准确的,且只计算前7阶的结果也不足以判断最佳阶数。当然,利用上面的方法逐个计算是很耗时间的,实际上,有函数可以直接按照准则计算出合适的order,这个是针对ARMA模型的,我们后续再讨论。
AR模型的检验
如果模型是充分的,其残差序列应该是白噪声,根据我们第一章里介绍的混成检验,可以用来检验残差与白噪声的接近程度。先求出残差序列:
delta = results_AR.fittedvalues - change_data[15:] #取得误差项 plt.figure(figsize=(10, 6)) #plt.plot(change_data[17:], label='original value') #plt.plot(results_AR.fittedvalues, label='fitted value') plt.plot(delta, 'r', label='residual error') plt.legend(loc=0)
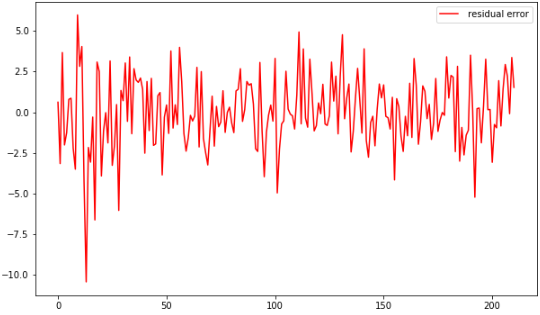
然后我们检查它是不是接近白噪声序列:
acf, q, p = sm.tsa.acf(delta, nlags=10, qstat=True) #计算自相关系数及p-value
out = np.c_[range(1, 11), acf[1:], q, p]
output = pd.DataFrame(out, columns=['lag', "ACF", "Q", "P-value"])
output = output.set_index('lag')
print(output)
lag ACF Q P-value 1.0 0.001303 0.000363 0.984792 2.0 -0.003122 0.002459 0.998771 3.0 0.013582 0.042318 0.997714 4.0 -0.014884 0.090414 0.999008 5.0 0.014418 0.135770 0.999656 6.0 0.007551 0.148269 0.999936 7.0 -0.003774 0.151407 0.999990 8.0 -0.014438 0.197556 0.999996 9.0 0.022536 0.310547 0.999996 10.0 -0.014879 0.360051 0.999999
观察p-value可知,该序列可以认为没有相关性,近似得可以认为残差序列接近白噪声。
拟合优度
调整后的拟合优度检验:
$$AdjR^2=1-\frac{\hat{\sigma}^2_{\epsilon}}{\hat{\sigma}^2_{r_t}}$$
右边分子代表残差的方差,分母代表${r_t}$的方差。adjR²值在0到1之间,越大说明拟合效果越好。计算该序列的adjR²值,发现效果并不好,这也符合我们的预期。
下面我们计算之前对日收益率的AR模型的拟合优度:
adjR = 1 - delta.var() / change_data[15:].var() print(adjR)
输出值为:0.05178424488182409,可以看出,模型的拟合程度并不好,当然,这并不重要,也许是这个序列并不适合用AR模型拟合。
AR模型的预测
我们首先得把原来的样本分为训练集和测试集,再来看预测效果,还是以之前的数据为例:
train = change_data[:-10] test = change_data[-10:] output = sm.tsa.AR(train).fit() output.predict() predicts = output.predict(216, 225, dynamic=True) #共226个数据 compare = pd.DataFrame() compare['original'] = change_data[-10:] compare['predict'] = predicts print(compare)
original predict 0 1.608146 0.853237 1 0.388352 -0.585180 2 -1.726237 0.435650 3 1.406797 0.482424 4 -0.406002 0.967699 5 -3.883607 -0.727744 6 -1.830801 0.412699 7 -0.174712 -0.076781 8 -2.877610 0.223773 9 -1.677702 -0.055838
compare.plot()
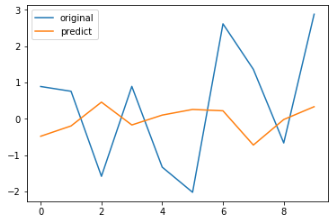
该模型的预测结果是很差。那么我们是不是可以通过其他模型获得更好的结果呢?我们将在下一部分继续介绍。
滑动平均模型(Moving Average, MA)
MA模型的理解
让我们以另一个例子来理解移动平均时间序列模型:一个公司生产了一批类型在市场上很容易买到的包,在竞争激烈的市场。这个包的销量在很多天都是0,于是,在某一天,这家公司做了一个实验,生产了一个不同类型的包,这种包在市场上任何地方找不到,因此,他可以一下子卖掉了1000个。这个包的需求特别高,很快库存快要完了。这天结束了还有100个包没卖掉。我们把这个误差成为时间点误差。接下来的几天仍有几个客户购买这种包。随着时间的推移,这个袋子已经失去了它的吸引力。下面通过一个简单的公式来描述这个场景:
$$x(t)=beta*error(t-1)+error(t)$$
如果我们尝试绘制这个图表,它会看起来像这样:
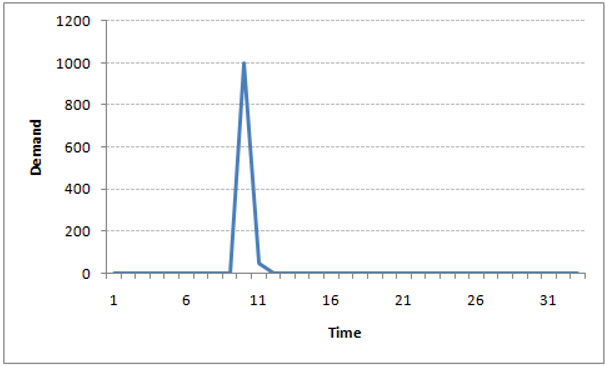
注意到MA和AR模型的区别了吗?在MA模型中,噪声/冲击随着时间的推移而迅速消失。AR模型对冲击具有持久的影响。
这里我们直接给出MA(q)模型的形式:
$$r_t=c_0+a_t-\theta_1a_{t-1}-\cdots-\theta_qa_{t-q}$$
$c_0$为一个常数项。这里的$a_t$,是AR模型$t$时刻的扰动或者说新息,则可以发现,该模型,使用了过去q个时期的随机干扰或预测误差来线性表达当前的预测值。
MA模型的性质
平稳性
MA模型总是弱平稳的,因为他们是白噪声序列(残差序列)的有限线性组合。因此,根据弱平稳的性质可以得出两个结论:
$$E(r_t)=c_0$$
$$Var(r_t)=(1+\theta_1^2+\theta_2^2+\cdots+\theta_q^2)\sigma_a^2$$
自相关函数
对q阶的MA模型,其自相关函数ACF总是q步截尾的。因此MA(q)序列只与其前q个延迟值线性相关,从而它是一个”有限记忆”的模型。这一点可以用来确定模型的阶次,后面会介绍。
可逆性
当满足可逆条件的时候,MA(q)模型可以改写为AR(p)模型。这里不进行推导,给出1阶和2阶MA的可逆性条件。
1阶:$|\theta_1|<1$
2阶:$|\theta_2|<1,\theta_1+\theta_2<1$
MA模型的的阶数确定
之前我们知道,通过计算偏自相关函数(pACF)可以粗略确定AR模型的阶数。而对于MA模型,需要采用自相关函数(ACF)进行定阶。
fig2 = plt.figure(figsize=(12, 6)) ax2 = fig2.add_subplot(111) fig2 = sm.graphics.tsa.plot_acf(change_data, lags=40, ax=ax2)
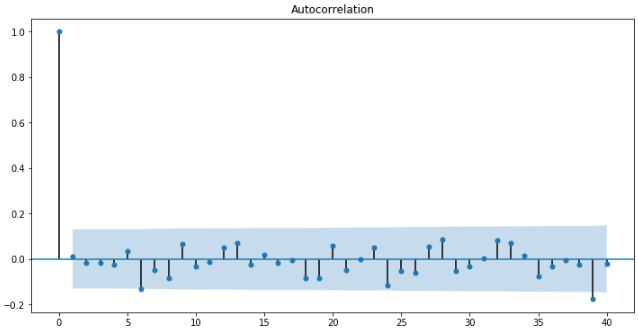
可以发现还是不太明显,这里以6阶为列,作出MA模型与原日涨跌幅的图像:
results_MA = sm.tsa.ARMA(change_data, (0, 6)).fit() #取ARMA模型中AR的阶数为0,MA的阶数为6 plt.figure(figsize=(12, 6)) plt.plot(change_data, 'b', label='changepct') plt.plot(results_MA.fittedvalues, 'r', label='MA model') plt.legend()
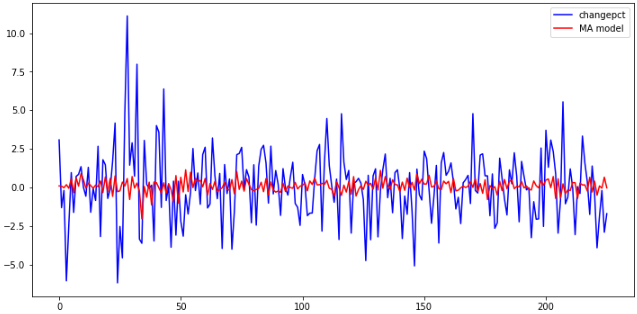
MA模型的预测
由于sm.tsa中没有单独的MA模块,我们利用ARMA模块,只要将其中AR的阶p设为0即可。函数sm.tsa.ARMA中的输入参数中的order(p,q),代表了AR和MA的阶次。模型阶次增高,计算量急剧增长,因此这里就建立6阶的模型作为示例。我们用最后10个数据作为out-sample的样本,用来对比预测值。
train = change_data[:-10] test = change_data[-10:] chgdataModel_MA = sm.tsa.ARMA(train, (0, 6)).fit() #取ARMA模型中AR的阶数为0,MA的阶数为6
我们先来看看拟合效果:
delta = chgdataModel_MA.fittedvalues - train score = 1 - delta.var() / train.var() print(score)
可以看出,score为0.028525493755446107远小于1,拟合效果不好。然后我们用建立的模型进行预测最后10个数据:
predicts_MA = chgdataModel_MA.predict(216, 225, dynamic=True) compare_MA = pd.DataFrame() compare_MA['original'] = test compare_MA['predict_MA'] = predicts_MA print(compare_MA)
可以看出,建立的模型效果很差,就算只看涨跌方向,正确率也不足。该模型不适用于原数据。没关系,如果真的这么简单能预测股价日涨跌才奇怪了~关于MA的内容只做了简单介绍,下面主要介绍ARMA模型。
自回归-滑动平均模型(ARMA)
AR模型与MA模型的不同
AR和MA模型之间的主要区别是基于不同时间点的时间序列对象之间的相关性。x(t)与x(t-n)的相关性总为0,这直接源于x(t)和x(t-n)之间的协方差对于MA模型来说是零。然而,AM模型中x(t)与x(t-1)的相关性随着时间的推移变得越来越小。不管是否有AR模型或MA模型,这种差异都可以被利用。
在有些应用中,我们需要高阶的AR或MA模型才能充分地描述数据的动态结构,这样问题会变得很繁琐。为了克服这个困难,提出了自回归滑动平均(ARMA)模型。基本思想是把AR和MA模型结合在一起,使所使用的参数个数保持很小。模型的形式为:
$$r_t=\phi_0+\sum_{i=1}^p\phi_ir_{t-i}+a_t+\sum_{i=1}^q\theta_ia_{t-i}$$
其中,{$a_t$}为白噪声序列,$p$和$q$都是非负整数。AR和MA模型都是ARMA(p,q)的特殊形式。
利用向后推移算子$B$(后移算子$B$,即上一时刻),上述模型可写成:
$$(1-\phi_1B-\cdots-\phi_pB^p)r_t=\phi_0+(1-\theta_1B-\cdots-\theta_qB^q)a_t$$
这时候我们求$r_t$的期望,得到:
$$E(r_t)=\frac{\phi_0}{1-\phi_1-\cdots-\phi_p}$$
和上期我们的AR模型一样。因此有着相同的特征方程:
$$1-\phi_1x-\phi_2x^2-\cdots-\phi_px^p=0$$
该方程所有解的倒数称为该模型的特征根,如果所有的特征根的模都小于1,则该ARMA模型是平稳的。有一点很关键:ARMA模型的应用对象应该为平稳序列!下面的步骤都是建立在假设原序列平稳的条件下的。
一旦我们得到平稳时间序列,我们必须回答:是AR还是MA过程?
ACF是不同滞后函数之间的总关联图。例如,在GDP问题上,时间点T的GDP是x(t)。我们对x(t)与x(t-1)、x(t-2)等的相关性很感兴趣。现在让我们来反思一下上面所学的内容。在移动平均序列的滞后n中,x(t)与x(t-n-1)之间不存在任何相关。因此,总相关图在第n次滞后处截止。因此,很容易找到一个MA系列的滞后。对于AR序列,这种相关性将逐渐下降而没有任何截止值。
如果发现每个滞后的部分相关,则在AR级数的程度之后会被切断。例如,如果我们有AR系列,如果我们排除第一滞后x(t-1)的影响,则我们的第二滞后x(t-2)与x(t)无关。因此,偏相关函数(PACF)在第一滞后急剧下降。下面是一些例子来澄清你对这个概念的任何怀疑:
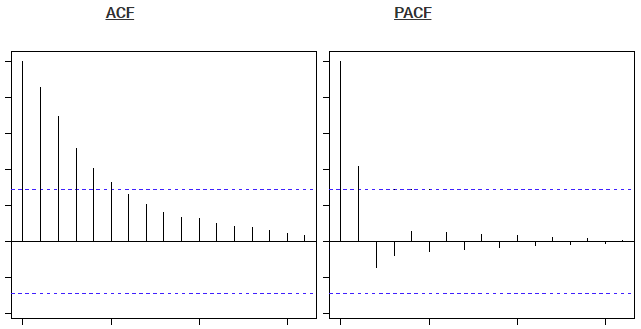
上面的蓝线显示出明显不同于零的值。显然,上面的图在第二滞后之后在PACF曲线上有一个截止,这意味着这主要是AR过程。
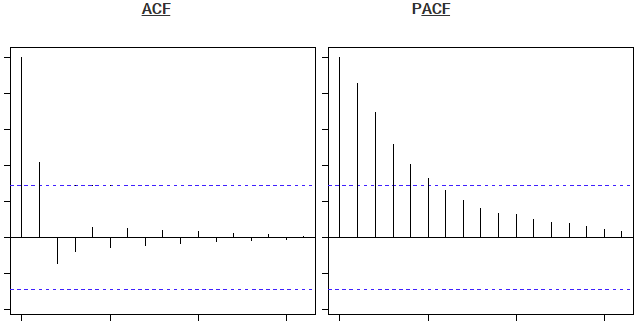
显然,上面的图在第二滞后之后在ACF曲线上有一个截止,这意味着这主要是MA过程。
ARMA模型的阶数确定
PACF、ACF判断模型阶数
我们通过观察PACF和ACF截尾,分别判断p、q的值。(限定滞后阶数40)
fig = plt.figure(figsize=(12,12)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(change_data, lags=30, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(change_data, lags=30, ax=ax2)
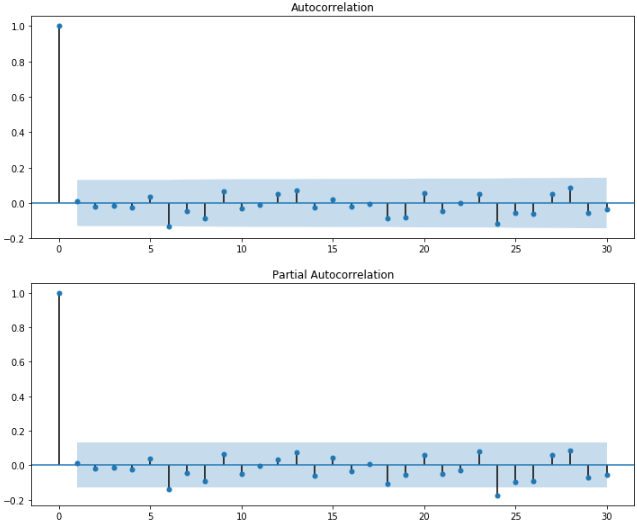
可以看出,模型的阶次应该为(6,24)。然而,这么高的阶次建模的计算量是巨大的。为什么不再限制滞后阶数小一些?如果lags设置为25,20或者更小时,阶数为(0,0),显然不是我们想要的结果。
综合来看,由于计算量太大,在这里就不使用(6,24)建模了。采用另外一种方法确定阶数。
信息准则定阶
关于信息准则,已有过一些介绍。下面,我们分别应用以上3种法则,为我们的模型定阶,数据仍然是日涨跌幅序列。为了控制计算量,我们限制AR最大阶不超过6,MA最大阶不超过4。但是这样带来的坏处是可能为局部最优。
import warnings
warnings.filterwarnings("ignore")
sm.tsa.arma_order_select_ic(change_data, max_ar=6, max_ma=4, ic='aic')['aic_min_order'] #AIC
#(5,4)
sm.tsa.arma_order_select_ic(change_data, max_ar=6, max_ma=4, ic='bic')['bic_min_order'] #BIC
#(0,0)
sm.tsa.arma_order_select_ic(change_data, max_ar=6, max_ma=4, ic='hqic')['hqic_min_order'] #HQIC
#(0,0)
可以看出,AIC求解的模型阶次为(5,4)。我们这里就以AIC准则为准~至于到底哪种准则更好,可以分别建模进行对比~
ARMA模型的预测和检验
预测的流程和MA流程一致,这里不再重复。预测结果的拟合优度得分仍然很低,但是从预测图上来看,好像比之前强了一点,至少在中间部分效果还不错。
可能的原因有:
- 信息准则定阶时,为减少计算量,我们设定了AR和MA模型的最大阶数,这样得到的阶数只是局部最优解。
- ARMA模型不足以预测股价的变化趋势(这也正常,不然人人都可以赚大钱了)
差分自回归滑动平均模型(Auto-Regressive Integrated Moving Averages,ARIMA)
到目前为止,我们研究的序列都集中在平稳序列。即ARMA模型研究的对象为平稳序列。如果序列是非平稳的,就可以考虑使用ARIMA模型。ARIMA比ARMA仅多了个”I”,代表着其比ARMA多一层内涵:也就是差分。一个非平稳序列经过d次差分后,可以转化为平稳时间序列。d具体的取值,我们得分被对差分1次后的序列进行平稳性检验,若果是非平稳的,则继续差分。直到d次后检验为平稳序列。
平稳时间序列的ARIMA预测的只不过是一个线性方程(如线性回归)。模型有三个主要参数:
- Number of AR (Auto-Regressive) terms (p):现在点使用多少个过往数据计算。AR条件仅仅是因变量的滞后。如:如果 P 等于 5,那么预测 x(t)将是 x(t-1)…x(t-5)。
- Number of MA (Moving Average) terms (q):使用多少个过往的残余错误值。MA条件是预测方程的滞后预测错误。如:如果 q 等于 5,预测 x(t)将是 e(t-1)…e(t-5),e(i) 是移动平均叔在第 i 个瞬间和实际值的差值。
- Number of Differences (d):为时间序列成为平稳时所做的差分次数。有非季节性的差值,这种情况下我们采用一阶差分。
ARIMA 模型分析框架
下图的框架展示了如何一步一步的“做一个时间序列分析”
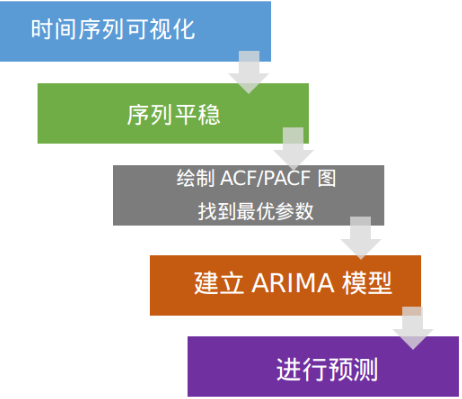
前三步我们在前文已经讨论了。尽管如此,这里还是需要简单说明一下:
第一步:时间序列可视化
在构建任何类型的时间序列模型之前,分析其趋势是至关重要的。我们感兴趣的细节与系列中的任何趋势、季节性或随机行为有关。
第二步:时间序列平稳
一旦我们知道了模式、趋势、周期。我们就可以检查序列是否平稳。Dicky-Fuller 是一种很流行的检验方式。如果发现序列是非平稳序列怎么办?
这里有三种比较常用的技术来让一个时间序列平稳。
1、消除趋势:这里我们简单的删除时间序列中的趋势成分。例如,我的时间序列的方程是:
$$x(t)=(mean+trend*t)+error$$
我们只需删除括号中的部分,并为其余部分建立模型。
2、差分:这是常用的去除非平稳性的技术。这里我们是对序列的差分的结果建立模型而不是真正的序列。例如:
$$x(t)-x(t-1)=ARMA(p,q)$$
这种差异称为 AR(I)MA 中的积分部分。现在,我们有三个参数:
- p: AR
- d: I
- q: MA
3、季节性:季节性直接被纳入 ARIMA 模型中。下面的应用部分我们再讨论这个。
第三步:找到最优参数
使用 ACF 和 PACF 图可以找到参数 p、d、q。这种方法的一个补充是,如果 ACF 和 PACF 逐渐减小,则表明我们需要使时间序列平稳并将值引入到“d”。
第四步:建立 ARIMA 模型
找到了这些参数,我们现在就可以尝试建立 ARIMA 模型了。从上一步找到的值可能只是一个近似估计的值,我们需要探索更多 (p,d,q)的组合。最小的 BIC 和 AIC 的模型参数才是我们要的。我们也可以尝试一些具有季节性成分的模型。在这里,在 ACF/PACF 图中我们会注意到一些季节性的东西。
第五步:预测
一旦我们有了最后的 ARIMA 模型,我们现在就可以预测未来的时间点。如果模型工作正常,我们也可以用可视化趋势来验证。
ARIMA 模型参数 p、d、q
看完上面的介绍你一定对于如何确定 ARIMA 模型的参数 p、d、q 还有疑问。接下来讲解何确定 p、d、q 参数。
实验数据:链接: https://pan.baidu.com/s/14Nt8aU3NbgzBt2lA_jmB6Q 提取码: 8rbt读取并观察数据
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
data = pd.read_csv("arima-demo.csv", parse_dates=['date'], index_col='date')
print(data.head())
data.plot(figsize=(12,6))
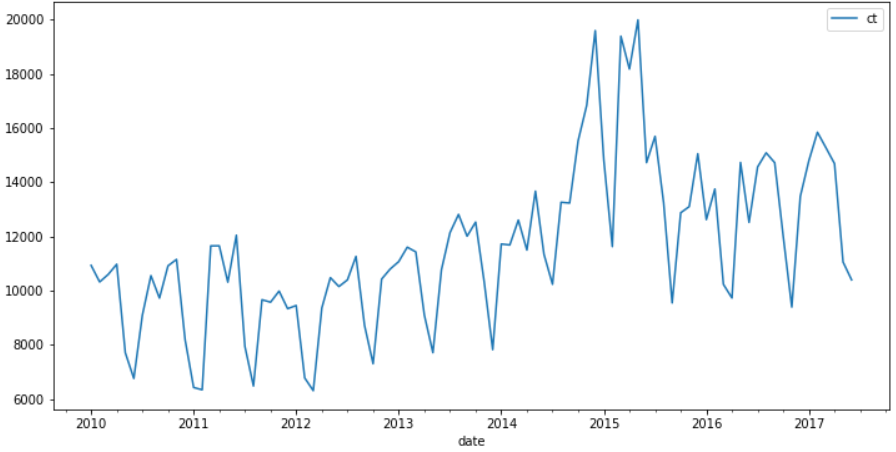
从上图可知,存在一定的增长趋势。
时间序列的差分 d
ARIMA 模型对时间序列的要求是平稳型。因此,当你得到一个非平稳的时间序列时,首先要做的即是做时间序列的差分,直到得到一个平稳时间序列。如果你对时间序列做 d 次差分才能得到一个平稳序列,那么可以使用 ARIMA(p,d,q) 模型,其中 d 是差分次数。
1 阶差分:
diff1 = data.diff(1) diff1.plot(figsize=(12,6))
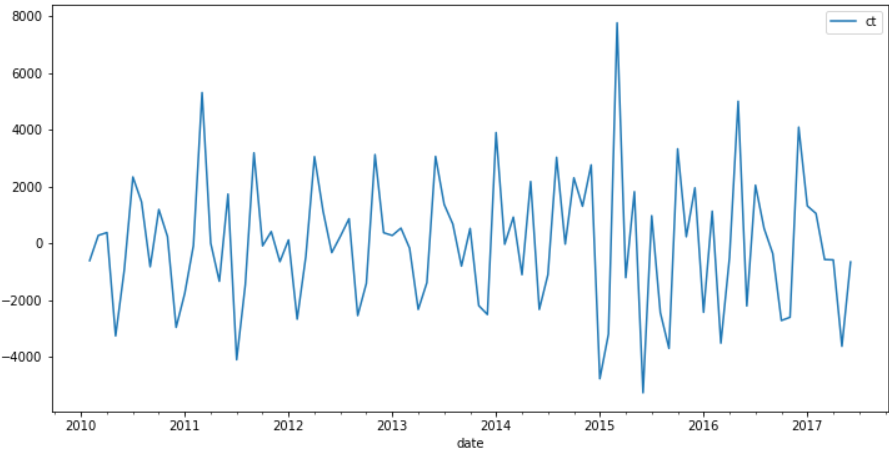
目测已经平稳,再来看看 2 阶差分的效果:
diff2 = data.diff(2) diff2.plot(figsize=(12,6))
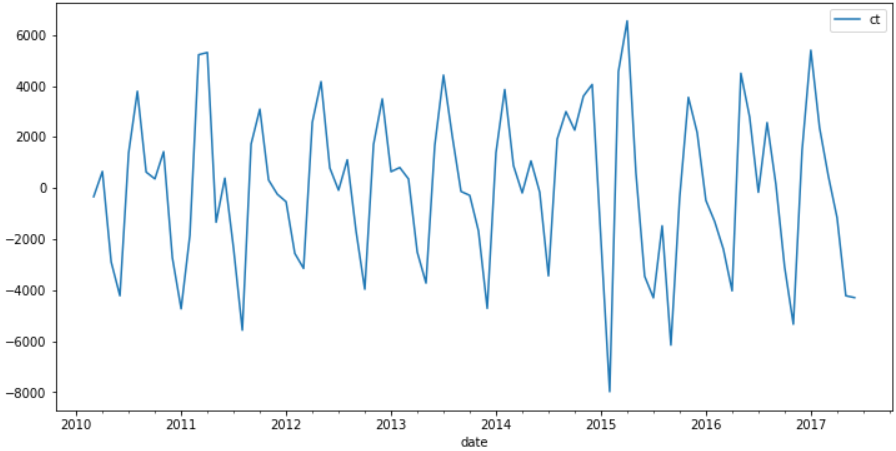
可以看到二阶差分侯差异不大,所以这里 d 设置为 1 即可。
阶数 p 和阶数 q
如何确定差分阶数和常数项:
- 假如时间序列在很高的 lag(10 以上)上有正的 ACF,则需要很高阶的差分
- 假如 lag-1 的 ACF 是 0 或负数或者非常小,则不需要很高的差分,假如 lag-1 的 ACF 是 -0.5 或更小,序列可能 overdifferenced。
- 最优的差分阶数一般在最优阶数下标准差最小(但并不是总数如此)
- 模型不查分意味着原先序列是平稳的;1 阶差分意味着原先序列有个固定的平均趋势;二阶差分意味着原先序列有个随时间变化的趋势
- 模型没有差分一般都有常数项;有两阶差分一般没常数项;假如 1 阶差分模型非零的平均趋势,则有常数项
如何确定 AR 和 MA 的阶数:
- 假如 PACF 显示截尾或者 lag-1 的 ACF 是正的(此时序列仍然有点 underdifferenced),则需要考虑 AR 项;PACF 的截尾项表明 AR 的阶数
- 假如 ACF 显示截尾或者 lag-1 的 ACF 是负的(此时序列有点 overdifferenced),则需要加 MA 项,ACF 的截尾项表明 AR 的阶数
- AR 和 MA 可以相互抵消对方的影响,所以假如用 AR-MA 模型去拟合数据,仍然需要考虑加些 AR 或 MA 项。尤其在原先模型需要超过 10 次的迭代去 converge。
- 假如在 AR 部分有个单位根(AR 系数和大约为 1),此时应该减少一项 AR 增加一次差分
- 假如在 MA 部分有个单位根(MA 系数和大约为 1),此时应该减少一项 AR 减少一次差分
- 假如长期预测出现不稳定,则可能 AR、MA 系数有单位根
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的 ARIMA 模型,即 ARIMA 模型中合适的 p,q。
第一步我们要先检查平稳时间序列的自相关图和偏自相关图。
diff1.dropna(inplace=True) fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(diff1, lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(diff1, lags=40, ax=ax2)
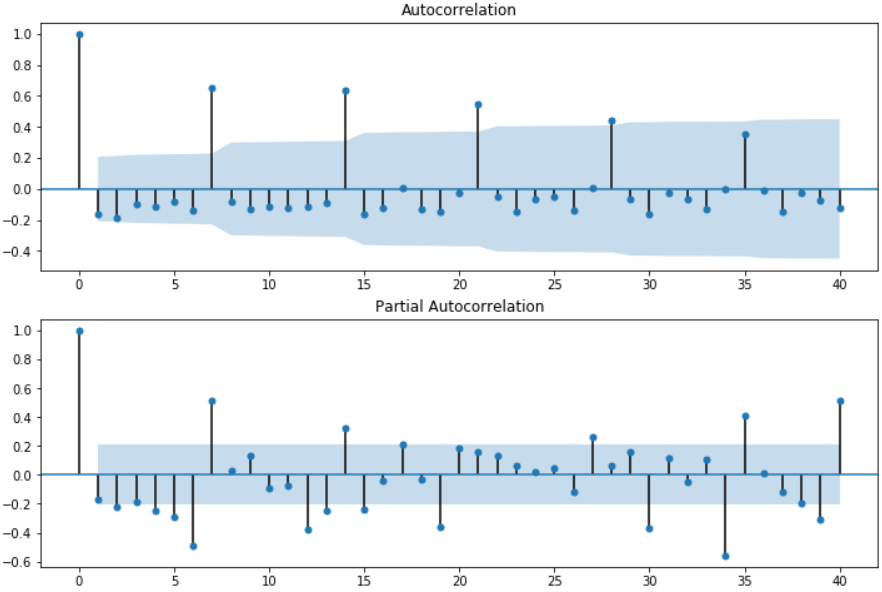
其中lags表示滞后的阶数,以上分别得到acf图和pacf图。通过两图观察得到:
- 自相关图显示滞后有3(4)个阶超出了置信边界
- 偏相关图显示在滞后1至7阶(lags 1,2,…,7)时的偏自相关系数超出了置信边界,从lag 7之后偏自相关系数值缩小至0
则有以下模型可以供选择:
- ARMA(0,1)模型:即自相关图在滞后1阶之后缩小为0,且偏自相关缩小至0,则是一个阶数q=1的移动平均模型;
- ARMA(7,0)模型:即偏自相关图在滞后7阶之后缩小为0,且自相关缩小至0,则是一个阶层p=3的自回归模型;
- ARMA(7,1)模型:即使得自相关和偏自相关都缩小至零。则是一个混合模型。
为了确定哪个模型最合适,可以采用信息准测AIC、BIC、HQIC判定:
arma_mod70 = sm.tsa.ARMA(diff1, (7,0)).fit()
print("arma_mod70:", arma_mod70.aic, arma_mod70.bic, arma_mod70.hqic)
arma_mod01 = sm.tsa.ARMA(diff1, (0,1)).fit()
print("arma_mod01:", arma_mod01.aic, arma_mod01.bic, arma_mod01.hqic)
arma_mod71 = sm.tsa.ARMA(diff1, (7,1)).fit()
print("arma_mod71:", arma_mod71.aic, arma_mod71.bic, arma_mod71.hqic)
arma_mod70: 1579.7025547690232 1602.1002820966125 1588.7304359010805
arma_mod01: 1632.3203732818517 1639.7862823910482 1635.3296669925376
arma_mod71: 1581.0916055163707 1605.9779692136922 1591.12258455199
可以看到ARMA(7,0)的aic,bic,hqic均最小,因此是最佳模型。
ARIMA模型的校验
在指数平滑模型下,观察ARIMA模型的残差是否是平均值为0且方差为常数的正态分布(服从零均值、方差不变的正态分布),同时也要观察连续残差是否(自)相关。
残差的自相关与偏自相关
对ARMA(7,0)模型所产生的残差做自相关图:
resid = arma_mod70.resid #残差 fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)
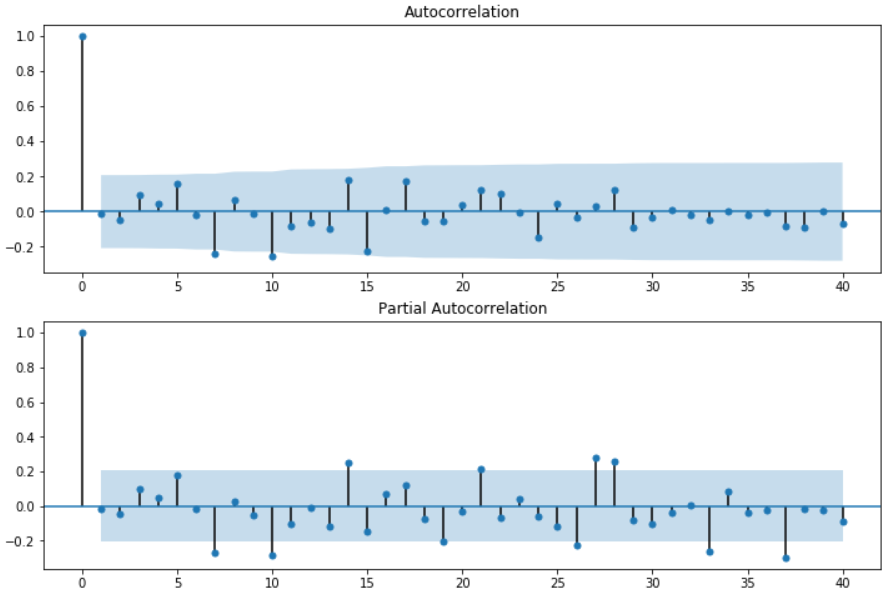
看一看到大部分都在置信空间内,部分超出也只超出一点点。
D-W检验
Durbin-Watson检验,简称D-W检验,是目前检验自相关性最常用的方法,但它只使用于检验一阶自相关性。当DW值显著的接近于O或4时,则存在自相关性,而接近于2时,则不存在(一阶)自相关性。
print(sm.stats.durbin_watson(resid)) #2.024244082702278
观察是否符合正态分布
这里使用QQ图,它用于直观验证一组数据是否来自某个分布,或者验证某两组数据是否来自同一(族)分布。在教学和软件中常用的是检验数据是否来自于正态分布。
from statsmodels.graphics.api import qqplot fig = plt.figure(figsize=(12,6)) ax = fig.add_subplot(111) fig = qqplot(resid, line='q', ax=ax, fit=True)
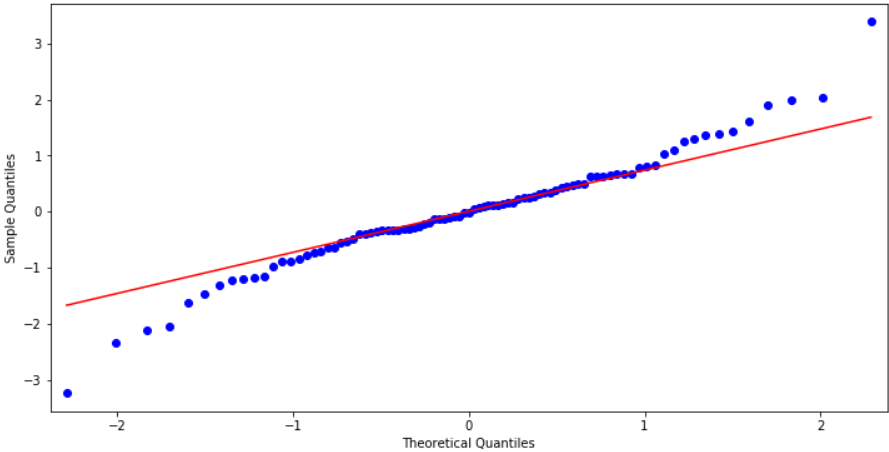
Ljung-Box检验
Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验,我们常常采用的方法还包括计算ACF和PCAF并观察其图像,但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数,判断序列总体的相关性或者说随机性是否存在。时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型,其残差被假定为高斯白噪声序列,所以当我们用ARIMA模型去拟合数据时,拟合后我们要对残差的估计序列进行LB检验,判断其是否是高斯白噪声,如果不是,那么就说明ARIMA模型也许并不是一个适合样本的模型。
import numpy as np
r, q, p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
ACQ Prob(> Q) lag 1.0 -0.014445 0.019203 0.889787 2.0 -0.047441 0.228719 0.891937 3.0 0.097778 1.129072 0.770061 4.0 0.047514 1.344178 0.853837 5.0 0.156219 3.697174 0.593785 6.0 -0.017855 3.728282 0.713391 7.0 -0.241230 9.475812 0.220274 8.0 0.068078 9.939217 0.269318 9.0 -0.012041 9.953895 0.354231 10.0 -0.256684 16.708543 0.081067 11.0 -0.085178 17.461885 0.094936 12.0 -0.063577 17.887029 0.119164 13.0 -0.096512 18.879634 0.126883 14.0 0.181119 22.422039 0.070348 15.0 -0.223097 27.869400 0.022401 16.0 0.012916 27.887910 0.032608 17.0 0.176769 31.402779 0.017833 18.0 -0.053140 31.724897 0.023694 19.0 -0.057704 32.110150 0.030374 20.0 0.037425 32.274556 0.040459 21.0 0.120519 34.004510 0.036199 22.0 0.102662 35.278536 0.036225 23.0 -0.007830 35.286058 0.048710 24.0 -0.148547 38.035517 0.034383 25.0 0.046254 38.306261 0.043173 26.0 -0.032621 38.443060 0.055055 27.0 0.032381 38.580025 0.069141 28.0 0.124968 40.653492 0.057760 29.0 -0.092711 41.813707 0.058361 30.0 -0.033602 41.968698 0.072016 31.0 0.011216 41.986264 0.090054 32.0 -0.016597 42.025405 0.110574 33.0 -0.047033 42.345328 0.127733 34.0 0.001922 42.345872 0.154137 35.0 -0.022258 42.420173 0.181558 36.0 -0.003481 42.422025 0.213721 37.0 -0.083009 43.495231 0.214345 38.0 -0.089174 44.758050 0.209260 39.0 0.005255 44.762523 0.242730 40.0 -0.065663 45.475168 0.254607
检验的结果就是看最后一列前十二行的检验概率(一般观察滞后1~12阶),如果检验概率小于给定的显著性水平,比如0.05就拒绝原假设,其原假设是相关系数为零。就结果来看,如果取显著性水平大于0.05,那么相关系数与零没有显著差异,即为白噪声序列。
ARIMA模型实战,通过ACF和PCF确定参数
测试数据使用上面平稳序列使用的AirPassengers数据。
绘制ACF和PACF图
时间序列的自回归函数和偏自回归函数可以在差分后绘制为:
# ACF and PACF plots:
from statsmodels.tsa.stattools import acf, pacf
lag_acf = acf(ts_log_diff, nlags=20)
lag_pacf = pacf(ts_log_diff, nlags=20, method='ols')
# Plot ACF:
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0, linestyle='--', color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)), linestyle='--', color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)), linestyle='--', color='gray')
plt.title('Autocorrelation Function')
# Plot PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0, linestyle='--', color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)), linestyle='--', color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)), linestyle='--', color='gray')
plt.title('Partial Autocorrelation Function')
plt.tight_layout()
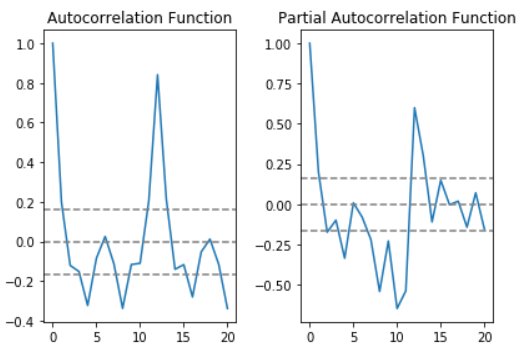
在这个例子中,0刻度线上线的2条虚线为置信区间,用来确定“p”和“q”的值。
- p:部分自相关函数表第一次截断的上层置信区间是滞后值。如果你仔细看,该值是p=0
- q:自相关函数表第一次截断的上层置信区间是滞后值。如果你仔细看,该值是q=1
现在开始搭建ARIMA的三个模型,及计算各自的RSS(这里的RSS是指残差值,而不是实际序列)
自回归(AR)模型
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(ts_log, order=(0, 1, 0))
results_AR = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_AR.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_AR.fittedvalues-ts_log_diff)**2))
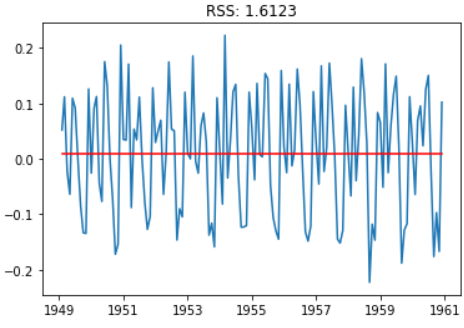
移动平均数(MA)模型
model = ARIMA(ts_log, order=(0, 1, 1))
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_MA.fittedvalues-ts_log_diff)**2))
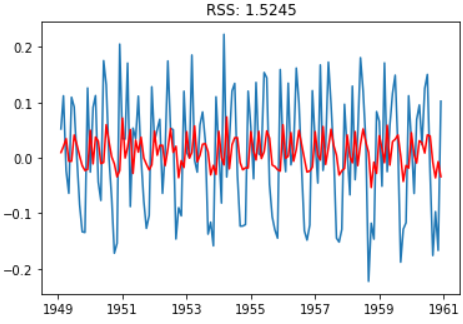
ARMA组合
在本例中,由于AR的p值为0,所以组合的结果与MA一致:
model = ARIMA(ts_log, order=(0, 1, 1))
results_ARIMA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red')
plt.title('RSS: %.4f'% sum((results_ARIMA.fittedvalues-ts_log_diff)**2))
转化为原数据空间
前面模型采用的数据都是转化后的数据,为了得到最终的结果,需要将数据转化为原数据空间。第一步将预测结果保存为序列。
predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True) print(predictions_ARIMA_diff.head())
TravelDate 1949-02-01 0.009726 1949-03-01 0.020485 1949-04-01 0.034537 1949-05-01 -0.005924 1949-06-01 -0.006085 dtype: float64
注意这些是从‘1949-02-01’开始而不是第一个月。为什么?这是因为我们将第一个月份取为滞后值,一月前面没有可以减去的元素。一个简单的解决方法是先确定索引的累积和,然后将它添加到基数。累积和的计算方式如下:
predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum() print(predictions_ARIMA_diff_cumsum.head())
TravelDate 1949-02-01 0.009726 1949-03-01 0.030211 1949-04-01 0.064748 1949-05-01 0.058824 1949-06-01 0.052739 dtype: float64
将差分转换为对数尺度的方法是这些差值连续地添加到基数。(第一个元素是基数本身)
predictions_ARIMA_log = pd.Series(ts_log.iloc[0], index=ts_log.index) predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum, fill_value=0) predictions_ARIMA_log.head()
TravelDate 1949-01-01 4.718499 1949-02-01 4.728225 1949-03-01 4.748710 1949-04-01 4.783247 1949-05-01 4.777323 dtype: float64
最后一步是将指数与原序列比较。
predictions_ARIMA = np.exp(predictions_ARIMA_log)
plt.plot(ts)
plt.plot(predictions_ARIMA)
plt.title('RMSE: %.4f'% np.sqrt(sum((predictions_ARIMA-ts)**2)/len(ts)))
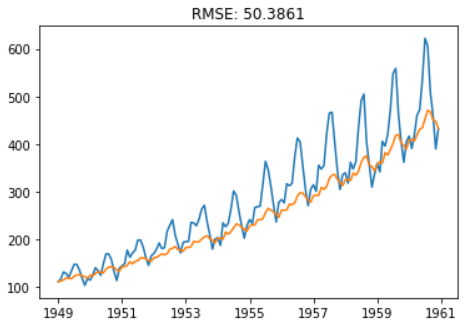
ARIMA模型实战,基于”分解”进行未来预测
前面讲到了,分解出来的df测试值要优于移动平均和移动加权平均,这里就使用”分解”后的数据进行进一步的预测。
对残差值进行预测
from statsmodels.tsa.arima_model import ARIMA residual.dropna(inplace=True) model_ARIMA = ARIMA(residual, (0,1,1)).fit(disp=-1, method='css') predictions_ARIMA = model_ARIMA.predict(start='1950-01-01', end='1962-04-01') plt.plot(residual) plt.plot(predictions_ARIMA)
这里的(p,d,q)与就使用上一篇文章中的(0,1,1)。预测后的数据绘制出来为:
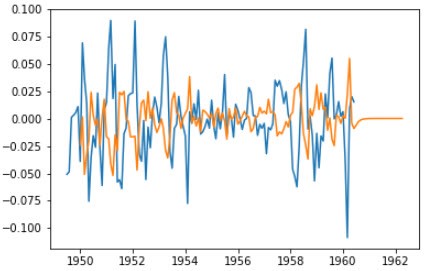
在残差预测的基础上加上趋势和季节数据
predictions_ARIMA = predictions_ARIMA.add(trend, fill_value=0).add(seasonal, fill_value=0) predictions_ARIMA = np.exp(predictions_ARIMA) plt.plot(data['Passengers'], color='blue') plt.plot(predictions_ARIMA, color='red')
绘制出来的图像如下:
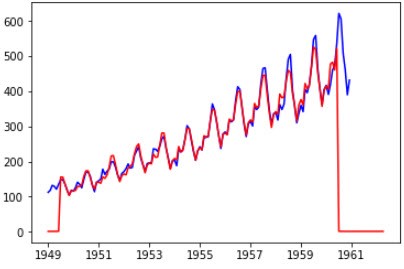
可以看到在中间匹配的还可以,而开头和最后预测结果比较异常,通过查看trend、seasonal的数据可发现其存在数据缺失。trend在1960-06之后便没有数据了,seasonal在1960-12之后也结束了,所以会导致最终的数据在1960-06之后便为0了。
print(trend) print(seasonal)
对trend和seasonal进行预测
我们看看trend的形状:
plt.plot(trend)
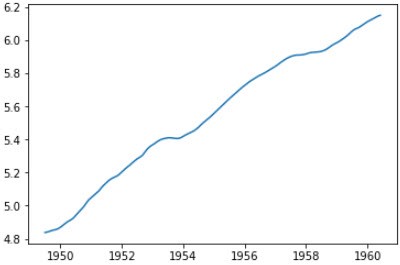
上面趋势近似线性,我们可以用线性拟合来预测1960-06之后的数据:
trend.dropna(inplace=True)
from sklearn.linear_model import LinearRegression
x = pd.Series(range(trend.size), index=trend.index)
x = x.to_frame()
linreg = LinearRegression()
linereg = linreg.fit(x, trend)
x = pd.Series(range(0,154), index=(pd.period_range('1949-07', periods=154, freq='M'))
x = x.to_frame()
res_predict = linereg.predict(x)
trend2 = pd.Series(res_predict, index=x.index).to_timestamp()
plt.plot(trend, color='blue')
plt.plot(trend2, color='red')
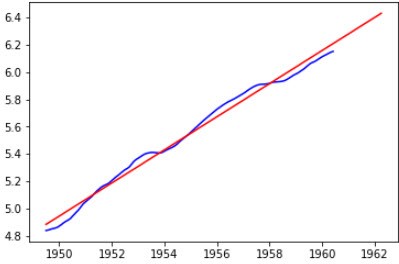
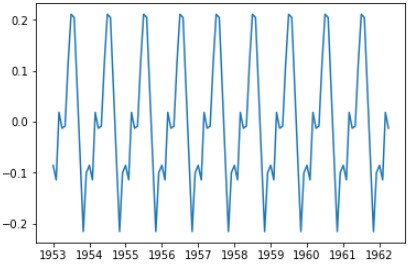
由于seasonal是周期性的,直接用shift即可:
index1 = pd.date_range(start='1949-01-01', end='1962-04-01', freq='MS') seasonal = seasonal.reindex(index1) seasonal = seasonal.shift(24) plt.plot(seasonal)
周期图如下图:
在预测残差的基础上,重新添加trend和seasonal
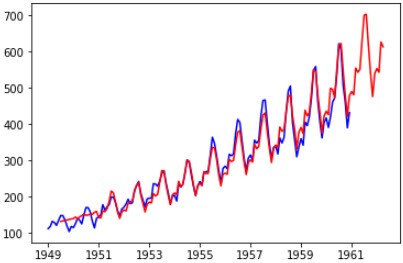
model_ARIMA = ARIMA(residual, (0,1,1)).fit(disp=-1, method='css') predictions_ARIMA = model_ARIMA.predict(start='1950-01-01', end='1962-04-01') predictions_ARIMA = predictions_ARIMA.add(trend2, fill_value=0).add(seasonal, fill_value=0) predictions_ARIMA = np.exp(predictions_ARIMA) plt.plot(data['Passengers'], color='blue') plt.plot(predictions_ARIMA, color='red')
最终预测效果为:
ARIMA模型实战,基于网格搜索确定参数
确定ARIMA参数值
从上面的ACF和PACF可大致确定ARIMA的参数,p=偏自相关截尾的lag。如果偏自相关截尾后,自相关仍然拖尾,考虑增加p;q=自相关截尾的lag。如果自相关截尾后,偏自相关仍然拖尾,考虑增加q。以上仅是理论上的说法,具体最合适的p,q,还是要以AIC、BIC或预测结果残差最小来循环确定。ARIMA模型是通过优化AIC,BIC,HQIC等得出的,一般来说AIC较小的模型拟合度较好,但拟合度较好不能说明预测能力好。
from statsmodels.tsa.arima_model import ARIMA #导入ARIMA模型
d = 1 #一阶差分后平稳,所以d=1。p,q参数使用循环暴力调参确定最佳值
pdq_result = pd.DataFrame()
for p in range(0,5):
for q in range(0,5):
try:
model = ARIMA(ts_week_log, order=(p,d,q)) #ARIMA的参数:order=p,d,q
results_ARIMA = model.fit()
pdq_result = pdq_result.append(pd.DataFrame(
{'p':[p], 'd':[d], 'q':[q], 'AIC':[results_ARIMA.aic], 'BIC':[results_ARIMA.bic],
'HQIC':[results_ARIMA.hqic]}))
#print(results_ARIMA.summary()) #summary2()也可以使用
except:
pass
print(pdq_result)
pdq AIC BIC HQIC 0 0 10 -13939.315506 -13927.843765 -13935.132034 0 0 11 -14083.366353 -14066.158742 -14077.091145 0 0 12 -14083.421767 -14060.478286 -14075.054823 0 0 13 -14081.931844 -14053.252492 -14071.473164 0 0 14 -14080.862357 -14046.447135 -14068.311941 0 1 10 -14083.792730 -14066.585119 -14077.517522 0 1 11 -14083.699762 -14060.756281 -14075.332818 0 1 12 -14082.602763 -14053.923412 -14072.144084 0 1 14 -14078.946543 -14038.795451 -14064.304391 0 2 10 -14083.401327 -14060.457845 -14075.034383 0 2 11 -14081.986100 -14053.306749 -14071.527420 0 2 12 -14081.512486 -14047.097264 -14068.962070 0 3 10 -14082.610717 -14053.931365 -14072.152037 0 3 11 -14080.785531 -14046.370309 -14068.235115 0 3 12 -14087.953053 -14047.801961 -14073.310901 0 3 13 -14086.313032 -14040.426069 -14069.579144 0 4 10 -14080.937459 -14046.522237 -14068.387043 0 4 11 -14078.958559 -14038.807467 -14064.316408 0 4 12 -14086.257204 -14040.370241 -14069.523316 0 4 14 -14082.963600 -14025.604897 -14062.046240
从上面的结果看,(p,d,q)比较适合选择(3,1,2)。所以用(3,1,2)参数比较拟合的数据和原始数据:
model = ARIMA(ts_week_log, order=(3,1,2)) #ARIMA的参数:order=p,d,q results_ARIMA = model.fit() plt.plot(ts_week_log_diff) plt.plot(results_ARIMA.fittedvalues, color='red') #fittedvalues返回的是d次差分后的序列,因此和ts_week_log_diff比较 residuals = pd.DataFrame(results_ARIMA.resid) #拟合的数据和原始数据ts_week_log的残差 plt.show()
计算拟合后残差的自相关和偏自相关
acf_pacf(residuals, lags=10, title='Residuals') #等于acf_pacf(results_ARIMA.fittedvalues-ts_week_log_diff, lags=10, title='Residuals')
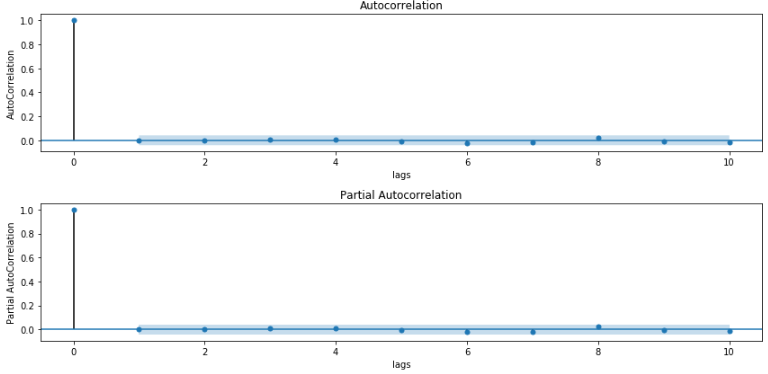
上图中我们看到完全的没有拖尾了。因为ARIMA模型会使拟合和原始数据的残差变为白噪声,所以残差的核密度(概率密度)为正态分布:
print('Residuals Summary:\n', residuals.describe())
residuals.plot(kind='kde')#概率密度图 kde
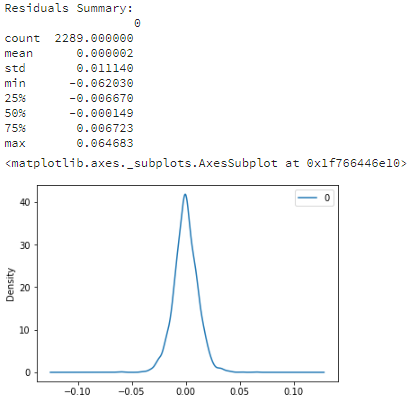
将拟合的值逆向转化并可视化:
predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)#复制Log和差分后的预测值
predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()#一阶差分的逆向转换为累计和
predictions_ARIMA_log = pd.Series(ts_week_log.iloc[0], index=ts_week_log.index)#将一个新序列的每个元素都填充为ts_week_log的第一个元素
predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum, fill_value=0)#将累计和追加到第一个元素上,还原log序列。其中的空值填充为0
predictions_ARIMA = np.exp(predictions_ARIMA_log)#进行指数运算,还原为原始值
plt.plot(ts_week)
plt.plot(predictions_ARIMA)
plt.title('RMSE: %.4f'%np.sqrt(sum((predictions_ARIMA-ts_week)**2)/len(ts_week)))
plt.show()
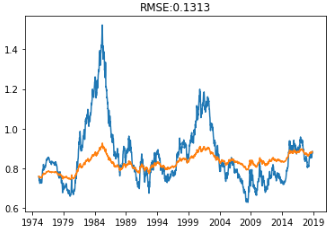
预测结果
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.arima_model import ARIMA
pdq = (3, 1, 2)
test_point = 15#测试点数
size = len(ts_week_log)-15
train, test = ts_week_log[0:size], ts_week_log[size:len(ts_week_log)]#切分数据集
model = ARIMA(train, order=pdq)
model_fit = model.fit()
predictions = model_fit.predict(start=size, end=size+test_point-1, dynamic=True).tolist()
error = mean_squared_error(test, predictions)
print('Printing Mean Squared Error of Predictions...')
predictions_series = pd.Series(predictions, index=test.index)#predictions没有Index,无法在图上显示出来,必须先追加Index
fig, ax = plt.subplots()
ax.set(title='Spot Exchange Rate, Euro into USD', xlabel='Date', ylabel='Euro into USD')
ax.plot(ts_week[-50:], 'o', label='observed')
ax.plot(np.exp(euro_predictions_series), 'g', label='rolling one-step out-of-sample forecast')
legend = ax.legend(loc='upper left')
legend.get_frame().set_facecolor('w')
SARIMAX
SARIMAX模型简介
ARIMA是用于单变量时间序列数据预测的最广泛使用的预测方法之一。尽管该方法可以处理具有趋势的数据,但它不支持具有季节性组件的时间序列。支持对该系列季节性组成部分进行直接建模的ARIMA扩展称为(SARIMA(Seasonal AutoRegressive Integrated Moving Averages with eXogenous regressors.)。它增加了三个新的参数来指定系列季节性成分的自回归(AR),差分(I)和移动平均(MA),以及季节性周期的附加参数。
ARIMA->SARIMA->SARIMAX:
- S是Seasonal,就是季节性、周期性的意思
- X是eXogenous,外部信息的意思
所以SARIMAX和ARIMA比就是增加了周期性,并且使用了外部信息来增强模型的预测能力
SARIMAX模型的使用
SARIMAX模型与ARIMA最大的不同是,会多出季节性参数。需要提供的参数为:
趋势参数:(与ARIMA模型相同)
- p:趋势自回归阶数
- d:趋势差分阶数
- q:趋势移动平均阶数
季节性参数:
- P:季节性自回归阶数
- D:季节性差分阶数
- Q:季节性移动平均阶数
- m:单个季节期间的时间步数
季节性ARIMA模型使用等于季节数的滞后差异来消除加性季节效应。与滞后1差分去除趋势一样,滞后差分引入移动平均项。季节性ARIMA模型包括滞后S处的自回归和移动平均项。SARIMA模型的符号指定为:SARIMA(p,d,q)(P,D,Q)m,其中m参数会影响P,D和Q参数。例如,月度数据的m为12表示每年的季节周期。
如何确定季节性部分:
- 假如序列有显著是季节性模式,则需要用季节性差分,但是不要使用两次季节性差分或总过超过两次差分(季节性和非季节性)
- 假如差分序列在滞后s处有正的ACF,s是季节的长度,则需要加入SAR项;假如差分序列在滞后s处有负的ACF,则需要加入SMA项,如果使用了季节性差异,则后一种情况很可能发生,如果数据具有稳定和合乎逻辑的季节性模式。如果没有使用季节性差异,前者很可能会发生,只有当季节性模式不稳定时才适用。应该尽量避免在同一模型中使用多于一个或两个季节性参数(SAR+SMA),因为这可能导致过度拟合数据和/或估算中的问题。
参考链接:http://people.duke.edu/~rnau/arimrule.htm
SARIMAX模型实战
实验数据:美国夏威夷莫纳罗亚火山天文台空气样本中大气二氧化碳数据(该数据收集了1958年3月至2001年12月的二氧化碳样本数据。重要的是statsmodels中自带此部分数据)
加载数据与序列可视化
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
data = sm.datasets.co2.load_pandas().data
data = data['co2'].resample('MS').mean()
data = data.fillna(data.bfill())
print(data.head())
data.plot(figsize=(12,6))
plt.show()
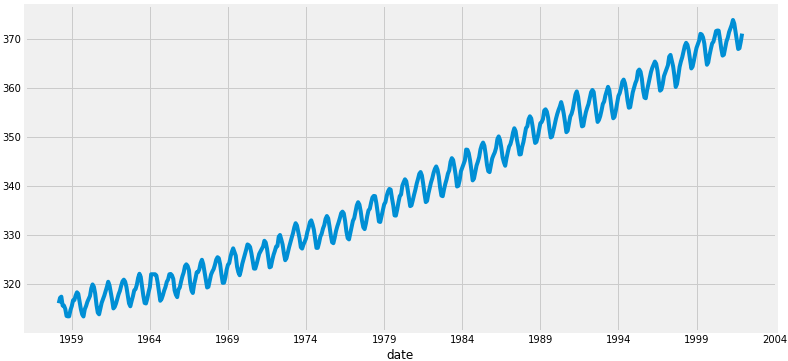 这里涉及到的内容有:
这里涉及到的内容有:
从绘制的图形看,整体的数据呈上升趋势,并且存在一定的季节性波动。
为模型选择最优参数
在上面的文章中详细介绍了ARIMA模型及,对应的(p,d,q)参数,方案是采用ACF和PACF图来确定具体的参数值。这里采用了另外一种方法”网格搜索”,通过迭代不同参数的组合来获取最佳参数。
# Define the p, d and q parameters to take any value between 0 and 2 p = d = q = range(0, 2) # Generate all different combinations of p, q and q triplets pdq = list(itertools.product(p, d, q)) print(pdq) # Generate all different combinations of seasonal p, q and q triplets seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))] print(seasonal_pdq)
接下来我们就可以通过不同的参数组合来对SARIMAX进行评估。在评估和比较不同参数的模型时,我们可以使用AIC值来评估。该值将在模型中直接返回。在这里AIC的值越小,则模型越优。
import warnings
warnings.filterwarnings("ignore") # specify to ignore warning messages
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
model = sm.tsa.statespace.SARIMAX(data, order=param, seasonal_order=param_seasonal, enforce_stationarity=False, enforce_invertibility=False)
results = model.fit()
print('ARIMA{}x{}-AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
由于某些参数组合可能会产生数值错误,所以在这里显式地禁用了警告消息,上述代码执行后获得的结果:
ARIMA(0,0,0)x(0,0,0,12) - AIC:7612.583429881011 ARIMA(0,0,0)x(0,0,1,12) - AIC:6787.343624031752 ARIMA(0,0,0)x(0,1,0,12) - AIC:1854.828234141261 ARIMA(0,0,0)x(0,1,1,12) - AIC:1596.711172763898 ARIMA(0,0,0)x(1,0,0,12) - AIC:1058.9388921320026 ARIMA(0,0,0)x(1,0,1,12) - AIC:1056.2878557033246 ARIMA(0,0,0)x(1,1,0,12) - AIC:1361.6578978072075 ARIMA(0,0,0)x(1,1,1,12) - AIC:1044.7647912998186 ARIMA(0,0,1)x(0,0,0,12) - AIC:6881.048755126321 ARIMA(0,0,1)x(0,0,1,12) - AIC:6072.662327947137 ARIMA(0,0,1)x(0,1,0,12) - AIC:1379.1941067330986 ARIMA(0,0,1)x(0,1,1,12) - AIC:1241.4174716851521 ARIMA(0,0,1)x(1,0,0,12) - AIC:1084.9453872064087 ARIMA(0,0,1)x(1,0,1,12) - AIC:780.4316223926196 ARIMA(0,0,1)x(1,1,0,12) - AIC:1119.5957893630987 ARIMA(0,0,1)x(1,1,1,12) - AIC:807.0912988896297 ARIMA(0,1,0)x(0,0,0,12) - AIC:1675.8086923024293 ARIMA(0,1,0)x(0,0,1,12) - AIC:1240.2211199194085 ARIMA(0,1,0)x(0,1,0,12) - AIC:633.4425586468699 ARIMA(0,1,0)x(0,1,1,12) - AIC:337.793854858494 ARIMA(0,1,0)x(1,0,0,12) - AIC:619.9501759055394 ARIMA(0,1,0)x(1,0,1,12) - AIC:376.9283760898942 ARIMA(0,1,0)x(1,1,0,12) - AIC:478.3296906672489 ARIMA(0,1,0)x(1,1,1,12) - AIC:323.07764996953097 ARIMA(0,1,1)x(0,0,0,12) - AIC:1371.187260233786 ARIMA(0,1,1)x(0,0,1,12) - AIC:1101.8410734303056 ARIMA(0,1,1)x(0,1,0,12) - AIC:587.9479709744935 ARIMA(0,1,1)x(0,1,1,12) - AIC:302.49490008406354 ARIMA(0,1,1)x(1,0,0,12) - AIC:584.4333533493711 ARIMA(0,1,1)x(1,0,1,12) - AIC:337.1999050779197 ARIMA(0,1,1)x(1,1,0,12) - AIC:433.0863608210692 ARIMA(0,1,1)x(1,1,1,12) - AIC:281.5190053393452 ARIMA(1,0,0)x(0,0,0,12) - AIC:1676.8881767362054 ARIMA(1,0,0)x(0,0,1,12) - AIC:1241.9353188506311 ARIMA(1,0,0)x(0,1,0,12) - AIC:624.2602350563734 ARIMA(1,0,0)x(0,1,1,12) - AIC:341.2896611730041 ARIMA(1,0,0)x(1,0,0,12) - AIC:579.3896901160358 ARIMA(1,0,0)x(1,0,1,12) - AIC:370.591911050293 ARIMA(1,0,0)x(1,1,0,12) - AIC:476.0500429124218 ARIMA(1,0,0)x(1,1,1,12) - AIC:329.5844988945166 ARIMA(1,0,1)x(0,0,0,12) - AIC:1372.6085881684037 ARIMA(1,0,1)x(0,0,1,12) - AIC:1199.4888202249872 ARIMA(1,0,1)x(0,1,0,12) - AIC:586.4485732044088 ARIMA(1,0,1)x(0,1,1,12) - AIC:305.62738298712236 ARIMA(1,0,1)x(1,0,0,12) - AIC:586.5467067203238 ARIMA(1,0,1)x(1,0,1,12) - AIC:400.3606781886424 ARIMA(1,0,1)x(1,1,0,12) - AIC:433.54694646294087 ARIMA(1,0,1)x(1,1,1,12) - AIC:284.35964168784733 ARIMA(1,1,0)x(0,0,0,12) - AIC:1324.311112732457 ARIMA(1,1,0)x(0,0,1,12) - AIC:1060.935191442204 ARIMA(1,1,0)x(0,1,0,12) - AIC:600.7412682874252 ARIMA(1,1,0)x(0,1,1,12) - AIC:312.1329632683155 ARIMA(1,1,0)x(1,0,0,12) - AIC:593.6637754853627 ARIMA(1,1,0)x(1,0,1,12) - AIC:349.209146507186 ARIMA(1,1,0)x(1,1,0,12) - AIC:440.1375884358338 ARIMA(1,1,0)x(1,1,1,12) - AIC:293.56145595783397 ARIMA(1,1,1)x(0,0,0,12) - AIC:1262.6545542448305 ARIMA(1,1,1)x(0,0,1,12) - AIC:1052.0636724058634 ARIMA(1,1,1)x(0,1,0,12) - AIC:581.3099935252751 ARIMA(1,1,1)x(0,1,1,12) - AIC:295.9374058139739 ARIMA(1,1,1)x(1,0,0,12) - AIC:576.8647112079228 ARIMA(1,1,1)x(1,0,1,12) - AIC:327.90491219439946 ARIMA(1,1,1)x(1,1,0,12) - AIC:444.12436865154666 ARIMA(1,1,1)x(1,1,1,12) - AIC:277.7802201071108
从上面返回的结果中,我们发现ARIMA(1,1,1)x(1,1,1,12)返回的AIC为277.78,值最小。因此,我们应该认为这是我们所考虑的所有模型中的最佳选择。
拟合ARIMA模型
通过“网格搜索”我们找到了最佳拟合模型的参数,接下里我们将最佳参数值输入到一个新的SARIMAX模型:
model = sm.tsa.statespace.SARIMAX(data, order=(1,1,1), seasonal_order=(1,1,1,12), enforce_stationarity=False, enforce_invertibility=False) results = model.fit() print(results.summary().tables[1])
输出内容为:
============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 0.3182 0.092 3.442 0.001 0.137 0.499 ma.L1 -0.6254 0.077 -8.163 0.000 -0.776 -0.475 ar.S.L12 0.0010 0.001 1.732 0.083 -0.000 0.002 ma.S.L12 -0.8769 0.026 -33.812 0.000 -0.928 -0.826 sigma2 0.0972 0.004 22.632 0.000 0.089 0.106 ==============================================================================
从SARIMAX输出结果得到的summary属性返回大量信息,但我们将把注意力集中在coef列上。在这里每列的P值都比0.05小或接近0.05,因此我们可以保留模型中的所有权重。在拟合季节ARIMA模型(以及其他相关的模型)时,重要的是要运行模型诊断,以确保模型所做的假设是正确的。plot_diagnostics()允许我们快速生成模型诊断并调查任何异常行为。
results.plot_diagnostics(figsize=(12,12)) plt.show()
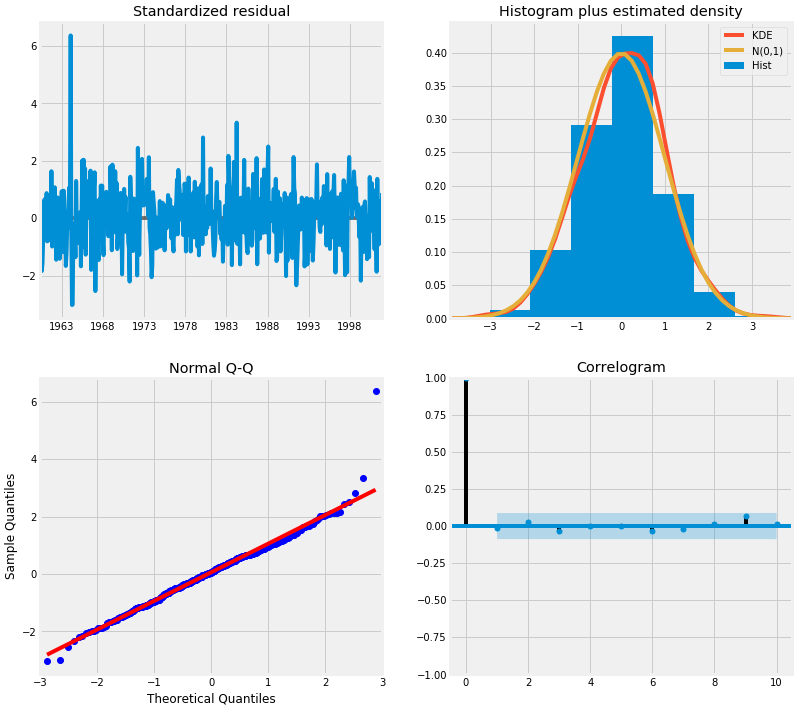
这里我们主要要确保残差稳定,且平均分布为0。上面的模型诊断表明:
- 右上角的红色KDE线和黄色N(0,1)线非常的接近(N(0,1)表示,平均值为0,标准差为1),表明残差是正态分布。
- 左下角对的QQ分位图表明,从N(0,1)的标准正态分布抽取的样本,残差(蓝点)的有序分布服从线性趋势。同样,这是一个强烈的迹象表明,残差是正态分布。
- 随着时间的推移(左上图)残差不会显示任何明显的季节性,似乎是白噪声。这通过右下角的自相关(即相关图)证实了这一点,它表明时间序列的残差与其自身的滞后版本有很低的相关性。
这些观察结果使我们得出结论,我们的模型产生了令人满意的结果,可以帮助我们预测未来的数据。
备注:虽然我们得到了令人满意的拟合参数,但是ARIMA模型的一些参数还是可以改变,以改进我们的模型拟合。例如,我们的网格搜索只考虑受限制的参数组合集,所以如果我们扩大网格搜索,我们可能会找到更好的模型。
验证预测
我们已经获得了我们时间序列的模型,现在可以用来产生预测。我们首先将预测值与时间序列的实际值进行比较,这将有助于我们了解我们的预测的准确性。get_prediction()和conf_int()属性允许我们获得时间序列预测的值和相关的置信区间。
pred = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=False)
pred_ci = pred.conf_int()
代码中设置从1998年1月开始预测,通过dynamic=False设置后续的每一个都是使用1998年1月之前的数据预测生产的。
我们可以绘制二氧化碳时间序列的实际值和预测值,以评估我们做得如何。
ax = data['1990':].plot(label='Observed', figsize=(12,6))
pred.predicted_mean.plot(ax=ax, label='One-step ahead Forecast', alpha=.7)
ax.fill_between(pred_ci.index,
pred_ci.iloc[:,0],
pred_ci.iloc[:,1], color='k', alpha=.2)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
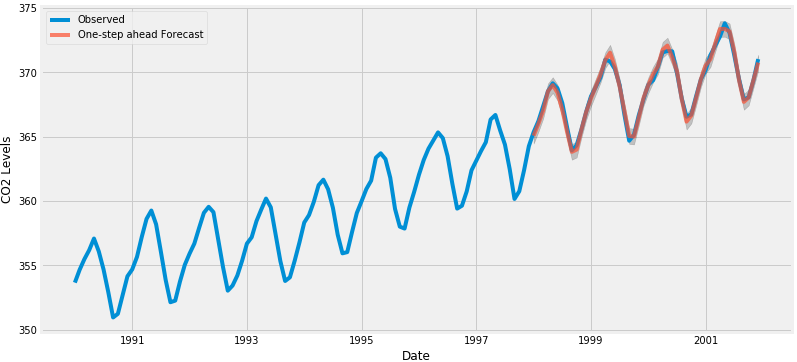
总体而言,我们的预测值与真实值保持一致,呈现总体增长趋势。量化我们的预测的准确性也是有用的。我们将使用MSE(均方误差)来评估预测的准确性。
data_forecasted = pred.predicted_mean
data_truth = data['1998-01-01':]
# Compute the mean square error
mse = ((data_forecasted - data_truth)**2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))
这里预测的MSE值为0.07,是接近0的非常低的值。0的MSE是估计器将以完美的精度预测参数的观测值,这将是一个理想的场景但通常不可能。在这种情况下,我们只使用时间序列中的信息到某一点,之后,使用先前预测时间点的值生成预测。然而,使用动态预测可以获得更好地表达我们的真实预测能力。在下面的代码块中,我们指定从1998年1月起开始计算动态预测和置信区间。
pred_dynamic = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=True, full_results=True)
pred_dynamic_ci = pred_dynamic.conf_int()
ax = data['1990':].plot(label='Observed', figsize=(12,6))
pred_dynamic.predicted_mean.plot(label='Dynamic Forecast', ax=ax)
ax.fill_between(pred_dynamic_ci.index,
pred_dynamic_ci.iloc[:,0],
pred_dynamic_ci.iloc[:,1], color='k', alpha=.25)
ax.fill_betweenx(ax.get_ylim(), pd.to_datetime('1998-01-01'), data.index[-1],
alpha=.1, zorder=-1)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
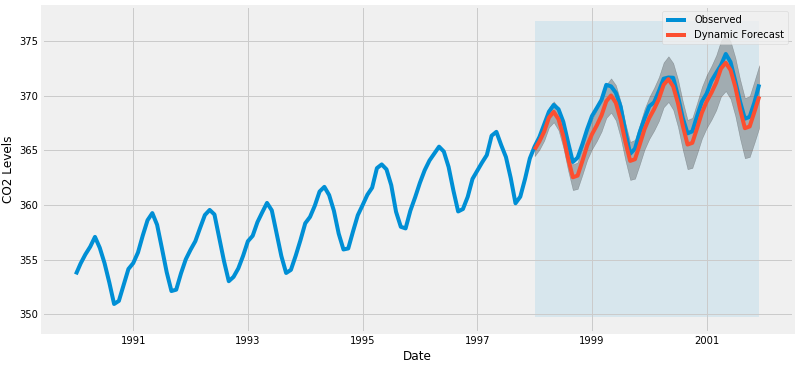
我们看到即使使用动态预测,总体预测也是准确的。所有预测值(红线)与实际值(蓝线)相当吻合,并且在我们预测的置信区间内。我们再次通过计算MSE量化我们预测的准确性:
# Extract the predicted and true values of our time series
data_forecasted = pred_dynamic.predicted_mean
data_truth = data['1998-01-01':]
# Compute the mean square error
mse = ((data_forecasted - data_truth)**2).mean()
print('The Mean Squared Error of our forecasts is {}'.format(round(mse, 2)))
从动态预测获得的预测值产生的MSE为1.01。要比非动态要高,这个也在预料之中,原因是可供参考的历史数据较少。
采用动态或非动态的预测都证实了时间序列模型的有效。然而,关于时间序列预测的大部分兴趣是能够及时预测未来价值观。
预测及可视化
在本教程的最后一步,我们将介绍如何利用季节性ARIMA时间序列模型来预测未来的价值。我们的时间序列对象的get_forecast()属性可以计算预先指定数量的”步数”的预测值。
# Get forecast 500 steps ahead in future
pred_uc = results.get_forecast(steps=500)
# Get confidence intervals of forecasts
pred_ci = pred_uc.conf_int()
我们可以使用此代码的输出绘制其未来值的时间序列和预测。
ax = data.plot(label='Observed', figsize=(12, 6))
pred_uc.predicted_mean.plot(ax=ax, label='Forecast')
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.25)
ax.set_xlabel('Date')
ax.set_ylabel('CO2 Levels')
plt.legend()
plt.show()
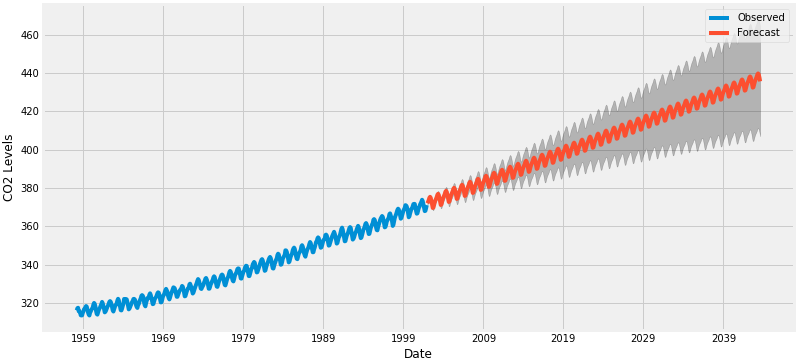
我们所作的预测和相关的置信区间现在都可以用来进一步理解时间序列,并预测将会发生什么。我们的预测显示,预计时间序列将以稳定的速度持续增长。
参考链接:
- A Complete Tutorial on Time Series Modeling in R
- [python]时间序列分析之ARIMA
- A Guide to Time Series Forecasting with ARIMA in Python 3
- statespace.sarimax.SARIMAX
- A Gentle Introduction to SARIMA for Time Series Forecasting in Python
- How to Grid Search SARIMA Model Hyperparameters for Time Series Forecasting in Python
- SARIMAX: Introduction
- Seasonal ARIMA with Python
- Predicting Spot Exchange Rates with ARIMA
- A Gentle Introduction to Autocorrelation and Partial Autocorrelation




写得真好,深入浅出,学习了!
写的很好,就是小白需要自己多加辨别,错别字和误打错的词有些多,容易干扰思路。
请问加权移动平均为什么就不会出现前11个月遗漏的问题呀,不是也设置窗口12了吗