地理空间数据分组：mapclassify

mapclassify简介

mapclassify 是一个 Python 库，主要作用是为空间数据提供分类和分级的方法，以便在地图上进行可视化和分析。通过将连续的数值数据分成离散的类别或等级，mapclassify 能够帮助用户更清晰地理解和展示数据的空间分布和特征。在上篇交通数据可视化包TransBigData的文章中讲到的GeoPandas 的scheme参数就是使用mapclassify实现的。

其主要作用是：

• 数据分类和分。Mapclassify 提供了多种分类算法，将连续的数值数据分成若干类别或等级，这些方法包括但不限于：
  • 等间距分类（Equal Interval）：将数据范围均匀地分成若干个相等的区间。
  • 分位数分类（Quantiles）：按照数据的分布，将数据分成具有相等数量观测值的区间。
  • 自然断点（Natural Breaks）：通过最小化类内方差的方法自动确定分类断点。
  • 自定义断点（User Defined）：用户可以根据具体需求自定义断点。
  • 头尾断点（Head/tail Breaks）：适用于具有幂律分布的数据分类。
  • …
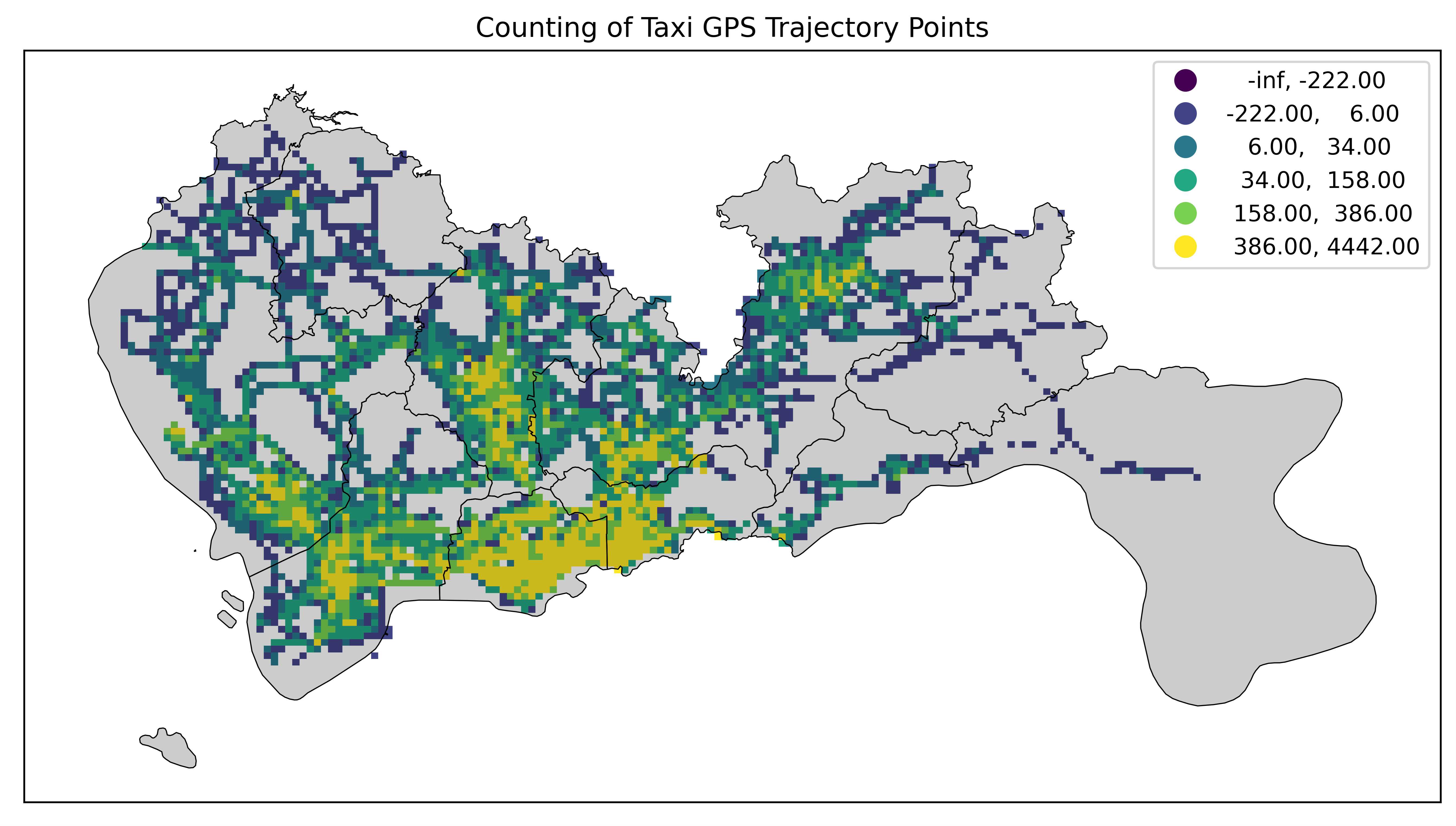
• 支持空间数据可视化。通过将数值数据分级，mapclassify 使得用户可以更方便地在地图上进行数据可视化。例如，使用 Choropleth 图表（区块图）展示不同区域的数值数据分布情况。
• 帮助进行空间分析。通过分类和分级，mapclassify 可以帮助用户更好地分析空间数据的特征和规律。例如，通过自然断点分类，可以识别出数据中的自然分组结构，从而更好地理解数据的分布。
• 性能优化。Mapclassify 提供高效的算法，能够处理大型数据集，确保分类操作的速度和准确性。这样，用户在面对大量空间数据时，依然可以快速获得分类结果。
• 误差分析和评价。Mapclassify 提供误差分析工具，帮助用户评估分类方案的合理性和准确性。通过误差分析，用户可以选择最适合自己数据特征的分类方法。
• 与其他库的无缝集成。Mapclassify 能够与其他常用的地理信息处理库（如 GeoPandas、CartoPy）和可视化库（如 Matplotlib）无缝集成，使其在 GIS 和空间数据分析工作流程中占据重要地位。

本次研究mapclassify主要是其与数据分箱和一维数据的聚类有很多补充类的启示。

mapclassify分类方法详解

Mapclassify 提供了多种方法来对数值型数据进行分类和分级，以便在地图上进行可视化和分析。

• BoxPlot(y[, hinge])：BoxPlot Map Classification，使用箱线图（Box Plot）的方法进行分类。hinge参数用于设置箱线图的铰链位置，通常为1.5，可以调整以控制分类的离群点检测。
• EqualInterval(y[, k])：Equal Interval Classification，将数据范围均匀地分成k 个相等的区间。这种方法适用于数据分布较为均匀的情况。
• FisherJenks(y[, k])：Fisher Jenks optimal classifier – mean based，基于平均值的 Fisher-Jenks 最优分类方法，通过最小化类内方差来确定分类断点。这种方法适用于数据分布不均匀的情况。
• FisherJenksSampled(y[, k, pct, …])：Fisher Jenks optimal classifier – mean based using random sample，与FisherJenks 类似，但使用随机样本进行分类，从而提高处理大型数据集的效率。
• greedy(gdf[, strategy, balance, …])：Color GeoDataFrame using various strategies of greedy (topological) colouring，使用贪心算法对 GeoDataFrame 进行着色，适用于拓扑着色问题，提供多种策略和参数调整。
• HeadTailBreaks(y)：Head/tail Breaks Map Classification for Heavy-tailed Distributions，适用于重尾分布数据的分类方法，基于幂律分布的特性。
• JenksCaspall(y[, k])：Jenks Caspall Map Classification，使用 Jenks-Caspall 算法进行分类，通过迭代优化类间和类内方差来确定分类断点。
• JenksCaspallForced(y[, k])：Jenks Caspall Map Classification with forced movements，与JenksCaspall 类似，但强制移动断点以进一步优化分类。
• JenksCaspallSampled(y[, k, pct])，Jenks Caspall Map Classification using a random sample：使用随机样本进行 Jenks-Caspall 分类，提高处理大型数据集的效率。
• MaxP(y[, k, initial, seed1, seed2])：MaxP Map Classification，基于最大化模块度（Modularity）的方法进行分类，适用于检测数据中的自然分组。
• MaximumBreaks(y[, k, mindiff])：Maximum Breaks Map Classification，基于最大值差异进行分类，寻找数据中的最大差异点作为分类断点。
• NaturalBreaks(y[, k, initial])：Natural Breaks Map Classification，通过最小化类内方差来确定自然断点，适用于数据分布不均匀的情况。
• Percentiles(y[, pct])：Percentiles Map Classification，根据百分位数进行分类，将数据分成若干百分位区间。
• PrettyBreaks(y[, k])：未具体说明，通常指的是生成“漂亮”的分类断点，使得分类结果更具可读性。
• Quantiles(y[, k])：Quantile Map Classification，将数据按分位数分成具有相等数量观测值的区间，适用于数据分布较为均匀的情况。
• StdMean(y[, multiples, anchor])：Standard Deviation and Mean Map Classification，基于平均值和标准差进行分类，通过设置multiples 和 anchor 参数来控制分类边界。
• UserDefined(y, bins[, lowest])：User Specified Binning，用户自定义分类断点，提供灵活的分类方法，根据具体需求进行数据分级。

BoxPlot

BoxPlot 是 Mapclassify 提供的一种基于箱线图（Box Plot）的数据分类方法。箱线图是一种图形工具，用于显示数据分布的五个主要统计量：最小值（minimum），第一四分位数（Q1），中位数（median），第三四分位数（Q3）和最大值（maximum），以及离群值（outliers）。BoxPlot 分类方法利用这些统计量对数据进行分级。

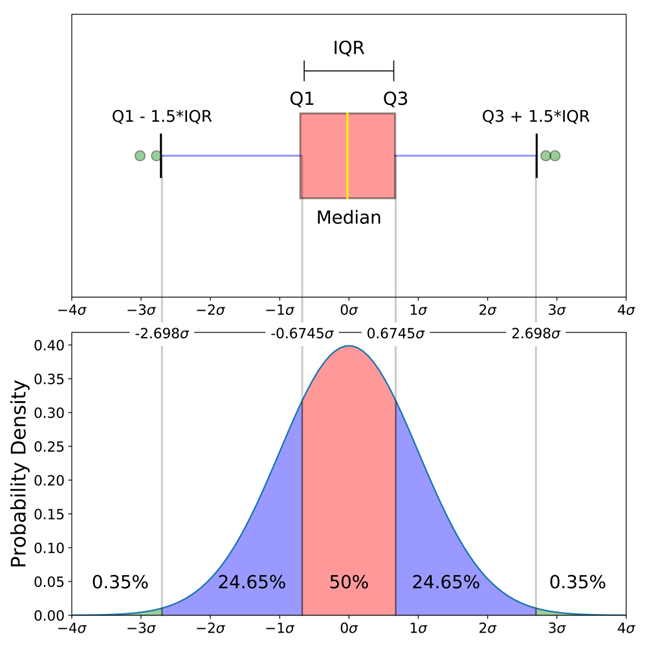
主要特点

• 基于统计量：BoxPlot 分类方法利用数据的几个关键统计量（如四分位数和中位数）来划分区间。
• 检测离群值：箱线图本身能够有效检出离群值，这在 BoxPlot 分类中也得到了体现。
• 适用于分布不均匀的数据：通过使用四分位数，可以有效处理分布不均匀的数据。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• hinge（可选）：设置箱线图的铰链位置，通常为1.5，表示四分位距的1.5倍，用于确定离群值的范围。

实现原理

BoxPlot 分类通过以下步骤实现：

• 计算四分位数：
  • 第一四分位数（Q1）：数据中第25百分位数的值。
  • 中位数（Median 或 Q2）：数据中第50百分位数的值。
  • 第三四分位数（Q3）：数据中第75百分位数的值。
• 计算四分位距（IQR）：
  • IQR = Q3 – Q1
• 确定离群值范围：
  • 下界：Q1 – hinge * IQR
  • 上界：Q3 + hinge * IQR
• 划分区间：
  • 基于上述统计量，将数据划分为不同的区间，包括离群值区间和正常值区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用箱线图分类方法
classifier = mapclassify.BoxPlot(data, hinge=1.5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('BoxPlot Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 有效检测离群值：能够自动识别并分类离群值。
• 适用于不均匀分布：通过使用四分位数和四分位距，可以有效处理不均匀分布的数据。
• 基于统计量：利用描述性统计量进行分类，具有较好的解释性。

缺点：

• 对数据分布敏感：如果数据中存在非常极端的离群值，可能会影响分类结果。
• 参数依赖：需要调整hinge 参数以适应不同数据集。

适用场景

BoxPlot 分类方法适用于以下场景：

• 数据探索性分析：快速识别数据中的离群值和主要分布区间。
• 地理信息系统（GIS）：在地图上展示空间数据的分布情况时，特别是当数据有明显的离群值时。
• 统计分析：分析数据的分布特征和离群值，提供更多数据洞察。

EqualInterval

EqualInterval 是 Mapclassify 提供的一种数据分类方法，用于将数据范围均匀地分成若干个相等的区间。这种方法在数据分布相对均匀或希望每个分类区间的宽度相同的情况下非常有用。

主要特点

• 均匀分割：将数据范围从最小值到最大值按等间距分割，每个区间的宽度相等。
• 简单直观：这种方法简单易懂，适合快速了解数据的基本分布情况。
• 适用于均匀分布：当数据分布较为均匀时，EqualInterval 能较好地反映数据的整体情况。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。

实现原理

EqualInterval 的实现原理是计算数据的最小值和最大值，然后将整个数据范围按等间距分割。例如，如果数据的最小值为 min_val，最大值为 max_val，区间数为 k，则每个区间的宽度为：

$$\text{interval width} = \frac{\text{max_val} – \text{min_val}}{k}$$

然后，以 min_val 为起点，按等间距划分区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.rand(100) * 100  # 产生 0 到 100 之间的随机数

# 使用等间距分类方法，分成5个区间
classifier = mapclassify.EqualInterval(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('Equal Interval Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 简单直观：分类方法简单明了，无需复杂计算。
• 易于解释：每个区间的宽度相同，方便解释和理解。

缺点：

• 对异常值敏感：如果数据中存在异常值（极值），可能导致大多数数据点集中在少数几个区间中。
• 不适合非均匀分布：对于分布不均匀的数据，EqualInterval 可能无法有效反映数据的实际分布特征。

适用场景

EqualInterval 适用于对均匀分布的数据进行简单分类和可视化。例如：

• 地理信息系统（GIS）：将地图上的数值数据（如温度、降雨量等）按等间距分级，生成 Choropleth 地图。
• 数据探索性分析：快速了解数据的基本分布情况。

FisherJenks

FisherJenks 是 Mapclassify 提供的一种数据分类方法，旨在通过最小化类内方差（即每个分类内部的数据差异）来优化分类结果。该方法特别适用于数据分布不均匀的情况，通过寻找最佳的分割点，使得每个分类的内部差异最小，而分类之间的差异最大，从而更好地反映数据的实际分布。

主要特点

• 最小化类内方差：Fisher-Jenks 方法通过最小化每个分类内部的数据差异来确定最佳分割点。
• 优化分类效果：这种方法能够有效地处理不均匀分布的数据，提供更具代表性的分类结果。
• 广泛应用：常用于统计分析、地理信息系统（GIS）和各种需要数据分级的领域。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。

实现原理

Fisher-Jenks 分类方法的实现原理包括以下步骤：

• 初始分割：将数据按某种初始策略进行分割。
• 计算类内方差：计算每个分类内部的方差，并求和得到总类内方差。
• 最小化类内方差：通过动态规划算法，调整分割点位置，以最小化总类内方差。
• 重复迭代：不断调整和优化分割点，直到找到使总类内方差最小的分割方案。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 Fisher-Jenks 分类方法，分成5个区间
classifier = mapclassify.FisherJenks(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('Fisher-Jenks Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 优化分类效果：通过最小化类内方差，提高分类的代表性和准确性。
• 适用于不均匀分布：能够有效处理分布不均匀的数据，提供更合理的分类结果。
• 自动化：无需手动调整参数，算法自动确定最佳分割点。

缺点：

• 计算复杂度高：由于采用动态规划算法，计算量相对较大，处理大型数据集时可能较慢。
• 对离群值敏感：如果数据中存在极端离群值，可能会影响分类结果。

适用场景

Fisher-Jenks 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是当数据分布不均匀时。
• 统计分析：优化数据分级，提高分类的代表性和准确性。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。

FisherJenksSampled

FisherJenksSampled 是 Mapclassify 提供的一种基于 Fisher-Jenks 方法的数据分类变体。它通过对数据进行随机抽样来减少计算量，从而提高处理大型数据集时的效率。这种方法在保持 Fisher-Jenks 分类准确性的同时，通过样本数据的优化减少了计算资源的消耗，非常适合大规模数据集的分类。

主要特点

• 基于抽样：通过从数据集中抽取一个子样本进行分类，显著减少了计算量。
• 效率提高：特别适用于大型数据集的分类任务，能够在较短时间内提供合理的分类结果。
• 继承 Fisher-Jenks 优势：仍然通过最小化类内方差来优化分类结果，保持了 Fisher-Jenks 方法的高代表性和准确性。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。
• pct：抽样的百分比，指定从原始数据集中抽取多少百分比的数据作为样本。默认值通常为10%（即1）。
• 其他参数：可以包括随机种子等，用于控制抽样的随机性。

实现原理

FisherJenksSampled 分类方法的实现原理包括以下步骤：

• 随机抽样：从原始数据集中按指定百分比抽取一个子样本。
• 初始分割：对抽样数据按某种初始策略进行分割。
• 计算类内方差：计算样本数据中每个分类内部的方差，并求和得到总类内方差。
• 最小化类内方差：通过动态规划算法，调整分割点位置，以最小化总类内方差。
• 应用到全数据集：使用样本数据上找到的最佳分割点对整个数据集进行分类。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(1000) * 10 + 50  # 正态分布的随机数，大型数据集

# 使用 Fisher-Jenks Sampled 分类方法，分成5个区间，抽样10%的数据
classifier = mapclassify.FisherJenksSampled(data, k=5, pct=0.1)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('Fisher-Jenks Sampled Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 处理大型数据集：通过抽样，大幅减少了计算量，提高了处理速度。
• 高效：在保证分类结果合理性的前提下，显著提高了大数据集的处理效率。
• 继承 Fisher-Jenks 优势：仍然保持了 Fisher-Jenks 方法的高代表性和准确性。

缺点：

• 依赖样本代表性：分类结果的准确性依赖于所抽取样本的代表性。如果样本不具有代表性，可能影响分类效果。
• 随机性影响：抽样过程中存在随机因素，不同的抽样结果可能会导致略有不同的分类断点。

适用场景

FisherJenksSampled 分类方法适用于以下场景：

• 大型数据集：在处理大规模数据集时，通过抽样提高分类效率。
• 地理信息系统（GIS）：在地图上展示大规模空间数据的分布情况。
• 统计分析：对大规模数据进行优化分级，提高分类的代表性和准确性。
• 市场分析：分析大型市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。

greedy

mapclassify.greedy 是 Mapclassify 库中的一种基于贪心算法（Greedy Algorithm）的分类方法，专门用于解决地理信息系统（GIS）中的拓扑着色问题。拓扑着色问题涉及如何为地图上的区域（如国家、省份或行政区）分配颜色，以确保相邻区域具有不同的颜色。贪心算法通过一种迭代的、局部最优的方式进行着色，以求整体上的合理性和效率。

主要特点

• 贪心算法：利用贪心算法的简单性和高效性，逐步为地图上的区域分配颜色。
• 拓扑着色：特别适用于 GIS 中的拓扑着色问题，确保相邻区域具有不同的颜色。
• 多种策略：支持多种不同的贪心策略，用户可以根据实际需求选择最适合的策略。

参数

• gdf：GeoDataFrame，包含地理空间数据，需要进行着色的区域。
• strategy：指定贪心算法的具体策略，如largest_first、random_sequential 等。
• balance：用于控制平衡性的参数，可能影响颜色分配的结果。
• 其他参数：可能包括颜色数量、随机种子等，用于控制着色过程中的细节。

实现原理

mapclassify.greedy 实现原理包括以下步骤：

• 初始化：读取地理空间数据，构建区域之间的邻接关系图。
• 选择策略：根据用户指定的strategy，决定区域的着色顺序。
• 贪心着色：按顺序为每个区域选择一个颜色，确保相邻区域具有不同的颜色。
• 重复迭代：继续为剩余的区域选择颜色，直到所有区域都被着色。

示例代码

import geopandas as gpd
import mapclassify
import matplotlib.pyplot as plt

# 读取 GeoDataFrame 数据
gdf = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))

# 使用 greedy 方法进行拓扑着色
gdf['colors'] = mapclassify.greedy(gdf, strategy='largest_first')

# 可视化着色结果
gdf.plot(column='colors', legend=True, figsize=(10, 6), cmap='tab20')
plt.title('Greedy Topological Coloring')
plt.show()

优缺点

优点：

• 高效：贪心算法简单高效，适合处理大规模地理空间数据。
• 易于实现：算法实现简单，易于理解和使用。
• 多策略支持：支持多种不同的贪心策略，灵活性高。

缺点：

• 局部最优：贪心算法只能保证局部最优解，并不一定能找到全局最优解。
• 策略依赖：不同的策略可能会导致不同的着色结果，需要根据具体情况选择合适的策略。
• 颜色分配：在某些情况下，可能需要较多的颜色来确保相邻区域颜色不同。

适用场景

mapclassify.greedy 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上进行区域分配和着色，以确保相邻区域具有不同的颜色。
• 网络图着色：除了地理数据，还可以用于图论中的节点着色问题，确保相邻节点颜色不同。
• 资源分配问题：在某些资源分配和调度问题中，可以利用贪心算法的高效性和灵活性。

HeadTailBreaks

HeadTailBreaks 是 Mapclassify 提供的一种数据分类方法，适用于分布不均匀的数据，特别是具有长尾分布的数据。其核心思想是通过反复分割数据的头部（高频部分）和尾部（低频部分），以适应数据的自然分布规律。这种方法特别适用于处理具有幂律分布或对数正态分布的数据，如城市人口、财富分布等。

主要特点

• 适应长尾分布：特别适用于长尾分布或幂律分布的数据，能够更好地反映数据的实际分布情况。
• 递归分割：通过递归地分割数据的头部和尾部，形成多个分类区间。
• 自动化：无需用户指定分类的区间数，算法自动确定适当的分类数量。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• initial：初始分割点，默认为数据的均值（mean）。也可以根据具体数据特征选择其他分割点。

实现原理

HeadTailBreaks 分类方法的实现原理包括以下步骤：

• 计算初始分割点：通常为数据的均值或中位数。
• 分割数据：将数据分割为头部（大于等于初始分割点）和尾部（小于初始分割点）。
• 递归处理：对头部数据重复上述分割过程，直到头部数据不再满足分割条件（即头部数据的数量低于某个阈值或方差过小）。
• 形成区间：结合各次分割点，形成最终的分类区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.pareto(a=2, size=100) * 100  # 幂律分布数据

# 使用 HeadTailBreaks 分类方法
classifier = mapclassify.HeadTailBreaks(data)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('HeadTailBreaks Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 适应自然分布：能够自动适应数据的自然分布，特别适合长尾分布的数据。
• 自动化：无需指定分类的区间数，算法自动确定适当的分类数量。
• 递归分割：通过递归分割，提高了分类的精确性和代表性。

缺点：

• 计算复杂度：递归分割过程可能会增加计算复杂度，处理非常大规模数据时可能较慢。
• 对异常值敏感：对异常值敏感，如果数据中存在极端值，可能影响分类结果。
• 参数选择：初始分割点的选择可能影响分类效果，需要根据具体数据特征进行调整。

适用场景

HeadTailBreaks 分类方法适用于以下场景：

• 长尾分布数据：对具有长尾分布或幂律分布的数据进行分类，如城市人口、财富分布等。
• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是分布不均匀的数据。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。

JenksCaspall

JenksCaspall 是一种数据分类方法，属于 Mapclassify 库的一部分。该方法结合了 Jenks 自然断点分类法和 Caspall 的改进方案，以最小化每个分类内部的方差，同时最大化分类之间的方差，从而使得数据的分类更加合理和具有代表性。

主要特点

• 最小化类内方差：通过最小化每个分类内部的数据差异来确保分类的代表性。
• 最大化类间方差：通过最大化分类之间的数据差异来提高分类的区分度。
• 改进算法：结合了 Jenks 自然断点方法和 Caspall 的改进方案，提供更优的分类结果。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。
• initial：初始分类方法，可以选择’random’、’kmeans’ 等。

实现原理

JenksCaspall 分类方法的实现原理包括以下步骤：

• 初始分类：根据指定的方法对数据进行初始分类，如使用随机分类或 k-means 聚类。
• 计算类内方差：计算每个分类内部的方差，并求和得到总类内方差。
• 优化分类：通过迭代优化，最小化总类内方差，同时最大化分类之间的方差。
• 调整和收敛：不断调整分类的边界，直到达到收敛条件，即总类内方差不再显著减少。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 JenksCaspall 分类方法，分成5个区间
classifier = mapclassify.JenksCaspall(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('JenksCaspall Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 优化分类效果：通过最小化类内方差和最大化类间方差，提高分类的代表性和区分度。
• 适应性强：能够处理各种类型的数据，特别是分布不均匀的数据。
• 自动化：无需手动调整参数，算法自动确定最佳分割点。

缺点：

• 计算复杂度高：优化过程需要多次迭代，计算量较大，处理大型数据集时可能较慢。
• 对初始分类敏感：初始分类方法的选择可能影响最终分类结果，需要根据具体数据特征进行调整。

适用场景

JenksCaspall 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是分布不均匀的数据。
• 统计分析：对各种类型的数据进行优化分级，提高分类的代表性和区分度。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。

JenksCaspallForced

JenksCaspallForced 是 Mapclassify 库中的一种数据分类方法，结合了 Jenks 自然断点分类法和 Caspall 的强制分割策略。该方法在既定的分类数量下，强制优化数据的分割点，以最小化类内方差（即每个分类内部的数据差异）和最大化类间方差（即分类之间的数据差异）。这种方法特别适用于需要强制固定分类数量的场景，如地理信息系统（GIS）中的地图着色和市场分析中的客户分级。

主要特点

• 强制分类数量：强制指定分类数量，而不是让算法自行决定分类数量。
• 最小化类内方差：通过最小化每个分类内部的数据差异，提高分类的代表性和准确性。
• 最大化类间方差：通过最大化分类之间的数据差异，提高分类的区分度。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。用户需要强制指定该参数。
• initial：初始分类方法，可以选择’random’、’kmeans’ 等。

实现原理

JenksCaspallForced 分类方法的实现原理包括以下步骤：

• 初始分类：根据指定的方法对数据进行初始分类，如使用随机分类或 k-means 聚类。
• 计算类内方差：计算每个分类内部的方差，并求和得到总类内方差。
• 强制优化：通过强制迭代优化，最小化总类内方差，同时保持用户指定的分类数量。
• 调整和收敛：不断调整分类的边界，直到达到收敛条件，即总类内方差不再显著减少。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 JenksCaspallForced 分类方法，强制分成5个区间
classifier = mapclassify.JenksCaspallForced(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('JenksCaspallForced Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 优化分类效果：通过最小化类内方差和最大化类间方差，提高分类的代表性和区分度。
• 强制控制：能够强制指定分类数量，适应特定场景的需求。
• 自动化：无需手动调整参数，算法自动优化分割点。

缺点：

• 计算复杂度高：优化过程需要多次迭代，计算量较大，处理大型数据集时可能较慢。
• 对初始分类敏感：初始分类方法的选择可能影响最终分类结果，需要根据具体数据特征进行调整。

适用场景

JenksCaspallForced 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是需要强制固定分类数量的场景。
• 统计分析：对各种类型的数据进行优化分级，提高分类的代表性和区分度。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。
• 资源分配：在资源有限的情况下，强制将资源分配到固定数量的类别中，以优化使用效率。

JenksCaspallSampled

JenksCaspallSampled 是 Mapclassify 库中的一种数据分类方法，它结合了 Jenks 自然断点分类法和 Caspall 的改进策略，同时引入了抽样技术，以提高处理大型数据集时的效率。该方法通过对数据进行随机抽样来减少计算量，从而在保持分类效果的同时提升处理速度。

主要特点

• 基于抽样：通过从数据集中抽取一个子样本进行分类，显著减少了计算量。
• 优化分类效果：通过最小化类内方差和最大化类间方差，提高分类的代表性和区分度。
• 高效处理大数据：特别适用于大型数据集，通过抽样技术提高处理速度。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。
• pct：抽样的百分比，指定从原始数据集中抽取多少百分比的数据作为样本。默认值通常为10%（即1）。
• initial：初始分类方法，可以选择’random’、’kmeans’ 等。

实现原理

JenksCaspallSampled 分类方法的实现原理包括以下步骤：

• 随机抽样：从原始数据集中按指定百分比抽取一个子样本。
• 初始分类：对抽样数据根据指定的方法进行初始分类，如使用随机分类或 k-means 聚类。
• 计算类内方差：计算样本数据中每个分类内部的方差，并求和得到总类内方差。
• 优化分类：通过迭代优化，最小化总类内方差，同时最大化分类之间的方差。
• 应用到全数据集：使用样本数据上找到的最佳分割点对整个数据集进行分类。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(1000) * 10 + 50  # 正态分布的随机数，大型数据集

# 使用 JenksCaspallSampled 分类方法，分成5个区间，抽样10%的数据
classifier = mapclassify.JenksCaspallSampled(data, k=5, pct=0.1)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('JenksCaspallSampled Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 高效处理大数据：通过抽样技术，大幅减少计算量，提高处理速度。
• 优化分类效果：通过最小化类内方差和最大化类间方差，提高分类的代表性和区分度。
• 自动化：无需手动调整参数，算法自动确定最佳分割点，适应性强。

缺点：

• 依赖样本代表性：分类结果的准确性依赖于所抽取样本的代表性。如果样本不具有代表性，可能影响分类效果。
• 计算复杂度仍然较高：尽管通过抽样减少了计算量，但优化过程中的迭代计算仍然可能较为复杂。
• 对初始分类敏感：初始分类方法的选择可能影响最终分类结果，需要根据具体数据特征进行调整。

适用场景

JenksCaspallSampled 分类方法适用于以下场景：

• 大型数据集：在处理大规模数据集时，通过抽样提高分类效率。
• 地理信息系统（GIS）：在地图上展示大规模空间数据的分布情况。
• 统计分析：对大规模数据进行优化分级，提高分类的代表性和区分度。
• 市场分析：分析大型市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。

MaxP

MaxP 是 Mapclassify 库中的一种数据分类方法，专门用于优化空间聚类。它基于空间自相关的原则，通过最大化区域内部的统计相似性（如人口、收入等属性），并最小化区域之间的统计差异，来实现数据的空间聚类。这种方法特别适用于地理信息系统（GIS）中的区域划分和空间分析。

主要特点

• 最大化空间相似性：通过最大化每个聚类内部的数据相似性，提高聚类的代表性。
• 最小化空间差异性：通过最小化聚类之间的数据差异，增强聚类的区分度。
• 适应空间数据：特别适用于处理具有空间属性的数据，优化空间聚类效果。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：聚类的数量，即将数据分成多少个聚类。用户需要指定该参数。
• initial：初始聚类方法，可以选择’random’、’kmeans’ 等。
• spatial_weights：一个空间权重矩阵，用于衡量区域之间的空间关系。

实现原理

MaxP 分类方法的实现原理包括以下步骤：

• 初始聚类：根据指定的方法对数据进行初始聚类，如使用随机分类或 k-means 聚类。
• 计算空间相似性：利用空间权重矩阵计算每个聚类内部的相似性。
• 优化聚类：通过迭代优化，最大化每个聚类内部的数据相似性，同时最小化聚类之间的数据差异。
• 调整和收敛：不断调整聚类的边界，直到达到收敛条件，即聚类内部的相似性不再显著增加。

示例代码

import mapclassify
import numpy as np
import geopandas as gpd
import libpysal

# 生成一些模拟空间数据
gdf = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
data = gdf['pop_est'].values  # 使用人口数据进行聚类

# 创建空间权重矩阵
w = libpysal.weights.Queen.from_dataframe(gdf)

# 使用 MaxP 分类方法，分成5个聚类
classifier = mapclassify.MaxP(data, w, k=5)

# 获取分类结果（每个聚类的标签）
labels = classifier.labels
print("聚类标签:", labels)

# 将结果添加到 GeoDataFrame 并进行可视化
gdf['cluster'] = labels
gdf.plot(column='cluster', legend=True, cmap='tab20')
plt.title('MaxP Classification')
plt.show()

优缺点

优点：

• 优化空间聚类：通过最大化聚类内部的相似性和最小化聚类之间的差异，提高空间聚类的代表性和区分度。
• 适应空间数据：特别适用于处理具有空间属性的数据，提供更合理的聚类结果。
• 自动化：无需手动调整参数，算法自动确定最佳聚类边界，适应性强。

缺点：

• 计算复杂度高：优化过程需要多次迭代，计算量较大，处理大型数据集时可能较慢。
• 依赖空间权重矩阵：分类效果依赖于空间权重矩阵的质量，构建权重矩阵可能需要额外的计算和数据准备。
• 对初始聚类敏感：初始聚类方法的选择可能影响最终聚类结果，需要根据具体数据特征进行调整。

适用场景

MaxP 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是需要进行优化空间聚类的场景。
• 统计分析：对具有空间属性的数据进行优化分级，提高聚类的代表性和区分度。
• 市场分析：分析具有空间属性的市场数据（如销售数据、客户分布等），识别数据中的模式和趋势。
• 城市规划：在城市规划和管理中，对区域进行合理划分和分类，提高资源分配的效率。

MaximumBreaks

MaximumBreaks 是 Mapclassify 库中的一种数据分类方法，旨在最大化数据分类中的统计断点。其核心思想是通过最大化相邻组之间的差异，来找到最显著的断点，从而将数据划分为若干类别。这种方法特别适用于需要识别数据集中重要变化点和显著差异的场景。

主要特点

• 最大化断点差异：通过最大化相邻组之间的差异，找出最显著的断点。
• 适应性强：能够处理各种类型的数据，特别是那些需要识别显著变化点的数据。
• 自动化：无需手动指定分类的区间数，算法自动确定最佳分类区间。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。用户需要指定该参数。
• initial：初始分类方法，可以选择’random’、’kmeans’ 等。

实现原理

MaximumBreaks 分类方法的实现原理包括以下步骤：

• 排序数据：将数据按升序或降序排列。
• 计算差异：计算相邻数据点之间的差异。
• 确定断点：找出差异最大的 k-1 个断点，这些断点将数据分割成 k 个区间。
• 分组：根据确定的断点，将数据分成若干类别。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 MaximumBreaks 分类方法，分成5个区间
classifier = mapclassify.MaximumBreaks(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('MaximumBreaks Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 识别显著变化点：能够有效识别数据中的显著变化点，提供更有意义的分类结果。
• 适应性强：能够处理各种类型的数据，适用于多种应用场景。
• 自动化：无需手动指定分类的区间数，算法自动确定最佳分类区间。

缺点：

• 对异常值敏感：对数据中的异常值较为敏感，可能会影响分类结果。
• 计算复杂度高：在大型数据集上，计算相邻数据点之间的差异并确定断点的过程可能较为复杂。
• 需要指定区间数：用户需要预先指定分类的区间数，可能需要根据具体应用场景进行调整。

适用场景

MaximumBreaks 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是需要识别显著变化点的场景。
• 统计分析：对各种类型的数据进行分级，提高分类的代表性和区分度。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的显著变化点和趋势。
• 时间序列分析：在时间序列数据中识别显著的变化点，如经济数据、气候数据等。

NaturalBreaks

NaturalBreaks，也称为 Jenks 自然断点分类法，是 Mapclassify 库中的一种数据分类方法，旨在通过最小化每个分类内部的方差和最大化分类之间的方差，来优化数据的分割。此方法特别适用于需要识别数据集中自然分布模式的场景，如地理信息系统（GIS）中的地图着色和统计数据的分类。

主要特点

• 最小化类内方差：通过最小化每个分类内部的数据差异，提高分类的代表性。
• 最大化类间方差：通过最大化分类之间的数据差异，提高分类的区分度。
• 适应性强：能够处理各种类型的数据，特别适用于数据分布不均匀的场景。
• 自动化：无需手动调整参数，算法自动确定最佳分割点。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。

实现原理

NaturalBreaks 分类方法的实现原理包括以下步骤：

• 排序数据：将数据按升序或降序排列。
• 初始分类：根据指定的分类数量，对数据进行初步分割。
• 计算类内方差：计算每个分类内部的方差，并求和得到总类内方差。
• 优化分割点：通过迭代优化，最小化总类内方差，同时最大化分类之间的方差。
• 调整和收敛：不断调整分类的边界，直到达到收敛条件，即总类内方差不再显著减少。

示例代码

以下是如何在 Python 中使用 mapclassify 库的 NaturalBreaks 方法对数据进行分类的示例：

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 NaturalBreaks 分类方法，分成5个区间
classifier = mapclassify.NaturalBreaks(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('NaturalBreaks Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 优化分类效果：通过最小化类内方差和最大化类间方差，提高分类的代表性和区分度。
• 适应性强：能够处理各种类型的数据，特别适用于分布不均匀的数据。
• 自动化：无需手动调整参数，算法自动确定最佳分割点。

缺点：

• 计算复杂度高：优化过程需要多次迭代，计算量较大，处理大型数据集时可能较慢。
• 对异常值敏感：对数据中的异常值较为敏感，可能影响分类结果。

适用场景

NaturalBreaks 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，特别是需要识别自然分布模式的场景。
• 统计分析：对各种类型的数据进行分级，提高分类的代表性和区分度。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的自然模式和趋势。
• 经济分析：在经济数据中识别自然的分布特征，如收入分布、消费支出等。

Percentiles

Percentiles 是 Mapclassify 库中的一种数据分类方法，通过将数据按百分比区间进行分割。它将数据分成若干百分位数区间，使得每个区间内包含的数据量相等。这种方法在处理数据分布不均匀和需要将数据按相对位置进行分类的场景中非常有效。

主要特点

• 等量分类：每个区间包含相等数量的数据点，确保分类的均匀性。
• 适应性强：适用于分布不均匀的数据，按相对位置进行分类。
• 直观易懂：分类结果简单明了，易于解释。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个百分位数区间。默认值通常是4（即四分位数），但可以根据实际需要进行调整。

实现原理

Percentiles 分类方法的实现原理包括以下步骤：

• 排序数据：将数据按升序排列。
• 计算百分位数：根据指定的分类数量，计算每个百分位数的边界值。例如，四分位数将数据分为四个区间，每个区间包含相等数量的数据点。
• 分组：根据计算得到的百分位数边界值，将数据分成若干区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 Percentiles 分类方法，分成4个区间（四分位数）
classifier = mapclassify.Percentiles(data, k=4)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('Percentiles Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 等量分类：每个区间包含相等数量的数据点，确保分类的均匀性。
• 适应性强：适用于分布不均匀的数据，按相对位置进行分类。
• 直观易懂：分类结果简单明了，易于解释。

缺点：

• 对异常值敏感：对数据中的异常值较为敏感，可能影响分类结果。
• 可能忽略实际分布：在某些情况下，按百分位数进行分类可能会忽略数据的实际分布模式。

适用场景

Percentiles 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，按相对位置进行分类。
• 统计分析：对各种类型的数据进行等量分级，提高分类的均匀性。
• 市场分析：分析市场数据（如销售数据、客户分布等），按相对位置和分布进行分类。
• 社会经济分析：在收入、消费等经济数据中，按相对位置进行分类。

PrettyBreaks

PrettyBreaks 是 Mapclassify 库中的一种数据分类方法，旨在创建美观且易于理解的数据分割点。它根据数据的范围和用户指定的分类数量，自动生成若干个“漂亮”的断点，使得分类结果更加直观和美观。这种方法特别适用于需要将数据进行可视化展示的场景，如地理信息系统（GIS）的地图着色和统计图表的绘制。

主要特点

• 美观易懂：生成的断点通常是简单的整数或具有较少小数位的数值，便于理解和展示。
• 自动化：无需手动调整断点，算法自动生成最佳的分割点。
• 适应性强：适用于各种类型的数据，特别是需要进行可视化展示的场景。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个区间。默认值通常是5，但可以根据实际需要进行调整。

实现原理

PrettyBreaks 分类方法的实现原理包括以下步骤：

• 确定数据范围：计算数据的最小值和最大值。
• 生成美观断点：根据数据的范围和指定的分类数量，自动生成若干个美观的断点。这些断点通常是简单的整数或具有较少小数位的数值。
• 分组：根据生成的断点，将数据分成若干区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 PrettyBreaks 分类方法，分成5个区间
classifier = mapclassify.PrettyBreaks(data, k=5)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('PrettyBreaks Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 美观易懂：生成的断点通常是简单的整数或具有较少小数位的数值，便于理解和展示。
• 自动化：无需手动调整断点，算法自动生成最佳的分割点。
• 适应性强：适用于各种类型的数据，特别是需要进行可视化展示的场景。

缺点：

• 对数据分布依赖较少：该方法主要关注断点的美观性，可能忽略数据的实际分布特征。
• 有限的灵活性：在某些复杂的数据场景中，生成的断点可能不完全符合用户的具体需求。

适用场景

PrettyBreaks 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，生成美观的分类断点，便于理解和展示。
• 统计分析：对各种类型的数据进行美观分级，提高分类结果的直观性和可解释性。
• 市场分析：分析市场数据（如销售数据、客户分布等），生成美观的分类断点，便于展示数据的分布特征。
• 数据可视化：在生成统计图表时，生成美观的分类断点，提高图表的美观性和易读性。

Quantiles

Quantiles 是 Mapclassify 库中的一种数据分类方法，旨在通过将数据按等量的方式进行分割。它将数据分成若干个区间（即分位数区间），使得每个区间内包含的观测值数量相等。这种方法在处理分布不均匀的数据时非常有效，能够确保每个分类区间内包含的观测值数量相等。

主要特点

• 等量分类：每个区间包含相等数量的数据点，确保分类的均匀性。
• 适应性强：适用于分布不均匀的数据，按相对位置进行分类。
• 直观易懂：分类结果简单明了，易于解释。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的区间数，即将数据分成多少个分位数区间。默认值通常是4（即四分位数），但可以根据实际需要进行调整。

实现原理

Quantiles 分类方法的实现原理包括以下步骤：

• 排序数据：将数据按升序排列。
• 计算分位点：根据指定的分类数量，计算每个分位数的边界值。例如，四分位数将数据分为四个区间，每个区间包含相等数量的数据点。
• 分组：根据计算得到的分位数边界值，将数据分成若干区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 Quantiles 分类方法，分成4个区间（四分位数）
classifier = mapclassify.Quantiles(data, k=4)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('Quantiles Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 等量分类：每个区间包含相等数量的数据点，确保分类的均匀性。
• 适应性强：适用于分布不均匀的数据，按相对位置进行分类。
• 直观易懂：分类结果简单明了，易于解释。

缺点：

• 对异常值敏感：对数据中的异常值较为敏感，可能影响分类结果。
• 可能忽略实际分布：在某些情况下，按分位数进行分类可能会忽略数据的实际分布模式。

适用场景

Quantiles 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，按相对位置进行分类。
• 统计分析：对各种类型的数据进行等量分级，提高分类的均匀性。
• 市场分析：分析市场数据（如销售数据、客户分布等），按相对位置和分布进行分类。
• 社会经济分析：在收入、消费等经济数据中，按相对位置进行分类。

StdMean

StdMean 是 Mapclassify 库中的一种数据分类方法，它通过使用均值和标准差来确定分类的界限。这种方法将数据按照与均值的标准差距离进行分割，对于识别数据中的异常值和离群点特别有用。其分类结果能够直观地展示出数据的集中趋势和离散程度。

主要特点

• 基于统计特性：利用均值和标准差进行分类，能够直观地展示数据的集中趋势和离散程度。
• 识别异常值：有助于识别数据中的异常值和离群点。
• 自动化：无需手动调整参数，算法自动生成分类的断点。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• k：分类的标准差倍数。默认情况下，通常进行 ±1、±2 和 ±3 标准差的分类，但可以根据实际需要进行调整。

实现原理

StdMean 分类方法的实现原理包括以下步骤：

• 计算均值和标准差：对数据集计算均值和标准差。
• 确定断点：根据均值和标准差，确定分类的断点。通常，断点为均值加减一个或多个标准差的倍数。例如，±1、±2 和 ±3 标准差。
• 分组：根据确定的断点，将数据分成若干区间。

示例代码

以下是如何在 Python 中使用 mapclassify 库的 StdMean 方法对数据进行分类的示例：

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 使用 StdMean 分类方法，默认情况下进行 ±1、±2 和 ±3 标准差的分类
classifier = mapclassify.StdMean(data)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('StdMean Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 基于统计特性：利用均值和标准差进行分类，能够直观地展示数据的集中趋势和离散程度。
• 识别异常值：有助于识别数据中的异常值和离群点。
• 自动化：无需手动调整参数，算法自动生成分类的断点。

缺点：

• 对正态分布假设依赖较大：该方法假设数据呈正态分布，对于非正态分布的数据，分类结果可能不够准确。
• 对异常值敏感：极端值会影响均值和标准差，从而影响分类结果。

适用场景

StdMean 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的集中趋势和离散程度，帮助识别异常区域。
• 统计分析：对各种类型的数据进行基于均值和标准差的分级，直观地展示数据的集中趋势和离散程度。
• 市场分析：分析市场数据（如销售数据、客户分布等），识别数据中的异常值和离群点。
• 社会经济分析：在收入、消费等经济数据中，识别数据的集中趋势和离散程度，帮助识别异常值。

UserDefined

UserDefined 是 Mapclassify 库中的一种数据分类方法，允许用户根据自己的需求手动定义分类的断点。这种方法提供了最大的灵活性，适用于用户对数据分割有特定要求的场景。通过手动设置断点，用户可以精确控制数据的分类方式，以满足特定的分析需求或展示目的。

主要特点

• 最大灵活性：用户可以手动定义断点，精确控制数据的分类方式。
• 适应性强：适用于各种类型的数据，特别是用户对分类有特定要求的场景。
• 简单直接：容易理解和使用，通过手动设置断点来控制分类。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• bins：用户定义的分类断点列表，必须按升序排列。断点的数量和位置由用户自行决定。

实现原理

UserDefined 分类方法的实现原理包括以下步骤：

• 排序数据：将数据按升序排列。
• 用户定义断点：根据用户提供的断点列表，将数据分成若干区间。
• 分组：根据用户定义的断点，将数据分成若干区间。

示例代码

import mapclassify
import numpy as np
import matplotlib.pyplot as plt

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50  # 正态分布的随机数

# 用户定义的分类断点
user_bins = [30, 40, 50, 60, 70]

# 使用 UserDefined 分类方法
classifier = mapclassify.UserDefined(data, bins=user_bins)

# 获取分类结果（每个区间的上限值）
bins = classifier.bins
print("分类断点:", bins)

# 可视化分类结果
plt.hist(data, bins=bins, edgecolor='black')
plt.title('UserDefined Classification')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

优缺点

优点：

• 最大灵活性：用户可以手动定义断点，精确控制数据的分类方式。
• 适应性强：适用于各种类型的数据，特别是用户对分类有特定要求的场景。
• 简单直接：容易理解和使用，通过手动设置断点来控制分类。

缺点：

• 依赖用户经验：分类效果依赖于用户对数据的理解和断点的选择。
• 不适合自动化：需要用户手动定义断点，不适合完全自动化的数据处理流程。

适用场景

UserDefined 分类方法适用于以下场景：

• 地理信息系统（GIS）：在地图上展示空间数据的分布情况，用户可以根据特定需求手动设置分类断点。
• 统计分析：对各种类型的数据进行手动分级，满足特定的分析需求。
• 市场分析：分析市场数据（如销售数据、客户分布等），根据特定的业务需求手动设置分类断点。
• 教育目的：在教学和培训中，演示如何通过手动设置断点来影响数据分类。

mapclassify其他功能

mapclassify.KClassifiers(y[, pct])

KClassifiers 函数用于评估所有分类器，并基于 Goodness of Absolute Deviation Fit (GADF) 选择最优分类器。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• pct：一个阈值，默认为8。用于确定何时停止计算 GADF。

返回

• 返回一个对象，其中包含所有评估的分类器及其性能。

示例代码

import mapclassify
import numpy as np

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50

# 评估所有分类器并选择最佳的一个
kclassifiers = mapclassify.KClassifiers(data, pct=0.8)
best_classifier = kclassifiers.best
print("最佳分类器:", best_classifier)

mapclassify.Pooled(Y[, classifier])

Pooled 函数用于在多个列上应用全局分箱。即将多个数据列视为一个整体，并基于全局数据范围进行分箱。

参数

• Y：待分类的数据集，通常是一个二维数组或 DataFrame。
• classifier：指定的分类器，默认为Quantiles。

返回

• 返回一个分类结果对象，包含所有列的分箱结果。

示例代码

import mapclassify
import numpy as np
import pandas as pd

# 生成一些模拟数据
data = pd.DataFrame({
    'col1': np.random.randn(100) * 10 + 50,
    'col2': np.random.randn(100) * 5 + 60
})

# 使用全局分箱
pooled = mapclassify.Pooled(data)
print("全局分箱结果:", pooled.bins)

mapclassify.classify(y, scheme[, k, pct, …])

classify 函数用于使用指定的分类方案对数据进行分类。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• scheme：分类方案，如Quantiles, EqualInterval, FisherJenks 等。
• k：区间数，对某些分类方案是可选参数。
• pct：百分比阈值，用于某些分类方案。

返回

• 返回一个分类结果对象，包含分类断点和分类标签。

示例代码

import mapclassify
import numpy as np

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50

# 使用指定的分类方案进行分类
classified = mapclassify.classify(data, 'Quantiles', k=4)
print("分类断点:", classified.bins)

mapclassify.gadf(y[, method, maxk, pct])

gadf 函数用于评估分类器的 Goodness of Absolute Deviation Fit (GADF)，并找到使 GADF 大于指定百分比的最小区间数 k。

参数

• y：待分类的数据，通常是一个数值型数组或序列。
• method：分类方法，默认为Quantiles。
• maxk：最大区间数，默认为10。
• pct：GADF 的阈值百分比，默认为8。

返回

• 返回一个包含 GADF 评估结果的对象。

示例代码

import mapclassify
import numpy as np

# 生成一些模拟数据
data = np.random.randn(100) * 10 + 50

# 评估分类器的 GADF
gadf_result = mapclassify.gadf(data, method='Quantiles', maxk=10, pct=0.8)
print("GADF 评估结果:", gadf_result)

参考链接：

• API reference — mapclassify v2.7.0 Manual (pysal.org)