什么是分箱?
数据分箱(Data Binning)是一种数据预处理技术,用于将连续变量分组为一系列“箱”或“区间”,以便于分析。其实分箱的概念其实很好理解,它的本质上就是把数据进行分组。分箱就是把数据按特定的规则进行分组,实现数据的离散化,增强数据稳定性,减少过拟合风险。逻辑回归中进行分箱是非常必要的,其他树模型可以不进行分箱。
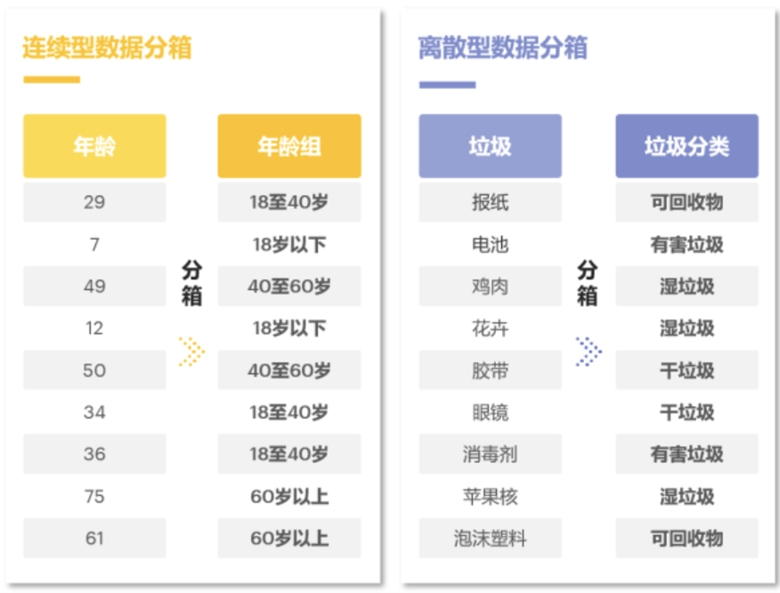
在实际建模中,分箱一般都是针对连续型数据(如价格、销量、年龄)进行的。但是从理论上,分箱也可以对类别型数据进行。比如,有些分类型数据可取的值非常多,像中国的城市这种数据,这种情况下可以通过分箱,比如城市可以被划分为一线城市、二线城市、三级城市等。
分箱(Binning)是将连续数据划分成离散的组,通常用于数据预处理和特征工程中。分箱的主要价值在于:
- 减小数据噪声和异常值的影响:分箱能够将数据离散化,从而减小数据中噪声和异常值的影响。这能够使模型更稳定和准确。
- 提高模型的解释性:分箱能够将连续数据转化为离散数据,使得模型的解释性更强。例如,可以将某个指标分成多个等级,从而更好地解释该指标的含义和作用。
- 提高模型的泛化能力:分箱能够减小模型的复杂度,从而避免过拟合和欠拟合问题,提高模型的泛化能力。
- 提高特征的稳定性和可靠性:分箱能够将连续数据转化为离散数据,使得特征的稳定性和可靠性更高。例如,在某些场景下,连续数据可能因为采集误差等原因出现抖动,而分箱能够减小这种影响。
- 更好地满足业务需求:分箱可以根据具体的业务需求进行划分,例如,将某个指标分成多个等级,以适应不同的业务场景和需求。
综上所述,分箱在数据预处理和特征工程中具有重要的价值,能够提高模型的稳定性、解释性、泛化能力和可靠性,并更好地满足业务需求。
常见分箱方法
等宽分箱(Equal-width binning)
等宽分箱是将数据划分为固定大小的区间。这通常需要指定区间的数量或宽度。等宽分箱能够快速划分数据,并且适用于数值分布均匀的数据。

下面是等宽分箱的示例代码:
import numpy as np
import pandas as pd
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.randint(1, 100, 100)})
# 等宽分箱
n_bins = 5
data['bin'] = pd.cut(data['value'], n_bins, labels=False)
在这个示例中,pd.cut函数用于将data[‘value’]等宽分为n_bins个区间,并返回每个值所在的区间序号(从0开始)。
等频分箱(Equal Frequency Binning)
等频分箱是将数据划分为固定数量的区间,每个区间包含相同数量的数据点。这个方法能够在处理数据分布不均匀的情况下,避免某些区间的数据点过多或过少的问题。

下面是等频分箱的示例代码:
import numpy as np
import pandas as pd
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.randint(1, 100, 100)})
# 等频分箱
n_bins = 5
data['bin'] = pd.qcut(data['value'], n_bins, labels=False)
在这个示例中,pd.qcut函数用于将data[‘value’]等频分为n_bins个区间,并返回每个值所在的区间序号(从0开始)。
基于聚类分箱(Clustering Binning)
聚类分箱是一种基于聚类算法的分箱方法,它能够自动将数据分为若干组,每组内的数据点相似度较高。这个方法适用于数据分布不均匀或数据自身不具有明显的规律性的情况。
下面是聚类分箱的示例代码:
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.randint(1, 100, 100)})
# 聚类分箱
n_bins = 5
kmeans = KMeans(n_clusters=n_bins, random_state=0).fit(data[['value']])
data['bin'] = kmeans.labels_
在这个示例中,使用sklearn.cluster.KMeans函数将数据划分为n_bins个簇,并将每个数据点分配到最近的簇中。最终,每个数据点都被分配到一个区间中。
基于决策树分箱(Decision tree-based binning)
基于决策树的分箱(Decision tree-based binning)是一种使用决策树来进行数据分箱的方法。它的主要思想是,利用决策树对数据进行递归划分,并将同一子树中的数据划分到同一个箱中,从而实现数据的分箱和离散化。
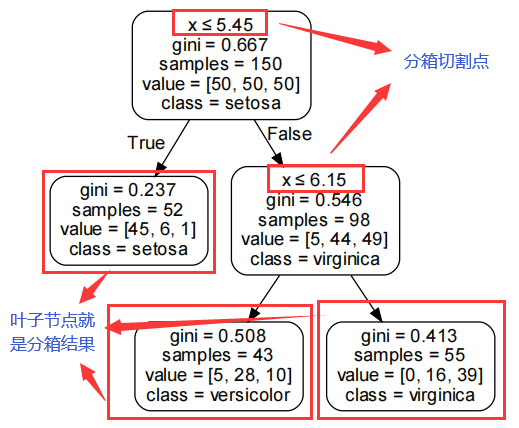
具体来说,基于决策树的分箱主要包括以下步骤:
- 构建决策树:首先,使用决策树算法(如CART、5、ID3等)对原始数据进行建树,得到一棵决策树。
- 选择叶节点:在决策树中选择叶节点作为分箱的基本单元。一般情况下,叶节点的样本量要达到一定的阈值,以保证分箱的稳定性和可靠性。
- 合并叶节点:为了得到更少的箱,可以将相邻的叶节点进行合并,直到得到预定的箱数。
- 确定分箱边界:对于每个箱,可以使用箱中数据的最大值或最小值作为分箱的边界,或者使用所有叶节点的分裂点作为分箱的边界。
- 计算最优分箱结果:根据业务需求和模型准确度等要求,可以使用不同的评估指标(如均方差、信息增益、基尼系数等)来计算最优的分箱结果。
基于决策树的分箱方法具有以下优点:
- 可以自动适应数据特征:基于决策树的分箱方法不需要对数据进行预处理和归一化,能够自适应地处理离散和连续变量,并根据数据的实际情况进行分箱。
- 可以处理高维数据:基于决策树的分箱方法能够处理高维数据,并将其离散化为少数几个变量,从而提高模型的效率和稳定性。
- 可以提高模型可解释性:基于决策树的分箱方法能够将模型的分箱过程可视化,并提高模型的可解释性。
基于决策树的分箱方法也有一些缺点:
- 分箱结果依赖于决策树的质量:基于决策树的分箱方法依赖于决策树的质量,如果决策树构造不好,分箱结果可能不准确。
- 箱数的选择比较困难:基于决策树的分箱方法需要选择合适的箱(叶节点)数,而这个选择比较困难,需要根据具体问题进行判断。
总的来说,基于决策树的分箱方法是一种简单而有效的数据离散化方法,能够在不降低模型精度的前提下,提高模型的可解释性和稳定性。
下面是使用Python中的sklearn库进行决策树分箱的代码示例:
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.normal(0, 1, 100)})
# 构建决策树
clf = DecisionTreeRegressor(max_depth=2, random_state=0)
clf.fit(data[['value']], data['value'])
# 获取分箱结果
bins = clf.tree_.threshold[clf.tree_.feature != -2]
bins = np.insert(bins, 0, float('-inf'))
bins = np.append(bins, float('inf'))
# 对数据进行分箱
data['bin'] = pd.cut(data['value'], bins, labels=False)
在这个示例中,我们首先生成了一些标准正态分布的数据,并使用DecisionTreeRegressor函数构建了一棵深度为2的决策树。然后,我们获取了决策树的分裂点,将其作为分箱的边界,并使用pd.cut函数对数据进行分箱。最终,我们得到了数据的分箱结果,可以将其用于模型训练和预测。
卡方分箱(Chi-Square Binning)
卡方分箱(Chi-Square Binning)是一种将连续变量离散化为分类变量的方法。它基于卡方检验,将连续变量划分成若干组,使每组中的变量之间相似度较高,不同组之间的差异较大。
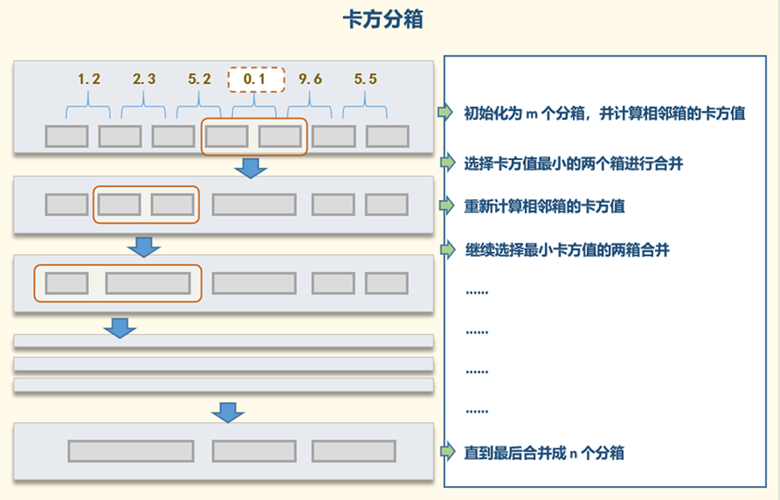
卡方分箱的基本思想是:将一维连续变量按照某种方式分成若干组,然后对于每两组计算卡方值,卡方值越大表示两组之间差异越大,分组效果越好。最终,得到的每组之间的卡方值可以作为离散化的依据,将相似度高的变量放在同一组中。
卡方分箱的主要步骤包括:
- 将连续变量排序:将连续变量按照大小排序,确定分割点。
- 初始化分组:将变量分成k组,每组包含n个样本。
- 计算卡方值:对于相邻的两个组,计算它们之间的卡方值,找到卡方值最小的一对组,将它们合并为一组。
- 重复直到满足停止条件:不断重复步骤3,直到满足停止条件。
卡方分箱的停止条件可以选择卡方值的阈值、组的数量或某些业务需求等。
卡方分箱的优点包括:
- 不需要指定分组数量,可以自适应地进行分组。
- 分组结果较为稳定,不容易受到数据分布的影响。
- 分组效果较好,可以提高模型的泛化能力和解释性。
卡方分箱的缺点包括:
- 计算量较大,需要处理大量数据,并进行复杂的卡方检验。
- 分组结果不一定最优,可能存在多个最优分组方案。
- 分组过程对分布的敏感度较高,不适用于数据分布不均匀的情况。
下面是一个使用Python进行卡方分箱的示例代码:
import pandas as pd
import numpy as np
from scipy.stats import chi2_contingency
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.normal(0, 1, 100)})
# 卡方分箱
n_bins = 5
group = pd.qcut(data['value'], n_bins, labels=False)
for i in range(n_bins-1):
while True:
if len(np.unique(group)) <= 2:
break
freq_table = pd.crosstab(group, columns=data['value'])
chi2, p, dof, expected = chi2_contingency(freq_table)
if chi2 <= chi2_critical:
break
else:
idx = np.argmin(expected.sum(axis=1))
group[group == idx] = np.unique(group)[-2]
data['bin'] = group
在这个示例中,我们首先使用pd.qcut函数将数据分为n组,并将每组赋予一个唯一的标签。然后,我们不断计算相邻两组之间的卡方值,并将卡方值最小的两组进行合并,直到满足停止条件。最终,我们得到了数据的分箱结果,可以将其用于模型训练和预测。
值得注意的是,卡方分箱通常需要调整分组的数量和卡方检验的阈值,以得到最优的分箱结果。同时,卡方分箱也可以与其他分箱方法结合使用,以得到更好的效果。
最大KS分箱
最大KS分箱是一种将连续变量离散化为分类变量的方法,其主要目的是将连续变量划分成若干组,每组中的样本不同类别之间的”差异性”最大。
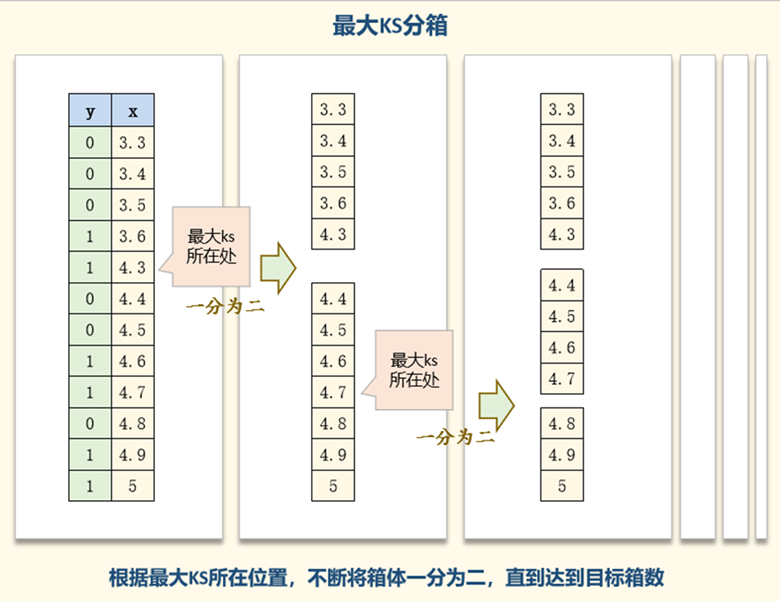
最大KS分箱的基本思想是:将一维连续变量按照某种方式分成若干组,然后对于每两组计算KS值(Kolmogorov-Smirnov Test),找到KS值最大的一对组,并将它们进行合并。重复这一过程,直到满足停止条件。最终,得到的每组之间的KS值可以作为离散化的依据,将差异性高的变量放在同一组中。
最大KS分箱的主要步骤包括:
- 将连续变量排序:将连续变量按照大小排序,确定分割点。
- 初始化分组:将变量分成k组,每组包含n个样本。
- 计算KS值并合并组:计算相邻的两组之间的KS值,找到KS值最大的一对组,将它们合并为一组。
- 重复直到满足停止条件:不断重复步骤3,直到满足停止条件。
最大KS分箱的停止条件可以选择KS值的阈值或组的数量等。
最大KS分箱的优点包括:
- 不需要指定分组数量,可以自适应地进行分组。
- 分组结果较为稳定,不容易受到数据分布的影响。
- 分组效果较好,可以提高模型的泛化能力和解释性。
最大KS分箱的缺点包括:
- 计算量较大,需要处理大量数据,并进行复杂的KS检验。
- 分组结果不一定最优,可能存在多个最优分组方案。
- 分组过程对分布的敏感度较高,不适用于数据分布不均匀的情况。
下面是一个使用Python进行最大KS分箱的示例代码:
import pandas as pd
import numpy as np
from scipy.stats import ks_2samp
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.normal(0, 1, 100)})
# 最大KS分箱
n_bins = 5
group = pd.qcut(data['value'], n_bins, labels=False)
while True:
if len(np.unique(group)) <= 2:
break
ks_value = []
for j in range(1, len(np.unique(group))):
group1 = data.loc[group < j, 'value']
group2 = data.loc[group >= j, 'value']
ks, p_value = ks_2samp(group1, group2)
ks_value.append(ks)
if np.max(ks_value) <= ks_critical:
break
else:
idx = np.argmax(ks_value) + 1
group[group >= idx] += 1
data['bin'] = group
在这个示例中,我们首先使用 pd.qcut 函数将数据分为 nn 组,并将每组赋予一个唯一的标签。然后,我们不断计算相邻两组之间的 KS 值,并将 KS 值最大的两组进行合并,直到满足停止条件。最终,我们得到了数据的分箱结果,可以将其用于模型训练和预测。
值得注意的是,最大 KS 分箱通常需要调整分组的数量和 KS 检验的阈值,以得到最优的分箱结果。同时,最大 KS 分箱也可以与其他分箱方法结合使用,以得到更好的效果。
Best-KS 分箱
Best-KS 分箱是一种将连续变量离散化为分类变量的方法,其主要目的是将连续变量划分成若干组,每组中的样本不同类别之间的“差异性”最大。
Best-KS 分箱的基本思想是:将一维连续变量按照某种方式分成若干组,然后对于每两组计算 KS 值(Kolmogorov-Smirnov Test),KS 值越大表示两组之间差异越大,分组效果越好。最终,得到的每组之间的 KS 值可以作为离散化的依据,将差异性高的变量放在同一组中。
Best-KS 分箱的主要步骤包括:
- 将连续变量排序:将连续变量按照大小排序,确定分割点。
- 初始化分组:将变量分成 k 组,每组包含 n 个样本。
- 计算 KS 值:对于相邻的两个组,计算它们之间的 KS 值(Kolmogorov-Smirnov Test),找到 KS 值最大的一对组,将它们合并为一组。
- 重复直到满足停止条件:不断重复步骤 3,直到满足停止条件。
Best-KS 分箱的停止条件可以选择 KS 值的阈值、组的数量或某些业务需求等。
Best-KS 分箱的优点包括:
- 不需要指定分组数量,可以自适应地进行分组。
- 分组结果较为稳定,不容易受到数据分布的影响。
- 分组效果较好,可以提高模型的泛化能力和解释性。
Best-KS 分箱的缺点包括:
- 计算量较大,需要处理大量数据,并进行复杂的 KS 检验。
- 分组结果不一定最优,可能存在多个最优分组方案。
- 分组过程对分布的敏感度较高,不适用于数据分布不均匀的情况。
下面是一个使用 Python 进行 Best-KS 分箱的示例代码:
import pandas as pd
import numpy as np
from scipy.stats import ks_2samp
# 生成一些示例数据
data = pd.DataFrame({'value': np.random.normal(0, 1, 100)})
# Best-KS 分箱
n_bins = 5
group = pd.qcut(data['value'], n_bins, labels=False)
for i in range(n_bins-1):
while True:
if len(np.unique(group)) <= 2:
break
ks_value = []
for j in range(1, len(np.unique(group))):
group1 = data.loc[group < j, 'value']
group2 = data.loc[group >= j, 'value']
ks, p_value = ks_2samp(group1, group2)
ks_value.append(ks)
if np.max(ks_value) <= ks_critical:
break
else:
idx = np.argmax(ks_value) + 1
group[group >= idx] += 1
data['bin'] = group
在这个示例中,我们首先使用 pd.qcut 函数将数据分为 nn 组,并将每组赋予一个唯一的标签。然后,我们不断计算相邻两组之间的 KS 值,并将 KS 值最大的两组进行合并,直到满足停止条件。最终,我们得到了数据的分箱结果,可以将其用于模型训练和预测。
值得注意的是,Best-KS 分箱通常需要调整分组的数量和 KS 检验的阈值,以得到最优的分箱结果。同时,Best-KS 分箱也可以与其他分箱方法结合使用,以得到更好的效果。
Best-KS 分箱和最大 KS 分箱有什么区别?
- Best-KS 分箱的基本思想是:将一维连续变量按照某种方式分成 kk 组,计算每两组之间的 KS 值(Kolmogorov-Smirnov Test),找到 KS 值最大的一对组,将它们合并为一组。重复这个过程,直到满足停止条件。最终,得到的每组之间的 KS 值可以作为离散化的依据,将差异性高的变量放在同一组。
- 最大 KS 分箱的基本思想是:将一维连续变量按照某种方式分成 kk 组,计算相邻的两组之间的 KS 值,找到 KS 值最大的一对组,并将它们合并为一组。重复这个过程,直到满足停止条件。最终,得到的每组之间的 KS 值可以作为离散化的依据,将差异性高的变量放在同一组中。
因此,Best-KS 分箱和最大 KS 分箱的区别在于计算 KS 值的依据。Best-KS 分箱是在 kk 组中找到 KS 值最大的一对组进行合并,而最大 KS 分箱是在相邻的两组中找到 KS 值最大的一对组进行合并。在实际应用中,Best-KS 分箱适用于分组数量较多的情况,而最大 KS 分箱适用于分组数量较少的情况。除此之外,Best-KS 分箱和最大 KS 分箱在分组结果的解释性和泛化能力方面也有差异。Best-KS 分箱更注重每组之间的差异性,分组结果更具有解释性,而最大 KS 分箱更注重整体的 KS 值,分组结果更具有泛化能力。因此,在实际应用中,需要根据具体的业务需求和数据特征选择合适的分组方法。