Sklearn 提供了一些机器学习方法,可用于奇异(Novelty)点或异常(Outlier)点检测,包括 OneClassSVM、IsolationForest、LocalOutlierFactor(LOF) 等。其中 OneClassSVM 可用于 Novelty Detection,而后两者可用于 Outlier Detection。
- novelty detection:当训练数据中没有离群点,我们的目标是用训练好的模型去检测另外新发现的样本
- outlier detection:当训练数据中包含离群点,模型训练时要匹配训练数据的中心样本,忽视训练样本中的其它异常点
OneClassSVM
OneClassSVM 是一個非监督学习的算法,顾名思义训练数据只有一个分类。透过这些正常样本的特征取学习一个决策边界,再透过这个边界去判别新的数据是否与训练数据类似。超出边界即视为异常。
OneClassSVM 的训练集不应该掺杂异常点,因为模型可能会去匹配这些异常点。但在数据维度很高,或者对相关数据分布没有任何假设的情况下,OneClassSVM 也可以作为一种很好的 outlier detection 方法。在 one-class classification 中,仅仅只有一类的信息是可以用于训练,其他类别的(总称 outlier)信息是缺失的,也就是区分两个类别的边界线是通过仅有的一类数据的信息学习得到的。
那么没有类别标签,我们如何寻找划分的超平面以及寻找支持向量呢?OneClassSVM 这个问题的解决思路有很多。这里只讲解一种特别的思路 SVDD, 对于 SVDD 来说,我们期望所有不是异常的样本都是正类别,同时它采用一个超球体而不是一个超平面来做划分,该算法在特征空间中获得数据周围的球形边界,期望最小化这个超球体的体积,从而最小化异常点数据的影响。
假设产生的超球体参数为中心 o 和对应的超球体半径 r>0,超球体体积 V(r) 被最小化,中心 o 是支持向量的线性组合;跟传统 SVM 方法相似,可以要求所有训练数据点$x_i$到中心的距离严格小于 r,但同时构造一个惩罚系数为 C 的松弛变量$\xi_i$,优化问题如下所示:
$$\underbrace{min}_{r,o}V(r)+C\sum\limits_{i=1}^m\xi_i$$
$$||x_i-o||_2\leq r+\xi_i,\;\;i=1,2,…m$$
$$\xi_i\geq 0,\;\;i=1,2,…m$$
和之前讲的支持向量机类似的求解方法,在采用拉格朗日对偶求解之后,可以判断新的数据点 z 是否在类内,如果 z 到中心的距离小于或者等于半径 r, 则不是异常点,如果在超球体以外,则是异常点。
在 sklearn 中,我们可以用 svm 包里面的 OneClassSVM 来做异常点检测。OneClassSVM 也支持核函数,所以普通 SVM 里面的调参思路在这里也适用。
代码示例:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# Generate train data
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# Generate some regular novel observations
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size
# plot the line, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
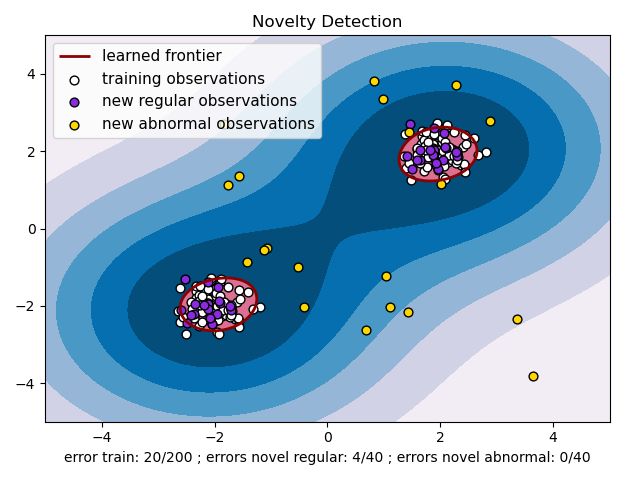
plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu) # 绘制异常样本的区域
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred') # 绘制正常样本和异常样本的边界
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred') # 绘制正常样本的区域
s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s, edgecolors='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s,
edgecolors='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s,
edgecolors='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
["learned frontier", "training observations",
"new regular observations", "new abnormal observations"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel(
"error train: %d/200; errors novel regular: %d/40;"
"errors novel abnormal: %d/40"
%(n_error_train, n_error_test, n_error_outliers))
plt.show()
参考链接:
IsolationForest(隔离森林)
Isolation Forest (以下简称 iForest) 主要是利用集成学习的思路来做异常点检测,目前几乎成为异常点检测算法的首选项。iForest 适用于连续数据(Continuous numerical data)的异常检测,将异常定义为“容易被孤立的离群点(more likely to be separated)可以理解为分布稀疏且离密度高的群体较远的点。用统计学来解释,在数据空间里面,分布稀疏的区域表示数据发生在此区域的概率很低,因此可以认为落在这些区域里的数据是异常的。通常用于网络安全中的攻击检测和流量异常等分析,金融机构则用于挖掘出欺诈行为。对于找出的异常数据,然后要么直接清除异常数据,如数据清理中的去噪数据,要么深入分析异常数据,比如分析攻击,欺诈的行为特征。
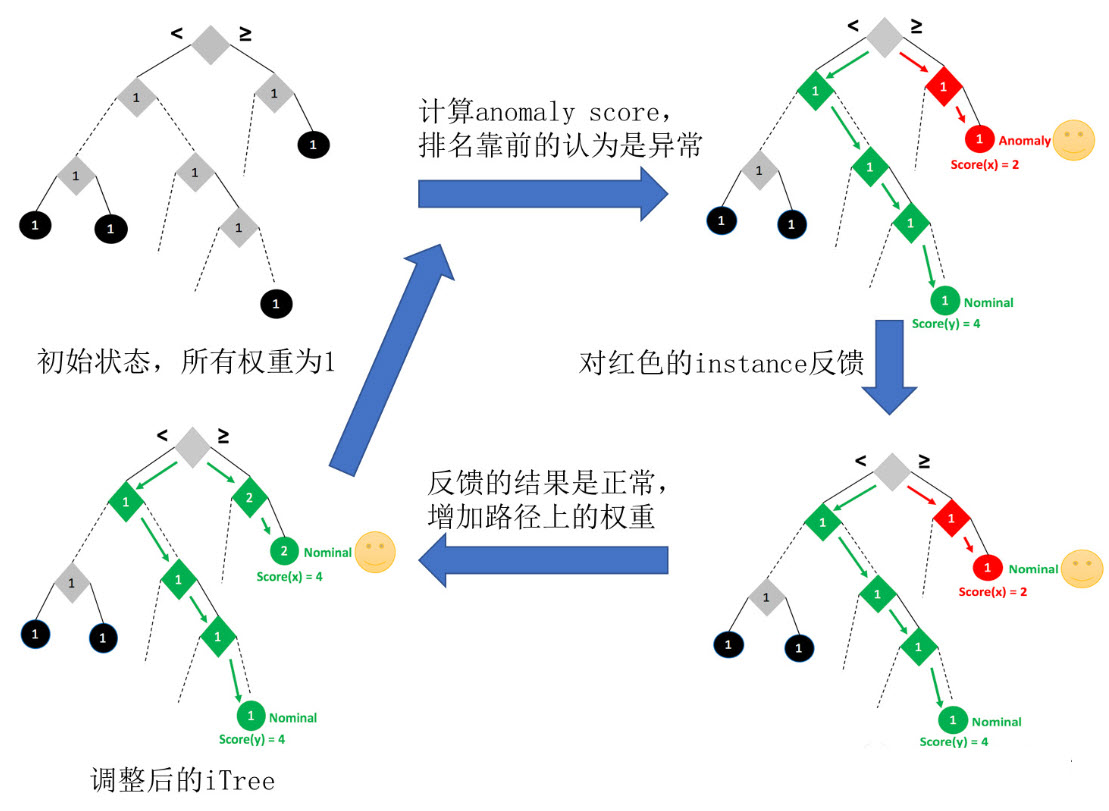
算法本身并不复杂,主要包括第一步训练构建随机森林对应的多颗决策树,这些决策树一般叫 iTree,第二步计算需要检测的数据点 x 最终落在任意第 t 颗 iTree 的层数 ht(x)。然后我们可以得出 x 在每棵树的高度平均值 h(x)。第三步根据 h(x) 判断 x 是否是异常点。
- 第一步构建决策树的过程,方法和普通的随机森林不同。首先采样决策树的训练样本时,普通的随机森林要采样的样本个数等于训练集个数。但是 iForest 不需要采样这么多,一般来说,采样个数要远远小于训练集个数。原因是我们的目的是异常点检测,只需要部分的样本我们一般就可以将异常点区别出来了。另外就是在做决策树分裂决策时,由于我们没有标记输出,所以没法计算基尼系数或者和方差之类的划分标准。这里我们使用的是随机选择划分特征,然后在基于这个特征再随机选择划分阈值,进行决策树的分裂。直到树的深度达到限定阈值或者样本数只剩一个。
- 第二步计算要检测的样本点在每棵树的高度平均值 h(x)。首先需要遍历每一颗 iTree,得到检测的数据点 x 最终落在任意第 t 颗 iTree 的数层数 $h_t(x)$。这个 $h_t(x)$ 代表的是树的深度,也就是离根节点越近,则 $h_t(x)$ 越小,越靠近底层,则 $h_t(x)$ 越大,根节点的高度为
- 第三步是据 h(x) 判断 x 是否是异常点。我们一般用下面的公式计算 x 的异常概率分值:$s(x,m)=2^{-\frac{h(x)}{c(m)}}$,s(x,m) 的取值范围是 [0,1],取值越接近于 1,则是异常点的概率也越大。其中,m 为样本个数。的表达式为:$c(m)=2\ln(m-1)+\xi-2\frac{m-1}{m}$,$\xi$ 是欧拉常数。
从 $s(x,m)$ 表示式可以看出,如果高度 $h(x)\to0$,则 $s(x,m)\to1$,即是异常点的概率是 100%,如果高度 $h(x)\to m-1$,则 $s(x,m)\to0$,即不可能是异常点。如果高度 $h(x)\to c(m)$,则 $s(x,m)\to0.5$,即是异常点的概率是 50%,一般我们可以设置 $s(x,m)$ 的一个阈值然后去调参,这样大于阈值的才认为是异常点。
在 sklearn 中,我们可以用 ensemble 包里面的 IsolationForest 来做异常点检测。
示例代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
rng = np.random.RandomState(42)
# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))
# fit the model
clf = IsolationForest(max_samples=100, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white',
s=20, edgecolor='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green',
s=20, edgecolor='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red',
s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([b1, b2, c],
["training observations",
"new regular observations","new abnormal observations"],
loc="upper left")
plt.show()
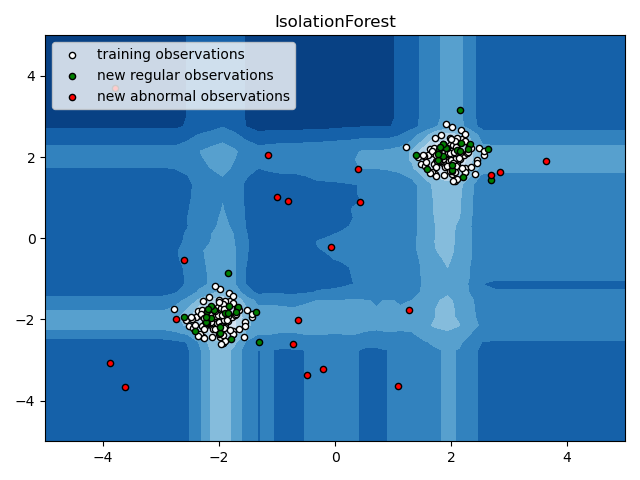
iForest 目前是异常点检测最常用的算法之一,它的优点非常突出,它具有线性时间复杂度。
- iForest 具有线性时间复杂度,因为是 ensemble 的方法,所以可以用在含有海量数据的数据集上面,通常树的数量越多,算法越稳定。由于每棵树都是相互独立生成的,因此可以部署在大规模分布式系统上来加速运算。
- iForest 不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度,建完树后仍然有大量的维度信息没有被使用,导致算法可靠性降低。高维空间还可能存在大量噪音维度或者无关维度(irrelevant attributes),影响树的构建。对这类数据,建议使用子空间异常检测(Subspace Anomaly Detection)技术。此外,切割平面默认是 axis-parallel 的,也可以随机生成各种角度的切割平面。
- IForest 仅对 Global Anomaly 敏感,即全局稀疏点敏感,不擅长处理局部的相对稀疏点(Local Anomaly)。
- iForest 推动了重心估计(Mass Estimation)理论,目前在分类聚类和异常检测中都取得显著效果。
参考链接:
- sklearn.ensemble.IsolationForest.html#sklearn.ensemble.IsolationForest
- Python 机器学习笔记:异常点检测算法——Isolation Forest
Local Outlier Factor(局部离群因子)
LocalOutlierFactor(LOF)是基于密度的经典算法(Breuning et.al. 2000)。在LOF之前的异常检测算法大多是基于统计方法的,或者是借用了一些聚类算法用于异常点的识别(比如,DBSCAN,OPTICS)。但是,基于统计的异常检测算法通常需要假设数据服从特定的概率分布,这个假设往往是不成立的。而聚类的方法通常只能给出0/1的判断(即:是不是异常点),不能量化每个数据点的异常程度。相比较而言,基于密度的LOF算法要更简单、直观。它不需要对数据的分布做太多要求,还能量化每个数据点的异常程度(outlierness)。
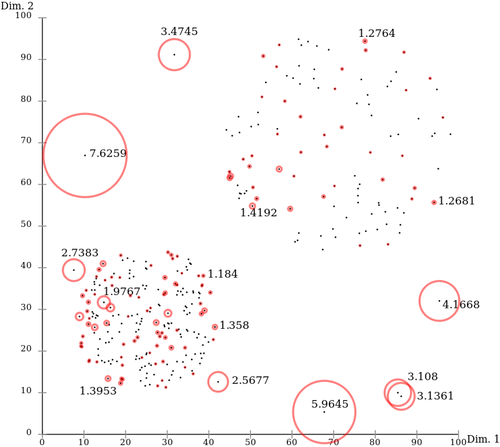
LOF算法是一种无监督的异常检测方法,它计算给定数据点相对于其邻居的局部密度偏差。每个样本的异常分数称为局部异常因子。异常分数是局部的,取决于样本相对于周围邻域的隔离程度。确切地说,局部性由k近邻给出,并使用距离估计局部密度。通过将样本的局部密度与其邻居的局部密度进行比较,可以识别密度明显低于其邻居的样本,,这些样本就被当做是异常样本点。
算法原理如下:
- 计算k-distance of p:计算点p的第k距离,也就距离样本点p第k远的点的距离,不包括p;
- 计算k-distance neighborhood of p:计算点p的第k邻域距离,就是p的第k距离以内的所有点,包括第k距离;
- 计算reach-distance:可达距离,若小于第k距离,则可达距离为第k距离,若大于第k距离,则可达距离为真实距离,公式如下(说明:d(p,o)为p到o的距离):$reach-distance_k(p,o)=max\{k-istance(o),d(p,o)\$。点o到点p的第k可达距离,至少是点o的第k距离,或者为o与p间的真实距离。
- 计算local reachability density:局部可达密度。$d_k(p)=\frac{1}{\frac{1}{|Nk(p)|}\sum_{o\in Nk(p)}reach-istance_k(p,o)}$。表示点p的第k邻域内点到点p的平均可达距离的倒数。
- 计算local outlier factor:局部离群因子。$F_k(p)=\frac{1}{|Nk(p)|}∑_{o\in Nk(p)}\frac{lrd_k(o)}{lrd_k(p)}=\frac{∑_{o\in Nk(p)}lrd_k(o)}{|Nk(p)|}\cdot\frac{1}{lrd_k(p)}$。表示点p的邻域点Nk(p)的局部可达密度与点p的局部可达密度之比的平均数。
示例代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
from scipy import stats
#构造训练样本
n_samples = 200 #样本总数
outliers_fraction = 0.25 #异常样本比例
n_inliers = int((1.-outliers_fraction)*n_samples)
n_outliers = int(outliers_fraction*n_samples)
rng = np.random.RandomState(42)
X = 0.3*rng.randn(n_inliers//2,2)
X_train = np.r_[X+2,X-2] #正常样本
X_train = np.r_[X_train,np.random.uniform(low=-6,high=6,size=(n_outliers,2))] #正常样本加上异常样本
#fit the model
clf = LocalOutlierFactor(n_neighbors=35,contamination=outliers_fraction)
y_pred = clf.fit_predict(X_train)
scores_pred = clf.negative_outlier_factor_
threshold = stats.scoreatpercentile(scores_pred,100*outliers_fraction) #根据异常样本比例,得到阈值,用于绘图
#plot the level sets of the decision function
xx,yy = np.meshgrid(np.linspace(-7,7,50),np.linspace(-7,7,50))
Z = clf._decision_function(np.c_[xx.ravel(),yy.ravel()]) #类似scores_pred的值,值越小越有可能是异常点
Z = Z.reshape(xx.shape)
plt.title("Local Outlier Factor (LOF)")
#plt.contourf(xx,yy,Z,cmap=plt.cm.Blues_r)
plt.contourf(xx,yy,Z,levels=np.linspace(Z.min(),threshold,7),cmap=plt.cm.Blues_r) #绘制异常点区域,值从最小的到阈值的那部分
a = plt.contour(xx,yy,Z,levels=[threshold],linewidths=2,colors='red') #绘制异常点区域和正常点区域的边界
plt.contourf(xx,yy,Z,levels=[threshold,Z.max()],colors='palevioletred') #绘制正常点区域,值从阈值到最大的那部分
b = plt.scatter(X_train[:-n_outliers,0],X_train[:-n_outliers,1],c='white',
s=20,edgecolor='k')
c = plt.scatter(X_train[-n_outliers:,0],X_train[-n_outliers:,1],c='black',
s=20,edgecolor='k')
plt.axis('tight')
plt.xlim((-7,7))
plt.ylim((-7,7))
plt.legend([a.collections[0],b,c],
['learned decision function','true inliers','true outliers'],
loc="upper left")
plt.show()
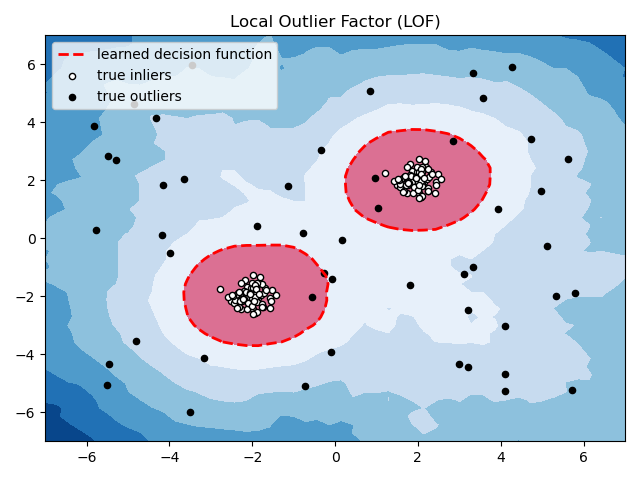
参考链接:
Fitting an elliptic envelope(椭圆模型拟合)
实现异常值检测的一种常见方式是假设内围数据来自已知分布(例如,数据服从高斯分布)。从这个假设来看,我们通常试图定义数据的“形状”,并且可以将异常观测定义为足够远离拟合形状的观测。
scikit-learn提供了covariance.EllipticEnvelope对象,它能拟合出数据的稳健协方差估计,从而为中心数据点拟合出一个椭圆,忽略中心模式之外的点。例如,假设内围数据服从高斯分布,它将稳健地(即不受异常值的影响)估计内围位置和协方差。从该估计得到的马氏距离用于得出异常度量。该策略如下图所示:
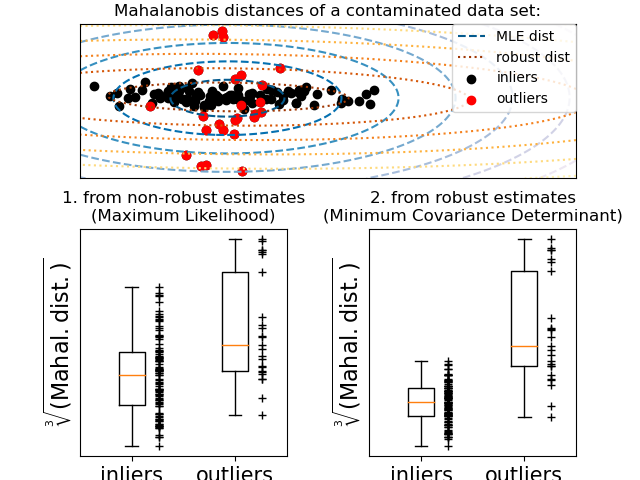
import numpy as np
import matplotlib.pyplot as plt
from sklearn.covariance import EmpiricalCovariance, MinCovDet
n_samples = 125
n_outliers = 25
n_features = 2
# generate data
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)
# fit a Minimum Covariance Determinant (MCD) robust estimator to data
robust_cov = MinCovDet().fit(X)
# compare estimators learnt from the full dataset with true parameters
emp_cov = EmpiricalCovariance().fit(X)
##############################################################################
# Display results
fig = plt.figure()
plt.subplots_adjust(hspace=-.1, wspace=.4, top=.95, bottom=.05)
# Show dataset
subfig1 = plt.subplot(3, 1, 1)
inlier_plot = subfig1.scatter(X[:, 0], X[:, 1],
color='black', label='inliers')
outlier_plot = subfig1.scatter(X[:, 0][-n_outliers:], X[:, 1][-n_outliers:],
color='red', label='outliers')
subfig1.set_xlim(subfig1.get_xlim()[0], 11.)
subfig1.set_title("Mahalanobis distances of a contaminated dataset:")
# Show contours of the distance functions
xx, yy = np.meshgrid(np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
np.linspace(plt.ylim()[0], plt.ylim()[1], 100))
zz = np.c_[xx.ravel(), yy.ravel()]
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = subfig1.contour(xx, yy, np.sqrt(mahal_emp_cov),
cmap=plt.cm.PuBu_r,
linestyles='dashed')
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = subfig1.contour(xx, yy, np.sqrt(mahal_robust_cov),
cmap=plt.cm.YlOrBr_r, linestyles='dotted')
subfig1.legend([emp_cov_contour.collections[1], robust_contour.collections[1],
inlier_plot, outlier_plot],
['MLE dist', 'robust dist', 'inliers', 'outliers'],
loc="upper right", borderaxespad=0)
plt.xticks(())
plt.yticks(())
# Plot the scores for each point
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
subfig2 = plt.subplot(2, 2, 3)
subfig2.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=.25)
subfig2.plot(np.full(n_samples - n_outliers, 1.26),
emp_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig2.plot(np.full(n_outliers, 2.26),
emp_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig2.axes.set_xticklabels(('inliers', 'outliers'), size=15)
subfig2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
subfig2.set_title("1. from non-robust estimates\n(Maximum Likelihood)")
plt.yticks(())
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
subfig3 = plt.subplot(2, 2, 4)
subfig3.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]],
widths=.25)
subfig3.plot(np.full(n_samples - n_outliers, 1.26),
robust_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig3.plot(np.full(n_outliers, 2.26),
robust_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig3.axes.set_xticklabels(('inliers', 'outliers'), size=15)
subfig3.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
subfig3.set_title("2. from robust estimates\n(Minimum Covariance Determinant)")
plt.yticks(())
plt.show()
参考链接:
异常检测算法比较
示例代码:
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor
rng = np.random.RandomState(42)
# Example settings
n_samples = 200
outliers_fraction = 0.25
clusters_separation = [0, 1, 2]
# define two outlier detection tools to be compared
classifiers = {
"One-Class SVM": svm.OneClassSVM(nu=0.95 * outliers_fraction + 0.05,
kernel="rbf", gamma=0.1),
"Robust covariance": EllipticEnvelope(contamination=outliers_fraction),
"Isolation Forest": IsolationForest(max_samples=n_samples,
contamination=outliers_fraction,
random_state=rng),
"Local Outlier Factor": LocalOutlierFactor(
n_neighbors=35,
contamination=outliers_fraction)}
# Compare given classifiers under given settings
xx, yy = np.meshgrid(np.linspace(-7, 7, 100), np.linspace(-7, 7, 100)
n_inliers = int((1. - outliers_fraction) * n_samples)
n_outliers = int(outliers_fraction * n_samples)
ground_truth = np.ones(n_samples, dtype=int)
ground_truth[-n_outliers:] = -1
# Fit the problem with varying cluster separation
for i, offset in enumerate(clusters_separation):
np.random.seed(42)
# Data generation
X1 = 0.3 * np.random.randn(n_inliers // 2, 2) - offset
X2 = 0.3 * np.random.randn(n_inliers // 2, 2) + offset
X = np.r_[X1, X2]
# Add outliers
X = np.r_[X, np.random.uniform(low=-6, high=6, size=(n_outliers, 2))]
# Fit the model
plt.figure(figsize=(9, 7))
for i, (clf_name, clf) in enumerate(classifiers.items()):
# fit the data and tag outliers
if clf_name == "Local Outlier Factor":
y_pred = clf.fit_predict(X)
scores_pred = clf.negative_outlier_factor_
else:
clf.fit(X)
scores_pred = clf.decision_function(X)
y_pred = clf.predict(X)
# 选取预定的前25%的分数的分界线作为阈值
threshold = stats.scoreatpercentile(scores_pred, 100 * outliers_fraction)
# 计算误差
n_errors = (y_pred != ground_truth).sum()
# 绘制等高线
if clf_name == "Local Outlier Factor":
# decision_function is private for LOF
Z = clf._decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
subplot = plt.subplot(2, 2, i + 1)
subplot.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),
cmap=plt.cm.Blues_r)
# 用红线画阈值边界
a = subplot.contour(xx, yy, Z, levels=[threshold],
linewidths=2, colors='red')
# 用橙色填充阈值区域内的背景
subplot.contourf(xx, yy, Z, levels=[threshold, Z.max()],
colors='orange')
b = subplot.scatter(X[:-n_outliers, 0], X[:-n_outliers, 1], c='white',
s=20, edgecolor='k')
c = subplot.scatter(X[-n_outliers:, 0], X[-n_outliers:, 1], c='black',
s=20, edgecolor='k')
subplot.axis('tight')
subplot.legend(
[a.collections[0], b, c],
['learned decision function', 'true inliers', 'true outliers'],
prop=matplotlib.font_manager.FontProperties(size=10),
loc='lower right')
subplot.set_xlabel("%d. %s (errors: %d)" % (i + 1, clf_name, n_errors))
subplot.set_xlim((-7, 7))
subplot.set_ylim((-7, 7))
plt.subplots_adjust(0.04, 0.1, 0.96, 0.94, 0.1, 0.26)
plt.suptitle("Outlier detection")
plt.show()