什么是 SVD?
奇异值分解(singular value decomposition)是线性代数中一种重要的矩阵分解,在生物信息学、信号处理、金融学、统计学等领域有重要应用,SVD 都是提取信息的强度工具。在机器学习领域,很多应用与奇异值都有关系,比如推荐系统、数据压缩(以图像压缩为代表)、搜索引擎语义层次检索的 LSI 等等。
SVD 的原理
矩阵相关知识
正交与正定矩阵
- 正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等。两个向量正交的意思是两个向量的内积为 0。
- 正定矩阵:如果对于所有的非零实系数向量 z,都有 $z^T\mathbf{A}z>0$,则称矩阵$\mathbf{A}$是正定的。正定矩阵的行列式必然大于 0,所有特征值也必然>0。相对应的,半正定矩阵的行列式必然≥0。
转置与共轭转置
矩阵的转置(transpose)是最简单的一种矩阵变换。简单来说,若 $m\times n$ 的矩阵 $\mathbf{M}$ 的转置记为 $M^T$;则 $\mathbf{M}^T$ 是一个 $n\times m$ 的矩阵,并且 $\mathbf{M}_{i,j}=\mathbf{M}^T_{j,i}$。因此,矩阵的转置相当于将矩阵按照主对角线翻转;同时,我们不难得出 $\mathbf{M}=(\mathbf{M}^T)^T$。

矩阵的共轭转置(conjugate transpose)可能是倒数第二简单的矩阵变换。共轭转置只需要在转置的基础上,再叠加复数的共轭即可。因此,若以 $\mathbf{M}^{\mathsf{H}}$ 记矩阵 $\mathbf{M}$ 的共轭转置,则有 $\mathbf{M}_{i,j}=\overline{\bigl(\mathbf{M}^{\mathsf{H}}\bigr)_{j,i}}$。
酉矩阵
酉矩阵(unitary matrix)是一种特殊的方阵,它满足 $\mathbf{U}\mathbf{U}^{\mathsf{H}}=\mathbf{U}^{\mathsf{H}}\mathbf{U}=I_n$。不难看出,酉矩阵实际上是推广的正交矩阵(orthogonal matrix);当酉矩阵中的元素均为实数时,酉矩阵实际就是正交矩阵。另一方面,由于 $\mathbf{M}\mathbf{M}^{-1}=\mathbf{M}^{-1}\mathbf{M}=I_n$,所以酉矩阵 $\mathbf{U}$ 满足 $\mathbf{U}^{-1}=\mathbf{U}^{\mathsf{H}}$,事实上,这是一个矩阵是酉矩阵的充分必要条件。
正规矩阵
同酉矩阵一样,正规矩阵(normal matrix)也是一种特殊的方阵,它要求在矩阵乘法的意义下与它的共轭转置矩阵满足交换律。这也就是说,若矩阵 $\mathbf{M}$ 满足如下条件,则称其为正规矩阵:$\mathbf{M}\mathbf{M}^{\mathsf{H}}=\mathbf{M}^{\mathsf{H}}\mathbf{M}$。显而易见,复系数的酉矩阵和实系数的正交矩阵都是正规矩阵。显而易见,正规矩阵并不只有酉矩阵或正交矩阵。例如说,矩阵 $\mathbf{M}=\begin{pmatrix}1&1&0\\0&1&1\\1&0&1\end{pmatrix}$ 即是一个正规矩阵,但它显然不是酉矩阵或正交矩阵;因为 $\mathbf{M}\mathbf{M}^{\mathsf{H}}=\begin{pmatrix}2&1&1\\1&2&1\\1&1&2\end{pmatrix}=\mathbf{M}^{\mathsf{H}}\mathbf{M}$。
谱定理和谱分解
矩阵的对角化是线性代数中的一个重要命题。谱定理(spectral theorem)给出了方阵对角化的一个结论:若矩阵 $\mathbf{M}$ 是一个正规矩阵,则存在酉矩阵 $\mathbf{U}$,以及对角矩阵 $\mathbf{\Lambda}$,使得 $\mathbf{M}=\mathbf{U}\mathbf{\Lambda}\mathbf{U}^{\mathsf{H}}$。这也就是说,正规矩阵,可经由酉变换,分解为对角矩阵;这种矩阵分解的方式,称为谱分解(spectral decomposition)。
SVD 奇异值分解
谱定理给出了正规矩阵分解的可能性以及分解形式。然而,对于矩阵来说,正规矩阵是要求非常高的。因此,谱定理是一个非常弱的定理,它的适用范围有限。在实际生产中,我们遇到的很多矩阵都不是正规矩阵。对于这些矩阵,谱定理就失效了。作为谱定理的泛化,SVD 分解对于原矩阵的要求就要弱得多。
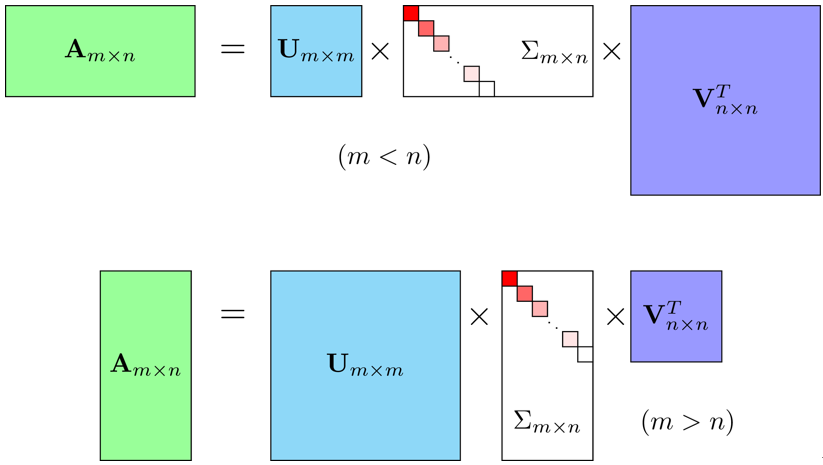
假设 $\mathbf{M}$ 是一个 $m\times n$ 的矩阵,其中的元素全部属于数域 $\mathbb{K}$(实数域 $\mathbb{R}$ 或复数域 $\mathbb{C}$)。那么,存在 $m\times m$ 的酉矩阵 $\mathbf{U}$ 和 $n\times n$ 的酉矩阵 $\mathbf{V}$ 使得:
$$M_{m×n}=U_{m×m}\Sigma_{m×n}V^T_{n×n}$$
其中 $\mathbf{\Sigma}$ 是 $m\times n$ 的非负实数对角矩阵;并且 $\mathbf{\Sigma}$ 对角线上的元素 $\mathbf{\Sigma}_{i,i}$ 是 $\mathbf{M}$ 的奇异值。一般来说,我们偏好将这些奇异值按从大到小的顺序排列,这样一来 $\mathbf{\Sigma}$ 就由 $\mathbf{M}$ 唯一确定了。
另一方面,因为 U 和 V 都是酉矩阵,所以 U 和 V 的列向量分别张成 Km 和 Kn 的一组标准正交基。我们将 U 的列向量记作 u⃗i,1⩽i⩽m;将 V 的列向量记作 v⃗j,1⩽j⩽n;同时,将 Σ 对角线上的第 i 个元素记作 σk,1⩽k⩽min(m,n)。那么,SVD 分解实际可以将矩阵 M 写作一个求和形式:
$$\mathbf{M}=\sum_{i=1}^{\min(m,n)}\sigma_i\vec{u}_i\vec{v}_i^{\mathsf{T}}$$
SVD 的计算方法
SVD 与特征值
现在,假设矩阵 $\mathbf{M}_{m\times n}$ 的 SVD 分解是 $\mathbf{M}=\mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\mathsf{H}}$,那么,我们有
$$\begin{aligned}\mathbf{M}\mathbf{M}^{\mathsf{H}}&{}=\mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\mathsf{H}}\mathbf{V}\mathbf{\Sigma}^{\mathsf{H}}\mathbf{U}^{\mathsf{H}}=\mathbf{U}(\mathbf{\Sigma}\mathbf{\Sigma}^{\mathsf{H}})\mathbf{U}^{\mathsf{H}}\\\mathbf{M}^{\mathsf{H}}\mathbf{M}&{}=\mathbf{V}\mathbf{\Sigma}^{\mathsf{H}}\mathbf{U}^{\mathsf{H}}\mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\mathsf{H}}=\mathbf{V}(\mathbf{\Sigma}^{\mathsf{H}}\mathbf{\Sigma})\mathbf{V}^{\mathsf{H}}\\\end{aligned}$$
这也就是说,$\mathbf{U}$ 的列向量(左奇异向量),是 $\mathbf{M}\mathbf{M}^{\mathsf{H}}$ 的特征向量;同时,$\mathbf{V}$ 的列向量(右奇异向量),是 $\mathbf{M}^{\mathsf{H}}\mathbf{M}$ 的特征向量;另一方面,$\mathbf{M}$ 的奇异值($\mathbf{\Sigma}$ 的非零对角元素)则是 $\mathbf{M}\mathbf{M}^{\mathsf{H}}$ 或者 $\mathbf{M}^{\mathsf{H}}\mathbf{M}$ 的非零特征值的平方根。
如何计算 SVD
有了这些知识,我们就能手工计算出任意矩阵的 SVD 分解了;具体来说,算法如下:
- 计算 $\mathbf{M}\mathbf{M}^{\mathsf{H}}$ 和 $\mathbf{M}^{\mathsf{H}}\mathbf{M}$;
- 分别计算 $\mathbf{M}\mathbf{M}^{\mathsf{H}}$ 和 $\mathbf{M}^{\mathsf{H}}\mathbf{M}$ 的特征向量及其特征值;
- $\mathbf{M}\mathbf{M}^{\mathsf{H}}$的特征向量组成$\mathbf{U}$;而$\mathbf{M}^{\mathsf{H}}\mathbf{M}$的特征向量组成$\mathbf{V}$;
- 对$\mathbf{M}\mathbf{M}^{\mathsf{H}}$和$\mathbf{M}^{\mathsf{H}}\mathbf{M}$的非零特征值求平方根,对应上述特征向量的位置,填入$\mathbf{\Sigma}$的对角元。
实际计算看看
现在,我们来试着计算$\mathbf{M}=\begin{bmatrix}2&4\\1&3\\0&0\\0&0\end{bmatrix}$的奇异值分解。计算奇异值分解,需要计算$\mathbf{M}$与其共轭转置的左右积;这里主要以$\mathbf{M}\mathbf{M}^{\mathsf{H}}$为例。
首先,我们需要计算$\mathbf{M}\mathbf{M}^{\mathsf{H}}$:
$$\mathbf{W}=\mathbf{M}\mathbf{M}^{\mathsf{H}}=\begin{bmatrix}2&4\\1&3\\0&0\\0&0\end{bmatrix}\begin{bmatrix}2&1&0&0\\4&3&0&0\end{bmatrix}=\begin{bmatrix}20&14&0&0\\14&10&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}$$
现在,我们要求 W 的特征值与特征向量。根据定义$\mathbf{W}\vec{x}=\lambda\vec{x}$;因此$(\mathbf{W}-\lambda\mathbf{I})\vec{x}=\vec{0}$。这也就是说:
$$\begin{bmatrix}20-\lambda&14&0&0\\14&10-\lambda&0&0\\0&0&-\lambda&0\\0&0&0&-\lambda\end{bmatrix}\vec{x}=\vec{0}$$
根据线性方程组的理论,若要该关于$\vec{x}$的方程有非零解,则要求系数矩阵的行列式为 0;也就是:
$$\begin{vmatrix}20-\lambda&14&0&0\\14&10-\lambda&0&0\\0&0&-\lambda&0\\0&0&0&-\lambda\end{vmatrix}=\begin{vmatrix}20-\lambda&14\\14&10-\lambda\\\end{vmatrix}\begin{vmatrix}-\lambda&0\\0&-\lambda\\\end{vmatrix}=0$$
这也就是$$\bigl((20-\lambda)(10-\lambda)-196\bigr)\lambda^2=0$$;解得$\lambda_{1}=\lambda_{2}=0$,$\lambda_{3}=15+\sqrt{221}\approx29.866$,$\lambda_{4}=15-\sqrt{221}\approx0.134$。将特征值代入原方程,可解得对应的特征向量;这些特征向量即作为列向量,形成矩阵:
$$\mathbf{U}=\begin{bmatrix}-0.82&-0.58&0&0\\-0.58&0.82&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$$
同理可解得(注意,$\mathbf{M}\mathbf{M}^{\mathsf{T}}$和$\mathbf{M}^{\mathsf{T}}\mathbf{M}$的特征值相同)
$$\mathbf{V}=\begin{bmatrix}-0.40&-0.91\\-0.91&0.40\end{bmatrix}$$
以及$\mathbf{\Sigma}$上的对角线元素由$\mathbf{W}$的特征值的算术平方根组成;因此有:
$$\mathbf{\Sigma}=\begin{bmatrix}5.46&0\\0&0.37\\0&0\\0&0\end{bmatrix}$$
因此我们得到矩阵$\mathbf{M}$的 SVD 分解(数值上做了近似):
$$\begin{bmatrix}2&4\\1&3\\0&0\\0&0\end{bmatrix}\approx\begin{bmatrix}-0.82&-0.58&0&0\\-0.58&0.82&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}5.46&0\\0&0.37\\0&0\\0&0\end{bmatrix}\begin{bmatrix}-0.40&-0.91\\-0.91&0.40\end{bmatrix}$$
SVD 的应用实战
本次实战内容为基于模型的协同过滤算法。假设我们用 m 个用户,n 个商品,每个用户对每个商品的评分可以组成一个 m*n 的二维矩阵。当然,这个矩阵中会有非常多的值是不知道的,可能是用户没有用过这个商品,也有可能用户使用后没有进行评分。如下图所示:

图中空白位置即未知的值。接下来,我们需要做的是根据这个残缺的二维矩阵中已知的值,预测出未知的值,即预测出每一个用户对每一个商品的评分。可以想象,当矩阵被预测值补充完整之后,矩阵的每一行即表示一个用户对所有商品的评分,可以从这些评分中提取评分最高的几个商品推荐给用户,这样我们就完成了一个推荐系统模型。接下来,就是如何通过已知值预测未知值的问题了,这里我们采用矩阵分解的方式,如图所示:
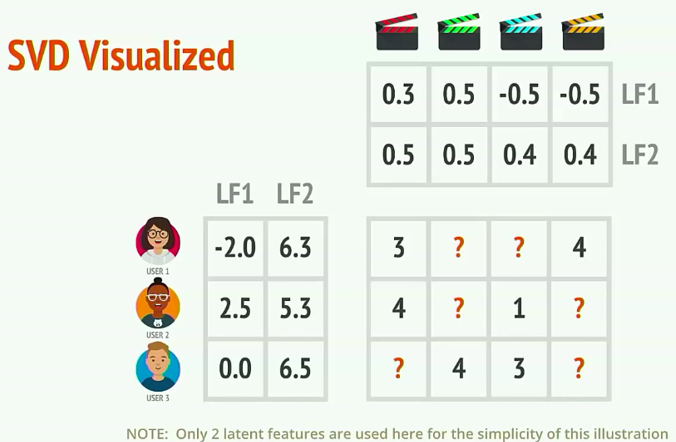
中间矩阵可以拆分为左边和上边两个矩阵的乘积,这就是奇异值分解,一个矩阵总是可以拆分成两个矩阵相乘。
第一步:安装 Python 组件及准备数据
1、安装 Python 推荐系统库:Surprise(Simple Python Recommendation System Engine)
pip install scikit-surprise
2、准备训练数据
用到的数据集 movieslen 100k:https://grouplens.org/datasets/movielens/
Surprise 自带数据集就支持 movieslen,运行如下代码:
from surprise import Dataset
# 加载 movielens 数据
data = Dataset.load_builtin('ml-100k')
交互窗口提示如下内容:
Dataset ml-100k could not be found. Do you want to download it? [Y/n]
输入 Y 以后会自动将数据集下载下来并可直接使用。
第二步:使用 SVD 进行模型训练
from surprise import SVD
from surprise import Dataset
from surprise.model_selection import cross_validate, train_test_split
from surprise import accuracy
data = Dataset.load_builtin('ml-100k')
# 拆分训练集与测试集,75%的样本作为训练集,25%的样本作为测试集
# 这里的train_set的类型是surprise.dataset.Trainset类型,我们可以查看数据的基本信息
# train_set.n_users
# Out[2]: 943
# train_set.n_items
# Out[3]: 1637
# 这说明我们要用于训练的样本共有943个用户,1637个商品。
train_set, test_set = train_test_split(data, test_size=.25)
# 训练模型,指定有35个隐含特征,使用训练集进行训练
# 35隐含特征是指,原本943*1637的矩阵会被拆分成943*35和35*1637的两个矩阵乘积。
# n_factors值可以任意指定只要不超过943即可,但是设置不同的值将会拟合出不同的模型,需要选择使结果较优的值。
# n_factors我一般选择ceiling(m*n,1/4)用来测试
model = SVD(n_factors=35)
# 5折验证,输出结果
# 输出的内容为:
# Evaluating RMSE, MAE of algorithm SVD on 5 split(s).
# Fold 1 Fold 2 Fold 3 Fold 4 Fold 5 Mean Std
# RMSE (testset) 0.9310 0.9320 0.9364 0.9329 0.9402 0.9345 0.0034
# MAE (testset) 0.7327 0.7357 0.7387 0.7357 0.7375 0.7361 0.0020
# Fit time 4.93 4.36 4.27 4.14 4.30 4.40 0.27
# Test time 0.24 0.31 0.30 0.20 0.19 0.25 0.05
cross_validate(model, data, measures=['RMSE', 'MAE'], cv=5, verbose=True)
# 使用训练集进行训练
model.fit(train_set)
# 模型训练完成后也可以查看拆分出来的两个矩阵
# model.pu.shape
# Out[2]: (943, 35)
# model.qi.shape
# Out[3]: (1637, 35)
# 使用测试集进行测试
# 输出的内容为:RMSE: 0.9413
predictions = model.test(test_set)
accuracy.rmse(predictions)
第三步:根据模型结果进行推荐
uid = str(196) # raw user id (as in the ratings file). They are **strings**!
iid = str(302) # raw item id (as in the ratings file). They are **strings**!
# 获取指定用户和电影的评级结果.
# 输出内容:
# user: 196 item: 302 r_ui=4.00 est=4.05 {'was_impossible': False}
pred = model.predict(uid, iid, r_ui=4, verbose=True)
SVD的缺点
SVD分解是早期推荐系统研究常用的矩阵分解方法,不过该方法具有以下缺点,因此很难在实际系统中应用。
- 该方法首要需要用一个简单的方法补全稀松评分矩阵。一般来说,推荐系统中的评分矩阵是非常稀疏的,一般都有95%以上的元素是缺失的。而一旦补全,评分矩阵就会变成一个稠密矩阵,从而使评分矩阵的存储需要非常大的空间,这种空间的需求在实际系统中是不可能接受的。
- 该方法依赖的SVD分解方法的计算复杂度较高,特别是在稠密的大规模矩阵上更是非常慢。一般来说,这里的SVD分解用于1000维以上的矩阵就已经非常慢了,而实际系统动辄上千万的用户和几百万的物品,所以这一方法无法使用。如果仔细研究这方面的论文可以发现,实验都是在几百个用户、几百个商品的数据集上进行的。
如何解决SVD存在的问题,请听下回分解。
参考链接: