条件随机场CRF及CRF++安装与使用

条件随机场(conditional random field, CRF)是用来标注和划分序列结构数据的概率化结构模型。言下之意，就是对于给定的输出，标识序列Y和观测序列X，条件随机场通过定义条件概率P(Y|X)，而不是联合概率分布P(X, Y)来描述模型。从定义中看出：CRF考虑一件东西，不但要考虑自身，还要考虑周围的情况。举个例子，我们做命名实体识别，例句：“Google的总部在硅谷”。我们知道地址是“硅谷”，其他位置的词对我们识别“硅谷”有啥帮助呢？例如，“硅谷”前面是“在”，是不是这个字后面经常接地址呢？“在”前面的词是不是应该是名词？这样的综合考虑，就是CRF中的特征选择或者叫特征模板。简要的说，CRF算法，需要解决三个问题：

特征的选择。在CRF中，很重要的工作就是找特征函数，然后利用特征函数来构建特征方程。在自然语言处理领域，特征函数主要是指一个句子s，词在句子中的位置i，当前词的标签 $l_{i}$，前一个词的标签$l_{i-1}$。
参数训练。在每一个特征函数之前，都有一个参数，也就是训练它们的权重。CRF的参数训练，可以采用梯度下降法。
解码。解码问题，如果来一个句子，遍历所有可能的分割，会导致计算量过大。因此，可以采用类似viterbi这样的动态规划算法，来提高效率。

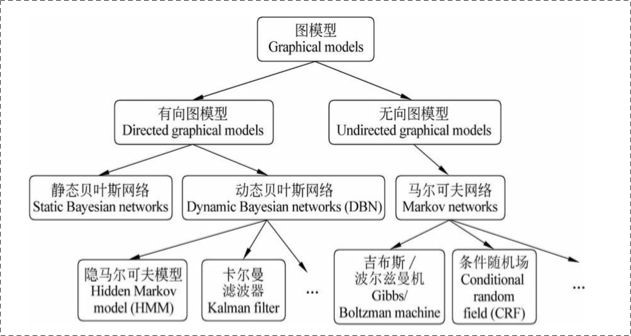
概率图模型

概率模型是将学习任务归结为计算变量的概率分布的模型。在该模型中，利用已知的变量推测位置变量的分布称为推断。

假定关心的标量为Y，可观测变量集合为O，其他变量为R，那么就可以将模型分为两种：

生成式考虑联合分布P(Y,R,O)
判别式考虑条件分布P(Y,R|O)

给定观测变量，推断就是由上述分布去推测条件概率分布P(Y|O)

由于直接求解该模型的复杂度是指数级别的，因此我们需要有一套能够简洁紧凑表达变量关系的工具，其中的代表就是概率图模型。它利用图作为标识，用结点来表示随机变量，边来表示随机变量之间的关系，概率图主要分为两类：

贝叶斯网，使用有向无环图（常用于变量间存在显式因果关系的情况）
马尔科夫网，使用无向图（常用于变量之间存在相关性但没有明显因果性）

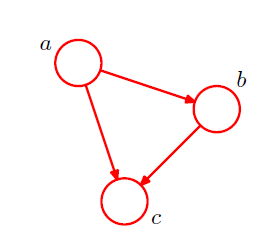
考虑三个随机变量a,b,c，其联合概率分布为：

$$P(a,b,c)=P(c\mid a,b)P(a,b)=P(c\mid a,b)P(b\mid a)P(a)$$

对每个随机变量引入一个结点，然后为每个结点关联上式右侧对应的条件概率。
对于每个条件概率分布，在图中添加一个链接（箭头）：箭头的起点是条件概率的条件代表的结点。
对于因子P(a)，因为它不是条件概率，因此没有输入的链接。
如果存在一个从结点a到结点b 的链接，则称结点a是结点b的父结点，结点b是结点a的子结点。
可以看到，上式的左侧关于随机变量a,b,c是对称的，但是右侧不是。

实际上通过对P(a,b,c)的分解，隐式的选择了一个特定的顺序（即a,b,c）。如果选择一个不同的顺序，则得到一个不同的分解方式，因此也就得到一个不同的图的表现形式。

对于K个随机变量的联合概率分布，有：

$$P(X_1,X_2,\cdots,X_K)=P(X_K\mid X_1,X_2,\cdots,X_{K-1})\cdots P(X_2\mid X_1)P(X_1)$$

它对应于一个具有K个结点的有向图。
- 每个结点对应于公式右侧的一个条件概率分布。
- 每个结点的输入链接包含了所有的编号低于它的结点。
这个有向图是全链接的，因为每对结点之间都存在一个链接。
实际应用中，真正有意义的信息是图中的链接的缺失，因为：
- 全链接的计算量太大。
- 链接的缺失代表了某些随机变量之间的不相关或者条件不相关。
设结点$X_i$的父结点集合为$\Psi_{X_i}$，则所有随机变量的联合概率分布为：$P(X_1,X_2,\cdots,X_K)=\prod_{k=1}^KP(X_k\mid \Psi_{X_k})$

前面讨论的是：每个结点对应于一个变量。可以很容易的推广到每个结点代表一个变量的集合（或者关联到一个向量）的情形。可以证明：如果上式右侧的每一个条件概率分布都是归一化的，则这个表示方法整体总是归一化的。

概率图模型probabilistic graphical model 就是一类用图来表达随机变量相关关系的概率模型：

用一个结点表示一个或者一组随机变量。
结点之间的边表示变量间的概率相关关系。

概率图描述了：联合概率分布在所有随机变量上能够分解为一组因子的乘积的形式，而每个因子只依赖于随机变量的一个子集。

根据边的性质不同，概率图模型可以大致分为两类：

使用有向无环图表示随机变量间的依赖关系，称作有向图模型或者贝叶斯网络Bayesian network。有向图对于表达随机变量之间的因果关系很有用。
使用无向图表示随机变量间的相关关系，称作无向图模型或者马尔可夫网络Markov network 。无向图对于表达随机变量之间的软限制比较有用。

概率图模型的优点：

提供了一个简单的方式将概率模型的结构可视化。
通过观察图形，可以更深刻的认识模型的性质，包括条件独立性。
高级模型的推断和学习过程中的复杂计算可以利用图计算来表达，图隐式的承载了背后的数学表达式。

贝叶斯网络

贝叶斯网络Bayesian network借助于有向无环图来刻画特征之间的依赖关系，并使用条件概率表Conditional Probability Table:CPT来描述特征的联合概率分布。这里每个特征代表一个随机变量，特征的具体取值就是随机变量的采样值。

条件独立性

一个贝叶斯网$\mathcal B$由结构$\mathcal G$和参数$\Theta$两部分组成，即$\mathcal B=(\mathcal G,\Theta)$：

网络结构$\mathcal G$是一个有向无环图，其中每个结点对应于一个特征。若两个特征之间有直接依赖关系，则他们用一条边相连。
参数$\Theta$定量描述特征间的这种依赖关系。设特征$X_i$在$\mathcal G$中父结点的集合为$\Psi_{X_i}$，则$\Theta$包含了该特征的条件概率表：$\theta_{X_i\mid \Psi_{X_i}}=P(X_i\mid \Psi_{X_i})$

贝叶斯网结构有效地表达了特征间的条件独立性。

给定父结点集，贝叶斯网络假设每个特征与它的非后裔结点表达的特征是相互独立的。于是有：

$$P(\mathbb X)=P(X_1,X_2,\cdots,X_n)=\prod_{i=1}^{n}P(X_i\mid \Psi_{X_i})=\prod_{i=1}^{n}\theta_{X_i\mid \Psi_{X_i}}$$

推导过程：

$$P(\mathbb X)=P(X_1,X_2,\cdots,X_n)=P(X_1\mid X_2,\cdots,X_n)P(X_2,\cdots,X_n)\\ =P(X_1\mid \Psi_{X_1})P(X_2,\cdots,X_n)\\ =P(X_1\mid \Psi_{X_1})P(X_2\mid X_3,\cdots,X_n)P(X_3,\cdots,X_n)\\ =P(X_1\mid \Psi_{X_1})P(X_2\mid \Psi_{X_2})P(X_3,\cdots,X_n)=\cdots$$

贝叶斯网络中三个结点之间典型依赖关系如下图：

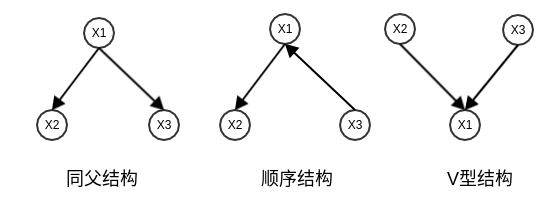
同父结构：给定父结点$X_1$的取值，则$X_2$与$X_3$条件独立，即：

$$P(X_2,X_3\mid X_1)=P(X_2\mid X_1)P(X_3\mid X_1)$$

顺序结构：给定中间结点$X_1$的取值，则$X_2$与$X_3$条件独立，即：

$$P(X_2,X_3\mid X_1)=P(X_2\mid X_1)P(X_3\mid X_1)$$

即：在$X_1$给定的条件下，$X_2$与$X_3$之间被阻断。因此它们关于$X_1$条件独立。

V 型结构：给定子结点$X_1$的取值，则$X_2$与$X_3$必定不是条件独立的。即：

$$P(X_2,X_3\mid X_1)\ne P(X_2\mid X_1)P(X_3\mid X_1)$$

事实上$X_2$与$X_3$是独立的（但不是条件独立的），即 $P(X_2,X_3)=P(X_2)P(X_3)$

为了分析有向图中结点之间的条件独立性，可以使用有向分离技术：

找出有向图中的所有V型结构，在V型结构的两个父结点之间加上一条无向边。
将所有的有向边改成无向边。

这样产生的无向图称作道德图moral graph。父结点相连的过程称作道德化moralization。基于道德图能直观、迅速的找到结点之间的条件独立性。

网络的学习

贝叶斯网络的学习可以分为参数学习和结构学习两部分：

参数学习比较简单。只需要通过对训练样本“计数”，估计出每个结点的条件概率表即可。但是前提是必须知道网络结构。
结构学习比较复杂，结构学习被证明是NP难问题。

贝叶斯网络的结构学习通常采用评分搜索来求解。先定义一个评分函数，以此评估贝叶斯网络与训练数据的契合程度。然后基于这个评分函数寻找结构最优的贝叶斯网。最常用的评分函数基于信息论准则：将结构学习问题视作一个数据压缩任务。学习的目标是找到一个能以最短编码长度描述训练集数据集的模型。这就是最小描述长度 Minimal Description Length:MDL准则。此时的编码长度包括了：描述模型自身所需要的字节长度，和使用该模型描述数据所需要的字节长度。

给定训练集$\mathbb D=\{(\mathbf {\vec x}_1,y_1),(\mathbf {\vec x}_2,y_2),\cdots,(\mathbf {\vec x}_N,y_N)\}$，贝叶斯网络$\mathcal B=(\mathcal G,\Theta)$在$\mathbb D$上的评分函数定义为：

$$score(\mathcal B\mid \mathbb D)=f(\theta) |\mathcal B|-L(\mathcal B\mid \mathbb D)$$

其中：

$f(\theta)$表示描述每个参数$\theta $所需的字节数
$|\mathcal B|$是贝叶斯网络的参数个数
$L(\mathcal B\mid\mathbb D)=\sum_{i=1}^{N}\log P(\mathbf {\vec x}_i)$ 是贝叶斯网$\mathcal B $的对数似然

因此：

第一项$f(\theta) |\mathcal B|$是计算编码贝叶斯网络$\mathcal B $所需要的字节数。
第二项$ -\sum_{i=1}^{N}\log P(\mathbf {\vec x}_i) $是计算$\mathcal B$所对应的概率分布P需要多少字节来描述$\mathbb D$。

现在结构学习任务转换为一个优化任务，即寻找一个贝叶斯网络$\mathcal B$使评分函数$score(\mathcal B\mid \mathbb D)$最小。问题是，从所有可能的网络结构空间中搜索最优贝叶斯网络结构是个NP难问题，难以快速求解。有两种方法可以在有限时间内求得近似解：

贪心算法。如从某个网络结构出发，每次调整一条边，直到评分函数不再降低为止。
增加约束。通过给网络结构增加约束来缩小搜索空间，如将网络结构限定为树形结构等。

贝叶斯网络训练好之后就能够用来进行未知样本的预测。最理想的是直接根据贝叶斯网络定义的联合概率分布来精确计算后验概率，但问题是这样的“精确推断”已经被证明是NP难的。此时需要借助“近似推断”，通过降低精度要求从而在有限时间内求得近似解，常用的近似推断为吉布斯采样(Gibbs sampling)。

马尔可夫随机场

根据前面的介绍，有向图模型可以将一组变量上的联合概率分布分解为局部条件概率分布的乘积。无向图模型也可以表示一个分解形式。马尔可夫随机场Markov Random Field:MRF是一种著名的无向图模型。

现实任务中，可能只知道两个变量之间存在相关关系，但是并不知道具体怎样相关，也就无法得到变量之间的依赖关系。

贝叶斯网络需要知道变量之间的依赖关系，从而对依赖关系（即条件概率）建模。
马尔科夫随机场并不需要知道变量之间的依赖关系。它通过变量之间的联合概率分布来直接描述变量之间的关系。

如：$X_1,X_2$两个变量的联合概率分布为：

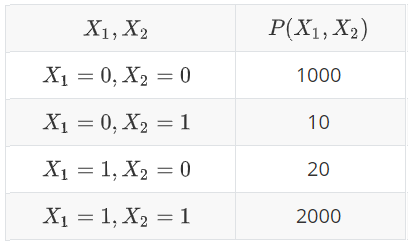
则这个分布表示：$X_1$和$X_2$取值相同的概率很大。事实上这里的$P(\cdot)$就是后面介绍的势函数。

它们的总和不一定为1。即：这个表格并未定义一个概率分布，它只是告诉我们某些配置具有更高的可能性。
它们并没有条件关系，它涉及到变量的联合分布的比例。

马尔科夫性

对结点A,B,C，若去掉结点C之后A,B分属于两个联通分支，则称结点A,B关于结点C条件独立，记作$A \perp B \mid C$。这一概念可以推广到集合。

分离集separating set：如下图所示，若从结点集 A中的结点到结点集B中的结点都必须经过结点集C中的结点，则称结点集A和结点集B被结点集C分离，C称作分离集。

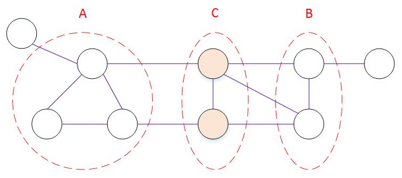
马尔可夫随机场有三个马尔可夫性定义：全局马尔科夫性、局部马尔科夫性、成对马尔科夫性

全局马尔可夫性

全局马尔可夫性global Markov property：给定两个变量子集和它们的分离集，则这两个变量子集关于分离集条件独立。令结点集A、B、C对应的变量集分别为$\mathbb X_A,\mathbb X_B,\mathbb X_C$，则$\mathbb X_A$和$\mathbb X_B$在给定$\mathbb X_C$的条件下独立，记作：$\mathbb X_A \perp \mathbb X_B \mid \mathbb X_C$

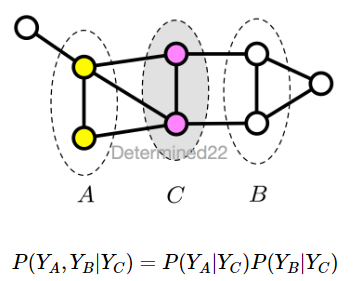
设结点集合A, B是在无向图G中被结点集合C分开的任意结点集合。结点集合A, B和C所对应的随机变量组分别是$Y_A$，$Y_B$和$Y_C$。全局马尔可夫性是指给定随机变量组$Y_C$条件下随机变量组$Y_A$，$Y_B$是条件独立的，即：

局部马尔可夫性

局部马尔可夫性local Markov property：给定某变量的邻接变量，则该变量与其他变量（既不是该变量本身，也不是邻接变量）关于邻接变量条件独立。即：令$\mathbb V$为图的结点集，n(v)为结点v在图上的邻接结点，$n^{*}(v)=n(v) \bigcup \{v\}$，则有：$\mathbb X_{v} \perp \mathbb X_{\mathbb V-n^{*}(v)} \mid \mathbb X_{n(v)}$

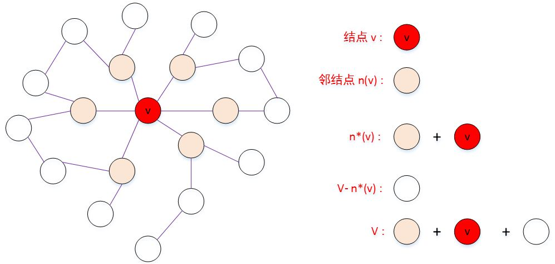
设v是无向图G中任意一个结点，W是与v有边连接的所有结点，O是v, W以外的其他所有结点。分别表示随机变量$Y_v$，以及随机变量组$Y_W$和$Y_O$。局部马尔可夫性是指在给定随机变量组$Y_W$的条件下随机变量$Y_v$与随机变量组$Y_O$是独立的，即：

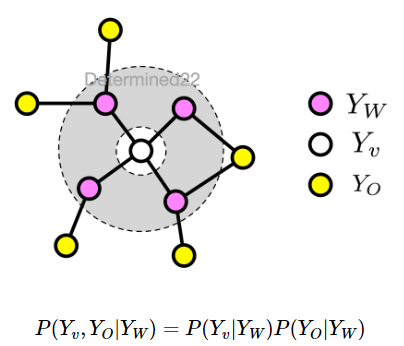
成对马尔可夫性

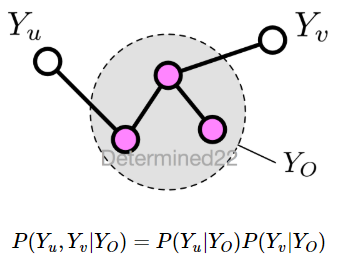
成对马尔可夫性pairwise Markov property：给定两个非邻接变量，则这两个变量关于其他变量（即不是这两个变量的任何其他变量）条件独立。即：令$\mathbb V$为图的结点集，令$\mathbb E$为图的边集。对图中的两个结点u,v，若$(u,v) \notin \mathbb E$, 则有：$\mathbb X_{u} \perp \mathbb X_{v} \mid \mathbb X_{\mathbb V-\{u,v\}}$

设u和v是无向图G中任意两个没有边连接的结点，结点u和v分别对应随机变量$Y_u$和$Y_v$，其他所有结点为O，对应的随机变量组是$Y_O$。成对马尔可夫性是指给定随机变量组v的条件下随机变量$Y_u$和$Y_v$是条件独立的，即：

极大团

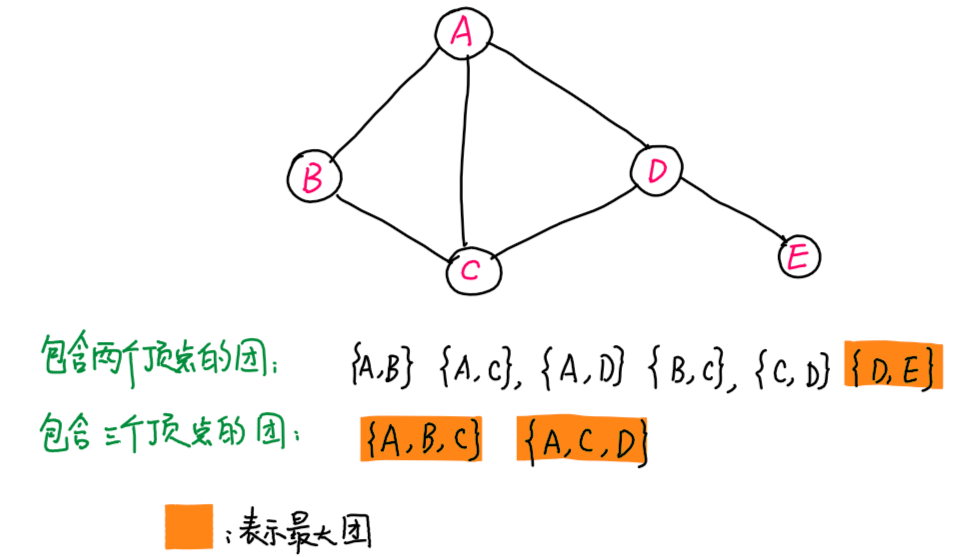
给定一张图G=(V,E)，和顶点集合的一个非空子集合$C\subset V$，如果C中任何两个顶点之间均有边链接，则称C为团(clique)；更进一步，若加入任何一个顶点$v \in G \backslash C$中的顶点，都使得$C \cup {v}$不再是团,则称C为最大团(maximal clique)。

上述定义比较抽象，可用下图辅助理解：

对于团，任何两点之间都有边链接。例如，由一条边连接的两个顶点，自然成为一个团，如{A,B}，{A,C}等
对于最大团，如果再增加任何一个顶点，就不再成为团。
- 对于团{A,B},还可以增加顶点C,形成团{A,B,C},该团中任何两点都有边连接。因此，{A,B}不是最大团
- 对于团{D,E},我们看到，增加任何一个顶点，无法保证两点之间有边存在，例如，增加点C，则{C,D,E}中，不存在边(C,E)，因此{D,E}是最大团。

考虑两个结点$X_i,X_j$，如果它们之间不存在链接，则给定图中其他所有结点，那么这两个结点一定是条件独立的。因为这两个结点之间没有直接的路径，并且所有其他路径都通过了观测的结点。

该条件独立性表示为：

$$P(X_i,X_j\mid \mathbb X-\{X_i,X_j\})=P(X_i\mid \mathbb X-\{X_i,X_j\})P(X_j\mid\mathbb X-\{X_i,X_j\})$$

对于联合概率分布的分解，则一定要让$X_i,X_j$不能出现在同一个因子中，从而让属于这个图的所有可能的概率分布都满足条件独立性质。

这里引入团的概念：对于图中结点的一个子集，如果其中任意两个结点之间都有边连接，则称该结点子集为一个团clique。即：团中的结点集合是全连接的。若在一个团中加入团外的任何一个结点都不再形成团，则称该团为极大团maximal clique 。即：极大团就是不能被其他团所包含的团。显然，每个结点至少出现在一个极大团中。如下图所示：

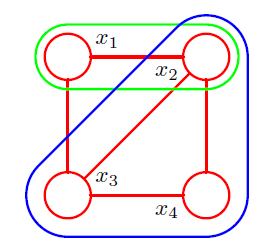
所有的团有：$\{X_1,X_2\},\{X_2,X_3\},\{X_3,X_4\},\{X_4,X_2\},\{X_1,X_3\},\{X_1,X_2,X_3\},\{X_2,X_3,X_4\}$
极大团有：$\{X_1,X_2,X_3\},\{X_2,X_3,X_4\}$

可以将联合概率分布分解的因子定义为团中变量的函数，也称作势函数。它是定义在随机变量子集上的非负实函数，主要用于定义概率分布函数。

在马尔可夫随机场中，多个变量之间的联合概率分布能够基于团分解为多个因子的乘积，每个因子仅和一个团相关。对于n个随机变量$\mathbb X=\{X_1,X_2,\cdots,X_n\}$，所有团构成的集合为$\mathcal C$，与团$\mathbb Q\in \mathcal C$对应的变量集合记作$\mathbb X_\mathbb Q$，则联合概率$P(\mathbb X)$定义为：

$$P(\mathbb X)=\frac 1Z \prod_{\mathbb Q\in \mathcal C} \psi_\mathbb Q(\mathbb X_\mathbb Q)$$

其中：

所有团构成了整个概率图（团包含了结点和连接），任意两个团之间不互相包含（但是可以相交）。
$\psi_\mathbb Q$为与团$\mathbb Q$对应的势函数，用于对团$\mathbb Q$中的变量关系进行建模。
$Z=\sum_{\mathbb X}\prod_{\mathbb Q\in \mathcal C} \psi_\mathbb Q(\mathbb X_\mathbb Q)$为规范化因子，确保$P(\mathbb X)$满足概率的定义。
实际应用中，Z的精确计算非常困难。但是很多任务往往并不需要获得Z的精确值。

在上述$P(\mathbb X)$计算公式中，团的数量会非常多。如：所有相互连接的两个结点都会构成一个团。这意味着有非常多的乘积项。注意到：若团$\mathbb Q$不是极大团，则它必被一个极大团$\mathbb Q^{*}$所包含。此时有：$\mathbb X_\mathbb Q \subseteq \mathbb X_{\mathbb Q^{*}}$。

于是：随机变量集合$\mathbb X_\mathbb Q$内部随机变量之间的关系不仅体现在势函数$\psi_{\mathbb Q}$中，也体现在势函数$\psi_{\mathbb Q^{*}}$中（这是根据势函数的定义得到的结论）。
于是：联合概率$P(\mathbb X)$可以基于极大团来定义。假定所有极大团构成的集合为$\mathcal C^{*}$，则有Hammersley-Clifford 定理：$P(\mathbb X)=\frac {1}{Z^{*}} \prod_{\mathbb Q\in \mathcal C^{*}} \psi_\mathbb Q(\mathbb X_\mathbb Q)$。其中：$Z^{*}=\sum_{\mathbb X}\prod_{\mathbb Q\in \mathcal C^{*}} \psi_\mathbb Q(\mathbb X_\mathbb Q)$ 为规范化因子，确保$P(\mathbb X)$满足概率的定义。

通常贝叶斯网络可以将因子定义成表格形态，而马尔可夫随机场将因子定义为势函数。因为马尔可夫随机场无法将因子表格化。

假设有n个随机变量$X_1,X_2,\cdots,X_n$，它们的取值都是$\{0,1\}$。假设马尔可夫随机场中它们是全连接的，则其联合概率分布需要$O(2^n)$个参数。如果表达成表格形态，横轴表示连接的一个端点、纵轴表示连接的另一个端点，则需要$O(n^2)$个参数。当n较大的时候，$O(n^2) \lt O(2^n)$，因此表格无法完全描述马尔可夫随机场的参数。

全局马尔可夫性的一个证明：

将上图简化为如下所示：

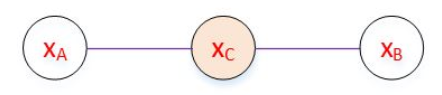
最大团有两个：$\{\mathbb X_{A},\mathbb X_{C}\},\{\mathbb X_{B},\mathbb X_{C}\}$，因此联合概率为：

$$P(\mathbb X_{A},\mathbb X_{B},\mathbb X_{C})=\frac 1Z\psi_{AC}(\mathbb X_{A},\mathbb X_{C})\psi_{BC}(\mathbb X_{B},\mathbb X_{C})$$

基于条件概率的定义有：

$$P(\mathbb X_{A},\mathbb X_{B}\mid \mathbb X_{C})=\frac{P(\mathbb X_{A},\mathbb X_{B},\mathbb X_{C})}{P(\mathbb X_{C})}$$

根据：

$$P(\mathbb X_{C})=\sum_{\mathbb X_{A}^{\prime}}\sum_{\mathbb X_{B}^{\prime}} P(\mathbb X_{A}^{\prime},\mathbb X_{B}^{\prime},\mathbb X_{C}) = \sum_{\mathbb X_{A}^{\prime}}\sum_{\mathbb X_{B}^{\prime}}\frac {1}{Z}\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C})\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C})$$

将$P(\mathbb X_{C})$和$P(\mathbb X_{A},\mathbb X_{B},\mathbb X_{C})$代入，有：

$$P(\mathbb X_{A},\mathbb X_{B}\mid \mathbb X_{C})=\frac{\psi_{AC}(\mathbb X_{A},\mathbb X_{C})\psi_{BC}(\mathbb X_{B},\mathbb X_{C}) }{\sum_{\mathbb X_{A}^{\prime}}\sum_{\mathbb X_{B}^{\prime}}\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C})\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C}) }\\ = \frac{\psi_{AC}(\mathbb X_{A},\mathbb X_{C})}{\sum_{\mathbb X_{A}^{\prime}}\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C})}\cdot \frac{\psi_{BC}(\mathbb X_{B},\mathbb X_{C}) }{\sum_{\mathbb X_{B}^{\prime}}\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C})}$$

考虑$P(\mathbb X_{A}\mid \mathbb X_{C})$：

$$P(\mathbb X_{A}\mid \mathbb X_{C})=\frac{P(\mathbb X_{A},\mathbb X_{C})}{P(\mathbb X_{C})}=\frac{\sum_{\mathbb X_{B}^{\prime}} P(\mathbb X_{A},\mathbb X_{B}^{\prime},\mathbb X_{C})}{\sum_{\mathbb X_{A}^{\prime}}\sum_{\mathbb X_{B}^{\prime}} P(\mathbb X_{A}^{\prime},\mathbb X_{B}^{\prime},\mathbb X_{C})}\\ = \frac{\sum_{\mathbb X_{B}^{\prime}}\frac 1Z\psi_{AC}(\mathbb X_{A},\mathbb X_{C})\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C}) }{\sum_{\mathbb X_{A}^{\prime}}\sum_{\mathbb X_{B}^{\prime}} \frac 1Z\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C})\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C}) }\\ =\frac{\psi_{AC}(\mathbb X_{A},\mathbb X_{C})\sum_{\mathbb X_{B}^{\prime}}\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C}) }{\left(\sum_{\mathbb X_{A}^{\prime}}\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C}) \right)\left(\sum_{\mathbb X_{B}^{\prime}}\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C})\right)}\\ =\frac{\psi_{AC}(\mathbb X_{A},\mathbb X_{C})}{\sum_{\mathbb X_{A}^{\prime}}\psi_{AC}(\mathbb X_{A}^{\prime},\mathbb X_{C})}$$

同理，可以推导出：

$$P(\mathbb X_{B}\mid \mathbb X_{C})=\frac{\psi_{BC}(\mathbb X_{B},\mathbb X_{C})}{\sum_{\mathbb X_{B}^{\prime}}\psi_{BC}(\mathbb X_{B}^{\prime},\mathbb X_{C}) }$$

于是有：

$$P(\mathbb X_{A},\mathbb X_{B}\mid \mathbb X_{C})=P(\mathbb X_{A}\mid \mathbb X_{C}) \cdot P(\mathbb X_{B}\mid \mathbb X_{C})$$

有向图和无向图模型都将复杂的联合分布分解为多个因子的乘积：

无向图模型的因子是势函数，需要全局归一化。优点是：势函数设计不受概率分布的约束，设计灵活。
有向图模型的因子是概率分布，不需要全局归一化。优点是：训练相对高效。

势函数

势函数$\psi_\mathbb Q(\mathbb X_\mathbb Q)$的作用是刻画变量集$\mathbb X_\mathbb Q$中变量之间的相关关系。与有向图的联合分布的因子不同，无向图中的势函数没有一个具体的概率意义。

这可以使得势函数的选择具有更大的灵活性，但是也产生一个问题：对于具体任务来说，如何选择势函数。
可以这样理解：将势函数看做一种度量：它表示局部变量的哪种配置优于其他配置。

势函数必须是非负函数（确保概率非负），且在所偏好的变量取值上具有较大的函数值。如：

$$\psi_{AC}( X_A, X_C)=\begin{cases} 2.0,& \text{if}\quad X_A= X_C\\ 0.1,& \text{otherwise} \end{cases} \\ \psi_{BC}( X_B, X_C)=\begin{cases} 0.1,& \text{if}\quad X_B= X_C\\ 1.5,& \text{otherwise} \end{cases}$$

该模型偏好变量$X_A, X_C$拥有相同的取值；偏好$X_B, X_C$拥有不同的取值。如果想获取较高的联合概率，则可以令$X_A$和$X_C$相同，且$X_B$和$X_C$不同。

通常使用指数函数来定义势函数：

$$\psi_\mathbb Q(\mathbb X_\mathbb Q)=e^{-H_\mathbb Q(\mathbb X_\mathbb Q)}$$

其中$H_\mathbb Q(\mathbb X_\mathbb Q)$是一个定义在变量集$\mathbb X_\mathbb Q$上的实值函数，称作能量函数。

指数分布被称作玻尔兹曼分布。联合概率分布被定义为势函数的乘积，因此总能量可以通过将每个最大团中的能量相加得到。这就是采取指数函数的原因，指数将势函数的乘积转换为能量函数的相加。

$H_\mathbb Q(\mathbb X_\mathbb Q)$常见形式为：

$$H_\mathbb Q(\mathbb X_\mathbb Q)=\sum_{u,v \in \mathbb Q,u\neq v} \alpha_{u,v}t_{u,v}(u,v)+\sum_{v \in \mathbb Q}\beta_vs_v(v)$$

其中：

$\alpha_{u,v},\beta_v$表示系数；$t_{u,v}(u,v),s_v(v)$表示约束条件。
上式第一项考虑每一对结点之间的关系；第二项考虑单个结点。

图像降噪应用

马尔可夫随机场可以应用于图像问题中：

每个像素都表示成一个结点，相邻像素之间相互影响。
像素之间并不存在因果关系，它们之间的作用是对称的。因此使用无向图概率模型，而不是有向图概率模型。

马尔可夫随机场的一个应用是图像降噪。如下图所示，左侧图片为原始图像，右侧图片为添加了一定噪音（假设噪音比例不超过 10%）的噪音图像。现在给定噪音图像，需要得到原始图像。

设随机变量$Y_i$表示噪音图像中的像素，随机变量$X_i$表示原始图像中的像素。其中：

i代表图片上的每个位置。
$Y_i,X_i\in \{+1,-1\}$。当它们取 +1 时，表示黑色；取-1 时，表示白色。

由于已知噪音图像，因此$Y_i$的分布是已知的。原始图像未知，则$X_i$的分布待求解。由于噪音图像是从原始图像添加噪音而来，因此我们认为：$Y_i$和$X_i$具有较强的关联。由于原始图像中，每个像素和它周围的像素值比较接近，因此$X_i$与它相邻的像素也存在较强的关联。因此我们假设：$X_i$只和它直接相邻的像素有联系（即：条件独立性质）。

因此得到一个具备局部马尔可夫性质的概率图模型。模型中具有两类团：

团$\{X_i,Y_i\}$：原始图像的像素和噪音图像的像素
团$\{X_i,X_j\}$：原始图像的像素和其直接相邻的像素

这两类团就是模型中的最大团。

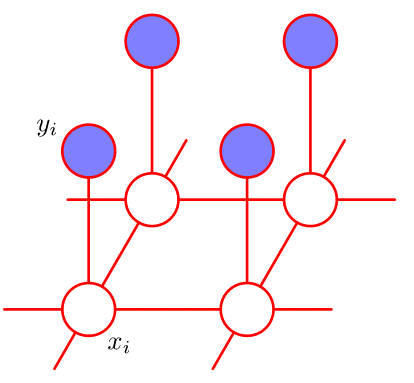
定义能量函数：

对于团$\{X_i,Y_i\}$，定义能量函数：$H_1(X_i,Y_i) =-\eta X_iY_i$。即：$X_i,Y_i$相同时，能量较低；$X_i,Y_i$不同时，能量较高。
对于团$\{X_i,X_j\}$，定义能量函数：$H_2(X_i,X_j) =-\beta X_iX_j$。即：$X_i,X_j$相同时，能量较低；$X_i,X_j$不同时，能量较高。
另外对于团$\{X_i,Y_i\}$，$\{X_i,X_j\}$这个整体，定义能量函数：$H_3(X_i)=hX_i$。即：$X_i$较大时，能量较高； $X_i$较小时，能量较低。

于是得到整体的能量函数为：

$$H(\mathbb X,\mathbb Y)=h \sum_{i} X_i-\beta\sum_{(i,j) \in \mathbb E} X_iX_j -\eta \sum_{i}X_iY_i$$

其中$\mathbb E$为原始图像的相邻像素连接得到的边。

考虑到$P(\mathbb X,\mathbb Y)=\frac {1}{Z^{*}} e^{-H(\mathbb X,\mathbb Y)}$，根据最大似然准则，则模型优化目标是：

$$\min_{X_i} H(\mathbb X,\mathbb Y) = \min_{X_i} h \sum_{i} X_i-\beta\sum_{(i,j) \in \mathbb E} X_iX_j -\eta \sum_{i}X_iY_i$$

对于能量函数最小化这个最优化问题，由于每个位置的$X_i$都可以取2 个值$\{+1,-1\}$，因此有$2^N$种取值策略，N为原始图像的像素数量。如果N较大，则参数的搜索空间非常巨大。实际任务中通过 ICM 算法、模拟退火算法、或者graph cuts 算法来解决这个参数搜索问题。

条件随机场 CRF

生成式概率图模型是直接对联合分布进行建模，如隐马尔可夫模型和马尔可夫随机场都是生成式模型。判别式概率图模型是对条件分布进行建模，如条件随机场Conditional Random Field:CRF。

条件随机场试图对多个随机变量（它们代表标记序列）在给定观测序列的值之后的条件概率进行建模：令$\mathbf X=\{ X_1, X_2,\cdots,X_n\}$为观测变量序列，$\mathbf Y=\{Y_1,Y_2,\cdots,Y_n\}$为对应的标记变量序列。条件随机场的目标是构建条件概率模型$P(\mathbf Y \mid \mathbf X)$。即：已知观测变量序列的条件下，标记序列发生的概率。

标记随机变量序列Y的成员之间可能具有某种结构：

在自然语言处理的词性标注任务中，观测数据为单词序列，标记为对应的词性序列（即动词、名词等词性的序列），标记序列具有线性的序列结构。
在自然语言处理的语法分析任务中，观测数据为单词序列，标记序列是语法树，标记序列具有树形结构。

令$\mathcal G=<\mathbb V,\mathbb E>$表示与观测变量序列X和标记变量序列Y对应的无向图，$Y_v$表示与结点v对应的标记随机变量，n(v)表示结点v的邻接结点集。若图$\mathcal G$中结点对应的每个变量$Y_v$都满足马尔可夫性，即：$P(Y_v\mid \mathbf X,\mathbf Y_{\mathbb V-\{v\}})=P(Y_v \mid \mathbf X,Y_{n(v)})$。则$(\mathbf Y,\mathbf X)$构成了一个条件随机场。

链式条件随机场

理论上讲，图$\mathcal G $可以具有任意结构，只要能表示标记变量之间的条件独立性关系即可。但在现实应用中，尤其是对标记序列建模时，最常用的是链式结构，即链式条件随机场chain-structured CRF。

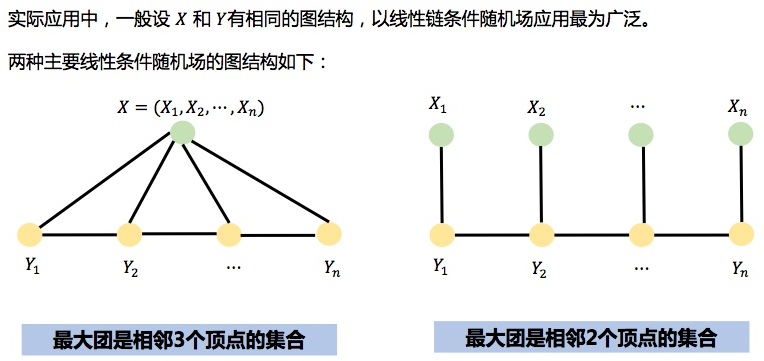如果没有特殊说明，这里讨论是基于链式条件随机场。

给定观测变量序列$\mathbf X=\{ X_1, X_2,\cdots,X_n\}$，链式条件随机场主要包含两种关于标记变量的团：

单个标记变量与$\mathbf X$构成的团：$\{Y_i,\mathbf X\},i=1,2,\cdots,n$
相邻标记变量与$\mathbf X$构成的团：$\{Y_{i-1},Y_i,\mathbf X\},i=2,\cdots,n$

与马尔可夫随机场定义联合概率的方式类似，条件随机场使用势函数和团来定义条件概率$\{Y_{i-1},Y_i,\mathbf X\},i=2,\cdots,n$。采用指数势函数，并引入特征函数feature function，定义条件概率：

$$P(\mathbf Y\mid \mathbf X)=\frac 1Z \exp\left(\sum_{j=1}^{K_1}\sum_{i=1}^{n-1}\lambda_jt_j(Y_i,Y_{i+1},\mathbf X,i)+\sum_{k=1}^{K_2}\sum_{i=1}^{n}\mu_ks_k(Y_i,\mathbf X,i)\right)$$

其中：

$t_j(Y_i,Y_{i+1},\mathbf X,i)$：在已知观测序列情况下，两个相邻标记位置上的转移特征函数transition feature function。它刻画了相邻标记变量之间的相关关系，以及观察序列X对它们的影响。位置变量i也对势函数有影响。比如：已知观测序列情况下，相邻标记取值(代词，动词)出现在序列头部可能性较高，而(动词，代词)出现在序列头部的可能性较低。
$s_k(Y_i,\mathbf X,i)$：在已知观察序列情况下，标记位置i上的状态特征函数status feature function。它刻画了观测序列X对于标记变量的影响。位置变量i也对势函数有影响。比如：已知观测序列情况下，标记取值名词出现在序列头部可能性较高，而动词出现在序列头部的可能性较低。
$\lambda_j,\mu_k$为参数Z为规范化因子（它用于确保上式满足概率的定义）。$K_1$为转移特征函数的个数，$K_2$为状态特征函数的个数。

特征函数通常是实值函数，用来刻画数据的一些很可能成立或者预期成立的经验特性。一个特征函数的例子（词性标注）：

$$t_j(Y_i,Y_{i+1},\mathbf X,i)=\begin{cases} 1,& \text{if} \quad Y_{i+1}=\text{[P]},\;Y_i=\text{[V]} \;\text{and}\; X_i=\text{“knock”}\\ 0,& \text{otherwise} \end{cases}\\ s_k(Y_i,\mathbf X,i)=\begin{cases} 1,& \text{if} \quad Y_i=\text{[V]} \;\text{and}\; X_i=\text{“knock”}\\ 0,& \text{otherwise} \end{cases}$$

转移特征函数刻画的是：第i个观测值$X_i$为单词 “knock” 时，相应的标记$Y_i$和$Y_{i+1}$很可能分别为[V]和[P] 。
状态特征函数刻画的是：第i个观测值$X_i$为单词 “knock” 时，标记$Y_i$很可能为[V] 。

条件随机场与马尔可夫随机场均使用团上的势函数定义概率，二者在形式上没有显著区别。条件随机场处理的是条件概率，马尔可夫随机场处理的是联合概率。

$P(\mathbf Y\mid \mathbf X)$的形式类似于逻辑回归。事实上，条件随机场是逻辑回归的序列化版本。

逻辑回归是用于分类问题的对数线性模型
条件随机场是用于序列化标注的对数线性模型

CRF 的简化形式

注意到条件随机场中的同一个特征函数在各个位置都有定义，因此可以对同一个特征在各个位置求和，将局部特征函数转化为一个全局特征函数。这样就可以将条件随机场写成权值向量和特征向量的内积形式，即条件随机场的简化形式。

设有$K_1$个转移特征函数，$K_2$个状态特征函数。令$K=K_1+K_2$，定义：

$$f_k(Y_i,Y_{i+1},\mathbf X,i)=\begin{cases} t_k(Y_i,Y_{i+1},\mathbf X,i),&k=1,2,\cdots,K_1\\ s_l(Y_i,\mathbf X,i),&k=K_1+l;l=1,2,\cdots,K_2 \end{cases}$$

CRF应用

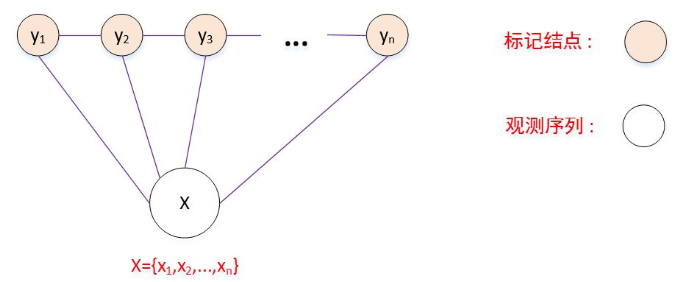
中文分词

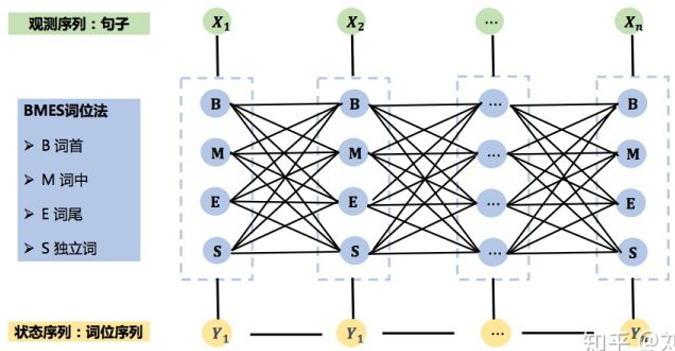
基本思想：每个字在构造一个特定的词语时都占据着一个确定的构词位置（即构词位）。常用的四位构词位：

基本原理：

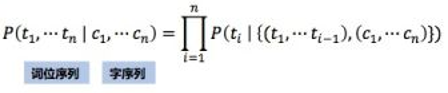
CRF中文分词的图结构：

命名实体识别

基于CRF的命名实体识别过程如下：

词的实体标注。首先把句子进行原子切分，然后对字（词）进行实体标注。
确定特征函数。接着确定特征模板。一般采用当前位置的前后n个位置上的词。‘
模型训练。训练CRF模型参数$W_k$

CDF命名实体识别的图结构：

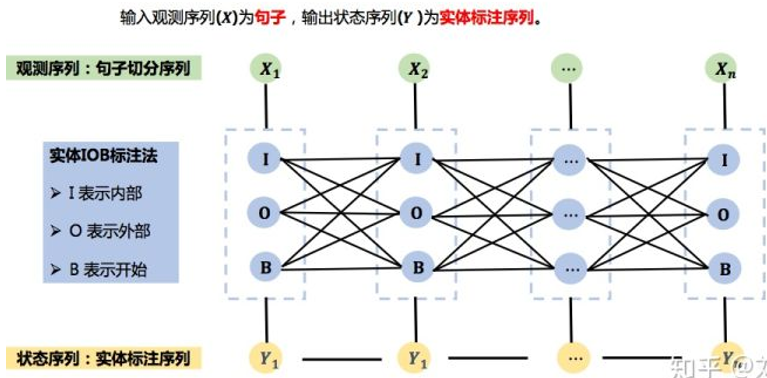
词性标注

基本思想：判定句子中的每个词的词性并进行标注。

基本原理：

对输入句子进行原子切分，得到原子切分序列
对字（词）进行词性标注
确定特征函数
训练CRF模型参数

CRF中文词性标注的图结构：

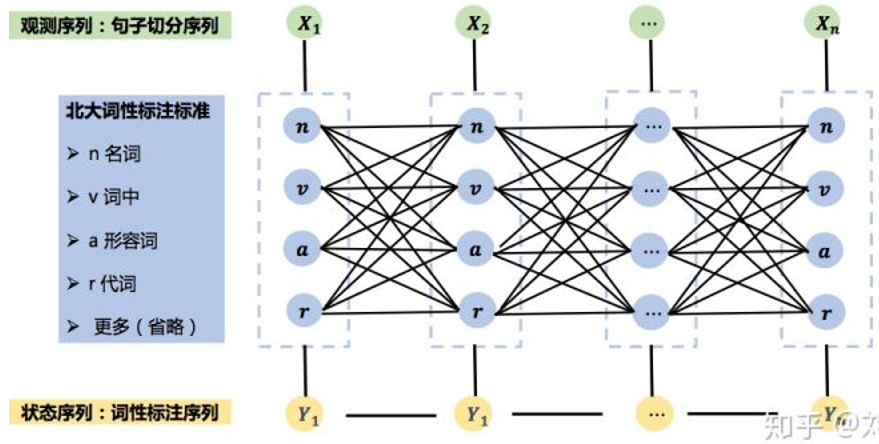
CRF的概括总结

CRF发展方向

机器学习阶段：CRF
深度学习阶段：BiLSTM-CRF、BiLSTM-CNN-CRF
Attention阶段：Transformer-CRF、BERT-BiLSTM-CRF

CRF++的安装

CRF++是著名的条件随机场的开源工具，也是目前综合性能最佳的CRF工具。

Windows下的安装

在Windows下的安装很简单，其实严格来讲不能说是安装。我们解压我们下载的压缩包文件到某一个目录下面。你可能会得到如下所示的文件，（版本不同，可能会有所不同。）

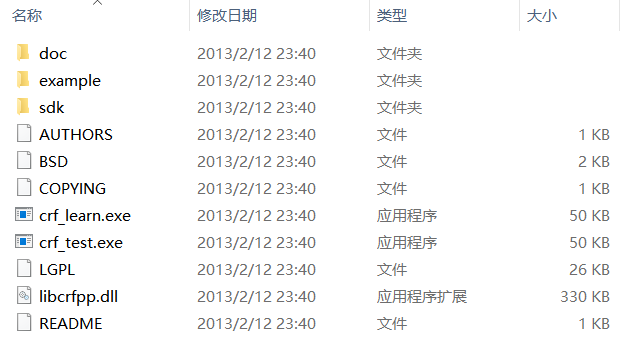
其中：（实际上，需要使用的就是crf_learn.exe，crf_test.exe和libcrfpp.dll，这三个文件。）

doc文件夹：就是官方主页的内容
example文件夹：有四个任务的训练数据（data）、测试数据(train.data)和模板文件(template),还有一个执行脚本文件exec.sh。
sdk文件夹：CRF++的头文件和静态链接库。
exe:CRF++的训练程序
exe:CRF++的测试程序
dll:训练程序和测试程序需要使用的静态链接库。

Linux下的安装

tar -zxvf CRF++-0.58.tar.gz
cd CRF++-0.58
./configure
make
sudo make install

默认安装的位置为：/usr/local/bin

安装Python包（此部分可省略）：

python setup.py build
python setup.py install

import CRFPP 直接向后报如下错误：

>>> import CRFPP
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/home/qw/anaconda3/lib/python3.7/site-packages/CRFPP.py", line 26, in <module>
    _CRFPP = swig_import_helper()
  File "/home/qw/anaconda3/lib/python3.7/site-packages/CRFPP.py", line 22, in swig_import_helper
    _mod = imp.load_module('_CRFPP', fp, pathname, description)
  File "/home/qw/anaconda3/lib/python3.7/imp.py", line 242, in load_module
    return load_dynamic(name, filename, file)
  File "/home/qw/anaconda3/lib/python3.7/imp.py", line 342, in load_dynamic
    return _load(spec)
ImportError: libcrfpp.so.0: cannot open shared object file: No such file or directory

解决方案：

sudo ln -s /usr/local/lib/libcrfpp.so.0 /usr/lib/

CRF++的使用

命令行使用

训练

./rf_learn template_file train_file model_file

这个训练过程的时间、迭代次数等信息会输出到控制台上（感觉上是crf_learn程序的输出信息到标准输出流上了），如果想保存这些信息，我们可以将这些标准输出流到文件上，命令格式如下：

./crf_learn template_file train_file model_file >> train_info_file

从上面可以看到，训练时需要传入的参数是template_file、train_file这两个文件，输出model_file文件。四个主要参数：

-a CRF-L2 or CRF-L1规范化算法选择。默认是CRF-L2。一般来说L2算法效果要比L1算法稍微好一点，虽然L1算法中非零特征的数值要比L2中大幅度的小。
-c float 这个参数设置CRF的hyper-parameter。c的数值越大，CRF拟合训练数据的程度越高。这个参数可以调整过度拟合和不拟合之间的平衡度。这个参数可以通过交叉验证等方法寻找较优的参数。
-f NUM 这个参数设置特征的cut-off threshold。CRF++使用训练数据中至少NUM次出现的特征。默认值为1。当使用CRF++到大规模数据时，只出现一次的特征可能会有几百万，这个选项就会在这样的情况下起到作用。
-p NUM 如果电脑有多个CPU，那么那么可以通过多线程提升训练速度。NUM是线程数量。

更详细介绍：

➜  bin ./crf_learn
CRF++: Yet Another CRF Tool Kit
Copyright (C) 2005-2013 Taku Kudo, All rights reserved.

Usage: ./crf_learn [options] files
 -f, --freq=INT              use features that occuer no less than INT(default 1)
 -m, --maxiter=INT           set INT for max iterations in LBFGS routine(default 10k) 设置INT为LBFGS的最大迭代次数 (默认10k)
 -c, --cost=FLOAT            set FLOAT for cost parameter(default 1.0) 设置FLOAT为代价参数，过大会过度拟合 (默认1.0)
 -e, --eta=FLOAT             set FLOAT for termination criterion(default 0.0001) 设置终止标准FLOAT(默认0.0001)
 -C, --convert               convert text model to binary model 将文本模式转为二进制模式
 -t, --textmodel             build also text model file for debugging 为调试建立文本模型文件
 -a, --algorithm=(CRF|MIRA)  select training algorithm (CRF|MIRA) 选择训练算法，默认为CRF-L2
 -p, --thread=INT            number of threads (default auto-detect)
 -H, --shrinking-size=INT    set INT for number of iterations variable needs to  be optimal before considered for shrinking. (default 20) 设置INT为最适宜的跌代变量次数 (默认20)
 -v, --version               show the version and exit 显示版本号并退出
 -h, --help                  show this help and exit 显示帮助并退出

测试

crf_test -m model_file test_files

同样，与crf_learn类似，输出的结果放到了标准输出流上，而这个输出结果是最重要的预测结果信息（预测文件的内容+预测标注），同样可以使用重定向，将结果保存下来，命令为：

crf_test -m model_file test_files >> result_file

在这里的参数有两个：-v 和-n,都是用来显示一些信息的。-v 可以用来预测标签概率值, -n可以显示不同可能序列的概率值。对于准确率、召回率、运行效率，没有影响。

训练语料格式

训练文件

样例：

训练文件由若干个句子组成（可以理解为若干个训练样例），不同句子之间通过换行符分隔，上图中显示出的有两个句子。每个句子可以有若干组标签，最后一组标签是标注，上图中有三列，即第一列和第二列都是已知的数据，第三列是要预测的标注，以上面例子为例是，根据第一列的词语和和第二列的词性，预测第三列的标注。涉及到标注的问题，这个就是很多paper要研究的了，比如命名实体识别就有很多不同的标注集。这个超出本文范围。

测试文件

测试文件与训练文件格式自然是一样的。与SVM不同，CRF++没有单独的结果文件，预测结果通过标准输出流输出了，因此将结果重定向到文件中。结果文件比测试文件多了一列，即为预测的标签，我们可以计算最后两列，一列的标注的标签，一列的预测的标签，来得到标签预测的准确率。

模板文件

1、模板基础

模板文件中的每一行是一个模板。每个模板都是由%x[row,col]来指定输入数据中的一个token。row指定到当前token的行偏移，col指定列位置。

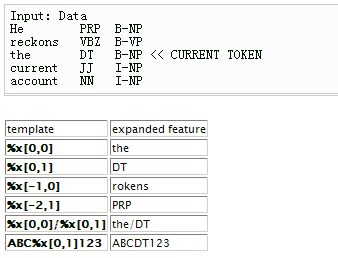
由上图可见，当前token是the这个单词。%x[-2,1]就就是the的前两行，1号列的元素（注意，列是从0号列开始的），即为PRP。

2、模板类型

有两种类型的模板，模板类型通过第一个字符指定。

Unigram template: first character, ‘U’

当给出一个”U01:%x[0,1]”的模板时，CRF++会产生如下的一些特征函数集合(func1 … funcN) 。

这几个函数我说明一下，%x[0,1]这个特征到前面的例子就是说，根据词语(第1列)的词性(第2列)来预测其标注(第3列)，这些函数就是反应了训练样例的情况，func1反映了“训练样例中，词性是DT且标注是B-NP的情况”，func2反映了“训练样例中，词性是DT且标注是I-NP的情况”。模板函数的数量是L*N，其中L是标注集中类别数量，N是从模板中扩展处理的字符串种类。

Bigram template: first character, ‘B’

这个模板用来描述二元特征。这个模板会自动产生当前output token和前一个output token的合并。注意，这种类型的模板会产生L * L * N种不同的特征。

Unigram feature 和 Bigram feature有什么区别呢？

unigram/bigram很容易混淆，因为通过unigram-features也可以写出类似%x[-1,0]%x[0,0]这样的单词级别的bigram(二元特征)。而这里的unigram和bigram features指定是uni/bigrams的输出标签。

unigram: |output tag| x |all possible strings expanded with a macro|
bigram: |output tag| x |output tag| x |all possible strings expanded with a macro|

这里的一元/二元指的就是输出标签的情况，这个具体的例子我还没看到，example文件夹中四个例子，也都是只用了Unigram，没有用Bigarm，因此感觉一般Unigram feature就够了。

3、模板例子

这是CoNLL 2000的Base-NP chunking任务的模板例子。只使用了一个bigram template (‘B’)。这意味着只有前一个output token和当前token被当作bigram features。“#”开始的行是注释，空行没有意义。

4、样例数据

example文件夹中有四个任务，basenp，chunking，JapaneseNE，seg。前两个是英文数据，后两个是日文数据。第一个应该是英文命名实体识别，第二个应该是英文分词，第三个应该是日文命名实体识别，第四个是日文分词。

CRF++实战：中文分词

使用人民日报的语料，为了方便切割，将其中的\t替换为了空格。对于语料有嵌套的标注，例如：[中央/n 电视台/n]nt，为了处理方便，只考虑最细粒度的分词结果，即当作是中央/n 电视台/n 两个词进行处理。

生成训练数据

通过下面python脚本，根据人民日报的语料库生成crf的测试和训练数据。原始数据中随机10%是测试数据，90%是训练数据。程序打印出来了不少调试信息，可以忽略。生成训练数据的时候，支持4tag和6tag两个格式，6tag的格式是：

S，单个词；B，词首；E，词尾；M1/M2/M，词中

4tag和6tag的区别就是没有词中顺序状态。具体代码：

data_dir = "./data/"


def split_word(words):
    li = list()
    for word in words:
        li.append(word)
    return li


# 4 tag
# S/B/E/M
def get4tag(li):
    length = len(li)
    if length == 1:
        return ['S']
    elif length == 2:
        return ['B', 'E']
    elif length > 2:
        li = list()
        li.append('B')
        for i in range(0, length - 2):
            li.append('M')
        li.append('E')
        return li


# 6 tag
# S/B/E/M/M1/M2
def get6tag(li):
    length = len(li)
    if length == 1:
        return ['S']
    elif length == 2:
        return ['B', 'E']
    elif length == 3:
        return ['B', 'M', 'E']
    elif length == 4:
        return ['B', 'M1', 'M', 'E']
    elif length == 5:
        return ['B', 'M1', 'M2', 'M', 'E']
    elif length > 5:
        li = list()
        li.append('B')
        li.append('M1')
        li.append('M2')
        for i in range(0, length - 4):
            li.append('M')
        li.append('E')
        return li


def save_data_file(train_obj, test_obj, is_test, word, handle, tag):
    if is_test:
        save_train_file(test_obj, word, handle, tag)
    else:
        save_train_file(train_obj, word, handle, tag)


def save_train_file(fiobj, word, handle, tag):
    if len(word) > 0:
        wordli = split_word(word)
        if tag == '4':
            tagli = get4tag(wordli)
        if tag == '6':
            tagli = get6tag(wordli)
        for i in range(0, len(wordli)):
            w = wordli[i]
            h = handle
            t = tagli[i]
            fiobj.write(w + '\t' + h + '\t' + t + '\n')
    else:
        # print 'New line'
        fiobj.write('\n')


# B,M,M1,M2,M3,E,S
def convert_tag(tag):
    tag = str(tag)
    fi_obj = open(data_dir + 'people-daily.txt', 'r', encoding='utf-8')
    train_obj = open(data_dir + tag + '.train.data', 'w', encoding='utf-8')
    test_obj = open(data_dir + tag + '.test.data', 'w', encoding='utf-8')

    arr = fi_obj.readlines()
    i = 0
    for a in arr:
        i += 1
        a = a.strip('\r\n\t ')
        if a == "":
            continue
        words = a.split(" ")
        test = False
        if i % 10 == 0:
            test = True
        for word in words:
            # print("---->", word)
            word = word.strip('\t ')
            if len(word) > 0:
                i1 = word.find('[')
                if i1 >= 0:
                    word = word[i1 + 1:]
                i2 = word.find(']')
                if i2 > 0:
                    w = word[:i2]
                word_hand = word.split('/')
                w, h = word_hand
                if ']' in h:
                    h = h.split("]")[0]
                if h == 'nr':  # ren min
                    # print 'NR',w
                    if w.find('·') >= 0:
                        tmpArr = w.split('·')
                        for tmp in tmpArr:
                            save_data_file(train_obj, test_obj, test, tmp, h, tag)
                    continue
                if h != 'm':
                    save_data_file(train_obj, test_obj, test, w, h, tag)

                if h == 'w':
                    save_data_file(train_obj, test_obj, test, "", "", tag)  # split

    train_obj.flush()
    test_obj.flush()


if __name__ == '__main__':
    # if len(sys.argv) < 2:
    #     print('tag[6,4] convert raw data to train.data and tag.test.data')
    # else:
    #     tag = sys.argv[1]
    #     convert_tag(tag)
    convert_tag(6)

使用模板

# Unigram  
U00:%x[-1,0]  
U01:%x[0,0]  
U02:%x[1,0]  
U03:%x[-1,0]/%x[0,0]  
U04:%x[0,0]/%x[1,0]  
U05:%x[-1,0]/%x[1,0]

训练和测试

./crf_learn -f 3 -c 4.0 template 6.train.data 6.model > 6.train.rst  
./crf_test -m 6.model 6.test.data > 6.test.rst

计算F值

if __name__ == "__main__":
    rst_file = './data/6.test.rst'
    with open(rst_file, "r") as f:
        lines = f.readlines()
        wc_of_test = 0
        wc_of_gold = 0
        wc_of_correct = 0
        flag = True

        for l in lines:
            if l == '\n': continue

            _, _, g, r = l.strip().split()

            if r != g:
                flag = False

            if r in ('E', 'S'):
                wc_of_test += 1
                if flag:
                    wc_of_correct += 1
                flag = True

            if g in ('E', 'S'):
                wc_of_gold += 1

        print("WordCount from test result:", wc_of_test)
        print("WordCount from golden data:", wc_of_gold)
        print("WordCount of correct segs :", wc_of_correct)

        # 查全率
        P = wc_of_correct / float(wc_of_test)
        # 查准率，召回率
        R = wc_of_correct / float(wc_of_gold)

        print("P = %f, R = %f, F-score = %f" % (P, R, (2 * P * R) / (P + R)))

输出结果：

WordCount from test result: 102966
WordCount from golden data: 102952
WordCount of correct segs : 97193
P = 0.943933, R = 0.944061, F-score = 0.943997

CRF++实战：地名实体识别

类似使用CRF实现分词和词性标注，地域识别也是需要生成相应的tag进行标注。这里使用的语料库是1998年1月人民日报语料集。最终学习出来的模型，对复杂的地名识别准确率（F值）非常低，推测是预料中对地名的标注多处是前后矛盾。例如 [华南/ns 地区/n]ns 标为地名实体，但是东北/f 地区/n 确分开标注，类似错误还有很多。

生成训练和测试数据

通过一个python脚本按照一定比例生成训练和测试数据，生成过程中按照BMES对语料进行标识，具体规则如下：

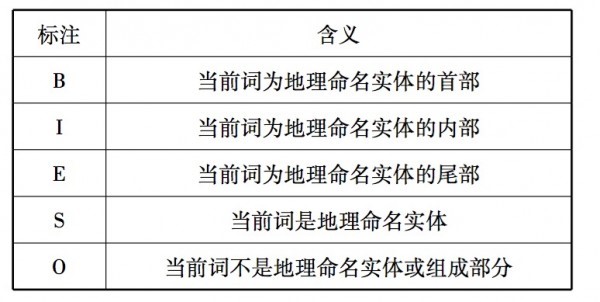
转换代码：

import sys

data_dir = "./data/"


def save_data_file(train_obj, test_obj, is_test, word, handle, tag):
    if is_test:
        save_train_file(test_obj, word, handle, tag)
    else:
        save_train_file(train_obj, word, handle, tag)


def save_train_file(fi_obj, word, handle, tag):
    if len(word) > 0 and word != "。" and word != "，":
        fi_obj.write(word + '\t' + handle + '\t' + tag + '\n')
    else:
        fi_obj.write('\n')


# 填充地点标注，非地点的不添加
def fill_local_tag(words, tags):
    pos = 0
    while True:
        if pos == len(words):
            break
        word = words[pos]
        left = word.find("[")
        if left == -1:
            w, h = word.split("/")
            if h == "ns":  # 单个词是地点
                tags[pos] = "LOC_S"
            pos += 1
        elif left >= 0:
            search_pos = pos
            for word in words[pos + 1:]:
                search_pos += 1
                if word.find("[") >= 0:
                    print("括号配对异常")
                    sys.exit(255)
                if word.find("]") >= 0:
                    break
            if words[search_pos].find("]") == -1:
                print("括号配对异常，搜索到句尾没有找都另一半括号")
                sys.exit(255)
            else:
                # 找到另一半，判断原始标注是不是ns，如果是就进行tag标注
                h = words[search_pos].split("]")[-1]  # 最后一个词性
                if h == "ns":
                    tags[pos] = "LOC_B"  # 添加首个词
                    for p in range(pos + 1, search_pos + 1):
                        tags[p] = "LOC_I"  # 中间词
                    tags[search_pos] = "LOC_E"  # 找到最后一个词
                else:
                    p = pos
                    for word in words[pos:search_pos + 1]:
                        w, h = word.strip("[").split("]")[0].split("/")
                        if h == "ns":
                            tags[p] = "LOC_S"
                        p += 1
            pos = search_pos + 1


def convert_tag():
    fi_obj = open(data_dir + 'people-daily.txt', 'r', encoding='utf-8')
    train_obj = open(data_dir + 'train.data', 'w', encoding='utf-8')
    test_obj = open(data_dir + 'test.data', 'w', encoding='utf-8')

    arr = fi_obj.readlines()
    i = 0
    for a in arr:
        i += 1
        a = a.strip('\r\n\t ')
        if a == "":
            continue
        words = a.split(" ")
        test = False
        if i % 5 == 0:
            test = True
        words = words[1:]
        if len(words) == 0:
            continue
        tags = ["O"] * len(words)
        fill_local_tag(words, tags)

        pos = -1
        for word in words:
            pos += 1
            word = word.strip('\t ')
            if len(word) == 0:
                print("Warning 发现空词")
                continue

            l1 = word.find('[')
            if l1 >= 0:
                word = word[l1 + 1:]

            l2 = word.find(']')
            if l2 >= 0:
                word = word[:l2]

            w, h = word.split('/')

            save_data_file(train_obj, test_obj, test, w, h, tags[pos])
        save_data_file(train_obj, test_obj, test, "", "", "")

    train_obj.flush()
    test_obj.flush()


if __name__ == '__main__':
    convert_tag()

模板文件

#Unigram
U01:%x[-1,0]
U02:%x[0,0]
U03:%x[1,0]
U04:%x[2,0]
U05:%x[-2,1]
U06:%x[-1,1]
U07:%x[0,1]
U08:%x[1,1]
U09:%x[2,1]
U0:%x[-2,0]
U10:%x[0,0]/%x[0,1]
U11:%x[-2,1]%x[-1,1]
U18:%x[0,0]/%x[-1,0]
U12:%x[0,0]%x[1,0]
U13:%x[0,1]%x[-1,0]
U14:%x[0,0]%x[1,1]
U15:%x[-1,0]%x[-1,1]
U16:%x[-1,0]%x[-2,0]
U17:%x[-2,0]%x[-2,1]
U18:%x[1,0]%x[2,0]
U19:%x[-1,0]%x[1,0]
U20:%x[1,0]%x[0,1]
U22:%x[-2,1]%x[0,1]
U23:%x[-1,1]%x[0,1]
U24:%x[-1,1]%x[1,1]
U25:%x[0,1]%x[1,1]
U26:%x[0,1]%x[2,1]
U27:%x[1,1]%x[2,1]

开始训练和测试

./crf_learn -f 4 -p 4 -c 3 template train.data model > train.rst 
./crf_test -m model test.data > test.rst

分类型计算F值

god_dic = {"LOC_S": 0, "LOC_B": 0, "LOC_I": 0, "LOC_E": 0}
pre_dic = {"LOC_S": 0, "LOC_B": 0, "LOC_I": 0, "LOC_E": 0}
correct_dic = {"LOC_S": 0, "LOC_B": 0, "LOC_I": 0, "LOC_E": 0}

if __name__ == "__main__":
    with open('./data/test.rst') as f:
        file = f.readlines()
        wc = 0
        loc_wc = 0
        wc_of_test = 0
        wc_of_gold = 0
        wc_of_correct = 0
        flag = True

        for l in file:
            wc += 1
            if l == '\n':
                continue
            _, _, g, r = l.strip().split()
            # 并不涉及到地点实体识别
            if "LOC" not in g and "LOC" not in r:
                continue
            loc_wc += 1
            if "LOC" in g:
                god_dic[g] += 1
            if "LOC" in r:
                pre_dic[r] += 1
            if g == r:
                correct_dic[r] += 1

        print("WordCount from result:", wc)
        print("WordCount of loc_wc  post :", loc_wc)
        print("真实位置标记个数：", god_dic)
        print("预估位置标记个数：", pre_dic)
        print("正确标记个数：", correct_dic)

        res = {"LOC_S": 0.0, "LOC_B": 0.0, "LOC_I": 0.0, "LOC_E": 0.0}

        all_gold = 0
        all_correct = 0
        all_pre = 0
        for k in god_dic:
            print("------ %s -------" % (k))
            R = correct_dic[k] / float(god_dic[k])
            P = correct_dic[k] / float(pre_dic[k])
            print("[%s] P = %f, R = %f, F-score = %f" % (k, P, R, (2 * P * R) / (P + R)))

            all_pre += pre_dic[k]
            all_correct += correct_dic[k]
            all_gold += god_dic[k]
        print("------ All -------")
        all_R = all_correct / float(all_gold)
        all_P = all_correct / float(all_pre)
        print("[%s] P = %f, R = %f, F-score = %f" % ("All", all_P, all_R, (2 * all_P * all_R) / (all_P + all_R)))

执行结果：

WordCount from result: 220612
WordCount of loc_wc  post : 5791
真实位置标记个数： {'LOC_S': 5262, 'LOC_B': 197, 'LOC_I': 95, 'LOC_E': 197}
预估位置标记个数： {'LOC_S': 5304, 'LOC_B': 136, 'LOC_I': 57, 'LOC_E': 149}
正确标记个数： {'LOC_S': 5233, 'LOC_B': 106, 'LOC_I': 42, 'LOC_E': 124}
------ LOC_S -------
[LOC_S] P = 0.986614, R = 0.994489, F-score = 0.990536
------ LOC_B -------
[LOC_B] P = 0.779412, R = 0.538071, F-score = 0.636637
------ LOC_I -------
[LOC_I] P = 0.736842, R = 0.442105, F-score = 0.552632
------ LOC_E -------
[LOC_E] P = 0.832215, R = 0.629442, F-score = 0.716763
------ All -------
[All] P = 0.975027, R = 0.957225, F-score = 0.966044

参考链接：CRF++地名实体识别（特征为词性和词）

CRF++实战：词性标注

训练和测试的语料都是人民日报98年标注语料，训练和测试比例是10：1，直接通过CRF++标注词性的准确率:0.933882。由于训练时间较慢，此部分未进行正式测试。

生成训练和测试数据

data_dir = "./data/"


def save_data_file(train_obj, test_obj, is_test, word, handle):
    if is_test:
        save_train_file(test_obj, word, handle)
    else:
        save_train_file(train_obj, word, handle)


def save_train_file(fi_obj, word, handle):
    if len(word) > 0 and word != "。" and word != "，":
        fi_obj.write(word + '\t' + handle + '\n')
    else:
        fi_obj.write('\n')


def convert_tag():
    fi_obj = open(data_dir + 'people-daily.txt', 'r')
    train_obj = open(data_dir + 'train.data', 'w')
    test_obj = open(data_dir + 'test.data', 'w')

    arr = fi_obj.readlines()
    i = 0
    for a in arr:
        i += 1
        a = a.strip('\r\n\t ')
        if a == "":
            continue
        words = a.split(" ")
        test = False
        if i % 10 == 0:
            test = True
        for word in words[1:]:
            word = word.strip('\t ')
            if len(word) > 0:
                i1 = word.find('[')
            if i1 >= 0:
                word = word[i1 + 1:]
            i2 = word.find(']')
            if i2 > 0:
                w = word[:i2]
            word_hand = word.split('/')
            w, h = word_hand
            if ']' in h:
                h = h.split("]")[0]
            if h == 'nr':  # ren min
                if w.find('·') >= 0:
                    tmp_arr = w.split('·')
                    for tmp in tmp_arr:
                        save_data_file(train_obj, test_obj, test, tmp, h)
                    continue
            save_data_file(train_obj, test_obj, test, w, h)
        save_data_file(train_obj, test_obj, test, "", "")

    train_obj.flush()
    test_obj.flush()


if __name__ == '__main__':
    convert_tag()

模板文件

# Unigram
U00:%x[-2,0]
U01:%x[-1,0]
U02:%x[0,0]
U03:%x[1,0]
U04:%x[2,0]
U05:%x[-1,0]/%x[0,0]
U06:%x[0,0]/%x[1,0]

执行训练

./crf_learn -f 3 -p 4 -c 4.0 template train.data model > train.rst  
./crf_test -m model test.data > test.rst

计算准确率

if __name__ == "__main__":
    with open("./data/test.rst", "r") as f:
        file = f.readlines()

        wc = 0
        wc_of_test = 0
        wc_of_gold = 0
        wc_of_correct = 0
        flag = True

        for l in file:
            if l == '\n':
                continue

            _, g, r = l.strip().split()

            if r != g:
                flag = False
            wc += 1

            if flag:
                wc_of_correct += 1
            flag = True

        print("WordCount from result:", wc)
        print("WordCount of correct post :", wc_of_correct)

        # 准确率
        P = wc_of_correct / float(wc)

        print("准确率:%f" % (P))

参考链接：CRF++词性标注

CRF++实战：依存句法分析

语料是清华大学的句法标注语料，包括训练集（train.conll）和开发集合文件（dev.conll），根据模板文件生成了将近两千万个特征，由于训练较慢，以下内容未做测试。

生成训练和开发语料

依存关系本身是一个树结构，每一个词看成一个节点，依存关系就是一条有向边。语料本身格式：

1	坚决	坚决	a	ad	_	2	方式	
2	惩治	惩治	v	v	_	0	核心成分	
3	贪污	贪污	v	v	_	7	限定	
4	贿赂	贿赂	n	n	_	3	连接依存	
5	等	等	u	udeng	_	3	连接依存	
6	经济	经济	n	n	_	7	限定	
7	犯罪	犯罪	v	vn	_	2	受事	
 
1	最高	最高	n	nt	_	3	限定	
2	人民	人民	n	nt	_	3	限定	
3	检察院	检察院	n	nt	_	4	限定	
4	检察长	检察长	n	n	_	0	核心成分	
5	张思卿	张思卿	n	nr	_	4	同位语

数据格式说明：

1、本次中文语义依存分析将在两个语料库上进行评测，其中THU文件夹内为清华大学语义依存网络语料，HIT文件夹内为哈尔滨工业大学依存语料库。
   每个语料库都包含三个文件，分别为train.conll，dev.conll和test.conll。
   train.conll为训练语料，用于模型训练；
   dev.conll为开发集，用于模型参数调优；
   test.conll用于测试，根据会议日程，暂不发布。
 
2、参赛者可以在两个语料的训练语料上上分别训练模型，也可以结合两个语料库的训练语料训练统一的模型。
 
3、所有数据文件均采用CONLL格式，UTF8编码。CONLL标注格式包含10列，分别为：
   ---------------------------------------------------------------------------------
   ID	FORM	LEMMA	CPOSTAG	POSTAG	FEATS	HEAD	DEPREL	PHEAD	PDEPREL	
---------------------------------------------------------------------------------
 
 
   本次评测只用到前８列，其含义分别为：
 
   1	ID	当前词在句子中的序号，１开始.
   2	FORM	当前词语或标点  
   3	LEMMA	当前词语（或标点）的原型或词干，在中文中，此列与FORM相同
   4	CPOSTAG	当前词语的词性（粗粒度）
   5	POSTAG	当前词语的词性（细粒度）
   6	FEATS	句法特征，在本次评测中，此列未被使用，全部以下划线代替。
   7	HEAD	当前词语的中心词
   8	DEPREL	当前词语与中心词的依存关系
 
   在CONLL格式中，每个词语占一行，无值列用下划线'_'代替，列的分隔符为制表符'\t'，行的分隔符为换行符'\n'；句子与句子之间用空行分隔。

通过python脚本生成所需要的训练数据和测试使用的开发数据：

# coding=utf-8
'''
词A依赖词B，A就是孩子，B就是父亲
'''

import sys

sentence = ["Root"]


def do_parse(sentence):
    if len(sentence) == 1: return
    for line in sentence[1:]:
        line_arr = line.strip().split("\t")
        # print line_arr
        c_id = int(line_arr[0])
        f_id = int(line_arr[6])
        # print c_id, f_id
        if f_id == 0:
            print("\t".join(line_arr[2:5]) + "\t" + "0_Root")
            continue
        # print sentence[f_id].strip().split("\t")[3:5]
        f_post, f_detail_post = sentence[f_id].strip().split("\t")[3:5]  # 得到父亲节点的粗词性和详细词性
        c_edge_post = f_post  # 默认是依赖词的粗粒度词性，但是名词除外；名词取细粒度词性
        if f_post == "n":
            c_edge_post = f_detail_post
        # 计算是第几个出现这种词行
        diff = f_id - c_id  # 确定要走几步
        step = 1 if f_id > c_id else -1  # 确定每一步方向
        same_post_num = 0  # 中间每一步统计多少个一样的词性
        cmp_idx = 4 if f_post == "n" else 3  # 根据是否是名词决定取的是粗or详细词性
        for i in range(0, abs(diff)):
            idx = c_id + (i + 1) * step
            if sentence[idx].strip().split("\t")[cmp_idx] == c_edge_post:
                same_post_num += step

        print("\t".join(line_arr[2:5]) + "\t" + "%d_%s" % (same_post_num, c_edge_post))
    print("")


for line in sys.stdin:
    line = line.strip()
    line_arr = line.split("\t")

    if line == "" or line_arr[0] == "1":
        # print sentence
        do_parse(sentence)
        sentence = ["Root"]

    if line == "":
        continue
sentence.append(line)

模板文件

# Unigram
U01:%x[0,0]
U02:%x[0,0]/%x[0,2]
U03:%x[-1,2]/%x[0,0]
U04:%x[-1,2]/%x[0,2]/%x[0,0]
U05:%x[0,0]/%x[1,2]
U06:%x[0,0]/%x[0,2]/%x[1,2]
U07:%x[-1,2]/%x[0,2]
U08:%x[-1,1]/%x[0,2]
U09:%x[0,2]/%x[1,2]
U10:%x[0,2]/%x[1,1]
U11:%x[-2,2]/%x[-1,2]/%x[0,2]/%x[1,2]
U12:%x[-1,2]/%x[0,2]/%x[1,2]/%x[2,2]
U13:%x[-2,2]/%x[-1,2]/%x[0,2]/%x[1,2]/%x[2,2]
U14:%x[-2,1]/%x[-1,2]/%x[0,2]
U15:%x[-1,2]/%x[0,2]/%x[1,2]
U16:%x[-1,1]/%x[0,2]/%x[1,1]
U17:%x[-1,2]/%x[1,2]

进行训练和测试过程

./crf_learn -f 3 -p 40 -c 4.0 template train.data model > train.rst  
./crf_test -m model dev.data > dev.rst

参考链接：CRF++依存句法分析

CRFPP在Windows环境下的安装

前面介绍CRF++的文章中，只介绍到了CRFPP在Linux环境下的安装。在测试DeepNLP这个工具的时候由于其依赖CRF++，需要安装CRF++，中间还是遇到蛮多问题的。记录下来供参考。

从网络上整理出来的安装流程：

下载Windows版CRF++(注意是.zip后缀的文件)
下载Linux版CRF++（文件名后缀为.tar.gz）
从Linux版本中复制出Python目录，并从Windows版CRF++中复制h和libcrfpp.lib文件到Python目录，并将libcrfpp.lib修改为crfpp.lib
从如下网址https://wnsgml972.github.io/c/c_windows_pthread.html 下载pthread文件，解压后在Pre-built.2\lib文件夹下找到对应系统的lib文件，同样复制到Python文件夹下，并将其改名为pthread.lib

然后在命令行窗口

python setup.py build
python setup.py install

将Windows版CRF++种的libcrfpp.dll复制到\Lib\site-packages文件夹下。

以上流程在执行第5部的时候发生了报错，报错信息如下：

(venv) PS D:\CodeHub\python> python .\setup.py build
running build
running build_py
running build_ext
building '_CRFPP' extension
D:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\BIN\x86_amd64\cl.exe /c /nologo /Ox /W3 /GL /DNDEBUG /MD -ID:\CodeHub\NLP\venv\include "-ID:\Program Files\Python37\include" "-ID:\Program Files\Python37\include" "-ID:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\INCLUDE" "-ID:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\ATLMFC\INCLUDE" "-IC:\Program Files (x86)\Windows Kits\include.0.10150.0\ucrt" "-IC:\Program Files (x86)\Windows Kits\NETFXSDK.6\include\um" "-IC:\Program Files (x86)\Windows Kits.1\include\shared" "-IC:\Program Files (x86)\Windows Kits.1\include\um" "-IC:\Program Files (x86)\Windows Kits.1\include\winrt" /EHsc /TpCRFPP_wrap.cxx /Fobuild\temp.win-amd64-3.7\Release\CRFPP_wrap.obj
CRFPP_wrap.cxx
D:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\BIN\x86_amd64\link.exe /nologo /INCREMENTAL:NO /LTCG /DLL /MANIFEST:EMBED,ID=2 /MANIFESTUAC:NO /LIBPATH:D:\CodeHub\NLP\venv\libs "/LIBPATH:D:\Program Files\Python37\libs" "/LIBPATH:D:\Program Files\Python37" /LIBPATH:D:\CodeHub\NLP\venv\PCbuild\amd64 "/LIBPATH:D:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\LIB\amd64" "/LIBPATH:D:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\ATLMFC\LIB\amd64" "/LIBPATH:C:\Program Files (x86)\Windows Kits\lib.0.10150.0\ucrt\x64" "/LIBPATH:C:\Program Files (x86)\Windows Kits\NETFXSDK.6\lib\um\x64" "/LIBPATH:C:\Program Files (x86)\Windows Kits.1\lib\winv6.3\um\x64" crfpp.lib pthread.lib /EXPORT:PyInit__CRFPP build\temp.win-amd64-3.7\Release\CRFPP_wrap.obj /OUT:build\lib.win-amd64-3.7\_CRFPP.cp37-win_amd64.pyd /IMPLIB:build\temp.win-amd64-3.7\Release\_CRFPP.cp37-win_amd64.lib
CRFPP_wrap.obj : warning LNK4197: 多次指定导出“PyInit__CRFPP”；使用第一个规范
  正在创建库 build\temp.win-amd64-3.7\Release\_CRFPP.cp37-win_amd64.lib 和对象 build\temp.win-amd64-3.7\Release\_CRFPP.cp37-win_amd64.exp
CRFPP_wrap.obj : error LNK2001: 无法解析的外部符号 "__declspec(dllimport) class CRFPP::Tagger * __cdecl CRFPP::createTagger(char const *)" (__imp_?createTagger@CRFPP@@YAPEAVTagger@1@PEBD@Z)
CRFPP_wrap.obj : error LNK2001: 无法解析的外部符号 "__declspec(dllimport) class CRFPP::Model * __cdecl CRFPP::createModel(char const *)" (__imp_?createModel@CRFPP@@YAPEAVModel@1@PEBD@Z)
CRFPP_wrap.obj : error LNK2001: 无法解析的外部符号 "__declspec(dllimport) char const * __cdecl CRFPP::getLastError(void)" (__imp_?getLastError@CRFPP@@YAPEBDXZ)
build\lib.win-amd64-3.7\_CRFPP.cp37-win_amd64.pyd : fatal error LNK1120: 3 个无法解析的外部命令
error: command 'D:\\Program Files (x86)\\Microsoft Visual Studio 14.0\\VC\\BIN\\x86_amd64\\link.exe' failed with exit status 1120

在此报错上我卡了很久，包括看源代码等都没有找到问题。于是下了一个别人整理好的文件，然后一下子就安装成功了。安装成功后回溯寻找报错原因，发现我自己从网上下载的Windows版CRF++种的crfpp.lib、libcrfpp.dll文件与别人打包好的文件存在差异。官方提供的是32位的版本，而我系统安装的Python版本为64位。最后附上打包好的安装文件，链接: https://pan.baidu.com/s/1IAhIG8Je0zeNvDTL3mBOQQ 提取码: 1ysa

安装完毕后在deepnlp中能正常调用，但是测试代码时报错。测试代码：

import CRFPP

try:
    # -v 3: access deep information like alpha,beta,prob
    # -nN: enable nbest output. N should be >= 2
    tagger = CRFPP.Tagger("-m ../model -v 3 -n2")

    # clear internal context
    tagger.clear()

    # add context
    tagger.add("Confidence NN")
    tagger.add("in IN")
    tagger.add("the DT")
    tagger.add("pound NN")
    tagger.add("is VBZ")
    tagger.add("widely RB")
    tagger.add("expected VBN")
    tagger.add("to TO")
    tagger.add("take VB")
    tagger.add("another DT")
    tagger.add("sharp JJ")
    tagger.add("dive NN")
    tagger.add("if IN")
    tagger.add("trade NN")
    tagger.add("figures NNS")
    tagger.add("for IN")
    tagger.add("September NNP")

    print("column size: ", tagger.xsize())
    print("token size: ", tagger.size())
    print("tag size: ", tagger.ysize())

    print("tagset information:")
    ysize = tagger.ysize()
    for i in range(0, ysize - 1):
        print("tag ", i, " ", tagger.yname(i))

    # parse and change internal stated as 'parsed'
    tagger.parse()

    print("conditional prob=", tagger.prob(), " log(Z)=", tagger.Z())

    size = tagger.size()
    xsize = tagger.xsize()
    for i in range(0, (size - 1)):
        for j in range(0, (xsize - 1)):
            print(tagger.x(i, j), "\t")
        print(tagger.y2(i), "\t")
        print("Details")
        for j in range(0, (ysize - 1)):
            print("\t", tagger.yname(j), "/prob=", tagger.prob(i, j), "/alpha=", tagger.alpha(i, j), "/beta=",
                  tagger.beta(i, j))
        print("\n")

    print("nbest outputs:")
    for n in range(0, 9):
        if (not tagger.next()):
            continue
        print("nbest n=", n, "\tconditional prob=", tagger.prob())
        # you can access any information using tagger.y()...

    print("Done")

except RuntimeError as e:
    print("RuntimeError: ", e)

报错内容：

RuntimeError:&nbsp; ..\..\CRF++-0.58\feature_index.cpp(193) [mmap_.open(model_filename)] e:\ai\crf++-0.58\mmap.h(110) [hFile != INVALID_HANDLE_VALUE] CreateFile() failed: ../model

解决方案：

将以下测试代码种的模型路径由相对路径改为绝对路径：

# tagger = CRFPP.Tagger("-m ../model -v 3 -n2")
tagger = CRFPP.Tagger("-m D:\\CodeHub\\NLP\\data\\model -v 3 -n2")

其中model文件可以在Linux环境下由CRF++-0.58\example\basenp\exec.sh 训练获得。需要注意要将exec.sh文件中删除 rm -f model

其他参考：

条件随机场CRF及CRF++安装与使用

概率图模型

贝叶斯网络

条件独立性

网络的学习

马尔可夫随机场

马尔科夫性

极大团

势函数

图像降噪应用

条件随机场 CRF

链式条件随机场

CRF 的简化形式

CRF应用

中文分词

命名实体识别

词性标注

CRF的概括总结

CRF发展方向

CRF++的安装

CRF++的使用

命令行使用

训练语料格式

CRF++实战：中文分词

生成训练数据

使用模板

训练和测试

计算F值

CRF++实战：地名实体识别

生成训练和测试数据

模板文件

开始训练和测试

分类型计算F值

CRF++实战：词性标注

生成训练和测试数据

模板文件

执行训练

计算准确率

CRF++实战：依存句法分析

生成训练和开发语料

模板文件

进行训练和测试过程

CRFPP在Windows环境下的安装

相关文章:

Windows Node.js+Yarn的安装与配置

开源文档生成工具Sphinx

Flask学习之Werkzeug

发表回复 取消回复

发表回复取消回复