逻辑回归算法的名字里虽然带有“回归”二字，但实际上逻辑回归算法是用来解决分类问题的。简单来说，逻辑回归（Logistic Regression）是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。注意，这里用的是“可能性”，而非数学上的“概率”，logisitc回归的结果并非数学定义中的概率值，不可以直接当做概率值来用（逻辑回归是基于分布假设建立的，假设在现实案例中并不是那么容易满足，所以，很多情况下，我们得出的逻辑回归输出值，无法当作真实的概率，只能作为置信度来使用）。该结果往往用于和其他特征值加权求和，而非直接相乘。
逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。逻辑回归假设因变量y服从伯努利分布，而线性回归假设因变量y服从高斯分布。因此与线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。
逻辑回归的优缺点
优点：
- 速度快，适合二分类问题
- 简单易于理解，直接看到各个特征的权重
- 能容易地更新模型吸收新的数据
缺点：
- 对数据和场景的适应能力有局限性，不如决策树算法适应性那么强
逻辑回归算法原理
假设函数（Hypothesis function）
首先我们要先介绍一下Sigmoid函数，也称为逻辑函数（Logistic function）：
$$g(z)=\frac{1}{1+e^{-z}}$$
其函数曲线如下：
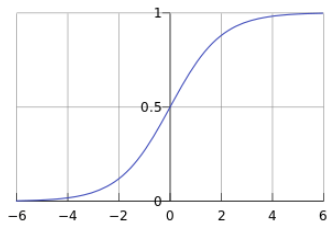
从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0,1]之间，在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要。
逻辑回归的假设函数形式如下：
$$h_\theta(x)=g(\theta^Tx), g(z)=\frac{1}{1+e^{-z}}$$
所以：
$$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$$
其中x是我们的输入，$\theta$为我们要求取的参数。一个机器学习的模型，实际上是把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是：
$$P(y=1|x;\theta)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$$
这个函数的意思就是在给定x和$\theta$的条件下y=1的概率。这里g(h)就是我们上面提到的sigmoid函数，与之相对应的决策函数为：
$$y^*=1, if P(y=1|x)>0.5$$
选择0.5作为阈值是一个一般的做法，实际应用时特定的情况可以选择不同阈值，如果对正例的判别准确性要求高，可以选择阈值大一些，对正例的召回要求高，则可以选择阈值小一些。
决策边界（Decision Boundary）
决策边界，也称为决策面，是用于在N维空间，将不同类别样本分开的平面或曲面。注意：决策边界是假设函数的属性，由参数决定，而不是由数据集的特征决定。这里我们引用Andrew Ng课程上的两张图来解释这个问题：
线性决策边界
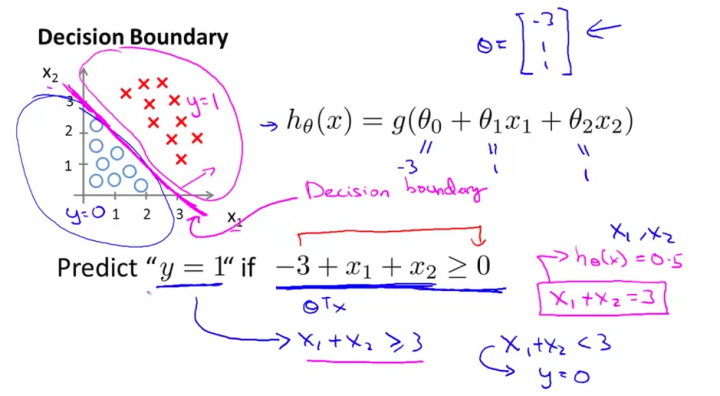
这里决策边界为:$-3+x_1+x_2=0$
非线性决策边界
这里决策边界为:$-1+x_1^2+x_2^2=0$
上面两张图很清晰的解释了什么是决策边界，决策边界其实就是一个方程，在逻辑回归中，决策边界由$\theta^Tx=0$定义：
$$P(y=1|x;\theta)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$$
这里我们要注意理解一下假设函数和决策边界函数的区别与联系。决策边界是假设函数的属性，由假设函数的参数（$\theta$）决定。
在逻辑回归中，假设函数$h=g(z)$用于计算样本属于某类别的可能性；决策函数$y^*=1, if P(y=1|x)>0.5$用于计算（给出）样本的类别；决策边界$\theta^Tx=0$是一个方程，用于标识出分类函数（模型）的分类边界。
损失函数（Cost Function）
逻辑回归的假设为：$h_\theta(x)=1/(1+e^{-\theta^Tx})$，我们的任务是找到一个“合适”的$\theta$来使这个假设尽可能地解决我们的问题。例如分类任务，我们希望决策边界能最大程度将数据区分开。那么数学上怎么表达这种需求呢？在线性回归中，一般采用均方误差用来评价一个$\theta$的好坏：
$$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}{\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2}$$
即$J(\theta)$越小，认为$\theta$越好。那为什么不直接把逻辑回归的$h_\theta(x)$代入均方误差呢？原因是这样产生的$J(\theta)$是非凸函数(non-convex)。我们举个例子：
samples = [(-5,1), (-20,0), (-2,1)]
def sigmoid(theta, x):
return 1/(1+math.e**(-theta*x))
def cost(theta):
diffs = [(sigmoid(theta,x)-y) for x,y in samples]
return sum(diff*diff for diff in diffs)/len(samples)/2
X = np.arange(-1,1,0.01)
Y = np.array([cost(theta) for theta in X])
plt.plot(X,Y)
plt.show()
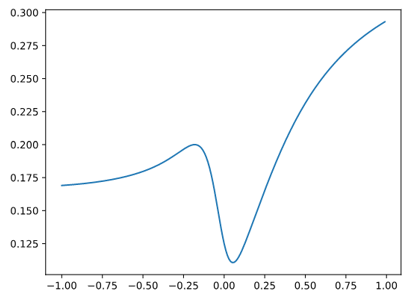可以看出这个损失函数是非凸的，局部最小值不等于全局最小值，因此使用梯度下降法难以求解。因此逻辑回归模型使用如下的损失函数，
$$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}{Cost(h_\theta(x^{(i)}),y)}$$
$$Cost(h_\theta(x),y)=\begin{cases}-\log(h_\theta(x)),&\text{if}\ y=1\\-\log(1-h_\theta(x)),&\text{if}\ y=0\end{cases}$$
写成统一的形式：
$$J(\theta)=-\frac{1}{m}\Big[\sum_{i=1}^{m}{y^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))}\Big]$$
那么损失函数是如何影响决策的呢？首先，损失函数是对hθ(x)给出错误结论的惩罚。因此损失越小，一般就认为hθ(x)的结论就越正确。而上面这个式子意味着，损失越小，最后得到的hθ(x)曲面会越”贴近”数据点，换言之会”越陡”：
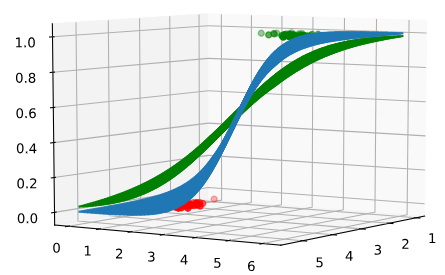
这幅图中，$J(\theta_{blue})
和线性回归类似，我们使用梯度下降算法来求解逻辑回归模型参数。关于梯度下降的详细信息见线性回归文章中的相关内容。
正则化（Regularization）
当模型的参数过多时，很容易遇到过拟合的问题。这时就需要有一种方法来控制模型的复杂度，典型的做法在优化目标中加入正则项，通过惩罚过大的参数来防止过拟合。
$$J(\theta)=-\frac{1}{N}\sum{y\log{g(\theta^Tx)}+(1-y)\log{(1-g(\theta^Tx))}}+\lambda\Vert w\Vert_p$$
一般情况下，取p=1或p=2，分别对应L1，L2正则化，两者的区别可以从下图中看出来，L1正则化（左图）倾向于使参数变为0，因此能产生稀疏解。
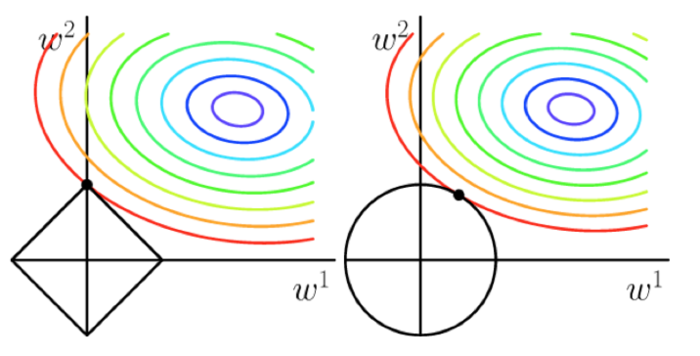
关于正则化的详细内容见岭回归、Lasso回归文章中的详细内容。
使用Scikit-Learn进行逻辑回归
在scikit-learn里，逻辑回归模型由类sklearn.linear_model.LogisticRegression实现。
正则项权重
正则项权重$\lambda$，在LogisticRegression里有个参数C与此对应，但成反比。即C值越大，正则项的权重越小，模型容易出现过拟合；C值越小，正则项权重越大，模型容易出现欠拟合。
L1/L2范数
创建逻辑回归模型时，有个参数penalty，其取值有’l1’或’l2’，这个实际上就是指定我们前面介绍的正则项的形式。
最简单的使用方法：
from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression nb_samples = 500 X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1) X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25) lr = LogisticRegression() lr.fit(X_train, Y_train) train_score = lr.score(X_train, Y_train) #模型对训练样本得准确性 test_score = lr.score(X_test, Y_test) #模型对测试集的准确性 print(train_score) print(test_score)
对于参数优化，可以选择LogisticRegressionCV或GridSearchCV
GridSearchCV：
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
import numpy as np
iris = load_iris()
param_grid = {
'penalty': ["l1", "l2"],
'C': np.power(10.0, np.arange(-10, 10))
}
gs = GridSearchCV(estimator=LogisticRegression(), param_grid=param_grid, scoring='accuracy', cv=10)
gs.fit(iris.data, iris.target)
print(gs.best_estimator_)
LogisticRegressionCV：
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegressionCV
from sklearn.model_selection import KFold
import numpy as np
iris = load_iris()
fold = KFold(n_splits=5, shuffle=True, random_state=777)
searchCV = LogisticRegressionCV(
Cs=list(np.power(10.0, np.arange(-10, 10)))
, penalty='l2'
, scoring='roc_auc'
, cv=fold
, random_state=777
, max_iter=10000
, fit_intercept=True
, solver='newton-cg'
, tol=10
)
searchCV.fit(iris.data, iris.target)
print('Max auc_roc:', searchCV.scores_[1].mean(axis=0).max())
参考链接：
