在处理较为复杂的数据的回归问题时,普通的线性回归算法通常会出现预测精度不够,如果模型中的特征之间有相关关系,就会增加模型的复杂程度。当数据集中的特征之间有较强的线性相关性时,即特征之间出现严重的多重共线性时,用普通最小二乘法估计模型参数,往往参数估计的方差太大,此时,求解出来的模型就很不稳定。在具体取值上与真值有较大的偏差,有时会出现与实际意义不符的正负号。
在线性回归中如果参数$\theta$过大、特征过多就会很容易造成过拟合,如下如所示:
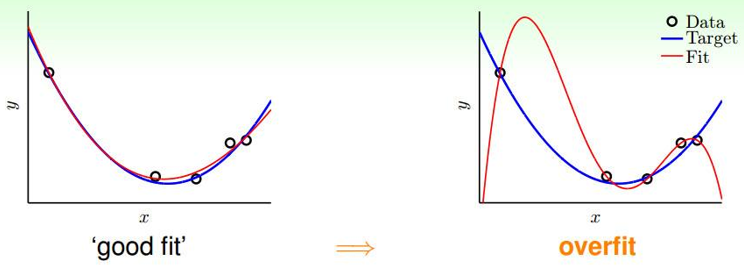
正则化
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解$\theta$的过程中出现的$(X^TX)$不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的。
在日常机器学习任务中,如果数据集的特征比样本点还多,$(X^TX)^{-1}$的时候会出错。岭回归最先用来处理特征数多于样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里通过引入$\lambda$限制了所有$\theta^2$之和,通过引入该惩罚项,能够减少不重要的参数,这个技术在统计学上也叫作缩减(shrinkage)。和岭回归类似,另一个缩减LASSO也加入了正则项对回归系数做了限定。
为了防止过拟合($\theta$过大),在目标函数$J(\theta)$后添加复杂度惩罚因子,即正则项来防止过拟合。正则项可以使用L1-norm(Lasso)、L2-norm(Ridge),或结合L1-norm、L2-norm(ElasticNet)。
Lasso:使用L1-norm正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda\sum_{j}^{n}|\theta_j|$$
Ridge:使用L2-norm正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda\sum_{j}^{n}\theta_j^2$$
ElasticNet:结合l1-norm、l2-norm进行正则
$$J(\theta)=\frac{1}{2}\sum_{i}^{m}(y^{(i)}-\theta^Tx^{(i)})^2+\lambda(\rho\sum_{j}^{n}|\theta_j|+(1-\rho)\sum_{j}^{n}\theta_j^2)$$
简单的理解正则化:
- 正则化的目的:防止过拟合
- 正则化的本质:约束(限制)要优化的参数
关于第1点,过拟合指的是给定一堆数据,这堆数据带有噪声,利用模型去拟合这堆数据,可能会把噪声数据也给拟合了,这点很致命,一方面会造成模型比较复杂,另一方面,模型的泛化性能太差了,遇到了新的数据让你测试,你所得到的过拟合的模型,正确率是很差的。
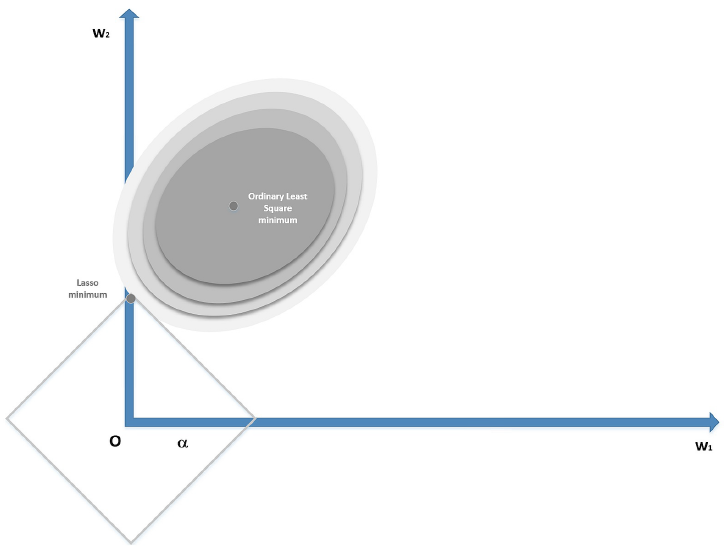
关于第2点,本来解空间是全部区域,但通过正则化添加了一些约束,使得解空间变小了,甚至在个别正则化方式下,解变得稀疏了。这一点不得不提到一个图,相信我们都经常看到这个图,但貌似还没有一个特别清晰的解释,这里我尝试解释一下,图如下:
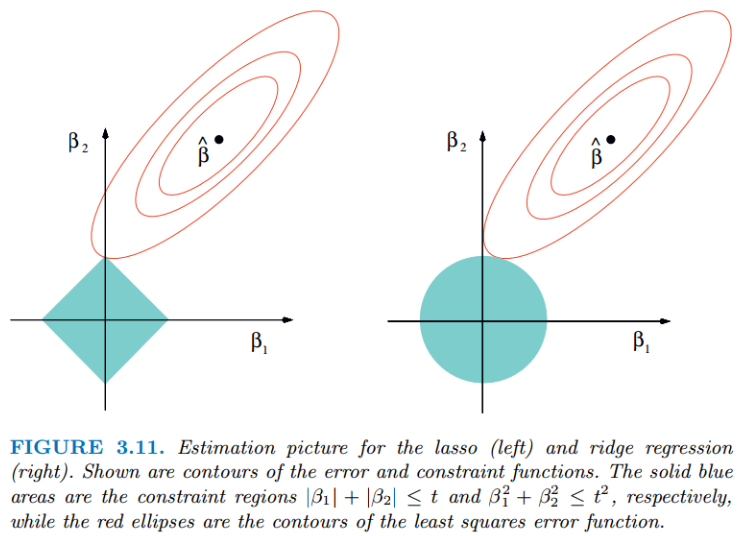
上图中左边为Lasso回归,右边为岭回归。红色的椭圆和蓝色的区域的切点就是目标函数的最优解,我们可以看到,如果是圆,则很容易切到圆周的任意一点,但是很难切到坐标轴上,因此没有稀疏;但是如果是菱形或者多边形,则很容易切到坐标轴上,因此很容易产生稀疏的结果。这也说明了为什么L1范式会是稀疏的。这样就解释了为什么lasso可以进行特征选择。岭回归虽然不能进行特征筛选,但是对$\theta$的模做约束,使得它的数值会比较小,很大程度上减轻了overfitting的问题。
这里的$\beta_1$,$\beta_2$都是模型的参数,要优化的目标参数,蓝色部分区域,其实就是解空间,正如上面所说,这个时候,解空间”缩小了”,你只能在这个缩小了的空间中,寻找使得目标函数最小的$\beta_1$,$\beta_2$。再看看那红色的圆圈,再次提醒大家,这个坐标轴和特征(数据)没关系,它完全是参数的坐标系,每一个圆圈上,可以取无数个$\beta_1$,$\beta_2$,这些$\beta_1$,$\beta_2$有个共同的特点,用它们计算的目标函数值是相等的。那个红色的圆心,就是实际最优参数,但是由于我们对解空间做了限制,所以最优解只能在”缩小的”解空间中产生。
以两个变量为例,解释岭回归的几何意义:
1、没有约束项时。模型参数$\beta_1$,$\beta_2$已经经过标准化。残差平方和RSS可以表示为$\beta_1$,$\beta_2$的一个二次函数,数学上可以用一个抛物面表示。
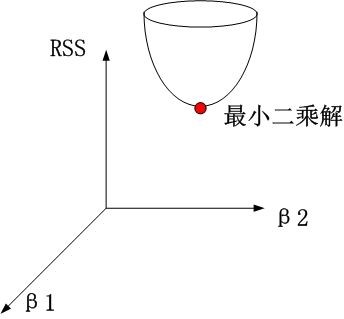
2、岭回归时。约束项为$\beta_1^2+\beta_2^2\leq t$,对应着投影为$\beta_1$,$\beta_2$平面上的一个圆,即下图中的圆柱。
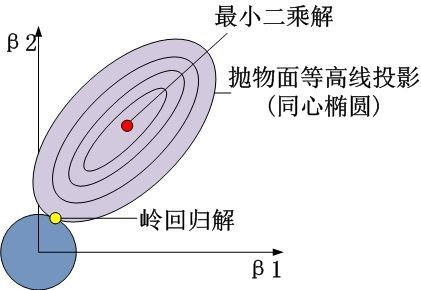
可见岭回归解与原先的最小二乘解是有一定距离的。
使用Scikit-Learn进行岭回归、Lasso回归和ElasticNet回归
岭回归
岭(Ridge)回归再普通最小二乘法的损失函数中增加了额外的缩减惩罚项,以限制L2范数的平方项。
$$L(\bar{w})=\left\|X\bar{w}-\bar{y}\right\|_2^2+\alpha\left\|\bar{w}\right\|_2^2$$
在这种情况下,X是将所有样本作为列向量的矩阵,w表示权重向量。系数$\alpha$表示正则化的强弱正则化。
from sklearn.linear_model import Ridge from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split boston = load_boston() X = boston.data y = boston.target #把数据分为训练数据集和测试数据集(20%数据作为测试数据集) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3) model = Ridge(alpha=0.01, normalize=True) model.fit(X_train, y_train) train_score = model.score(X_train, y_train) #模型对训练样本得准确性 test_score = model.score(X_test, y_test) #模型对测试集的准确性 print(train_score) print(test_score)
其中alpha的值为岭系数,scikit-learn提供了类RidgeCV,它可以自动执行网格搜索,来寻找最佳值:
from sklearn.linear_model import RidgeCV from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split boston = load_boston() X = boston.data y = boston.target #把数据分为训练数据集和测试数据集(20%数据作为测试数据集) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3) model = RidgeCV(alphas=[1.0, 0.5, 0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001], normalize=True) model.fit(X_train, y_train) print(model.alpha_)
Lasso回归
Lasso回归加入w的L1范数作为惩罚项,以确定系数中的数目较多的无用项(零值):
$$L(\bar{w})=\frac{1}{2n}\left\|X\bar{w}-\bar{y}\right\|_2^2+\alpha\left\|\bar{w}\right\|_1$$
具体代码与Ridge回归类似,这里不再复述。
ElasticNet回归
ElasticNet将Lasso和Ridge组成一个具有两种惩罚因素的单一模型:一个与L1范数成比例,另外一个与L2范数成比例。使用这种方式方法所得到的模型就像纯粹的Lasso回归一样稀疏,但同时具有与岭回归提供的一样的正则化能力。它的损失函数是:
$$L(\bar{w})=\frac{1}{2n}\left\|X\bar{w}-\bar{y}\right\|_2^2+\alpha\beta\left\|\bar{w}\right\|_1+\frac{\alpha(1-\beta)}{2}\left\|\bar{w}\right\|_2^2$$
从上面的公式可知,ElasticNet使用时需要提供$\alpha$和$\beta$两个参数。在$\beta$中参数的名称为l1_ratio:
from sklearn.datasets import load_boston
from sklearn.linear_model import LassoCV, ElasticNetCV
boston = load_boston()
#Find the optimal alpha value for Lasso regression
lscv = LassoCV(alphas=(1.0, 0.1, 0.01, 0.001, 0.005, 0.0025, 0.001, 0.00025), normalize=True)
lscv.fit(boston.data, boston.target)
print('Lasso optimal alpha: %.3f' % lscv.alpha_)
#Find the optimal alpha and l1_ratio for ElasticNet
encv = ElasticNetCV(alphas=(0.1, 0.01, 0.005, 0.0025, 0.001), l1_ratio=(0.1, 0.25, 0.5, 0.75, 0.8), normalize=True)
encv.fit(boston.data, boston.target)
print('ElasticNet optimal alpha: %.3f and L1 ratio: %.4f' % (encv.alpha_, encv.l1_ratio_))
参考链接: