线性回归是统计学总最常用的算法之一。从根本上来说,当你想表示两个变量间数学关系时,就可以使用线性回归。当你使用它时,你首先假设输出变量(有时称为响应变量、因变量或标签)和预测变量(有时称为自变量、解释变量或特征)之间存在线性关系。当然这种线性关系也可能存在于一个输出变量和数个预测变量之间。输出变量于预测变量之间存在线性关系是一个大胆的假设,同时也是一个最简单的假设。从数学表示形式来看,线性函数比非线性函数更加简单。线性模型作为最简单的参数化方法,始终值得关注。这是因为很多问题,甚至本质是非线性的问题,也可以采用线性模型解决。
在线性回归中,数据采用线性函数的方式进行数据建模,对于模型中的未知参数也采用数据进行估计。对于一个多变量的线性回归模型可以表示为如下公式:
$$Y_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+…+\beta_pX_{ip}+\varepsilon_i,i=1,2,…,n$$
其中,Y是X的线性函数,$\varepsilon_i$是误差项。线性则是$Y_i$的条件均值,在参数$\beta$里是线性的。有些函数模型看起来并不一定是线性回归但是通过代数转换可以转换为线性回归模型。对于一个简单的线性回归,可以表示为如下:
$$Y_i=\alpha+\beta x_i$$
对于单变量的线性回归,是目前最容易理解的线性模型,其回归式如下:
$$Y=\alpha+\beta x+\varepsilon$$
线性回归是回归分析中最为广泛使用的模型,在结果预测及函数关系的应用中较为频繁。
对于线性回归算法,我们希望从训练数据中学习到线性回归方程,即:
$$y=b+\sum_{i=1}^{n}w_ix_i$$
其中,b称为偏置,$w_i$为回归系数。对于上式,令$x_0=1$则上式可以表示为:
$$y=\sum_{i=0}^{n}w_ix_i$$
在线性回归模型中,其目的是求出线性模型回归方程,即求出线性回归方程中的回归系数$w_i$。线性回归的评价是指如何度量预测值(Prediction)于标签(Label)之间的接近程序,线性回归模型的损失函数可以是绝对损失(Absolute Loss)或者平方损失(Squared Loss)。其中,绝对损失函数为:
$$l=|y-\hat{y}|$$
其中,$\hat{y}$为预测值,且:$\hat{y}=\sum_{i=0}^{n}w_ix_i$
平方损失函数为:
$$l=(y-\hat{y})^2$$
由于平方损失处处可导,通常使用平方误差作为线性回归模型的损失函数。假设有m个训练样本,每个样本中有n-1个特征,则平方误差可以表示为:
$$l=\frac{1}{2}\sum_{i=1}^{m}(y^i-\sum_{j=0}^{n-1}w_jx_j^i)^2$$
对于如上的损失函数,线性回归的求解是希望求得平方误差最小值。
最小二乘法
最小二乘法也称作最小平方法,最常用的是普通最小二乘法(Ordinary Least Square),它是一种数学中的优化方法,试图找到一个或一组估计值,使得实际值与估计值尽可能相似,距离最小,目的是通过已有的数据来预测未知数据。一般通过一条多元一次的直线方程来计算,在二维坐标中即二元一次方程。例如,在二维坐标中,非常多的点分散在其中,试图绘制一条直线,使得这些分散的点到直线上的距离最小。这里的距离最小并非点到直线的垂直距离最短,而是点到直接的y轴距离最短,即通过该点并与y轴平行的直线,点到该y轴平行线与直线交点的距离最短。
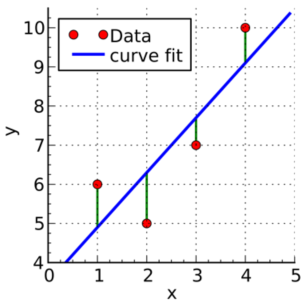
最小二乘法的核心思想是通过最小化误差的平方和,试图找到最可能的函数方程。例如,在二维坐标系中存在五个数据点(10,20),(11,23),(12,25),(13,27),(14,26),希望找出一条该五个点距离最短的直线,根据二元一次方程:$y=ax+b$。将五个点分别带入该二元方程得到如下:
$$20=10a+b$$
$$23=11a+b$$
$$25=12a+b$$
$$27=13a+b$$
$$26=14a+b$$
由于最小二乘法是尽可能使得等号两边的方差值最小,因此:
$$S(a,b)=[20-(10a+b)]^2+[23-(11a+b)]^2+[25-(12a+b)]^2+[27-(13a+b)]^2+[26-(14a+b)]^2$$
因此求最小值即可通过对$S(a,b)$求偏导数获得,并得一阶倒数得值为0,因此:
$$\frac{\partial S}{\partial a}=1460a+120b-2936$$
$$\frac{\partial S}{\partial b}=12a+10b-242$$
即得到关于求解未知变量a、b的二元一次方程:
$$\left\{\begin{matrix}1460a+120b=2936\\12a+10b=242\end{matrix}\right.$$
通过计算上述二元一次方法即得到a=0.0243,b=24.1708。因此,在上述五个点中,通过最小二乘法得到直线方程:y=24.1708+0.0243x是使得五个点到该直线距离最小的直线。
最小二乘解法
对于线性回归模型,假设训练集中有m个训练样本,每个训练样本中有n-1个特征,可以使用矩阵的表示方法,预测函数可以表示为:$Y=XW$,其损失函数表示为:$(Y-XW)^T(Y-XW)$。
其中,标签Y为m×1的矩阵,训练特征X为m×n的矩阵,回归系数W为n×1的矩阵。在最小二乘法中,对W求导,即:
$$\frac{d}{dW}(Y-XW)^T(Y-XW)=X^T(Y-XW)$$
令其为0,得到:
$$\hat{W}=(X^TX)^{-1}X^TY$$
Python实现:
def least_square(feature, label):
'''最小二乘法
input: feature(mat):特征
label(mat):标签
output: w(mat):回归系数
'''
w = (feature.T * feature).I * feature.T * label
return w
最小二乘法虽然看似是一个直线方程的问题,但是在实际应用中却应用非常广泛,因为它得到的方程可以视为一个函数模型,该函数模型可以对后续的工作带来极大的便利。上述过程均是通过线性问题的求解方式进行阐述,但是在更多时候,需要解决的问题不是一个线性问题,它需要通过多项式拟合的方式进行处理,但是原理和求解方式均一致。当样本数据不断增加后,计算量会明显增加,在阶数更高时计算扯则更为复杂,为解决更多问题,基千最小二乘法衍生出了移动最小二乘法、加权最小二乘法及偏最小二乘法等。除最小二乘法外,梯度下降也是线性回归中的方法之一。
梯度下降法
什么是梯度下降法
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e.找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
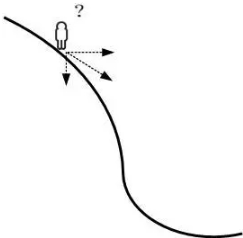 在微积分里面,对多元函数的参数求$\partial$偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y),分别对x,y求偏导数,求得的梯度向量就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})^T$,简称grad f(x,y)或者$\bigtriangledown f(x,y)$。对于在点$(x_0,y_0)$的具体梯度向量就是$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0})^T$,或者$\bigtriangledown f(x_0,y_0)$。如果是3个参数的向量梯度,就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})^T$,以此类推。
在微积分里面,对多元函数的参数求$\partial$偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y),分别对x,y求偏导数,求得的梯度向量就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})^T$,简称grad f(x,y)或者$\bigtriangledown f(x,y)$。对于在点$(x_0,y_0)$的具体梯度向量就是$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0})^T$,或者$\bigtriangledown f(x_0,y_0)$。如果是3个参数的向量梯度,就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})^T$,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点$(x_0,y_0)$,沿着梯度向量的方向就是$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0})^T$的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是$-(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0})^T$的方向,梯度减少最快,也就是更加容易找到函数的最小值。
对于凸优化问题来说,导数为0(梯度为0向量)的点,就是优化问题的解。为了找到这个解,我们沿着梯度的反方向进行线性搜索,每次搜索的步长为某个特定的数值$\alpha$,直到梯度与0向量非常接近为止。上面描述的这个方法就是梯度下降法。迭代算法的步骤如下:
- 当$i=0$,自己设置初始点$\textbf{x}^0=(x_1^0,x_2^0,\cdots,x_n^0)$,设置步长(也叫做学习率)$\alpha$,设置迭代终止的误差忍耐度tol。
- 计算目标函数$f$在点$x_i$上的梯度$\nabla f_{\textbf{x}^i}$。
- 计算$\textbf{x}^{i+1}$,公式如下:$\textbf{x}^{i+1}=\textbf{x}^{i}-\alpha\nabla f_{\textbf{x}^i}$
- 计算梯度$\nabla f_{\textbf{x}^{i+1}}$。如果$\|\nabla f_{\textbf{x}^{i+1}}\|_2\leq tol$则迭代停止,最优解的取值为$\textbf{x}^{i+1}$;如果梯度的二范数大于tol,那么i=i+1,并返回第(3)步。
梯度下降法的类型
基于如何使用数据计算代价函数的导数,梯度下降法可以被定义为不同的形式(various variants)。确切地说,根据使用数据量的大小(the amount of data),时间复杂度(time complexity)和算法的准确率(accuracy of the algorithm),梯度下降法可分为:
- 批量梯度下降法(Batch Gradient Descent, BGD);
- 随机梯度下降法(Stochastic Gradient Descent, SGD);
- 小批量梯度下降法(Mini-Batch Gradient Descent, MBGD)。
批量梯度下降法BGD
这是梯度下降法的基本类型,这种方法使用整个数据集(the complete dataset)去计算代价函数的梯度。每次使用全部数据计算梯度去更新参数,批量梯度下降法会很慢,并且很难处理不能载入内存(don’t fit in memory)的数据集。
批量梯度下降法的损失函数为:
$$\frac{\partial J(\theta)}{\partial {\theta}_j}=\sum_{i=1}^{m}(h_\theta(x^i)-y^i)x_j^i$$
进一步得到批量梯度下降的迭代式为:
$${\theta}’_j=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta_j}=\theta_j=\alpha\sum_{i=1}^{m}(h_\theta(x^i)-y^i)x_j^i$$
其中,m是训练样本(training examples)的数量。
每迭代一步,都要用到训练集所有的数据,如果样本数目很大,那么可想而知这种方法的迭代速度!
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
- 如果训练集有3亿条数据,你需要从硬盘读取全部数据到内存中;
- 每次一次计算完求和后,就进行参数更新;
- 然后重复上面每一步;
- 这意味着需要较长的时间才能收敛;
- 特别是因为磁盘输入/输出(disk I/O)是系统典型瓶颈,所以这种方法会不可避免地需要大量的读取。
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
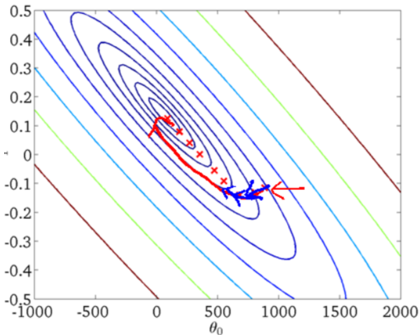
上图是每次迭代后的等高线图,每个不同颜色的线表示代价函数不同的值。运用梯度下降会快速收敛到圆心,即唯一的一个全局最小值。
下面的Python代码实现了批量梯度下降法:
import numpy as np
def gradient_descent(alpha, x, y, ep=0.0001, max_iter=10000):
converged = False
iter = 0
m = x.shape[0] # number of samples
# initial theta
t0 = np.random.random(x.shape[1])
t1 = np.random.random(x.shape[1])
# total error, J(theta)
J = sum([(t0 + t1*x[i] - y[i])**2 for i in range(m)])
# Iterate Loop
while not converged:
# for each training sample, compute the gradient (d/d_theta j(theta))
grad0 = 1.0/m * sum([(t0 + t1*x[i] - y[i]) for i in range(m)])
grad1 = 1.0/m * sum([(t0 + t1*x[i] - y[i])*x[i] for i in range(m)])
# update the theta_temp
temp0 = t0 - alpha * grad0
temp1 = t1 - alpha * grad1
# update theta
t0 = temp0
t1 = temp1
# mean squared error
e = sum([(t0 + t1*x[i] - y[i])**2 for i in range(m)])
if abs(J - e) <= ep:
print('Converged, iterations:', iter, '!!!')
converged = True
J = e # update error
iter += 1 # update iter
if iter == max_iter:
print('Max interactions exceeded!')
converged = True
return t0, t1
小批量梯度下降法MBGD
小批量梯度下降法是最广泛使用的一种算法,该算法每次使用m个训练样本(称之为一批)进行训练,能够更快得出准确的答案。小批量梯度下降法不是使用完整数据集,在每次迭代中仅使用m个训练样本去计算代价函数的梯度。一般小批量梯度下降法所选取的样本数量在50到256个之间,视具体应用而定。
- 减少了参数更新时的变化,能够更加稳定地收敛。
- 能利用高度优化的矩阵,进行高效的梯度计算。
随机初始化参数后,按如下伪码计算代价函数的梯度:
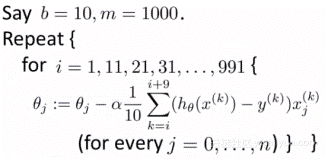 这里 b 表示一批训练样本的个数,m 是训练样本的总数。
这里 b 表示一批训练样本的个数,m 是训练样本的总数。
随机梯度下降法 SGD
批量梯度下降法被证明是一个较慢的算法,所以,我们可以选择随机梯度下降法达到更快的计算。随机梯度下降法的第一步是随机化整个数据集。在每次迭代仅选择一个训练样本去计算代价函数的梯度,然后更新参数。即使是大规模数据集,随机梯度下降法也会很快收敛。随机梯度下降法得到结果的准确性可能不会是最好的,但是计算结果的速度很快。在随机化初始参数之后,使用如下方法计算代价函数的梯度:
$${\theta}'_j=\theta_j+\frac{1}{m}(y^i-h_\theta(x^i))x_j^i$$
批量梯度下降会最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小。随机梯度下降会最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向,但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。
随机梯度下降法的优化过程为:
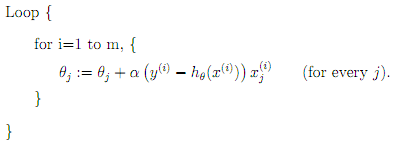
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将 theta 迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代 10 次的话就需要遍历训练样本 10 次。但是,SGD 伴随的一个问题是噪音较 BGD 要多,使得 SGD 并不是每次迭代都向着整体最优化方向。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
从迭代的次数上来看,SGD 迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:
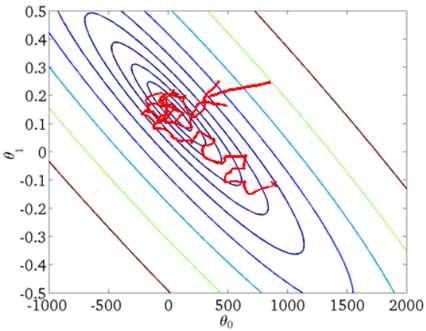
参考链接:http://sofasofa.io/tutorials/python_gradient_descent/index.php
牛顿法
除了前面说的梯度下降法,牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法的基本思想是利用迭代点 $x_k$ 处的一阶导数(梯度)和二阶导数(Hessen 矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法下降的速度比梯度下降的快,而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。
基本牛顿法
基本牛顿法是一种基于导数的算法,它每一步的迭代方向都是沿着当前点函数值下降的方向。对于一维的情形,对于一个需要求解的优化函数 f(x),求函数的极值的问题可以转化为求导函数 ${f}'(x)=0$。对函数 f(x) 进行泰勒展开到二阶,得到:
$$f(x)=f(x_k)+{f}'(x_k)(x-x_k)+\frac{1}{2}f^n(x_k)(x-x_k)^2$$
对上式求导并令其为 0,则为:
$${f}'(x)+{f}''(x_k)(x-x_k)=0$$
即得到:
$$x=x_k-\frac{{f}'(x_k)}{{f}''(x_k)}$$
这就是牛顿法的更新公式。
基本牛顿法的流程
- 给定终止误差值 $0\leq\varepsilon\leq1$,初始点 $x_0\in\mathbb{R}^n$,令 k=0;
- 计算 $g_k=\nabla f(x_k)$,若 $\left\|g_k\right\|\leq\varepsilon$,则停止,输出 $x^*\approx x_k$;
- 计算 $G_k=\nabla^2 f(x_k)$,并求解线性方程组 $G_k d=-g_k$ 得解 $d_k$;
- 令 $x_{k+1}=x_k+d_k,k=k+1$,并转 2。
全局牛顿法
牛顿法最突出的优点是收敛速度快,具有局部二阶收敛性,但是,基本牛顿法初始点需要足够"靠近"极小点,否则,有可能导致算法不收敛,此时就引入了全局牛顿法。全局牛顿法的流程为:
- 给定终止误差值 $0\leq\varepsilon\leq1$,$\delta\in(0,1)$,$\sigma\in(0,0.5)$,初始点 $x_0\in\mathbb{R}^n$,令 k=0;
- 计算 $g_k=\nabla f(x_k)$,若 $\left\|g_k\right\|\leq\varepsilon$,则停止,输出 $x^*\approx x_k$;
- 计算 $G_k=\nabla^2 f(x_k)$,并求解线性方程组 $G_k d=-g_k$ 得解 $d_k$;
- 设 $m_k$ 是不满足下列不等式的最小非负整数 m:$f(x_k+\delta^m d_k)\leq f(x_k)+\sigma\delta^m g_k^T d_k$
- 令 $\alpha_k=\delta^{m_k},x_{k+1}=x_k+\alpha_k d_k,k=k+1$,并转 2。
全局牛顿法的具体实现:
def newton(feature, label, iterMax, sigma, delta):
'''牛顿法
input: feature(mat):特征
label(mat):标签
iterMax(int):最大迭代次数
sigma(float), delta(float):牛顿法中的参数
output: w(mat):回归系数
'''
n = np.shape(feature)[1]
w = np.mat(np.zeros((n, 1)))
it = 0
while it <= iterMax:
# print it
g = first_derivativ(feature, label, w) # 一阶导数
G = second_derivative(feature) # 二阶导数
d = -G.I * g
m = get_min_m(feature, label, sigma, delta, d, w, g) # 得到最小的 m
w = w + pow(sigma, m) * d
if it % 10 == 0:
print "\t----itration:", it, ", error:", get_error(feature, label, w)[0, 0]
it += 1
return w
在程序中,函数 newton 利用全局牛顿法对线性回归模型中的参数进行学习,函数 newton 的输入为训练特征 feature、训练的目标值 label、全局牛顿法的最大迭代次数 iterMax 以及全局牛顿法的两个参数 sigma 和 delta。函数 newton 的输出是线性回归模型的参数 w。在函数 newton 中需要计算损失函数的一阶导数,计算损失函数的二阶导数,,同时需要计算最小的 m 值,最终根据上述的值更新权重。
def get_min_m(feature, label, sigma, delta, d, w, g):
'''计算步长中最小的值 m
input: feature(mat):特征
label(mat):标签
sigma(float), delta(float):全局牛顿法的参数
d(mat):负的一阶导数除以二阶导数值
g(mat):一阶导数值
output: m(int):最小 m 值
'''
m = 0
while True:
w_new = w + pow(sigma, m) * d
left = get_error(feature, label, w_new)
right = get_error(feature, label, w) + delta * pow(sigma, m) * g.T * d
if left <= right:
break
else:
m += 1
return m
程序实现了全局牛顿法中最小 m 值的确定,在函数 get_min_m 中,其输入为训练数据的特征 feature,训练数据的目标值 label,全局牛顿法的参数 sigma、delta、d 以及损失函数的一阶导数值 g。其输出是最小的 m 值 m。在计算的过程中,计算损失函数值时使用到了 get_error 函数,其具体实现:
```html def get_error(feature, label, w): '''计算误差 input:feature(mat):特征 label(mat):标签 w(mat):线性回归模型的参数 output:损失函数值 ''' return (label - feature * w).T * (label - feature * w) / 2
Armijo搜索
给定$\delta\in(0,1)$,$\sigma \in(0,0.5)$,令步长因子$\alpha_k=\delta^{m_k}$,其中$m_k$是满足下列不等式的最小非负整数:$f(x_k+\delta^m d_k)\leq f(x_k)+\sigma\delta^m g_k^T d_k$
利用全局牛顿法求解线性回归模型
假设有m个训练样本,其中,每个样本有n-1个特征,则线性回归模型的损失函数为:
$$l=\frac{1}{2}\sum_{i=1}^{m}(y^i-\sum_{j=0}^{n-1}w_j x_j^i)^2$$
若是利用全局牛顿法求解线性回归模型,需要计算线性回归模型损失函数的一阶导数和二阶导数,其一阶导数为:
$$\frac{\partial l}{\partial w_j}=-\sum_{i=1}^{m}[(y^i-\sum_{j=0}^{n-1}w_j\cdot x_j^i)*x_j^i]$$
损失函数的二阶导数为:
$$\frac{\partial l}{\partial w_j\partial w_k}=\sum_{i=1}^{m}(x_j^i\cdot x_k^i)$$
相关代码:
def first_derivative(feature, label, w): '''计算一阶导函数的值 input:feature(mat):特征 label(mat):标签 output:g(mat):一阶导数值 ''' m, n = np.shape(feature) g = np.mat(np.zeros((n, 1))) for i in xrange(m): err = label[i, 0] - feature[i, ] * w for j in xrange(n): g[j, ] -= err * feature[i, j] return g def second_derivative(feature): '''计算二阶导函数的值 input:feature(mat):特征 output:G(mat):二阶导数值 ''' m, n = np.shape(feature) G = np.mat(np.zeros((n, n))) for i in xrange(m): x_left = feature[i, ].T x_right = feature[i, ] G += x_left * x_right return G
first_derivative实现了损失函数一阶导数值的求解。在函数first_derivative中,其输入为训练数据的特征feature和训练数据的目标值label,其输出为损失函数的一阶导数g,其中g是一个n×1的向量。
second_derivative函数实现了损失函数二阶导数值的计算。在函数second_derivative中,其输入为训练数据的特征feature,输出为损失函数的二阶导数G,其中G是一个n×n的矩阵。
局部加权线性回归
在线性回归中会出现欠拟合的情况,有些方法可以用来解决这样的问题。局部加权线性回归(LWLR)就是这样的一种方法。局部加权线性回归采用的是给预测点附近的每个点赋予一定的权重,此时的回归系数可以表示为:
$$\hat{W}=(X^TMX)^{-1}X^TMY$$
M为给每个点的权重。
LWLR使用核函数来对附近的点赋予更高的权重,常用的有高斯核,对应的权重为:
$$w(i,i)=\exp(\frac{\left|X^{(i)-x}\right|}{-2k^2})$$
这样的权重矩阵只含对角元素。
局部加权线性回归的具体实现:
import numpy as np def lwlr(feature, label, k): '''局部加权线性回归 input:feature(mat):特征 label(mat):标签 k(int):核函数的系数 output:predict(mat):最终的结果 ''' m = np.shape(feature)[0] predict = np.zeros(m) weights = np.mat(np.eye(m)) for i in xrange(m): for j in xrange(m): diff = feature[i, ] - feature[j, ] weights[j, j] = np.exp(diff * diff.T / (-2.0 * k**2)) xTx = feature.T * (weights * feature) ws = xTx.I * (feature.T * (weights * label)) predict[i] = feature[i, ] * ws return predict
使用Scikit-Learn进行线性回归分析
这里使用SkLearn自带得数据集进行测试:
from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression boston = load_boston() X = boston.data y = boston.target print(X.shape) #样本个数及特征数 print(boston.feature_names) #特征标签名字 #把数据分为训练数据集和测试数据集(20%数据作为测试数据集) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3) model = LinearRegression() model.fit(X_train, y_train) train_score = model.score(X_train, y_train) #模型对训练样本得准确性 test_score = model.score(X_test, y_test) #模型对测试集的准确性 print(train_score) print(test_score)
模型优化
多项式与线性回归
当线性回归模型太简单导致欠拟合时,我们可以增加特征多项式来让线性回归模型更好的拟合数据。比如两个特征$x_1, x_2$,可以增加两特征的乘积$x_1\cdot x_2$作为新特征$x_3$。我们还可以增加$x_1^2$作为另外一个新特征$x_4$。
在scikit-learn里,线性回归是由类sklearn.linear_model.LinearRegression实现,多项式由类sklearn.preprocessing.PolynomialFeatures实现。那么要怎么添加多项式特征呢?我们需要用一个管道把两个类串起来,即用sklearn.pipeline.Pipeline把两个模型串起来。一个Pipeline可以包含多个处理节点,在scikit-learn里,除了最后一个节点外,其他的节点都必须实现'fit()'和'transform()'方法,最后一个节点只需要实现fit()方法即可。当训练样本数据送进Pipeline里进行处理时,它会逐个调用节点的fit()和transform()方法,然后调用最后一个节点的fit()方法来拟合数据。
数据归一化
```当线性回归模型有多个输入特征时,特别是使用多项式添加特征时,需要对数据进行归一化处理。比如,特征$x_1$的范围在[1,4]之间,特征$x_2$的范围在[1,2000]之间,这种情况下,可以让$x_1$除以4来作为新特征$x_1$,同时让$x_2$除以2000来作为新特征$x_2$,该过程称为特征缩放(feature scaling)。可以使用特征缩放来对训练样本进行归一化处理,处理后的特征值范围在[0,1]之间。
归一化处理的目的是让算法收敛更快,提升模型拟合过程中的计算效率。进行归一化处理后,当有个新的样本需要计算预测值时,也需要先进行归一化处理,再通过模型来计算预测值,计算出来的预测值要再乘以归一化处理的系数,这样得到的数据才是真实的预测数据。
在scikit-learn里,使用LinearRegression进行线性回归时,可以指定normalize=True来对数据进行归一化处理。具体可查阅scikit-learn文档。
优化后代码:
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
boston = load_boston()
X = boston.data
y = boston.target
print(X.shape) #样本个数及特征数
print(boston.feature_names) #特征标签名字
#把数据分为训练数据集和测试数据集(20%数据作为测试数据集)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)
def polynomial_model(degree=1):
polynomial_features = PolynomialFeatures(degree=degree, include_bias=False)
linear_regression = LinearRegression(normalize=True)
pipeline = Pipeline([("polynomial_features", polynomial_features), ("linear_regression", linear_regression)])
return pipeline
model = polynomial_model(degree=2)
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train) #模型对训练样本得准确性
test_score = model.score(X_test, y_test) #模型对测试集的准确性
print(train_score)
print(test_score)
使用二阶多项式训练后样本分数和测试分数都提高了,看来模型得到了优化,改为三阶后,针对训练样本的分数达到了1,而针对测试样本的得分数却是负数。说明这个模型已经过拟合。