数据, 术→技巧, 机器学习, 法→原理

机器学习算法之朴素贝叶斯

钱魏Way · · 1,705 次浏览

[LATEXPAGE]

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

贝叶斯定理

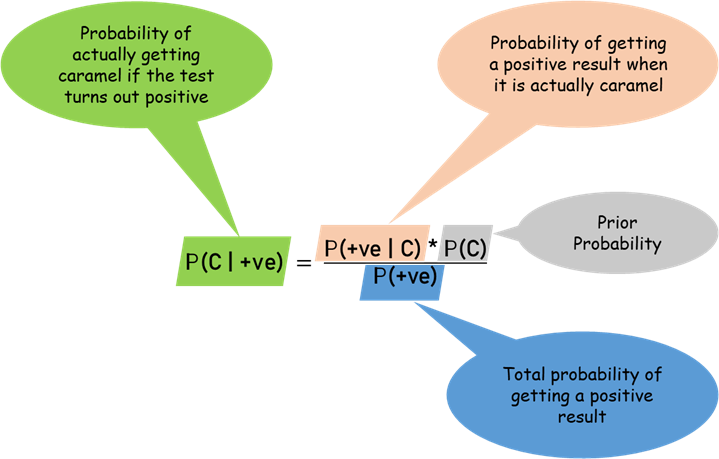
贝叶斯定理实际上就是计算“条件概率” 的公式。条件概率（Conditional Probability）是指在事件 B 发生的情况下，事件 A 发生的概率，用 P (A|B) 表示，读作在 B 条件下的 A 的概率。

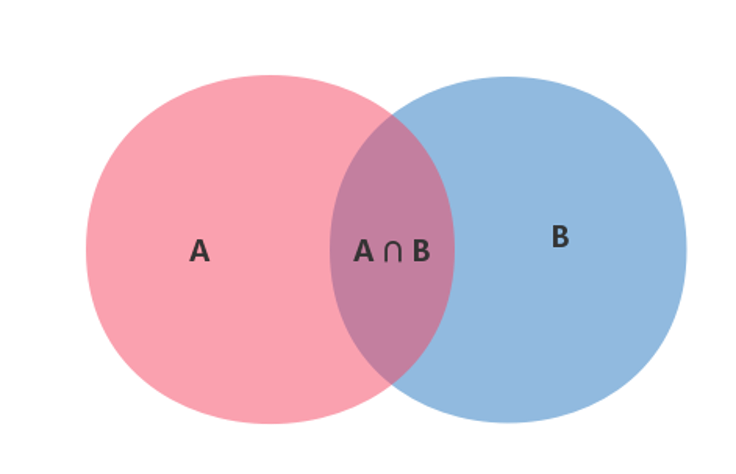
根据上图，可以很清楚地看到在事件 B 发生的情况下，事件 A 发生的概率就是 $P(A \cap B)$除以 $P (B)$。

$$P(A | B)=\frac{P(A \cap B)}{P(B)}$$

同时，$P (A \cap B)$又可以由$P (A \cap B)=P (B | A) P (A)$表示，然后我们就可以推得贝叶斯公式：

$$P(A | B)=\frac{P(B | A) P(A)}{P(B)}$$

贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出 $P (A|B)$，$P (B|A)$ 则很难直接得出，但我们更关心 $P (B|A)$，贝叶斯定理就为我们打通从 $P (A|B)$ 获得 $P (B|A)$ 的道路。

在分类任务中，我们可以把贝叶斯定理换一个更清楚的形式：

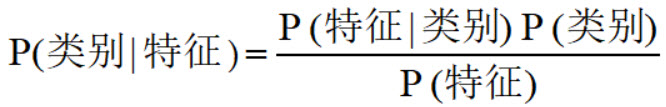
朴素贝叶斯分类器

朴素贝叶斯，英文叫Naive Bayes。之所以称为 “朴素” 是因为整个形式化过程只做最原始、最简单的假设。朴素贝叶斯算法是假设输入变量之间是相互独立的，没有概率依存关系。（若相互依存，那叫贝叶斯网络）。是监督学习里面的一种分类算法，使用场景为：给定训练集(X,Y)，其中每个样本x都包含n维特征，即$x=(x_1,x_2,…,x_n)$，标签集合含有k种类别，即$y=(y_1,y_2,…,y_k)$。如果现在来了一个新的样本x，我们如何判断它属于哪个类别？解决思路是：从概率的角度看，这个问题就是给定x，它属于哪个类别的概率最大。那么问题就转化为求解$ P(y_1|x),P(y_2|x),…,P(y_k|x)$中最大的那个，即求后验概率最大的那个：

$$\mathop{argmax}_{y} P(y|x)$$

所以朴素贝叶斯分类器就是求上式的最大值，根据贝叶斯公式将上面式子展开后如下：

$$ P(y|x_1,…,x_n) = \frac{P(y)P(x_1,…,x_n|y)}{P(x_1,…,x_n)}$$

可以看到，上面的式子中：

  • $P(y)$是先验概率，可以直接根据数据集计算出来。
  • $P(x_1,…,x_n)$如何计算？
  • $P(x_1,…,x_n|y)$如何计算?

首先来看$P(x_1,…,x_n|y)$的计算。这里需要用到条件联合概率分解公式：

$$P(XY|Z) = P(X|YZ)P(Y|Z)$$

$$P(UVWX|YZ) = P(U|VWXYZ)P(V|WXYZ)P(W|XYZ)P(X|YZ)P(Y|Z)$$

利用条件联合概率分解公式：

$$P(x_1,…,x_n|y) = P(x_1|x_2,…,x_n,y)P(x_2|x_3,…,x_n,y)…P(x_n|y)$$

上面式子很难计算，所以朴素贝叶斯理论对条件概率分布做了独立性假设，就是在我们的场景下各个维度特征 $x_1,…,x_n$相互独立，即：

$$P(x_i|y,x_1,…,x_{i-1},x_{i+1},…,x_n) = P(x_i|y)$$

有了上面的假设，之前那个难计算的公式就好计算了：

$$P(x_1,…,x_n|y) = P(x_1|x_2,…,x_n,y)P(x_2|x_3,…,x_n,y)…P(x_n|y) =P(x_1|y)P(x_2|y)…P(x_n|y) = \frac{P(y)\prod_{i=1}^n P(x_i|y)}{P(x_1,…,x_n)}$$

对于确定的输入，不论y取哪个值，${P(x_1,…,x_n)}$都是一样的，所以：

$$P(x_1,…,x_n|y) \propto P(y)\prod_{i=1}^n P(x_i|y)$$

所以新样例$x=(x_1,…,x_n)$所属的类别y的计算公式为：

$$\hat y= \mathop{argmax}_{y} P(y|x)\prod_{i=1}^n P(x_i|y)$$

所以，NB分类器最后就是求先验概率$P(y)$和$x_i$的条件概率$P(x_i|y)$，这两个概率都是可以计算的。

三种不同的朴素贝叶斯

朴素贝叶斯一共有三种方法，分别是高斯朴素贝叶斯、多项式分布贝叶斯、伯努利朴素贝叶斯，在介绍不同方法的具体参数前，我们先看看这三种方法有什么区别。这三种分类方法其实就是对应三种不同的数据分布类型。

高斯朴素贝叶斯

高斯朴素贝叶斯算法是假设特征属性为连续值时，而且分布服从高斯分布（正态分布）。正态分布的概率密度函数如图所示：

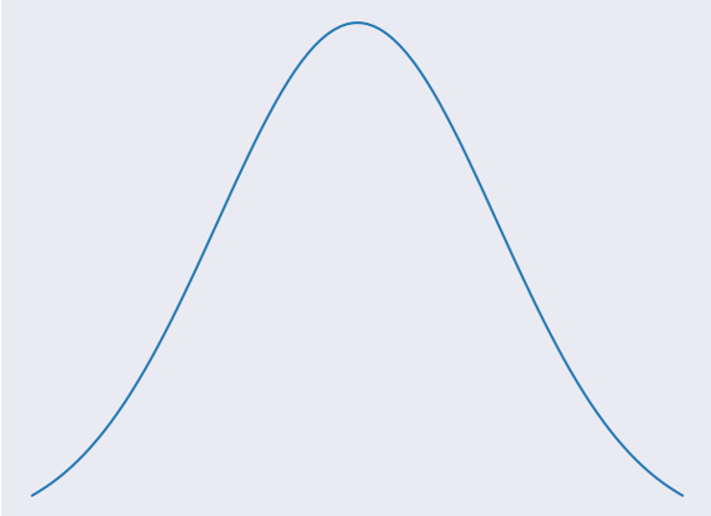
可以看出，正态分布像一个钟形，均值所对应的概率密度函数最高。我们假定某个特征I服从均值为$\mu$,方差为$\sigma ^2$的正态分布，记为$N(\mu ,\sigma ^2)$。针对公式：

$$P(y_k|X) =  = \frac{P(y_k)\prod_{i=1}^{N}P(a_i|y_k)}{P(X)}$$

我们可以假定样本X的特征I符合正态分布，此时上式中的$P(a_i|y_k)$的计算会变得十分容易：

$$P（a_i|y_k） = \frac{1}{2\pi(\sigma_{yk})^2}*e^-\frac{(a_i-\mu_{yk})^2}{2(\sigma_{yk})^2}$$

如上所示，其中$(\sigma_{yk})^2$代表类别为$y_k$的样本中，第I维特征的方差。$\mu$代表类别为$y_k$的样本中，第I维特征的均值。

SKlearn中的方法：

class sklearn.naive_bayes.GaussianNB(priors=None)
  • priors:先验概率大小，如果没有给定，模型则根据样本数据自己计算（利用极大似然法）。

示例代码：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d" % (X_test.shape[0], (y_test != y_pred).sum()))

多项式分布贝叶斯

当我们的特征都是分类型特征的时候，可以使用多项式模型。我们可以用它来计算特征中分类的出现频率。特别的是当特征只有两种的时候，我们将会使用多项式模型中的伯努利模型。

在多项式模型中，对于样本X的第I个特征，$P(a_i|y_k)$的计算十分容易：

$$P（a_i|y_k） = \frac{N(y_k,a_i)}{N(y_k)}$$

如上所示，其中$N(y_k,a_i)$代表类别为$y_k$的样本中，第I维特征取值是$a_i$的个数，$N(y_k)$ 代表类别为$y_k$的样本个数。

SKlearn中的方法：

class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
  • alpha:先验平滑因子，默认等于1，当等于1时表示拉普拉斯平滑。
  • fit_prior:是否去学习类的先验概率，默认是True
  • class_prior:各个类别的先验概率，如果没有指定，则模型会根据数据自动学习， 每个类别的先验概率相同，等于类标记总个数N分之一。

示例代码：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import ComplementNB

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
cnb = ComplementNB()
y_pred = cnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d" % (X_test.shape[0], (y_test != y_pred).sum()))

伯努利朴素贝叶斯

与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是1或0。伯努利模型中，条件概率$ P(x_i|y)$的计算方式时：

  • 当特征值$x_i=1$时，$P(x_i|y)=P(x_i=1|y)$
  • 当特征值$x_i=0$时，$P(x_i|y)=1-P(x_i=1|y)$

SKlearn中的方法：

class sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
  • alpha:平滑因子，与多项式中的alpha一致。
  • binarize:样本特征二值化的阈值，默认是0。如果不输入，则模型会认为所有特征都已经是二值化形式了；如果输入具体的值，则模型会把大于该值的部分归为一类，小于的归为另一类。
  • fit_prior:是否去学习类的先验概率，默认是True
  • class_prior:各个类别的先验概率，如果没有指定，则模型会根据数据自动学习， 每个类别的先验概率相同，等于类标记总个数N分之一。

示例代码：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import BernoulliNB

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
bnb = BernoulliNB()
y_pred = bnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d" % (X_test.shape[0], (y_test != y_pred).sum()))

朴素贝叶斯算法优缺点

优点：

  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
  • 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类
  • 算法逻辑简单,易于实现，分类过程中时空开销小

缺点：

  • 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进
  • 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳
  • 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率
  • 对输入数据的表达形式很敏感

参考链接：

相关文章:

  1. 机器学习算法之决策树分类
  2. 机器学习聚类算法之Mean Shift
  3. 机器学习之距离与相似度计算
  4. 高维数据降维及可视化工具t-SNE
  5. 层次聚类改进算法之CURE
朴素贝叶斯算法 机器学习 概率计算 贝叶斯 贝叶斯分类算法 贝叶斯定理
Python模板引擎jinja2
Flask学习之上下文
Flask学习之路由

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注