先前对于生存分析的理解比较片面,虽然知道生存分析不仅仅适用于预料行业,对于用户留存的也有一定的范围,当时的理解是只适合订阅制的网站用来分析用户留存,但是仔细分析后发现适用场景还是蛮多的。其中个人觉得最大的作用应该是模式发现。
什么是生存分析?
生存分析(英语:Survival analysis)是指根据试验或调查得到的数据对生物或人的生存时间进行分析和推断,研究生存时间和结局与众多影响因素间关系及其程度大小的方法,也称生存率分析或存活率分析。
产生背景
假设有一种治疗心脏病的新药M,我们希望探寻这个药是否能够改善患者的某个指标(例如生存时间Time)。那么最简单的想法就是:将患者随机分组为A,B两组,A组给药,B组给安慰剂(对照)。并在最后分别检测A、B组的平均生存时间。如果A组整体好于B组(例如使用t检验),则我们认为该药有效。事情不总随人愿,如果A组中的一位奶奶在治疗期间(例如开始治疗三个月后)不幸出车祸死亡,而B组中的一位爷爷家属不同意继续治疗(例如开始治疗后五个月)并进行终止,这会对我们的数据产生什么影响呢?最直观地来看:我们没办法再用t检验了!因为t检验需要找到两组数据的平均数,而出车祸的奶奶我们应该用什么数字呢?三个月吗?这未免太不科学。然而,直接删掉又是十分不理智的。因为这会让我们损失信息。顺便一提,我觉得信息这个概念在统计中实在太重要了。如何从数据中获取更多的信息是统计学一直孜孜不倦追求的目标。这三个月给我们的信息是:该奶奶至少活了三个月!如果直接删掉这个样本,对整体的数据信息是有损失的。考虑一个极端情况,如果数据集中的全部样本都是如上所述的情况,那怎么办呢?盲目的删除这会提高模型的方差,以至于降低估计精度。
解决方案
比起常见的数据,生存分析的主要不同在于一种特殊的因变量。一般而言,这种因变量被称为Time to Event data,也就是某个事件发生的时间。而上述数据的特殊情况(老奶奶问题)我们称之为删失(censoring)。删失是指开始时间或结束时间没有被精准观测,从而导致数据不完备的情况。例如在上述情况中,我们只知道$T_i>3$,而不知道 $T_i$ 的具体数字。总之,生存分析主要关注于处理一种特殊的时间数据,并且时间数据可能带有部分删失属性。事实上这种数据是很常见的,最多的被应用在医药分析领域,甚至需要药品说明书上都有生存分析的影子。而删失情况就更为常见了,在临床观察过程中,不可能每天都仔细地盯住患者,这会耗费大量人力物力,而人作为有思想的独立个体,多多少少可能导致中途退出药物实验等情况,这些都会导致删失。
为了更好理解这句话,我们用上帝视角假设下面一组医药行业情况。我们关心的因变量是用药后的生存时间。
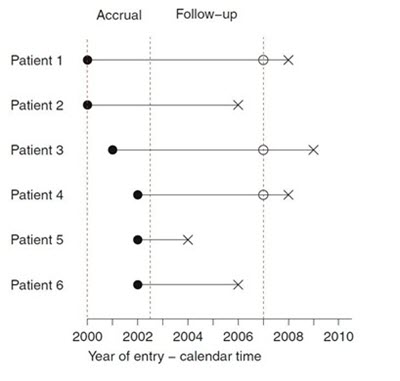
实心圈代表加入实验的时间,空心圈代表离开实验时间,叉代表死亡时间。从左至右第一根虚线是开启实验的时间,第二根是结束加人的时间,第三根是结束观测的时间。可以看出,我们结束观测之外有事件(死亡)发生,我们根本没办法得到完整而真实的数据!上图我们通过上帝视角假设了在观测区之外的情况,而我们真实看到的情况其实是下图:
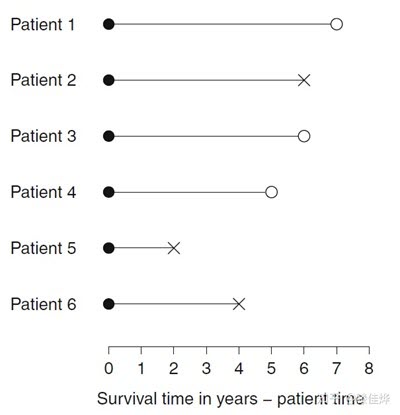
可以注意到,在观测区之外的事件我们一概不知(例如患者一的真实死亡时间)。因此每个患者可能会有生存时间和删失时间两个数据中的一个,我们将其标记为status。将上述观测图变为如下表格:
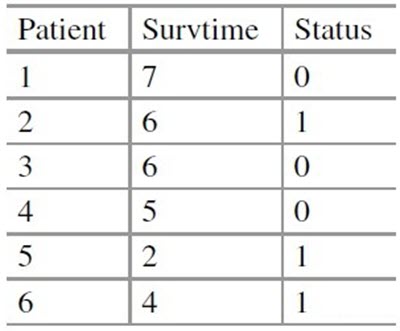
上表就是我们经常分析的生存数据(Survival Data)。我们一般将其表示成 $\{t_i,\delta_i,x_i\}_{i=1}^n$。其中:
- $t_i$代表了跟进时间(following-up time),是生存时间T_i与删失时间C_i的较小值
- $\delta_i$代表了状态(status),$if t_i=T_i, \delta_i=1; if t_i=C_i, \delta_i=0.$
- $x_i$代表了协变量(covariates),包括感兴趣的其他变量(如身高血压肺活量……)
从上述删失情况我们需要注意到:由于数据种类的不同,一些常见的处理就没有意义了!例如平均值,方差等等。但是中位数很有可能还是有意义的。
基本概念
起始时间和失效事件
- 起始事件(initial event):反应生存时间起始特征的事件,如疾病确诊、某种疾病治疗开始等。
- 失效事件(failure event):常被简称为事件,研究者规定的终点结局,医学研究中可以是患者死亡,也可以是疾病的发生、某种治疗的反应、疾病的复发等。在生存分析随访研究过程中,一部分研究对象可观察到死亡,可以得到准确的生存时间,它提供的信息是完全的,这种事件称为失效事件,也称之为死亡事件、终点事件。
失效事件和起始事件是相对而言的,它们都由研究目的决定,须在设计时明确规定,并在研究期间严格遵守,不能随意改变。
- 服药→痊愈
- 手术切除→死亡
- 染毒→死亡
- 化疗→缓解
- 缓解→复发
- …
生存时间
广义上指某个起点事件开始到某个终点事件发生所经历的时间,度量单位可以是年、月、日、小时等,常用符号t所示。这个时间也未必是通常意义上的时间,也可以是和时间相关的变量。比如距离等,具体要根据研究目的而定义。
- 分布类型不易确定。一般不服从正态分布,多数情况下不服从任何规则的分布类型。
- 影响因素多而复杂且不易控制。
- 根据研究对象的结局,生存时间数据可分为两种类型:
- 完全数据(Completed Data):从观察起点到发生死亡事件所经历的时间。
- 不完全数据(Incomplete Data):生存时间观察过程的截止不是由于死亡事件,而是由其他原因引起的。
- 不完全数据分为:删失数据(censored Data)和截尾数据(truncated Data)。
- 不完全主要原因:
- 失访:指失去联系;
- 退出:死于非研究因素或非处理因素而退出研究;
- 终止:设计时规定的时间已到而终止观察,但研究对象仍然存活。
删失/截尾(Censoring)
由于某些原因在随访中并没有观测到失效事件而不知道确切的生存时间,此部分数据即删失数据。常见原因有失访、患者退出试验、事件发生是由于非研究性疾病(如研究病人发生脑卒中后的生存时间,结果病人因为车祸死亡)、研究结束时研究对象仍未发生失效事件。删失数据的生存时间为起始事件到截尾点所经历的时间。
- 删失分类:
- 左删失(left censored):研究对象在某一时刻开始接受观察,但是在该时间点之前,研究所感兴趣的事件已经发生,无法明确具体时间。
- 右删失(right censored):在进行随访观察中,研究对象观察的起始时间已知,但终点事件发生的时间未知,无法获取具体的生存时间,只知道生存时间大于观察时间。
- 区间删失(interval censored):在实际的研究中,如果不能够进行连续的观察随访,只能预先设定观察时间点,研究人员仅能知道每个研究对象在两次随访区间内是否发生终点事件,而不知道准确的发生时间。
- 截尾是所有样本的综合特性,指的是观察的总体是有偏的,只有当事件的失效时间出现在观测区间内,我们才能知道这个事件及其观测数据的存在。
- 左截尾(left truncation):只能观测到一个时间点之后发生的失效事件。左截尾时间点之前发生的失效事件不知情/不关心(如样本来自退休中心,都是>60岁的老人)。
右截尾(right truncation):只能观测到一个时间点之前发生的失效事件。右截尾时间点之后发生的失效事件不知情/不关心
生存函数(Survival Function)与风险函数(Hazard Function)
生存函数也称为积累生存函数/概率(Cumulative Survival Function)或生存率,符号S(t),表示观察对象生存时间越过时间点t的概率,t=0时生存函数取值为1,随时间延长生存函数逐渐减小。以生存时间为横轴、生存函数为纵轴连成的曲线即为生存曲线。
风险函数表示生存时间达到t后瞬时发生失效事件的概率,用h(t)表示,h(t)=f(t)/S(t)。其中f(t)为概率密度函数(Probability Density Function),f(t)是F(t)的导数。F(t)为积累分布函数(Cumulative Distribution Function),F(t)=1-S(t),表示生存时间未超过时间点t的概率。累积风险函数H(t)=-logS(t)。
生存函数:
- 若含有删失数据,须分时段计算生存概率。假定观察对象在各个时段的生存时间独立,应用概率乘法定理将分时段的概率相乘得到生存率。
- 生存率与条件生存概率不同。条件生存概率是单个时段的结果,而生存率实质上是累积条件生存概率(cumulative probability of survival),是多个时段的累积结果。例如,3年生存率是第1年存活,第2年也存活,第3年还存活的可能性。
- 生存率s(t)的估计方法有参数法和非参数法。常用非参数法,非参数法主要有二个,即,乘积极限法与寿命表法,乘积极限法主要用于观察例数较少而未分组的生存资料,寿命表法适用于观察例数较多而分组的资料,不同的分组寿命表法的计算结果亦会不同,当分组资料中每一个分组区间中最多只有1个观察值时,寿命表法的计算结果与乘积极限法完全相同。
- 生存曲线(survival curve):以观察(随访)时间为横轴,以生存率为纵轴,将各个时间点所对应的生存率连接在一起的曲线图。生存曲线是一条下降的曲线,分析时应注意曲线的高度和下降的坡度。平缓的生存曲线表示高生
- 中位生存时间(Median Survival Time)/平均生存时间(Mean Survival Time):中位生存时间又称半数生存期,表示恰好一半个体未发生失效事件的时间,生存曲线上纵轴50%对应的时间。平均生存时间则表示生存曲线下的面积。
应用场景
生存分析,顾名思义,分析生存率、死亡率之类的。但这只是狭义的概念。事实上,并非所有领域都这么称呼,如社会学中经常会说事件史分析,在工业领域往往会说失效(failure)分析(所以你会发现很多软件中都是用failure和survival来标识死亡和生存)。其实都是一回事,只不过在医学中一般都叫做生存分析。
虽然名字叫生存分析,但并不是说只能分析生存、死亡的数据。所谓生存和死亡,是一个泛指。任何我们感兴趣的事件,只要有前面说的结局和结局发生时间,都可以用生存分析。
- 研究某病治疗后的复发情况,复发就是”死亡”,未复发就是”生存”。只要有复发的结局(是否复发)以及从治疗后到复发的时间,就可以用生存分析。
- 研究工作后升迁的因素有哪些,升迁就是”死亡”,未升迁就是”生存”。只要有升迁的结局(是否升迁)以及从开始工作到升迁的时间,就可以用生存分析。
- 研究戒烟后复吸的因素,复吸就是”死亡”,未复吸就是”生存”。只要有复吸的结局(是否复吸)以及从戒烟工作到复吸的时间,就可以用生存分析。
总的来说就是,只要你有一个感兴趣的结局(通常为发生和不发生),并能获得从某一时点到结局发生的时间长度,就可以用生存分析。
在互联网数据挖掘中,例如用survival analysis去预测信息在社交网络的传播程度,或者去预测用户流失的概率。
生存分析常用方法
由于生存数据是不同的数据,因此它们的方法也有各种。生存分析不是一种具体方法,而是特指的用于生存数据的很多种方法。
因变量为定量资料:
- 组间比较:t检验、方差分析
- 多因素分析:线性回归
因变量为定性资料:
- 组间比较:卡方检验
- 多因素分析:logistic回归
因边量为生存资料,同时包含定性资料(是否生存)和定量资料(生存时间):
- 组间比较:Kaplan-Meier
- 多因素分析:Cox回归
开始之前,我们再明确两个概念:
- 生存概率,即Survival probability,指的是研究对象从试验开始直到某个特定时间点仍然存活的概率,可见它是一个对时间t的函数,我们定义之为S(t);
- 风险概率,即Hazard probability,指的是研究对象从试验开始到某个特定时间t之前存活,但在t时间点发生观测事件如死亡的概率,它也是对时间t的函数,定义为H(t)。
接下来要讲的Kaplan-Meier方法主要关注S(t),而后面讲到的Cox风险比例模型则关注H(t)。
Kaplan-Meier模型
Kaplan Meier,是一种单因素生存分析。它可用于研究1个因素对于生存时间的影响,在医疗领域中使用广泛。
Kaplan–Meier方法,该方法是由Kaplan和Meier与1958年共同提出的,为理解方法的细节,我们先看下一张表(原文链接)。本例中我们以死亡作为观测事件,这张表也叫做life table.
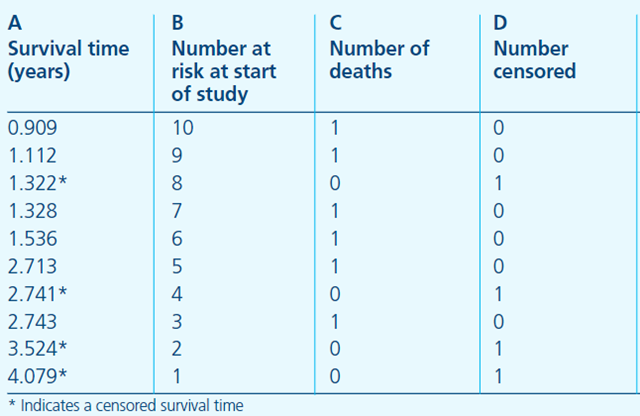
- A列是从试验开始起,持续的观测时间,星号代表在该时间有删失数据发生;
- B列是指在A列对应的时间开始之前所有存活的研究对象个数,也可以叫做at risk的人数,表示当前具有死亡风险的有效人群,是排除了已经死亡和删失的数据之后剩余的人数;
- C列为恰好在A列对应的时间死亡的人数,
- D列即表明在该时间点删失的个数。第一行则可以解读为,在909年这个时间点之前,本来有10个患者,在0.909这个时间点(或其之后的一小段时间区间)死亡了一个人,没有删失数据,意味着还剩9人;随后,只要有新增死亡或删失数据,则在表中新建一行,记录时间和人数。
我们先不引入Kaplan–Meier公式,大家可以先尝试自己去思考下如何计算每个时间节点的生存概率,即S(t)。比如在1.536年这个时间点,即表中的第五行,病人在该点的生存概率是多少呢?很容易可以想到,要想在1.536这个时间点存活,他/她必须在1.536之前的所有时间点存活才行,也就是说在0.909、1.112、1.322、1.328这几个时间点,病人都必须存活。那么在1.536这个时间点的生存概率P实际上就等于在包括1.536在内的所有之前的时间点都不死亡的概率乘积,即:
P(存活至1.536) = P(0.909时不死亡) * P(1.112时不死亡) * P(1.322时不死亡) * P(1.328时不死亡) * P(1.536时不死亡)
对于某个特定时间点不死亡的概率,可以用1–死亡概率来估算,举个例子:
P(0.909时不死亡) = 1 – P(0.909时死亡) = 1 – (0.909时死亡的人数)/(0.909之前的所有人数) = 1 – 1/10 = 0.9 P(1.112时不死亡) = 1 – P(1.112时死亡) = 1 – (1.112时死亡的人数)/(1.112之前的所有人数) = 1 – 1/9 = 0.89
需要注意的是,删失数据发生时,由于当前时间点没有发生死亡人数,该时间点对累计的生存概率不产生贡献。但由于总人数减少,会对下一个时间点的生存概率产生影响。如:
P(1.322时不死亡)=1–P(1.322时死亡)=1–(1.322时死亡的人数)/(1.322之前的所有人数)=1–0/9=1
当我们计算出每个时间点不死亡的概率之后,我们就可以通过连续乘积算出每个时间点的生存概率,即存活至该时间点的概率。如下表所示:
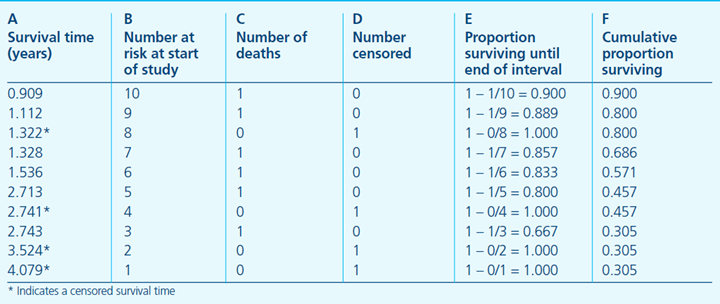
该表中 E列即不死亡概率,F列则表示累积的生存概率,可以看到随着时间增加,死亡人数增多,越到后期,生存概率越低,这是符合常理的。另外需要注意,在删失发生时,生存概率时没有变化的。
其实我们刚才的思路就是Kaplan–Meier方法的主要思路,基于刚才的表格,我们也可以用数学公式来表示。一共有m个时间点,每个时间点用下标i来表示,i为从1到m的整数,生存概率$S(t_i)$可以表示为:
$$S(t_i)=S(t_{i-1}(1-\frac{d_i}{n_i})$$
其中,$t_i$表示第i个时间点,$n_i$表示在$t_i$之前的有效人数,$d_i$表示在$t_i$死亡的人数,$S(t_{i-1})$表示在上一个时间点i-1的生存概率。
根据这一公式,我们可以画图来展示生存率的变化情况,即Kaplan-Meier生存曲线,如下图所示:
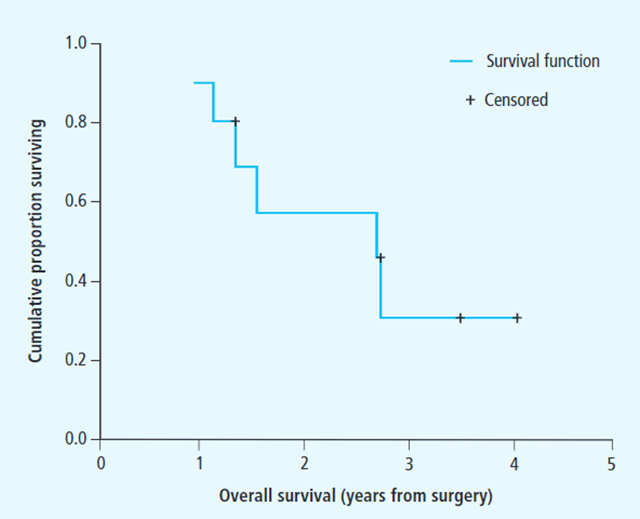
图中横轴即时间轴,纵轴是累积存活比例,也就是生存概率,加号表示删失数据。一般来说,生存分析是要比较不同组之间的一个生存情况,因此Kaplan-Meier生存曲线一般不止一条曲线,如下图所示:
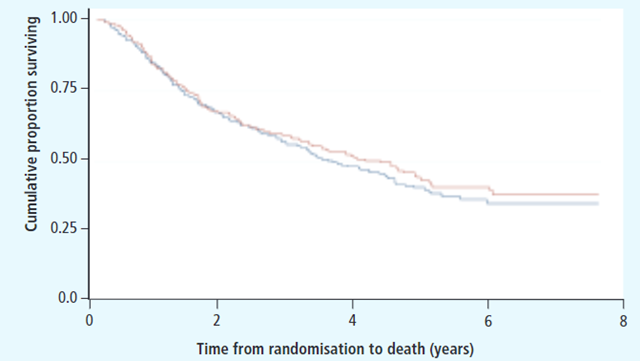
图中不同颜色表示不同的两组病人,在时间轴上生存情况的不同表现。该图中,红色和蓝色的线基本上重叠在一起,后期红色线稍微高一点,也就是说红色组的后期生存概率更高,病人死亡的相对慢一点。可以想象,如果某一组的生存情况特别差,那么它的生存曲线应该是一条极速下降的阶梯状。然而我们知道,在统计学中必须要有量化的指标来衡量差异及其显著性,不能仅通过观测来确定两组之间是否存在差异。
最直观的是来统计中位生存时间,即生存率在50%时所对应的生存时间,如下图所示:
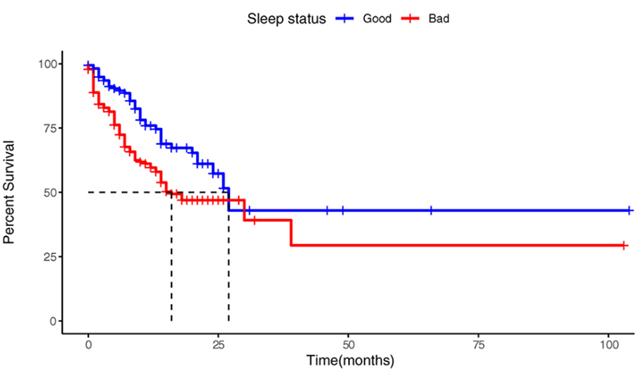
不同组别对应的中位生存时间不同,可以一定程度上反应出不同组别死亡风险的不同。如果想比较整体生存时间分布是否存在统计学差异,一般我们可以采用Logrank统计方法来对生存数据进行统计分析。
Logrank方法是由Nathan Mantel最初提出的,它是一种非参数检验,中文翻译为对数秩检验,主要用来比较两组样本的生存时间分布的差异。Logrank实际计算形式可能有不同的变体,我们这里介绍一种版本,实际上是卡方检验的一种应用场景。Logrank检验的零假设是指两组的生存时间分布完全一致,当我们通过计算拒绝零假设时,就可以认为两组的生存时间分布存在统计学差异。我们可以通过以下公式计算某组病人在某个时间点的期望死亡人数:
$$E_{1t}=N_{1t}*(O_t/N_t)$$
其中:
- $E_{1t}$是指第一组中,在时刻t,期望死亡人数;
- $N_{1t}$指第一组中t时刻at risk的人数,即t之前的存活人数;
- $O_t$则指两组(第一组和第二组)总的观测到的实际死亡人数;
- $N_t$指两组总的at risk的人数,或t时间之前两组的总人数。
如果你认真观察了公式,你就会觉得它其实浅显易懂,因为两组生存概率分布一致,因此两组总的at risk人数和两组总的死亡人数的比例,应该和单组的at risk人数和总死亡人数的比例是一致的,这也就是为什么通过两组总的比例和其中一组总的at risk的人数,就可以得到这一组期望死亡的人数,也就是上面公式所讲的内容。
有了每个时间点的死亡期望值之后,我们构造如下的卡方值:
$$\chi^2=\sum\frac{(\sum O_{jt}-\sum E_{jt})^2}{\sum E_{jt}}$$
在该公式中,外层的$\sum$是对不同组的一个叠加,内层的三个$\sum$都是对不同时间点的叠加;j代表的是第j组,比如服药组和对照组就可以分别对应j=1和j=2;这里分子上的$\sum O_{jt}$是指在j组所有时间点的观测死亡人数相加之和,是对不同时间点t对应的观测值的一个累加,比如t分别对应1天、2天、3天等等;$\sum E_{jt}$是指在j组所有时间点期望死亡人数相加之和。观测人数和期望人数的差值,就代表了实际情况与我们假设情况是否一致,如果假设是对的,即不同组的生存时间分布是完全一致的,那么观测人数和期望人数的差值会是非常小的。因为差值有正有负,所以对它取平方,这样就不会出现抵消的情况。另外,由于100和120之间相差的20,和1000和1020之间相差的20,情况并不完全一样,100和120之间的20占比达到20%,而1000和1020之间相差的20占比只达到了2%,为了让这两种情况可比较,再加一个分母即$\sum E_{jt}$,相当于转换成百分比;最后把不同组别得到的值加起来,就得到X2 值。通过查表可根据$\chi^2$值来判断是否需要拒绝零假设。
除Logrank检验之外,一种生存时间分布的常用检验包括Breslow检验,其实也就是Wilcoxon检验,与Logrank不同的是,在每个时间点统计观测人数和期望人数时,他会给它们乘以一个权重因子,即当前时间点的at risk的总人数,然后再把所有时间点加起来去统计卡方值。可以想象随着时间点越靠后,at risk的总人数会越小,因此权重越少,对X2 值的贡献就越小。因此Breslow检验对试验前期的差异要更加敏感,而相对来说Logrank对后期相对更敏感一些,因为它的所有时间点的权重参数都是1。在实际使用中,我们可以使用不同的方法从多个角度对数据去进行探究。
说到这里,Kaplan–Meier的多数知识我们已经覆盖到了。但还有一个方面可能会引起同学们的注意,如下图所示:
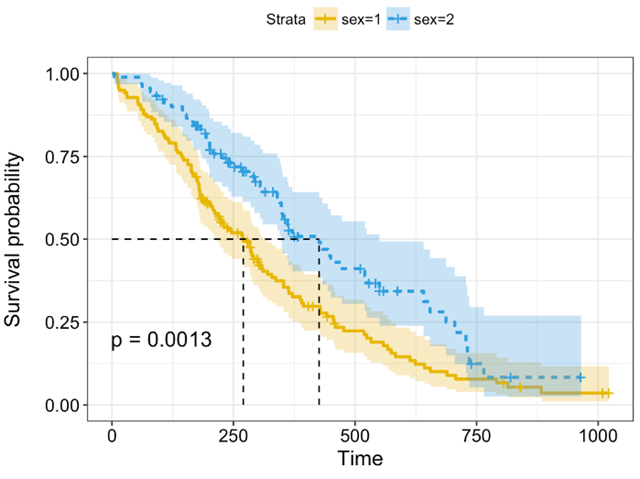 大家可能会问,上图中生存曲线周围的浅色区间是什么?实际上,上图中生存曲线周围的浅色区间即其对应的95%置信区间。首先我们需要理解为什么每个节点的生存概率会存在置信区间,因为我们假设每个时间点的生存概率是符合一种特定的分布,那么每次观测到某个时间点的结果就相当于是一次随机抽样,因为我们已经知道了生存概率对于时间t的函数S(t),通过估算标准误,我们就可以估算出某个时间点的误差范围(Margin of Error),从而得到一个特定概率的置信区间。
大家可能会问,上图中生存曲线周围的浅色区间是什么?实际上,上图中生存曲线周围的浅色区间即其对应的95%置信区间。首先我们需要理解为什么每个节点的生存概率会存在置信区间,因为我们假设每个时间点的生存概率是符合一种特定的分布,那么每次观测到某个时间点的结果就相当于是一次随机抽样,因为我们已经知道了生存概率对于时间t的函数S(t),通过估算标准误,我们就可以估算出某个时间点的误差范围(Margin of Error),从而得到一个特定概率的置信区间。
针对生存概率分布数据的置信区间估计,一种基于Greenwood提出的公式为:
$$\begin{aligned}&\widehat{S}(t)\pm z_{\alpha/2}\sqrt{\widehat{\operatorname{Var}}[\widehat{S}(t)]}\quad\text{where}\\&\widehat{\operatorname{Var}}[\widehat{S}(t)]=\widehat{S}(t)^2\sum_{t_i\leq t}\frac{d_i}{n_i(n_i-d_i)}\end{aligned}$$
其中S(t)即为生存概率函数,是我们之前解释过的不死亡概率的累计乘积。$z_{\alpha/2}$是正态分布的$\alpha/2-th$分位数,可以查表得到。
除了上面公式提到的置信区间计算方法,还有一种指数型Greenwood公式,可以解决之前计算的置信区间可能不在(0,1)区间的问题,两个公式的具体内容和推导都可以参考链接.
到目前为止,我们已经讲了生存分析的基础知识,包括生存分析应用场景、删失数据说明、生存概率和风险概率、Kaplan–Meier曲线、Log Rank和Breslow检验以及置信区间估计。但我们以上讲解的内容都是只针对单变量的,也就是说Kaplan-Meier、Log Rank只能针对单一的变量进行分析,要么按性别分组,要么按不同药物分组,但无法同时考察多个因素,或对某些可能有影响的因素进行调整。比如我们要考察新冠病毒在湖北省内外的预后差异,假设我们不知道任何其他信息,但有理由怀疑湖北省和其他省份的人口成分可能存在差异,比如湖北省老人更多、儿童更多(假设),那我们就不能直接简单的拿湖北的病例和其他省的病例去比较,必须同时考虑年龄、性别的影响,也就是说要对年龄、性别做出调整,这是之前用Log Rank无法做到的,此时Cox比例风险回归模型就要闪亮登场了。
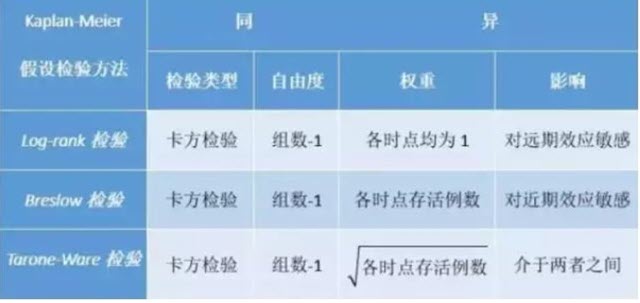
在Kaplan-Meier生存分析中有三种检验方法:log-rank、breslow、tarone。有时候会出现三种检验方法结果不一致的情况,到底取哪一个结果呢?
总的来说,这三种假设检验的方法都和属于卡方检验的方法,都需要计算各观察时间的实际死亡数和预计死亡数,并套用卡方统计量计算的公式。其计算所得统计量同样符合自由度=组数-1的卡方分布。但不同的是,每种方法的统计量具体算法不一样。Kaplan-Meier法会根据观察时点(每个病例对应随访时间)顺序,把生存资料从小到大排列来进行分析,根据时间顺序计算实际死亡数和预计死亡数。
- Log Rank检验各时点的权重均为“1”。就是不考虑各观察时点开始时存活的人数对统计模型的影响。也就是每个时点死亡情况的变化对整个模型的贡献是一样的。
- Breslow检验则在Log Rank检验的基础上增加了权重,并设置权重为各时点开始时存活的人数。也就是开始存活人数多的时点死亡情况的变化对整个模型的贡献较大,而开始存活人数少的时点死亡情况的变化对整个模型的贡献较小。
- Tarone-Ware检验是权重的取值方法介于以上两种方法之间,设置权重为各时点开始时存活的人数的平方根。同样是开始存活人数多的时点死亡情况的变化对整个模型的贡献较大,而开始存活人数少的时点死亡情况的变化对整个模型的贡献较小。只是开始存活人数多的时点对整个模型的贡献不如Breslow检验大。
上面都看不懂?没关系,我们都知道在生存分析里随着观察时间或随访时间的推移,观察时点开始时尚存活的人数会越来越少。因此,相对而言,Breslow检验研究开始时(开始存活人数多)组间差异对卡方值的影响更大,而Log Rank检验相对Breslow检验和Tarone-Ware检验,则研究后期组间差异对卡方值影响更大。也就是说,一开始粘在一起随时间推移越来越开的生存曲线Log Rank检验要比Breslow检验更容易得到差异有统计学意义的结果;而开始相差较大,随着时间推移越来越接近的生存曲线则是Breslow检验比Log Rank检验更容易得到差异有统计学意义的结果。
Cox回归
下面我们讲解Cox比例风险回归模型,英文名叫Proportional Hazards Regression analysis或Cox Proportional-Hazards Model,是由Cox于1972年提出的。我们这里简称其为Cox模型。
Cox模型是一种半参数模型,因为它的公式中既包括参数模型又包括非参数模型。简单说下参数模型和非参数模型的相同与区别。相同点是它们都是用来描述某种数据分布情况的;不同点在于,参数模型的参数是有限维度的,即有限个参数就可以表示模型分布,比如正态分布里的均值和标准差;而非参数模型的参数则属于某个无限维的空间,无法用有限参数来表示,不同的数据会得到不同的分布估计,比如决策树、随机森林等等,我们无法用有限的参数来表示所有可能的分布情况。来看看Cox模型的公式就知道为什么Cox模型是一种半参数模型了。
$$h(t)=h_0(t)\times\exp(b_1x_1+b_2x_2+…+b_px_p)$$
其中t是生存时间,$x_1$,$x_2$到$x_p$指的是具有预测效应的多个变量,$b_1$,$b_2$到$b_p$则是每个变量对应的effect size即效应量,可以理解为结果的影响程度,后面会解释。$h(t)$就是不同时间t的hazard,即风险值。而$h_0(t)$是基准风险函数,也就是说在其他协变量$x_1,x_2,…,x_p$都为0时,即不起作用时,衡量风险值的函数。根据公式我们可以看到指数部分是参数模型,因为其参数个数有限,即$b_1$,$b_2$到$b_p$,而基准风险函数$h_0(t)$由于其未确定性,可根据不同数据来使用不同的分布模型,因此是非参数模型。所以说,Cox模型是一种半参数模型。
一个需要注意的地方在于,并不是所有的生存分析数据都可以用Cox模型来分析,它是需要满足一定的假设的,大家可以带着这个疑问继续阅读,我们在文章最后对此会进行讨论。
现在我们知道了风险函数$h(t)$的公式,先解读一下这个公式。h(t)首先是基于时间变化的,t是自变量;对于某个病人,不同时间的死亡风险是不一样的,这非常好理解,肿瘤病人肯定是随着病程的进展,复发率、死亡率都会不断提高。我们可以回忆以下之前做Kaplan-Meier的那个表格,在最后的时间点生存率也越来越低,意味着风险越来越高。其次除了时间,不同年龄、性别、血压等指征不同的病人,死亡风险也不一样。比如这次的新冠病毒Covid-19,年纪越大致死率越高,这也就是为什么Cox模型要把诸多可能影响生存率的因素都当作协变量引入到公式中去,在该公式中即$x_1,x_2,…,x_p$。我们的主要目标是通过一定方法来找到合适的$h_0(t)$,以及所有协变量的系数$b_1,b_2,…,b_p$。实际上cox模型是需要用到极大似然估计等计算方法,首先构建特定的似然函数,通过梯度下降等方法来求解模型的参数,使得函数求解值最大。
假设我们已经通过计算得到了合适的$h_0(t)$和协变量系数,如何去解读结果呢?我们可以比较某个协变量$x_1$在不同值时对应的不同风险比(hazard ratio),这里比较$x_1$和$x_1+1$,即若$x_1$增加1个单位,增加前后的风险比是:
$$\text{hazard ratio}=\frac{h_0(t)*\exp(b_1(x_1+1)+b_2x_2+…+b_px_p)}{b_0(t)*\exp(b_1x_1+b_2x_2+…+b_px_p)}=\frac{\exp(b_1(x_1+1)+b_2x_2+…+b_px_p}{\exp(b_1x_1+b_2x_2+…+b_px_p)}=\exp(b_1)$$
上式中,我们对$x_1+1$和$x_1$这两个不同的值对应的风险比进行了计算,通过化简可知$x_1+1$和$x_1$对应的风险比实际上等于$\exp(b_1)$,也就是e的$b_1$次方;简单的讲,假如$x_1$指的是年龄,那么对于年龄51岁(x+1)和年龄50岁(x)的人,可能死亡的风险比为$exp(b_1)$。
- 如果$b_1>0$,则$\exp(b_1)>1$,意味着年龄+1,死亡风险增加;
- 如果$b_1=0$,则$\exp(b_1)=1$,意味着年龄变化对死亡风险不起作用。
如果$b_1<0$,则$\exp(b_1)<1$,意味着年龄+1,死亡风险降低;
因此,我们知道,对于每一个协变量,如果它的系数为正,表明对应的变量增加时,会增加病人的死亡风险(或其他事件风险,如复发、转移等);如果它的系数为负,表明对应的变量值增加时,会降低病人的死亡风险。
下面的表格是一个计算结果:
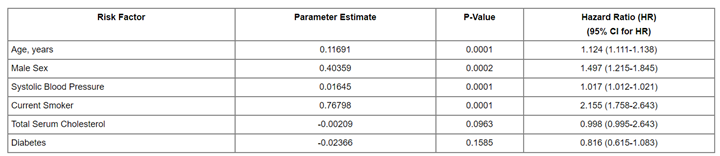
可以看到该表格中,一些风险因子包括年龄、性别、血压(收缩压)、是否抽烟、血清总胆固醇以及是否患有糖尿病,经过Cox模型计算,得到各个风险因子的参数估计,如年龄对应的参数为0.11691,也就是之前公式中的系数为0.11691,大于0表示年龄增加会增加风险,风险比(hazard ratio)为exp(0.11691)=1.124,即表格最后一列,该数值大于1,同样表明年龄增加会导致风险增加。对于二分类变量,即只有0和1,比如男性为1,女性为0,这样的变量与连续变量在Cox模型中的结果解读是一致的,如果性别对应的协变量系数大于0,表明性别值越高风险越大,也就是说男性的风险高与女性。除了关注系数外,同时需要关注的是p value,即该参数估计是否具有统计学显著性,常用来统计的方法是Likelihood ratio test,同时也有使用Wald test,和 score logrank statistics。简单介绍一下Likelihood ratio test,中文名叫似然比检验,核心思想是:为了判断都某个新变量的引入是否对于模型有效,比较变量加入前和加入后,似然函数最大值的比较,如果没有出现最大值的降低,那么则可能对模型有效,进而统计其显著性。
我们之前提到过,使用Cox模型是需要满足一定的条件的。相信大家看到这里应该已经有了答案,最重要的一个假设条件是:任意两人的风险比例是不随事件变化的,这也是为什么Cox模型全名叫Cox比例风险回归模型。举例来说,如果某个人的死亡风险比另一个人高两倍,那么不论什么时候,这个人的死亡风险都是另一个人的两倍。这样的假设我们可以从之前的公式中看到,hazard ratio推导的结果是不包括时间t的。这是Cox模型可用的一个基本假设。实际情况并非一定如此,对吧?因此我们在做Cox模型之前,最好对数据进行一个解读,看看是否满足当前假设。既然不同人之间的风险比例固定,那么一个最简单的例子就是任意分组情况下,两组的Kaplan–Meier曲线不应该相交叉,如果曲线相交叉,说明两组的生存概率关系随事件发生了变化,亦即风险比随时间发生变化,与假设相悖。然而,在实际应用中,由于样本量较小时,生存曲线会引入较大的误差,因此该判断方法有可能失效。一个更加复杂的方法为complementary log-log plot,即横轴为$\ln(t)$,纵轴为$\ln(-\ln(S(t)))$。经过推导:
$$\begin{aligned}h(t)&=h_0(t)\exp(\beta X)\\H(t)&=H0(t)\exp(\beta X)\\\log H(t)&=\log H_0(t)+\beta X\\\log[-\log S(t)]&=\log[-\log S_0(t)]+\beta X\end{aligned}$$
我们可知,不同组中,$\log(-\log(S(t)))$对于t的曲线,只有$\beta X$不同,而其与时间t无关,所以两条曲线应该近似平行或等距。
除了画生存曲线观察数据之外,我们还可以通过Schoenfeld残差来检查风险是否成比例。以及检验变量与时间的交互来作用来衡量风险比例是否固定,这里不做展开。对于不符合固定风险比例的数据,可以使用时依协变量或分层Cox模型来计算。
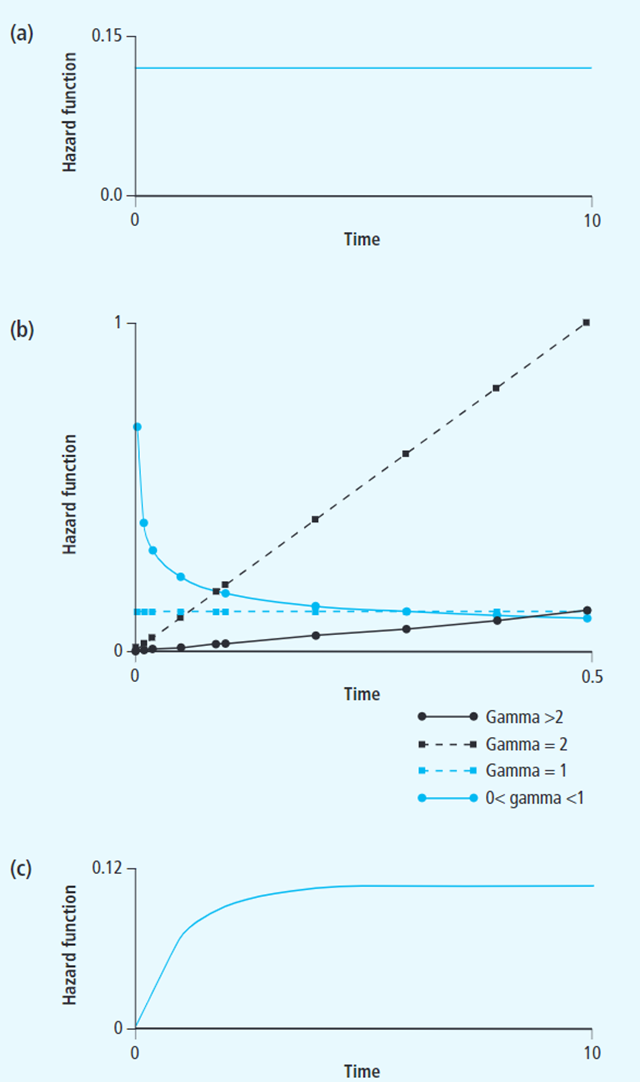
对于生存分析,除了Cox模型外,还有一些其他可用的参数模型。与Cox模型不同,这些参数模型往往给定了可能的风险函数分布,比如指数分布、Weibull和Gompertz分布,然后进一步去估计对应的模型参数。如下图所示,a为指数分布,其hazard ratio为恒定值,在实际中很少应用;b为Weibull分布,可通过不同的参数调整分布的走向;c为Gompertz分布。相对于Cox模型,使用这些模型的优点在于分布曲线可根据参数推断,可得到更多信息,比如:前期死亡率高后期死亡率低,也就是说可以得到更多关于风险分布的信息,而Cox模型只能得到有限信息,如风险比及其显著性。使用这些全参数模型的缺点也是明显的,即固定的分布不一定能满足实际的数据情况,可能带来更多的误差。再实际使用情况中,可根据不同情况进行选择。
使用PySurvival分析用户流失
这里使用的工具是PySurvival,首先遇到的问题是PySurvival包安装的非常的困难:
- Python版本:官方说是7~3.7,实际上的3.8也可以。但是超过3.8就会存在问题
- Windows上安装一直不成功。所以在WLS中进行的安装
PySurvival内部自带了一个数据集,我们就是用内部数据来分析。自带的数据来自一家Saas服务公司的客户数据,该公司的主要商业模式是每月收费。
1、加载需要使用到的包(依赖)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from pysurvival.datasets import Dataset
from pysurvival.utils.display import correlation_matrix, compare_to_actual, integrated_brier_score, create_risk_groups
from pysurvival.utils.metrics import concordance_index
from pysurvival.models.survival_forest import ConditionalSurvivalForestModel
import warnings
warnings.filterwarnings("ignore")
pd.set_option("display.precision", 2)
np.set_printoptions(precision=2, suppress=True)
pd.options.display.float_format='{:,.0f}'.format
2、加载并查看数据
df0 = Dataset("churn").load()
df0.tail()
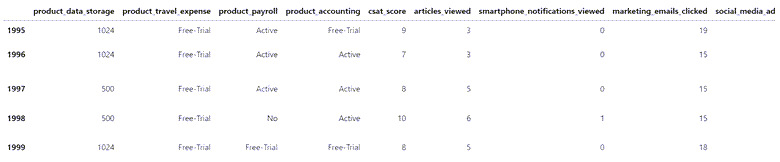
RangeIndex: 2000 entries, 0 to 1999 Data columns (total 14 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 product_data_storage 2000 non-null int64 1 product_travel_expense 2000 non-null object 2 product_payroll 2000 non-null object 3 product_accounting 2000 non-null object 4 csat_score 2000 non-null int64 5 articles_viewed 2000 non-null int64 6 smartphone_notifications_viewed 2000 non-null int64 7 marketing_emails_clicked 2000 non-null int64 8 social_media_ads_viewed 2000 non-null int64 9 minutes_customer_support 2000 non-null float64 10 company_size 2000 non-null object 11 us_region 2000 non-null object 12 months_active 2000 non-null float64 13 churned 2000 non-null float64 dtypes: float64(3), int64(6), object(5) memory usage: 218.9+ KB
数据由13列组成,其中5列是分类变量。Pandas的info()函数显示数据框不包含空值。
| 特征类别 | 特征名称 | 类型 | 描述 |
| Time | months_active | numerical | Number of months since the customer started his/her subscription |
| Event | churned | categorical | Specifies if the customer stopped doing business with the company |
| Products | product_data_storage | numerical | Amount of cloud data storage purchased in Gigabytes |
| Products | product_travel_expense | categorical | Indicates if the customer is actively using and paying for the Travel and Expense management services or not. (‘Active’, ‘Free-Trial’, ‘No’) |
| Products | product_payroll | categorical | Indicates if the customer is actively using and paying for the Payroll management services or not. (‘Active’, ‘Free-Trial’, ‘No’) |
| Products | product_accounting | categorical | Indicates if the customer is actively using and paying for the Accounting services or not. (‘Active’, ‘Free-Trial’, ‘No’) |
| Satisfaction | csat_score | numerical | Customer Satisfaction Score (CSAT) is the measure of how products and services supplied by the company meet customer expectations. |
| Satisfaction | minutes_customer_support | numerical | Minutes the customer spent on the phone with the company customer support |
| Marketing | articles_viewed | numerical | Number of articles the customer viewed on the company website. |
| Marketing | smartphone_notifications_viewed | numerical | Number of smartphone notifications the customer viewed |
| Marketing | marketing_emails_clicked | numerical | Number of marketing emails the customer opened on |
| Marketing | social_media_ads_viewed | numerical | Number of social media ads the customer viewed |
| Customer information | company_size | categorical | Size of the company |
| Customer information | us_region | categorical | Region of the US where the customer’s headquarter is located |
当我们尝试识别构成流失风险的模式时,两列将作为我们的目标变量:
- “churned”,用于识别过去未续订的客户
- “months_active”,它添加了一个时间维度,我们希望沿着该维度跟踪客户流失风险
其他列代表影响客户流失风险的特征。我们想要确定哪些特征值组合——哪些客户资料——将流失概率提高了多少。
df0.describe()
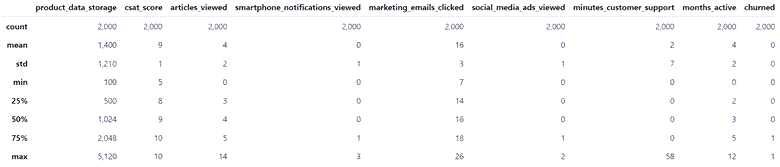
查看数值类的列,看分布:
def plot_nums(df):
numcols = list(df.dtypes[df.dtypes != np.object].index)
for col in numcols:
fig, ((ax1, ax2)) = plt.subplots(1, 2, figsize=(15, 4))
x = df[numcols].values
ax1.boxplot(x)
ax1.set_title("{}".format(col))
ax2.hist(x, bins=20)
ax2.set_title("{}".format(col))
plt.show()
plot_nums(df0)
查看类列型数据:
df0.describe(include='object').T
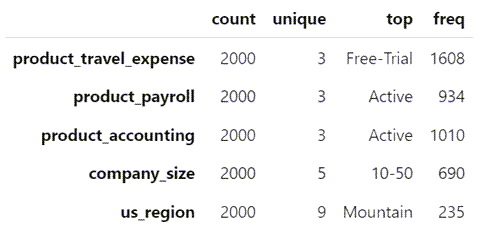
当我们查看类别数据时,发现每列中唯一值的数量很少,使它们更容易转换为数值。
数据预处理:针对类别型数据使用one-hot进行编码:
# backup the original data before modifications df1 = df0.copy() # create numerical columns from categories via one-hot encoding catcols = list(df1.dtypes[df1.dtypes == np.object].index) df1 = pd.get_dummies(df1, columns=catcols, drop_first=True) df1.info() <class 'pandas.core.frame.DataFrame'> RangeIndex: 2000 entries, 0 to 1999 Data columns (total 27 columns): # Column Non-Null Count Dtype ---------------------------- 0 product_data_storage 2000 non-null int64 1 csat_score 2000 non-null int64 2 articles_viewed 2000 non-null int64 3 smartphone_notifications_viewed 2000 non-null int64 4 marketing_emails_clicked 2000 non-null int64 5 social_media_ads_viewed 2000 non-null int64 6 minutes_customer_support 2000 non-null float64 7 months_active 2000 non-null float64 8 churned 2000 non-null float64 9 product_travel_expense_Free-Trial 2000 non-null uint8 10 product_travel_expense_No 2000 non-null uint8 11 product_payroll_Free-Trial 2000 non-null uint8 12 product_payroll_No 2000 non-null uint8 13 product_accounting_Free-Trial 2000 non-null uint8 14 product_accounting_No 2000 non-null uint8 15 company_size_10-50 2000 non-null uint8 16 company_size_100-250 2000 non-null uint8 17 company_size_50-100 2000 non-null uint8 18 company_size_self-employed 2000 non-null uint8 19 us_region_EastSouthCentral 2000 non-null uint8 20 us_region_MiddleAtlantic 2000 non-null uint8 21 us_region_Mountain 2000 non-null uint8 22 us_region_NewEngland 2000 non-null uint8 23 us_region_Pacific 2000 non-null uint8 24 us_region_SouthAtlantic 2000 non-null uint8 25 us_region_WestNorthCentral 2000 non-null uint8 26 us_region_WestSouthCentral 2000 non-null uint8 dtypes: float64(3), int64(6), uint8(18) memory usage: 175.9 KB
查看数值情况:
df1.select_dtypes(exclude="object").nunique() product_data_storage 6 csat_score 6 articles_viewed 13 smartphone_notifications_viewed 4 marketing_emails_clicked 20 social_media_ads_viewed 3 minutes_customer_support 217 months_active 13 churned 2 product_travel_expense_Free-Trial 2 product_travel_expense_No 2 product_payroll_Free-Trial 2 product_payroll_No 2 product_accounting_Free-Trial 2 product_accounting_No 2 company_size_10-50 2 company_size_100-250 2 company_size_50-100 2 company_size_self-employed 2 us_region_EastSouthCentral 2 us_region_MiddleAtlantic 2 us_region_Mountain 2 us_region_NewEngland 2 us_region_Pacific 2 us_region_SouthAtlantic 2 us_region_WestNorthCentral 2 us_region_WestSouthCentral 2 dtype: int64
3、数据加工处理:确定目标列和在特征中取出目标
我们通过分离目标变量来完成我们的数据整理工作:
- “事件”——在我们的示例中,“churned”=1或0
- 时间维度:“months_active”
然后第6行中的numpy函数setdiff1d()从所有列名列表中删除“churned”和“months_active”,留下特征列列表。
# target variables: months_active and churns time_column = 'months_active' event_column = 'churned' # list of feature columns: excluding the target columns features = np.setdiff1d(df1.columns, [time_column, event_column]).tolist() X = df1[features] X.tail()
4、查看特征间的相关性
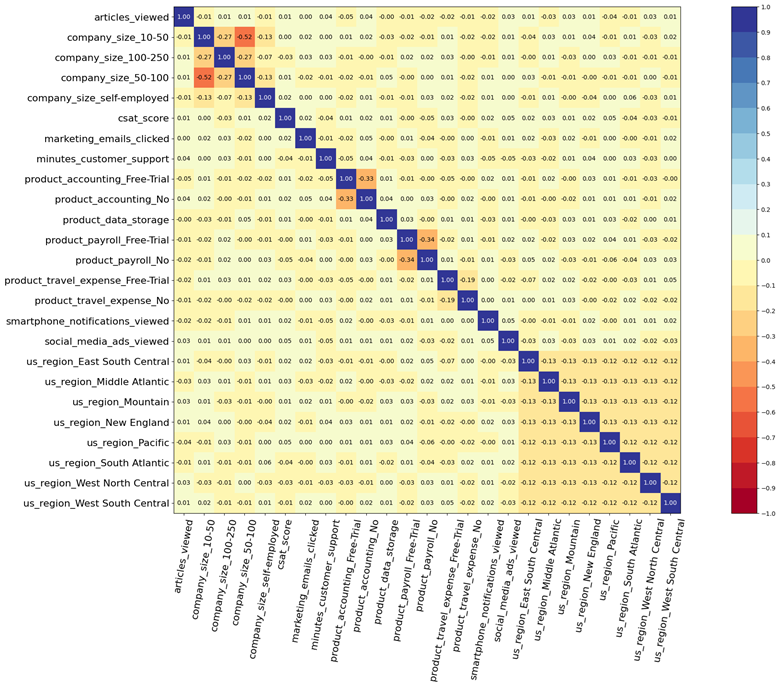
在PySurvival自带的函数中,我们找到了相关矩阵。它显示了特征的对齐程度。如果任何一对表现出惊人的高相关性,接近1.0,我们应该删除其中一个以处理它们的多重共线性。在我们的例子中,中型和大型客户公司之间的最高相关性没有超过0.52。这不是一个惊人的水平,所以我们继续我们的分析。
# correlation matrix of the features correlation_matrix(df1[features], figure_size=(30, 15), text_fontsize=10)
5、准备模型数据
数据预处理:区分训练集和验证集
# sklearn: train vs test split N = df1.shape[0] idx_train, idx_test = train_test_split(range(N), test_size=0.35) df_train = df1.loc[idx_train].reset_index(drop=True) df_test = df1.loc[idx_test].reset_index(drop=True) # features, times (months active), and churn events: isolate the X, T and E variables X_train, X_test = df_train[features], df_test[features] T_train, T_test = df_train[time_column], df_test[time_column] # when did the Churn event occur? E_train, E_test = df_train[event_column], df_test[event_column] # v did the Churn event occur?
6、训练模型
生存问题增加了一个困难:模型必须处理审查数据。当数据集达到观察期结束时,许多(希望是大多数)客户不会流失。他们的流失事件仍未被观察到,并将发生在未知的未来日期。因此,数据集是右删失的。
为了处理审查,生存模型使用修改后的配置:
- 传统的回归模型对两个数据数组X和y进行操作:回归量X和目标向量y。
- 而生存模型对三个变量X、E和T进行操作:
- 特征数组X(由代表属性或客户资料的列组成)
- 二进制事件指示符向量E(1或0),表示是否已为客户记录流失事件;
- 时间向量T=min(t,c),其中t表示事件时间,c表示审查时间
生存模型预测感兴趣的事件在时间t发生的概率。
# fitting a survival forest model model = ConditionalSurvivalForestModel(num_trees=200) model.fit( X_train, T_train, E_train, max_features="sqrt", # number of features randomly chosen at each split (int, float, "sqrt", "log2", or "all") max_depth=5, # min_node_size=20, # minimum number of samples at leaf node alpha=0.05, # significance threshold to allow splitting seed=42, # seed for random variable generator sample_size_pct=0.63, # % of original samples used in each tree building num_threads=-1 # number of jobs to run; if -1, then all available cores will be used )
4、测试模型质量
C-index,英文名全称concordance index,中文里有人翻译成一致性指数,最早是由范德堡大学(Vanderbilt University)生物统计教教授Frank E Harrell Jr 1996年提出,主要用于计算生存分析中的COX模型预测值与真实之间的区分度(discrimination),和大家熟悉的AUC其实是差不多的;在评价肿瘤患者预后模型的预测精度中用的比较多。
C-index的计算方法是把所研究的资料中的所有研究对象随机地两两组成对子,以生存分析为例,两个病人如果生存时间较长的一位其预测生存时间长于另一位,或预测的生存概率高的一位的生存时间长于另一位,则称之为预测结果与实际结果相符,称之为一致。
C-index在0.5-1之间(任意配对随机情况下一致与不一致刚好是0.5的概率)。0.5为完全不一致,说明该模型没有预测作用,1为完全一致,说明该模型预测结果与实际完全一致。一般情况下C-index:
- 在50-0.70为准确度较低
- 在71-0.90之间为准确度中等
- 高于90则为高准确度
跟相关系数有点类似。
Brier Score(mean squared error)跟L2 loss很像。
$$BS=\frac{1}{N}\sum_{t=1}^N(\hat{y}_t-y_t)^2$$
$$L2 loss=\sum_{t=1}^N(\hat{y}_t-y_t)^2$$
Brier Score的出来的范围是[0,1]之间,然后Brier Score越小则模型准确率越高。
因为BS(t)是只考虑在时间点t的时候BS是多少,但是生存概率是一个时间范围内,如果我们想知道整个时间段的生存概率是否正确,我们可以用IBS
当我们只考虑uncensor病人,也就是有event的病人:
$$IBS(\tau,V_U,\hat{S}(\cdot\mid\cdot))=\frac{1}{\tau}\int_0^\tau BS_t(V_U,\hat{S}(t\mid\cdot))dt$$
# testing: model quality - prediction error measures by concordance index and Brier score
ci = concordance_index(model, X_test, T_test, E_test)
print("concordance index: {:.2f}".format(ci))
ibs = integrated_brier_score(model, X_test, T_test, E_test, t_max=12, figure_size=(15,5))
print("integrated Brier score: {:.2f}".format(ibs))
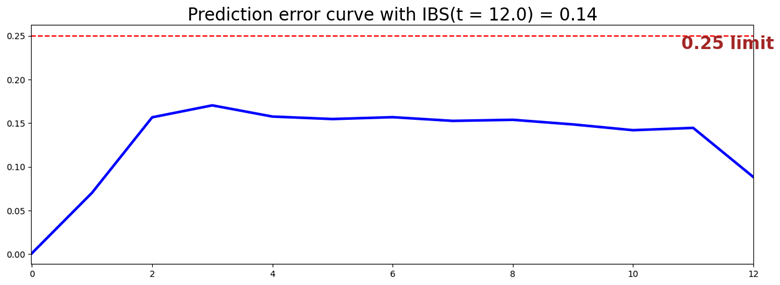
- concordance index: 0.83
- integrated Brier score: 0.14
PySurvival的compare_to_actual 方法沿时间轴绘制风险客户的预测和实际数量。它还计算三个准确度指标,RMSE、MAE和中值绝对误差。在内部,它计算Kaplan-Meier估计量以确定源数据的实际生存函数。
# testing: model quality - actual vs predicted churn events
res = compare_to_actual(
model,
X_test,
T_test,
E_test,
is_at_risk=False, # True: return the expected number of customers at risk
figure_size=(16,6),
metrics=["rmse","mean","median"]) # root mean square error, mean abs error, median abs error
print("accuracy metrics:")
_ = [print(k, ":", f'{v:.2f}') for k, v in res.items()]
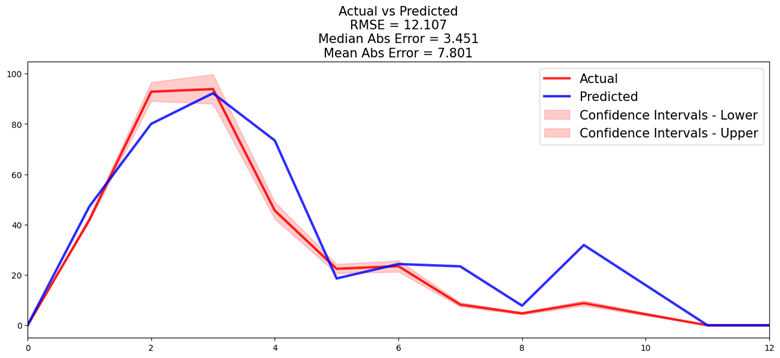
accuracy metrics: root_mean_squared_error: 12.11 median_absolute_error: 3.45 mean_absolute_error: 7.80
6、模型结果:特征重要性
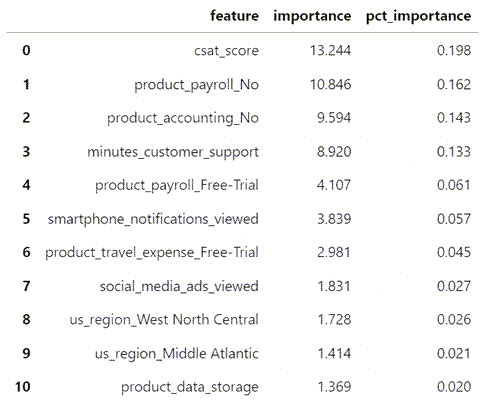
拟合模型报告数据框中每个特征的重要性。重要性衡量特征对流失风险的影响。正重要性分数会增加风险,负分数会减轻风险。
“pct_importance”列标识在0到1的范围内校准相对重要性。相对重要性加起来为1.0。
- csat_score——通过营销调查衡量的客户满意度得分——与客户流失风险密切相关。
- product_payroll_No和product_accounting_No,不清楚这整个维度具体什么意思。
- minutes_customer_support表示那些在取消订阅之前经常向支持热线投诉的客户存在高流失风险。
# model results: variable importance
# positive: increase the risk; negative: alleviate the risk
pd.options.display.float_format = '{:,.3f}'.format
model.variable_importance_table
7、预测个体的生存函数、危险函数和风险评分
如果我们将时间变量t设置为None,那么PySurvival将计算数据帧中所有时间段的函数值并显示它们的趋势——在我们的示例中长达12个月。
# survival function, hazard function and risk score for a randomly drawn individual
k = np.random.choice(df1.index)
# t = number of time periods for which to show the probabilities
# if t = None, then t = maximum number of "months active" in dataset
svf = model.predict_survival(X.values[k,:], t=None) # survival function over time
hzf = model.predict_hazard(X.values[k,:], t=None) # hazard function over time
risk = model.predict_risk(X.values[k,:]) # risk score (scalar)
df_risk = pd.DataFrame()
df_risk["svf"] = svf.flatten().tolist()
df_risk["hzf"] = hzf.flatten().tolist()
df_risk.insert(2, "risk", risk.item())
print("risk score, and survival and hazard functions over time, for customer", k, ":")
df_risk
8、计算每个用户的在4个时期的生存函数和风险分值
# compute every customer's survival function and risk score for 4 chosen periods (active months)
T = [1, 3, 6, 12]
for t in T:
svf = model.predict_survival(X.values, t=t) # survival function over time
df1["svf"+str(t)] = svf
df1["risk"] = model.predict_risk(X.values) # risk score
df1.tail()
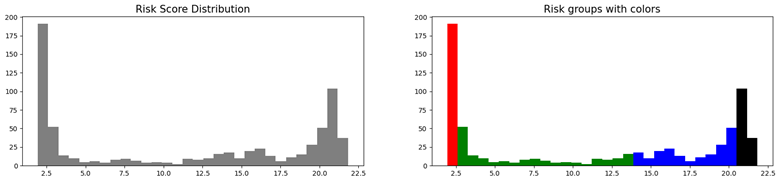
按用户的质量进行分组:
# predictions: customer quartiles, grouped by their risk scores
q1 = df1["risk"].quantile(0.25)
q2 = df1["risk"].quantile(0.50)
q3 = df1["risk"].quantile(0.75)
q4 = df1["risk"].max()
risk_groups = create_risk_groups(
model=model,
X=X_test,
use_log=False,
num_bins=30,
figure_size=(20,4),
q1={'lower_bound':0, 'upper_bound':q1, 'color':'red'},
q2={'lower_bound':q1, 'upper_bound':q2, 'color':'green'},
q3={'lower_bound':q2, 'upper_bound':q3, 'color':'blue'},
q4={'lower_bound':q3, 'upper_bound':q4, 'color':'black'}
)
使用Lifelines进行生存分析实战
lifelines简介
lifelines是Python中使用较多的生存分析包,其核心功能主要有:
| 模块 | 描述 | 类型 | 方法 |
| survival function | 研究对象从试验开始直到某个特定时间点仍然存活的概率 | 参数估计 | Exponential, Log-Logistic, Log-Normal and Splines |
| 非参数估计 | Kaplan-Meier估计 | ||
| cumulative hazard | 风险函数的估计值 | 参数估计 | Exponential, Log-Logistic, Log-Normal and Splines |
| 非参数估计 | Nelson-Aalen估计 | ||
| Survival regression | 会加入额外的协变量(如年龄、国家等)与另一个变量进行回归 | 比例回归 | Cox比例风险回归模型,指数回归模型,Weibull回归模型,Poisson回归模型 |
| 非比例回归 | 含参数与半参模型:Aalen’s Additive model模型、Cox Time Varying时变模型、AFT (accelerated failure time model)加速失效模型 |
数据预览
数据集:IBM Watson电信客户演示数据集WA_Fn-UseC_-Telco-Customer-Churn.csv
对于每个客户,我们需要两个重要的数据点进行生存分析:
- “Tenure”:观察数据时他们成为客户的时间
- “Churn”:观察数据时客户是否离开
1、加载数据看一些基础的数据情况
import pandas as pd
data = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
data.info()
data.head() #列太多,看不全
data.head().transpose() #行转列,显示TOP5数据
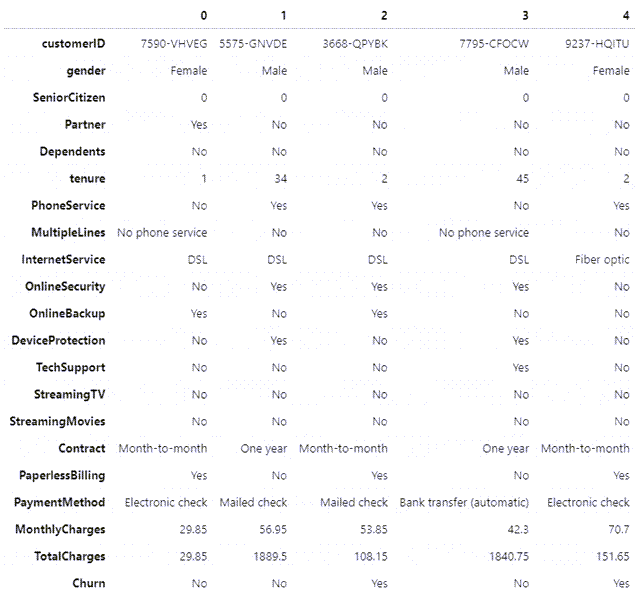
2、去除不需要的customerID列
data['customerID'].duplicated().any() #判断是否有重复
data = data.drop("customerID", axis=1) #去除列
3、数据类型转化及去除空值行
data.TotalCharges = pd.to_numeric(data.TotalCharges, errors='coerce') #将字符串数值转化为数字 data.isnull().sum() #统计null值数量 data.dropna(inplace=True)
4、显示类别型特征的类别情况
summary_categorical = []
for column in data.columns:
if data[column].dtype == object:
summary_categorical.append(column)
print(data[column].value_counts())
print(f"----------------------------------")
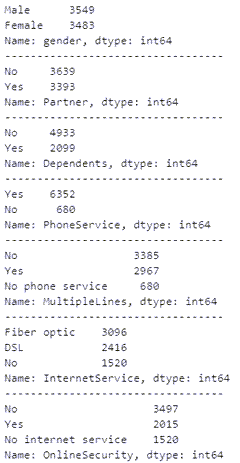
二值类类别特征的转换:
data['gender'].replace(to_replace='Male', value=1, inplace=True)
data['gender'].replace(to_replace='Female', value=0, inplace=True)
binary_features = ['Partner','Dependents','PhoneService','MultipleLines','OnlineSecurity','OnlineBackup','DeviceProtection','TechSupport',
'StreamingTV','StreamingMovies','PaperlessBilling','Churn']
for feat in binary_features:
data[feat].replace(to_replace='Yes', value=1, inplace=True)
data[feat].replace(to_replace=r'No', value=0, regex=True, inplace=True)
data.head().transpose()
其他类别型特征转换:
data_dummies = pd.get_dummies(data) data_dummies.head() data_dummies.info()
5、查看特征间的相关性
import matplotlib.pyplot as plt
import seaborn as sns
corr = data_dummies.corr()
sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot=True, annot_kws={'size':12})
heat_map = plt.gcf()
heat_map.set_size_inches(20,15)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
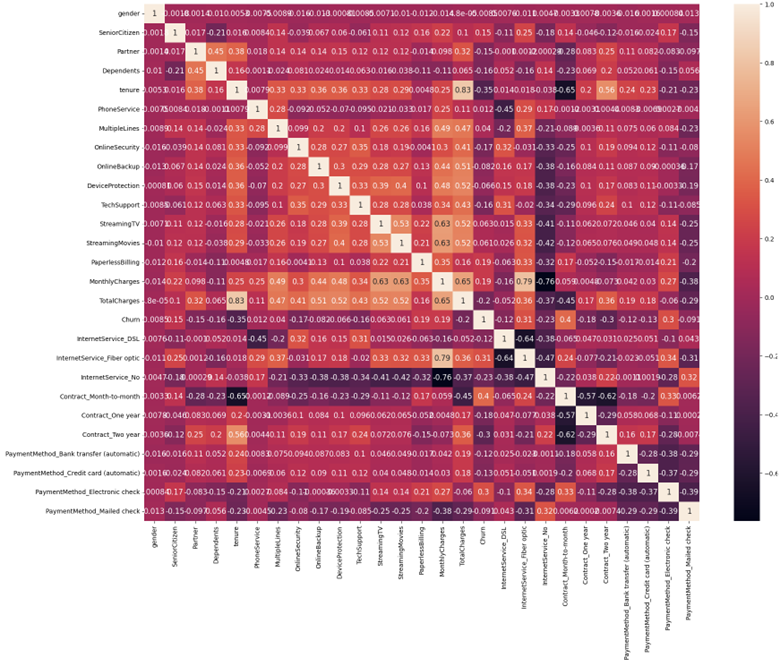
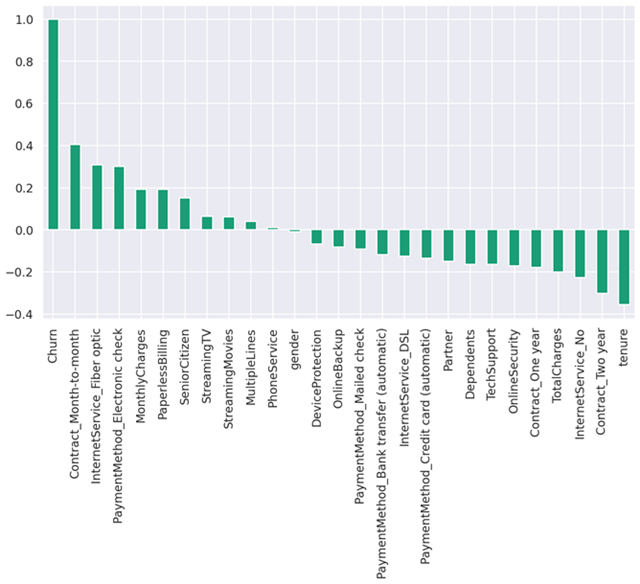
查看与”Churn”的相关性:
#Checking again Correlation of "Churn" with other variables on a different plot sns.set(style='darkgrid', context='talk', palette='Dark2') plt.figure(figsize=(15,8)) data_dummies.corr()['Churn'].sort_values(ascending=False).plot(kind='bar')
类别型特征与”Churn”的相关性:
columns_to_visualise = ['gender','SeniorCitizen','Partner','Dependents',
'PhoneService','MultipleLines','InternetService','OnlineSecurity',
'OnlineBackup','DeviceProtection','TechSupport','StreamingTV',
'StreamingMovies','Contract','PaperlessBilling','PaymentMethod']
for column in columns_to_visualise:
plot_data = data.groupby([column,'Churn']).size().reset_index().pivot(columns='Churn', index=column, values=0)
plot_data.plot.bar(stacked=True, rot=45)
plt.show()
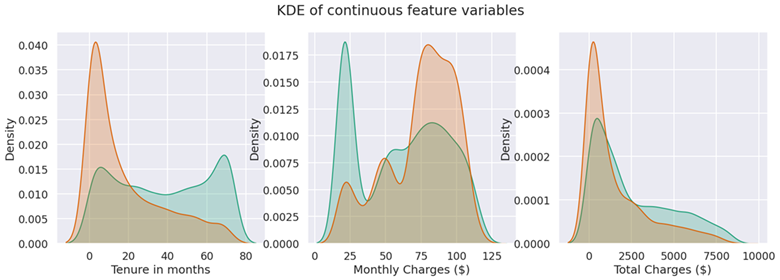
数值型特征与”Churn”的相关性:
# Visualise the numerical features
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20, 6))
fig.suptitle("KDE of continuous feature variables")
# tenure
sns.kdeplot(data['tenure'].loc[data['Churn'] == 0], label='not churn', fill=True, ax=ax1)
sns.kdeplot(data['tenure'].loc[data['Churn'] == 1], label='churn', fill=True, ax=ax1)
ax1.set_xlabel("Tenure in months")
# monthly charges
sns.kdeplot(data['MonthlyCharges'].loc[data['Churn'] == 0], label='not churn', fill=True, ax=ax2)
sns.kdeplot(data['MonthlyCharges'].loc[data['Churn'] == 1], label='churn', fill=True, ax=ax2)
ax2.set_xlabel("Monthly Charges ($)")
# total charges
sns.kdeplot(data['TotalCharges'].loc[data['Churn'] == 0], label='not churn', fill=True, ax=ax3)
sns.kdeplot(data['TotalCharges'].loc[data['Churn'] == 1], label='churn', fill=True, ax=ax3)
ax3.set_xlabel("Total Charges ($)")
数值型特征的分布情况:
# Check for any outliers in any of the continuous variables continuous_labels = ['tenure', 'MonthlyCharges', 'TotalCharges'] i = 1 plt.figure(figsize=(15, 15)) for var in continuous_labels: # plotting boxplot for each variable plt.subplot(3, 4, i) plt.boxplot(data[var], whis=5) plt.title(var) i += 1 plt.tight_layout()
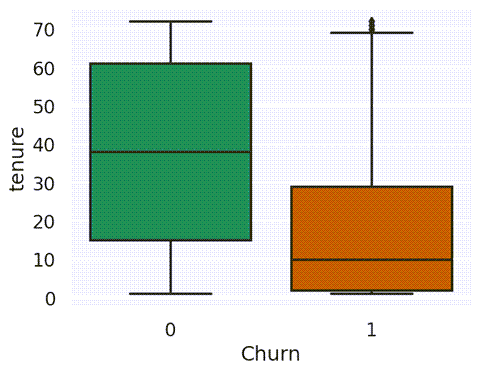
continuous_labels = ['tenure', 'MonthlyCharges', 'TotalCharges'] for var in continuous_labels: sns.boxplot(x=data['Churn'], y=data[var]) plt.show()
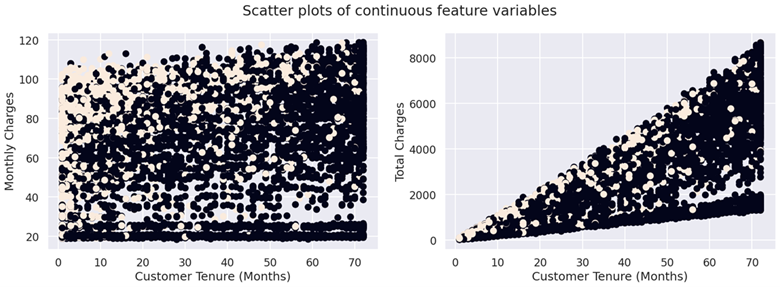
# Visualise scatterplots of tenure against monthly and total charges based on churn
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
fig.suptitle("Scatterplots of continuous feature variables")
# MonthlyCharges
ax1.scatter(data['tenure'], data['MonthlyCharges'], c=data['Churn'])
ax1.set_xlabel('Customer Tenure (Months)')
ax1.set_ylabel('Monthly Charges')
# TotalCharges
ax2.scatter(data['tenure'], data['TotalCharges'], c=data['Churn'])
ax2.set_xlabel('Customer Tenure (Months)')
ax2.set_ylabel('Total Charges');
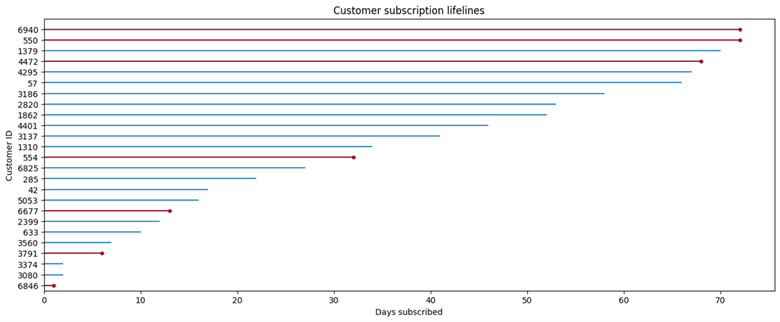
随机显示25个用户的生存情况:
import matplotlib.pyplot as plt
from lifelines.plotting import plot_lifetimes
time = data['tenure'].sample(25, replace=False)
status = data['Churn'].sample(25, replace=False)
plt.figure(figsize=(16, 6));
plot_lifetimes(time, status)
plt.xlabel('Days subscribed');
plt.ylabel('Customer ID');
plt.title('Customer subscription lifelines')
使用逻辑回归进行流失预测
1、准备数据并进行逻辑回归
# Using the dataframe where we had created dummy variables
y = data_dummies['Churn'].values
X = data_dummies.drop(columns=['Churn'])
# Scaling all the variables to a range of 0 to 1
from sklearn.preprocessing import MinMaxScaler
features = X.columns.values
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(X)
X = pd.DataFrame(scaler.transform(X))
X.columns = features
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=101, stratify=y)
print('length of X_train and x_test:', len(X_train), len(X_test))
print('length of y_train and y_test:', len(y_train), len(y_test))
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn import metrics
model = LogisticRegression(solver='lbfgs', max_iter=1000)
result = model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print("Prdiction:", metrics.accuracy_score(y_test, y_pred))
print("Precision:", metrics.precision_score(y_test, y_pred))
print("Recall:", metrics.recall_score(y_test, y_pred))
print('Intercept:' + str(result.intercept_)) # reporting the intercept
print('Regression:' + str(result.coef_)) # reporting the co-efficients
2、查看模型的质量
import itertools
import numpy as np
# Evaluation of Model - Confusion Matrix Plot
def plot_confusion_matrix(cm, classes, title='Confusion matrix', normalize=False, cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, prediction_test)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['No Churn','Churn'], title='Confusion matrix, with normalized data')
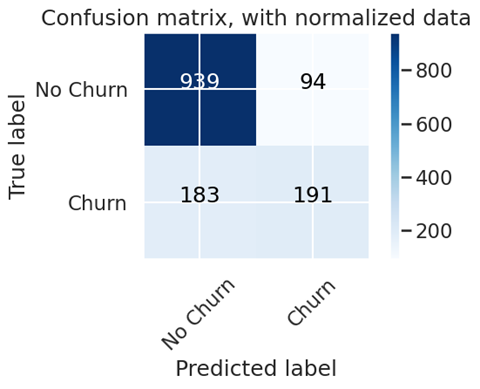
输出重要的特征:
# To get the weights of all the variables weights = pd.Series(model.coef_[0], index=X.columns.values) weights.sort_values(ascending=False)
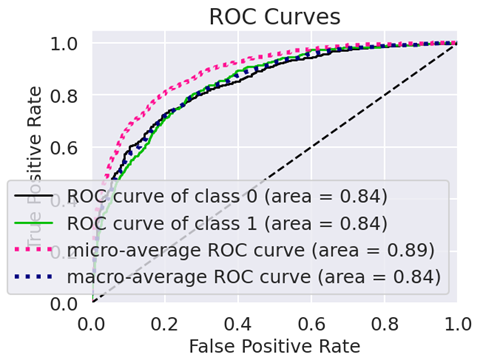
查看ROC图:
# !pip install scikit-plot import scikitplot as skplt # to make things easy y_pred_proba = model.predict_proba(X_test) skplt.metrics.plot_roc_curve(y_test, y_pred_proba)
3、将数据调整到平衡后再进行一轮模型测试
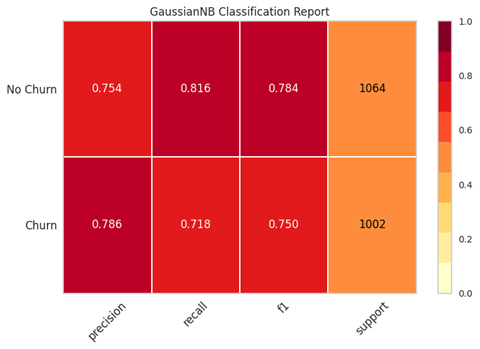
data_dummies['Churn'].value_counts() from sklearn.utils import resample data_majority = data_dummies[data_dummies['Churn'] == 0] data_minority = data_dummies[data_dummies['Churn'] == 1] data_minority_upsampled = resample(data_minority, replace=True, n_samples=5163, # same number of samples as majority class random_state=1) # set the seed for random resampling # Combine resampled results data_upsampled = pd.concat([data_majority, data_minority_upsampled]) data_upsampled['Churn'].value_counts() data_upsampled.head().transpose() from sklearn.metrics import classification_report train, test = train_test_split(data_upsampled, test_size=0.20) train_y_upsampled = train['Churn'].values test_y_upsampled = test['Churn'].values train_x_upsampled = train.drop(columns=['Churn']) test_x_upsampled = test.drop(columns=['Churn']) logisticRegr_balanced = LogisticRegression(solver='lbfgs', max_iter=1000) logisticRegr_balanced.fit(X=train_x_upsampled, y=train_y_upsampled) test_y_pred_balanced = logisticRegr_balanced.predict(test_x_upsampled) # !pip install yellowbrick from sklearn.naive_bayes import GaussianNB from yellowbrick.classifier import ClassificationReport classes = ['Churn', 'NoChurn'] # Instantiate the classification model and visualizer bayes = GaussianNB() visualizer = ClassificationReport(bayes, classes=classes, support=True) visualizer.fit(train_x_upsampled, train_y_upsampled) # Fit the visualizer and the model visualizer.score(test_x_upsampled, test_y_upsampled) # Evaluate the model on the test data g = visualizer.poof() # Draw/show/poof the data
from sklearn.metrics import roc_auc_score
# Get class probabilities for both models
test_y_prob = model.predict_proba(X_test)
test_y_prob_balanced = model.predict_proba(test_x_upsampled)
# We only need the probabilities for the positive class
test_y_prob = [p[1] for p in test_y_prob]
test_y_prob_balanced = [p[1] for p in test_y_prob_balanced]
print('Unbalanced model AUROC: ' + str(roc_auc_score(y_test, test_y_prob)))
print('Balanced model AUROC: ' + str(roc_auc_score(test_y_upsampled, test_y_prob_balanced)))
from sklearn.model_selection import cross_val_score
# evaluate the model using 10-fold cross-validation
scores = cross_val_score(result, X_train, y_train, scoring='accuracy', cv=10)
print('10 fold cross-validation scores:', scores)
print('Mean of scores:', scores.mean())
为什么不使用OLS线性回归?
OLS通过绘制最小化平方误差项总和的回归线来工作。然而,对于未观察到的数据,无法知道误差项,因此不可能最小化这些值。
简单地将审查日期作为所有受试者已知的有效最后一天,或者更糟糕的是放弃所有被审查的受试者可能会使我们的结果产生偏差。
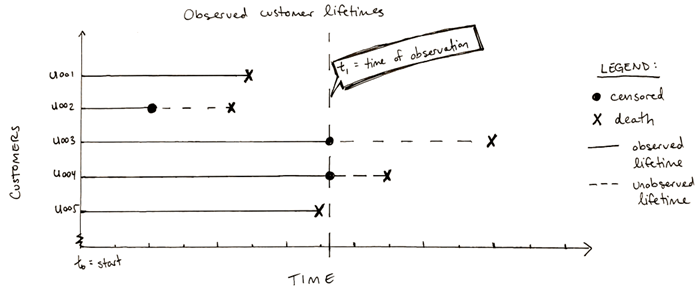
在上图中,U002从丢失到跟进(可能是由于,例如,由于帐户上的一个未解决的技术问题导致客户在数据提取时的状态未知)被审查,U003和U004被审查因为他们是现有客户。截至t1,只有U001和U005都观察到了出生和死亡。如图所示,丢弃未观察到的数据会低估客户的生命周期并使我们的结果产生偏差。
生存分析完美地处理事件审查。被审查的顾客是没有观察到死亡的顾客。这可能发生的主要方式是如果客户的生命周期在观察时尚未完成。(注意在临床试验中,失访或退出研究的患者也被认为是审查过的。)
生存分析在我们可以定义的情况下效果很好:
- “出生”事件:对于我们的应用程序,这将是客户与公司签订合同
- “死亡”事件:对我们而言,“死亡”是客户结束与公司的关系
使生存分析优于其他回归模型的组成部分是它处理数据审查的能力。
Kaplan-Meier (KM) 生存分析
Kaplan是完全参数化的,也是计算生存或“无流失”的最简单方法。Kaplan-Meier生存曲线定义为在给定时间长度内“没有流失”的概率,同时考虑许多小区间的时间。对于每个时间间隔,“无流失”概率计算为保留的用户数除以有离开风险的用户数。
对于每个主题(或客户或用户)只能有一个“出生”(注册、激活或注册)和一个“死亡”(无论是否观察到)的任何问题,第一个最好的起点是Kaplan-Meier曲线。这将使我们能够估计一个或多个队列的“生存函数”,它是生存分析中最常用的统计技术之一。
Kaplan-Meier的优点:
- 需要最少的功能集。Kaplan-Meier只需要事件发生的时间(死亡或审查)以及出生和事件之间的生命周期。
- 许多时间序列分析难以实施。Kaplan-Meier只需要所有事件都在同一时间段内发生
- 自动处理类别不平衡(死亡与审查事件的任何比例都可以)
- 因为它是一种非参数方法,所以很少对数据的基本分布做出假设
Kaplan-Meier的缺点:
- 无法估计感兴趣的生存预测关系的差异幅度(无风险比或相对风险)
- 在事件发生时间研究中,不能同时考虑每个受试者的多个因素,也不能控制混杂因素
- 假设审查和生存之间是独立的,这意味着在时间t,那些被审查的人应该与那些没有被审查的人有相同的预后。
- 因为它是一个非参数模型,所以在底层数据分布已知的问题上,它不如竞争技术那么有效或准确
import lifelines
from lifelines import KaplanMeierFitter
# fitting kmf to churn data
t = data['tenure']
churn = data['Churn']
kmf = lifelines.KaplanMeierFitter()
kmf.fit(t, churn, label='Estimate for Average Customer')
# plotting kmf curve
fig, ax = plt.subplots(figsize=(10,7))
kmf.plot(ax=ax)
ax.set_title('Kaplan-Meier Survival Curve—All Customers')
ax.set_xlabel('Customer Tenure-Months')
ax.set_ylabel('Customer Survival Chance(%)')
plt.show()
我们将通过首先绘制样本的KM曲线来开始我们的生存分析,该曲线向我们显示普通客户在特定时间点的历史生存概率。请记住,协变量的存在对KM曲线没有影响,因为它只与持续时间和事件标志有关。通常,在实践中,首先查看KM曲线以了解我们的数据,然后再通过CPH模型进行更深入的分析。我们针对所有客户的第一条KM曲线,置信区间为5%,如下所示:
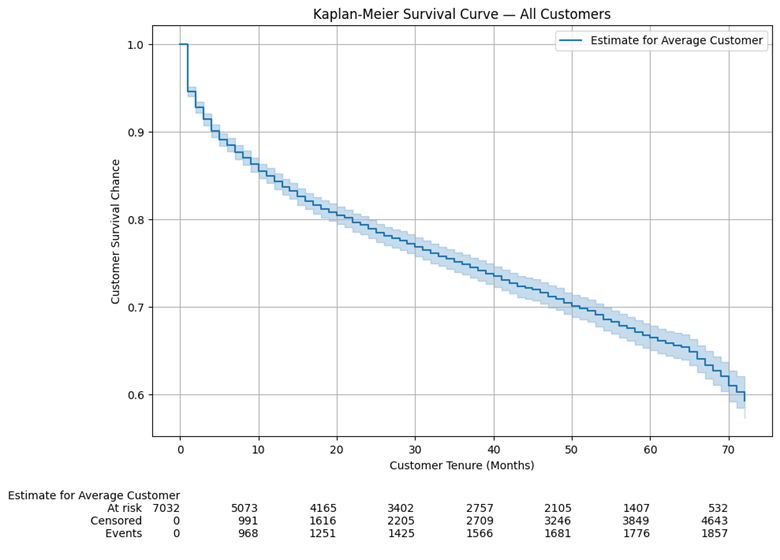
图底部的行显示了一些附加信息,解释如下:
- 处于风险中:观察到的任期超过该时间点的客户数量。例如,532位客户的任期超过70个月
- 已审查:未流失的任期等于或小于该时间点的客户数量。例如,3,860名客户的任期为60个月或更短,但他们当时并没有流失
- 事件:使用期限等于或小于该时间点的客户数量,该时间点已经流失。例如,1,681名客户的任期为50个月或更短,并且在那时已经流失
在这一点上,我们不知道我们的哪些协变量对我们客户的生存机会有重大影响(CPH模型将帮助我们)。但是,直观地我们知道,可以预期拥有更长的固定期限合同会影响客户的生存概率。为了检查这种潜在影响,我们将为Contract列的每个唯一值绘制KM曲线:
# save indices for each contract type
idx_m2m = data['Contract'] == 'Month-to-month'
idx_1y = data['Contract'] == 'One year'
idx_2y = data['Contract'] == 'Two year'
# plot the 3 KM plots for each category
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(10,10))
kmf_m2m = lifelines.KaplanMeierFitter()
ax = kmf_m2m.fit(durations=data.loc[idx_m2m,'tenure'], event_observed=data.loc[idx_m2m,'Churn'], label='Month-to-month').plot(ax=ax)
kmf_1y = lifelines.KaplanMeierFitter()
ax = kmf_1y.fit(durations=data.loc[idx_1y,'tenure'], event_observed=data.loc[idx_1y,'Churn'], label='One year').plot(ax=ax)
kmf_2y = lifelines.KaplanMeierFitter()
ax = kmf_2y.fit(durations=data.loc[idx_2y,'tenure'], event_observed=data.loc[idx_2y,'Churn'], label='Two year').plot(ax=ax)
# display title and labels
ax.set_title('KM Survival Curve by Contract Duration')
ax.set_xlabel('Customer Tenure (Months)')
ax.set_ylabel('Customer Survival Chance')
plt.grid()
lifelines.plotting.add_at_risk_counts(kmf_m2m, kmf_1y, kmf_2y, ax=ax)
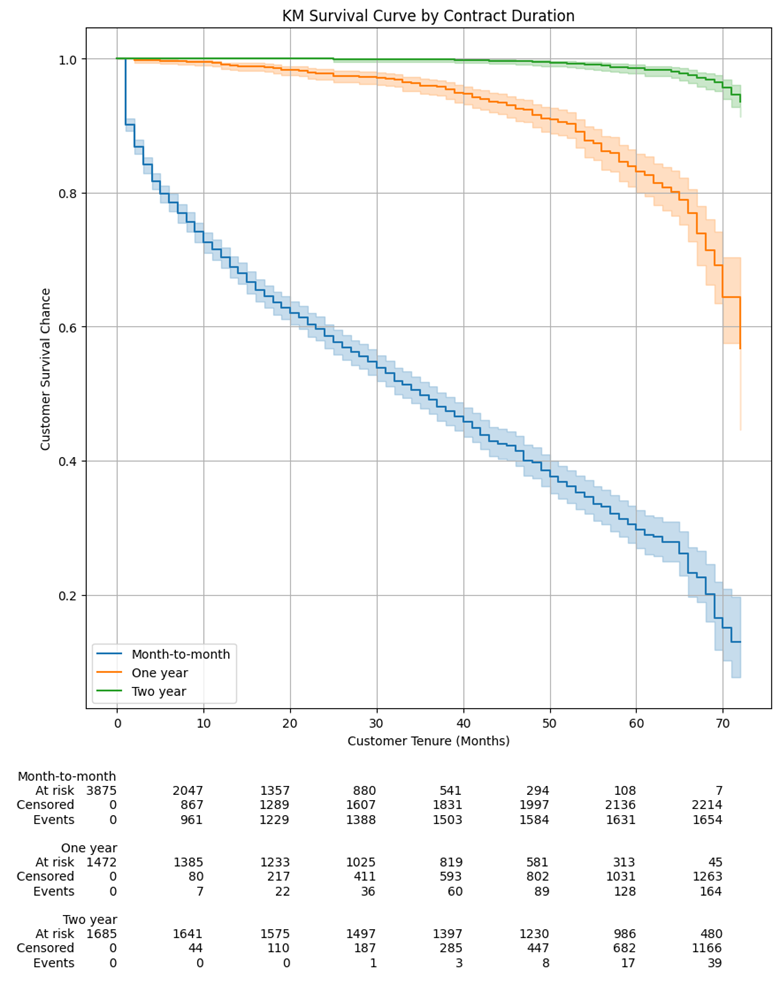
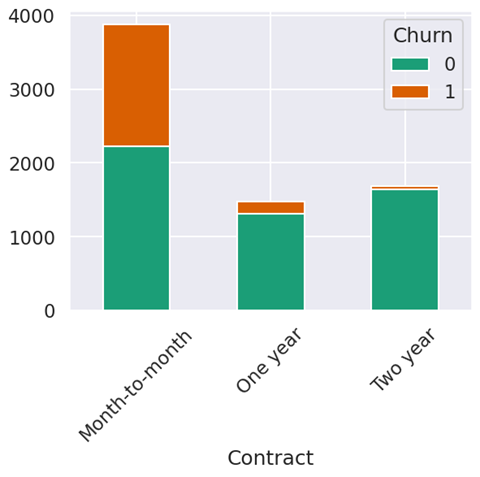
正如预期的那样,我们在这里看到的生存曲线大不相同,随着时间的推移,每月合同客户的生存概率急剧下降。即使在三年后(准确地说是40个月):
- 签订2年合同的客户几乎有100%的生存概率
- 签订1年合同的客户有超过95%的生存概率
- 每月合同的客户只有大约45%的生存概率
Cox模型
1、应用模型并显示模型效果
Cox模型就像scikit-learn中的模型一样通过模型的print_summary方法访问以下模型摘要:
# 去掉共线特征 data_dummies.drop(columns=['InternetService_Fiber optic','Contract_Month-to-month','PaymentMethod_Electronic check'], inplace=True) data.info() # Instantiate and fit CPH model cph = lifelines.CoxPHFitter() cph.fit(data_dummies, duration_col='tenure', event_col='Churn') # Print model summary cph.print_summary(model='base model', decimals=3, columns=['coef','exp(coef)','p'])

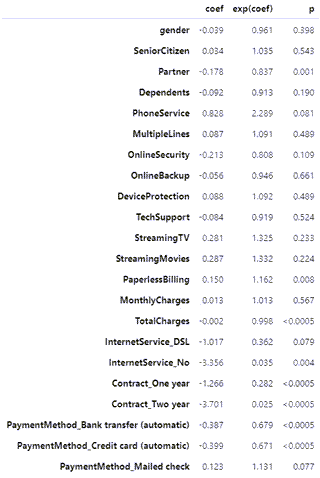

上述模型摘要列出了CPH模型分析的所有one-hot编码协变量。让我们看看这里提供的关键信息:
- 模型系数(coef列)告诉我们每个协变量如何影响风险。协变量为正coef表示具有该特征的客户更有可能流失,反之亦然
- exp(coef)是风险比,解释为变量每增加一个单位的风险比例,00是中性的。例如,1.325的风险比StreamingMovies意味着订阅流媒体电影服务的客户取消其服务的可能性高出32.5%。从我们的角度来看,exp(coef)低于1.0是好的,这意味着客户在存在该协变量的情况下不太可能取消
- 模型一致性929的解释与逻辑回归的AUROC类似:
- 接近5是随机预测的预期结果
- 越接近0,1.0显示出完美的预测一致性越好。
0.929 的一致性基本上意味着我们的模型在未经审查的数据上正确预测了 100 对中的 92.9 对。它基本上评估了模型的区分能力,即它在区分活着的和流失的对象方面有多好。比较两个不同的模型很有用。然而,concordance 并没有说明我们的模型校准得有多好——我们稍后会评估这一点。
这里的一对是指我们数据中所有可能的客户对。考虑一个示例,我们有五个未经审查的客户:A、B、C、D 和 E。从这五个客户中,我们总共可以有十个可能的配对:(A,B), (A,C), (A,D), (A,E), (B,C), (B,D), (B,E), (C,D), (C,E) 和 (D,E)。如果 E 被删失,则一致性指数计算将排除与 E 相关的对,并将考虑分母中剩余的八对。
2、确认比例危害 (PH) 假设
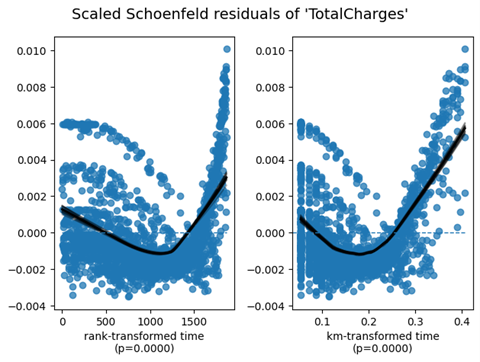
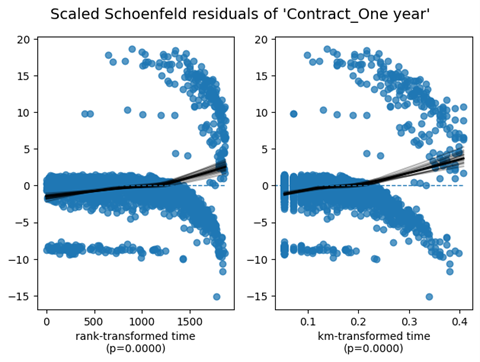
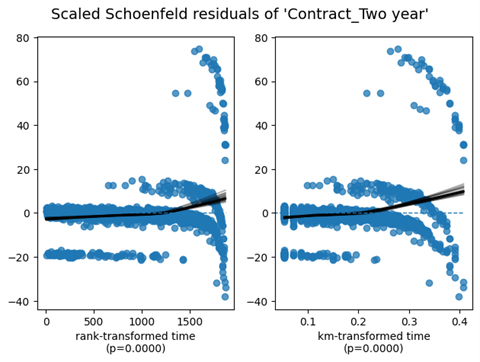
回想一下上面解释过的 CPH 模型的比例风险假设。可以使用基于缩放的 Schoenfeld 残差的统计测试和图形诊断来检查 PH 假设。该假设得到残差和时间之间不显着的关系(例如,p>0.05)的支持,并被显着的关系(例如,p<0.05)驳斥。
在不涉及许多技术细节的情况下,我将只关注实际应用。PH 假设可以通过 lifelines’ check_assumptions 方法在拟合的 CPH 模型上进行检查。执行此方法将返回不满足 PH 假设的协变量的名称,一些关于如何纠正潜在的 PH 违规的通用建议,以及对于每个违反 PH 假设的变量,缩放 Schoenfeld 残差与时间的可视图转换(一条平线证实了 PH 假设)。有关详细信息,请参阅此内容。
在检查我们模型的 PH 假设后,我们发现我们的 3 个协变量不符合它。但是,出于项目的目的,我们将忽略这些警告,因为我们的最终目标是生存预测,而不是确定推断或相关性以了解协变量对生存持续时间和结果的影响。
# Check model assumptions, with a threshold of 0.001 (i.e. only highlight extreme significances - rationale explained after the results) cph.check_assumptions(data_dummies, p_value_threshold=0.001, show_plots=True) The ``p_value_threshold`` is set at 0.001. Even under the null hypothesis of no violations, some covariates will be below the threshold by chance. This is compounded when there are many covariates. Similarly, when there are lots of observations, even minor deviances from the proportional hazard assumption will be flagged. With that in mind, it's best to use a combination of statistical tests and visual tests to determine the most serious violations. Produce visual plots using ``check_assumptions(..., show_plots=True)`` and looking for non-constant lines. See link [A] below for a full example.
| null_distribution | chisquared | ||||
| degrees_of_freedom | 1 | ||||
| model | <lifelines.CoxPHFitter: fitted with 7032 total… | ||||
| test_name | proportional_hazard_test | ||||
| test_statistic | p | -log2(p) | |||
| Contract_Oneyear | km | 115.75 | <0.005 | 87.26 | |
| rank | 102.16 | <0.005 | 77.37 | ||
| Contract_Twoyear | km | 152.13 | <0.005 | 113.70 | |
| rank | 122.65 | <0.005 | 92.28 | ||
| Dependents | km | 0.19 | 0.66 | 0.59 | |
| rank | 0.19 | 0.66 | 0.60 | ||
| DeviceProtection | km | 0.26 | 0.61 | 0.71 | |
| rank | 1.12 | 0.29 | 1.79 | ||
| InternetService_DSL | km | 0.66 | 0.42 | 1.26 | |
| rank | 1.79 | 0.18 | 2.47 | ||
| InternetService_No | km | 3.06 | 0.08 | 3.64 | |
| rank | 5.38 | 0.02 | 5.62 | ||
| MonthlyCharges | km | 0.33 | 0.57 | 0.82 | |
| rank | 0.08 | 0.78 | 0.35 | ||
| MultipleLines | km | 0.58 | 0.45 | 1.17 | |
| rank | 2.44 | 0.12 | 3.08 | ||
| OnlineBackup | km | 0.70 | 0.40 | 1.31 | |
| rank | 1.81 | 0.18 | 2.49 | ||
| OnlineSecurity | km | 0.56 | 0.45 | 1.14 | |
| rank | 2.06 | 0.15 | 2.72 | ||
| PaperlessBilling | km | 0.41 | 0.52 | 0.93 | |
| rank | 0.76 | 0.38 | 1.39 | ||
| Partner | km | 2.66 | 0.10 | 3.28 | |
| rank | 4.72 | 0.03 | 5.07 | ||
| PaymentMethod_Banktransfer(automatic) | km | 0.14 | 0.71 | 0.50 | |
| rank | 0.06 | 0.81 | 0.31 | ||
| PaymentMethod_Creditcard(automatic) | km | 1.22 | 0.27 | 1.90 | |
| rank | 2.37 | 0.12 | 3.02 | ||
| PaymentMethod_Mailedcheck | km | 0.57 | 0.45 | 1.15 | |
| rank | 1.76 | 0.18 | 2.44 | ||
| PhoneService | km | 0.83 | 0.36 | 1.47 | |
| rank | 2.26 | 0.13 | 2.92 | ||
| SeniorCitizen | km | 3.62 | 0.06 | 4.13 | |
| rank | 2.03 | 0.15 | 2.70 | ||
| StreamingMovies | km | 0.47 | 0.49 | 1.02 | |
| rank | 1.41 | 0.23 | 2.09 | ||
| StreamingTV | km | 0.81 | 0.37 | 1.45 | |
| rank | 1.91 | 0.17 | 2.58 | ||
| TechSupport | km | 1.18 | 0.28 | 1.85 | |
| rank | 2.93 | 0.09 | 3.53 | ||
| TotalCharges | km | 154.94 | <0.005 | 115.74 | |
| rank | 20.49 | <0.005 | 17.35 | ||
| gender | km | 0.00 | 0.98 | 0.03 | |
| rank | 0.16 | 0.69 | 0.54 | ||
1. Variable 'TotalCharges' failed the non-proportional test: p-value is <5e-05. Advice 1: the functional form of the variable 'TotalCharges' might be incorrect. That is, there may be non-linear terms missing. The proportional hazard test used is very sensitive to incorrect functional forms. See documentation in link [D] below on how to specify a functional form. Advice 2: try binning the variable 'TotalCharges' using pd.cut, and then specify it in `strata=['TotalCharges', ...]` in the call in `.fit`. See documentation in link [B] below. Advice 3: try adding an interaction term with your time variable. See documentation in link [C] below. Bootstrapping lowess lines. May take a moment... 2. Variable 'Contract_Oneyear' failed the non-proportional test: p-value is <5e-05. Advice: with so few unique values (only 2), you can include `strata=['Contract_Oneyear', ...]` in the call in `.fit`. See documentation in link [E] below. Bootstrapping lowess lines. May take a moment... 3. Variable 'Contract_Twoyear' failed the non-proportional test: p-value is <5e-05. Advice: with so few unique values (only 2), you can include `strata=['Contract_Twoyear', ...]` in the call in `.fit`. See documentation in link [E] below. Bootstrapping lowess lines. May take a moment... --- [A] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html [B] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Bin-variable-and-stratify-on-it [C] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Introduce-time-varying-covariates [D] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Modify-the-functional-form [E] https://lifelines.readthedocs.io/en/latest/jupyter_notebooks/Proportional%20hazard%20assumption.html#Stratification [27]: [[<AxesSubplot: xlabel='rank-transformed time\n(p=0.0000)'>, <AxesSubplot: xlabel='km-transformed time\n(p=0.0000)'>], [<AxesSubplot: xlabel='rank-transformed time\n(p=0.0000)'>, <AxesSubplot: xlabel='km-transformed time\n(p=0.0000)'>], [<AxesSubplot: xlabel='rank-transformed time\n(p=0.0000)'>, <AxesSubplot: xlabel='km-transformed time\n(p=0.0000)'>]]
3、CPH模型验证
lifelines库有一个内置函数来执行我们拟合模型的k折交叉验证。使用一致性指数作为评分参数运行它会导致十倍的平均一致性指数为0.928。
Concordance Index没有说明模型的校准——即预测概率与实际真实概率的差距有多大?我们可以绘制一条校准曲线来检查我们的模型在任何给定时间正确预测概率的倾向。sklearn现在让我们使用’calibration_curve函数在t=12处绘制校准曲线:
from sklearn.calibration import calibration_curve
plt.figure(figsize=(10, 10))
ax1 = plt.subplot2grid((3, 1), (0, 0), rowspan=2)
# Plot the perfectly calibrated line with 0 intercept and 1 slope
ax1.plot([0, 1], [0, 1], ls='--', label='Perfectly calibrated')
# Calculate the churn probabilities at the end of 12th month. predict_survival_function gives us the survival probability, which we have deducted from 1 to get the churn probability
probs = 1 - np.array(cph.predict_survival_function(data_dummies, times=12).T)
actual = data['Churn']
# For each decile, the calibration curve will plot the mean predicted churn probability on the x-axis and its corresponding proportion of observations that actually churned on y-axis, in each bin
fraction_of_positives, mean_predicted_value = calibration_curve(actual, probs, n_bins=10, strategy='quantile')
ax1.plot(mean_predicted_value, fraction_of_positives, marker='s', ls='-', label='Cox PH')
ax1.set_ylabel("Actual fraction of positives")
ax1.set_xlabel("Predicted churn probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend(loc="lower right")
ax1.set_title('Calibration plots (reliability curve) for the 12th month')
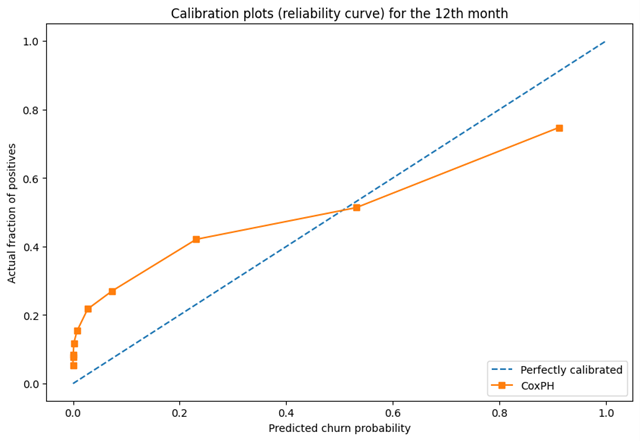
鉴于我们的数据在流失客户和非流失客户之间的倾斜分布,我们将calibration_curve的strategy参数设置为‘quantile’。这将确保每个bin将根据第12个月的预测流失概率具有相同数量的样本。这是可取的,否则,考虑到流失/非流失客户之间的不平衡类别分布,我们将拥有不具有代表性的等宽箱。
上面的校准图向我们显示,对于绘制的前7个十分位数,我们的CPH模型低估了流失风险,而高估了后两个。
总体而言,校准曲线看起来还不错。让我们通过计算Brier分数来确认它,我们发现它是0.17(0是理想的Brier分数),一点也不差!
我们还可以绘制每个月的Brier分数,如下所示:
from sklearn.metrics import brier_score_loss
# calculate Brier Score
brier_score = brier_score_loss(data_dummies['Churn'], 1 - np.array(cph.predict_survival_function(data_dummies, times=12).T), pos_label=1)
print('The Brier Score of our CPH Model is {:.2f} at the end of 12 months'.format(brier_score))
brier_score_dict = {}
# Loop over all the months
for i in range(1, 73):
score = brier_score_loss(data_dummies['Churn'], 1 - np.array(cph.predict_survival_function(data_dummies, times=i).T), pos_label=1)
brier_score_dict[i] = [score]
# Convert the dict to a DF
brier_score_df = pd.DataFrame(brier_score_dict).T
# Plot the Brier Score over time
fig, ax = plt.subplots()
ax.plot(brier_score_df)
ax.set(xlabel='Month', ylabel='Brier Score', title='Cox PH Model Calibration Over Time')
ax.grid()
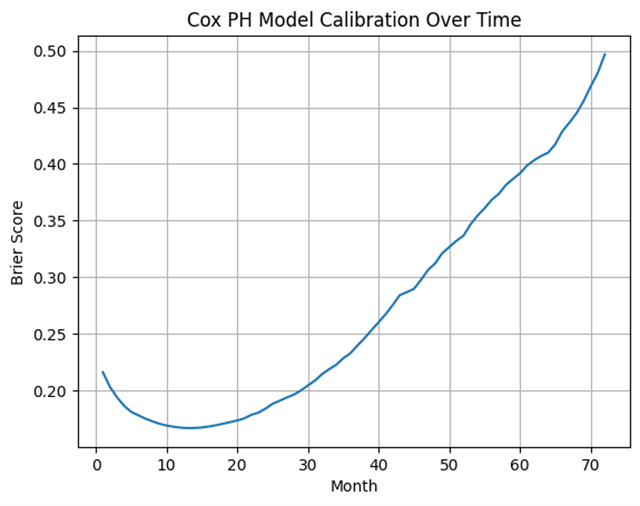
我们可以看到,我们的模型在5到20个月之间进行了合理的校准。
4、CPH模型可视化
现在让我们可视化CPH模型中分析的所有协变量的系数和风险比:
# Let's plot the coefficient outputs and their respective confidence intervals
fig_coef, ax_coef = plt.subplots(figsize=(12, 7))
ax_coef.set_title('Survival Regression: Coefficients and Confidence Intervals')
cph.plot(ax=ax_coef)
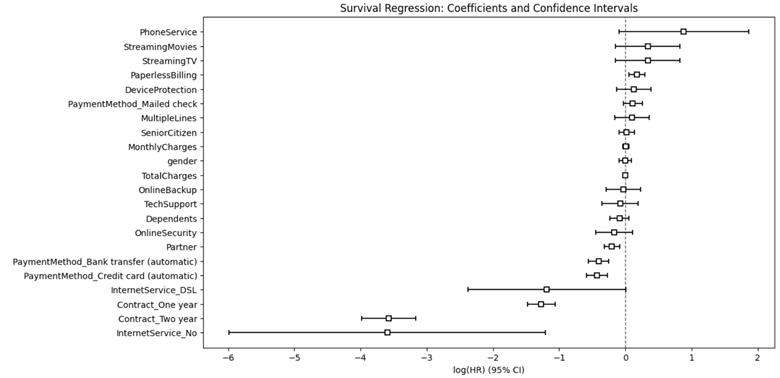
通过该图,我们可以快速识别对预测流失至关重要的特定客户特征。
可能导致流失的协变量:
- PhoneService
- StreamingMovies
- StreamingTV
- PaperlessBilling
- DeviceProtection
- PaymentMothod_Mailedcheck
可能有助于留住客户的协变量:
- intertnetService_No
- Contact_TwoYear
- Contact_OneYear
- intertnetService_DSL
- PaymentMothod_Creditcard(automatic)
- PaymentMothod_Banktransfer(automatic)
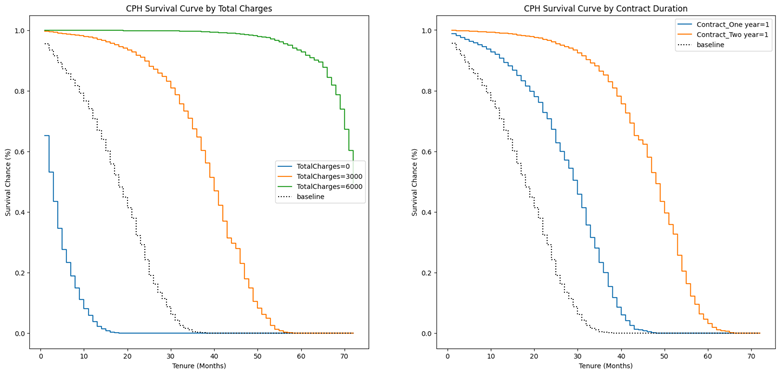
现在让我们绘制并可视化在指定水平的生存曲线上改变协变量的效果以及基线生存曲线:
# Define figure and axes
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(20, 9))
# TotalCharges
cph.plot_partial_effects_on_outcome('TotalCharges', values=[0, 3000, 6000], ax=ax1)
ax1.set_title('CPH Survival Curve by TotalCharges')
ax1.set_xlabel('Tenure (Months)')
ax1.set_ylabel('Survival Chance (%)')
# Contract
cph.plot_partial_effects_on_outcome(['Contract_Oneyear', 'Contract_Twoyear'], values=[[1, 0], [0, 1]], ax=ax2) # we have two arrays in values, 1 for each of the covariate. eq to np.eye(2)
ax2.set_title('CPH Survival Curve by Contract Duration')
ax2.set_xlabel('Tenure (Months)')
ax2.set_ylabel('Survival Chance (%)')
4、客户流失预测和预防
所以现在我们知道我们可以关注哪些协变量来降低我们现有的右删失客户的流失风险,即那些还没有流失的客户。让我们首先绘制 PaymentMethod、Contract、InternetService 和 PhoneService 的 KM 曲线:
kmf = lifelines.KaplanMeierFitter()
# We will use the data_kmf that we kept aside for this moment before feature engineering
# function for creating KM curves segmented by categorical variables
def plot_categorical_KM_Curve(feature, t='tenure', event='Churn', df=data, ax=None):
for cat in df[feature].unique():
idx = df[feature] == cat
kmf.fit(df[idx][t], event_observed=df[idx][event], label=cat)
kmf.plot(ax=ax, label=cat)
# call the above function and plot 4 KM Curves
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize=(20, 10))
# PaymentMethod
plot_categorical_KM_Curve(feature='PaymentMethod', ax=ax1)
ax1.set_title('Kaplan-Meier Survival Curve by PaymentMethod')
ax1.set_xlabel('Customer Tenure (Months)')
ax1.set_ylabel('Customer Survival Chance (%)')
# Contract
plot_categorical_KM_Curve(feature='Contract', ax=ax2)
ax2.set_title('Kaplan-Meier Survival Curve by Contract Duration')
ax2.set_xlabel('Customer Tenure (Months)')
ax2.set_ylabel('Customer Survival Chance (%)')
# InternetService
plot_categorical_KM_Curve(feature='InternetService', ax=ax3)
ax3.set_title('Kaplan-Meier Survival Curve by InternetService')
ax3.set_xlabel('Customer Tenure (Months)')
ax3.set_ylabel('Customer Survival Chance (%)')
# PhoneService
plot_categorical_KM_Curve(feature='PhoneService', ax=ax4)
ax4.set_title('Kaplan-Meier Survival Curve by PhoneService')
ax4.set_xlabel('Customer Tenure (Months)')
ax4.set_ylabel('Customer Survival Chance (%)')
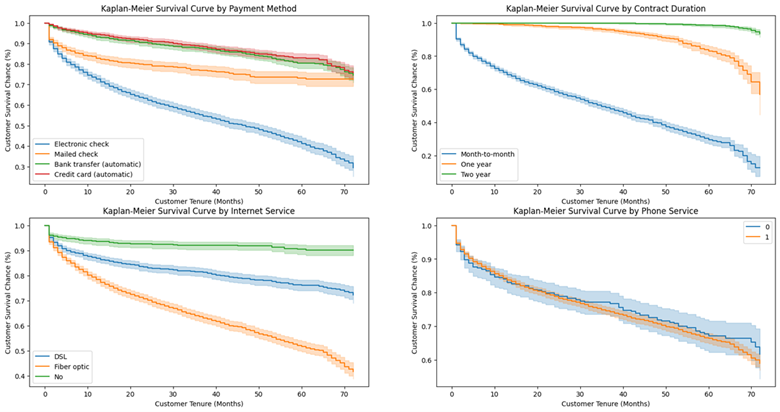
方案:
- 鼓励客户通过银行转帐或信用卡设置自动付款
- 让客户签订1年或2年的合同
- 关于互联网服务,首先我们应该分析一下DSL或光纤互联网订阅用户流失率较高的根本原因——可能是服务质量差、价格高、客户服务不足等。我们也应该这样做互联网服务盈利能力分析。最佳行动方案取决于该分析。
- 有或没有电话服务的客户的生存曲线似乎没有太大的统计差异
5、分析审查客户
现在,我们将把重点转向审查过的和仍然活跃的客户,以确定他们可以预期在未来流失的月份,以及我们为增加他们的保留机会所做的工作。
我们将使用该 predict_survival_function 方法来预测这些客户在给定各自协变量的情况下的未来生存曲线。也就是说,估计我们客户的剩余寿命。
predict_survival_function 的输出将是一个矩阵,其中包含每个剩余客户在特定未来时间点的生存概率,直至我们数据中的最大历史持续时间。因此,如果我们的数据中的最长持续时间是70个月,predict_survival_function 那么将从今天开始预测接下来的70个月。该方法还允许我们通过参数计算未来特定月份的生存概率(有助于回答诸如我们希望在接下来的3个月和6个月末保留多少客户等问题)
censored_data = data_dummies[data_dummies['Churn'] == 0] censored_data_last_obs = censored_data['tenure'] conditioned_sf = cph.predict_survival_function(censored_data, conditional_after=censored_data_last_obs) conditioned_sf
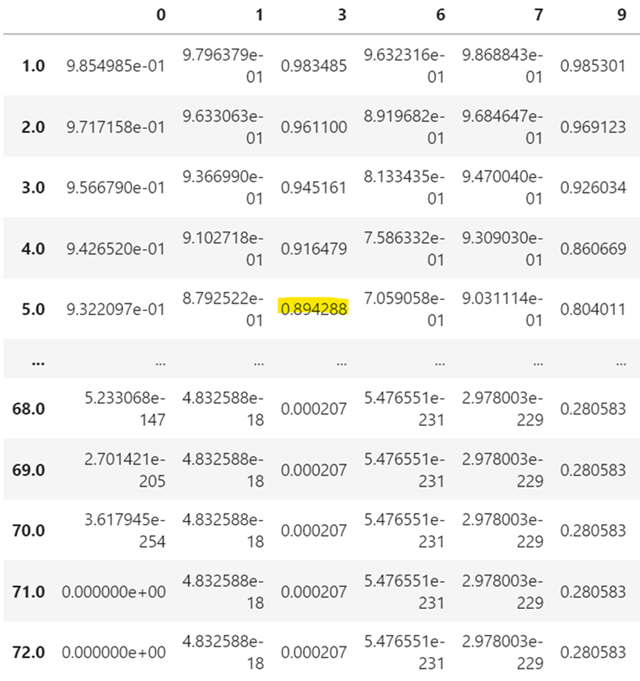
预计第3列中的客户在5个月后存活的概率为89.43%.
6、计算预期损失
我们可以使用这些生存概率来确定每个客户的生存可能性低于某个阈值的特定月份。根据用例,我们可以选择任何百分位数,但对于我们的项目,我们将通过 median_survival_times 方法使用中位数。qth_survival_times 可用于任何其他百分位数。
# Predict the month where the survival probability falls below the median predictions_50 = lifelines.utils.median_survival_times(conditioned_sf) predictions_50 # Use the following if we wanted to assign any other threshold, i.e. month when the survival function reaches the qth percentile # predictions_25 = lifelines.utils.qth_survival_times(0.25, conditioned_sf) # 25% survival chance

inf基本上意味着这个客户几乎可以肯定还活着。
接下来,我们将执行以下操作:
- 将转置后的输出 median_survival_times 与 CustomerID 和各自的 MonthlyCharges(我们一开始就放在一边)连接起来。这将使我们能够将我们的预测与每个特定客户及其每月费用联系起来。
- 通过将每月费用乘以他们的预期流失月份来计算每个客户在今天流失时的预期损失。
- 对于 inf 预期流失月份的客户,替换 inf 为启发式,可能是 24,对应于 2 年的合同。如果他们今天离开我们,假设他们将在我们身边至少呆 24 个月,这将使我们能够估计这些客户的相关预期损失。
我们的数据按预期损失的降序排序,现在看起来像这样:
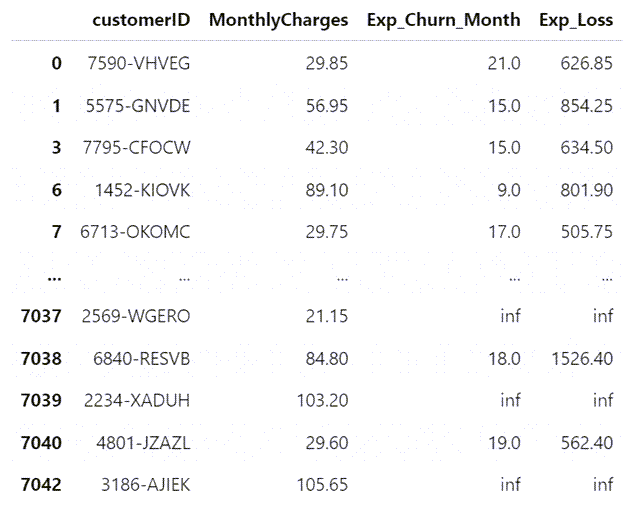
# We can use this single row and by joining it to our data DF, we can investigate the predicted remaining value a customer has for the business
# Note that we will also append our censored customer IDs that we kept aside at the beginning of the model so as to properly identify our customers
customer_predictions = pd.concat([customerID[['customerID', 'MonthlyCharges']], predictions_50.T], axis=1)
# Rename the column returned by median_survival_times function
customer_predictions.rename(columns={0.5: 'Exp_Churn_Month'}, inplace=True)
# Add another column for the expected loss if these customers were to leave us today
customer_predictions['Exp_Loss'] = customer_predictions['MonthlyCharges'] * customer_predictions['Exp_Churn_Month']
customer_predictions
# Assign 24 to inf values in Exp_Churn_Month customer_predictions['Exp_Churn_Month'].replace([np.inf, -np.inf], 24, inplace=True) # Recalculate the customer_predictions table and sort it customer_predictions['Exp_Loss'] = customer_predictions['MonthlyCharges'] * customer_predictions['Exp_Churn_Month'] customer_predictions.sort_values(by=['Exp_Loss'], ascending=False)
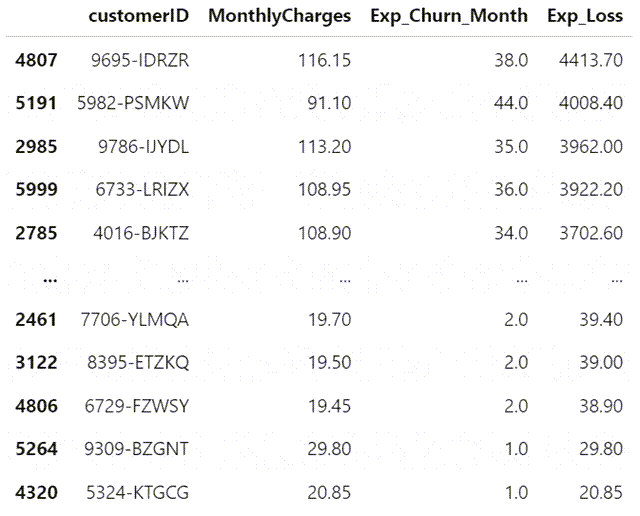
我们现在已经确定了如果他们今天离开我们会对我们构成最高货币风险的客户。
7、计算预计收入提升
我们能做些什么来留住他们?我们的 CPH 模型的系数和相关的知识管理生存曲线表明我们需要关注哪些特征来留住我们现有的客户。但是,如果我们能够说服我们的客户注册这些可以防止客户流失的特定功能,那么现在让我们尝试估算一下金钱收益。
因此,如果我们可以让没有以下功能的客户订阅/登录,我们将估计以下功能的潜在收入增长。
- 1 年的合同
- 2 年的合同
- DSL
- 通过银行转账自动付款
- 通过信用卡自动付款
我们现在将通过假设场景下的嵌套循环计算上述每个协变量和每个客户的潜在提升。例如,如果他签订了一份为期一年的合同,我们可以计算修改后的预期流失月份,以防他没有签订一年的合同。
我们最初的提升分析结果如下:
# Store the column names to be analysed in a list
upgrades = ['Contract_Oneyear', 'Contract_Twoyear', 'InternetService_DSL', 'PaymentMethod_Banktransfer(automatic)', 'PaymentMethod_Creditcard(automatic)']
# Define an empty dictionary to hold the results
results_dict = {}
# For each of the potential upgrades, loop through each individual customer to determine the increase in expected median churn month
for customer in customer_predictions.index:
actual = censored_data.loc[[customer]] # save the actual cutomer data as a series
change = censored_data.loc[[customer]] # same as actual but this series will be used to evaluate hypothetical scenarios
results_dict[customer] = [cph.predict_median(actual, conditional_after=censored_data_last_obs[customer])] # calculate the base median churn month
for upgrade in upgrades:
change[upgrade] = 1 if list(change[upgrade]) == 0 else 1 # hypothetical scenario where customer signs up for this particular upgrade
results_dict[customer].append(cph.predict_median(change, conditional_after=censored_data_last_obs[customer])) # calculate the revised median churn month under the above hypothetical scenario
change = censored_data.loc[[customer]] # bring the change series back to the original state (i.e. undo the effect of the hypothetical scenario)
# Convert dictionary to a DF and transpose the resultant DF back to the required format (each customer in a separate row)
results_df = pd.DataFrame(results_dict).T
# add 'baseline' to the beginning of upgrades list. This new list will be used to rename the columns of results_df
column_names = upgrades
column_names.insert(0, 'baseline')
results_df.columns = column_names
# Concat this new df with customer_predictions DF
upgrade_analysis = pd.concat([customer_predictions, results_df], axis=1)
upgrade_analysis
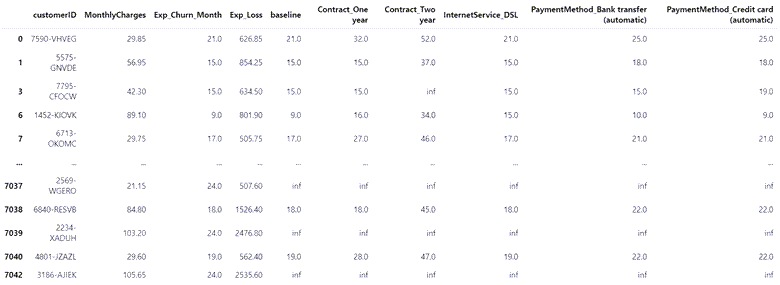
现在,如果我们可以注册特定功能(在其他条件不变的情况下),我们就可以为每个客户修改预期流失月份。例如,如果我们可以让客户7590-VHVEG签署一份为期一年的合同,在其他条件不变的情况下,我们可以期望客户7590-VHVEG与我们再呆11个月。或者,如果他设置自动付款,在其他条件不变的情况下,他预计会再逗留4个月。
如前所述,我们有一些流失风险低的非常好的客户,inf以基准月份的值表示。我们暂时不需要将营销工作集中在他们身上。因此,我们将它们排除在进一步分析之外。
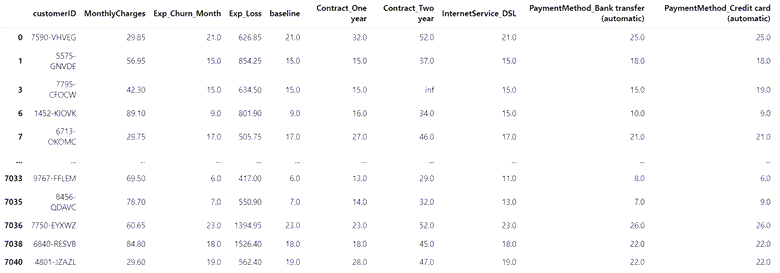
让我们更进一步,看看每次潜在升级在预期修改后的生命周期内对客户的财务影响,而不仅仅是预期的额外几个月。这是一个简单的计算,我们将每个协变量的基线和修订的流失月之间的差异乘以每月费用。
# replace inf values in baseline column with NaN before dropping these rows upgrade_analysis['baseline'].replace([np.inf, -np.inf], np.nan, inplace=True) upgrade_analysis.dropna(subset=['baseline'], axis=0, inplace=True) upgrade_analysis
# Calculate the difference in months between baseline and each feature's revised tenures and multiple this difference by MonthlyCharges upgrade_analysis['1yrContractUplift'] = (upgrade_analysis['Contract_Oneyear'] - upgrade_analysis['baseline']) * upgrade_analysis['MonthlyCharges'] upgrade_analysis['2yrContractUplift'] = (upgrade_analysis['Contract_Twoyear'] - upgrade_analysis['baseline']) * upgrade_analysis['MonthlyCharges'] upgrade_analysis['InternetService_DSLUplift'] = (upgrade_analysis['InternetService_DSL'] - upgrade_analysis['baseline']) * upgrade_analysis['MonthlyCharges'] upgrade_analysis['PaymentMethod_Bank_transferUplift'] = (upgrade_analysis['PaymentMethod_Banktransfer(automatic)'] - upgrade_analysis['baseline']) * upgrade_analysis['MonthlyCharges'] upgrade_analysis['PaymentMethod_Credit_cardUplift'] = (upgrade_analysis['PaymentMethod_Creditcard(automatic)'] - upgrade_analysis['baseline']) * upgrade_analysis['MonthlyCharges'] upgrade_analysis
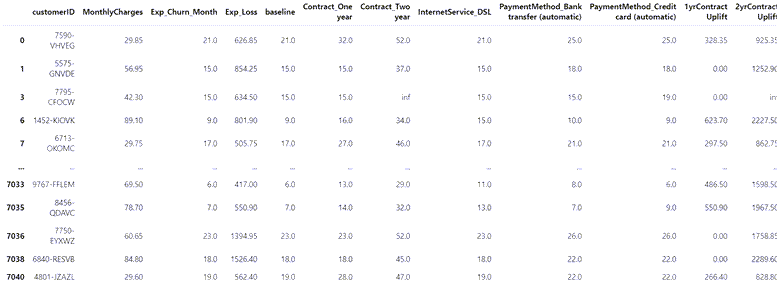
所以现在我们知道客户7590-VHVEG的以下信息:
- 如果他签署一份为期一年的合同,在其他条件不变的情况下,他预计会增加35美元的额外收入
- 如果他签署一份为期2年的合同,在其他条件不变的情况下,他的预期寿命将增加35美元
- 如果他转换为其中一种自动付款方式,在其他条件不变的情况下,他的预期寿命将增加4美元
参考链接:



