Scikit-Learn 提供了多种特征选择方法,主要分为以下几类,结合具体场景和算法特性进行选择:
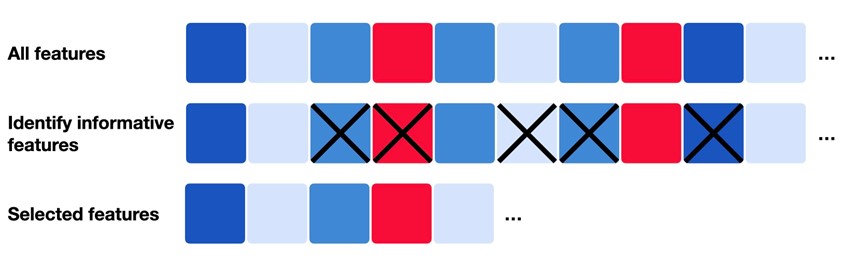
过滤法 (Filter Methods)
基于统计指标评估特征重要性,独立于模型。
方差阈值 (Variance Threshold)
方差阈值(Variance Threshold)是 Scikit-Learn 提供的一种简单但高效的过滤式特征选择方法,其核心思想是:移除数据集中方差低于预设阈值的特征(即变化程度过小的特征)。这类特征通常对模型预测的贡献极小,甚至可能引入噪声。
方差阈值是特征选择的“第一道过滤器”,适合快速清理明显无用的特征,尤其在高维数据中能显著降低计算复杂度。但在实际应用中,需结合业务背景和后续模型效果,避免过度依赖单一方法。
核心原理
方差(Variance):统计学中衡量数据离散程度的指标。公式:
$$\text{Var}(X) = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2$$
其中, $\bar{x}$ 为特征列的平均值。
阈值(Threshold):用户设定的方差下限。若某特征的方差小于此阈值,则被判定为“低价值特征”并移除。
适用场景
- 去除常数特征:例如所有样本的取值为同一数值(方差为 0)。
- 去除近似常数特征:例如 99% 的样本取相同值,仅 1% 不同。
- 预处理高维数据:如文本分类中的稀疏矩阵(One-Hot 编码后可能产生大量低方差特征)。
参数设置
- threshold:默认值为 0,表示仅移除方差为 0 的特征。
- 若数据已标准化(均值为 0,方差为 1),可设置threshold=0.8 过滤方差较小的特征。
- 若数据未标准化,需结合特征实际分布调整阈值。
使用示例
示例 1:基础用法
import numpy as np
from sklearn.feature_selection import VarianceThreshold
# 创建示例数据(4 个特征)
X = np.array([
[0, 0.5, 0, 3], # 特征 0: 方差为 0(常数)
[0, 0.6, 4, 3], # 特征 1: 方差 ≈ 0.003
[0, 0.4, 1, 3] # 特征 2: 方差 ≈ 2.89
[0, 0.5, 2, 3] # 特征 3: 方差为 0(常数)
])
# 初始化方差阈值选择器(移除方差 < 0.1 的特征)
selector = VarianceThreshold(threshold=0.1)
# 应用选择器
X_new = selector.fit_transform(X)
print("原始形状:", X.shape) # 输出: (4, 4)
print("筛选后形状:", X_new.shape) # 输出: (4, 1)(仅保留特征 2)
print("保留的特征索引:", selector.get_support(indices=True)) # 输出: [2]
示例 2:结合标准化
from sklearn.preprocessing import StandardScaler # 先标准化数据(均值为 0,方差为 1) scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 设置阈值过滤方差 < 0.8 的特征 selector = VarianceThreshold(threshold=0.8) X_new = selector.fit_transform(X_scaled)
优缺点
| 优点 | 缺点 |
| 计算效率高,适合高维数据初步筛选。 | 仅考虑特征自身方差,忽略与目标变量的关系。 |
| 无需模型参与,无监督方法。 | 阈值需人工设定,依赖经验或实验调优。 |
| 有效去除无信息特征的干扰。 | 可能误删低方差但重要的特征(需谨慎)。 |
注意事项
- 缺失值处理:方差计算默认不支持缺失值,需提前填充(如用均值、中位数)。
- 数据标准化:若特征量纲差异大(如年龄 vs 收入),需先标准化避免方差被量纲主导。
- 组合其他方法:常与其他特征选择方法(如卡方检验、L1 正则化)结合使用。
单变量统计检验 (Univariate Statistical Tests)
单变量统计检验(Univariate Statistical Tests)是特征选择中过滤法(Filter Methods)的一种,其核心思想是独立评估每个特征与目标变量之间的统计相关性,保留最相关的特征。这类方法计算高效、无需依赖模型,适用于初步筛选特征。
核心原理
- 单变量(Univariate):每次仅分析一个特征与目标变量之间的关系,忽略特征之间的相互作用。
- 统计检验:通过假设检验或信息论指标,量化特征与目标变量的关联强度。
- 筛选策略:选择得分最高的前K 个特征(SelectKBest)或前 百分比 的特征(SelectPercentile)。
常用统计检验方法
Scikit-Learn 的 SelectKBest 和 SelectPercentile 支持多种统计检验,需根据问题类型(分类/回归)选择:
分类问题
| 检验方法 | 描述 |
| 卡方检验 (chi2) | 检验特征与目标变量的独立性(适用于非负特征,如词频或类别编码)。 |
| 互信息 (mutual_info_classif) | 衡量特征与目标变量的信息共享量,支持连续和离散特征,无需数据分布假设。 |
| F 检验 (f_classif) | 基于方差分析(ANOVA),检验特征均值在不同类别间的差异。 |
回归问题
| 检验方法 | 描述 |
| F 检验 (f_regression) | 检验特征与目标变量的线性相关性(基于线性模型的F值)。 |
| 互信息 (mutual_info_regression) | 衡量特征与目标变量的非线性信息共享量。 |
Scikit-Learn 实现
核心类
- SelectKBest:选择得分最高的前K 个特征。
- SelectPercentile:选择得分最高的前百分比 的特征。
- 参数:
- score_func:指定统计检验函数(如chi2, f_classif)。
- k(或percentile):设置保留的特征数量或比例。
代码示例
from sklearn.feature_selection import SelectKBest, chi2
# 示例:分类问题中选择前 5 个特征(卡方检验)
selector = SelectKBest(score_func=chi2, k=5)
X_new = selector.fit_transform(X, y) # 必须传入目标变量 y
# 查看得分和选择的特征
print("特征得分:", selector.scores_)
print("保留的特征索引:", selector.get_support(indices=True))
关键统计检验详解
卡方检验 (Chi-Square)
- 原理:检验特征与目标变量的独立性。原假设(H₀):特征与目标变量无关。卡方值越高,拒绝H₀的证据越强,说明特征与目标相关性强。
- 公式:$\chi^2 = \sum \frac{(O_i – E_i)^2}{E_i}$
- 其中,$O_i$是观察频数,$E_i$ 是期望频数。
- 适用场景:
- 特征和目标均为离散型(如分类变量)。
- 特征需为非负值(例如词频、类别计数)。
互信息 (Mutual Information)
- 原理:基于信息论,衡量特征与目标变量的共享信息量。互信息值越高,说明特征对目标的预测能力越强。
- 公式:$I(X; Y) = \sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x, y)}{p(x)p(y)}$
- 优点:
- 可捕捉非线性关系(如曲线关系)。
- 支持连续和离散特征。
- 适用场景:复杂关系的数据(传统线性检验可能失效)。
F 检验 (ANOVA)
- 原理:通过方差分析,比较不同类别(分类问题)或连续值(回归问题)的特征均值差异。F 值越高,说明特征与目标的线性相关性越强。
- 公式(分类问题):$F = \frac{\text{组间方差}}{\text{组内方差}}$
- 适用场景:
- 特征与目标变量存在线性关系。
- 数据满足正态性假设(近似满足即可)。
皮尔逊相关系数(f_regression)
- 原理:
- 计算特征与目标变量之间的线性相关系数(F值形式)。
- 基于协方差和标准差计算:$r = \frac{\text{cov}(X,Y)}{\sigma_X \sigma_Y}$
- 将其转换为F值(用于排序特征重要性):$F = \frac{r^2}{1 – r^2} \times (n – 2)$
- F值越大,线性相关性越强。
- 适用场景:
- 回归问题,特征与目标变量之间为线性关系。
- 例如:房价预测中面积与价格的线性关联。
- 注意事项:
- 仅能检测线性关系,无法捕捉非线性关联。
- 对异常值敏感,需提前处理。
其他评分函数
方差分析(f_classif 和 f_regression)
分类和回归问题均可使用,但具体实现不同(如上述ANOVA F值和皮尔逊F值)。
基于模型的评分(如随机森林重要性)
虽然不是 SelectKBest 的内置函数,但可通过自定义评分函数实现:
from sklearn.ensemble import RandomForestClassifier
def model_based_score(X, y):
model = RandomForestClassifier()
model.fit(X, y)
return model.feature_importances_
使用场景与策略
适用场景
- 高维数据预处理:如文本分类(TF-IDF 矩阵)、基因表达数据。
- 快速特征筛选:在复杂模型(如深度学习)训练前减少特征数量。
- 探索性分析:识别与目标变量强相关的特征。
选择策略
- 分类问题:优先尝试卡方检验或互信息。
- 回归问题:优先使用F检验或互信息。
- 非线性关系:使用互信息避免漏掉重要特征。
- 稀疏数据:卡方检验更适合非负特征(如文本数据)。
优缺点
| 优点 | 缺点 |
| 计算速度快,适合大规模数据。 | 忽略特征间的交互作用(可能遗漏重要组合)。 |
| 无需训练模型,无监督/监督均可。 | 对某些检验方法的数据分布有假设(如卡方)。 |
| 可解释性强(得分直观反映相关性)。 | 可能选择冗余特征(如两个高度相关的特征)。 |
注意事项
- 数据预处理:
- 卡方检验要求特征为非负值,必要时进行归一化或二值化。
- 标准化数据可能提升F检验的稳定性。
- 缺失值处理:需提前填充缺失值(如均值、众数)。
- 阈值选择:
- 通过交叉验证或网格搜索选择最优k 或 percentile。
- 观察得分分布,避免保留大量低分特征。
- 结合其他方法:
- 先使用单变量检验过滤,再用嵌入法(如L1正则化)进一步筛选。
完整代码示例
分类问题(鸢尾花数据集)
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest, chi2
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 选择前 2 个特征(卡方检验)
selector = SelectKBest(chi2, k=2)
X_new = selector.fit_transform(X, y)
print("原始特征形状:", X.shape) # (150, 4)
print("筛选后特征形状:", X_new.shape) # (150, 2)
print("特征得分:", selector.scores_) # [ 10.82 3.71 116.31 67.05]
print("保留的特征索引:", selector.get_support(indices=True)) # [2, 3]
回归问题(波士顿房价数据集)
from sklearn.datasets import fetch_california_housing
from sklearn.feature_selection import SelectKBest, f_regression
# 加载数据
data = fetch_california_housing()
X, y = data.data, data.target
# 选择前 3 个特征(F检验)
selector = SelectKBest(f_regression, k=3)
X_new = selector.fit_transform(X, y)
print("特征得分:", selector.scores_) # 例如 [103.99, 8.01, 154.91, ...]
包装法 (Wrapper Methods)
通过迭代训练模型选择特征子集,依赖模型性能。
递归特征消除 (Recursive Feature Elimination, RFE)
递归特征消除(Recursive Feature Elimination, RFE)是一种包装式(Wrapper)特征选择方法,其核心思想是通过迭代训练模型,逐步移除对模型贡献最小的特征,最终得到最优特征子集。相较于过滤法,RFE 依赖模型的性能评估特征重要性,通常能获得更精准的特征子集,但计算成本更高。
核心原理
- 递归(Recursive):通过多轮迭代逐步减少特征数量。
- 特征消除(Feature Elimination):每轮训练模型后,移除最不重要的特征(如权重或重要性最低的特征)。
- 模型驱动:需要依赖基模型(如线性回归、SVM、随机森林等)提供特征重要性评估。
算法步骤
- 初始化:
- 指定基模型(如LogisticRegression)和要保留的特征数量 n_features_to_select。
- 若未指定n_features_to_select,默认保留一半特征。
- 训练模型:
- 使用当前特征集训练模型。
- 获取特征重要性(如线性模型的系数coef_ 或树模型的 feature_importances_)。
- 剔除最不重要特征:移除重要性排名最低的 1 个或多个特征。
- 重复迭代:重复步骤 2-3,直到剩余特征数量达到预设值。
- 输出结果:最终保留的特征集合及其重要性排名。
Scikit-Learn 实现
核心类
- RFE:手动指定要保留的特征数量。
- RFECV:通过交叉验证自动选择最优特征数量。
- 常用参数:
- estimator:基模型(需支持返回特征重要性)。
- n_features_to_select:最终保留的特征数量。
- step:每轮迭代移除的特征数量(默认 1)。
- verbose:控制日志输出。
代码示例
基本用法(分类问题)
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
# 初始化基模型(需支持 coef_ 或 feature_importances_)
model = LogisticRegression()
# 创建 RFE 选择器,保留 5 个特征
selector = RFE(estimator=model, n_features_to_select=5, step=1)
# 训练并选择特征
X_new = selector.fit_transform(X, y)
# 查看结果
print("保留特征数量:", selector.n_features_)
print("特征重要性排名:", selector.ranking_) # 1 表示保留,数字越大表示越早被剔除
print("保留特征索引:", selector.support_)
自动选择最优特征数量(RFECV)
from sklearn.feature_selection import RFECV
# 使用交叉验证自动选择最优特征数量
selector = RFECV(
estimator=model,
step=1,
cv=5, # 5 折交叉验证
scoring="accuracy" # 评估指标(分类问题用 accuracy,回归用 r2)
)
selector.fit(X, y)
print("最优特征数量:", selector.n_features_)
print("特征重要性排名:", selector.ranking_)
关键细节
基模型选择
- 线性模型(如LogisticRegression、LinearRegression):使用系数绝对值 coef_ 作为重要性指标。适用于特征间独立性较强的场景。
- 树模型(如RandomForestClassifier、XGBoost):使用 feature_importances_ 作为重要性指标。能捕捉非线性关系,但计算成本较高。
- 支持向量机(SVM):使用权重向量的平方(coef_**2)作为重要性指标,适用于高维数据。
特征重要性评估
- 线性模型:系数大小反映特征对目标的贡献程度(需先标准化数据确保可比性)。
- 树模型:基于特征在分裂节点中的信息增益或基尼不纯度减少量计算重要性。
参数调优
- step:
- 设为 1:每轮移除 1 个特征(精细但耗时)。
- 设为更大值(如 10% 特征数量):加速迭代,但可能跳过局部最优。
- n_features_to_select:
- 若不确定,使用RFECV 自动确定最优数量。
优缺点
| 优点 | 缺点 |
| 模型驱动,特征子集针对性强,预测性能高。 | 计算成本高,尤其特征数量多或基模型复杂时。 |
| 可捕捉特征间的交互效应。 | 依赖基模型的准确性(若模型差,选择结果差)。 |
| 支持自动选择最优特征数量(RFECV)。 | 树模型可能对高基数特征或噪声特征过拟合。 |
使用场景
- 特征数量中等(<1000):计算资源允许的情况下。
- 模型解释性要求高:需明确哪些特征对预测最关键。
- 特征间存在复杂交互:如医疗诊断、金融风控等领域。
注意事项
- 数据标准化:使用线性模型时,需先标准化数据(StandardScaler),确保特征重要性可比。
- 基模型选择:
- 优先选择简单快速模型(如线性模型)作为基模型,减少计算时间。
- 若数据存在非线性关系,使用树模型或带核函数的SVM。
- 处理共线性:RFE 可能无法有效处理高度相关的特征(可能同时保留或剔除相关特征)。
- 交叉验证:务必使用RFECV 避免过拟合,尤其在特征数量较少时。
完整示例(乳腺癌数据集)
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFECV
# 加载数据
data = load_breast_cancer()
X, y = data.data, data.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 初始化基模型(随机森林)
model = RandomForestClassifier(n_estimators=100, random_state=42)
# 创建 RFECV 选择器
selector = RFECV(
estimator=model,
step=1,
cv=5,
scoring="accuracy",
n_jobs=-1 # 并行计算
)
selector.fit(X_train, y_train)
# 评估效果
X_train_selected = selector.transform(X_train)
X_test_selected = selector.transform(X_test)
model.fit(X_train_selected, y_train)
accuracy = model.score(X_test_selected, y_test)
print("最优特征数量:", selector.n_features_)
print("测试集准确率:", accuracy)
嵌入法 (Embedded Methods)
模型训练过程中自动选择重要特征。
L1 正则化 (Lasso)
嵌入法中的 L1 正则化(Lasso,Least Absolute Shrinkage and Selection Operator) 是一种通过在模型训练过程中自动进行特征选择的方法,其核心思想是通过添加 L1 正则化项,使得部分特征的系数被压缩为零,从而剔除不重要的特征。
核心原理
数学公式
对于线性回归模型,Lasso 的损失函数为:
$$J(\beta) = \frac{1}{2n} \sum_{i=1}^{n} (y_i – \beta_0 – \sum_{j=1}^{p} \beta_j x_{ij})^2 + \alpha \sum_{j=1}^{p} |\beta_j|$$
- 第一项:均方误差(MSE),衡量模型预测误差。
- 第二项:L1 正则化项,对系数绝对值求和,惩罚大系数。
- $\alpha$:正则化强度,控制稀疏性($\alpha$越大,系数越趋向于零)。
稀疏性解释
- 几何视角:L1 正则化的约束区域(菱形)在顶点处与损失函数等高线相切时,容易导致某些系数为 0。
- 优化视角:L1 正则化的非光滑性使得梯度下降时,部分系数直接被“压缩”至零。
特征选择机制
- 系数归零:L1 正则化倾向于将不重要的特征系数设为 0,保留系数非零的特征。
- 自动选择:训练结束后,非零系数对应的特征即为被选中的特征。
- 适用于:高维数据(特征数p > 样本数 n)和存在冗余特征的场景。
Scikit-Learn 实现
回归问题(Lasso)
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
# 数据标准化(L1 正则化对特征尺度敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 初始化 Lasso 模型
lasso = Lasso(alpha=0.1) # alpha 控制正则化强度
lasso.fit(X_scaled, y)
# 获取非零系数对应的特征
selected_features = [i for i, coef in enumerate(lasso.coef_) if coef != 0]
print("保留特征索引:", selected_features)
分类问题(L1 逻辑回归)
from sklearn.linear_model import LogisticRegression # 使用 L1 正则化的逻辑回归 logistic_l1 = LogisticRegression(penalty='l1', solver='liblinear', C=1.0) logistic_l1.fit(X_scaled, y) # 获取非零系数特征 selected_features = [i for i, coef in enumerate(logistic_l1.coef_[0]) if coef != 0]
关键参数与调优
- $\alpha$(或 C):
- alpha(Lasso)或C=1/alpha(逻辑回归)控制正则化强度。
- 调优方法:通过交叉验证(如LassoCV)选择最优值。
from sklearn.linear_model import LassoCV # 自动选择 alpha lasso_cv = LassoCV(cv=5, alphas=[0.1, 0.5, 1.0]).fit(X_scaled, y) optimal_alpha = lasso_cv.alpha_
- 标准化:必须对特征进行标准化(如 StandardScaler),避免因尺度差异导致误压缩系数。
优缺点
| 优点 | 缺点 |
| 自动特征选择,无需额外步骤。 | 对高度相关的特征可能随机选择一个,忽略其他。 |
| 适合高维数据,计算效率较高。 | 需要调整 \alpha,依赖交叉验证。 |
| 提供特征重要性(系数绝对值大小)。 | 若真实关系非线性,可能表现不佳。 |
与 L2 正则化(Ridge)对比
| 特性 | L1 正则化(Lasso) | L2 正则化(Ridge) |
| 正则化项 | $\alpha \sum |\beta_j|$ | $\alpha \sum \beta_j^2$ |
| 系数稀疏性 | 是(部分系数为 0) | 否(系数接近 0 但不为 0) |
| 特征选择 | 直接实现特征选择 | 无法直接选择特征 |
| 适用场景 | 高维数据、特征冗余 | 处理共线性、防止过拟合 |
| 几何约束区域 | 菱形(顶点处稀疏) | 圆形(平滑收缩) |
注意事项
共线性问题:
- 若多个特征高度相关,Lasso 可能随机选择其中一个,其余系数归零。
- 可考虑使用Elastic Net(L1 + L2 正则化)平衡选择与稳定性:
from sklearn.linear_model import ElasticNet enet = ElasticNet(alpha=0.1, l1_ratio=0.5) # l1_ratio 控制 L1/L2 混合比例
非线性关系:Lasso 仅捕捉线性关系,若存在非线性依赖,需结合特征工程(如多项式特征)。
模型评估:特征选择后需重新训练模型(如使用交叉验证),避免信息泄露。
实际应用示例
糖尿病数据集特征选择
from sklearn.datasets import load_diabetes
from sklearn.linear_model import LassoCV
# 加载数据
data = load_diabetes()
X, y = data.data, data.target
# 标准化
X_scaled = StandardScaler().fit_transform(X)
# 使用 LassoCV 选择特征
lasso_cv = LassoCV(cv=5, random_state=42).fit(X_scaled, y)
selected_features = [i for i, coef in enumerate(lasso_cv.coef_) if coef != 0]
print("原始特征数:", X.shape[1]) # 10
print("保留特征数:", len(selected_features)) # 可能保留 3-5 个
print("非零系数特征索引:", selected_features)
基于树模型的特征重要性
基于树模型的特征重要性(Tree-based Feature Importance)是一种通过树结构算法(如决策树、随机森林、梯度提升树)评估特征对目标变量预测贡献程度的方法。这类方法属于嵌入法(Embedded Methods),在模型训练过程中自动评估特征重要性,无需额外计算步骤。
基于树模型的特征重要性是一种高效且直观的特征选择与解释工具,尤其适合非线性数据和复杂特征交互的场景。使用时需注意共线性和高基数特征的影响,结合交叉验证和置换重要性验证结果稳定性。对于需要高可解释性的任务(如风控、医疗诊断),可进一步使用 SHAP 或 LIME 等工具深入分析特征贡献。
核心原理
树模型通过递归分割数据,构建决策规则以最小化预测误差(回归)或最大化类别纯度(分类)。特征重要性反映了每个特征在这些分割中的贡献程度:
- 分裂贡献:每次特征被选为分裂节点时,计算其对目标(如基尼不纯度减少、信息增益)的优化程度。
- 累计评估:汇总所有树中该特征的总贡献,并进行归一化处理。
常见树模型的特征重要性计算
基尼重要性(Gini Importance)
- 适用模型:决策树、随机森林(分类任务)。
- 计算方法:
- 对每个特征,统计其在所有树节点中作为分裂特征的次数。
- 每次分裂时,计算分裂前后基尼不纯度的减少量(即信息增益)。
- 累加所有分裂的基尼不纯度减少量,并归一化为总和为 1 的重要性分数。
- 公式(单次分裂的基尼不纯度减少):
$$\Delta Gini = Gini_{parent} – ( \frac{N_{left}}{N_{parent}} Gini_{left} + \frac{N_{right}}{N_{parent}} Gini_{right})$$
- $Gini_{parent}$:父节点的基尼不纯度。
- $N_{left}, N_{right}$:分裂后左右子节点的样本数。
平均不纯度减少(Mean Decrease Impurity, MDI)
- 适用模型:回归和分类任务(如随机森林、梯度提升树)。
- 原理:与基尼重要性类似,但适用于不同不纯度指标(如均方误差 MSE)。
- 归一化:所有特征的重要性总和为 1。
置换重要性(Permutation Importance)
- 原理:通过打乱某特征的取值,观察模型性能下降程度。性能下降越多,特征越重要。
- 优点:不依赖模型内部结构,适用于任何模型。
- 缺点:计算成本较高,需多次置换和评估。
Scikit-Learn 实现
随机森林示例
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 加载数据
data = load_iris()
X, y = data.data, data.target
feature_names = data.feature_names
# 训练模型
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X, y)
# 获取特征重要性
importances = model.feature_importances_
# 可视化
plt.figure(figsize=(10, 6))
plt.barh(feature_names, importances)
plt.xlabel("Feature Importance (MDI)")
plt.title("Random Forest Feature Importance")
plt.show()
输出结果示例
Feature ranking: 1. petal length (cm) : 0.44 2. petal width (cm) : 0.40 3. sepal length (cm) : 0.11 4. sepal width (cm) : 0.05
关键特性
优点
- 捕捉非线性关系:树模型可自动识别特征与目标的非线性关联。
- 自动处理交互作用:特征组合的重要性通过多次分裂体现。
- 无需标准化:树模型对特征尺度不敏感。
- 可解释性:直观展示特征贡献度。
缺点
- 高基数特征偏差:类别型特征若类别数多(如用户ID),可能被误判为高重要性。
- 共线性影响:若多个特征高度相关,重要性可能分散到各特征。
- 样本敏感:小样本或噪声数据可能导致重要性不稳定。
使用场景
- 特征初筛:快速识别对预测贡献大的特征。
- 可解释性分析:在金融、医疗等领域解释模型决策依据。
- 高维数据:处理特征数远大于样本数的数据集(需调整树参数防止过拟合)。
注意事项
- 数据预处理:
- 类别型特征需编码(如独热编码、目标编码)。
- 缺失值需填充(树模型可处理,但显式填充更可控)。
- 模型参数调整:
- 增加n_estimators(树的数量)提升重要性评估稳定性。
- 限制max_depth 避免过拟合导致重要性偏差。
- 验证方法:
- 结合交叉验证:多次训练模型,观察重要性排名是否一致。
- 对比置换重要性:验证 MDI 结果的可靠性。
与过滤法、包装法的对比
| 方法 | 计算效率 | 捕捉非线性 | 抗共线性 | 可解释性 |
| 树模型特征重要性 | 高 | 是 | 弱 | 高 |
| 过滤法(如卡方检验) | 极高 | 否 | 强 | 中 |
| 包装法(如 RFE) | 低 | 是 | 中 | 中 |
高级技巧
多模型重要性对比
from sklearn.ensemble import GradientBoostingClassifier
# 训练梯度提升树
gb_model = GradientBoostingClassifier(n_estimators=100, random_state=42)
gb_model.fit(X, y)
gb_importances = gb_model.feature_importances_
# 对比随机森林与GBDT的重要性
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(feature_names, importances)
plt.title("Random Forest Importance")
plt.subplot(1, 2, 2)
plt.barh(feature_names, gb_importances)
plt.title("GBDT Importance")
plt.show()
使用 SHAP 值增强解释
SHAP(SHapley Additive exPlanations)提供更细粒度的特征贡献分析: import shap # 创建 SHAP 解释器 explainer = shap.TreeExplainer(model) shap_values = explainer.shap_values(X) # 可视化单个样本的特征贡献 shap.initjs() shap.force_plot(explainer.expected_value[0], shap_values[0][0, :], X[0, :], feature_names=feature_names)
SelectFromModel
SelectFromModel 是 Scikit-Learn 中一种基于模型的嵌入式特征选择方法,其核心思想是利用训练好的模型自动筛选重要特征,根据特征重要性(如线性模型的系数、树模型的特征重要性)或特定阈值过滤掉低贡献特征。SelectFromModel 是一种高效、灵活的特征选择方法,尤其适合与树模型或 L1 正则化结合使用。其优势在于:
- 快速降维:无需复杂迭代,直接利用模型内在评估指标。
- 广泛兼容性:支持多种模型(线性、树、SVM 等)。
- 自动化流程:可嵌入机器学习管道(Pipeline),简化代码。
实际应用中需注意基模型的选择、数据标准化及阈值调优,必要时结合交叉验证确保稳定性。对于需要高精度特征排序的场景,可进一步与递归特征消除(RFE)或 SHAP 值分析结合使用。
核心原理
- 模型驱动:依赖于基模型(如 Lasso、随机森林、SVM 等)提供的特征重要性指标。
- 阈值筛选:通过设定阈值(绝对数值或比例),保留重要性高于阈值的特征。
- 自动化流程:将特征选择嵌入模型训练过程,无需额外迭代或交叉验证(但需注意基模型需提前训练或支持动态评估)。
工作流程
- 训练基模型:使用完整特征集训练一个模型(如随机森林)。
- 获取特征重要性:提取模型的coef_(线性模型)或 feature_importances_(树模型)。
- 设定阈值:手动指定或通过启发式方法(如中位数、均值)确定阈值。
- 筛选特征:保留重要性高于阈值的特征,形成最终特征子集。
Scikit-Learn 实现
核心类
from sklearn.feature_selection import SelectFromModel
关键参数
| 参数 | 说明 |
| estimator | 基模型(需支持 coef_ 或 feature_importances_ 属性)。 |
| threshold | 重要性阈值,可设为数值、”median”、”mean” 或 “1.25*mean” 等。 |
| prefit | 若为 True,直接使用已训练好的模型;默认 False(重新训练模型)。 |
| max_features | 可选,最多保留的特征数量(覆盖 threshold 的设定)。 |
使用示例
基于树模型的特征选择
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
# 加载数据
data = load_breast_cancer()
X, y = data.data, data.target
feature_names = data.feature_names
# 训练基模型(随机森林)
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X, y)
# 创建 SelectFromModel 选择器,阈值设为中位数
selector = SelectFromModel(estimator=model, threshold="median")
X_selected = selector.fit_transform(X, y)
# 输出结果
print("原始特征数:", X.shape[1]) # 30
print("保留特征数:", X_selected.shape[1]) # 约 15
print("保留特征:", feature_names[selector.get_support()])
结合 L1 正则化的线性模型
from sklearn.linear_model import LassoCV
from sklearn.preprocessing import StandardScaler
# 标准化数据(L1 正则化对尺度敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 训练 LassoCV 模型(自动选择正则化强度)
lasso = LassoCV(cv=5).fit(X_scaled, y)
# 创建 SelectFromModel 选择器,阈值设为均值
selector = SelectFromModel(estimator=lasso, threshold="mean")
X_selected = selector.fit_transform(X_scaled, y)
# 输出非零系数特征
print("保留特征数:", X_selected.shape[1]) # 约 5-10
阈值设定策略
| 阈值类型 | 说明 |
| threshold=0.1 | 保留重要性 > 0.1 的特征(需根据基模型调整范围)。 |
| threshold=”median” | 保留重要性高于中位数的特征。 |
| threshold=”mean” | 保留重要性高于均值的特征。 |
| threshold=”1.25*mean” | 自定义表达式,如保留重要性高于均值 1.25 倍的特征。 |
| max_features=10 | 直接指定最多保留 10 个特征(忽略阈值)。 |
与其他特征选择方法的对比
| 方法 | 计算效率 | 模型依赖 | 特征交互处理 | 适用场景 |
| SelectFromModel | 高 | 强 | 支持(依赖基模型) | 快速筛选、高维数据、非线性 |
| 递归特征消除(RFE) | 低 | 强 | 支持 | 精确子集搜索、中小数据集 |
| 过滤法(如卡方检验) | 极高 | 无 | 不支持 | 预筛选、独立特征评估 |
优缺点
| 优点 | 缺点 |
| 快速高效,适合高维数据。 | 依赖基模型的准确性(若模型差,选择结果差)。 |
| 支持非线性模型(如树模型、SVM)。 | 阈值需手动调整或依赖经验规则。 |
| 自动捕捉特征交互效应。 | 对共线性特征可能随机选择或同时保留。 |
使用场景
- 高维数据降维:如基因表达数据(数万特征)中快速筛选关键特征。
- 模型解释性增强:保留对预测贡献最大的特征,简化模型。
- 预处理加速:减少后续复杂模型(如神经网络)的训练时间。
注意事项
- 标准化数据:使用线性模型(如 Lasso)时,务必先标准化特征(StandardScaler),否则系数不可比。
- 共线性处理:若特征高度相关,SelectFromModel可能仅选择其中一个,需结合业务理解或使用 Elastic Net。
- 基模型选择:
- 线性模型(Lasso、逻辑回归):适合特征独立或线性关系强的场景。
- 树模型(随机森林、XGBoost):捕捉非线性关系和特征交互。
- SVM:适用于高维数据,但计算成本较高。
- 动态阈值调优:结合交叉验证和网格搜索(GridSearchCV)优化阈值或max_features:
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
pipeline = Pipeline([
('scaler', StandardScaler()),
('selector', SelectFromModel(LassoCV())),
('classifier', RandomForestClassifier())
])
params = {
'selector__threshold': [0.01, 0.1, "mean", "median"]
}
grid = GridSearchCV(pipeline, params, cv=5)
grid.fit(X, y)
完整示例(乳腺癌数据集)
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载数据
data = load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 基模型:随机森林
base_model = RandomForestClassifier(n_estimators=100, random_state=42)
base_model.fit(X_train, y_train)
# 使用 SelectFromModel 选择特征
selector = SelectFromModel(estimator=base_model, threshold="median")
X_train_selected = selector.fit_transform(X_train, y_train)
X_test_selected = selector.transform(X_test)
# 训练简化后的模型
reduced_model = RandomForestClassifier(n_estimators=100, random_state=42)
reduced_model.fit(X_train_selected, y_train)
# 评估效果
accuracy = reduced_model.score(X_test_selected, y_test)
print("保留特征数:", X_train_selected.shape[1]) # 约 15
print("测试集准确率:", accuracy) # 与原模型相近(约 96%)
其他工具
移除共线性特征
在机器学习中,共线性特征(高度相关的特征)会导致模型不稳定、参数估计方差增大、可解释性下降等问题。常用的共线性检测与处理方法包括 相关系数法 和 方差膨胀因子(VIF)。以下是详细实现方法(含代码示例),包括自定义实现和库函数调用。
相关系数法
通过计算特征之间的皮尔逊相关系数,设定阈值去除高相关特征。
原理
- 皮尔逊相关系数:衡量两个特征之间的线性相关性,范围[-1, 1]。
- 阈值设定:通常设定绝对值为7~0.9,超过阈值则认为共线性显著。
- 处理逻辑:
- 计算所有特征对的相关系数矩阵。
- 若两个特征相关系数超过阈值,删除其中一个(或根据业务逻辑选择保留)。
代码实现
import numpy as np
import pandas as pd
def remove_correlated_features_corr(df, threshold=0.8):
"""
基于相关系数去除高相关特征
:param df: DataFrame,包含所有特征
:param threshold: 相关系数阈值
:return: 去除共线性特征后的 DataFrame
"""
corr_matrix = df.corr().abs() # 计算绝对值相关系数矩阵
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(bool)) # 取上三角矩阵
to_drop = [column for column in upper.columns if any(upper[column] > threshold)] # 记录需删除的特征
return df.drop(columns=to_drop)
# 示例
data = {
'A': [1, 2, 3, 4, 5],
'B': [1.1, 2.1, 3.1, 4.1, 5.1], # 与 A 高度相关
'C': [5, 4, 3, 2, 1],
'D': [2, 3, 4, 5, 6]
}
df = pd.DataFrame(data)
df_filtered = remove_correlated_features_corr(df, threshold=0.9)
print("原始特征:", df.columns.tolist()) # ['A', 'B', 'C', 'D']
print("保留特征:", df_filtered.columns.tolist()) # ['A', 'C', 'D'](B 被删除)
优点
- 简单直观,计算高效。
- 适合快速筛选线性相关特征。
缺点
- 只能检测两两之间的线性关系,无法处理多重共线性(多个特征组合相关)。
- 阈值需人工设定,可能误删重要特征。
方差膨胀因子(VIF)
通过计算每个特征的 VIF 值,衡量其受其他特征线性影响的程度。
原理
- VIF 公式:$VIF_i = \frac{1}{1 – R_i^2}$
- 其中$R_i^2$ 是将第 i 个特征作为因变量,其他特征作为自变量进行线性回归的决定系数。
- 阈值设定:
- VIF < 5:低共线性。
- 5 ≤ VIF < 10:中度共线性。
- VIF ≥ 10:高共线性(需删除或处理)。
自定义代码实现
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant
def calculate_vif(df, threshold=5, max_iter=10):
"""
逐步删除高 VIF 特征
:param df: DataFrame,包含所有特征
:param threshold: VIF 阈值
:param max_iter: 最大迭代次数
:return: 去除高 VIF 特征后的 DataFrame
"""
df_numeric = df.select_dtypes(include=[np.number]) # 仅保留数值型特征
df_numeric = df_numeric.dropna(axis=1, how='any') # 删除含缺失值的列
features = df_numeric.columns.tolist()
for _ in range(max_iter):
vif = [variance_inflation_factor(df_numeric.values, i) for i in range(df_numeric.shape[1])]
max_vif = max(vif)
if max_vif < threshold:
break
# 删除 VIF 最大的特征
max_idx = vif.index(max_vif)
feature_to_remove = features[max_idx]
df_numeric = df_numeric.drop(columns=feature_to_remove)
features.remove(feature_to_remove)
return df_numeric
# 示例
df_vif_filtered = calculate_vif(df, threshold=5)
print("保留特征:", df_vif_filtered.columns.tolist()) # ['C', 'D'](A和B因共线性被删除)
使用库函数简化
def calculate_vif_quick(df, threshold=5):
"""
快速计算 VIF 并删除高共线性特征
"""
df_const = add_constant(df) # statsmodels 需要添加截距项
vif = pd.DataFrame()
vif["Feature"] = df_const.columns
vif["VIF"] = [variance_inflation_factor(df_const.values, i) for i in range(df_const.shape[1])]
vif = vif[vif["Feature"] != "const"] # 忽略截距项
features_to_keep = vif[vif["VIF"] <= threshold]["Feature"].tolist()
return df[features_to_keep]
对比与选择
| 方法 | 适用场景 | 优点 | 缺点 |
| 相关系数法 | 快速去除两两线性相关特征 | 计算快,易实现 | 无法处理多重共线性 |
| VIF | 检测并处理多重共线性 | 更全面,适合复杂线性关系 | 计算成本高,需逐步删除 |
实际应用建议
- 预处理阶段:先用相关系数法去除明显高相关特征。
- 精细处理:对剩余特征使用 VIF 进一步筛选。
- 结合业务逻辑:某些高相关特征可能代表业务关键指标(如销售额和利润),需人工判断是否保留。
注意事项
- 数据预处理:
- 删除缺失值或填充(VIF 计算不支持缺失值)。
- 标准化特征(线性回归对尺度敏感)。
- 非线性关系:
- 相关系数和 VIF 仅检测线性共线性,无法处理非线性依赖(如多项式关系)。
- 高维数据问题:
- 当特征数p > 样本数 n 时,VIF 可能无法计算(因矩阵奇异),需先降维。
- 替代方法:
- 主成分分析(PCA):将共线性特征转换为正交成分,但牺牲可解释性。
- L1 正则化(Lasso):自动压缩冗余特征的系数至零(见前文)。
完整流程示例
步骤 1:加载数据并计算相关系数
import pandas as pd
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
df = df.iloc[:, :10] # 仅取前10个特征用于示例
# 相关系数法去重
df_corr_filtered = remove_correlated_features_corr(df, threshold=0.85)
print("相关系数法保留特征数:", df_corr_filtered.shape[1])
步骤 2:进一步用 VIF 筛选
# VIF 去重
df_vif_filtered = calculate_vif(df_corr_filtered, threshold=5)
print("VIF 法保留特征数:", df_vif_filtered.shape[1])
步骤 3:验证模型效果
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(df_vif_filtered, data.target, test_size=0.2, random_state=42)
# 训练模型
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 评估准确率
print("测试集准确率:", accuracy_score(y_test, y_pred))
通过 相关系数法 和 VIF 可有效去除共线性特征,提升模型稳定性和可解释性。实际应用中需根据数据规模、共线性类型和业务需求选择方法,必要时结合 PCA 或正则化技术。对于高维数据,建议优先使用相关系数法快速筛选,再通过 VIF 或模型嵌入法(如 Lasso)进一步优化。
特征组合优化
在特征选择中,过滤法(Filter Methods)和包装法(Wrapper Methods)各有优劣。将两者结合(如 先通过方差阈值过滤低方差特征,再用递归特征消除(RFE))可以兼顾效率与精度,适用于高维数据或计算资源有限的场景。
通过 方差阈值(过滤法) + RFE(包装法) 的组合,可在保证特征选择精度的前提下显著提升效率,尤其适合高维数据(如基因数据、文本 TF-IDF 矩阵)。关键步骤包括:
- 快速初筛:用方差阈值剔除低信息量特征。
- 精细筛选:基于模型性能的 RFE 选择最优子集。
- 参数调优:通过网格搜索平衡特征数量与模型性能。
实际应用中需结合数据特点、模型类型和业务需求灵活调整流程,必要时引入嵌入法或特征工程方法(如多项式扩展)进一步提升效果。
方法原理
过滤法(方差阈值)
- 目标:快速剔除明显无意义的特征(如方差接近0的常量特征)。
- 优点:计算简单、高效,无需依赖模型。
- 公式:保留方差大于阈值的特征:$\text{Var}(X_j) = \frac{1}{n} \sum_{i=1}^n (x_{ij} – \mu_j)^2$
- 若$\text{Var}(X_j) < \text{threshold}$,删除特征 $X_j$。
包装法(递归特征消除,RFE)
- 目标:基于模型性能逐步剔除对预测贡献小的特征。
- 优点:捕捉特征与模型的关系,选择最优子集。
- 步骤:
- 使用全部特征训练模型。
- 根据特征重要性(如线性模型的系数)排序。
- 移除重要性最低的特征。
- 重复上述过程,直到剩余指定数量的特征。
组合优势
- 效率提升:过滤法快速减少特征维度,降低后续 RFE 的计算成本。
- 精度保障:RFE 在精简后的特征集中进行精细化筛选,避免遗漏重要特征。
实现步骤
- 数据预处理:标准化(可选,对线性模型必要)。
- 过滤法:使用方差阈值剔除低方差特征。
- 包装法:应用 RFE 进一步选择特征。
- 模型训练与评估:验证最终特征子集的效果。
代码示例(Scikit-Learn)
数据加载与预处理
from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler # 加载数据 data = load_breast_cancer() X, y = data.data, data.target feature_names = data.feature_names # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 标准化(对线性模型必要) scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test)
方差阈值过滤
from sklearn.feature_selection import VarianceThreshold
# 设置方差阈值(过滤方差 < 0.1 的特征)
selector_var = VarianceThreshold(threshold=0.1)
X_train_filtered = selector_var.fit_transform(X_train_scaled)
X_test_filtered = selector_var.transform(X_test_scaled)
# 获取保留的特征索引和名称
retained_indices = selector_var.get_support(indices=True)
retained_features = feature_names[retained_indices]
print("方差阈值保留特征数:", len(retained_features)) # 示例输出:25(原30个)
递归特征消除(RFE)
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
# 初始化基模型(如逻辑回归)
model = LogisticRegression(max_iter=1000, random_state=42)
# 设置 RFE 选择器(最终保留5个特征)
selector_rfe = RFE(estimator=model, n_features_to_select=5, step=1)
selector_rfe.fit(X_train_filtered, y_train)
# 获取最终选择的特征
final_features = retained_features[selector_rfe.support_]
print("RFE 最终特征:", final_features)
# 示例输出:['mean radius', 'mean perimeter', 'mean concave points', 'worst radius', 'worst concave points']
模型训练与评估
# 提取最终特征子集
X_train_final = selector_rfe.transform(X_train_filtered)
X_test_final = selector_rfe.transform(X_test_filtered)
# 训练模型
model.fit(X_train_final, y_train)
accuracy = model.score(X_test_final, y_test)
print("测试集准确率:", accuracy) # 示例输出:0.956
参数调优
通过网格搜索优化方差阈值和 RFE 保留特征数:
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
# 创建流水线(标准化 + 方差阈值 + RFE + 分类器)
pipeline = Pipeline([
('scaler', StandardScaler()),
('variance_threshold', VarianceThreshold()),
('rfe', RFE(estimator=LogisticRegression(max_iter=1000, random_state=42))),
('classifier', LogisticRegression(max_iter=1000, random_state=42))
])
# 参数网格
params = {
'variance_threshold__threshold': [0.01, 0.1, 0.5], # 方差阈值
'rfe__n_features_to_select': [5, 10, 15] # RFE保留特征数
}
# 网格搜索
grid = GridSearchCV(pipeline, params, cv=5, scoring='accuracy')
grid.fit(X_train, y_train)
# 输出最优参数和准确率
print("最优参数:", grid.best_params_) # 示例:{'rfe__n_features_to_select':5, 'variance_threshold__threshold':0.1}
print("最优准确率:", grid.best_score_) # 示例:0.964
优缺点对比
| 方法 | 优点 | 缺点 |
| 单独过滤法 | 计算极快,适合高维数据初筛。 | 可能误删重要特征(尤其非线性关系)。 |
| 单独包装法 | 特征选择与模型性能强相关,结果更优。 | 计算成本高,特征多时效率低。 |
| 组合方法 | 平衡效率与精度,适合工程落地。 | 需调参(阈值、保留特征数)。 |
注意事项
- 数据标准化:若使用线性模型(如逻辑回归)作为 RFE 的基模型,必须标准化数据,否则系数不可比。
- 基模型选择:
- 线性模型(如逻辑回归、SVM):适合捕捉线性关系,计算快。
- 树模型(如随机森林):适合非线性关系,但计算成本高。
- 阈值设定:方差阈值过低可能导致过滤无效,过高可能丢失重要特征。可结合数据分布(如观察特征方差直方图)调整。
- 业务对齐:若某些低方差特征在业务上有特殊意义(如关键指标),需人工干预保留。
高级扩展
嵌入法(Embedded Methods)结合
在过滤法和包装法基础上,可加入 L1 正则化(如 Lasso)进一步压缩冗余特征:
from sklearn.linear_model import LassoCV
# 流水线:方差阈值 + Lasso 特征选择
pipeline = Pipeline([
('scaler', StandardScaler()),
('variance_threshold', VarianceThreshold(threshold=0.1)),
('lasso', LassoCV(cv=5)),
('classifier', LogisticRegression(max_iter=1000))
])
特征交叉与多项式扩展
对过滤后的特征进行组合(如多项式特征),再用 RFE 筛选:
from sklearn.preprocessing import PolynomialFeatures
# 流水线:方差阈值 + 多项式扩展 + RFE
pipeline = Pipeline([
('scaler', StandardScaler()),
('variance_threshold', VarianceThreshold(threshold=0.1)),
('poly', PolynomialFeatures(degree=2, interaction_only=True)),
('rfe', RFE(estimator=LogisticRegression(max_iter=1000))),
('classifier', LogisticRegression(max_iter=1000))
])
选择策略建议
- 高维数据:先使用VarianceThreshold或单变量方法过滤,再结合嵌入法。
- 模型解释性要求高:优先过滤法或L1正则化。
- 计算资源充足:尝试包装法(如RFECV)获得最优子集。
参考链接:



