类别型特征(categorical feature)主要是指职业,血型等在有限类别内取值的特征。它的原始输入通常是字符串形式,大多数算法模型不接受数值型特征的输入,针对数值型的类别特征会被当成数值型特征,从而造成训练的模型产生错误。
Label encoding
LabelEncoding是使用字典的方式,将每个类别标签与不断增加的整数相关联,即生成一个名为class_的实例数组的索引。
Scikit-learn中的LabelEncoder是用来对分类型特征值进行编码,即对不连续的数值或文本进行编码。其中包含以下常用方法:
- fit(y):fit可看做一本空字典,y可看作要塞到字典中的词。
- fit_transform(y):相当于先进行fit再进行transform,即把y塞到字典中去以后再进行transform得到索引值。
- inverse_transform(y):根据索引值y获得原始数据。
- transform(y):将y转变成索引值。
from sklearn.preprocessing import LabelEncoder le = LabelEncoder() city_list = ["paris", "paris", "tokyo", "amsterdam"] le.fit(city_list) print(le.classes_) #输出为:['amsterdam' 'paris' 'tokyo'] city_list_le = le.transform(city_list) #进行Encode print(city_list_le) #输出为:[1 1 2 0] city_list_new = le.inverse_transform(city_list_le) #进行decode print(city_list_new) #输出为:['paris' 'paris' 'tokyo' 'amsterdam']
多列数据编码方式:
import pandas as pd
from sklearn.preprocessing import LabelEncoder
df = pd.DataFrame({
'pets': ['cat', 'dog', 'cat', 'monkey', 'dog', 'dog'],
'owner': ['Champ', 'Ron', 'Brick', 'Champ', 'Veronica', 'Ron'],
'location': ['San_Diego', 'New_York', 'New_York', 'San_Diego', 'San_Diego',
'New_York']
})
d = {}
le = LabelEncoder()
cols_to_encode = ['pets', 'owner', 'location']
for col in cols_to_encode:
df_train[col] = le.fit_transform(df_train[col])
d[col] = le.classes_
Pandas的factorize()可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。factorize函数的返回值是一个tuple(元组),元组中包含两个元素。第一个元素是一个array,其中的元素是标称型元素映射为的数字;第二个元素是Index类型,其中的元素是所有标称型元素,没有重复。
import numpy as np import pandas as pd df = pd.DataFrame(['green', 'bule', 'red', 'bule', 'green'], columns=['color']) pd.factorize(df['color']) #(array([0, 1, 2, 1, 0], dtype=int64), Index(['green', 'bule', 'red'], dtype='object')) pd.factorize(df['color'])[0] #array([0, 1, 2, 1, 0], dtype=int64) pd.factorize(df['color'])[1] #Index(['green', 'bule', 'red'], dtype='object')
LabelEncoding只是将文本转化为数值,并没有解决文本特征的问题:所有的标签都变成了数字,算法模型直接将根据其距离来考虑相似的数字,而不考虑标签的具体含义。使用该方法处理后的数据适合支持类别性质的算法模型,如LightGBM。
序列编码(OrdinalEncoding)
OrdinalEncoding即最为简单的一种思路,对于一个具有m个category的Feature,我们将其对应地映射到[0,m-1]的整数。当然OrdinalEncoding更适用于OrdinalFeature,即各个特征有内在的顺序。例如对于”学历”这样的类别,”学士”、”硕士”、”博士”可以很自然地编码成[0,2],因为它们内在就含有这样的逻辑顺序。但如果对于“颜色”这样的类别,“蓝色”、“绿色”、“红色”分别编码成[0,2]是不合理的,因为我们并没有理由认为“蓝色”和“绿色”的差距比“蓝色”和“红色”的差距对于特征的影响是不同的。
ord_map = {'Gen1': 1, 'Gen2': 2, 'Gen3': 3, 'Gen4': 4, 'Gen5': 5, 'Gen6': 6}
df['GenerationLabel'] = df['Generation'].map(gord_map)
独热编码(One-Hot Encoding)
在实际的机器学习的应用任务中,特征有时候并不总是连续值,有可能是一些分类值,如性别可分为male和female。在机器学习任务中,对于这样的特征,通常我们需要对其进行特征数字化,比如有如下三个特征属性:
- 性别:[“male”,”female”]
- 地区:[“Europe”,”US”,”Asia”]
- 浏览器:[“Firefox”,”Chrome”,”Safari”,”InternetExplorer”]
对于某一个样本,如[“male”,”US”,”InternetExplorer”],我们需要将这个分类值的特征数字化,最直接的方法,我们可以采用序列化的方式:[0,1,3]。但是,即使转化为数字表示后,上述数据也不能直接用在我们的分类器中。因为,分类器往往默认数据是连续的,并且是有序的。按照上述的表示,数字并不是有序的,而是随机分配的。这样的特征处理并不能直接放入机器学习算法中。
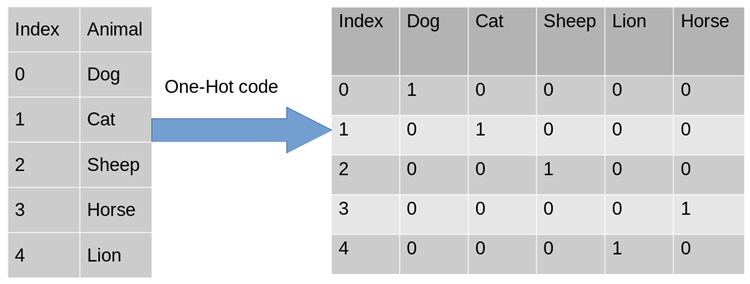
为了解决上述问题,其中一种可能的解决方法是采用独热编码(One-Hot Encoding)。独热编码,又称为一位有效编码。其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。可以这样理解,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征。并且,这些特征互斥,每次只有一个激活。因此,数据会变成稀疏的。
对于上述的问题,性别的属性是二维的,同理,地区是三维的,浏览器则是四维的,这样,我们可以采用One-Hot编码的方式对上述的样本[“male”,”US”,”InternetExplorer”]编码,male则对应着[1,0],同理US对应着[0,1,0],InternetExplorer对应着[0,0,0,1]。则完整的特征数字化的结果为:[1,0,0,1,0,0,0,0,1]。
为什么能使用One-Hot Encoding?
- 使用 one-hot 编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,也是基于的欧式空间。
- 将离散型特征使用 one-hot 编码,可以会让特征之间的距离计算更加合理。比如,有一个离散型特征,代表工作类型,该离散型特征,共有三个取值,不使用 one-hot 编码,计算出来的特征的距离是不合理。那如果使用 one-hot 编码,显得更合理。
独热编码优缺点
- 优点:独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有 0 和 1,不同的类型存储在垂直的空间。
- 缺点:当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA(主成分分析) 来减少维度。而且 One-Hot Encoding+PCA 这种组合在实际中也非常有用。
One-Hot Encoding 的使用场景
- 独热编码用来解决类别型数据的离散值问题。将离散型特征进行 one-hot 编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用 one-hot 编码就可以很合理的计算出距离,那么就没必要进行 one-hot 编码,比如,该离散特征共有 1000 个取值,我们分成两组,分别是 400 和 600, 两个小组之间的距离有合适的定义,组内的距离也有合适的定义,那就没必要用 one-hot 编码。
- 基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting 等。对于决策树来说,one-hot 的本质是增加树的深度,决策树是没有特征大小的概念的,只有特征处于他分布的哪一部分的概念。
基于 Scikit-learn 的 onehotencoding
LabelBinarizer:将对应的数据转换为二进制型,类似于 onehot 编码,这里有几点不同:
- 可以处理数值型和类别型数据
- 输入必须为 1D 数组
- 可以自己设置正类和父类的表示方式
from sklearn.preprocessing import LabelBinarizer lb = LabelBinarizer() city_list = ["paris", "paris", "tokyo", "amsterdam"] lb.fit(city_list) print(lb.classes_) # 输出为:['amsterdam' 'paris' 'tokyo'] city_list_le = lb.transform(city_list) # 进行 Encode print(city_list_le) # 输出为: # [[0 1 0] # [0 1 0] # [0 0 1] # [1 0 0]] city_list_new = lb.inverse_transform(city_list_le) # 进行 decode print(city_list_new) # 输出为:['paris' 'paris' 'tokyo' 'amsterdam']
OneHotEncoder 只能对数值型数据进行处理,需要先将文本转化为数值(Label encoding)后才能使用,只接受 2D 数组:
import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
def LabelOneHotEncoder(data, categorical_features):
d_num = np.array([])
for f in data.columns:
if f in categorical_features:
le, ohe = LabelEncoder(), OneHotEncoder()
data[f] = le.fit_transform(data[f])
if len(d_num) == 0:
d_num = np.array(ohe.fit_transform(data[[f]]))
else:
d_num = np.hstack((d_num, ohe.fit_transform(data[[f]]).A))
else:
if len(d_num) == 0:
d_num = np.array(data[[f]])
else:
d_num = np.hstack((d_num, data[[f]]))
return d_num
df = pd.DataFrame([
['green', 'Chevrolet', 2017],
['blue', 'BMW', 2015],
['yellow', 'Lexus', 2018],
])
df.columns = ['color', 'make', 'year']
df_new = LabelOneHotEncoder(df, ['color', 'make', 'year'])
基于 Pandas 的 onehotencoding
其实如果我们跳出 scikit-learn,在 pandas 中可以很好地解决这个问题,用 pandas 自带的 get_dummies 函数即可
import pandas as pd
df = pd.DataFrame([
['green', 'Chevrolet', 2017],
['blue', 'BMW', 2015],
['yellow', 'Lexus', 2018],
])
df.columns = ['color', 'make', 'year']
df_processed = pd.get_dummies(df, prefix_sep="_", columns=df.columns[:-1])
print(df_processed)
get_dummies 的优势在于:
- 本身就是 pandas 的模块,所以对 DataFrame 类型兼容很好
- 不管你列是数值型还是字符串型,都可以进行二值化编码
- 能够根据指令,自动生成二值化编码后的变量名
get_dummies 虽然有这么多优点,但毕竟不是 sklearn 里的 transformer 类型,所以得到的结果得手动输入到 sklearn 里的相应模块,也无法像 sklearn 的 transformer 一样可以输入到 pipeline 中进行流程化地机器学习过程。
频数编码(Frequency Encoding/Count Encoding)
将类别特征替换为训练集中的计数(一般是根据训练集来进行计数,属于统计编码的一种,统计编码,就是用类别的统计特征来代替原始类别,比如类别 A 在训练集中出现了 100 次则编码为 100)。这个方法对离群值很敏感,所以结果可以归一化或者转换一下(例如使用对数变换)。未知类别可以替换为 1。
频数编码使用频次替换类别。有些变量的频次可能是一样的,这将导致碰撞。尽管可能性不是非常大,没法说这是否会导致模型退化,不过原则上我们不希望出现这种情况。
import pandas as pd
data_count = data.groupby('城市')['城市'].agg({'频数':'size'}).reset_index()
data = pd.merge(data, data_count, on='城市', how='left')
目标编码(Target Encoding/Mean Encoding)
目标编码(target encoding),亦称均值编码(mean encoding)、似然编码(likelihood encoding)、效应编码(impact encoding),是一种能够对高基数(high cardinality)自变量进行编码的方法 (Micci-Barreca 2001)。
如果某一个特征是定性的(categorical),而这个特征的可能值非常多(高基数),那么目标编码(Target encoding)是一种高效的编码方式。在实际应用中,这类特征工程能极大提升模型的性能。
一般情况下,针对定性特征,我们只需要使用 sklearn 的 OneHotEncoder 或 LabelEncoder 进行编码。
LabelEncoder 能够接收不规则的特征列,并将其转化为从 0 到 n-1 的整数值(假设一共有 n 种不同的类别);OneHotEncoder 则能通过哑编码,制作出一个 m*n 的稀疏矩阵(假设数据一共有 m 行,具体的输出矩阵格式是否稀疏可以由 sparse 参数控制)。
定性特征的基数(cardinality)指的是这个定性特征所有可能的不同值的数量。在高基数(high cardinality)的定性特征面前,这些数据预处理的方法往往得不到令人满意的结果。
高基数定性特征的例子:IP 地址、电子邮件域名、城市名、家庭住址、街道、产品号码。
主要原因:
- LabelEncoder 编码高基数定性特征,虽然只需要一列,但是每个自然数都具有不同的重要意义,对于 y 而言线性不可分。使用简单模型,容易欠拟合(underfit),无法完全捕获不同类别之间的区别;使用复杂模型,容易在其他地方过拟合(overfit)。
- OneHotEncoder 编码高基数定性特征,必然产生上万列的稀疏矩阵,易消耗大量内存和训练时间,除非算法本身有相关优化(例:SVM)。
如果某个类别型特征基数比较低(low-cardinality features),即该特征的所有值去重后构成的集合元素个数比较少,一般利用 One-hot 编码方法将特征转为数值型。One-hot 编码可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost 对于基数较低的类别型特征也是采用后一种实现。
显然,在高基数类别型特征(high cardinality features)当中,比如 userID,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行 One-hot 编码。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称 TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用 TS 作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对 TS 数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在 LightGBM 当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称 GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
- 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对 GS 进行计算
- 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别
为了克服这些缺点,LightGBM 以损失部分信息为代价将所有的长尾类别归为一类,作者声称这样处理高基数类别型特征时比 One-hot 编码还是好不少。不过如果采用 TS 特征,那么对于每个类别只需要计算和存储一个数字。因此,采用 TS 作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS 也被广泛应用在点击预测任务当中,这个场景当中的类别型特征有用户、地区、广告、广告发布者等。接下来我们着重讨论 TS,暂时将 One-hot 编码和 GS 放一边。
以下是计算公式:
$$s=\frac{1}{1+\exp(-\frac{n-mdl}{a})}$$
$$\hat{s}^k=prior*(1-s)+s*\frac{n^+}{n}$$
其中 n 代表的是该某个特征取值的个数,$n^+$代表某个特征取值下正 Label 的个数,mdl 为一个最小阈值,样本数量小于此值的特征类别将被忽略,prior 是 Label 的均值。注意,如果是处理回归问题的话,$\frac{n^+}{n}$可以处理成相应该特征下 label 取值的 average/max。对于 k 分类问题,会生成对应的 k-1 个特征。
此方法同样容易引起过拟合,以下方法用于防止过拟合:
- 增加正则项 a 的大小
- 在训练集该列中添加噪声
- 使用交叉验证
目标编码属于有监督的编码方式,如果运用得当则能够有效地提高预测模型的准确性 (Pargent, Bischl, and Thomas 2019);而这其中的关键,就是在编码的过程中引入正则化,避免过拟合问题。
例如类别 A 对应的标签 1 有 200 个,标签 2 有 300 个,标签 3 有 500 个,则可以编码为:2/10, 3/10, 3/6。中间最重要的是如何避免过拟合(原始的 target encoding 直接对全部的训练集数据和标签进行编码,会导致得到的编码结果太过依赖与训练集),常用的解决方法是使用 2 levels of cross-validation 求出 target mean,思路如下:
- 把 train data 划分为 20-folds(举例:in fold: fold#2-20, out of fold: fold#1)
- 将每一个 in fold(fold#2-20)再次划分为 10-folds(举例:inner_infold: fold#2-10, Inner_oof: fold#1)
- 计算 10-folds 的 inner out of folds 值(举例:使用 inner_infold#2-10 的 target 的均值,来作为 inner_oof#1 的预测值)
- 对 10 个 inner out of folds 值取平均,得到 inner_oof_mean
- 计算 oof_mean(举例:使用 in fold#2-20 的 inner_oof_mean 来预测 out of fold#1 的 oof_mean
- 将每一个 in fold(fold#2-20)再次划分为 10-folds(举例:inner_infold: fold#2-10, Inner_oof: fold#1)
- 将 train data 的 oof_mean 映射到 test data 完成编码
比如划分为 10 折,每次对 9 折进行标签编码然后用得到的标签编码模型预测第 10 折的特征得到结果,其实就是常说的均值编码。
目标编码尝试对分类特征中每个级别的目标总体平均值进行测量。这意味着,当每个级别的数据更少时,估计的均值将与“真实”均值相距更远,方差更大。
from category_encoders import TargetEncoder import pandas as pd from sklearn.datasets import load_boston # prepare some data bunch = load_boston() y_train = bunch.target[0:250] y_test = bunch.target[250:506] X_train = pd.DataFrame(bunch.data[0:250], columns=bunch.feature_names) X_test = pd.DataFrame(bunch.data[250:506], columns=bunch.feature_names) # use target encoding to encode two categorical features enc = TargetEncoder(cols=['CHAS', 'RAD']) # transform the datasets training_numeric_dataset = enc.fit_transform(X_train, y_train) testing_numeric_dataset = enc.transform(X_test)
BetaTargetEncoding
Kaggle 竞赛 Avito Demand Prediction Challenge 第 14 名的 solution 分享:14th Place Solution: The Almost Golden Defenders。和 target encoding 一样,beta target encoding 也采用 target mean value(among each category)来给 categorical feature 做编码。不同之处在于,为了进一步减少 target variable leak,beta target encoding 发生在在 5-fold CV 内部,而不是在 5-fold CV 之前:
- 把 train data 划分为 5-folds(5-fold cross validation)
- target encoding based on infold data
- train model
- get out of fold prediction
同时 beta target encoding 加入了 smoothing term,用 bayesian mean 来代替 mean。Bayesian mean (Bayesian average) 的思路:某一个 category 如果数据量较少 (<N_min),noise 就会比较大,需要补足数据,达到 smoothing 的效果。补足数据值=prior mean。N_min 是一个 regularization term,N_min 越大,regularization 效果越强。
另外,对于 target encoding 和 beta target encoding,不一定要用 target mean (or bayesian mean),也可以用其他的统计值包括 medium, frqequency, mode, variance, skewness, and kurtosis—或任何与 target 有 correlation 的统计值。
# train->training dataframe
# test->test dataframe
# N_min->smoothing term, minimum sample size, if sample size is less than N_min, add up to N_min
# target_col->target column
# cat_cols->categorical colums
# Step 1: fill NA in train and test dataframe
# Step 2: 5-fold CV (beta target encoding within each fold)
kf = KFold(n_splits=5, shuffle=True, random_state=0)
for i, (dev_index, val_index) in enumerate(kf.split(train.index.values)):
# split data into dev set and validation set
dev = train.loc[dev_index].reset_index(drop=True)
val = train.loc[val_index].reset_index(drop=True)
feature_cols = []
for var_name in cat_cols:
feature_name = f'{var_name}_mean'
feature_cols.append(feature_name)
prior_mean = np.mean(dev[target_col])
stats = dev[[target_col, var_name]].groupby(var_name).agg(['sum', 'count'])[target_col].reset_index()
### beta target encoding by Bayesian average for dev set
df_stats = pd.merge(dev[[var_name]], stats, how='left')
df_stats['sum'].fillna(value=prior_mean, inplace=True)
df_stats['count'].fillna(value=1.0, inplace=True)
N_prior = np.maximum(N_min - df_stats['count'].values, 0) # prior parameters
dev[feature_name] = (prior_mean * N_prior + df_stats['sum']) / (N_prior + df_stats['count']) # Bayesian mean
### beta target encoding by Bayesian average for val set
df_stats = pd.merge(val[[var_name]], stats, how='left')
df_stats['sum'].fillna(value=prior_mean, inplace=True)
df_stats['count'].fillna(value=1.0, inplace=True)
N_prior = np.maximum(N_min - df_stats['count'].values, 0) # prior parameters
val[feature_name] = (prior_mean * N_prior + df_stats['sum']) / (N_prior + df_stats['count']) # Bayesian mean
### beta target encoding by Bayesian average for test set
df_stats = pd.merge(test[[var_name]], stats, how='left')
df_stats['sum'].fillna(value=prior_mean, inplace=True)
df_stats['count'].fillna(value=1.0, inplace=True)
N_prior = np.maximum(N_min - df_stats['count'].values, 0) # prior parameters
test[feature_name] = (prior_mean * N_prior + df_stats['sum']) / (N_prior + df_stats['count']) # Bayesian mean
# Bayesian mean is equivalent to adding N_prior data points of value prior_mean to the dataset.
del df_stats, stats
# Step 3: train model (K-fold CV), get oof prediction
M-Estimate Encoding
M-Estimate Encoding 相当于一个简化版的 Target Encoding:
$$\hat{x}^k=\frac{n^{+}+prior*m}{y^{+}+m}$$
其中 $y^+$ 代表所有正 Label 的个数,m 是一个调参的参数,m 越大过拟合的程度就会越小,同样的在处理连续值时 $n^+$ 可以换成 label 的求和,$y^+$ 换成所有 label 的求和。
James-Stein Encoding
James-Stein Encoding 同样是基于 target 的一种算法。算法的思想很简单,对于特征的每个取值 k 可以根据下面的公式获得:
$$\hat{x}^k=(1-B)*\frac{n^+}{n}+B*\frac{y^+}{y}$$
其中 B 由以下公式估计:
$$B=\frac{Var[y^k]}{Var[y^k]+Var[y]}$$
但是它有一个要求是 target 必须符合正态分布,这对于分类问题是不可能的,因此可以把 y 先转化成概率的形式。或者在实际操作中,使用 grid search 的方法选择一个比较好的 B 值。
Weight of Evidence Encoder
Weight Of Evidence 同样是基于 target 的方法。
使用 WOE 作为变量,第 i 类的 WOE 等于:
$$WOE_i=\log(\frac{B_i/B_{total}}{G_i/G_{total}})=\log(\frac{B_i/G_i}{B_{total}/G_{total}})$$
WOE 特别合适逻辑回归,因为 Logit=log(odds)。WOE 编码的变量被编码为统一的维度(是一个被标准化过的值),变量之间直接比较系数即可。
Leave-one-out Encoder (LOO or LOOE)
这个方法类似于 SUM 的方法,只是在计算训练集每个样本的特征值转换时都要把该样本排除(消除特征某取值下样本太少导致的严重过拟合),在计算测试集每个样本特征值转换时与 SUM 相同。可见以下公式:
$$\hat{x}_i^k=\frac{\sum_{j\neq i}(y_i*(x_j==k))-y_i}{\sum_{j\neq i}x_j==k}$$
Binary Encoding
把每一类的序号用二进制进行编码,使用 log2N 维向量来编码 N 类。例如:(0,0) 代表第一类,(0,1) 代表第二类,(1,0) 代表第三类,(1,1) 代表第四类
Hashing Encoding
类似于 One-hot encoding,但是通过 hash 函数映射到一个低维空间,并且使得两个类对应向量的空间距离基本保持一致。使用低维空间来降低了表示向量的维度。
特征哈希可能会导致要素之间发生冲突。但哈希编码的优点是它不需要制定和维护原变量与新变量之间的映射关系。因此,哈希编码器的大小及复杂程度不随数据类别的增多而增多。
Probability Ratio Encoding
和 WOE 相似,只是去掉了 log,即:
$$PR_i=\frac{B_i/B_{total}}{G_i/G_{total}}=\frac{B_i/G_i}{B_{total}/G_{total}}$$
SumEncoder(DeviationEncoder, EffectEncoder)
求和编码通过比较某一特征取值下对应标签(或其他相关变量)的均值与标签的均值之间的差别来对特征进行编码。如果做不好细节,这个方法非常容易出现过拟合,所以需要配合留一法或者五折交叉验证进行特征的编码。还有根据方差加入惩罚项防止过拟合的方法。
HelmertEncoding
Helmert 编码通常在计量经济学中使用。在 Helmert 编码(分类特征中的每个值对应于 Helmert 矩阵中的一行)之后,线性模型中编码后的变量系数可以反映在给定该类别变量某一类别值的情形下因变量的平均值与给定该类别其他类别值的情形下因变量的平均值的差值。
Helmet 编码是仅次于 One-Hot Encoding 和 SumEncoder 使用最广泛的编码方法,与 SumEncoder 不同的是,它比较的是某一特征取值下对应标签(或其他相关变量)的均值与他之前特征的均值之间的差异,而不是和所有特征的均值比较。这个特征同样容易出现过拟合的情况。
CatBoostEncoding
对于可取值的数量比独热最大量还要大的分类变量,CatBoost 使用了一个非常有效的编码方法,这种方法和均值编码类似,但可以降低过拟合情况。它的具体实现方法如下:
- 将输入样本集随机排序,并生成多组随机排列的情况。
- 将浮点型或属性值标记转化为整数。
- 将所有的分类特征值结果都根据以下公式,转化为数值结果。
$$avgTarget=\frac{countInClass+prior}{totalCount+1}$$
其中 CountInClass 表示在当前分类特征值中,有多少样本的标记值是 1;Prior 是分子的初始值,根据初始参数确定。TotalCount 是在所有样本中(包含当前样本),和当前样本具有相同的分类特征值的样本数量。
更多信息:CatBoost 类别型特征处理逻辑
CatBoost 处理 Categorical features 总结:
- 首先,他们会计算一些数据的 statistics。计算某个 category 出现的频率,加上超参数,生成新的 numerical features。这一策略要求同一标签数据不能排列在一起(即先全是 0 之后全是 1 这种方式),训练之前需要打乱数据集。
- 第二,使用数据的不同排列(实际上是 4 个)。在每一轮建立树之前,先扔一轮骰子,决定使用哪个排列来生成树。
- 第三,考虑使用 categorical features 的不同组合。例如颜色和种类组合起来,可以构成类似于 blue dog 这样的 feature。当需要组合的 categorical features 变多时,catboost 只考虑一部分 combinations。在选择第一个节点时,只考虑选择一个 feature,例如 A。在生成第二个节点时,考虑 A 和任意一个 categorical feature 的组合,选择其中最好的。就这样使用贪心算法生成 combinations。
- 第四,除非向 gender 这种维数很小的情况,不建议自己生成 one-hot vectors,最好交给算法来处理。
参考链接:



