时序分析中的差分变换

差分变换（Difference Transformation）是一种数学工具，用于处理时间序列数据，尤其是在时间序列分析和信号处理中。差分变换的核心目的在于去除数据中的趋势和季节性成分，使得一个非平稳时间序列变得平稳。平稳性是指时间序列的统计特性（如均值、方差等）不随时间变化。

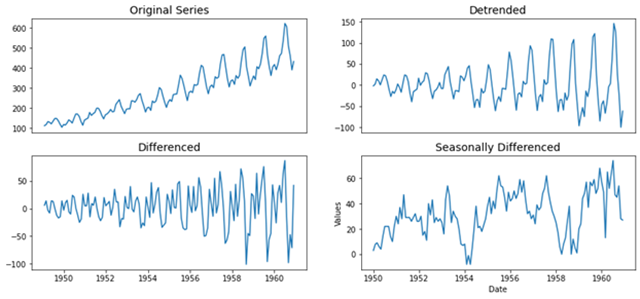
什么是差分变换？

差分变换涉及计算时间序列数据中一个观察值与前一个观察值之间的差异。一阶差分是最常见的差分变换，其定义如下：

对于一给定的时间序列 $\{X_t\}$，一阶差分序列 $\{Y_t\}$ 可以表示为：

$$Y_t = X_t – X_{t-1}$$

如果对差分过的序列再进行一次同样的差分操作，则称为二阶差分：

$$Z_t = Y_t – Y_{t-1} = (X_t – X_{t-1}) – (X_{t-1} – X_{t-2}) = X_t – 2X_{t-1} + X_{t-2}$$

如此类推，可以进行更高阶的差分。

差分变换的目的

• 降低数据的非平稳性：通过差分，可以去除或减弱时间序列中的趋势和季节性成分。
• 稳定方差：差分有时可以帮助稳定非常数方差的问题，这在金融时序数据中尤为常见。

差分变换的应用

• 趋势去除：如果时间序列存在线性或非线性趋势，一阶或更高阶的差分可以帮助去除这些趋势。
• 季节性调整：对于季节性时间序列，可以通过季节性差分（跨季节周期差分）去除季节性效应，例如月度数据采用12阶差分。
• 数据预处理：在应用ARIMA等模型进行预测之前，通常需要将非平稳时间序列转换为平稳序列。

差分变换的注意事项

• 差分变换可能导致数据丢失：每次差分都会导致序列的长度减少一个观察值。
• 过度差分可能会过度调整序列，导致数据中的信号被削弱，因此需要小心选择合适的差分阶数。
• 差分操作后，最终的时间序列应该检验平稳性，以确认差分的效果。

总而言之，差分变换是时间序列分析中的一项重要技术，对于实现数据平稳化和提高时序模型预测精度至关重要。在实际应用中，通常要结合单位根检验等其他统计方法来确定是否需要进行差分以及差分的阶数。

使用Python进行差分操作

在Python中进行差分操作，通常可以使用pandas库中的数据结构和函数。以下是一个简单的示例，展示了如何对时间序列数据进行一阶和二阶差分。

首先确保已经安装了pandas库，如果没有，可以使用pip安装：

import pandas as pd

# 假设我们有一组时间序列数据
data = {
    'date': ['2021-01-01', '2021-01-02', '2021-01-03', '2021-01-04', '2021-01-05'],
    'value': [100, 110, 120, 130, 125]
}

# 将数据转换为DataFrame
df = pd.DataFrame(data)

# 将date列转换为datetime类型，并设置为索引
df['date'] = pd.to_datetime(df['date'])
df.set_index('date', inplace=True)

# 执行一阶差分
df['first_difference'] = df['value'].diff()

# 执行二阶差分
df['second_difference'] = df['first_difference'].diff()

# 显示差分后的结果
print(df)

这个例子创建了一个简单的时间序列数据集，其中包括日期和对应的值。然后使用pandas的diff()函数进行一阶和二阶差分。这个函数默认计算的是一阶差分，对其结果再次调用diff()函数即可得到二阶差分。

diff()函数的输出会在第一行生成一个NaN值，因为第一个数据点之前没有数据来计算差值。在进行进一步的分析时，通常需要处理或删除这些NaN值。

差分后的DataFrame df 就包含了原始数据、一阶差分和二阶差分的结果。在实际应用中，你可能需要根据数据的具体情况选择合适的差分阶数。

使用差分消除季节性

要通过差分去除季节性，我们需要用到季节性差分，也就是在时间序列中，当前观测值与上一个季节相同位置的观测值之间进行差分。这种方法对于具有明显季节周期的数据来说非常有效。

以下是使用Python进行季节性差分的步骤：

• 确定季节性周期：首先，需要知道数据的季节性周期，例如，一个月的数据可能有月度季节性（周期为12），一周的数据可能有周季节性（周期为7）。
• 对数据进行季节性差分：使用pandas的diff()函数并指定周期参数进行差分。周期参数是指差分的步数，对于月度数据，如果想要去除年度季节性，周期就是12。

假设我们有一个月度时间序列数据集，并且我们想要去除年度季节性，我们可以这样做：

import pandas as pd

# 假设我们有一组带有月度季节性的时间序列数据
data = {
    'date': pd.date_range(start='2019-01-01', periods=24, freq='M'),
    'value': [...],  # 填入你的时间序列数据
}

# 创建DataFrame
df = pd.DataFrame(data)
df.set_index('date', inplace=True)

# 季节性周期，对于月度数据，年度季节性周期为12
seasonal_period = 12

# 执行季节性差分
df['seasonal_difference'] = df['value'].diff(seasonal_period)

# 查看差分结果
print(df)

此代码段中的seasonal_period = 12表明我们正在对数据进行年度季节性差分。diff(seasonal_period)函数将当前月的值与去年同月的值相减。

类似一阶或二阶差分，季节性差分也可能生成NaN值，因为前seasonal_period个观测值没有足够的数据来计算差分。同样，在进行时序分析或建模之前，这些NaN值需要被处理或移除。

进行季节性差分后，应该对时间序列数据进行平稳性检验（如ADF检验）来确认季节性差分的效果，并验证数据是否已经变得平稳。如果仍然不平稳，可能需要进行进一步的季节性差分或非季节性差分。

差分数据的还原

差分数据的还原是一个逆过程，涉及到将差分后的数据转换回原始的时间序列数据。这个过程要求我们拥有原始序列的起始点（或差分前的某些数据点），因为差分过程包含了数据丢失。

下面是如何使用Python还原一阶差分和季节性差分数据的步骤：

一阶差分数据还原

一阶差分数据的还原可以通过以下过程完成：

• 从原始时间序列中获取第一个观测值。
• 将差分后的第一个值加上原始序列的第一个值，得到原始序列的第二个值。
• 迭代此过程，直到所有差分数据都被还原。

使用pandas，可以通过cumsum()函数和原始数据点来实现：

import pandas as pd

# 差分后的数据（这里只是示例，你需要替换为实际的差分数据）
diff_data = [5, 7, -3, 10]

# 假设我们知道原始数据的第一个值
original_first_value = 100

# 创建差分数据的Series对象
diff_series = pd.Series(diff_data)

# 将第一个原始值作为差分序列的起点
restored_data = diff_series.cumsum() + original_first_value

# 将Series转换为list（如果需要）
restored_data_list = restored_data.tolist()

print(restored_data_list)

确保diff_data是从第二个原始值开始的差分数据，而original_first_value是原始序列的第一个值。

季节性差分数据还原

季节性差分数据的还原稍微复杂一些，因为它依赖于过去的一个季节周期的数据。以下是一个基本的步骤：

• 获取进行季节性差分之前周期内的所有数据点。
• 从差分序列的开始，将每个差分值加上季节周期前的对应值来还原原始数据。

以下是使用pandas进行季节性差分数据还原的示例：

# 假设这是季节性差分后的数据和原始数据中的一个季节周期（例如一年）
seasonal_diff = pd.Series([5, 3, -2, 8, -1, 2])
original_season = pd.Series([100, 105, 110, 115, 120, 125])  # 原始序列的季节周期数据

# 我们需要一个足够长的数组来存储还原的数据
restored = pd.Series(index=seasonal_diff.index, dtype=float)

# 季节周期，例如一年
seasonal_period = 6

# 还原季节性差分数据
for i in range(len(seasonal_diff)):
    if i < seasonal_period:
        # 使用原始季节周期的数据
        restored.iloc[i] = original_season.iloc[i] + seasonal_diff.iloc[i]
    else:
        # 使用前一个季节周期的还原数据
        restored.iloc[i] = restored.iloc[i - seasonal_period] + seasonal_diff.iloc[i]

print(restored)

在这个例子中，original_season代表了进行季节性差分之前的原始序列中的一个季节周期数据（如一年）。我们使用这个数据和差分数据seasonal_diff来还原出原始的时间序列数据。

请注意，根据数据的具体情况，差分的复原可能要复杂一些，特别是更高阶的差分或者同时存在季节性和非季节性差分时。在这种情况下，你可能需要按正确的顺序逐步还原每一次差分。

差分过程的注意事项

拆分次数的选择

选择正确的差分次数对于确保时间序列数据的平稳性和适宜性是非常关键的。差分次数过多或过少都可能对数据分析和预测模型的构建产生负面影响。以下是选择正确差分次数的一些方法和步骤：

• 视觉检查：
  • 先通过绘图观察时间序列的整体趋势和季节性特征。
  • 如果观察到明显的趋势或季节性，可以先应用一阶差分或季节性差分，并再次进行视觉检查。
• 单位根检验：
  • 使用统计测试，如ADF（Augmented Dickey-Fuller）检验、KPSS（Kwiatkowski-Phillips-Schmidt-Shin）检验，来检测时间序列的平稳性。
  • 如果测试结果表明时间序列是非平稳的，可以尝试进行一阶差分，然后重新进行单位根检验。
  • 重复此过程，直到测试表明时间序列是平稳的。
  • 对于季节性时间序列，可以使用季节性差分并结合单位根检验。
• 信息准则：
  • 应用诸如AIC（赤池信息准则）、BIC（贝叶斯信息准则）或HQIC（汉南-奎恩信息准则）等信息准则来选择差分次数。
  • 这些准则可以帮助你在拟合模型时选择最佳的差分次数，通常是选择使信息准则值最小的模型。
• 预测性能：
  • 尝试使用不同差分次数的数据来训练和验证预测模型，并比较它们的性能。
  • 选择提供最好预测结果的差分次数。
• 过度差分的警告：
  • 注意过度差分的风险，过度差分可能会使序列过于平坦，从而丢失重要信息。
  • 如果差分后的序列显示出过度的随机波动，这可能是过度差分的迹象。
  • 在这种情况下，你应该回退到较少的差分次数。

在实践中，选择差分次数通常是一个迭代的过程，在这个过程中，你可能需要结合上述方法来做出决策。始终记得，选择的差分次数应旨在使时间序列数据平稳，同时保留对构建预测模型有用的信息。

异常值的处理

处理差分过程中的异常值是一个重要的步骤，因为异常值可能会对模型的结果产生不成比例的影响。以下是处理差分过程中异常值的一些步骤和方法：

• 异常值检测：
  • 在差分前，先对原始数据进行异常值检测。可以使用统计方法，比如标准差、IQR（四分位数间距）或箱形图来识别异常值。
  • 还可以使用更复杂的方法，如基于模型的检测（例如基于聚类的方法、孤立森林等）。
• 异常值处理：
  • 一旦识别出异常值，需要决定如何处理它们。处理方法包括：
    • 删除：如果异常值数量不多，且可以合理地认为它们是由错误或罕见事件导致的，可以将其删除。
    • 修正：如果可以确定异常值的来源，可以修正这些数据点，使其与数据集中的其他值保持一致。
    • 替换：可以用中位数、均值或基于周围点的插值等方法来替换异常值。
    • 变换：对数据进行变换（例如对数变换）以减少异常值的影响。
  • 差分和模型建立：
    • 在处理完异常值之后，再进行差分操作。此时，差分后的序列应该更反映真实的序列特征，而不是被异常值所扭曲。
    • 建立时间序列模型，如ARIMA或季节性ARIMA（SARIMA）模型，并考虑异常值处理的影响。
  • 稳健性建模：
    • 考虑使用稳健性较强的时间序列模型，这些模型对异常值不那么敏感，如稳健的ARIMA模型。
  • 再次检查异常值：
    • 在差分和模型拟合后，再次检查残差是否含有异常值。
    • 异常值可能指示模型不足以捕捉数据中的所有动态，需要进行模型修正或进一步处理异常值。
  • 监控和调整：
    • 在模型投入使用后，定期监控预测错误，检查是否存在异常值的迹象，并根据需要调整模型。

总结来说，处理差分过程中的异常值应是一个系统的过程，需要在差分前后都进行异常值的检测和处理。通过适当的方法来处理异常值，可以有效提高时间序列分析和预测的准确性。

边界效应的处理

差分引起的边界效应通常发生在时间序列的起始和终止点，因为在这些位置上，差分操作可能会由于缺少必要的历史数据而导致结果不准确。以下是一些解决边界效应的策略：

• 数据填充：在差分之前，可以对序列的起始处进行填充，使用插值方法，如线性插值、样条插值或其他更复杂的方法来估计缺失值。填充的目的是为了在不引入较大误差的前提下，提供一个合理的数据点来支持差分操作。
• 数据扩展：如果你有访问历史数据的能力，可以尝试扩展时间序列数据集，通过获取序列开始之前的额外数据点来减少边界效应。
• 模型调整：在模型拟合阶段，特别是对于预测模型（如ARIMA），可以调整模型参数来尽量减少边界处的影响。
• 小心处理边界数据：在分析和解释模型结果时，对起始和终止点的数据结果给予特别关注，并小心处理这些点的预测值或估计值。
• 使用稳健的统计方法：采用稳健的统计方法可以减少异常值和边界效应的影响，例如，在进行差分或预测时可能选择使用中位数而不是平均值。
• 后处理：在差分后，可以对预测或分析的结果进行后处理，对于边界处的点可能需要进行平滑处理，例如可以使用移动平均或其他平滑技术。
• 避免差分：如果边界效应实在难以处理，可以考虑使用不涉及差分的其他方法来分析或预测时间序列，例如使用基于机器学习的模型。
• 对结果保持怀疑：最后，对起始和终止点的分析结果保持一定的怀疑态度，并在解释时谨慎。

在实际应用中，可能需要综合使用上述方法来最小化差分引起的边界效应。哪种方法更合适取决于具体的数据集、模型及其应用场景。

差分后的平稳性检测

差分是时间序列分析中常用的一种使非平稳序列变得平稳的方法。进行差分后，需要对序列的平稳性进行检验，以确保进一步的分析和模型构建基于平稳数据。以下是进行差分后平稳性检测的步骤和常用方法：

• 视觉检查：首先，通过绘制差分后的时间序列图来进行视觉检查。如果数据没有明显的趋势或季节性，并且在平均水平和方差上保持相对恒定，那么序列可能是平稳的。
• 描述性统计：查看差分后的序列统计摘要，包括均值、中位数、方差等，以及时间序列的自相关图（ACF）和偏自相关图（PACF）。平稳序列的ACF通常会较快地衰减至0。
• 单位根检验：实施单位根检验来正式检验时间序列的平稳性。常用的单位根测试包括：
  • ADF（Augmented Dickey-Fuller）检验：检验序列中是否存在单位根，如果p值显著（通常小于05），则可以拒绝单位根存在的原假设，认为序列是平稳的。
  • KPSS（Kwiatkowski-Phillips-Schmidt-Shin）检验：KPSS检验的原假设是序列是平稳的，如果p值显著，表明序列是非平稳的。
  • PP（Phillips-Perron）检验：与ADF检验类似，但在检验中对存在的自相关和异方差问题更为稳健。
• 检查季节性：如果原始序列存在季节性特征，可能需要执行季节性差分，并进行相应的平稳性检验。
• 模型拟合后的残差检验：如果你在差分后使用模型（如ARIMA）进行了拟合，那么可以检查模型残差的平稳性。理想情况下，拟合良好的模型残差应表现为白噪声。
• 综合判断：综合使用上述方法来判断差分后序列的平稳性。如果所有的检验和检查都表明序列是平稳的，则可以进行后续的分析和建模。

处理差分后的平稳性检测时，重要的是要注意平稳性的类型。严格意义上的平稳性（即强平稳性）要求序列的所有统计特性（均值、方差和协方差）都不随时间变化，而弱平稳性仅要求均值和方差恒定以及协方差只依赖于时间间隔。时间序列分析中通常关心的是后者。如果经过差分后的序列仍然不平稳，可能需要进一步的差分或采取其他方法来转换序列。

在Python中，你可以使用pandas库进行差分操作，使用matplotlib库进行绘图，使用statsmodels库进行平稳性检验。下面是相应的操作步骤：

首先，我们需要导入必要的库：

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 差分
df['diff_value'] = df['value'].diff()

# 移除由于差分产生的NaN值
df = df.dropna()
# 然后，你可以绘制差分后的序列以进行视觉检查：
plt.figure(figsize=(10,6))
plt.plot(df['diff_value'])
plt.title('Differenced Series')
plt.show()
# 接下来，你可以用自相关图（ACF）和偏自相关图（PACF）来检查差分后的序列：
plot_acf(df['diff_value'])
plt.show()

plot_pacf(df['diff_value'])
plt.show()
# 然后，你可以使用ADF检验来检查差分后序列的平稳性：
result = adfuller(df['diff_value'])
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))

如果ADF统计量小于临界值，或者p值显著（通常小于0.05），那么你可以拒绝存在单位根的原假设，这意味着差分后的序列是平稳的。

这只是一个基础的示例，具体的分析可能需要根据实际的时间序列数据进行调整。例如，如果原始系列具有季节性，你可能需要使用季节性差分，或者你可能需要使用不同的平稳性检验方法，如KPSS检验。

总之，差分是时间序列分析中的一个非常有用的工具，但它需要谨慎使用。正确应用差分方法并注意其潜在的陷阱，可以帮助你更好地理解数据，构建更有效的预测模型。