在观察数据的时候离散度是一个重要的指标。通常认为离散度越低数据会越好,但是现实场景并不如此。举个例子,比如某个电商网站有上万的商品,但是其每个商品的点评分离散度较低,那么将用户点评呈现给用户的价值就不是很大。
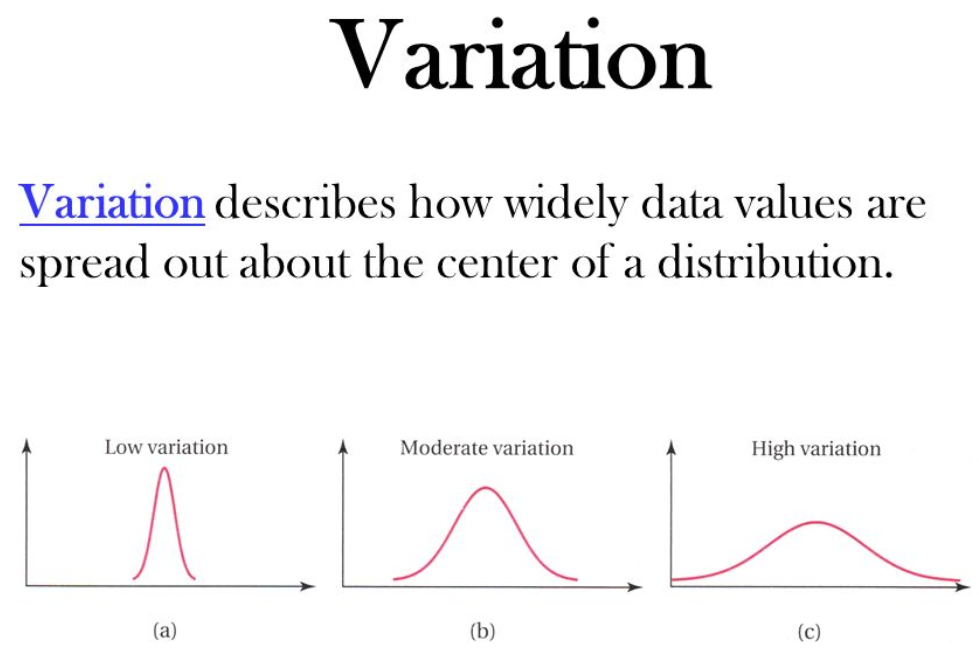
通常我们观察数据的时候使用均值、中位数、众数+离散度去观察数据。其中关于离散度有以下计算统计量:
极差(Range)
极差又称范围误差或全距(Range),以R表示,是用来表示统计资料中的变异量数(measures of variation),为最大值与最小值之间的差额,即最大值减最小值后所得数值。
$$R=x_{max}-x_{min}$$
极差只指明了测定值的最大离散范围,而未能利用全部测量值的信息,不能细致地反映测量值彼此相符合的程度,极差是总体标准偏差的有偏估计值,当乘以校正系数之后,可以作为总体标准偏差的无偏估计值,它的优点是计算简单,含义直观,运用方便,故在数据统计处理中仍有着相当广泛的应用。但是,它仅仅取决于两个极端值的水平,不能反映其间的变量分布情况,同时易受极端值的影响。
四分位距(interquartile range,IQR)
我们通常使用箱形图来表现一个数据集的分布特征:
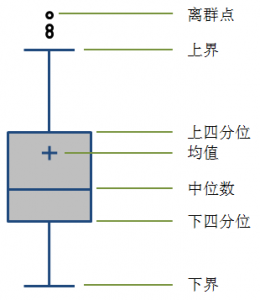
四分位距通常是用来构建箱形图,以及对概率分布的简要图表概述。对一个对称性分布数据(其中位数必然等于第三四分位数与第一四分位数的算术平均数),二分之一的四分差等于绝对中位差(MAD)。中位数是聚中趋势的反映。
一般中间矩形箱的上下两边分别为数据集的上四分位数(75%,Q3)和下四分位数(25%,Q1),中间的横线代表数据集的中位数(50%,Media,Q2),四分位距是使用Q3减去Q1计算得到:
$$IQR=Q3-Q1$$
如果将数据集升序排列,即处于数据集3/4位置的数值减去1/4位置的数值。四分位距规避了数据集中存在异常大或者异常小的数值影响极差对离散程度的判断,但四分位距还是单纯的两个数值相减,并没有考虑其他数值的情况,所以也无法比较完整地表现数据集的整体离散情况。
方差(Variance)
方差使用均值作为参照系,考虑了数据集中所有数值相对均值的偏离情况,并使用平方的方式进行求和取平均,避免正负数的相互抵消:
$$\sigma^2=\frac{\sum(x-\bar{x})^2}{n}$$
方差是最常用的衡量数据离散情况的统计量。
标准差(Standard Deviation)
方差得到的数值偏差均值取平方后的算术平均数,为了能够得到一个跟数据集中的数值同样数量级的统计量,于是就有了标准差,标准差就是对方差取开方后得到的:
$$\sigma=\sqrt{\frac{\sum(x-\bar{x})^2}{n}}$$
基于均值和标准差就可以大致明确数据集的中心及数值在中心周围的波动情况,也可以计算正态总体的置信区间等统计量。
平均差(Mean Deviation)
方差用取平方的方式消除数值偏差的正负,平均差用绝对值的方式消除偏差的正负性。平均差可以用均值作为参考系,也可以用中位数,这里使用均值:
$$MD=\frac{\sum\left|x-\bar{x}\right|}{n}$$
平均差相对标准差而言,更不易受极端值的影响,因为标准差是通过方差的平方计算而来的,但是平均差用的是绝对值,其实是一个逻辑判断的过程而并非直接计算的过程,所以标准差的计算过程更加简单直接。
离散系数(Coefficient of Variation,CV)
即变异系数,针对不同数据样本的标准差和方差,因数据衡量单位不同其结果自然无法直接进行对比,为出具一个相同的衡量指标,则进行了离散系数的计算。离散系数为一组数据的标准差与平均数之比:
$$CV=\frac{\sigma}{\mu}$$
变异系数的优势就在于作为一个无量纲量,可以比较度量单位不同的数据集之间的离散程度的差异;缺陷也是明显的,就是无法反应真实的绝对数值水平,同时对于均值是0的数据集无能为力。



