什么是正则化?
正则化(Regularization)是机器学习中一种防止模型过拟合的核心技术。它的核心思想是:在模型训练过程中,对模型的复杂度施加惩罚,让模型在“拟合数据”和“保持简单”之间找到平衡。简单来说,正则化就是给模型”戴上枷锁”,防止它学得太复杂,从而提升泛化能力。
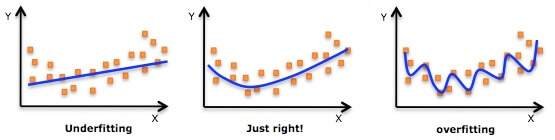
过拟合困境:当模型成为”书呆子”
在机器学习的世界里,模型如同求知若渴的学生。当给予充足的训练数据时,它们会贪婪地记忆每一个训练样本的细节。一个未受约束的深度神经网络,其参数数量可能高达数亿,就像拥有过目不忘能力的天才,能准确复述课本例题,却无法解答稍作变化的考题。这种现象在图像识别任务中尤为明显:未经正则化的CNN模型可能记住训练图片中每片树叶的纹理,却无法识别不同光照条件下的同一物体。过拟合的模型在训练集上达到95%的准确率,面对新数据时可能暴跌至60%,这种性能落差揭示了模型泛化能力的严重缺失。
正则化本质:智慧的约束之道
正则化的数学之美在于其简洁性。以最常见的L2正则化为例,其在损失函数中增加的权重平方和项($\lambda\sum w^2$),如同给每个参数系上弹性皮筋。当某个权重试图过度增长时,这个惩罚项会产生将其拉回的力。超参数λ扮演着调节松紧度的角色:λ=0时系统完全放开,λ过大则会导致模型”窒息”。
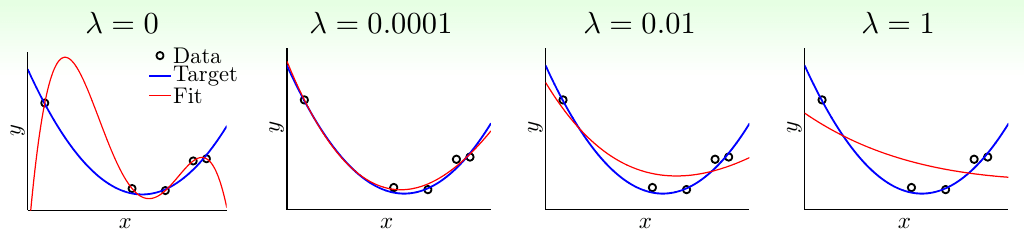
不同正则化方法构成了一套完整的约束体系:
- L1正则化通过绝对值惩罚诱导稀疏解,适合特征选择;
- 弹性网络(ElasticNet)融合L1和L2的优点;
- Dropout在神经网络训练中随机屏蔽神经元,模拟了生物神经系统的抗干扰机制。
这些方法共同构成了防止模型”走火入魔”的防御矩阵。
正则化的核心原理
数学形式
假设原始损失函数为L($\theta$),正则化后的损失函数变为:
$$L_{\text{new}}(\theta)=L(\theta)+\lambda\cdot R(\theta)$$
- $\lambda$:正则化系数(超参数),控制惩罚力度。
- $R(\theta)$:正则化项,常见的有L1范数、L2范数。
核心思想
通过添加正则化项,模型在优化时不仅要最小化原始损失(拟合数据),还要尽量让参数保持较小的值(控制复杂度)。这相当于在参数空间中施加约束,防止参数过大或过多。
两种经典正则化方法
L1正则化(Lasso)
L1正则化是机器学习中用于防止过拟合并促进模型稀疏性的重要技术。
基本概念
L1正则化在损失函数中添加模型权重绝对值之和作为惩罚项,即:
$$L_{\text{总}}=L(\text{损失})+\lambda\sum_{i=1}^n|w_i|$$
其中,$\lambda$是正则化强度参数,控制惩罚力度。
因其在回归中的应用,L1正则化也称为Lasso回归(Least Absolute Shrinkage and Selection Operator)。
稀疏性原理
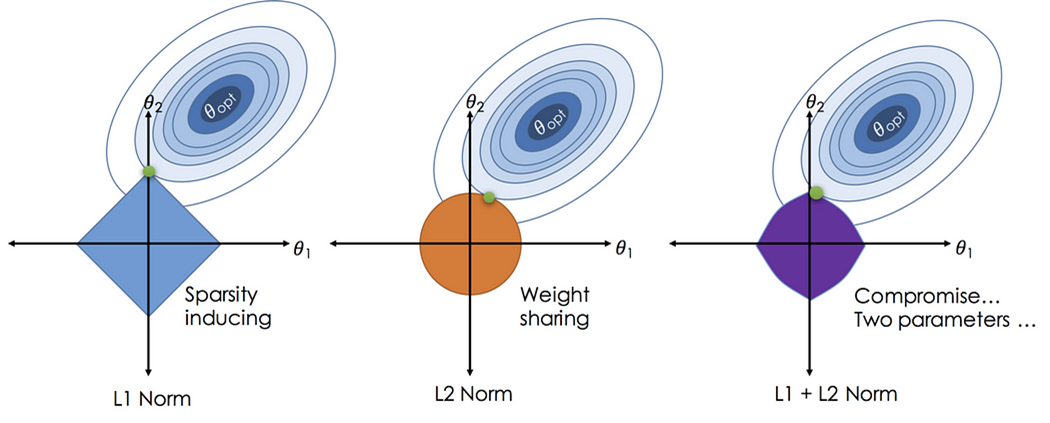
几何解释:在参数空间中,L1约束区域为菱形(顶点在坐标轴上),而损失函数的等高线与之相切时,易在顶点处相交,导致某些权重为0。
优化角度:L1的梯度为常数(±λ),更新时直接减去固定值,容易使权重归零;而L2的梯度与权重成正比,趋向于缩小但不归零。
概率视角:等价于参数服从拉普拉斯先验,该分布在零点处峰值更高,促使参数稀疏。
特点与优势
- 特征选择:自动筛选重要特征,将不重要特征的权重置零,提升模型解释性。
- 高维处理:适用于特征数远大于样本数的情况,通过稀疏性降低维度。
- 抗噪声:对异常值更具鲁棒性,因绝对值惩罚对大幅值不敏感。
应用场景
- 特征选择:当特征数量多且存在冗余时,L1可筛选关键特征。
- 模型简化:需要轻量级模型或明确解释性的场景(如医疗、金融)。
- 高维数据:如图像处理、文本分类中的高维稀疏数据。
局限性
- 共线性问题:若特征高度相关,L1可能随机选择其中一个,导致模型不稳定。
- 非凸优化:当特征数超过样本数时,可能无法恢复全部重要特征。
优化方法
- 次梯度下降:处理L1在零点不可导的问题,使用次梯度进行参数更新。
- 近端梯度下降:分解为可导损失项和L1项,对后者应用软阈值函数:
$$w_i=\text{sign}(w_i^*)\cdot\max(|w_i^*|-\lambda,0)$$
- 坐标下降法:逐维优化,固定其他参数,迭代求解每个权重。
参数调整
- λ的选择:通过交叉验证确定。λ越大,惩罚越强,更多权重被压缩至零。
L2正则化(Ridge)
L2正则化是机器学习中广泛使用的正则化技术,通过约束模型参数的范数来防止过拟合。
基本概念
定义:L2正则化在损失函数中添加模型权重平方和的惩罚项,公式为:
$$L_{\text{总}}=L(\text{原始损失})+\lambda\sum_{i=1}^n w_i^2$$
其中,$\lambda$是正则化强度参数,控制惩罚力度。
别名:在回归任务中称为岭回归(Ridge Regression),在神经网络中也称权重衰减(Weight Decay)。
平滑性原理
- 几何解释:在参数空间中,L2约束区域是一个圆形或超球体(所有参数平方和≤常数)。损失函数的等高线与L2约束区域相切时,最优解倾向于分布在参数空间的中心区域,使得权重值较小且分布均匀(而非稀疏)。
- 梯度下降视角:L2正则化项的梯度为$2\lambda w$,在参数更新时,每次迭代会额外减去$2\lambda w$,导致权重逐渐向零衰减。这一过程称为权重衰减,迫使模型学习更小的参数值。
- 概率视角:等价于对模型参数施加高斯先验分布(正态分布),假设参数服从均值为0、方差由$\lambda$控制的正态分布,通过最大后验估计(MAP)实现参数约束。
特点与优势
- 防止过拟合:通过限制权重幅度,降低模型对训练数据中噪声的敏感度。
- 处理共线性:当特征高度相关时,L2通过均匀压缩权重保持稳定性(L1可能随机丢弃特征)。
- 可导性:L2正则项处处可导,优化过程无额外复杂度(无需处理不可导点)。
- 凸优化保证:损失函数保持凸性,确保存在全局最优解。
应用场景
- 特征共线性:当特征之间存在强相关性时,L2 保持所有特征但压缩权重。
- 非稀疏场景:需保留所有特征信息(如自然语言处理中的词向量、图像像素)。
- 深度学习:作为默认正则化手段,防止神经网络权重过大(如卷积网络、全连接层)。
局限性
- 无特征选择:权重被压缩但不归零,无法自动筛选重要特征。
- 高维数据:当特征数远超样本数时,可能无法有效约束所有参数。
优化方法
梯度下降:直接在原始梯度中加入 L2 梯度项:
$$w \leftarrow w – \eta \left( \nabla L(\text{原始损失}) + 2 \lambda w \right)$$
其中, $\eta$ 是学习率。
解析解(线性回归):岭回归的闭式解为:
$$w = (X^T X + \lambda I)^{-1} X^T y$$
即使 $X^T X$ 不可逆,加入 $\lambda I$ 后仍可保证矩阵可逆。
参数调整
λ 的选择:
- λ→0:模型接近原始损失函数,可能过拟合。
- λ→∞:所有权重趋近于 0,模型欠拟合(仅保留偏置项)。
通过交叉验证在验证集上选择最佳 $\lambda$。
L1 与 L2 的对比
| 特性 | L2 正则化 | L1 正则化 |
| 惩罚项形式 | $\sum w_i^2$ | $\sum |w_i|$ |
| 解的性质 | 权重小而均匀 | 稀疏权重(部分归零) |
| 优化难度 | 可导,易优化 | 需处理不可导点(次梯度、近端方法) |
| 抗共线性 | 通过均匀压缩稳定模型 | 随机选择特征,可能不稳定 |
| 典型应用 | 岭回归、深度学习 | Lasso 回归、特征选择 |
实例理解
- 线性回归场景:假设两个强相关特征 $x_1$ 和 $x_2$,L2 正则化会为两者分配相近的小权重,而 L1 可能将其中一个权重置零。
- 神经网络训练:在图像分类任务中,L2 正则化约束卷积核权重,防止某些神经元过度响应特定模式,提升泛化能力。
下面是一组岭回归 (L1) 和 LASSO (L2) 回归的特征系数随着模型不断迭代而变化的动态展示。
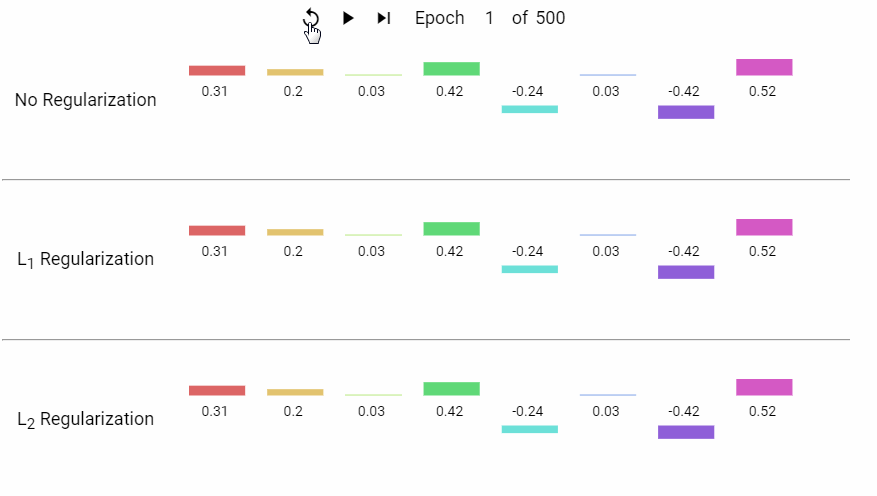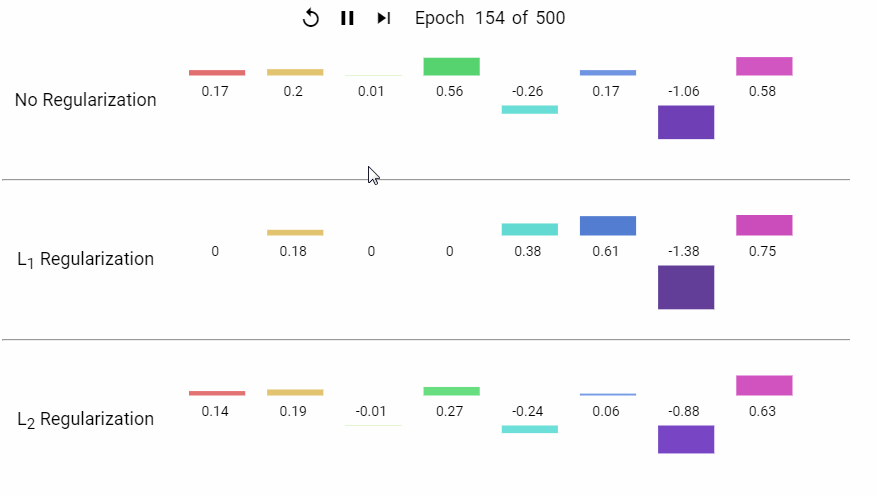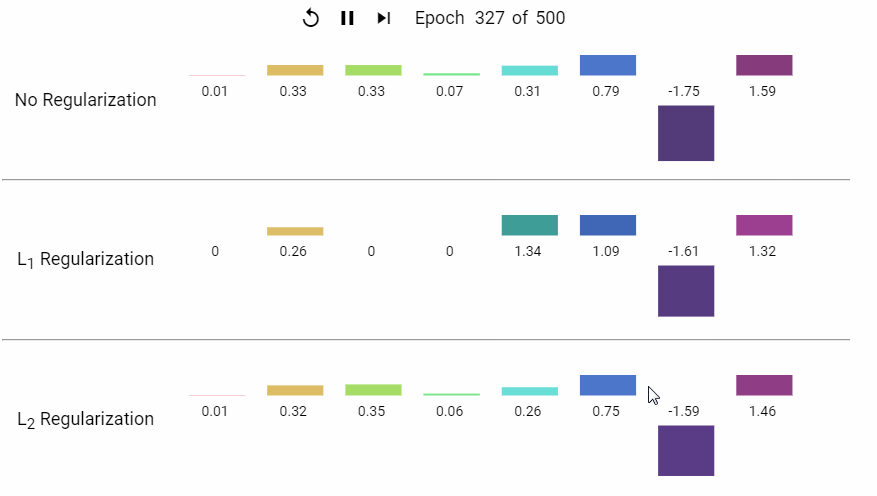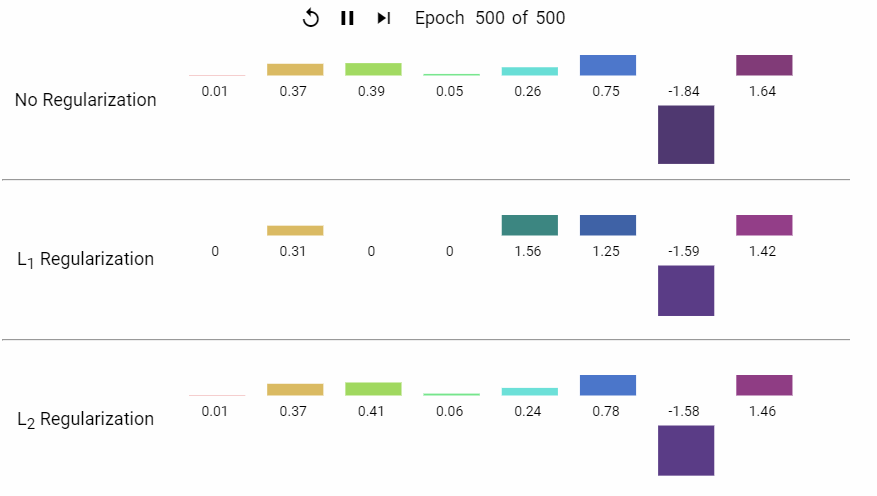
L2 正则化通过约束模型参数的平方和,促使权重趋向较小的均匀分布,从而降低模型复杂度、防止过拟合。其核心优势在于稳定共线性数据的解、保持所有特征信息,并适用于需要平滑权重分布的场景(如深度学习)。与 L1 正则化的稀疏性不同,L2 更注重整体模型的均衡性,是处理复杂数据关系的基石技术之一。实际应用中,需结合数据特性和任务目标选择正则化策略。
如何理解 L1 和 L2 正则?
搜索 L1 L2 正则,网上能找到的基本上都是一些框框圈圈的图,看上去很高大上,但是很难让人理解。这里就针对这样的图梳理自己的理解(不一定正确,如果错了,请指正)
对 L2 正则的理解
我们以 L2 正则为例,下图中,知识一个特征的正则展示,推广到多维原理类似。
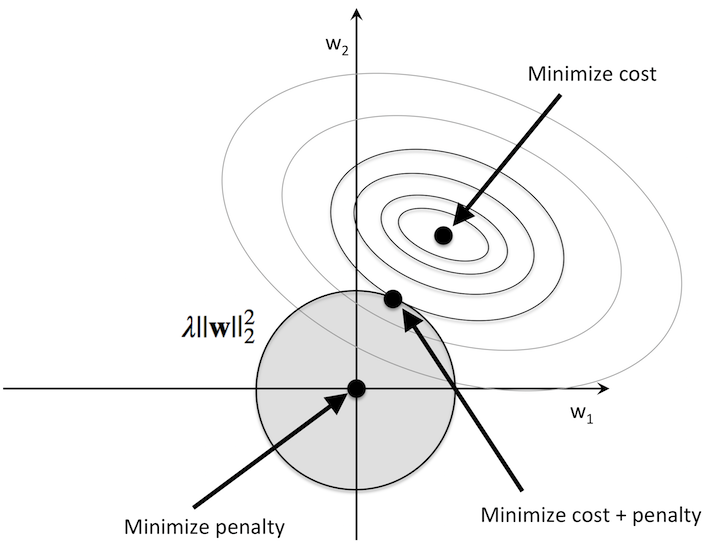
再没有加入 L2 正则前,这里的最优解就在最小损失的点上(图中 minimize cost 指向的点),但这个点可能存在过拟合问题。
围绕最小损失点周围的圆圈,我的理解类似等高线。同一圆圈上代表损失相同,圆圈越大代表损失越大。
从图中可以看到,在限定损失阈值的前提下,$w_1$ 和 $w_2$ 的解有无数个(极点只有有一个,但在一定误差范围内的解有无数个)
为了解决过拟合问题,我们可以让 $w_1$ 和 $w_2$ 的值尽可能的小。为什么系数小,能解决过拟合问题?你可以将 $w_1$ 和 $w_2$ 理解为系数,系数越大,杠杆率越高,波动越大,越容易产生过拟合。
等高线与基于原点的圆(L2 范数为圆形)相交的点即为 $w_1$ 和 $w_2$ 权重较小且较为均匀的点。
对 L1 正则的理解
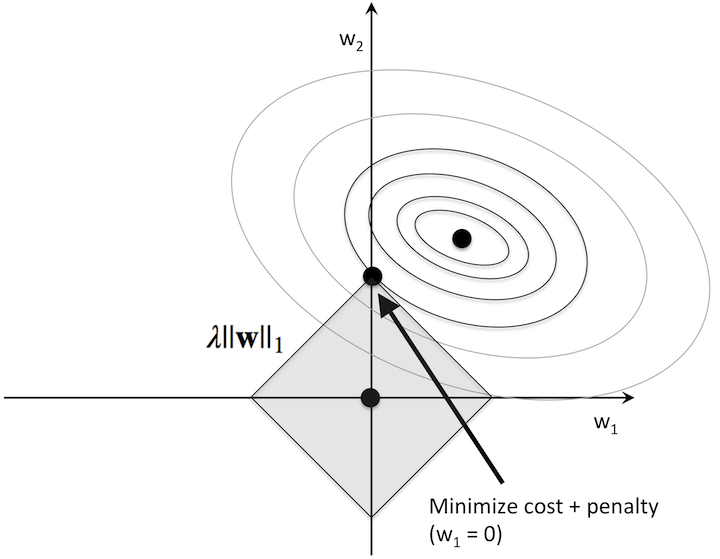
同样为了解决过拟合问题,L1 正则采用的是尽可能减少参数,在相同误差(损失)基础上,使得 $w_1$ 或 $w_2$ 的某一项为 0。当圆与菱形(L1 范数的图形为菱形)香蕉时,解大部分情况下再菱形的 4 个顶点。这样就可以通过减少特征数量,降低模型复杂度解决过拟合问题。
正则化为什么有效?
正则化通过在损失函数中引入对模型复杂度的惩罚,迫使模型在拟合数据的同时保持简单,从而在“学得太少”(欠拟合)和“学得太多”(过拟合)之间找到平衡。
- 从优化角度
- 正则化改变了损失函数的形状,使得参数空间中“简单模型”对应的区域更容易被优化器找到。
- 例如,L2 正则化会让损失函数的等高线更“圆滑”,梯度下降更稳定。
- 从几何角度
- L1 正则化:参数被约束在一个“菱形”区域内,最优解容易出现在顶点(某些参数为 0)。
- L2 正则化:参数被约束在一个“圆形”区域内,最优解靠近原点但非零。
- 从概率角度(贝叶斯解释)
- L1 正则化对应参数的拉普拉斯先验分布,假设参数服从稀疏分布。
- L2 正则化对应参数的高斯先验分布,假设参数服从均值为 0 的小方差分布。
参考链接: