在线性代数中,向量和矩阵是重要的概念。向量是一种特殊的矩阵,矩阵也是一种特殊的向量。一个n维向量,可以写成nx1的矩阵,或者1xn的矩阵,分别叫做列向量与行向量。单个向量可以视为一阶矩阵,多个向量组合在一起就组成了矩阵。向量是线性代数的基础,也是机器学习中最核心的概念之一。
向量是什么?
向量,也称为欧几里得向量、几何向量或矢量,既可以从代数角度去理解,也可以从几何角度去理解。
- 代数角度:向量是一个有序数组,n维向量中存了n个数,有先后次序之分
- 几何角度:向量是一个带方向(Direction),有长度(Magnitude)的箭头(长度也称为模)
向量没有绝对位置,也就是说当它出现在某个坐标系中,起点在何处并不会影响它本身。为了让向量的表达和计算更直观和方便,我们一般会将其起点设定在坐标系原点中。
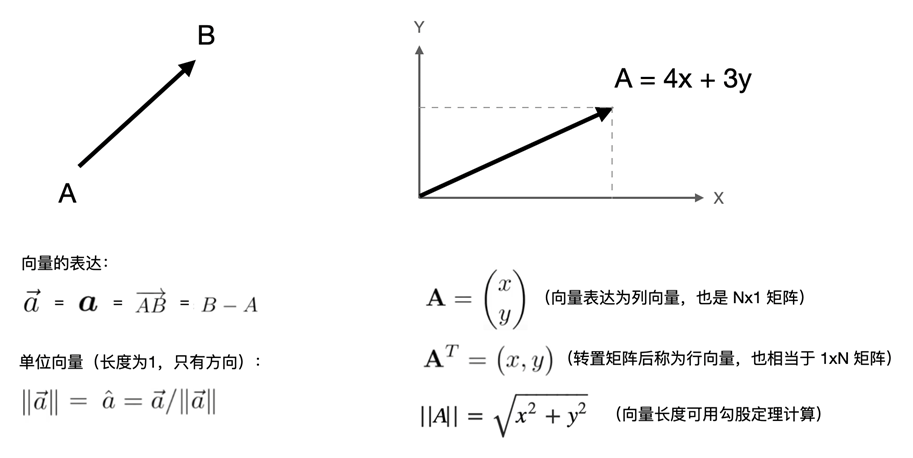
向量与点都可以表达为(x,y)或(x,y,z),虽然数学形式上相等,但几何意义完全不同:
- 点:有位置,没有实际大小或方向
- 向量:无位置,有实际大小和方向
- 联系:任何一个点都可以看作是从原点出发的向量
数学定义:向量是一个有方向和大小的量,可以看作是一组有序排列的数。例如:
$$\mathbf{v}=\begin{bmatrix}v_1\\v_2\\\vdots\\v_n\end{bmatrix}\quad\text{或}\quad\mathbf{v}=(v_1,v_2,\dots,v_n)$$
直观理解:向量像箭头,箭头长度是大小,箭头指向是方向。
机器学习中的应用:数据样本的特征表示(如房价预测中的面积、卧室数、地理位置等特征组成一个向量)。
特殊向量
零向量:所有元素为0,表示原点,记为$\mathbf{0}$。
单位向量:长度为1的向量,可通过$\frac{\mathbf{v}}{\|\mathbf{v}\|}$得到(标准化)。
向量的表示
行向量:水平排列,如([1,2,3])。
列向量:竖直排列,如$\begin{bmatrix}1\\2\\3\end{bmatrix}$。
注意:机器学习中通常默认用列向量,但在代码实现(如NumPy)中可能用行向量表示,需注意区分。
在机器学习的理论和代码实现中,向量方向的差异(列向量vs行向量)是一个常见的困惑点。理解这一差异的关键在于数学规范和工程实现的不同需求。
以下是一个清晰的解释:
数学中的规范:默认列向量
在数学和线性代数中,列向量是标准表示方式,原因如下:
- 矩阵乘法规则:矩阵(A)乘以列向量$\mathbf{x}$(形状$n\times1$时,结果是一个新的列向量(形状$m\times1$),即:
$$A_{m\times n}\cdot\mathbf{x}_{n\times1}=\mathbf{b}_{m\times1}$$
这种表示直接对应线性方程组$A\mathbf{x}=\mathbf{b}$的形式。
- 梯度计算:梯度(如损失函数对权重的导数)通常表示为列向量,以保持维度一致性。
- 几何意义:列向量更符合”向量是空间中的点”的直观几何理解。
代码实现中的行向量倾向
在编程(如Python/NumPy、PyTorch)中,数据存储和计算效率的考虑导致更常用行向量:
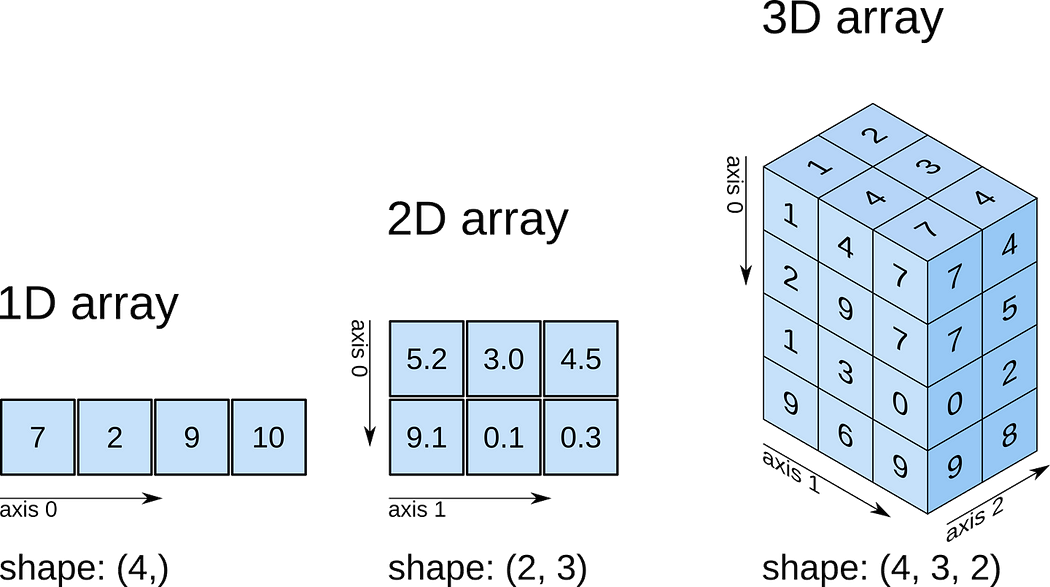
- 数据集的存储形式:数据集通常以矩阵形式存储,其中每一行是一个样本,每一列是一个特征。例如:
# 3个样本,每个样本2个特征 X = np.array([[1.0, 2.0], # 样本1 [3.0, 4.0], # 样本2 [5.0, 6.0]]) # 样本3
此时每个样本是行向量,这种布局便于批量计算。
- 内存连续性:计算机内存按行优先(Row-major)存储数据,行向量在内存中连续排列,计算效率更高。
- API设计:深度学习框架(如PyTorch、TensorFlow)的线性层(如Linear)默认接受行向量输入。
理论与代码的桥接
矩阵乘法的维度匹配
数学公式(列向量):
$$W_{m\times n}\cdot\mathbf{x}_{n\times1}=\mathbf{y}_{m\times1}$$
代码实现(行向量):
# X形状为(batch_size, n), W形状为(n, m) Y = X.dot(W) # 结果形状为(batch_size, m)
此时,每个样本(行)与权重矩阵\(W\)相乘,结果仍为行向量。
显式转置
如果需要将行向量转换为列向量,可以通过转置操作(但需注意维度):
x_row = np.array([1, 2, 3]) # 形状(3,) x_col = x_row.reshape(-1, 1) # 形状(3,1)(显式列向量)
常见场景示例
场景1:线性回归
数学公式(列向量):
$$y=\mathbf{w}^T\mathbf{x}+b$$
代码实现(行向量):
# X形状(num_samples, num_features) # w形状(num_features, 1) y_pred = X.dot(w) + b # 形状(num_samples, 1)
场景2:神经网络前向传播
数学公式(列向量):
$$\mathbf{h}=W\cdot\mathbf{x}+\mathbf{b}$$
代码实现(行向量):
# X形状(batch_size, input_dim) # W形状(input_dim, output_dim) h = X.dot(W) + b # 形状(batch_size, output_dim)
为什么容易混淆?
- 一维数组的歧义:在NumPy中,一维数组array([1,2,3])既不是行向量也不是列向量,转置(`.T`)不会改变形状。
- 权重矩阵的设计在代码中,权重矩阵的维度可能与数学公式中的相反(如数学中的$W_{m\times n}$对应代码中的(n,m))。
如何避免错误?
显式使用二维数组
x_row = np.array([[1, 2, 3]]) # 形状(1,3)(行向量) x_col = np.array([[1], [2], [3]]) # 形状(3,1)(列向量)
注意矩阵乘法运算符
- @或dot:严格遵循矩阵乘法规则。
- *:逐元素相乘,不是点积!
理解框架设计
例如PyTorch的nn.Linear层默认接受形状为(batch_size, input_dim)的输入。
向量的维度
定义:向量中元素的个数。例如,[2,5,-1]是三维向量。
几何意义:
- 二维/三维向量:可在平面/空间中可视化。
- 高维向量:无法直观可视化,但数学操作相同(如100维的词向量)。
机器学习中的应用:特征向量的维度对应数据特征的数量。
向量的基本运算
向量加减法
规则:对应位置的元素相加/减。
$$\begin{bmatrix}1\\2\end{bmatrix}+\begin{bmatrix}3\\4\end{bmatrix}=\begin{bmatrix}4\\6\end{bmatrix}$$
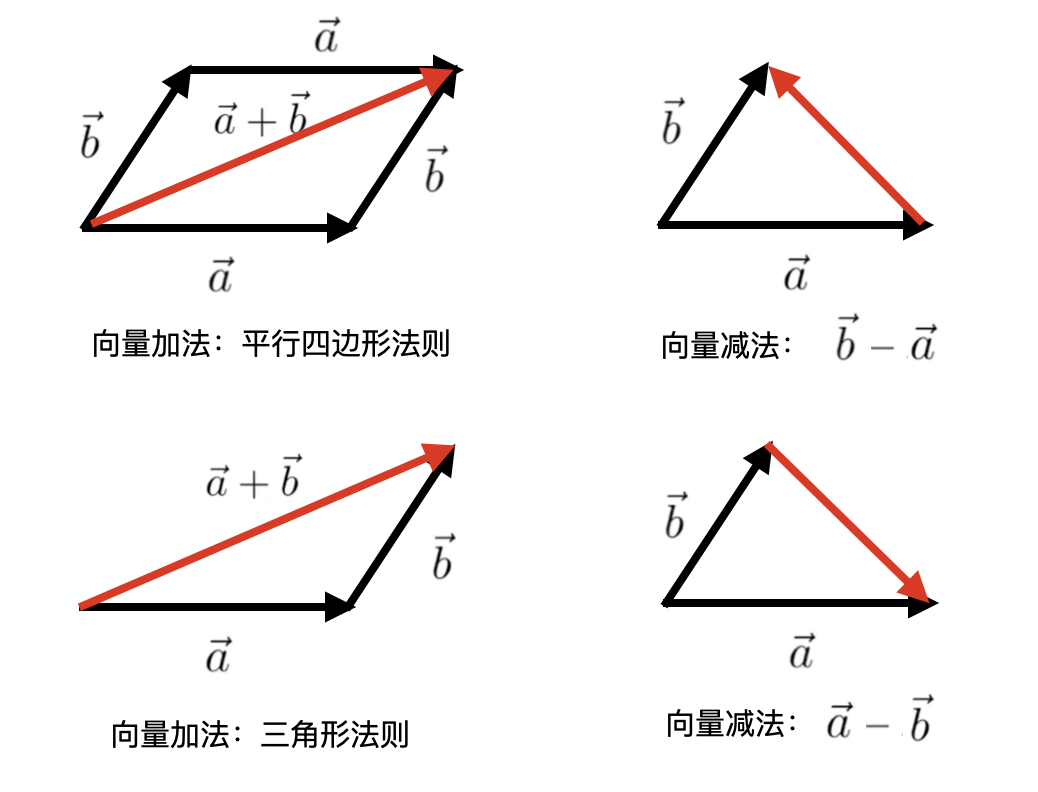
几何意义:向量的平移(三角形法则或平行四边形法则)。
标量乘法
规则:每个元素乘以标量(实数)。
$$2\cdot\begin{bmatrix}1\\-3\end{bmatrix}=\begin{bmatrix}2\\-6\end{bmatrix}$$
几何意义:缩放向量长度,方向可能反转(若标量为负)。
向量的点积(Dot Product)
向量点积几乎是应用的最广也最重要的向量运算了。其数学意义即分量乘积的和,最终计算出来的值是一个标量(常数)。
点积的定义
点积(也称为内积)是两个向量对应位置元素相乘后求和的结果。
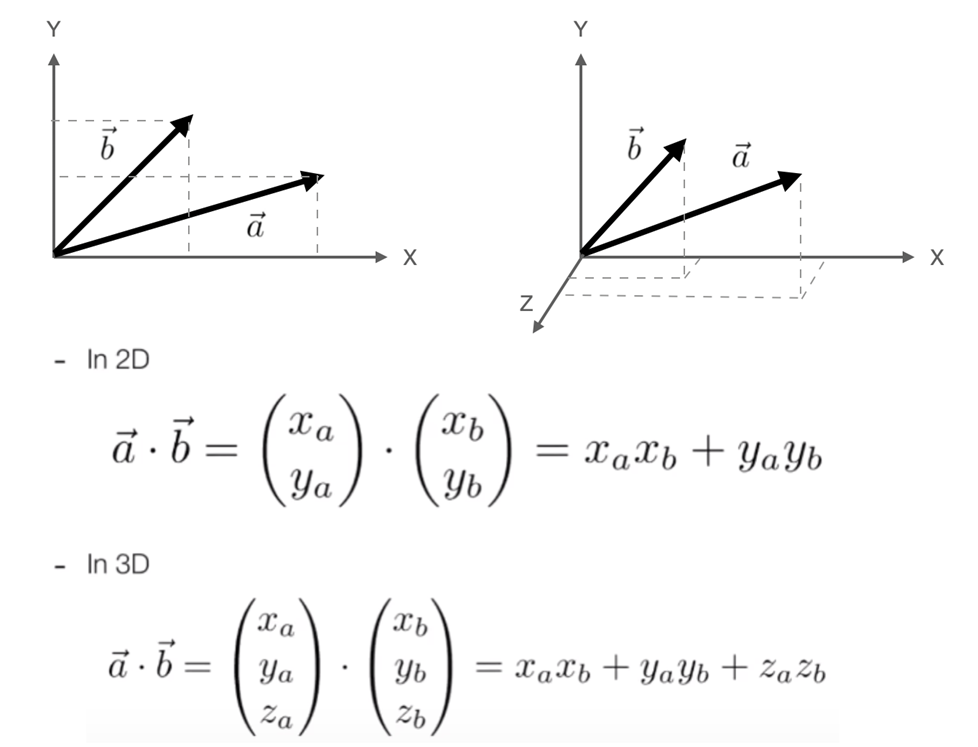
数学公式:
对于两个向量$\mathbf{a}=[a_1,a_2,\dots,a_n]$和$\mathbf{b}=[b_1,b_2,\dots,b_n]$,它们的点积为:
$$\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+\dots+a_nb_n$$
关键条件:两个向量必须维度相同。
点积的计算步骤
通过一个具体例子来理解计算过程:
假设$\mathbf{a}=[2,3]$,$\mathbf{b}=[4,1]$,计算它们的点积。
对应元素相乘:
- 第一个元素:$2\times4=8$
- 第二个元素:$3\times1=3$
相加求和:
$$8+3=11$$
所以,$\mathbf{a}\cdot\mathbf{b}=11$。
点积的几何意义
点积不仅是一个数值,还隐含着向量的几何关系。
公式:
$$\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta$$
其中:
- $\|\mathbf{a}\|$是向量$\mathbf{a}$的长度(模),
- $\theta$是两个向量的夹角。
几何解释:
- 夹角影响结果:
- 如果两向量同方向($\theta=0^\circ$),点积最大($\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|$)。
- 如果两向量垂直($\theta=90^\circ$),点积为0。
如果两向量反方向($\theta=180^\circ$),点积最小($\mathbf{a}\cdot\mathbf{b}=-\|\mathbf{a}\|\|\mathbf{b}\|$)。
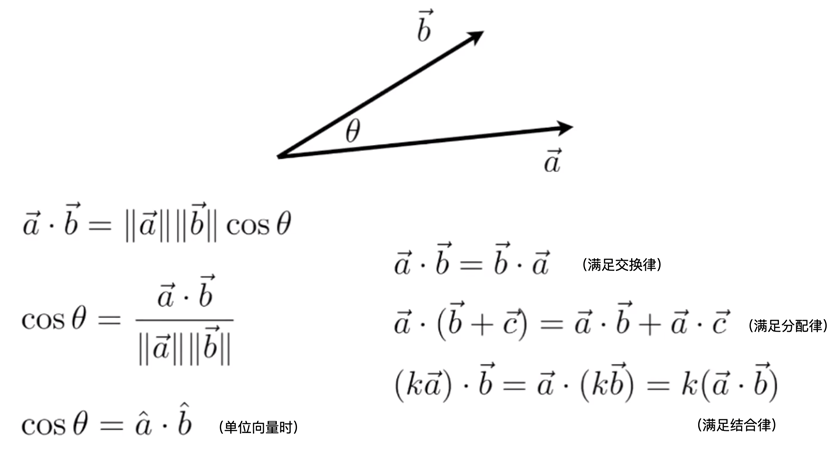
- 物理意义:点积可以理解为向量$\mathbf{a}$在向量$\mathbf{b}$方向上的投影长度乘以$\mathbf{b}$的长度。
点积的实战应用
计算相似度(如余弦相似度)
公式:
$$\cos\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}$$
结果范围:\([-1,1]\),值越大表示方向越相似。
应用场景:
- 文本相似度(词向量点积)。
- 推荐系统(用户偏好向量匹配)。
机器学习中的加权求和
神经网络:神经元的输入是权重向量和输入向量的点积。
例如:
$$z=w_1x_1+w_2x_2+\dots+w_nx_n=\mathbf{w}\cdot\mathbf{x}$$
这是神经网络中线性部分的核心计算。
几何判断
- 正交性检验:如果点积为0,两向量垂直。
- 方向一致性:点积为正表示锐角,为负表示钝角。
点积的代码实现
以Python的NumPy为例:
import numpy as np a = np.array([2, 3]) b = np.array([4, 1]) # 方法1:用np.dot() dot_product = np.dot(a, b) # 输出11 # 方法2:手动计算 dot_product_manual = sum(a * b) # 输出11 # 计算余弦相似度 norm_a = np.linalg.norm(a) # 计算a的模长(L2范数) norm_b = np.linalg.norm(b) cos_sim = dot_product / (norm_a * norm_b) # 输出约0.74
常见误区与重点总结
误区1:点积结果是向量
纠正:点积结果是一个标量(单个数值),不是向量。
误区2:点积只关注大小
纠正:点积同时反映方向关系(正负号表示夹角锐钝)。
重点总结
两个公式都要掌握:
- 代数公式:$\mathbf{a}\cdot\mathbf{b}=\sum a_ib_i$
- 几何公式:$\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta$
应用本质:点积是相似性度量和投影计算的核心工具。
向量的投影
向量的投影是线性代数中的重要概念,它描述了一个向量在另一个向量方向上的”影子”或分量。理解投影有助于分解向量、简化问题(如降维),并在机器学习、物理学等领域有广泛应用。
投影的定义
标量投影(投影长度)
向量a在向量b方向上的标量投影是一个标量,表示a在b方向上的长度:
$$\text{标量投影}=\|\mathbf{a}\|\cos\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|}$$
其中$\theta$是两向量的夹角,$\mathbf{a}\cdot\mathbf{b}$是点积。
向量投影(投影向量)
向量a在b方向上的向量投影是一个向量,方向与b相同,长度为标量投影:
$$\text{向量投影}=\left(\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|^2}\right)\mathbf{b}$$
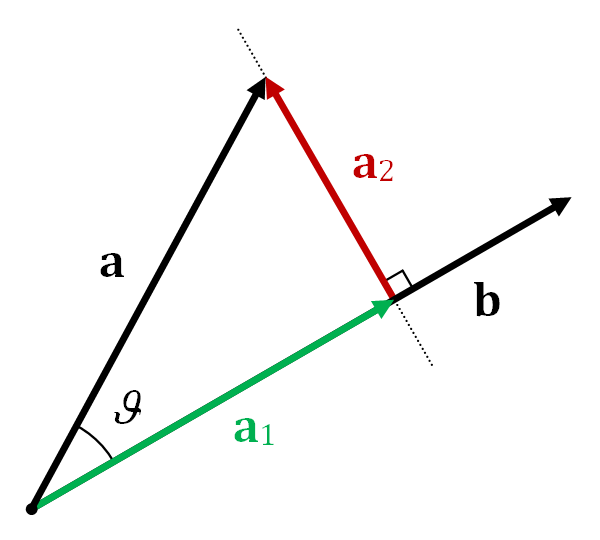
几何解释
想象一束光垂直于b的方向照射,a在b所在直线上的影子即为投影向量(下图中的$\text{proj}_{\mathbf{b}}\mathbf{a}$)。
原向量a可分解为两个正交分量:
$$\mathbf{a}=\text{proj}_{\mathbf{b}}\mathbf{a}+\mathbf{a}_\perp$$
其中$\mathbf{a}_\perp$是a垂直于b的分量。
计算步骤(示例)
假设向量$\mathbf{a}=[3,4]$,$\mathbf{b}=[1,0]$(x轴方向),计算a在b上的投影。
标量投影(投影长度)
$$\text{标量投影}=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|}=\frac{3\times1+4\times0}{\sqrt{1^2+0^2}}=3$$
向量投影(投影向量)
$$\text{向量投影}=\left(\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|^2}\right)\mathbf{b}=\frac{3}{1}[1,0]=[3,0]$$
数学推导
从点积的几何定义出发:
$$\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta$$
标量投影即为$\|\mathbf{a}\|\cos\theta$,代入点积公式:
$$\|\mathbf{a}\|\cos\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|}$$
向量投影的方向与b相同,因此乘以b的单位向量$\frac{\mathbf{b}}{\|\mathbf{b}\|}$:
$$\text{向量投影}=\left(\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|}\right)\frac{\mathbf{b}}{\|\mathbf{b}\|}=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|^2}\mathbf{b}$$
实际应用场景
机器学习中的降维
- 主成分分析(PCA):将高维数据投影到低维主成分方向,保留最大方差。
- 特征选择:投影到重要特征方向,去除冗余信息。
物理学中的力分解
- 将斜面上的重力分解为沿斜面方向和垂直方向的分量。
计算机图形学
- 3D物体在2D屏幕上的投影(如平行投影或透视投影)。
信号处理
- 从混合信号中提取特定频率成分(如傅里叶变换)。
代码实现(Python)
使用NumPy计算向量投影:
import numpy as np
def vector_projection(a, b):
"""计算向量a在向量b上的投影向量"""
scalar = np.dot(a, b) / np.linalg.norm(b)**2
projection = scalar * b
return projection
# 示例
a = np.array([3, 4])
b = np.array([1, 0])
proj = vector_projection(a, b) # 输出[3., 0.]
print("投影向量:", proj)
特殊情况与注意事项
- 零向量投影:若b是零向量,投影无定义(分母为零)。
- 垂直向量:若a与b垂直$(\cos90^\circ=0$),投影向量为零。
- 方向一致性:投影方向始终与b相同,若$\mathbf{a}\cdot\mathbf{b}<0$,投影方向与b相反。
正交分解
投影的一个自然结果是向量的正交分解,即:
$$\mathbf{a}=\text{proj}_{\mathbf{b}}\mathbf{a}+(\mathbf{a}-\text{proj}_{\mathbf{b}}\mathbf{a})$$
其中$\mathbf{a}-\text{proj}_{\mathbf{b}}\mathbf{a}$是a垂直于b的分量。
向量的叉积
向量的叉积(又称向量积、外积)是三维空间中两个向量的重要运算,结果是垂直于原向量的新向量。它在物理学、工程学和计算机图形学中有广泛应用(如力矩、法向量计算等)。和机器学习关系不大。
叉积的定义
数学公式
对于三维向量 $\mathbf{a}=[a_1,a_2,a_3]$ 和 $\mathbf{b}=[b_1,b_2,b_3]$,其叉积定义为:
$$\mathbf{a}\times\mathbf{b}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}=(a_2b_3-a_3b_2)\mathbf{i}-(a_1b_3-a_3b_1)\mathbf{j}+(a_1b_2-a_2b_1)\mathbf{k}$$
结果是一个向量,记为 $\mathbf{c}=\mathbf{a}\times\mathbf{b}$。
叉乘的数学意义即:分量交叉相乘再相减,结果仍然是一个向量,新向量的长度就是两个向量形成的平行四边形的面积。
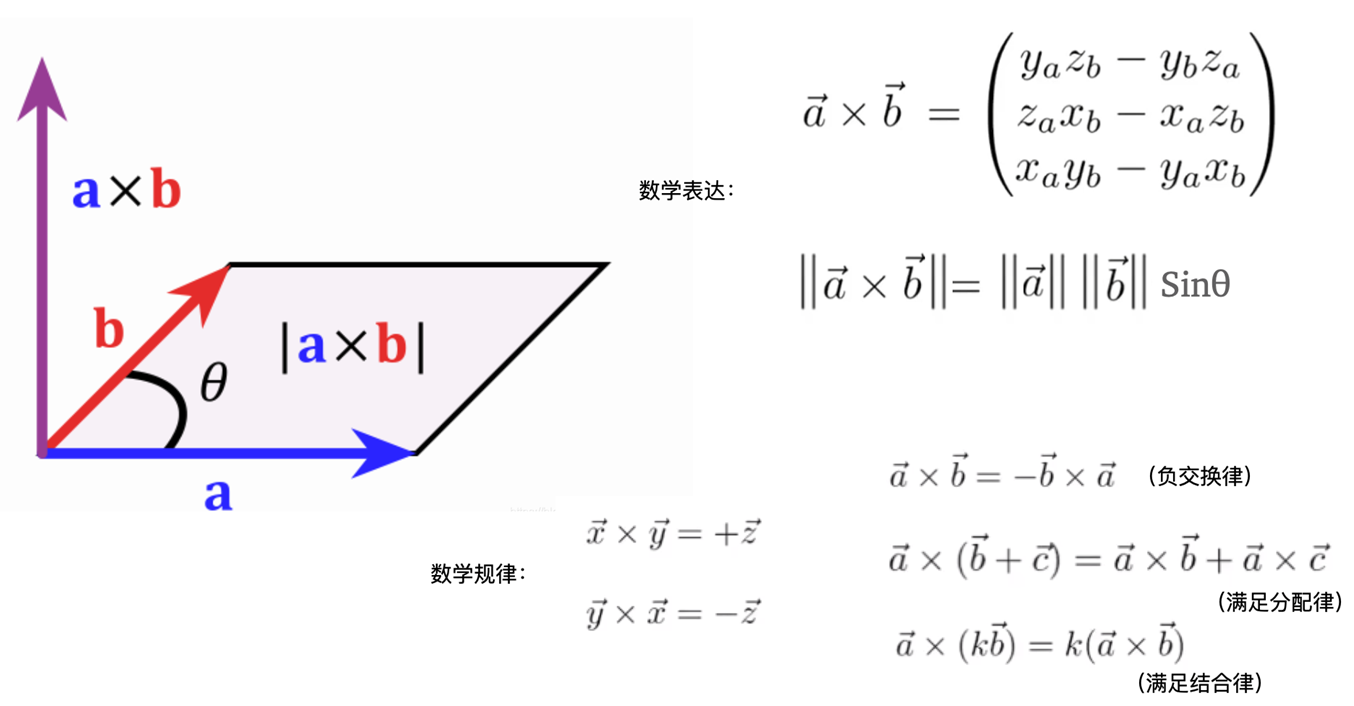
几何意义
方向:由右手定则确定(见下图)。
- 右手四指从 $\mathbf{a}$ 弯向 $\mathbf{b}$,拇指方向即 $\mathbf{c}$ 的方向。
模长:
$$\|\mathbf{a}\times\mathbf{b}\|=\|\mathbf{a}\|\|\mathbf{b}\|\sin\theta$$
- 表示 $\mathbf{a}$ 和 $\mathbf{b}$ 张成的平行四边形的面积。
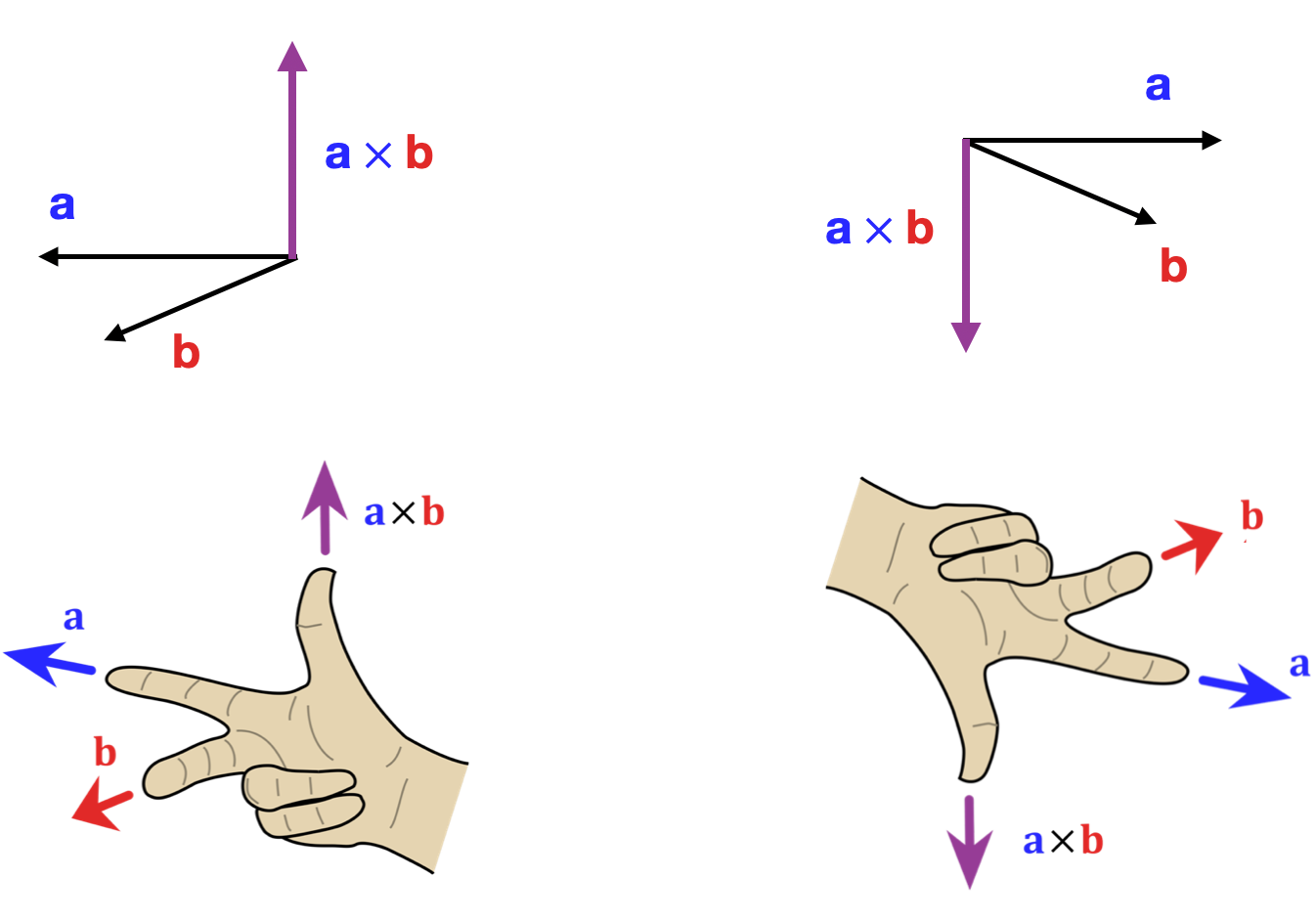
叉积的性质
- 反交换律:$\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}$
- 分配律:$\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}$
- 结合标量乘法:$(k\mathbf{a})\times\mathbf{b}=k(\mathbf{a}\times\mathbf{b})$
- 零向量:若两向量平行($\theta=0^\circ$ 或 $180^\circ$),叉积为零向量。
计算步骤(示例)
示例:计算 $\mathbf{a}=[1,2,3]$ 和 $\mathbf{b}=[4,5,6]$ 的叉积。
展开行列式计算:
$$\mathbf{a}\times\mathbf{b}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\1&2&3\\4&5&6\end{vmatrix}=\mathbf{i}(2\times6-3\times5)-\mathbf{j}(1\times6-3\times4)+\mathbf{k}(1\times5-2\times4)$$
逐项计算分量:
$$=\mathbf{i}(12-15)-\mathbf{j}(6-12)+\mathbf{k}(5-8)\\=-3\mathbf{i}+6\mathbf{j}-3\mathbf{k}\\=[-3,6,-3]$$
实际应用场景
计算平面的法向量
在三维图形学中,两个非平行向量的叉积可生成平面的法向量:
$$\mathbf{n}=\mathbf{a}\times\mathbf{b}$$
用于光照计算(如 Phong 着色模型)。
物理学中的力矩
力矩 $\mathbf{\tau}$ 是位置向量 $\mathbf{r}$ 和力 $\mathbf{F}$ 的叉积:
$$\mathbf{\tau}=\mathbf{r}\times\mathbf{F}$$
磁场中的洛伦兹力
带电粒子在磁场中的受力方向由叉积确定:
$$\mathbf{F}=q(\mathbf{v}\times\mathbf{B})$$
计算面积和体积
- 平行四边形面积:$\text{面积}=\|\mathbf{a}\times\mathbf{b}\|$
- 六面体体积:$\text{体积}=|(\mathbf{a}\times\mathbf{b})\cdot\mathbf{c}|$(混合积)
代码实现(Python)
使用 NumPy 计算叉积:
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# 计算叉积
cross_product = np.cross(a, b) # 输出 [-3, 6, -3]
print("叉积结果:", cross_product)
叉积与点积的对比
| 特性 | 点积(Dot Product) | 叉积(Cross Product) |
| 结果类型 | 标量 | 向量 |
| 几何意义 | 投影长度、夹角余弦 | 垂直向量、平行四边形面积 |
| 交换律 | $\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}$ | $\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}$ |
| 维度限制 | 任意维度 | 仅限三维(或七维,但极少使用) |
常见误区
- 二维向量叉积:严格来说,叉积仅定义在三维空间。二维叉积可视为三维叉积的 z 分量,但需明确上下文。
- 非三维空间:七维空间也存在叉积,但定义复杂且应用极少。
向量的范数(Norm)
在实数域中,数的大小和两个数之间的距离是通过绝对值来度量的。在解析几何中,向量的大小和两个向量之差的大小是“长度”和“距离”的概念来度量的。
其实“范数”的英语叫 Norm,Norm 在复数里,翻译成“模长”,所以“范数”本来应该叫“模数”。模数是机械行业的一个名称,齿轮之类的动力传动零件有一个重要参数就是模数,模数相同的齿轮才能正确啮合。而中文里有“模范”一词,“模”和“范”是同义字,所以就改成“范数”了。
向量范数(Vector Norm)是衡量向量“大小”或“长度”的核心工具,在机器学习中用于正则化、距离计算、特征缩放等任务。
向量范数是什么
范数(Norm)是对向量大小的数学度量,可以理解为向量的“长度”。不同的范数定义对应不同的衡量方式。
数学定义:
对于向量 $\mathbf{v}=(v_1,v_2,\dots,v_n)$,其 $L^p$ 范数定义为:
$$\|\mathbf{v}\|_p=\left(|v_1|^p+|v_2|^p+\dots+|v_n|^p\right)^{1/p}$$
其中 $p\geq1$ 是范数的阶数。
常见范数类型
L1 范数(曼哈顿距离)
定义:向量元素的绝对值之和。
$$\|\mathbf{v}\|_1=|v_1|+|v_2|+\dots+|v_n|$$
几何意义:在网格路径上行走的总距离(类似曼哈顿街区距离)。
应用:
- 稀疏特征选择(如Lasso回归)。
- 鲁棒性要求高的场景(对异常值不敏感)。
L2范数(欧氏距离)
定义:向量元素的平方和的平方根。
$$\|\mathbf{v}\|_2=\sqrt{v_1^2+v_2^2+\dots+v_n^2}$$
几何意义:空间中点到原点的直线距离。
应用:
- 正则化(如Ridge回归)。
- 计算相似度(如余弦相似度中的归一化)。
L∞范数(最大范数)
定义:向量元素的最大绝对值。
$$\|\mathbf{v}\|_\infty=\max(|v_1|,|v_2|,\dots,|v_n|)$$
几何意义:向量在任一坐标轴上的最大投影长度。
应用:限制最大误差(如图像生成中的像素值约束)。
几何直观:不同范数的”单位圆”
- L1范数:菱形(所有方向上的曼哈顿距离为1的点)。
- L2范数:圆形(所有方向上的欧氏距离为1的点)。
- L∞范数:正方形(所有坐标轴上的最大绝对值为1的点)。
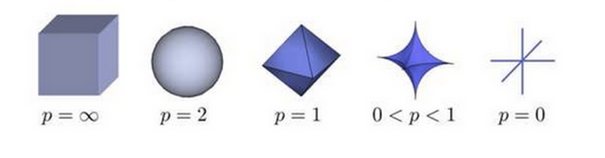
机器学习中的应用场景
正则化(防止过拟合)
L1正则化(Lasso):
$$\text{损失函数}+\lambda\|\mathbf{w}\|_1$$
倾向于产生稀疏权重向量(部分特征权重为0)。
L2正则化(Ridge):
$$\text{损失函数}+\lambda\|\mathbf{w}\|_2^2$$
倾向于让权重向量均匀缩小。
特征归一化
L2归一化:将向量缩放到单位长度(方向保留,大小统一)。
$$\mathbf{v}_{\text{norm}}=\frac{\mathbf{v}}{\|\mathbf{v}\|_2}$$
用于文本分类中的TF-IDF向量或词嵌入。
距离度量
- K近邻(KNN):使用L2范数计算样本间距离。
- 异常检测:使用L1范数衡量数据点的偏离程度。
Python代码示例
计算不同范数
import numpy as np
v = np.array([3, -4, 0])
# L1范数
l1_norm = np.linalg.norm(v, ord=1) # |3| + |-4| + |0| = 7
# L2范数
l2_norm = np.linalg.norm(v, ord=2) # sqrt(3² + (-4)² + 0²) = 5
# L∞范数
linf_norm = np.linalg.norm(v, ord=np.inf) # max(|3|, |-4|, |0|) = 4
print(f"L1: {l1_norm}, L2: {l2_norm}, L∞: {linf_norm}")
L2归一化示例
def normalize_l2(v):
norm = np.linalg.norm(v, ord=2)
return v / norm
v_normalized = normalize_l2(np.array([3, -4, 0])) # [0.6, -0.8, 0.0]
print("归一化后:", v_normalized)
关键总结
| 范数类型 | 公式 | 核心特点 | 应用场景 |
| L1 | 绝对值之和 | 稀疏性、抗噪声 | Lasso回归、特征选择 |
| L2 | 平方和的平方根 | 平滑性、几何直观 | Ridge回归、归一化 |
| L∞ | 最大绝对值 | 控制最大偏差 | 约束优化、图像处理 |
NumPy与向量计算
在机器学习和科学计算中,NumPy是Python的核心库之一,专门用于高效处理数组和矩阵运算。以下是使用NumPy进行向量计算的详细指南,涵盖基础操作和常见场景。
NumPy向量基础
向量在NumPy中的表示
NumPy中向量通过一维数组(ndarray)表示,但需注意行向量和列向量的维度区别:
- 行向量:形状为(n,),如 array([1, 2, 3])
- 列向量:形状为(n, 1),如 array([[1], [2], [3]])
import numpy as np # 创建行向量 row_vector = np.array([1, 2, 3]) # 形状(3,) # 创建列向量 col_vector = np.array([[1], [2], [3]]) # 形状(3, 1)
向量基本运算
向量加减法
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) # 加法 c = a + b # [5, 7, 9] # 减法 d = b - a # [3, 3, 3]
标量乘法
a = np.array([1, 2, 3]) scalar = 2 # 标量乘法 result = scalar * a # [2, 4, 6]
逐元素乘法(Hadamard积)
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) # 逐元素相乘 elementwise_product = a * b # [4, 10, 18]
点积(Dot Product)
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) # 方法1: np.dot() dot_product1 = np.dot(a, b) # 1*4 + 2*5 + 3*6 = 32 # 方法2: @运算符 dot_product2 = a @ b # 32
向量范数计算
L1范数(曼哈顿距离)
a = np.array([3, -4, 0]) l1_norm = np.linalg.norm(a, ord=1) # |3| + |-4| + |0| = 7
L2范数(欧氏距离)
l2_norm = np.linalg.norm(a, ord=2) # sqrt(3² + (-4)² + 0²) = 5
(3)L∞范数(最大绝对值)
linf_norm = np.linalg.norm(a, ord=np.inf) # max(|3|, |-4|, |0|) = 4
向量高级操作
向量标准化(L2归一化)
将向量缩放到单位长度:
a = np.array([3, -4, 0]) # 计算L2范数 norm = np.linalg.norm(a, ord=2) # 归一化 normalized = a / norm # [0.6, -0.8, 0.0]
向量广播(Broadcasting)
对不同形状的向量进行逐元素操作:
a = np.array([1, 2, 3]) # 形状(3,) b = np.array([10]) # 形状(1,) # 广播加法 result = a + b # [11, 12, 13]
向量拼接
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) # 水平拼接(行向量) h_stack = np.hstack([a, b]) # [1, 2, 3, 4, 5, 6] # 垂直拼接(列向量) v_stack = np.vstack([a, b]) # [[1, 2, 3], [4, 5, 6]]
向量统计计算
最大值/最小值
a = np.array([5, 2, 9, 1]) max_value = np.max(a) # 9 min_value = np.min(a) # 1
均值/方差
mean = np.mean(a) # 均值: 4.25 variance = np.var(a) # 方差: 8.1875
排序
sorted_a = np.sort(a) # [1, 2, 5, 9]
常见问题与技巧
行向量 vs 列向量
转换方法:
row = np.array([1, 2, 3]) col = row[:, None] # 形状(3, 1)
避免维度错误
使用 reshape() 调整维度:
a = np.array([1, 2, 3]) col_vector = a.reshape(-1, 1) # 形状(3, 1)
高效计算
优先使用 NumPy 内置函数(如 np.dot())替代循环,提升速度。
向量在机器学习中的应用
向量是机器学习的核心数学工具之一,几乎贯穿了数据表示、模型构建、特征工程、结果分析等所有环节。以下从具体场景出发,详细讲解向量在机器学习中的应用,并附示例代码加深理解。
数据表示:特征向量
应用场景:任何机器学习任务的第一步是将数据转换为数值形式,即特征向量。
结构化数据:每个样本的特征组成向量。
# 示例:房价预测的特征向量(面积, 卧室数, 房龄) sample = [120.5, 3, 5] # 形状(3,)
非结构化数据:
文本:词袋模型(Bag of Words)、TF-IDF、词嵌入(Word2Vec)。
# 使用 TF-IDF 将文本转为向量 from sklearn.feature_extraction.text import TfidfVectorizer corpus = ["machine learning", "deep learning"] vectorizer = TfidfVectorizer() X = vectorizer.fit_transform(corpus) # 稀疏向量表示
图像:像素值展平为向量(如 28×28 图像 → 784 维向量)。
# MNIST 图像展平为向量 from tensorflow.keras.datasets import mnist (X_train, y_train), _ = mnist.load_data() X_flatten = X_train.reshape(X_train.shape[0], -1) # 形状(60000, 784)
相似性计算
应用场景:推荐系统、聚类、异常检测等。
余弦相似度:通过向量点积计算方向相似性。
$$\cos(\theta)=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}$$
from sklearn.metrics.pairwise import cosine_similarity a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) similarity = cosine_similarity([a], [b])[0][0] # 约 0.974
欧氏距离:通过L2范数计算向量间距离。
$$\text{distance}=\|\mathbf{a}-\mathbf{b}\|_2$$
distance = np.linalg.norm(a - b) # 约 5.196
模型参数表示
应用场景:线性模型、神经网络等。
线性回归:权重向量 w 与特征向量点积得到预测值。
$$y=\mathbf{w}^T\mathbf{x}+b$$
#训练后的权重向量示例 w = np.array([0.5, -1.2, 3.1]) # 形状(3,) x = np.array([120, 3, 5]) # 输入特征 y_pred = np.dot(w, x) + 0.5 # 预测房价
神经网络:每层权重为矩阵,本质是多个向量组合。
#全连接层参数(输入2维,输出3维) weights = np.random.randn(2, 3) # 形状(2,3),每列为一个向量 biases = np.zeros(3)
正则化与稀疏性
应用场景:防止过拟合,提升模型泛化能力。
L1正则化(Lasso):通过L1范数惩罚项使权重向量稀疏化。
$$\text{Loss}=\text{MSE}+\lambda\sum|w_i|$$
from sklearn.linear_model import Lasso
model = Lasso(alpha=0.1) # alpha为λ
model.fit(X_train, y_train)
print("非零权重数量:", np.sum(model.coef_ != 0)) # 稀疏特征选择
L2正则化(Ridge):通过L2范数惩罚项平滑权重向量。
$$\text{Loss}=\text{MSE}+\lambda\sum w_i^2$$
降维与特征提取
应用场景:可视化、减少计算量、去除噪声。
主成分分析(PCA):将高维向量投影到低维正交基(主成分)。
from sklearn.decomposition import PCA pca = PCA(n_components=2) X_pca = pca.fit_transform(X) # 降维后的二维向量
词嵌入(WordEmbedding):将词语映射为低维稠密向量(如Word2Vec)。
#使用Gensim训练Word2Vec from gensim.models import Word2Vec sentences = [["machine", "learning"], ["deep", "learning"]] model = Word2Vec(sentences, vector_size=100, window=5) vector = model.wv["machine"] # 100维词向量
序列数据处理
应用场景:自然语言处理、时间序列预测。
循环神经网络(RNN):隐藏状态向量传递时序信息。
#简化的RNN隐藏状态更新 h_t = np.tanh(np.dot(W_hh, h_prev) + np.dot(W_xh, x_t) + b)
注意力机制:通过向量加权聚合上下文信息。
#计算注意力权重(Query与Key的点积) attention_weights = np.dot(Q, K.T) / np.sqrt(d_k)
图像与信号处理
应用场景:卷积神经网络(CNN)、特征提取。
卷积核:滤波器为向量或矩阵,与输入局部做点积。
#3x3卷积核(展平为9维向量) kernel = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]])
特征图:卷积结果可视为高维向量空间中的特征。
总结
向量在机器学习中的应用无处不在:
- 数据层:特征表示、相似性计算。
- 模型层:参数存储、正则化约束。
- 优化层:梯度下降方向为向量。
- 结果层:输出概率向量(如分类任务的Softmax结果)。
理解向量的运算(如点积、范数、投影)是掌握机器学习算法的关键数学基础。