三角函数回顾
六大三角函数
直角三角形定义
在一个直角三角形中,假设有一个锐角$\theta$,定义:
- 邻边(Adjacent):与角$\theta$相邻的边。
- 对边(Opposite):与角$\theta$相对的边。
- 斜边(Hypotenuse):直角三角形的最长边(对着直角)。
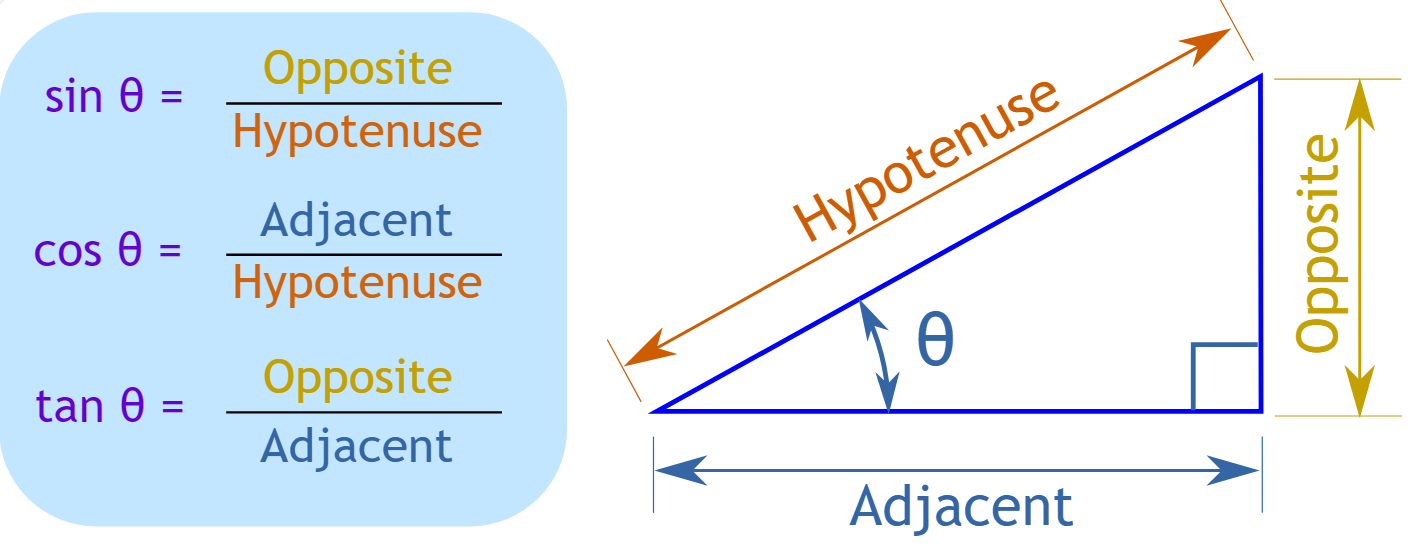
- 正弦(sinθ)=对边/斜边
- 余弦(cosθ)=邻边/斜边
- 正切(tanθ)=对边/邻边= $\frac{\sin\theta}{\cos\theta}$
- 余切(cotθ)=邻边/对边= $\frac{1}{\tan\theta}$
- 正割(secθ)=斜边/邻边= $\frac{1}{\cos\theta}$
- 余割(cscθ)=斜边/对边= $\frac{1}{\cos\theta}$
单位圆定义
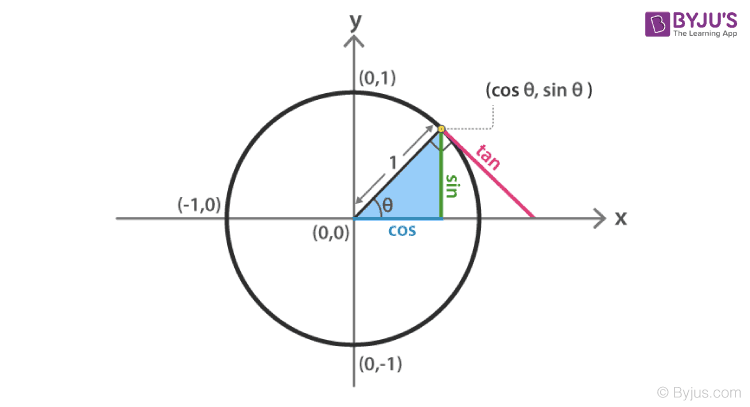
在单位圆(半径=1)中,角度 𝜃θ 终边交于点(x,y):
- sinθ=y
- cosθ=x
- tanθ=y/x
- cotθ=x/y
- secθ=1/x
- cscθ=1/y
单位圆中的sin和cos
将角度$\theta$放在单位圆(半径为1的圆)中,几何意义更加通用:
- 以坐标原点为中心,角$\theta$的终边(从x轴正方向逆时针旋转得到)与单位圆交于点(x,y)。
- 余弦(cosθ)是终边交点的x坐标。
- 正弦(sinθ)是终边交点的y坐标。

关键性质
- 任何角度都适用(包括超过90度的角和负角)。
- 符号规则:
- 第一象限(0°~90°):$\sin\theta>0,\cos\theta>0$
- 第二象限(90°~180°):$\sin\theta>0,\cos\theta<0$
- 第三象限(180°~270°):$\sin\theta<0,\cos\theta<0$
- 第四象限(270°~360°):$\sin\theta<0,\cos\theta>0$
几何意义总结
- cosθ:反映角度$\theta$在水平方向(x轴)的投影比例。例如:推箱子时,力的水平分量=力的大小×cosθ。
- sinθ:反映角度$\theta$在垂直方向(y轴)的投影比例。例如:斜坡上物体的重力沿斜坡的分量=重力×sinθ。
三角函数的图像与性质
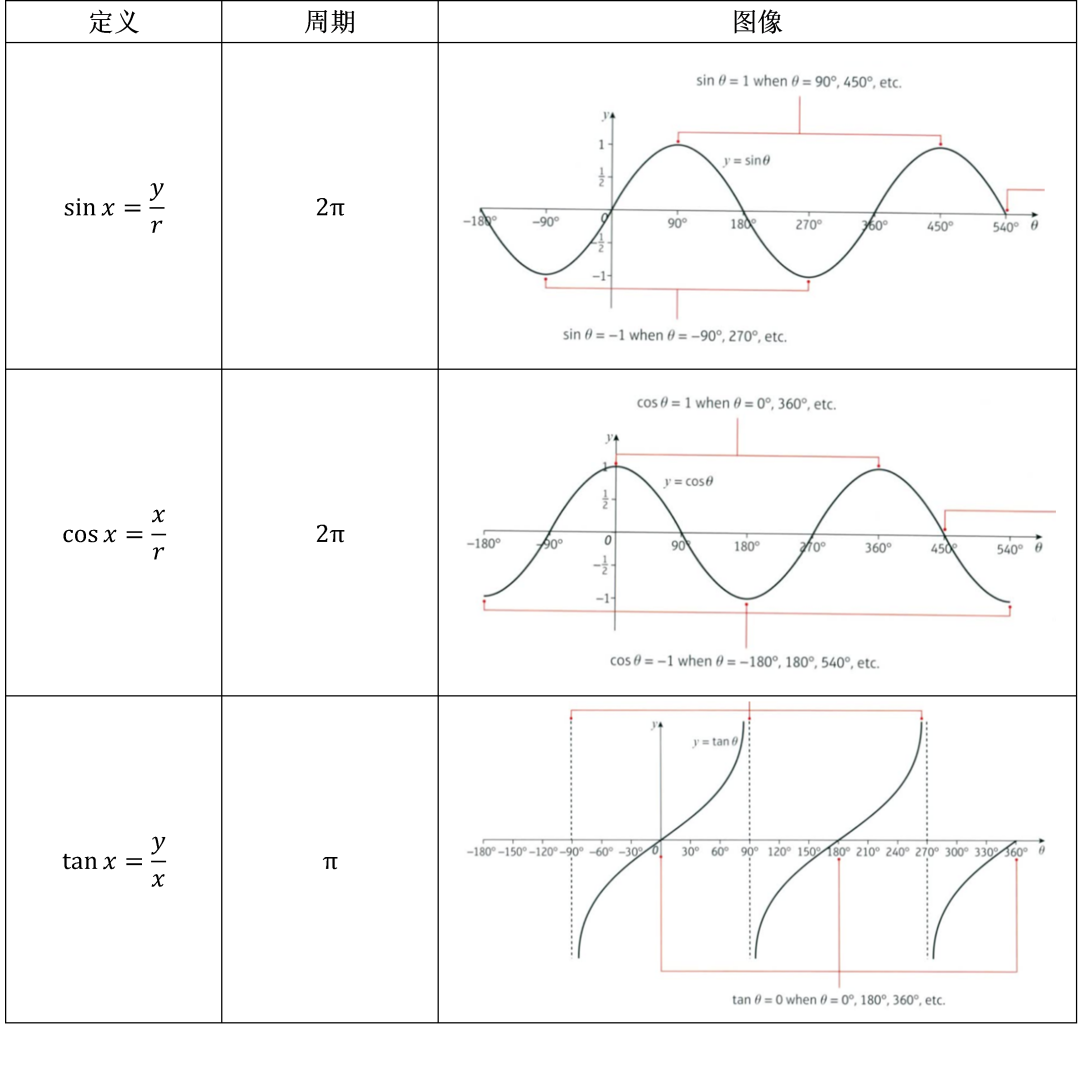
正弦函数(sinθ)
- 图像:周期性波浪线,周期$2\pi$,范围[−1,1]。
- 对称性:奇函数(关于原点对称)。
- 零点:$0,\pi,2\pi,\dots$
余弦函数(cosθ)
- 图像:类似正弦曲线,但起点在(0,1),周期$2\pi$,范围 [−1,1]。
- 对称性:偶函数(关于y轴对称)。
- 零点:$\pi/2,3\pi/2,\dots$
正切函数(tanθ)
- 图像:周期性曲线,周期$\pi$,在$\pi/2+k\pi$处有垂直渐近线。
- 定义域:$\theta\neq\pi/2+k\pi$
- 值域:全体实数$(-\infty,+\infty)$。
其他函数图像
- cotθ:与tanθ图像相似,但相位偏移𝜋/2。
- secθ和cscθ:分别在cosθ和sinθ的零点处有渐近线。
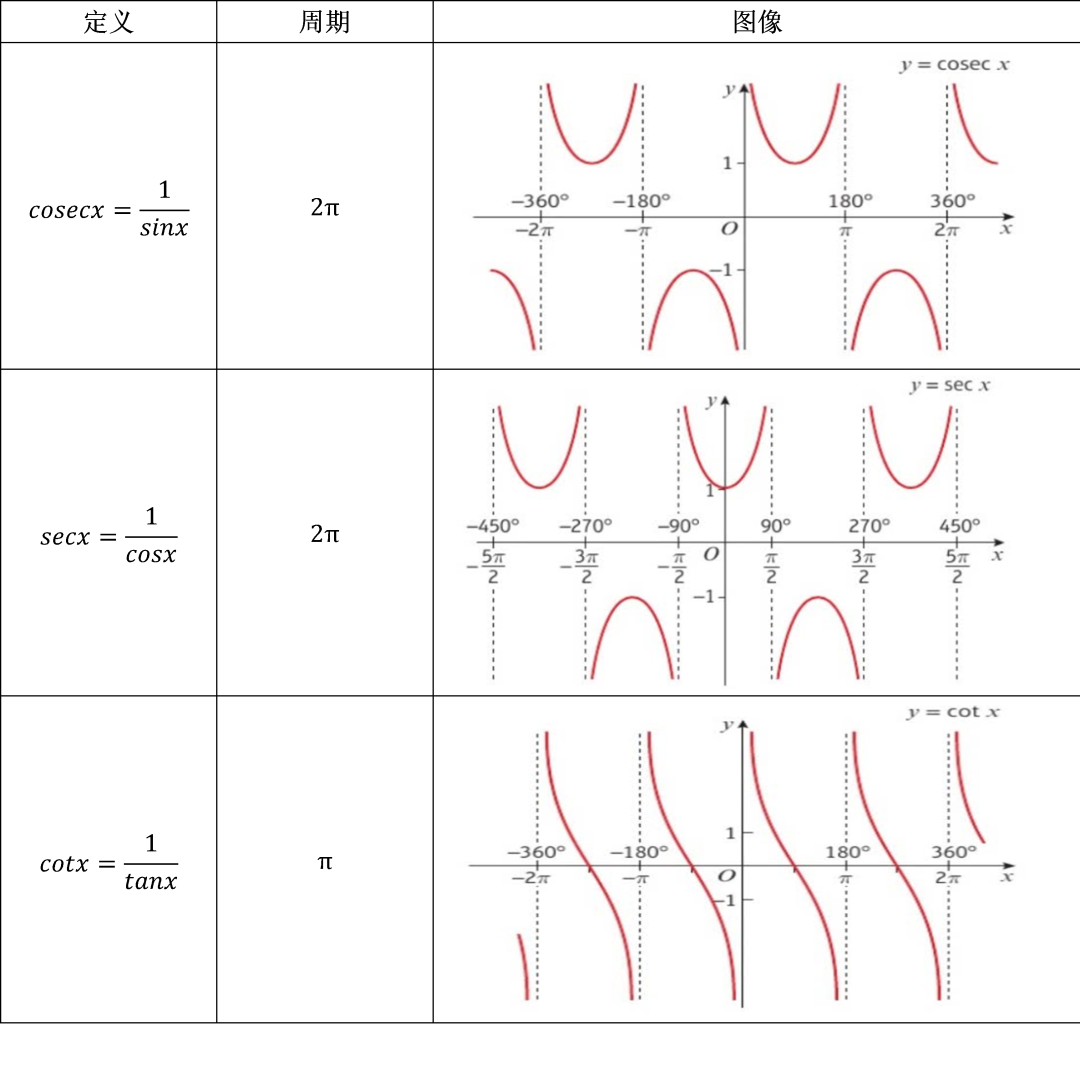
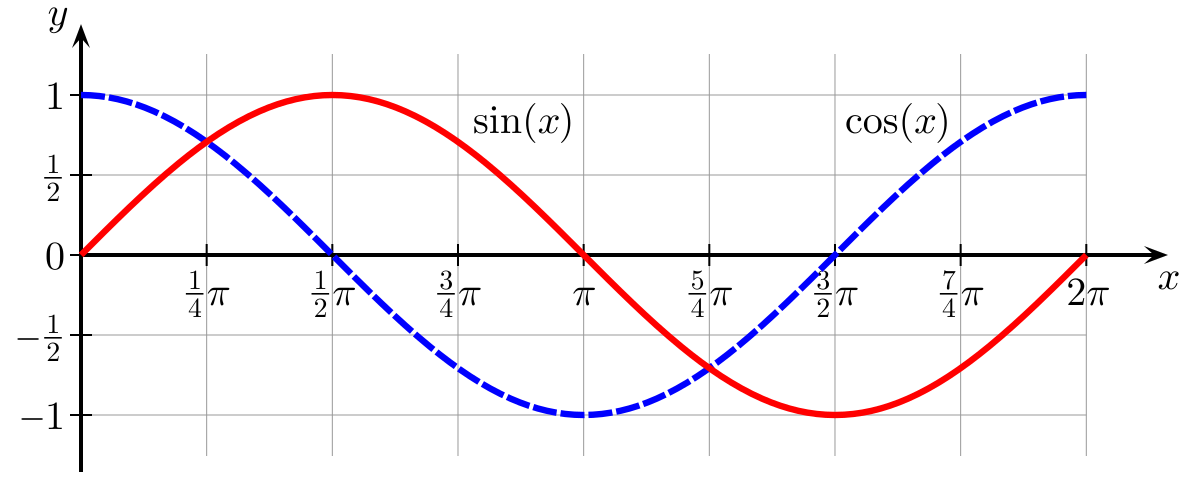
图像记忆法
- 余弦曲线(cosθ):关于y轴对称的波浪线,起点在(0,1)(0,1)。
- 正弦曲线(sinθ):关于原点对称的波浪线,起点在(0,0)(0,0)。
重要公式与恒等式
基本关系
倒数关系:
$$\sec\theta=\frac{1}{\cos\theta},\quad\csc\theta=\frac{1}{\sin\theta},\quad\cot\theta=\frac{1}{\tan\theta}$$
商数关系:
$$\tan\theta=\frac{\sin\theta}{\cos\theta},\quad\cot\theta=\frac{\cos\theta}{\sin\theta}$$
勾股定理:
$$\sin^2\theta+\cos^2\theta=1,\quad1+\tan^2\theta=\sec^2\theta,\quad1+\cot^2\theta=\csc^2\theta$$
角度转化:
$$\cos(-\theta)=\cos\theta,\quad\sin(-\theta)=-\sin\theta$$
和差角公式
$$\begin{aligned}\sin(A\pm B)&=\sin A\cos B\pm\cos A\sin B\\\cos(A\pm B)&=\cos A\cos B\mp\sin A\sin B\\\tan(A\pm B)&=\frac{\tan A\pm\tan B}{1\mp\tan A\tan B}\end{aligned}$$
倍角与半角公式
倍角公式:
$$\sin2\theta=2\sin\theta\cos\theta,\quad\cos2\theta=\cos^2\theta-\sin^2\theta$$
半角公式:
$$\sin\frac{\theta}{2}=\pm\sqrt{\frac{1-\cos\theta}{2}},\quad\cos\frac{\theta}{2}=\pm\sqrt{\frac{1+\cos\theta}{2}}$$
导数和积分
导数
$$\begin{aligned}\frac{d}{d\theta}\sin\theta&=\cos\theta\\\frac{d}{d\theta}\cos\theta&=-\sin\theta\\\frac{d}{d\theta}\tan\theta&=\sec^2\theta\\\frac{d}{d\theta}\cot\theta&=-\csc^2\theta\\\end{aligned}$$
积分
$$\begin{aligned}\int\sin\theta\,d\theta&=-\cos\theta+C\\\int\cos\theta\,d\theta&=\sin\theta+C\\\int\tan\theta\,d\theta&=-\ln|\cos\theta|+C\\\end{aligned}$$
反三角函数
反三角函数用于从已知的三角函数值求角度:
- arcsin(反正弦):定义域[-1,1],值域[-π/2,π/2]。
- arccos(反余弦):定义域[-1,1],值域[0,π]。
- arctan(反正切):定义域全体实数,值域(-π/2,π/2)。
示例:
- $\arcsin(0.5)=π/6$
- $\arccos(-1)=π$
- $\arctan(1)=π/4$
实际应用场景
- 物理学:
- 力的分解(如斜面上的重力分解)。
- 简谐振动(弹簧振子的运动方程)。
- 工程学:
- 交流电路分析(电压和电流的相位关系)。
- 信号处理(傅里叶变换中的正弦波合成)。
- 计算机图形学:
- 3D旋转(旋转矩阵中使用sin和cos)。
- 光照模型(计算光线与表面法线的夹角)。
- 地理测量:
- 三角定位(GPS、地图测绘)。
- 机器学习:
- 特征工程(周期性特征的编码,如时间序列的月份、星期)。
- 数据增强(图像旋转中的坐标变换)。
常见误区
- 角度单位混淆:区分弧度(radians)和角度(degrees),公式中默认用弧度。
- 反三角函数的多值性:如$\arcsin(0.5)$可能有多个解,但主值唯一。
三角函数与特征工程
在机器学习中,对时间相关的周期性特征(如小时、星期、月份)进行编码时,直接使用原始数值(例如用 1~12 表示月份)可能会引入误导性假设(如“12月”和“1月”在数值上相邻,但实际时间上是连续的)。三角函数编码(正弦/余弦变换)可以将周期性特征映射到连续的循环空间,保留时间的内在周期性。
周期性特征的问题
假设原始特征为小时(0~23),直接输入模型可能导致以下问题:
- 数值跳跃性:23点和0点相差1,但实际是连续的。
- 线性误解:模型可能认为“23点”和“0点”距离很远,但实际上它们是相邻的。
解决方案:三角函数编码
将周期性特征映射到正弦和余弦函数上,保留循环性:
将特征归一化到[0,2π]范围:
$$\text{弧度}=\frac{2\pi\times\text{原始值}}{\text{周期长度}}$$
例如,小时(周期24)的弧度为:$2\pi\times\text{小时}/24$
计算正弦和余弦值:
$$\sin(\text{弧度}),\quad\cos(\text{弧度})$$
同时使用两个函数可以消除单一函数的对称性歧义(如$\sin(0)=\sin(\pi)=0$)。
Python代码实现
生成示例数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 创建示例数据:时间特征(小时、星期、月份)
data = {
"hour": np.arange(0, 24),
"day_of_week": np.tile(np.arange(0, 7), 4)[:24], # 重复4次并截取前24个
"month": np.tile(np.arange(1, 13), 2)[:24] # 重复2次得到24个
}
df = pd.DataFrame(data)
定义周期性编码函数
def encode_cyclic_feature(df, col_name, period):
"""将周期性特征编码为sin和cos分量"""
# 计算弧度
radians = 2 * np.pi * df[col_name] / period
# 计算sin和cos
df[f"{col_name}_sin"] = np.sin(radians)
df[f"{col_name}_cos"] = np.cos(radians)
return df
# 对小时、星期、月份分别编码
df = encode_cyclic_feature(df, "hour", period=24)
df = encode_cyclic_feature(df, "day_of_week", period=7)
df = encode_cyclic_feature(df, "month", period=12)
# 查看结果
print(df[["hour", "hour_sin", "hour_cos"]].head(3))
输出示例:
hour hour_sin hour_cos 0 0 0.000000 1.000000 1 1 0.258819 0.965926 2 2 0.500000 0.866025
可视化编码效果
# 绘制小时的sin/cos编码效果
plt.figure(figsize=(10,4))
plt.scatter(df["hour"], df["hour_sin"], label="hour_sin")
plt.scatter(df["hour"], df["hour_cos"], label="hour_cos")
plt.xlabel("Original Hour")
plt.ylabel("Encoded Value")
plt.title("Cyclic Encoding of Hour")
plt.legend()
plt.grid()
plt.show()
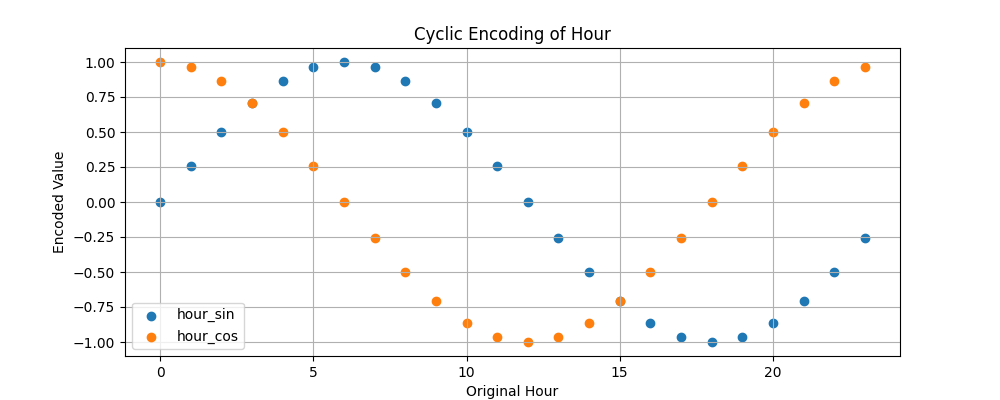
可以看到,23点和0点的编码值在正弦和余弦空间中是连续的。
编码原理详解
为什么同时使用sin和cos?
- 单一函数的局限性:单独使用sin 或 cos 会导致不同时间点具有相同的编码值(例如,sin(0)=sin(π)=0)。
- 互补性:同时使用sin 和 cos 可以消除歧义,确保每个时间点对应唯一的二维坐标。
几何意义
- 将时间特征映射到单位圆上的一个点,坐标由$(\sin(\theta),\cos(\theta))$决定。
- 周期性特征的相邻值在单位圆上相邻,保留时间连续性。
特征工程
将原始特征替换为 sin 和 cos 分量后,输入模型:
# 示例:使用编码后的特征训练模型 from sklearn.linear_model import LinearRegression # 假设X包含编码后的特征,y是目标变量 X = df[["hour_sin", "hour_cos", "day_of_week_sin", "day_of_week_cos", "month_sin", "month_cos"]] y = ... # 目标变量(如销售额) model = LinearRegression() model.fit(X, y)
优势
- 保留周期性:模型能理解23点和0点的连续性。
- 低维度:每个周期性特征仅增加2个维度(优于独热编码的高维度)。
对比其他编码方法
| 方法 | 优点 | 缺点 |
| 三角函数编码 | 保留周期性,低维度 | 需要计算sin/cos |
| 独热编码 | 简单直观 | 高维度,丢失顺序信息 |
| 数值直接输入 | 保留顺序 | 无法处理周期性跳跃 |
扩展:处理不规则周期
对于不规则周期(如每月的天数不同),可以按实际周期长度调整:
# 示例:月份的周期按实际天数调整(假设非闰年) month_days = [31,28,31,30,31,30,31,31,30,31,30,31] df["month_radians"] = 2*np.pi*(df["month"]-1)/month_days # 月份从1开始
掌握这种编码方式后,你可以更好地处理时间序列、传感器数据等周期性特征!如果需要对其他类型特征(如方位角)编码,方法类似。

这篇文章公式没有渲染
可能是js文件的镜像被屏蔽