在K-Means算法中,最终的聚类效果受初始的聚类中心的影响,K-Means++算法的提出,为选择较好的初始聚类中心提供了依据,但是算法中,聚类的类别个数k仍需事先制定,对于类别个数事先未知的数据集,K-Means和K-Means++将很难对其精确求解,对此,有一些改进的算法被提出来处理聚类个数k未知的情形。MeanShift算法,又被称为均值漂移算法,与K-Means算法一样,都是基于聚类中心的聚类算法,不同的是,MeanShift算法不需要事先制定类别个数k。
MeanShift的概念最早是由Fukunage在1975年提出的,在后来由Yizong Cheng对其进行扩充,主要提出了两点的改进:定义了核函数,增加了权重系数。核函数的定义使得偏移值对偏移向量的贡献随之样本与被偏移点的距离的不同而不同。权重系数使得不同样本的权重不同。
MeanShift算法在很多领域都有成功应用,例如图像平滑、图像分割、物体跟踪等,这些属于人工智能里面模式识别或计算机视觉的部分;另外也包括常规的聚类应用。
- 图像平滑:图像最大质量下的像素压缩;
- 图像分割:跟图像平滑类似的应用,但最终是将可以平滑的图像进行分离已达到前后景或固定物理分割的目的;
- 目标跟踪:例如针对监控视频中某个人物的动态跟踪;
- 常规聚类,如用户聚类等。
MeanShift算法理论
MeanShift向量
对于给定的$d$维空间$R^d$中的n个样本点$x_i,i=1,⋯,n$,则对于x点,其MeanShift向量的基本形式为:
$$M_h(x)=\frac{1}{k}\sum_{x_i\in S_h}(x_i-x)$$
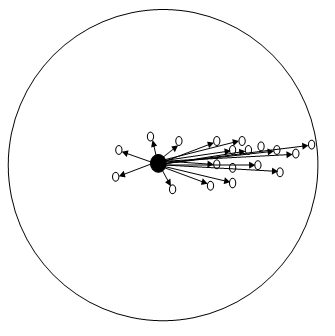
其中,$S_h$指的是一个半径为h的高维球区域,如上图中的圆形区域。$S_h$的定义为:
$$S_h(x)=(y\mid(y-x)(y-x)^T\leq h^2)$$
里面所有点与圆心为起点形成的向量相加的结果就是Meanshift向量。下图黄色箭头就是$M_h$(MeanShift向量)。
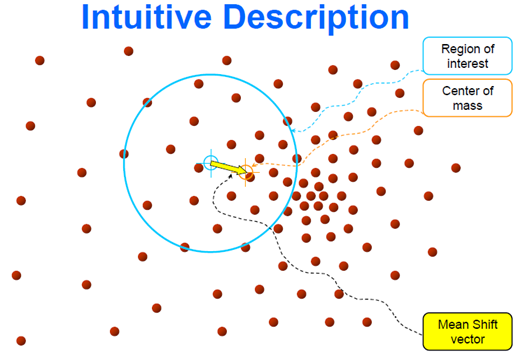
对于MeanShift算法,是一个迭代的步骤,即先算出当前点的偏移均值,将该点移动到此偏移均值,然后以此为新的起始点,继续移动,直到满足最终的条件。
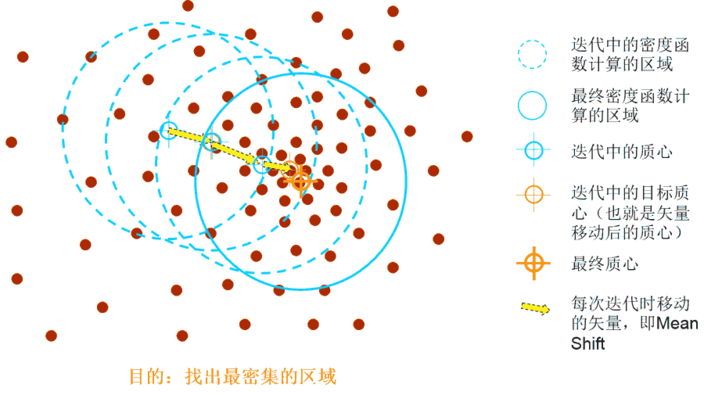
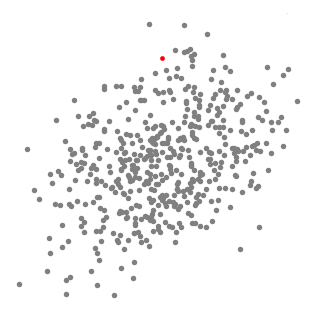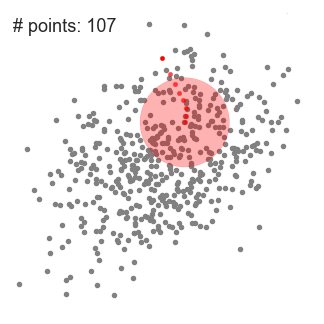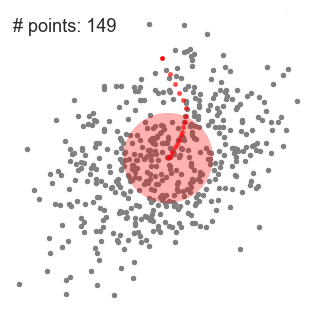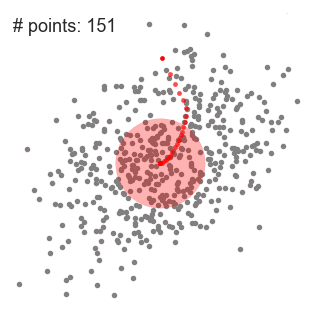
Mean-Shift聚类就是对于集合中的每一个元素,对它执行下面的操作:把该元素移动到它邻域中所有元素的特征值的均值的位置,不断重复直到收敛。准确的说,不是真正移动元素,而是把该元素与它的收敛位置的元素标记为同一类。
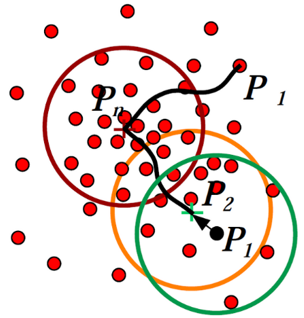
如上的均值漂移向量的求解方法存在一个问题,即在$S_h$的区域内,每一个样本点x对样本X的共享是一样的。而实际中,每一个样本点x对样本X的贡献是不一样的,这样的共享可以通过核函数进行度量。
核函数
在MeanShift算法中引入核函数的目的是使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。核函数是机器学习中常用的一种方式。核函数的定义如下所示:
X表示一个d维的欧式空间,x是该空间中的一个点$x=\{x_1,x_2,x_3\cdots,x_d\}$,其中,x的模$\|x\|^2=xx^T$,R表示实数域,如果一个函数K:X→R存在一个剖面函数k:[0,∞]→R,即
$$K(x)=k(\|x\|^2)$$
并且满足:
- k是非负的
- k是非增的
- k是分段连续的
那么,函数K(x)就称为核函数。
核函数有很多,下图中表示的每一个曲线都为一个核函数。
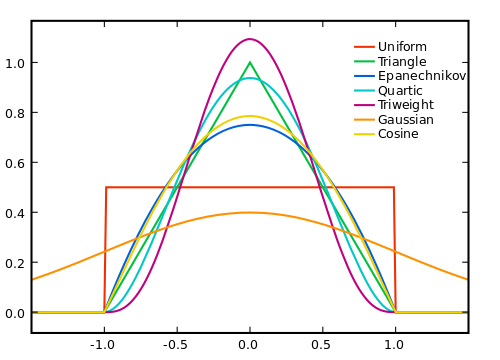
常用的核函数有高斯核函数。高斯核函数如下所示:
$$N(x)=\frac{1}{\sqrt{2\pi}h}e^{-\frac{x^2}{2h^2}}$$
其中,h称为带宽(bandwidth),不同带宽的核函数如下图所示:
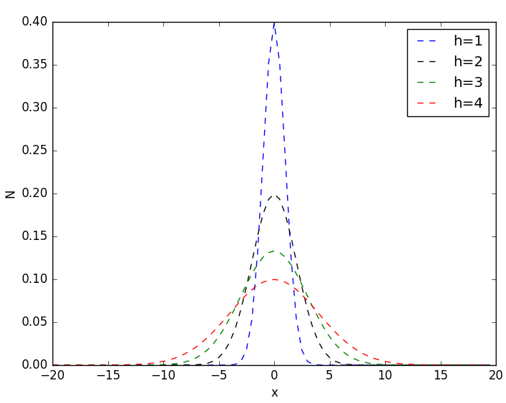
从高斯函数的图像可以看出,当带宽h一定时,样本点之间的距离越近,其核函数的值越大,当样本点之间的距离相等时,随着高斯函数的带宽h的增加,核函数的值在减小。
高斯核函数的Python实现:
# -*- coding: utf-8 -*- import numpy as np import math def gaussian_kernel(distance, bandwidth): '''高斯核函数 :param distance: 欧氏距离计算函数 :param bandwidth: 核函数的带宽 :return: 高斯函数值 ''' m = np.shape(distance)[0] # 样本个数 right = np.mat(np.zeros((m, 1))) # m*1矩阵 for i in range(m): right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth) right[i, 0] = np.exp(right[i, 0]) left = 1 / (bandwidth * math.sqrt(2 * math.pi)) gaussian_val = left * right return gaussian_val
引入核函数的MeanShift向量
假设在半径为 h 的范围 $S_h$ 范围内,为了使得每一个样本点 x 对于样本 X 的共享不一样,向基本的 MeanShift 向量形式中增加核函数,得到如下改进的 MeanShift 向量形式:
$$M_h(x)=\frac{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})(x_i-x)}{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})}$$
其中,$G(\frac{x_i-x}{h_i})$ 为核函数。通常,可以取 $S_h$ 为整个数据集范围。
计算 $M_h$ 时考虑距离的影响,同时也可以认为在所有的样本点 X 中, 重要性并不一样, 因此对每个样本还引入一个权重系数。如此以来就可以把 MeanShift 形式扩展为:
$$M_h(x)=\frac{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})w(x_i)(x_i-x)}{\sum_{i=1}^{n}G(\frac{x_i-x}{h_i})w(x_i)}$$
其中,$w(x_i)$ 是一个赋给采样点的权重。

聚类动画演示
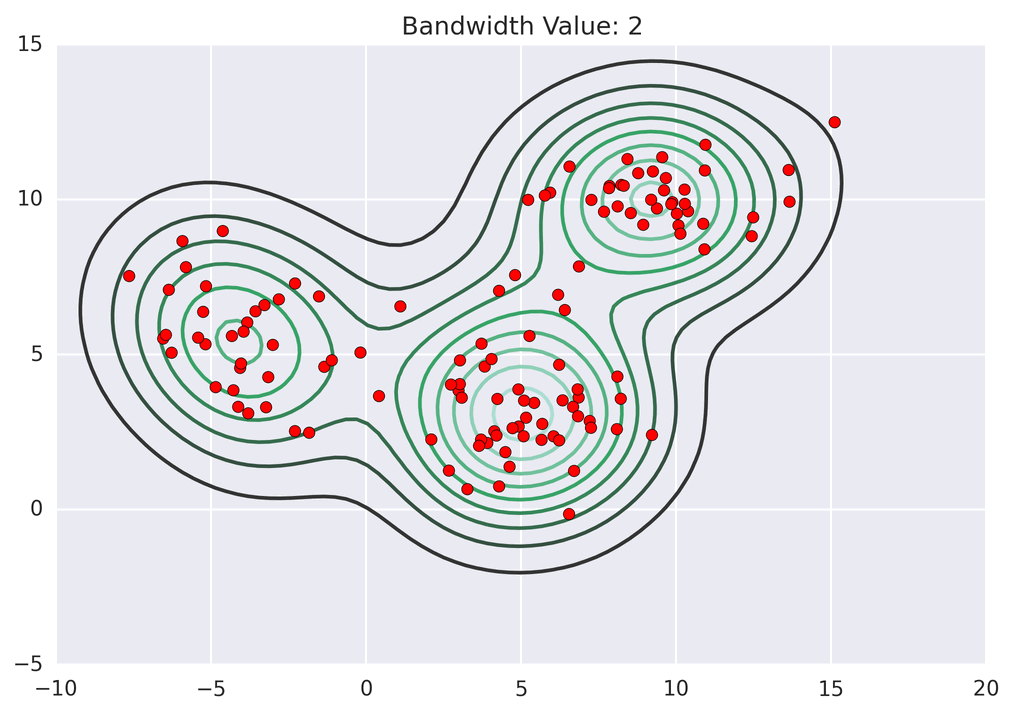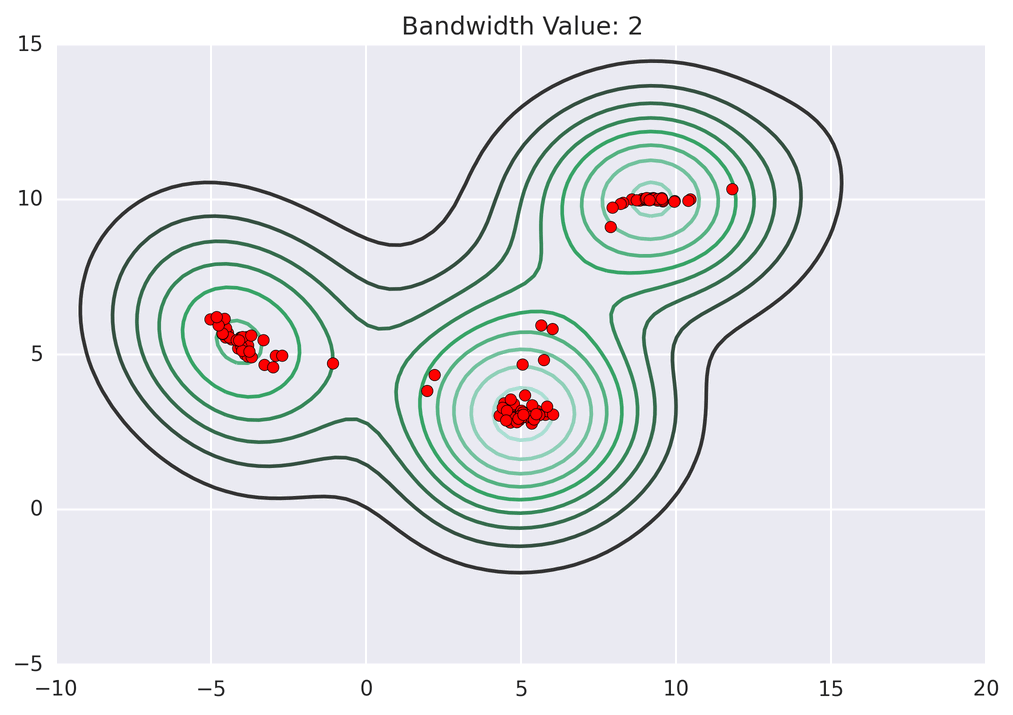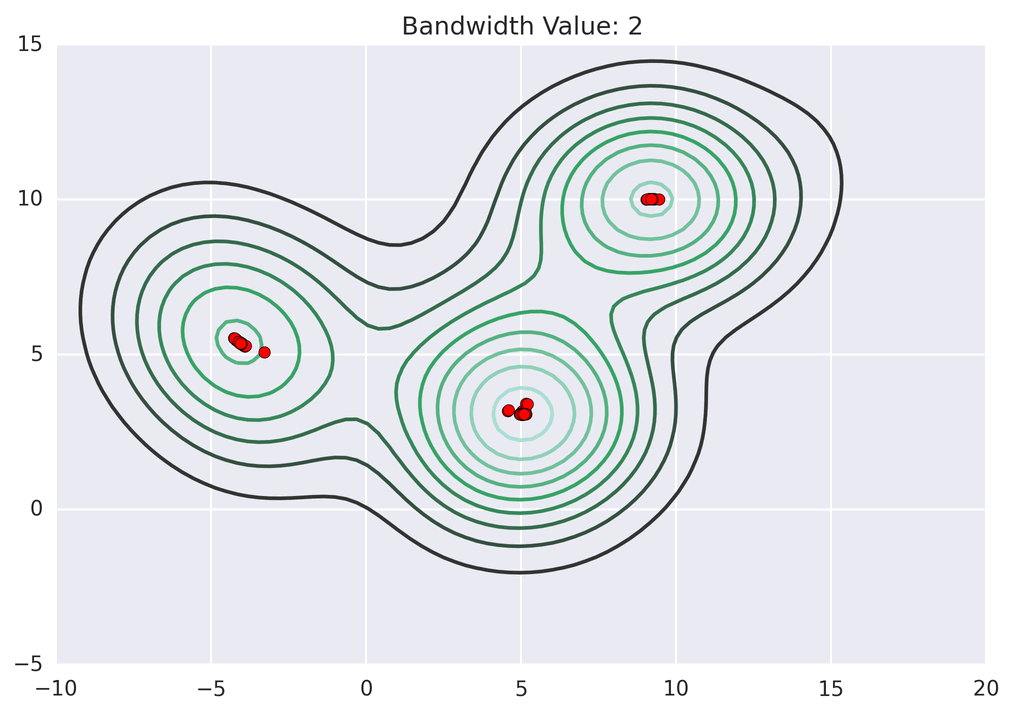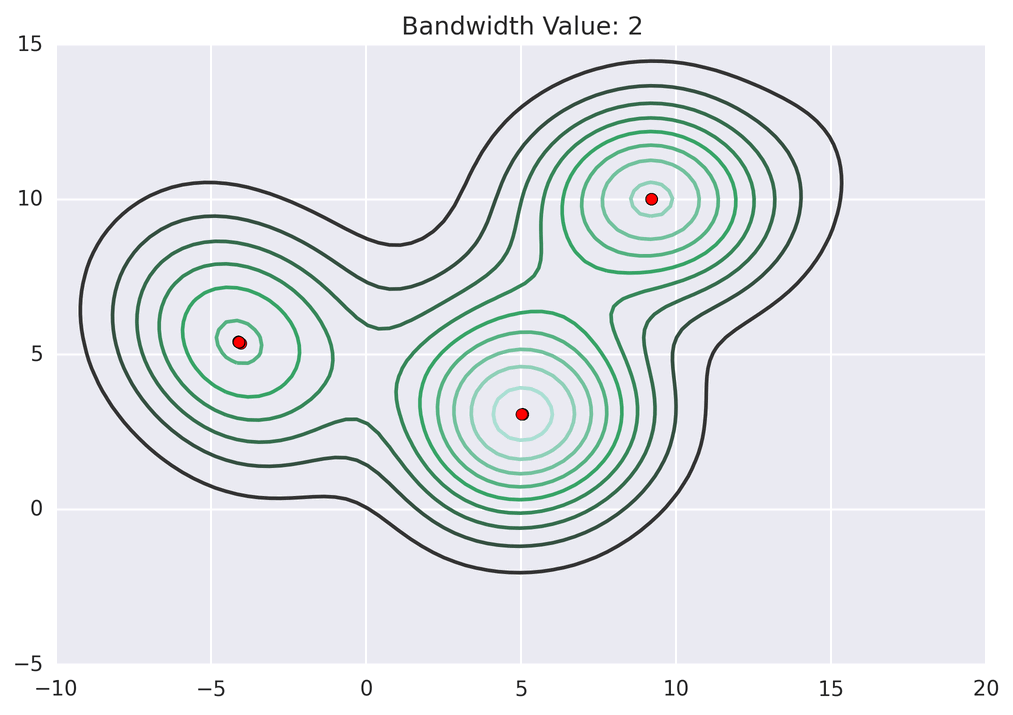
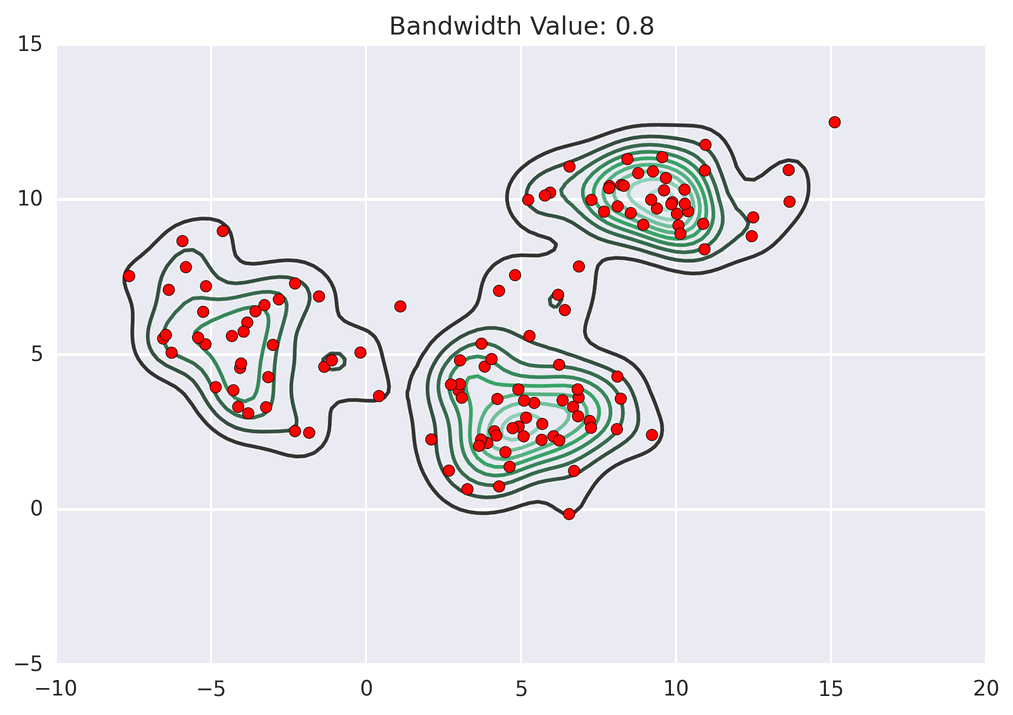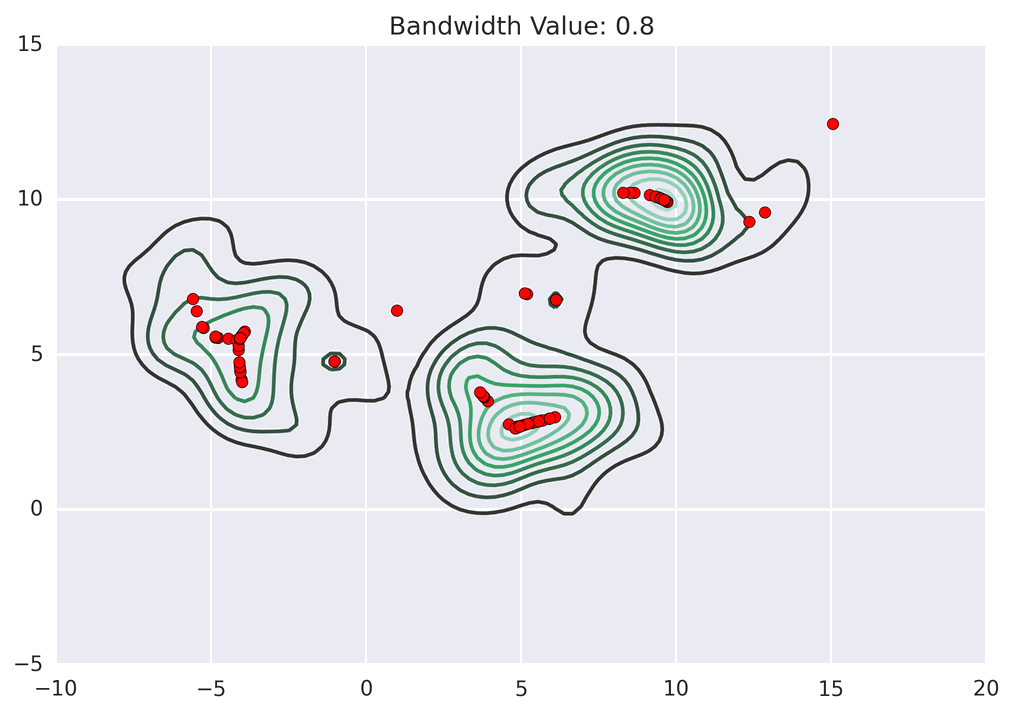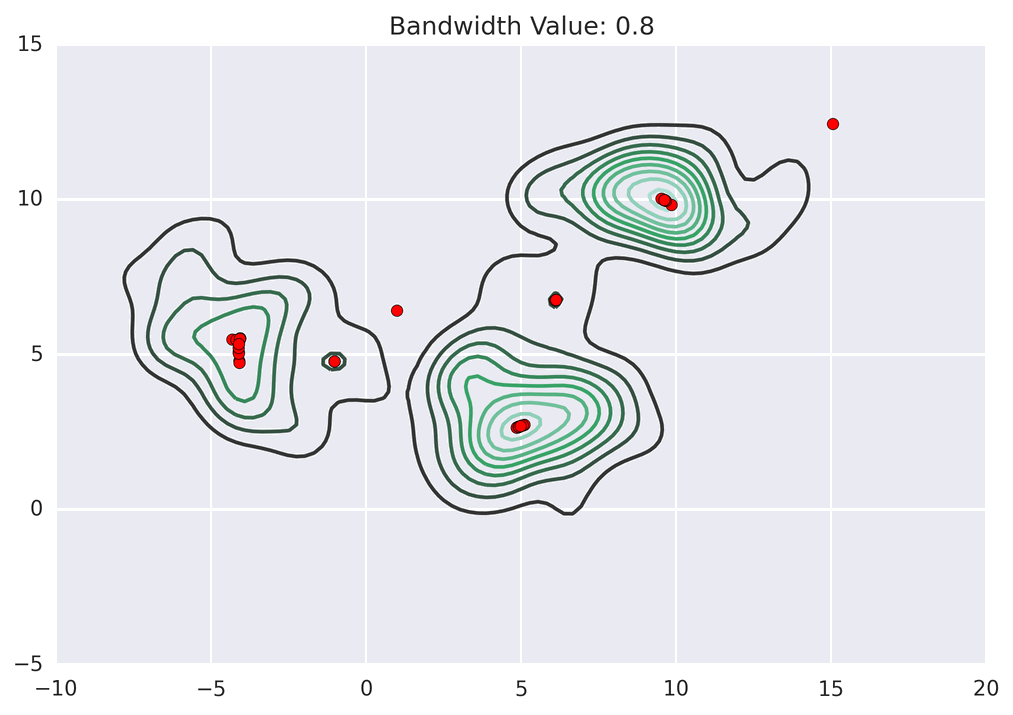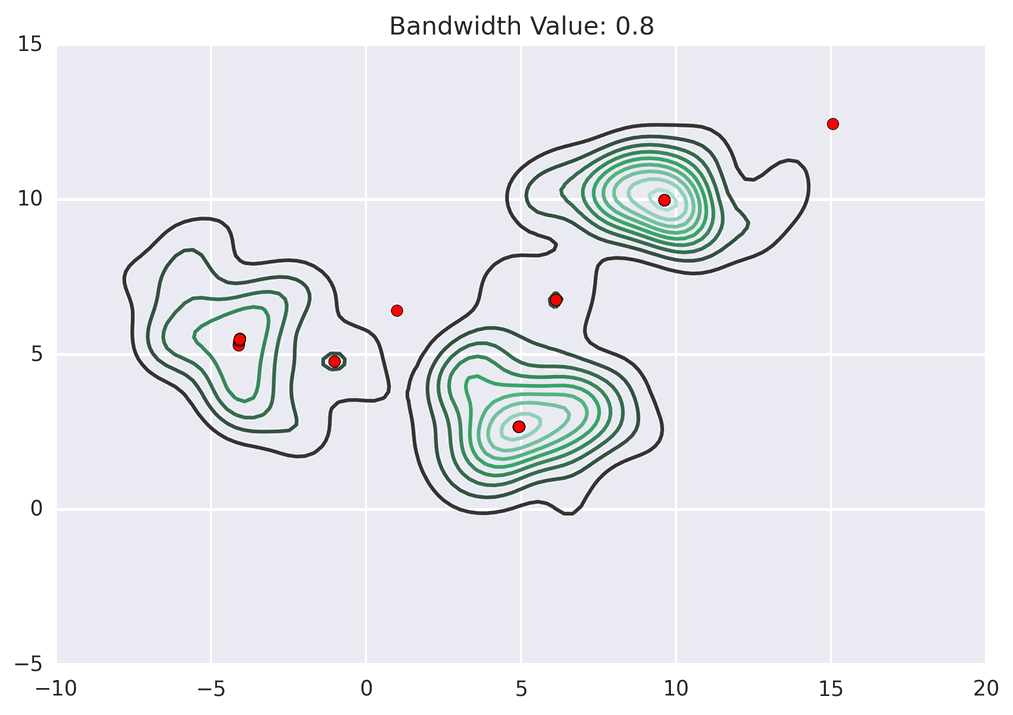
MeanShift 的代码实现
算法的Python 实现
import numpy as np
import math
MIN_DISTANCE = 0.00001 #最小误差
def euclidean_dist(pointA, pointB):
#计算 pointA 和 pointB 之间的欧式距离
total = (pointA - pointB) * (pointA - pointB).T
return math.sqrt(total)
def gaussian_kernel(distance, bandwidth):
'''高斯核函数
:param distance: 欧氏距离计算函数
:param bandwidth: 核函数的带宽
:return: 高斯函数值
'''
m = np.shape(distance)[0] #样本个数
right = np.mat(np.zeros((m, 1)))
for i in range(m):
right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth)
right[i, 0] = np.exp(right[i, 0])
left = 1 / (bandwidth * math.sqrt(2 * math.pi))
gaussian_val = left * right
return gaussian_val
def shift_point(point, points, kernel_bandwidth):
'''计算均值漂移点
:param point: 需要计算的点
:param points: 所有的样本点
:param kernel_bandwidth: 核函数的带宽
:return:
point_shifted:漂移后的点
'''
points = np.mat(points)
m = np.shape(points)[0] #样本个数
#计算距离
point_distances = np.mat(np.zeros((m, 1)))
for i in range(m):
point_distances[i, 0] = euclidean_dist(point, points[i])
#计算高斯核
point_weights = gaussian_kernel(point_distances, kernel_bandwidth)
#计算分母
all = 0.0
for i in range(m):
all += point_weights[i, 0]
#均值偏移
point_shifted = point_weights.T * points / all
return point_shifted
def group_points(mean_shift_points):
'''计算所属的类别
:param mean_shift_points: 漂移向量
:return: group_assignment:所属类别
'''
group_assignment = []
m, n = np.shape(mean_shift_points)
index = 0
index_dict = {}
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
if item_1 not in index_dict:
index_dict[item_1] = index
index += 1
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
group_assignment.append(index_dict[item_1])
return group_assignment
def train_mean_shift(points, kernel_bandwidth=2):
'''训练 MeanShift 模型
:param points: 特征数据
:param kernel_bandwidth: 核函数带宽
:return:
points:特征点
mean_shift_points:均值漂移点
group:类别
'''
mean_shift_points = np.mat(points)
max_min_dist = 1
iteration = 0
m = np.shape(mean_shift_points)[0] #样本的个数
need_shift = [True] * m #标记是否需要漂移
#计算均值漂移向量
while max_min_dist > MIN_DISTANCE:
max_min_dist = 0
iteration += 1
print("iteration:" + str(iteration))
for i in range(0, m):
#判断每一个样本点是否需要计算偏置均值
if not need_shift[i]:
continue
p_new = mean_shift_points[i]
p_new_start = p_new
p_new = shift_point(p_new, points, kernel_bandwidth) #对样本点进行偏移
dist = euclidean_dist(p_new, p_new_start) #计算该点与漂移后的点之间的距离
if dist > max_min_dist: #记录是有点的最大距离
max_min_dist = dist
if dist < MIN_DISTANCE: #不需要移动
need_shift[i] = False
mean_shift_points[i] = p_new
#计算最终的 group
group = group_points(mean_shift_points) #计算所属的类别
return np.mat(points), mean_shift_points, group
以上代码实现了基本的流程,但是执行效率很慢,正式使用时建议使用 scikit-learn 库中的 MeanShift。
scikit-learnMeanShift演示
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
data = []
f = open("k_means_sample_data.txt", 'r')
for line in f:
data.append([float(line.split(',')[0]), float(line.split(',')[1])])
data = np.array(data)
#通过下列代码可自动检测bandwidth值
#从data中随机选取1000个样本,计算每一对样本的距离,然后选取这些距离的0.2分位数作为返回值,当n_samples很大时,这个函数的计算量是很大的。
bandwidth = estimate_bandwidth(data, quantile=0.2, n_samples=1000)
print(bandwidth)
#bin_seeding设置为True就不会把所有的点初始化为核心位置,从而加速算法
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(data)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
#计算类别个数
labels_unique = np.unique(labels)
n_clusters = len(labels_unique)
print("number of estimated clusters: %d" % n_clusters)
#画图
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure(1)
plt.clf() #清楚上面的旧图形
#cycle把一个序列无限重复下去
colors = cycle('bgrcmyk')
for k, color in zip(range(n_clusters), colors):
#current_member表示标签为k的记为true反之false
current_member = labels == k
cluster_center = cluster_centers[k]
#画点
plt.plot(data[current_member, 0], data[current_member, 1], color + '.')
#画圈
plt.plot(cluster_center[0], cluster_center[1], 'o',
markerfacecolor=color, #圈内颜色
markeredgecolor='k', #圈边颜色
markersize=14) #圈大小
plt.title('Estimated number of clusters: %d' % n_clusters)
plt.show()
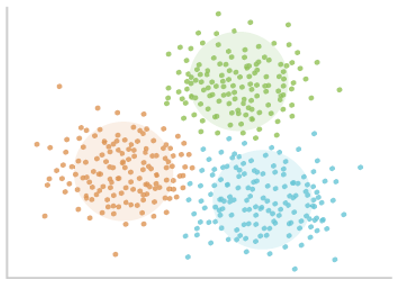
执行效果:
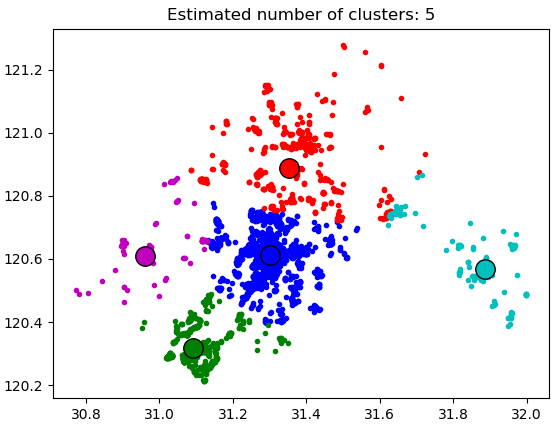
scikit-learn MeanShift源码分析
源码地址:https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/cluster/mean_shift_.py
def mean_shift(X, bandwidth=None, seeds=None, bin_seeding=False,
min_bin_freq=1, cluster_all=True, max_iter=300,
n_jobs=1):
"""Perform mean shift clustering of data using a flat kernel.
Read more in the :ref:`UserGuide`.
Parameters
----------
X : array-like, shape=[n_samples, n_features]
Input data.
bandwidth : float, optional
Kernel bandwidth.
If bandwidth is not given, it is determined using a heuristic based on
the median of all pairwise distances. This will take quadratic time in
the number of samples. The sklearn.cluster.estimate_bandwidth function
can be used to do this more efficiently.
seeds : array-like, shape=[n_seeds, n_features] or None
Points used as initial kernel locations. If None and bin_seeding=False,
each data point is used as a seed. If None and bin_seeding=True,
see bin_seeding.
bin_seeding : boolean, default=False
If true, initial kernel locations are not locations of all
points, but rather the location of the discretized version of
points, where points are binned onto a grid whose coarseness
corresponds to the bandwidth. Setting this option to True will speed
up the algorithm because fewer seeds will be initialized.
Ignored if seeds argument is not None.
min_bin_freq : int, default=1
To speed up the algorithm, accept only those bins with at least
min_bin_freq points as seeds.
cluster_all : boolean, default True
If true, then all points are clustered, even those orphans that are
not within any kernel. Orphans are assigned to the nearest kernel.
If false, then orphans are given cluster label -1.
max_iter : int, default 300
Maximum number of iterations, per seed point before the clustering
operation terminates (for that seed point), if has not converged yet.
n_jobs : int
The number of jobs to use for the computation. This works by computing
each of the n_init runs in parallel.
If -1 all CPUs are used. If 1 is given, no parallel computing code is
used at all, which is useful for debugging. For n_jobs below -1,
(n_cpus + 1 + n_jobs) are used. Thus for n_jobs=-2, all CPUs but one
are used.
.. versionadded:: 0.17
Parallel Execution using *n_jobs*.
Returns
-------
cluster_centers : array, shape=[n_clusters, n_features]
Coordinates of cluster centers.
labels : array, shape=[n_samples]
Cluster labels for each point.
Notes
-----
See examples/cluster/plot_mean_shift.py for an example.
"""
# 没有定义 bandwidth 执行函数 estimate_bandwidth 估计带宽
if bandwidth is None:
bandwidth = estimate_bandwidth(X, n_jobs=n_jobs)
# 带宽小于 0 就报错
elif bandwidth<= 0:
raise ValueError("bandwidth needs to be greater than zero or None,\
got %f" % bandwidth)
# 如果没有设置种子
if seeds is None:
# 通过 get_bin_seeds 选取种子
# min_bin_freq 指定最少的种子数目
if bin_seeding:
seeds = get_bin_seeds(X, bandwidth, min_bin_freq)
# 把所有点设为种子
else:
seeds = X
# 根据 shape 得到样本数量和特征数量
n_samples, n_features = X.shape
# 中心强度字典键为点值为强度
center_intensity_dict = {}
# 近邻搜索 fit 的返回值为
# radius 意思是半径表示参数空间的范围
# 用作于 radius_neighbors 可以理解为在半径范围内找邻居
nbrs = NearestNeighbors(radius=bandwidth, n_jobs=n_jobs).fit(X)
# 并行地在所有种子上执行迭代
# all_res 为所有种子的迭代完的中心以及周围的邻居数
# execute iterations on all seeds in parallel
all_res = Parallel(n_jobs=n_jobs)(
delayed(_mean_shift_single_seed)
(seed, X, nbrs, max_iter) for seed in seeds)
# 遍历所有结果
# copy results in a dictionary
for i in range(len(seeds)):
# 只有这个点的周围没有邻居才会出现 None 的情况
if all_res[i] is not None:
# 一个中心点对应一个强度(周围邻居个数)
center_intensity_dict[all_res[i][0]] = all_res[i][1]
# 要是一个符合要求的点都没有,就说明 bandwidth 设置得太小了
if not center_intensity_dict:
# nothing near seeds
raise ValueError("No point was within bandwidth=%f of any seed."
"Try a different seeding strategy\
or increase the bandwidth."
% bandwidth)
# POST PROCESSING: remove near duplicate points
# If the distance between two kernels is less than the bandwidth,
# then we have to remove one because it is a duplicate. Remove the
# one with fewer points.
# 按照强度来排序
# dict.items() 返回值形式为 [(key1, value1), (key2, value2)...]
# reverse 为 True 表示由大到小
# key 的 lambda 表达式用来指定用作比较的部分为 value
sorted_by_intensity = sorted(center_intensity_dict.items(),
key=lambda tup: tup[1], reverse=True)
# 单独把排好序的点分出来
sorted_centers = np.array([tup[0] for tup in sorted_by_intensity])
# 返回长度和点数量相等的 bool 类型 array
unique = np.ones(len(sorted_centers), dtype=np.bool)
# 在这些点里再来一次找邻居
nbrs = NearestNeighbors(radius=bandwidth,
n_jobs=n_jobs).fit(sorted_centers)#enumerate返回的是index,value
#还是类似于之前的找邻居不过这次是为了剔除相近的点就是去除重复的中心
#因为是按强度由大到小排好序的所以优先将靠前的当作确定的中心
for i, center in enumerate(sorted_centers):
if unique[i]:
neighbor_idxs = nbrs.radius_neighbors([center],
return_distance=False)[0]
#中心的邻居不能作为候选
unique[neighbor_idxs] = 0
#因为这个范围内肯定包含自己,所以要单独标为1
unique[i] = 1 #leave the current point as unique
#把筛选过后的中心拿出来就是最终的聚类中心
cluster_centers = sorted_centers[unique]
#分配标签:最近的类就是这个点的类
#ASSIGN LABELS: a point belongs to the cluster that it is closest to
#把中心放进去用kneighbors来找邻居
#n_neighbors标为1使找到的邻居数为1也就成了标签
nbrs = NearestNeighbors(n_neighbors=1, n_jobs=n_jobs).fit(cluster_centers)
#labels用来存放标签
labels = np.zeros(n_samples, dtype=np.int)
#所有点带进去求
distances, idxs = nbrs.kneighbors(X)
#cluster_all为True表示所有的点都会被聚类
if cluster_all:
#flatten可以简单理解如下
#>>> np.array([[[[1,2]],[[3,4]],[[5,6]]]]).flatten()
#array([1,2,3,4,5,6])
labels = idxs.flatten()
#为False就把距离大于bandwidth的点类别标为-1
else:
#先全标-1
labels.fill(-1)
#距离小于bandwidth的标False
bool_selector = distances.flatten() <= bandwidth
#标True的才能参与聚类
labels[bool_selector] = idxs.flatten()[bool_selector]
#返回的结果为聚类中心和每个样本的标签
return cluster_centers, labels
#separate function for each seed's iterative loop
def _mean_shift_single_seed(my_mean, X, nbrs, max_iter):
#对于每个种子,梯度上升,直到收敛或者到达max_iter次迭代次数
#For each seed, climb gradient until convergence or max_iter
bandwidth = nbrs.get_params()['radius']
#表示收敛时的阈值
stop_thresh = 1e-3 * bandwidth #when mean has converged
#记录完成的迭代次数
completed_iterations = 0
while True:
#radius_neighbors寻找my_mean周围的邻居
#i_nbrs是符合要求的邻居的下标
#Find mean of points within bandwidth
i_nbrs = nbrs.radius_neighbors([my_mean], bandwidth,
return_distance=False)[0]
#根据下标找点
points_within = X[i_nbrs]
#找不到点就跳出迭代
if len(points_within) == 0:
break #Depending on seeding strategy this condition may occur
#保存旧的均值
my_old_mean = my_mean #save the old mean
#移动均值,这就是mean-shift名字的由来,每一步的迭代就是计算新的均值点
my_mean = np.mean(points_within, axis=0)
#用欧几里得范数与阈值进行比较判断收敛或者
#判断迭代次数达到上限
#If converged or at max_iter, adds the cluster
if (extmath.norm(my_mean - my_old_mean) < stop_thresh or
completed_iterations == max_iter):
#返回收敛时的均值中心和周围邻居个数
#tuple表示转换成元组因为之后的center_intensity_dict键不能为列表
return tuple(my_mean), len(points_within)
#迭代次数增加
completed_iterations += 1
参考资料:

python实现并不是低效,是因为在带宽外面的点不能计算偏移量,缺少这个当然低效,并且导致结果有很大问题