机器学习之距离与相似度计算

[LATEXPAGE]

欧几里得距离

在数学中，欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。欧几里得距离有时候有称欧氏距离，在数据分析及挖掘中经常会被使用到，例如聚类或计算相似度。

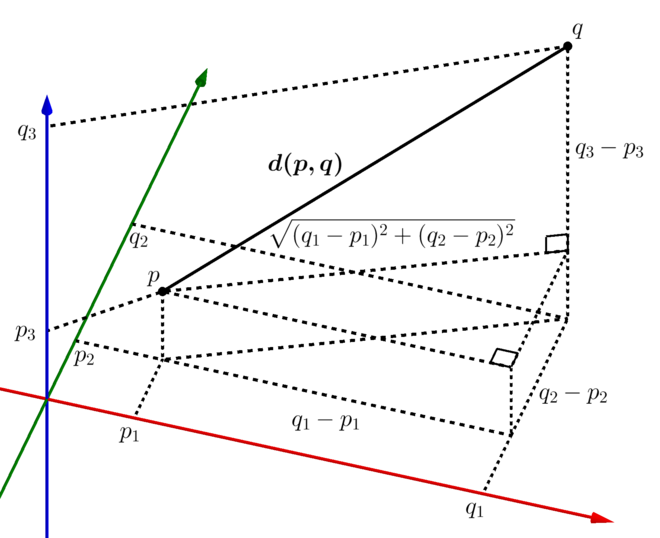
如果我们将两个点分别记作(p1,p2,p3,p4…)和(q1,q2,q3,14,…)，则欧几里得距离的计算公式为：

$E(p,q) = \sqrt{(p_1-q_1)^2+(p_2-q_2)^2+…+(p_n-q_n)^2}=\sqrt{\sum_{i=1}^{n}{(p_i-q_i)^2}}$

Python实现：

def eucliden(p, q):
    sumSq = 0.0
    
    #将差值的平方相加
    for i in range(len(p)):
        sumSq += (p[i] - q[i]) ** 2

    # 求平方根
    return sumSq ** 0.5

或者：

from math import *

def euclidean_distance(x, y):
    return sqrt(sum(pow(a - b, 2) for a, b in zip(x, y)))

print(euclidean_distance([0, 3, 4, 5], [7, 6, 3, -1]))

可以看到，欧几里得距离得到的结果是一个非负数，最大值是正无穷大，但是通常情况下相似度结果的取值范围在 [-1, 1] 之间。可以对它求倒数将结果转化到 (0, 1]之间。

$$\frac{1}{1+E(p,q)}$$

分母+1是为了避免遇到被0整除的错误。

标准化欧氏距离

标准化欧氏距离是针对简单欧氏距离的缺点（各维度分量的分布不一样）而作的一种改进方案。其实就是将各个分量都标准化。假设样本集X的均值(mean)为m，标准差(standard deviation)为s，那么X的“标准化变量”表示为：

$$X^*=\frac{X-m}{s}$$

即标准化后的值 = ( 标准化前的值－分量的均值) /分量的标准差

经过简单的推导就可以得到两个n维向量$a(a_1,a_2,…,a_n)$与$ b(b_1,b_2,…,b_n)$间的标准化欧氏距离的公式：

$$d(a,b) = \sqrt{\sum_{k=1}^{n}{(\frac{a_k-b_k}{s_k})^2}}$$

如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。

Python实现：

def normalized_euclidean(a, b):
    sumnum = 0
    for i in range(len(a)):
        avg = (a[i] - b[i]) / 2
        si = ((a[i] - avg) ** 2 + (b[i] - avg) ** 2) ** 0.5
        sumnum += ((a[i] - b[i]) / si) ** 2
    return sumnum ** 0.5

曼哈顿距离

曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

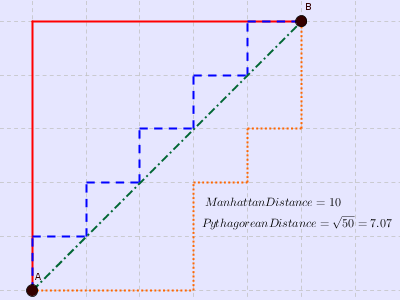
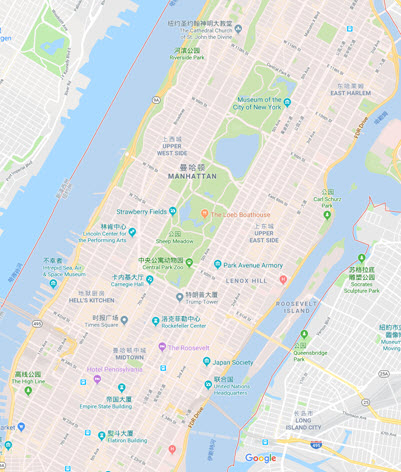
上图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和橙色代表等价的曼哈顿距离。通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”，此即曼哈顿距离名称的来源，同时，曼哈顿距离也称为城市街区距离(City Block distance)。正正方方的曼哈顿的地图：

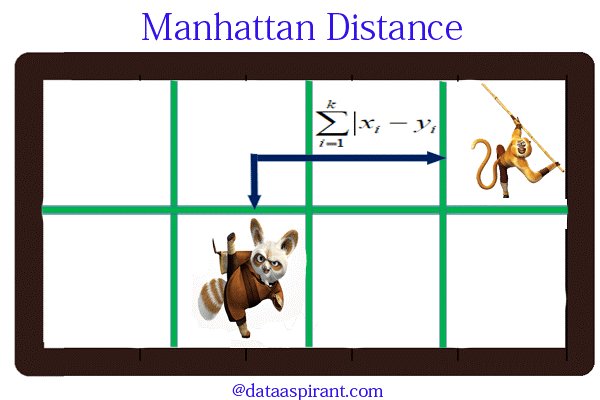
曼哈顿距离公式：

$$dist_{man}(x,y)=\sum_{i=1}^{n}{|x_i-y_i|}$$

曼哈顿距离的Python实现：

import numpy as np

def manhattan_distance(p_vec, q_vec):
    """
    This method implements the manhattan distance metric
    :param p_vec: vector one
    :param q_vec: vector two
    :return: the manhattan distance between vector one and two
    """
    return np.sum(np.fabs(p_vec - q_vec))

或

from math import *
 
def manhattan_distance(x,y):
    return sum(abs(a-b) for a,b in zip(x,y))

print(manhattan_distance([10,20,10],[10,20,20]))

汉明距离

汉明距离是以理查德·卫斯里·汉明的名字命名的，汉明在误差检测与校正码的基础性论文中首次引入这个概念这个所谓的距离，是指两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。

汉明距离有一个最为鲜明的特点就是它比较的两个字符串必须等长，否则距离不成立。它的核心原理就是如何通过字符替换（最初应用在通讯中实际上是二进制的0-1替换），能将一个字符串替换成另外一个字符串。维基百科给定了几个样例。(字符下标0为起始下标)

• “karolin” 和 “kathrin” 的汉明距离为(字符2 3 4替换)
• “karolin” 和 “kerstin” 的汉明距离为(字符1 3 4替换)
• 1011101 和 1001001 的汉明距离为(字符2 4替换)
• 2173896 和 2233796 的汉明距离为(字符1 2 4替换)

Python实现：

def hamming_distance(s1, s2):
    """Return the Hamming distance between equal-length sequences"""
    if len(s1) != len(s2):
        raise ValueError("Undefined for sequences of unequal length")
    return sum(el1 != el2 for el1, el2 in zip(s1, s2))

汉明距离主要应用在通信编码领域上，用于制定可纠错的编码体系。在机器学习领域中，汉明距离也常常被用于作为一种距离的度量方式。在LSH算法汉明距离也有重要的应用。

与汉明距离比较相近的是编辑距离。

切比雪夫距离

切比雪夫距离起源于国际象棋中国王的走法，国际象棋中国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格$(x_1, y_1)$走到B格$(x_2, y_2)$最少需要走几步？你会发现最少步数总是$max(| x_2-x_1 |,| y_2-y_1|) $步。有一种类似的一种距离度量方法叫切比雪夫距离。

若将国际象棋棋盘放在二维直角座标系中，格子的边长定义为1，座标的x轴及y轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置，和周围八个位置的切比雪夫距离都是1。

二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$间的切比雪夫距离：

$$d_{ab} = max(|x_1-x_2|, |y_1 – y_2|)$$

两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离：

$$d_{ab} = max(|x_{1i}-x_{2i}|)$$

可以看到当扩展到多维空间，其实切比雪夫距离就是当p趋向于无穷大时的闵可夫斯基距离：

$$dist(X,Y) = \lim_{p\rightarrow \infty }{(\sum_{i=1}^{n}{|x_i-y_i|^p})^{1/p}}=max(|x_i-y_i)$$

Python实现：

def chebyshev_distance(p, q):
    assert len(p) == len(q)
    return max([abs(x - y) for x, y in zip(p, q)])


def chebyshev_distance_procedural(p, q):
    assert len(p) == len(q)
    d = 0
    for x, y in zip(p, q):
        d = max(d, abs(x - y))
    return d

二维空间切比雪夫距离与曼哈顿距离的相互转化

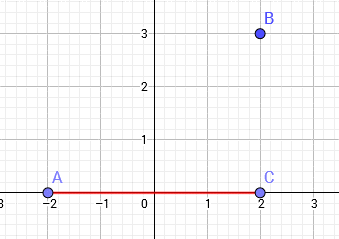
曼哈顿距离：设平面空间内存在两点，它们的坐标为$(x_1,y_1)$，$(x_2,y_2)$ 则$distance=|x_1−x_2|+|y_1−y_2|$ 。即两点横纵坐标差之和。如图所示，图中A,B两点的曼哈顿距离为AC+BC=4+3=7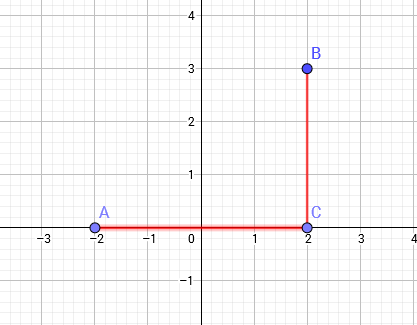

切比雪夫距离：设平面空间内存在两点，它们的坐标为$(x_1,y_1)$，$(x_2,y_2)$ 则$distance=max(|x_1−x_2|,|y_1−y_2|)$ 。即两点横纵坐标差的最大值 。distance=max(AC,BC)=AC=4。

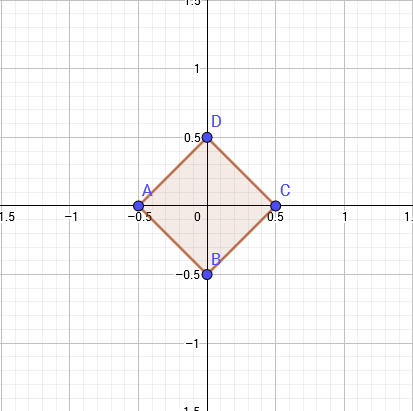
两者的定义看上去好像没有什么关系，但实际上，这两种距离可以相互转化。我们考虑最简单的情况，在一个二维坐标系中，设原点为(0,0)。如果用曼哈顿距离表示，则与原点距离为1的点会构成一个边长为1的正方形。

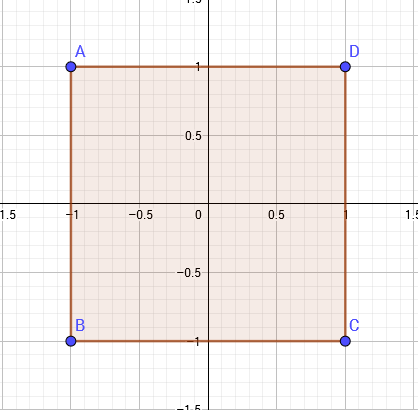
如果用切比雪夫距离表示，则与原点距离为1的点会构成一个边长为2的正方形。

仔细对比这两个图形，你会发现什么？第二个图像是由第一个图像放大后旋转45∘得到的。

将代表曼哈顿距离的正方形绕原点旋转45%，我们发现两个正方形现在是相似的。只要把代表曼哈顿距离的正方形扩大到原来的$\sqrt{2}$倍。

曼哈顿距离转化为切比雪夫距离：假设哈顿距离的正方形的四条边上的点A(x,y)，则旋转以后变为：

$$(x\cdot cos(45^\circ)-y\cdot sin(45^\circ),y\cdot cos(45^\circ)+x\cdot sin(45^\circ))=(x\cdot \frac{1}{\sqrt{2}}-y\cdot \frac{1}{\sqrt{2}},y\cdot \frac{1}{\sqrt{2}}+x\cdot \frac{1}{\sqrt{2}}) $$

在此基础上再扩大$\sqrt{2}$倍可得：${A}'(x-y,x+y) $

已知由曼哈顿距离转化为切比雪夫距离为：$A(x,y)\Rightarrow {A}'(x-y,x+y)$，则可以反推出切比雪夫距离转化为曼哈顿距离$$A(x,y)\Rightarrow {A}'(\frac{x-y}{2},\frac{x+y}{2})$$

马氏距离

马氏距离（Mahalanobis Distance）是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。有时也被称为马哈拉诺比斯距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。

一些基本概念：

• 方差：方差是标准差的平方，而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
• 协方差：标准差与方差是描述一维数据，当存在多维数据时，我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中，变量之间相关性的统计量。如果两个变量之间的协方差为正值，则这两个变量之间存在正相关，若为负值，则为负相关。

对于一个均值为$\mu =(\mu _{1},\mu _{2},\mu _{3},\dots ,\mu _{p})^{T}$，协方差矩阵为$\Sigma$的多变量向量$x=(x_{1},x_{2},x_{3},\dots ,x_{p})^{T}$，其马氏距离为：

$$D_{M}(x)={\sqrt {(x-\mu )^{T}\Sigma ^{-1}(x-\mu )}}$$

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为$\Sigma $的随机变量${\vec {x}}$与${\vec {y}}$的差异程度：

$$ d({\vec {x}},{\vec {y}})={\sqrt {({\vec {x}}-{\vec {y}})^{T}\Sigma ^{-1}({\vec {x}}-{\vec {y}})}}$$

如果协方差矩阵为单位矩阵，马氏距离就简化为欧氏距离；如果协方差矩阵为对角阵，其也可称为正规化的欧氏距离。

$$d({\vec {x}},{\vec {y}})={\sqrt {\sum _{i=1}^{p}{(x_{i}-y_{i})^{2} \over \sigma _{i}^{2}}}}$$

其中$ \sigma _{i}$是$x_{i}$的标准差。

Python实现：

import pandas as pd
import scipy as sp
from scipy.spatial.distance import mahalanobis

datadict = {
'country': ['Argentina', 'Bolivia', 'Brazil', 'Chile', 'Ecuador', 'Colombia', 'Paraguay', 'Peru', 'Venezuela'],
'd1': [0.34, -0.19, 0.37, 1.17, -0.31, -0.3, -0.48, -0.15, -0.61],
'd2': [-0.57, -0.69, -0.28, 0.68, -2.19, -0.83, -0.53, -1, -1.39],
'd3': [-0.02, -0.55, 0.07, 1.2, -0.14, -0.85, -0.9, -0.47, -1.02],
'd4': [-0.69, -0.18, 0.05, 1.43, -0.02, -0.7, -0.72, 0.23, -1.08],
'd5': [-0.83, -0.69, -0.39, 1.31, -0.7, -0.75, -1.04, -0.52, -1.22],
'd6': [-0.45, -0.77, 0.05, 1.37, -0.1, -0.67, -1.4, -0.35, -0.89]}

pairsdict = {
'country1': ['Argentina', 'Chile', 'Ecuador', 'Peru'],
'country2': ['Bolivia', 'Venezuela', 'Colombia', 'Peru']}

#DataFrame that contains the data for each country
df = pd.DataFrame(datadict)

#DataFrame that contains the pairs for which we calculate the Mahalanobis distance
pairs = pd.DataFrame(pairsdict)

#Add data to the country pairs
pairs = pairs.merge(df, how='left', left_on=['country1'], right_on=['country'])
pairs = pairs.merge(df, how='left', left_on=['country2'], right_on=['country'])

#Convert data columns to list in a single cell
pairs['vector1'] = pairs[['d1_x','d2_x','d3_x','d4_x','d5_x','d6_x']].values.tolist()
pairs['vector2'] = pairs[['d1_y','d2_y','d3_y','d4_y','d5_y','d6_y']].values.tolist()

mahala = pairs[['country1', 'country2', 'vector1', 'vector2']]

#Calculate covariance matrix
covmx = df.cov()
invcovmx = sp.linalg.inv(covmx)

#Calculate Mahalanobis distance
mahala['mahala_dist'] = mahala.apply(lambda x: (mahalanobis(x['vector1'], x['vector2'], invcovmx)), axis=1)

mahala = mahala[['country1', 'country2', 'mahala_dist']]

其他参考资料：

• http://kldavenport.com/mahalanobis-distance-and-outliers/
• https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.mahalanobis.html

根据马氏距离的定义，可以得到它的几个特点如下：

• 两点之间的马氏距离与原始数据的测量单位无关（不受量纲的影响）
• 标准化数据和中心化数据（即原始数据与均值之差）计算出的二点之间的马氏距离相同
• 可以排除变量之间的相关性的干扰
• 满足距离的四个基本公理：非负性、自反性、对称性和三角不等式
• 缺点是夸大了变化微小的变量的作用

考虑下面这张图，椭圆表示等高线，从欧几里得的距离来算，绿黑距离大于红黑距离，但是从马氏距离，结果恰好相反：

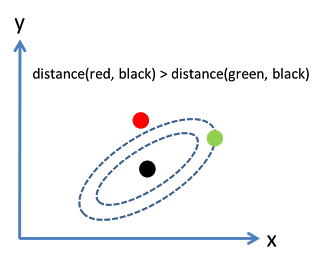
马氏距离实际上是利用 Cholesky transformation 来消除不同维度之间的相关性和尺度不同的性质。

下图是一个二元变量数据的散点图：

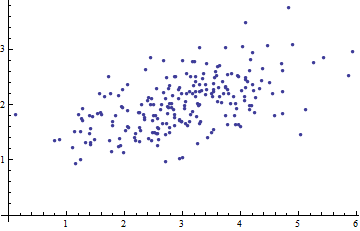
当我们将坐标轴拿掉，如下图：

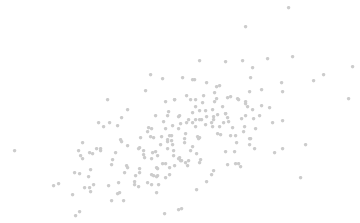
根据数据本身的提示信息来引入新的坐标轴：坐标的原点在这些点的中央（根据点的平均值算得）。第一个坐标轴（下图中蓝色的线）沿着数据点的“脊椎”，并向两端延伸，定义为使得数据方差最大的方向。第二个坐标轴（下图红色的线）会与第一个坐标轴垂直并向两端延伸。如果数据的维度超过了两维，那就选择使得数据方差是第二个最大的方向，以此类推。

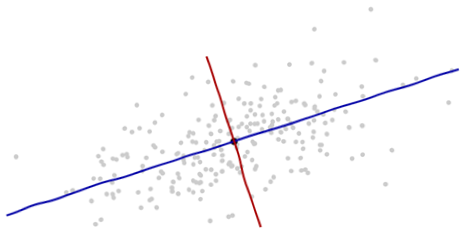
我们需要一个比例尺度。沿着每一个坐标轴的标准差来定义一个单位长度。使用“68-95-99.7法则”更容易找到合理的单位。（大约68%的点需要在离原点一个单位长度的范围内；大约95%的点需要在离原点两个单位的长度范围内；99.7的点需要在3个单位程度范围内。）为了以示参考，如下图：

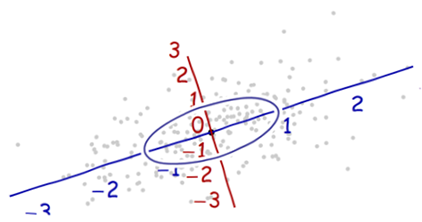
由于每个轴上的单位长度不相等，所以上图中距离原点一个单位的形成的轨迹并不是一个圆形。为了更好的呈现图表，我们将图片进行旋转。同时，并让每个轴方向上的单位长度相同：

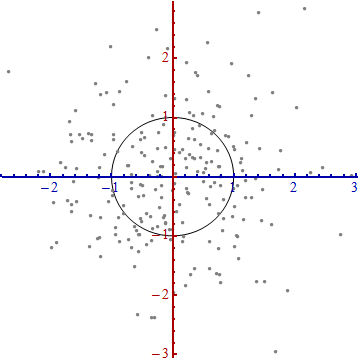
上面就是从散点图中构建坐标系统的过程，为的是方便进行测量。

说明：

• 沿着新坐标轴的单位向量是协方差矩阵的特征向量。注意到没有变形的椭圆，变成圆形后沿着特征向量用标准差（协方差的平方根）将距离长度分割。
• 坐标轴扩展的量是协方差矩阵的逆的特征值（平方根），同理的，坐标轴缩小的量是协方差矩阵的特征值。所以，点越分散，需要的将椭圆转成圆的缩小量就越多。
• 尽管上述的操作可以用到任何数据上，但是对于多元正态分布的数据表现更好。在其他情况下，点的平均值或许不能很好的表示数据的中心，或者数据的“脊椎”（数据的大致趋势方向）不能用变量作为概率分布测度来准确的确定。
• 原始坐标系的平移、旋转，以及坐标轴的伸缩一起形成了仿射变换（affine transformation）。除了最开始的平移之外，其余的变换都是基底变换，从原始的一个变为新的一个。
• 在新的坐标系中，多元正态分布像是标准正太分布，当将变量投影到任何一条穿过原点的坐标轴上。特别是，在每一个新的坐标轴上，它就是标准正态分布。从这点出发来看，多元正态分布彼此之实质性的差异就在于它们的维度。

参考链接：https://stats.stackexchange.com/questions/62092/bottom-to-top-explanation-of-the-mahalanobis-distance

兰氏距离

兰氏距离(Lance and Williams distance)堪培拉距离（Canberra Distance），被认为是曼哈顿距离的加权版本。

其定义公式为：

$$d(\mathbf {p} ,\mathbf {q} )=\sum _{i=1}^{n}{\frac {|p_{i}-q_{i}|}{|p_{i}|+|q_{i}|}}$$

通常兰氏距离对于接近于0（大于等于0）的值的变化非常敏感。与马氏距离一样，兰氏距离对数据的量纲不敏感。不过兰氏距离假定变量之间相互独立，没有考虑变量之间的相关性。

Python实现：

def canberra_distance(p, q):
    n = len(p)
    distance = 0
    for i in n:
        if p[i] == 0 and q[i] == 0:
            distance += 0
        else:
            distance += abs(p[i] - q[i]) / (abs(p[i]) + abs(q[i]))
    return distance

参考资料：

• https://en.wikipedia.org/wiki/Canberra_distance

闵可夫斯基距离

闵可夫斯基距离又称为闵氏距离（由于翻译问题，有时候也被称为明可夫斯基距离或明氏距离）。闵可夫斯基距离是欧氏空间中的一种测度，被看做是欧氏距离和曼哈顿距离的一种推广。闵氏距离不是一种距离，而是一组距离的定义。

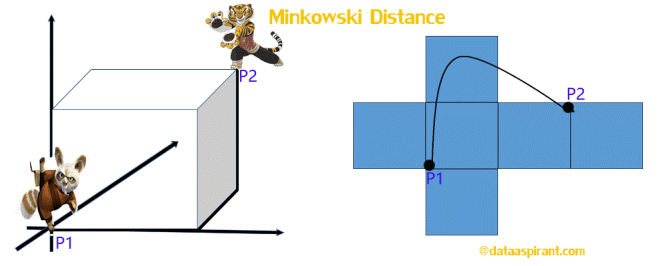
闵氏距离被看做是欧氏距离和曼哈顿距离的一种推广。公式中包含了欧氏距离、曼哈顿距离和切比雪夫距离。

闵可夫斯基距离的定义：

假设两点：

$$P=(x_{1},x_{2},\ldots ,x_{n}){\text{ and }}Q=(y_{1},y_{2},\ldots ,y_{n})\in \mathbb {R} ^{n}$$

明氏距离公式为：

$$\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{1/p}$$

p取1或2时的明氏距离是最为常用的，p=2即为欧氏距离，而p=1时则为曼哈顿距离。当p取无穷时的极限情况下，可以得到切比雪夫距离：

$$\lim _{p\to \infty }{\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac {1}{p}}}=\max _{i=1}^{n}|x_{i}-y_{i}|$$

我们知道平面上到原点欧几里得距离（p = 2）为 1 的点所组成的形状是一个圆，当 p 取其他数值的时候呢？

注意，当 p<1 时，闵可夫斯基距离不再符合三角形法则，举个例子：当 p<1, (0,0) 到 (1,1) 的距离等于 (1+1)^{1/p}>2, 而 (0,1) 到这两个点的距离都是 1。

闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行z-transform处理，即减去均值，除以标准差：

$$(x_1,y_1)x \mapsto x^2 (\frac{x_1-\mu _x}{\sigma _x},\frac{y_1-\mu _y}{\sigma _y})$$

其中 $\mu $为该维度上的均值，$\sigma$为该维度上的标准差。

可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。

闵氏距离的缺点主要有两个：

• 将各个分量的量纲(scale)，也就是“单位”当作相同看待了
• 没有考虑各个分量的分布（期望，方差等)可能是不同的

Python实现：

# Minkowski Distance implementation
#
# See: http://en.wikipedia.org/wiki/Minkowski_distance
#
# Returns the Minkowski distance between two vectors.
# 
# - p : first array
# - q : second array
# - n : distance order
#
# => returns: the distance between p and q.


def minkowski_distance(p, q, n):
    assert len(p) == len(q)
    return sum([abs(x - y) ^ n for x, y in zip(p, q)]) ^ 1 / n


def minkowski_distance_procedural(p, q, n):
    assert len(p) == len(q)
    s = 0
    for x, y in zip(p, q):
        s += abs(x - y) ^ n
    return s ^ (1 / n)

或：

from math import*
from decimal import Decimal
 
def nth_root(value, n_root):
    root_value = 1/float(n_root)
    return round (Decimal(value) ** Decimal(root_value),3)
 
def minkowski_distance(x,y,p_value):
    return nth_root(sum(pow(abs(a-b),p_value) for a,b in zip(x, y)),p_value)
 
print(minkowski_distance([0,3,4,5],[7,6,3,-1],3))

参考资料：

• https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.minkowski.html

“加权(weighted)”闵可夫斯基距离

当样本中不同属性的重要性不同时，可使用”加权距离”(weighted distance)

$$dist_{wmk}(x,y) = (\sum_{i=1}^{n}{W_i|x_i-y_i|^p})^{\frac{1}{p}}$$

$$\sum_{i=1}^{n}{w_i}=1$$

编辑距离

在做爬虫的时候，很容易保持一些相似的数据，这些相似的数据由于不完全一致，如果要通过人工一一的审核，将耗费大量的时间。编辑距离（Edit Distance），又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。一般来说，编辑距离越小，两个串的相似度越大。

例如将kitten一字转成sitting：（’kitten’ 和 ‘sitting’ 的编辑距离为3）

• sitten （k→s）
• sittin （e→i）
• sitting （→g）

Python中的Levenshtein包可以方便的计算编辑距离，包的安装：pip install python-Levenshtein

我们来使用下：

# -*- coding:utf-8 -*-
import Levenshtein
texta = '艾伦 图灵传'
textb = '艾伦•图灵传'
print Levenshtein.distance(texta,textb)

上面的程序执行结果为3，但是只改了一个字符，为什么会发生这样的情况？原因是Python将这两个字符串看成string类型，而在 string 类型中，默认的 utf-8 编码下，一个中文字符是用三个字节来表示的。解决办法是将字符串转换成unicode格式，即可返回正确的结果1。

# -*- coding:utf-8 -*-
import Levenshtein
texta = u'艾伦 图灵传'
textb = u'艾伦•图灵传'
print Levenshtein.distance(texta,textb)

接下来重点介绍下保重几个方法的作用：

Levenshtein.distance(str1, str2)

计算编辑距离（也称Levenshtein距离）。是描述由一个字串转化成另一个字串最少的操作次数，在其中的操作包括插入、删除、替换。算法实现：动态规划。

Levenshtein.hamming(str1, str2)

计算汉明距离。要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。

Levenshtein.ratio(str1, str2)

计算莱文斯坦比。计算公式  r = (sum – ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和，ldist是类编辑距离。注意这里是类编辑距离，在类编辑距离中删除、插入依然+1，但是替换+2。

Levenshtein.jaro(s1, s2)

计算jaro距离，Jaro Distance据说是用来判定健康记录上两个名字是否相同，也有说是是用于人口普查，我们先来看一下Jaro Distance的定义。

两个给定字符串S1和S2的Jaro Distance为：

$$d_{j}=\{\begin{array}{ll} 0 & \text { if } m=0 \\ \frac{1}{3}(\frac{m}{|s_{1}|}+\frac{m}{|s_{2}|}+\frac{m-t}{m}) & \text { otherwise } \end{array}$$

其中的m为s1, s2匹配的字符数，t是换位的数目。

两个分别来自S1和S2的字符如果相距不超过$\lfloor\frac{\max(|s_{1}|,|s_{2}|)}{2}\rfloor-1$

时，我们就认为这两个字符串是匹配的；而这些相互匹配的字符则决定了换位的数目t，简单来说就是不同顺序的匹配字符的数目的一半即为换位的数目t。举例来说，MARTHA与MARHTA的字符都是匹配的，但是这些匹配的字符中，T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符，t=2/2=1。

两个字符串的Jaro Distance即为：

$$d_{j}=\frac{1}{3}(\frac{6}{6}+\frac{6}{6}+\frac{6-1}{6})=0.944$$

Levenshtein.jaro_winkler(s1, s2)

计算Jaro–Winkler距离，而Jaro-Winkler则给予了起始部分就相同的字符串更高的分数，他定义了一个前缀p，给予两个字符串，如果前缀部分有长度为ι的部分相同，则Jaro-Winkler Distance为：

$$d_{w}=d_{j}+(\ell p(1-d_{j}))$$

• dj是两个字符串的Jaro Distance
• ι是前缀的相同的长度，但是规定最大为4
• p则是调整分数的常数，规定不能超过25，不然可能出现dw大于1的情况，Winkler将这个常数定义为0.1

这样，上面提及的MARTHA和MARHTA的Jaro-Winkler Distance为：

dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961

个人觉得算法可以完善的点：

• 去除停用词（主要是标点符号的影响）
• 针对中文进行分析，按照词比较是不是要比按照字比较效果更好？

其他参考资料：

• https://en.wikipedia.org/wiki/Jaro%E2%80%93Winkler_distance
• http://www.coli.uni-saarland.de/courses/LT1/2011/slides/Python-Levenshtein.html#Levenshtein-inverse

余弦相似度

余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

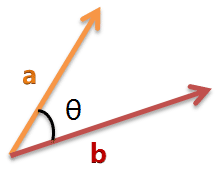
二维空间为例，上图的a和b是两个向量，我们要计算它们的夹角θ。余弦定理告诉我们，可以用下面的公式求得：

$$cos\theta = \frac{a^2+b^2-c^2}{2ab}$$

假定a向量是$[x_1, y_1]$，b向量是$[x_2, y_2]$，两个向量间的余弦值可以通过使用欧几里得点积公式求出：

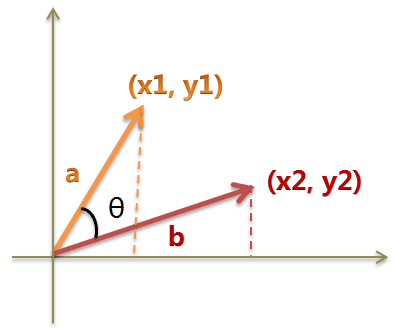向量a和向量b的夹角 的余弦计算如下：

$$\cos(\theta )={A\cdot B \over \|A\|\|B\|} = \frac{(x_1,y_1)\cdot (x_2,y_2)}{\sqrt{x_1^2+y_1^2}\times{\sqrt{x_2^2+y_2^2}}} = \frac{{x_1}{x_2}+{y_1}{y_2}}{\sqrt{x_1^2+y_1^2}\times{\sqrt{x_2^2+y_2^2}}}$$

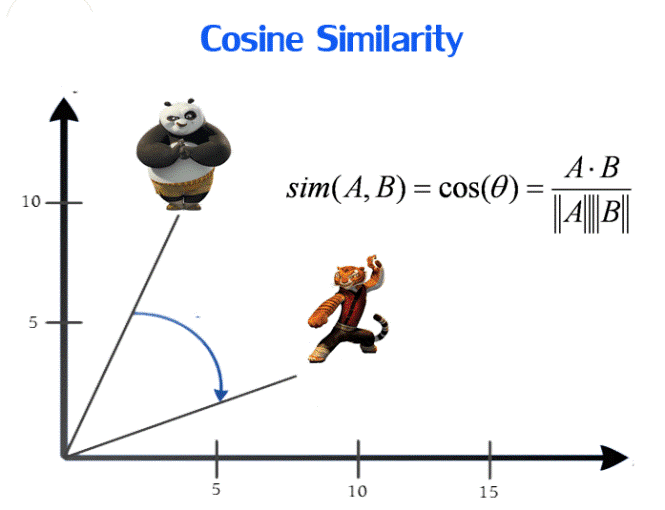
如果向量a和b不是二维而是n维，上述余弦的计算法仍然正确。假定A和B是两个n维向量，A是$ [A_1, A_2, …, A_n] $，B是$ [B_1, B_2, …, B_n]$ ，则A与B的夹角θ的余弦等于：

$$\cos(\theta )={A\cdot B \over \|A\|\|B\|}={\frac {\sum \limits _{i=1}^{n}{A_{i}\times B_{i}}}{{\sqrt {\sum \limits _{i=1}^{n}{(A_{i})^{2}}}}\times {\sqrt {\sum \limits _{i=1}^{n}{(B_{i})^{2}}}}}}$$

存在的问题：余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感。比如用户对内容评分，5分制。A和B两个用户对两个商品的评分分别为A：(1,2)和B：(4,5)。我们分别用两种方法计算相似度。使用余弦相似度得出的结果是0.98，看起来两者极为相似，但从评分上看X似乎不喜欢这两个东西，而Y比较喜欢。造成这个现象的原因就在于，余弦相似度没法衡量每个维数值的差异，对数值的不敏感导致了结果的误差。

Python实现：

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity


def cos_sim(a, b):
    """Takes 2 vectors a, b and returns the cosine similarity according
    to the definition of the dot product
    """
    dot_product = np.dot(a, b)
    norm_a = np.linalg.norm(a)
    norm_b = np.linalg.norm(b)
    return dot_product / (norm_a * norm_b)

# the counts we computed above
sentence_m = np.array([1, 1, 1, 1, 0, 0, 0, 0, 0])
sentence_h = np.array([0, 0, 1, 1, 1, 1, 0, 0, 0])
sentence_w = np.array([0, 0, 0, 1, 0, 0, 1, 1, 1])

# We should expect sentence_m and sentence_h to be more similar
print(cos_sim(sentence_m, sentence_h))  # 0.5
print(cos_sim(sentence_m, sentence_w))  # 0.25

# array.reshape(1, -1)
sentence_m = sentence_m.reshape(1, -1)
sentence_h = sentence_h.reshape(1, -1)
sentence_w = sentence_w.reshape(1, -1)

print(cosine_similarity(sentence_m, sentence_h))  # [[0.5]]
print(cosine_similarity(sentence_m, sentence_w))  #[[0.25]]

或：

from math import *
 
def square_rooted(x):
    return round(sqrt(sum([a*a for a in x])),3)
 
def cosine_similarity(x,y):
    numerator = sum(a*b for a,b in zip(x,y))
   denominator = square_rooted(x)*square_rooted(y)
   return round(numerator/float(denominator),3)
 
print(cosine_similarity([3, 45, 7, 2], [2, 54, 13, 15]))

修正余弦相似度

需要修正这种不合理性，就出现了调整余弦相似度，即所有维度上的数值都减去一个均值。

比如A和B对两部电影评分的均值分别是(1+4)/2=2.5,(2+5)/2=3.5。那么调整后为A和B的评分分别是：(-1.5,-1.5)和(1.5,2.5)，再用余弦相似度计算，得到-0.98，相似度为负值，显然更加符合现实。

修正的余弦相似度可以说就是对余弦相似度进行归一化处理的算法，公式如下：

$$s(i, j) = \frac {\sum_{u \in U}(R_{u,i} – R)(R_{u,j} – R)} {   \sqrt{\sum_{u \in U}(R_{u,i} – R_{u})^{2}}   \sqrt{\sum_{u \in U}(R_{u,j} – R_{u})^{2}} }$$

python实现：

import numpy as np
from scipy.spatial.distance import pdist, squareform

M = np.asarray([[2, 3, 4, 1, 0], 
                [0, 0, 0, 0, 5], 
                [5, 4, 3, 0, 0], 
                [1, 1, 1, 1, 1]])

M_u = M.mean(axis=1)
item_mean_subtracted = M - M_u[:, None]
similarity_matrix = 1 - squareform(pdist(item_mean_subtracted.T, 'cosine'))

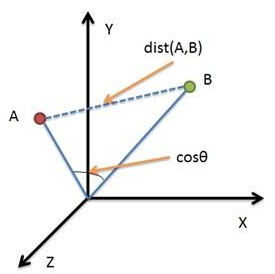
欧几里得距离和余弦相似度的区别

直观来说，欧几里得距离衡量空间点的直线距离，余弦距离衡量点在空间的方向差异。

参考链接：

• http://blog.christianperone.com/2013/09/machine-learning-cosine-similarity-for-vector-space-models-part-iii/

杰卡德相似度

Jaccard index, 又称为Jaccard相似系数（Jaccard similarity coefficient）用于比较有限样本集之间的相似性与差异性。Jaccard系数值越大，样本相似度越高。

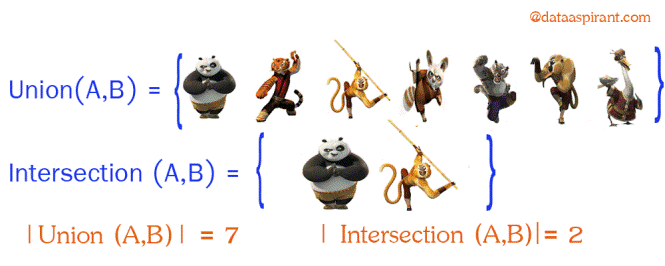
杰卡德相似系数

两个集合A和B交集元素的个数在A、B并集中所占的比例，称为这两个集合的杰卡德系数，用符号 J(A,B) 表示。杰卡德相似系数是衡量两个集合相似度的一种指标（余弦距离也可以用来衡量两个集合的相似度）。

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

Python实现：

def jaccard_sim(a, b):
    unions = len(set(a).union(set(b)))
    intersections = len(set(a).intersection(set(b)))
    return intersections / unions

a = ['x', 'y']
b = ['x', 'z', 'v']
print(jaccard_sim(a, b))

另外sklearn中也有相关实现，但是要求数据进行过encode处理，而且两个数组的长度也必须一样。

杰卡德距离

杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标，它是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数。

$$J_{\delta} =1-J(A,B)=\frac{|A\cup B|-|A\cap B|}{|A\cup B|}$$

杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

Python实现：

def jaccard_similarity(x,y):
    intersection_cardinality = len(set.intersection(*[set(x), set(y)]))
    union_cardinality = len(set.union(*[set(x), set(y)]))
    return intersection_cardinality/float(union_cardinality)
 
print(jaccard_similarity([0,1,2,5,6],[0,2,3,5,7,9]))

杰卡德系数扩展：Tanimoto系数

Tanimoto系数由Jaccard系数扩展而来，又称为广义Jaccard相似系数，计算方式如下：

$$E_j(A,B)=\frac{A\cdot B}{||A||^2+||B||^2-A\cdot B}$$

其中A、B分别表示为两个向量，集合中每个元素表示为向量中的一个维度，在每个维度上，取值通常是[0, 1]之间的值（如果取值是二值向量0或1，那么Tanimoto系数就等同Jaccard距离），$A\cdot B$表示向量乘积，$||A||^2$表示向量的模，即 $||A||^2 = \sqrt{\sum_{i=1}^{n}{A_i^2}}$

Tanimoto系数容易与余弦相似度混淆在Tanimoto系数计算公式中，如果把分母的$A\cdot B$去掉，并将$||A||^2+||B||^2$替换为$（||A||^2）*（||B||^2）$，就转成了余弦相似度（cosine similarity）。

$$similarity=cos(\theta )=\frac{A\cdot B}{||A||^2\times ||B||^2}=\frac{\sum_{i=1}^{n}{A_i\times B_i}}{\sqrt{\sum_{i=1}^{n}{(A_i)^2}}\times \sqrt{\sum_{i=1}^{n}{(B_i)^2}}}$$

Tanimoto系数Python实现：

import numpy as np
def tanimoto_coefficient(p_vec, q_vec):
    """
    This method implements the cosine tanimoto coefficient metric
    :param p_vec: vector one
    :param q_vec: vector two
    :return: the tanimoto coefficient between vector one and two
    """
    pq = np.dot(p_vec, q_vec)
    p_square = np.linalg.norm(p_vec)
    q_square = np.linalg.norm(q_vec)
    return pq / (p_square + q_square - pq)

参考资料：

• https://en.wikipedia.org/wiki/Jaccard_index
• http://dataaspirant.com/2015/04/11/five-most-popular-similarity-measures-implementation-in-python/

Dice系数

Dice距离用于度量两个集合的相似性，因为可以把字符串理解为一种集合，因此Dice距离也会用于度量字符串的相似性。此外，Dice系数的一个非常著名的使用即实验性能评测的F1值。Dice系数定义如下：

$$s = \frac{2|A\cap B|}{|A|+|B|}$$

其中分子是A与B的交集数量的两倍，分母为X和Y的长度之和，所以他的范围也在0到1之间。从公式看，Dice系数和Jaccard非常的类似。Jaccard是在分子和分母上都减去了|A∩B|。

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}=\frac{|A\cap B|}{|A|+|B|-|A\cap B|}$$

与Jaccard不同的是，相应的差异函数

$d=1-{\frac {2|X\cap Y|}{|X|+|Y|}}$

不是一个合适的距离度量措施，因为它没有三角形不等性的性质。例如给定 {a}, {b}, 和 {a,b}, 前两个集合的距离为1， 而第三个集合和其他任意两个集合的距离为三分之一。

与Jaccard类似, 集合操作可以用两个向量A和B的操作来表示:

$$s_{v}={\frac {2|A\cdot B|}{|A|^{2}+|B|^{2}}}$$

Python实现：

def dice_coefficient(a, b):
    """dice coefficient 2nt/na + nb."""
    a_bigrams = set(a)
    b_bigrams = set(b)
    overlap = len(a_bigrams & b_bigrams)
    return overlap * 2.0/(len(a_bigrams) + len(b_bigrams))

其他参考：

• https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.dice.html