层次聚类简介
层次聚类算法(Hierarchical Clustering)将数据集划分为一层一层的 clusters,后面一层生成的 clusters 基于前面一层的结果。层次聚类算法一般分为两类:
- Divisive 层次聚类:又称自顶向下(top-down)的层次聚类,最开始所有的对象均属于一个 cluster,每次按一定的准则将某个 cluster 划分为多个 cluster,如此往复,直至每个对象均是一个 cluster。
- Agglomerative 层次聚类:又称自底向上(bottom-up)的层次聚类,每一个对象最开始都是一个 cluster,每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster,如此往复,直至最终所有的对象都属于一个 cluster。
下图直观的给出了层次聚类的思想以及以上两种聚类策略的异同:
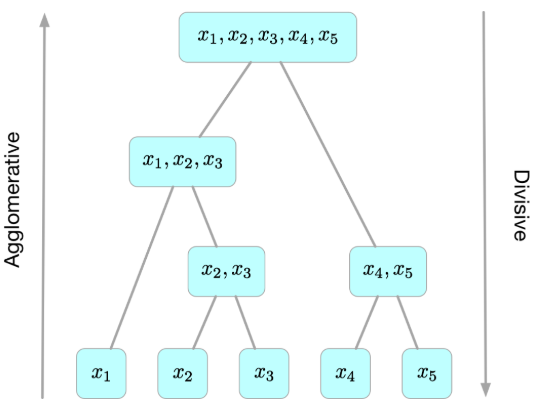
层次聚类算法是一种贪心算法(greedy algorithm),因其每一次合并或划分都是基于某种局部最优的选择。
自顶向下的层次聚类算法(Divisive)
Hierarchical K-means 算法
Hierarchical K-means 算法是“自顶向下”的层次聚类算法,用到了基于划分的聚类算法那 K-means,算法思路如下:
- 首先,把原始数据集放到一个簇 C,这个簇形成了层次结构的最顶层
- 使用 K-means 算法把簇 C 划分成指定的 K 个子簇$C_i,i=1,2,…,k$,形成一个新的层
- 对于步骤 2 所生成的 K 个簇,递归使用 K-means 算法划分成更小的子簇,直到每个簇不能再划分(只包含一个数据对象)或者满足设定的终止条件。
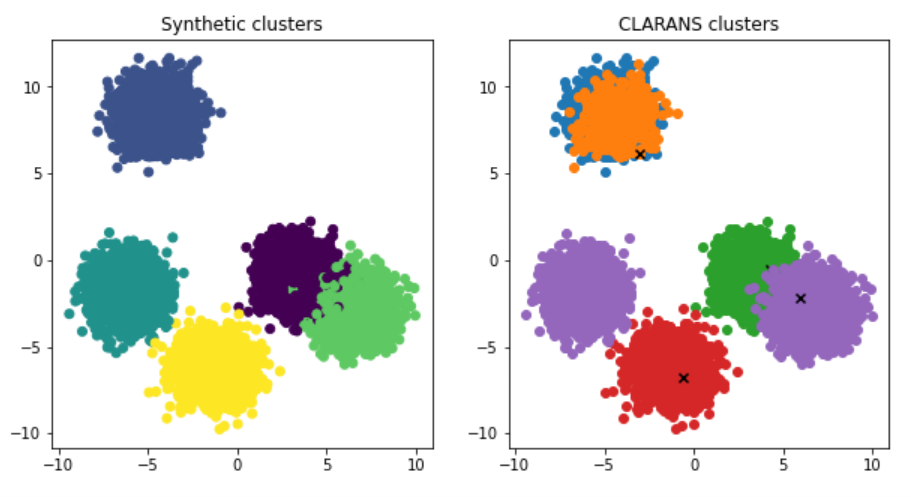
如下图,展示了一组数据进行了二次 K-means 算法的过程:
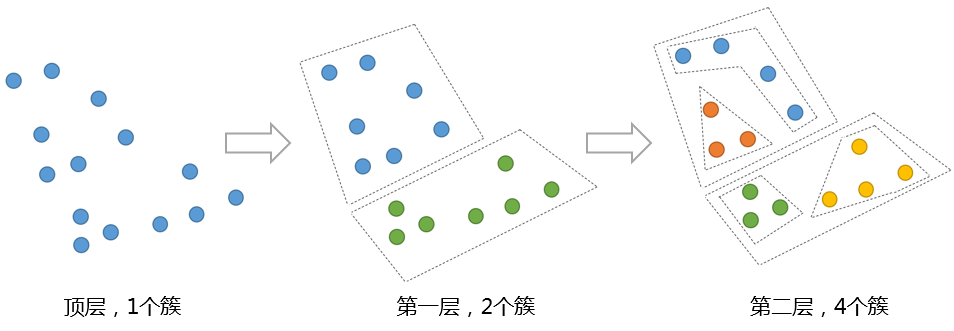
Hierarchical K-means 算法一个很大的问题是,一旦两个点在最开始被划分到了不同的簇,即使这两个点距离很近,在后面的过程中也不会被聚类到一起。
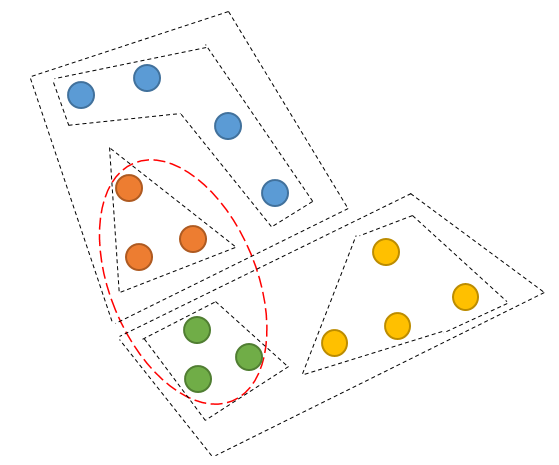
对于以上的例子,红色椭圆框中的对象聚类成一个簇可能是更优的聚类结果,但是由于橙色对象和绿色对象在第一次 K-means 就被划分到不同的簇,之后也不再可能被聚类到同一个簇。
Bisecting k-means 聚类算法,即二分 k 均值算法,是分层聚类(Hierarchical clustering)的一种。更多关于二分 k 均值法,可以查看聚类算法之 K-Means。
自底向上的层次聚类算法(Agglomerative)
层次聚类的合并算法通过计算两类数据点间的相似性,对所有数据点中最为相似的两个数据点进行组合,并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或类别进行组合,生成聚类树。
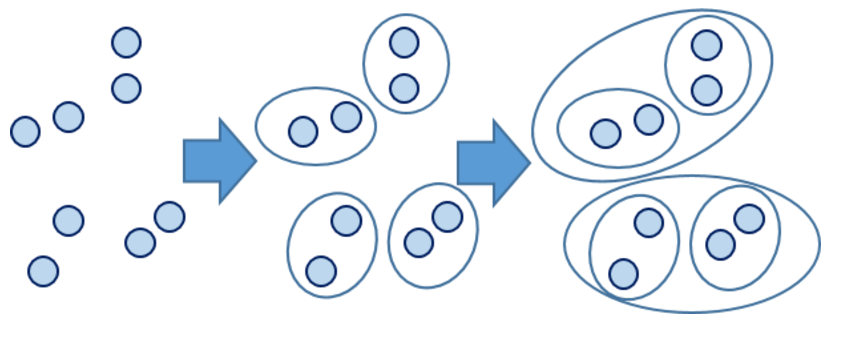
相比于 Hierarchical K-means 算法存在的问题,Agglomerative Clustering 算法能够保证距离近的对象能够被聚类到一个簇中,该算法采用的“自底向上”聚类的思路。
Agglomerative 算法示例
对于如下数据:
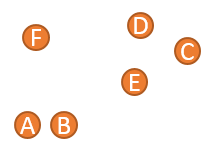
1、将 A 到 F 六个点,分别生成 6 个簇
2、找到当前簇中距离最短的两个点,这里我们使用单连锁的方式来计算距离,发现 A 点和 B 点距离最短,将 A 和 B 组成一个新的簇,此时簇列表中包含五个簇,分别是{A,B},{C},{D},{E},{F},如下图所示:
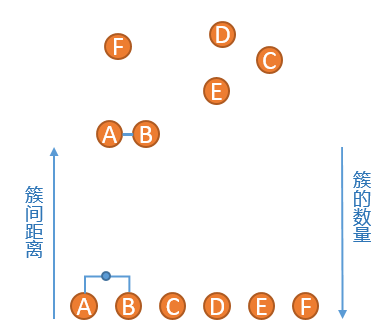
3、重复步骤 2、发现{C}和{D}的距离最短,连接之,然后是簇{C,D}和簇{E}距离最短,依次类推,直到最后只剩下一个簇,得到如下所示的示意图:
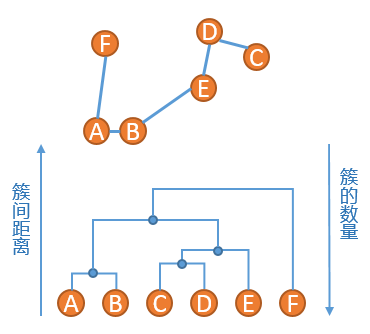
4、此时原始数据的聚类关系是按照层次来组织的,选取一个簇间距离的阈值,可以得到一个聚类结果,比如在如下红色虚线的阈值下,数据被划分为两个簇:簇{A,B,C,D,E}和簇{F}
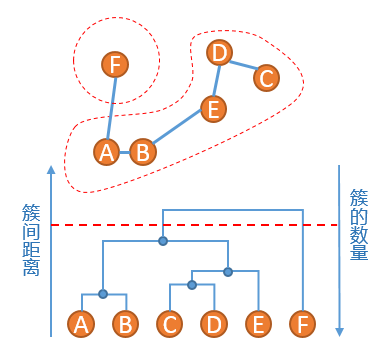
Agglomerative 聚类算法的优点是能够根据需要在不同的尺度上展示对应的聚类结果,缺点同 Hierarchical K-means 算法一样,一旦两个距离相近的点被划分到不同的簇,之后也不再可能被聚类到同一个簇,即无法撤销先前步骤的工作。另外,Agglomerative 性能较低,并且因为聚类层次信息需要存储在内存中,内存消耗大,不适用于大量级的数据聚类。
对象之间的距离衡量
衡量两个对象之间的距离的方式有多种,对于数值类型(Numerical)的数据,常用的距离衡量准则有 Euclidean 距离、Manhattan 距离、Chebyshev 距离、Minkowski 距离等等。
Cluster 之间的距离衡量
除了需要衡量对象之间的距离之外,层次聚类算法还需要衡量 cluster 之间的距离,常见的 cluster 之间的衡量方法有 Single-link 方法、Complete-link 方法、UPGMA(Unweighted Pair Group Method using arithmetic Averages)方法、WPGMA(Weighted Pair Group Method using arithmetic Averages)方法、Centroid 方法(又称 UPGMC,Unweighted Pair Group Method using Centroids)、Median 方法(又称 WPGMC,weighted Pair Group Method using Centroids)、Ward 方法。前面四种方法是基于图的,因为在这些方法里面,cluster 是由样本点或一些子 cluster(这些样本点或子 cluster 之间的距离关系被记录下来,可认为是图的连通边)所表示的;后三种方法是基于几何方法的(因而其对象间的距离计算方式一般选用 Euclidean 距离),因为它们都是用一个中心点来代表一个 cluster。
假设$C_i$和$C_j$为两个 cluster,则前四种方法定义的$C_i$和$C_j$之间的距离如下表所示:
| 方法 | 定义 |
| Single-link | $D(C_i,C_j)=\min_{x\in C_i,y\in C_j}d(x,y)$ |
| Complete-link | $D(C_i,C_j)=\max_{x\in C_i,y\in C_j}d(x,y)$ |
| UPGMA | $D(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i, y\in C_j} d(x,y)$ |
| WPGMA | 省略 |
简单的理解:
- SingleLinkage:方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
- CompleteLinkage:CompleteLinkage的计算方法与SingleLinkage相反,将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。CompleteLinkage的问题也与SingleLinkage相反,两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
- AverageLinkage:AverageLinkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两种方法更合理。
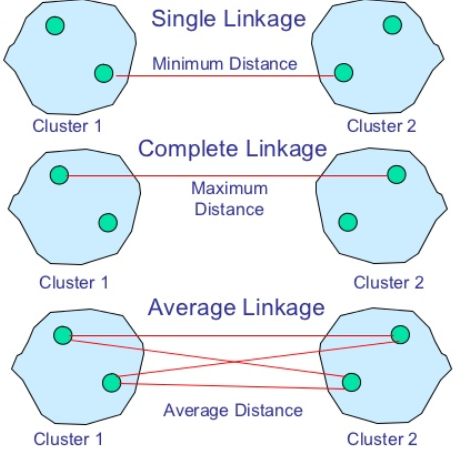
其中Single-link定义两个cluster之间的距离为两个cluster之间距离最近的两个对象间的距离,这样在聚类的过程中就可能出现链式效应,即有可能聚出长条形状的cluster;而Complete-link则定义两个cluster之间的距离为两个cluster之间距离最远的两个对象间的距离,这样虽然避免了链式效应,但其对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类;UPGMA正好是Single-link和Complete-link的一个折中,其定义两个cluster之间的距离为两个cluster之间两个对象间的距离的平均值;而WPGMA则计算的是两个cluster之间两个对象之间的距离的加权平均值,加权的目的是为了使两个cluster对距离的计算的影响在同一层次上,而不受cluster大小的影响(其计算方法这里没有给出,因为在运行层次聚类算法时,我们并不会直接通过样本点之间的距离之间计算两个cluster之间的距离,而是通过已有的cluster之间的距离来计算合并后的新的cluster和剩余cluster之间的距离,这种计算方法将由下一部分中的Lance-Williams方法给出)。
Centroid/UPGMC方法给每一个cluster计算一个质心,两个cluster之间的距离即为对应的两个质心之间的距离,一般计算方法如下:
$$D_{UPGMC}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum_{x\in C_i,y\in C_j}d(x,y)-\frac{1}{2{|C_i|}^2}\sum_{x,y\in C_i} d(x,y)-\frac{1}{2{|{C_j}|}^2}\sum_{x,y\in C_j}d(x,y)$$
当上式中的d(x,y)为平方Euclidean距离时,$D_{UPGMC}(C_i,C_j)$为$C_i$和$C_j$的中心点(每个cluster内所有样本点之间的平均值)之间的平方Euclidean距离。
Median/WPGMC方法为每个cluster计算质心时,引入了权重。
Ward方法提出的动机是最小化每次合并时的信息损失,具体地,其对每一个cluster定义了一个ESS(Error Sum of Squares)量作为衡量信息损失的准则,cluster C的ESS定义如下:
${ESS}(C)=\sum_{x\in C}(x-m_x)^{T}(x-m_x)$
其中$m_x$为C中样本点的均值。可以看到ESS衡量的是一个cluster内的样本点的聚合程度,样本点越聚合,ESS的值越小。Ward方法则是希望找到一种合并方式,使得合并后产生的新的一系列的cluster的ESS之和相对于合并前的cluster的ESS之和的增长最小。
常用Agglomerative算法
Lance-Williams方法
在Agglomerative层次聚类算法中,一个迭代过程通常包含将两个cluster合并为一个新的cluster,然后再计算这个新的cluster与其他当前未被合并的cluster之间的距离,而Lance-Williams方法提供了一个通项公式,使得其对不同的cluster距离衡量方法都适用。具体地,对于三个cluster$C_k$,$C_i$和$C_j$,Lance-Williams给出的$C_k$与$C_i$和$C_j$合并后的新cluster之间的距离的计算方法如下式所示:
$$D(C_k,C_i\cup C_j)=\alpha_iD(C_k,C_i)+\alpha_jD(C_k,C_j)+\beta D(C_i,C_j)+ \gamma|D(C_k,C_i)-D(C_k,C_j)|$$
其中,$\alpha_i,\alpha_j,\beta,\gamma$均为参数,随cluster之间的距离计算方法的不同而不同,具体总结为下表(注:$n_i$为cluster$C_i$中的样本点的个数):
| 方法 | 参数$\alpha_i$ | 参数$\alpha_j$ | 参数$\beta$ | 参数$\gamma$ |
| Single-link | 1/2 | 1/2 | 0 | -1/2 |
| Complete-link | 1/2 | 1/2 | 0 | 1/2 |
| UPGMA | $n_i/(n_i+n_j)$ | $n_j/(n_i+n_j)$ | 0 | 0 |
| WPGMA | 1/2 | 1/2 | 0 | 0 |
| UPGMC | $n_i/(n_i+n_j)$ | $n_j/(n_i+n_j)$ | $n_{i}n_{j}/(n_i+n_j)^2$ | 0 |
| WPGMC | 1/2 | 1/2 | 1/4 | 0 |
| Ward | $(n_k+n_i)/(n_i+n_j+n_k)$ | $(n_k+n_j)/(n_i+n_j+n_k)$ | $n_k/(n_i+n_j+n_k)$ | 0 |
其中Ward方法的参数仅适用于当样本点之间的距离衡量准则为平方Euclidean距离时,其他方法的参数适用范围则没有限制。
Naive算法
给定数据集$X=(x_1,x_2,…,x_n)$,Agglomerative层次聚类最简单的实现方法分为以下几步:
- 初始时每个样本为一个 cluster,计算距离矩阵 D,其中元素 $D_{ij}$ 为样本点 $x_i$ 和 $x_j$ 之间的距离
- 遍历距离矩阵 D,找出其中的最小距离(对角线上的除外),并由此得到拥有最小距离的两个 cluster 的编号,将这两个 cluster 合并为一个新的 cluster 并依据 Lance-Williams 方法更新距离矩阵 D(删除这两个 cluster 对应的行和列,并把由新 cluster 所算出来的距离向量插入 D 中),存储本次合并的相关信息
- 重复 2 的过程,直至最终只剩下一个 cluster。
当然,其中的一些细节这里都没有给出,比如,我们需要设计一些合适的数据结构来存储层次聚类的过程,以便于我们可以根据距离阈值或期待的聚类个数得到对应的聚类结果。可以看到,该 Naive 算法的时间复杂度为 $O(n^3)$(由于每次合并两个 cluster 时都要遍历大小为 $O(n^2)$ 的距离矩阵来搜索最小距离,而这样的操作需要进行 n-1 次),空间复杂度为 $O(n^2)$(由于要存储距离矩阵)。
当然,还有一些更高效的算法,它们用到了特殊设计的数据结构或者一些图论算法,是的时间复杂度降低到 $(n^2)$ 更低,例如 SLINK 算法(Single-link 方法),CLINK 算法(Complete-link 方法),BIRCH 算法(适用于 Euclidean 距离准则)等等。
利用 Scipy 实现层次聚类
1、生成测试数据
from sklearn.datasets import make_blobs import matplotlib.pyplot as plt centers = [[1, 1], [-1, -1], [1, -1]] X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0) plt.figure(figsize=(10, 8)) plt.scatter(X[:, 0], X[:, 1], c='b') plt.show()
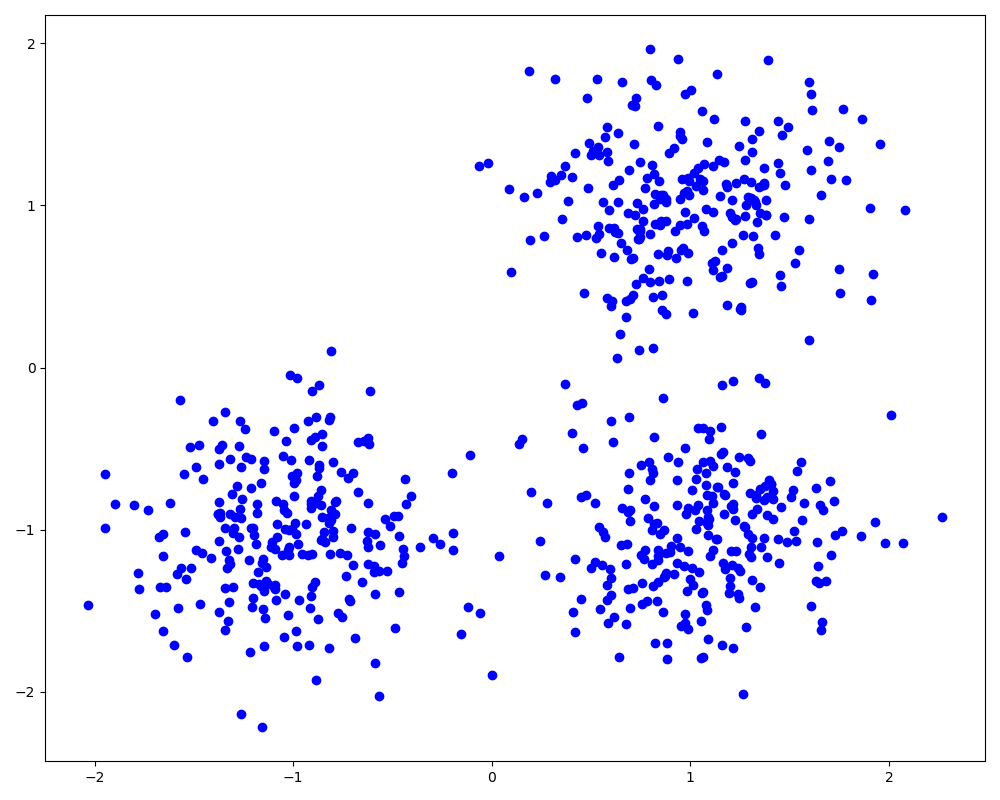
SciPy 里面进行层次聚类非常简单,直接调用 linkage 函数,一行代码即可搞定:
from scipy.cluster.hierarchy import linkage Z = linkage(X, method='ward', metric='euclidean') print(Z.shape) print(Z[:5])
以上即进行了一次 cluster 间距离衡量方法为 Ward、样本间距离衡量准则为 Euclidean 距离的 Agglomerative 层次聚类,其中 method 参数可以为 ‘single’、’complete’、’average’、’weighted’、’centroid’、’median’、’ward’ 中的一种,分别对应我们前面讲到的 Single-link、Complete-link、UPGMA、WPGMA、UPGMC、WPGMC、Ward 方法,而样本间的距离衡量准则也可以由 metric 参数调整。
linkage 函数的返回值 Z 为一个维度 (n-1)*4 的矩阵,记录的是层次聚类每一次的合并信息,里面的 4 个值分别对应合并的两个 cluster 的序号、两个 cluster 之间的距离以及本次合并后产生的新的 cluster 所包含的样本点的个数。
3、画出树形图
SciPy 中给出了根据层次聚类的结果 Z 绘制树形图的函数 dendrogram,我们由此画出本次实验中的最后 20 次的合并过程。
from scipy.cluster.hierarchy import dendrogram plt.figure(figsize=(10, 8)) dendrogram(Z, truncate_mode='lastp', p=20, show_leaf_counts=False, leaf_rotation=90, leaf_font_size=15, show_contracted=True) plt.show()
得到的树形图如下所示:
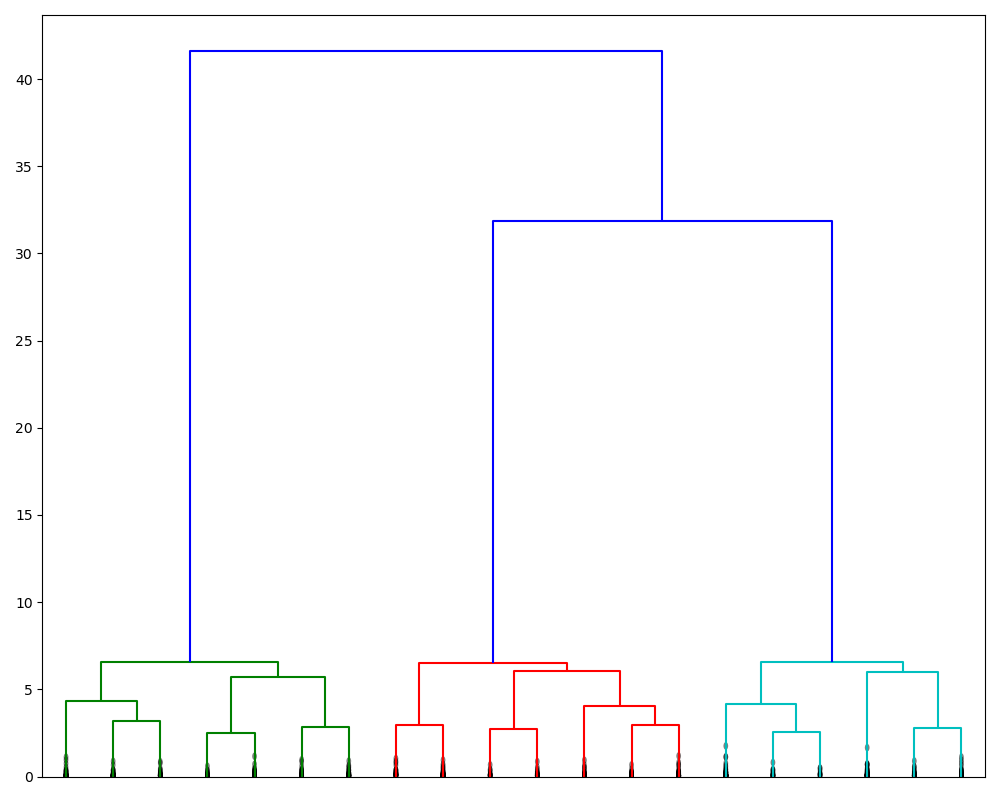
可以看到,该树形图的最后两次合并相比之前合并过程的合并距离要大得多,由此可以说明最后两次合并是不合理的;因而对于本数据集,该算法可以很好地区分出 3 个 cluster(和实际相符),分别在上图中由三种颜色所表示。
4、获取聚类结果
在得到了层次聚类的过程信息 Z 后,我们可以使用 fcluster 函数来获取聚类结果。可以从两个维度来得到距离的结果,一个是指定临界距离 d,得到在该距离以下的未合并的所有 cluster 作为聚类结果;另一个是指定 cluster 的数量 k,函数会返回最后的 k 个 cluster 作为聚类结果。使用哪个维度由参数 criterion 决定,对应的临界距离或聚类的数量则由参数 t 所记录。fcluster 函数的结果为一个一维数组,记录每个样本的类别信息。
from scipy.cluster.hierarchy import fcluster # 根据临界距离返回聚类结果 d = 15 labels_1 = fcluster(Z, t=d, criterion='distance') print(labels_1[:100]) # 打印聚类结果 print(len(set(labels_1))) # 看看在该临界距离下有几个 cluster # 根据聚类数目返回聚类结果 k = 3 labels_2 = fcluster(Z, t=k, criterion='maxclust') print(labels_2[:100]) list(labels_1) == list(labels_2) # 看看两种不同维度下得到的聚类结果是否一致 # 聚类的结果可视化,相同的类的样本点用同一种颜色表示 plt.figure(figsize=(10, 8)) plt.scatter(X[:, 0], X[:, 1], c=labels_2, cmap='prism') plt.show()
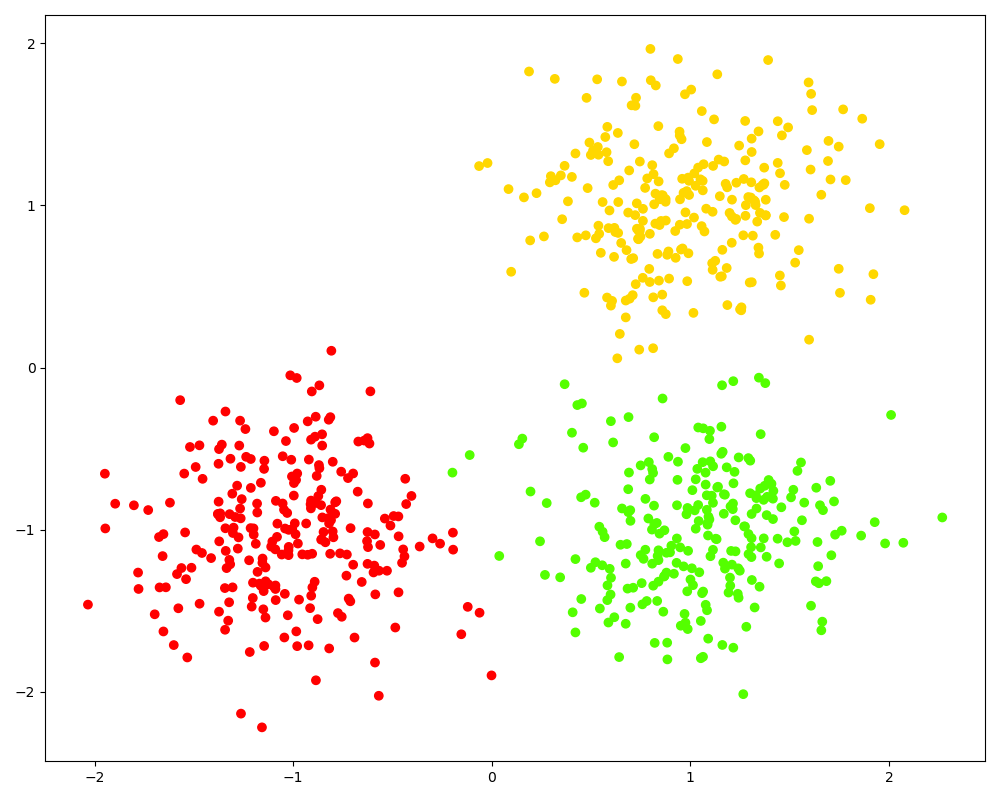
上图的聚类结果和实际的数据分布基本一致,但有几点值得注意,一是在聚类之前我们没法知道合理的聚类的数目或者最大的距离临界值,只有在得到全部的层次聚类信息并对其进行分析后我们才能预估出一个较为合理的数值;二是本次实验的数据集比较简单,所以聚类的结果较好,但对于复杂的数据集(比如非凸的、噪声点比较多的数据集),层次聚类算法有其局限性。
5、比较不同方法下的聚类结果
最后,我们对同一份样本集进行了 cluster 间距离衡量准则分别为 Single-link、Complete-link、UPGMA(Average)和 Ward 的 Agglomerative 层次聚类,取聚类数目为 3,代码如下:
from time import time
import numpy as np
from sklearn.datasets import make_blobs
from scipy.cluster.hierarchy import linkage, fcluster
from sklearn.metrics.cluster import adjusted_mutual_info_score
import matplotlib.pyplot as plt
# 生成样本点
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels = make_blobs(n_samples=750, centers=centers,
cluster_std=0.4, random_state=0)
# 可视化聚类结果
def plot_clustering(X, labels, title=None):
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='prism')
if title is not None:
plt.title(title, size=17)
plt.axis('off')
plt.tight_layout()
# 进行Agglomerative层次聚类
linkage_method_list = ['single', 'complete', 'average', 'ward']
plt.figure(figsize=(10, 8))
ncols, nrows = 2, int(np.ceil(len(linkage_method_list)/2))
plt.subplots(nrows=nrows, ncols=ncols)
for i, linkage_method in enumerate(linkage_method_list):
print('method %s:' % linkage_method)
start_time = time()
Z = linkage(X, method=linkage_method)
labels_pred = fcluster(Z, t=3, criterion='maxclust')
print('Adjust mutual information: %.3f' % adjusted_mutual_info_score(labels, labels_pred))
print('time used: %.3f seconds' % (time() - start_time))
plt.subplot(nrows, ncols, i+1)
plot_clustering(X, labels_pred, '%s linkage' % linkage_method)
plt.show()
可以得到4种方法下的聚类结果如图所示:

在上面的过程中,我们还为每一种聚类产生的结果计算了一个用于评估聚类结果与样本的真实类之间的相近程度的AMI(Adjust Mutual Information)量,该量越接近于1则说明聚类算法产生的类越接近于真实情况。程序的打印结果如下:
method single: Adjust mutual information: 0.002 time used: 0.010 seconds method complete: Adjust mutual information: 0.840 time used: 0.021 seconds method average: Adjust mutual information: 0.945 time used: 0.027 seconds method ward: Adjust mutual information: 0.956 time used: 0.021 seconds
从上面的图和AMI量的表现来看,Single-link方法下的层次聚类结果最差,它几乎将所有的点都聚为一个cluster,而其他两个cluster则都仅包含个别稍微有点偏离中心的样本点,这充分体现了Single-link方法下的”链式效应”,也体现了Agglomerative算法的一个特点,即”赢者通吃”(rich getting richer):Agglomerative算法倾向于聚出不均匀的类,尺寸大的类倾向于变得更大,对于Single-link和UPGMA(Average)方法尤其如此。由于本次实验的样本集较为理想,因此除了Single-link之外的其他方法都表现地还可以,但当样本集变复杂时,上述”赢者通吃”的特点会显现出来。
利用Sklearn实现层次聚类
除了Scipy外,scikit-learn也提供了层次聚类的方法sklearn.cluster.AgglomerativeClustering,使用示例:
from sklearn.datasets import make_blobs from sklearn.cluster import AgglomerativeClustering import matplotlib.pyplot as plt # 生成样本点 centers = [[1, 1], [-1, -1], [1, -1]] X, labels = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0) clustering = AgglomerativeClustering(n_clusters=3, linkage='ward').fit(X) plt.figure(figsize=(10, 8)) plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_, cmap='prism') plt.show()
参考链接: