Chameleon简介
Chameleon(变色龙)算法是一种两阶段层次聚类算法。在进行两个类簇合并时使用更高的标准,同时考虑了类簇之间的互连性(连接两个子簇的边的权重之和)和近似性(连接两个子簇的边的平均权重),具有发现任意形状和大小的簇的能力。算法的过程可分为两个阶段,第一阶段有数据集构造一个 K 近邻图 $G_k$,再通过一个图划分算法将 $G_k$ 划分成大量的子图,每个子图代表一个初始子簇,第二阶段通过一个凝聚的层次聚类算法反复的合并子簇来找到真正的聚类结果。具体过程如下:

Chameleon算法原理
Chamelon 是一种层次聚类算法,它采用动态建模来确定一对簇之间的相似度,从而实现聚类。那么,何为动态建模呢?要回答这个问题,我们首先要搞清楚簇的相似度依据是什么。在 Chamelon 中,簇的相似度依据如下两点评估:
- 簇中对象的连接情况
- 簇的邻近性
也就是说,如果两个簇的互连性都很高并且他们之间又靠的很近,那么就将其合并。因此,凭借这两点,我们就可以不用依赖一个静态的、用户提供的模型,而是可以自动的、适应的的去合并簇,从而实现聚类。
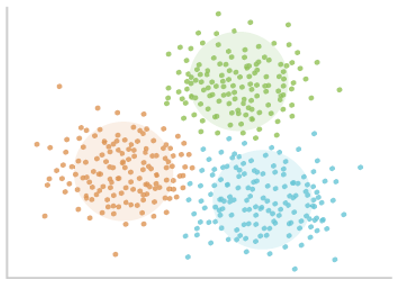
在 K-means 这种算法里面,我们是给定了簇的一个中心点的,然后再实现聚类和调优的。因此这种聚类方法就等同于我们是给定了一个“球形“(或者“类球形”),然后再去补充,修正它。这就是我们说的依赖一个静态的,用户提供的模型。而 Chamelon 呢,它是动态的考察自身和其他簇,然后动态的适应,合并簇。因此,他没有什么固定的模型,所以,基于这个特性,它可以发现任意形状的,高质量的簇。这也是这个算法一个巨大优势。
Chamelon 算法是一种多阶段层次聚类算法,同之前我们讲过的 BIRCH 算法一样,它也是分为 2 个主要阶段的。下面我们来具体看一看这个算法的原理。
- Chameleon 采用 K-最近邻图的方法来构建一个稀疏图(其中,图的每一个顶点代表一个数据对象,如果一个对象是另一个对象的 k 个最相似的对象之一,那么这两个顶点(对象)之间就存在一条边(这些边加权后反映对象间的相似度));
- Chameleon 使用一种图划分算法,把 k-个最近邻图划分成大量相对较小的子簇,使得边割最小(划分代价,说白了就是被切断的边上的权重之和最小)。
- Chameleon 使用一种凝聚层次聚类算法,其基于子簇的相似度(为了确定最相似的子簇,该算法考察每个簇的互连性和邻近性),反复地合并子簇。
其中,最后的一步(使用一种凝聚层次聚类算法,其基于子簇的相似度(互连性和邻近性)反复地合并子簇)应该是 Chameleon 算法能发现任意性状的聚类的关键所在。这里涉及到两个指标,即簇的互连性和簇的邻近性。
稀疏图
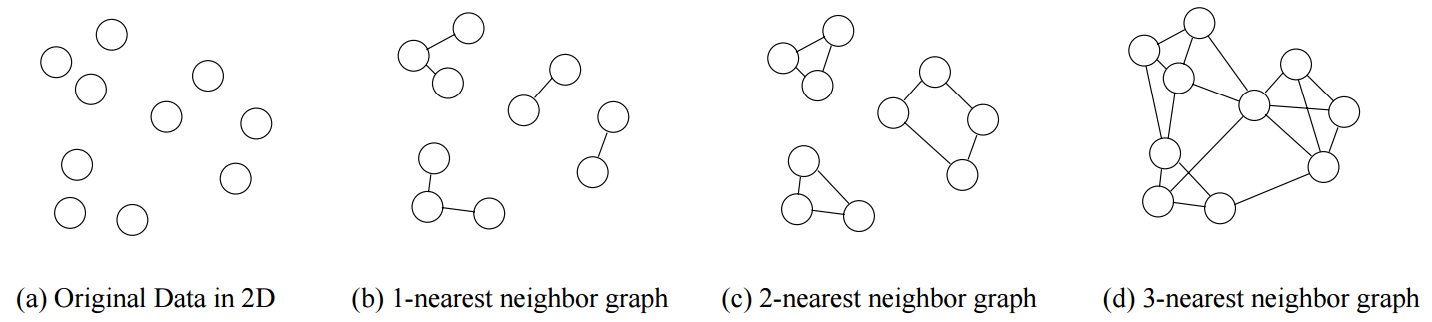
Chameleon 使用稀疏的 k 近邻图来对数据集进行建模,图中的每一个节点代表一个数据点,任意两个节点 v 和 u 之间存在每一条边代表 u 在 v 的 k 个最邻近的节点中。如下图,(a)是原始数据,(b)(c)(d)分别是 1,2,3 近邻图。
子簇相似性度量
Chameleon 使用相对互连性(Relative Interconnectivity)和相对近似性(Relative Closeness)来决定子簇之间的相似性,会选择 RI 和 RC 都高的子簇对进行合并。
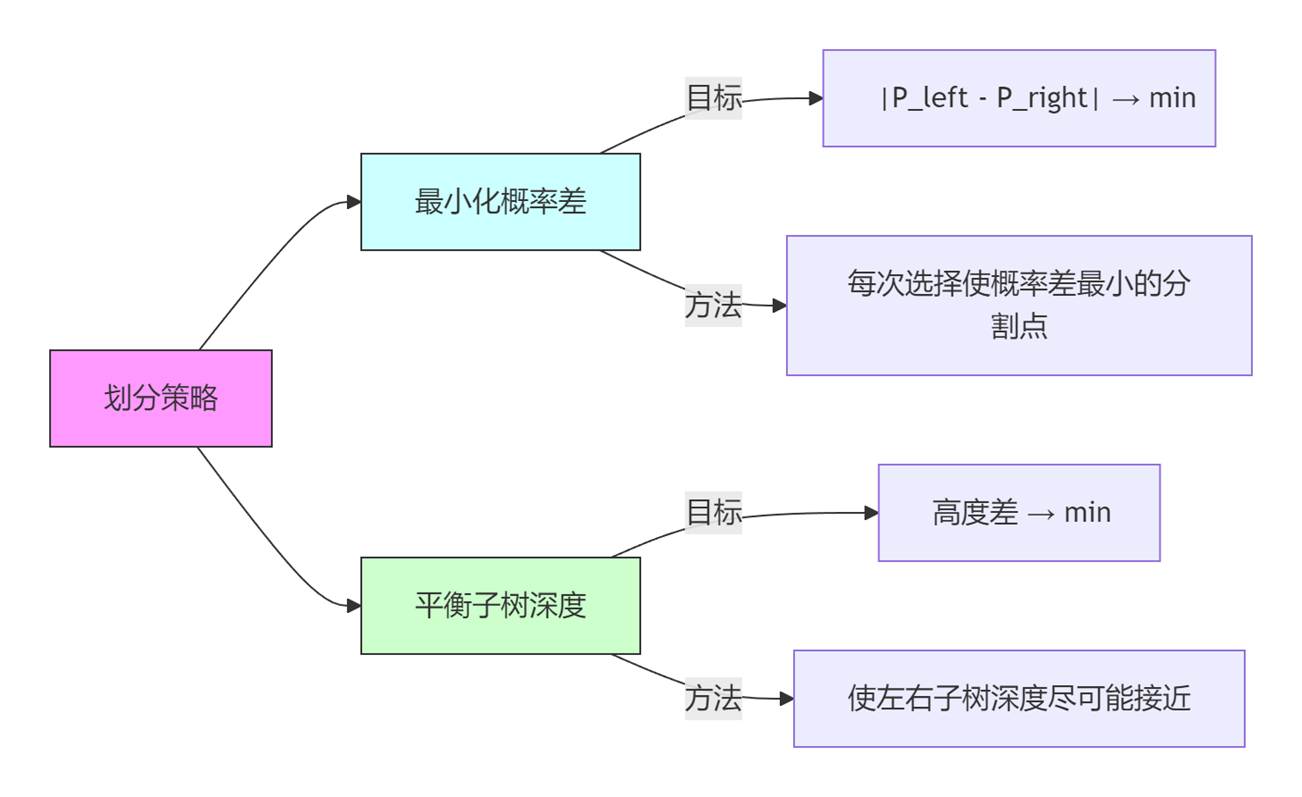
- 相对互连性:$RI(C_i,C_j)=\frac{EC(C_i,C_j)}{(|EC(C_i)|+|EC(C_j)|)/2}$。其中,$EC(C_i,C_j)$ 是连接簇 $C_i$ 和 $C_j$ 的边的权重之和,$EC(C_i)$ 是把簇 $C_i$ 划分成两个大小大致相等部分的最少边的权重之和。相对互连性解决的是簇之间形状不同和互连度不同的问题。
- 相对近似性:$RC(C_i,C_j)=\frac{\bar{S}EC(C_i,C_j)}{\frac{C_i}{C_i+C_j}\bar{S}EC(C_i)+\frac{C_j}{C_i+C_j}\bar{S}EC(C_j)}$。其中,$\bar{S}EC(C_i,C_j)$ 是连接簇 $C_i$ 和 $C_j$ 的边的平均权重,$\bar{S}EC(C_i)$ 是把簇 $C_i$ 划分成两个大小大致相等部分的最少边的平均权重。
Chameleon聚类过程
- 子图划分:Chameleon 使用 hMetis 算法根据最小化截断的边的权重之和来分隔 k 近邻图。
- 子簇合并:Chameleon 使用度量 $RI(C_i,C_j)\times RC(C_i,C_j)^{\alpha}$ 来选择合并的子簇,用这个度量是同时考虑到了两个子簇之间的互连性和近似性。
合并的过程如下:
- 给定度量函数如下 minMetric,
- 访问每个簇,计算他与邻近的每个簇的 RC 和 RI,通过度量函数公式计算出值 tempMetric。
- 找到最大的 tempMetric, 如果最大的 tempMetric 超过阈值 minMetric,将簇与此值对应的簇合并
- 如果找到的最大的 tempMetric 没有超过阈值,则表明此聚簇已合并完成,移除聚簇列表,加入到结果聚簇中。
- 递归步骤 2,直到待合并聚簇列表最终大小为空。
Chameleon算法总结
Chameleon 算法能高质量的发现一些任意形状的聚类,但里面的参数调整并不容易,图切分过程中的 k 值的选取并不那么直观,此外,算法的时间复杂度在 $O(n^2)$,在数据量过大时并不适用。
参考链接: