加密解密算法之RSA

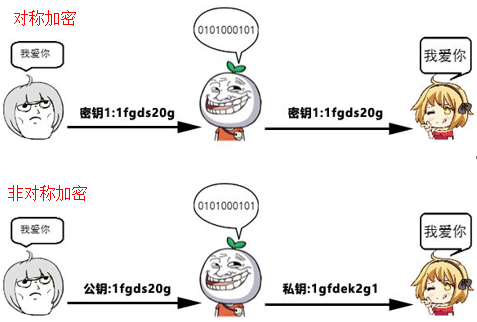
在了解RSA之前，需要先要对对称加密和非对称加密有个初步的了解。对称加密就是加密和解密使用同一个密钥。对称加密快而且方便，但是有个缺点，密钥容易被偷或被破解。非对称算法把密钥分成两个，一个自己持有叫私钥，另一个发给对方，还可以公开，叫公钥，用公钥加密的数据只能用私钥解开。

前面介绍的RC4、DES、AES都属于对称加密，而今天要学习的RSA则属于非对称加密的一种。

非对称加密的发展历史

1976年以前，所有的加密方法都是同一种模式：甲方选择某一种加密规则，对信息进行加密，乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称”密钥”），这被称为”对称加密算法”（Symmetric-key algorithm）。这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为”Diffie-Hellman密钥交换算法”。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。这种新的加密模式被称为”非对称加密算法”。

• 乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。
• 甲方获取乙方的公钥，然后用它对信息加密。
• 乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。从那时直到现在，RSA算法一直是最广为使用的”非对称加密算法”。毫不夸张地说，只要有计算机网络的地方，就有RSA算法。这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

RSA的数学原理

非对称加密算法核心原理其实就是设计一个数学难题，使得用公钥和明文推导密文很容易，但根据公钥、明文和密文推导私钥极其难。

互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。关于互质关系，不难得到以下结论：

• 任意两个质数构成互质关系，比如13和61。
• 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。
• 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。
• 1和任意一个自然数是都是互质关系，比如1和99。
• p是大于1的整数，则p和p-1构成互质关系，比如57和56。
• p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

欧拉函数

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）计算这个值的方法就叫做欧拉函数，以φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

φ(n) 的计算方法并不复杂，但是为了得到最后那个公式，需要一步步讨论。

• 第一种情况：如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。
• 第二种情况：如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。
• 第三种情况：如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则$\phi (p^k)=p^k-p^{(k-1)}$，比如 φ(8) = φ(2^3) =2^3 – 2^2 = 8-4 = 4。这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1)个，即1×p、2×p、3×p、…、p^(k-1)×p，把它们去除，剩下的就是与n互质的数。上面的式子还可以写成下面的形式：$\phi (p^k)=p^k-p^{(k-1)}=p^k(1-\frac{1}{p})$，可以看出，上面的第二种情况是 k=1 时的特例。
• 第四种情况：如果n可以分解成两个互质的整数之积，n = p1 × p2，则φ(n) = φ(p1p2) = φ(p1)φ(p2)，即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。这一条的证明要用到中国剩余定理，这里就不展开了，只简单说一下思路：如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。
• 第五种情况：因为任意一个大于1的正整数，都可以写成一系列质数的积。$n = p_1^{k1}p_2^{k2}…p_r^{kr}$，根据第4条的结论，得到$ \phi (n) = \phi (p_1^{k1})\phi (p_2^{k2})…\phi (p_r^{kr})$，再根据第3条的结论，得到$ \phi (n) = p_1^{k1}p_2^{k2}…p_r^{kr}(1-\frac{1}{p_1})(1-\frac{1}{p_2})…(1-\frac{1}{p_r})$，也就等于$ \phi (n) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})…(1-\frac{1}{p_r}))$，这就是欧拉函数的通用计算公式。比如，1323的欧拉函数，计算过程如下：$ \phi (1323) = \phi (3^3 * 7^2) = 1323(1-\frac{1}{3})(1-\frac{1}{7})=756$。

欧拉定理

欧拉函数的用处，在于欧拉定理。”欧拉定理”指的是：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：$ a^{\phi (n)}\equiv 1 \pmod{n}$，也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。欧拉定理的证明比较复杂，这里就省略了。我们只要记住它的结论就行了。欧拉定理可以大大简化某些运算。比如，7和10互质，根据欧拉定理，$ 7^{\phi (10)}\equiv 1 \pmod{10}$，已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。$ 7^{4k}\equiv 1 \pmod{10}$，因此，7的任意次方的个位数（例如7的222次方），心算就可以算出来。欧拉定理有一个特殊情况。假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成$ a^{p-1}\equiv 1 \pmod{p}$，这就是著名的费马小定理。它是欧拉定理的特例。欧拉定理是RSA算法的核心。理解了这个定理，就可以理解RSA。

模反元素

还剩下最后一个概念：如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。$ ab \equiv 1 \pmod{n}$，这时，b就叫做a的模反元素。比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。欧拉定理可以用来证明模反元素必然存在。$ a^\phi (n) = a * a^{\phi (n)-1} \equiv 1 \pmod{n}$，可以看到，a的 φ(n)-1 次方，就是a的模反元素。

算法原理

RSA算法基于一个事实：将两个大素数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。根据欧拉定理可知：只需 e * d mod φ(n) = 1，即可满足上式，如果我们选取素数 p, q，那么：n = p * q 容易计算，φ(n) = (p – 1) * (q – 1) 容易计算，很容易选取一个正整数 e，e 和 φ(n) 互质。当 e 和 φ(n) 互质时：由欧拉定理可很容易算出一个模反元素 d，满足 e * d mod φ(n) = 1。

RSA算法三个参数：n、e1、e2，n = p*q （p、q为2个大质数） n的二进制所占用的位数即秘钥的长度。e1与e2是一对相关的值，e1可以任意取，但要求e1与(p-1)(q-1)互质；要求(e2e1)mod((p-1)(q-1))=1。(n,e1),(n,e2)就是密钥对，其中(n,e1)为公钥，(n,e2)为私钥。

RSA的加密流程

非称加密算法的流程图：

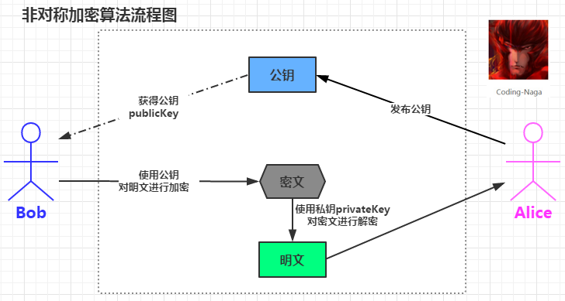
在此可以看到，非对称加密是通过两个密钥（公钥-私钥）来实现对数据的加密和解密的。公钥用于加密，私钥用于解密。对于非对称的加密和解密为什么可以使用不同的密钥来进行，这些都是数学上的问题了。不同的非对称加密算法也会应用到不同的数学知识。上面也对RSA中使用的数学问题做了一个小小的介绍。现在就来看看RSA算法是怎么来对数据进行加密的吧，如下是一幅RSA加密算法流程及加密过程图。

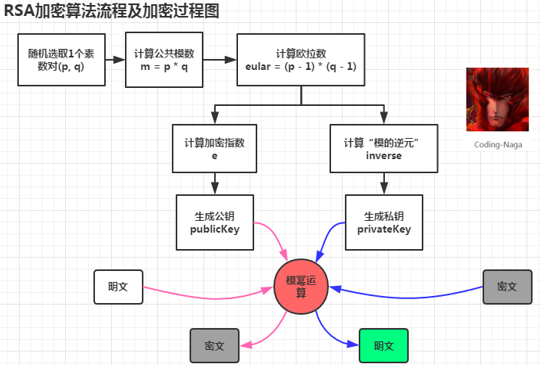
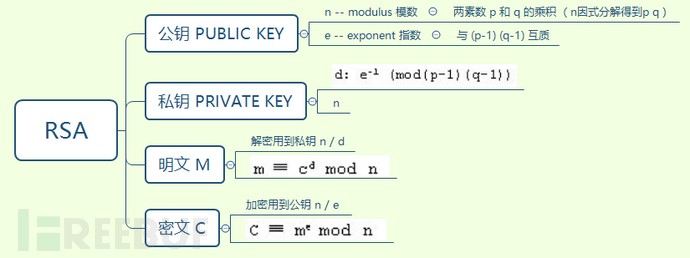
Cryptography and Network Security形象的描述了 RSA 流程：

+-------------------------------------------------------------------------------+
|                                 Key Generation                                |
|                                                                               |
|     Select p, q                               p and q both prime, p != q      |
|     Calculate n = p * q                                                       |
|     Calculate φ(n) = (p - 1) * (q - 1)                                        |
|     Select integer e                          e is relatively primte to φ(n)  |
|     Calculate d                               (d * e) mod n = 1               |
|     Public key                                PU = {e, n}                     |
|     Private key                               PR = {d, n}                     |
+-------------------------------------------------------------------------------+
+-------------------------------------------------------------------------------+
|                                  Encryption                                   |
|                                                                               |
|     Plaintext M                               M < n                           |
|     Ciphertext C                              C = M^e mod n                   |
+-------------------------------------------------------------------------------+
+-------------------------------------------------------------------------------+
|                                  Decryption                                   |
|                                                                               |
|     Ciphertext C                              C                               |
|     Plaintext M                               M = C^d mod n                   |
+-------------------------------------------------------------------------------+

RSA的应用

RSA作为非对称加密技术的代表，加解密的速度其实相当慢，只能对小块的数据进行加解密。但是其非对称的特点，满足公钥可以随处分发，只有公钥能解密私钥加密的数据，只有私钥能解密公钥加密的数据。所以很适合用来进行密钥分发和身份验证，这两个应用场景刚好相反。

• 用于对称秘钥分发的场景，其他人用公钥加密对称的秘钥，那么只有授权人才持有私钥，因此才能解密获得对应的秘钥，解决了AES密钥分发的难题；
• 对于身份验证的场景，授权人用私钥加密一段指令，其他人用公钥解密对应的数据，验证对应的指令与之前约定的某些特征一致，如果一致，那么可以确认这个指令就是授权人发出的。

Python理应PyCrypto实现RSA

RSA 公钥和私钥的生成

RSA的密文是对代码明文的数字的 E 次方求mod N 的结果。也就是将明文和自己做E次乘法，然后再将其结果除以 N 求余数，余数就是密文。RSA是一个简洁的加密算法。E 和 N 的组合就是公钥（public key）。对于RSA的解密，即密文的数字的 D 次方求mod N 即可，即密文和自己做 D 次乘法，再对结果除以 N 求余数即可得到明文。D 和 N 的组合就是私钥（private key）。算法的加密和解密还是很简单的，可是公钥和私钥的生成算法却不是随意的。使用 Pycrypto生成秘钥对很简单，我们分别为 Master和Ghost各生成一对属于自己的秘钥对。

from Crypto import Random
from Crypto.PublicKey import RSA

# 伪随机数生成器
random_generator = Random.new().read
# rsa算法生成实例
rsa = RSA.generate(1024, random_generator)

# master的秘钥对的生成
private_pem = rsa.exportKey()
with open('master-private.pem', 'wb') as f:
    f.write(private_pem)

public_pem = rsa.publickey().exportKey()
with open('master-public.pem', 'wb') as f:
    f.write(public_pem)

# ghost的秘钥对的生成
private_pem = rsa.exportKey()
with open('ghost-private.pem', 'wb') as f:
    f.write(private_pem)

public_pem = rsa.publickey().exportKey()
with open('ghost-public.pem', 'wb') as f:
f.write(public_pem)

当我们执行后，会在当前目录生成公钥和私钥，所生成的私钥和公钥大概是这样的：

-----BEGIN RSA PRIVATE KEY-----
MIICXgIBAAKBgQDOZ4ObgkZaH3ZexNj9WwAnXD4nDPBxPdyCSSehXvaM9ytSHpdP
RefVtRysq1J866DgzXA+mUUHXEzRfvRQHqZrCenqgsb2FGnCA7SkbLOp5c92ZLPi
DaET0/rZ7gkUCLZj1cRxXF8ZLyXgN7T8x7sAXyLa+tK0rt16UgOQuQbqjQIDAQAB
AoGBAJED/15Z+E3HfyX0TbQrpH8C+xP6rlARs4TCGxrwmm7OFdy7a3mh1tG6Tqwu
LmVgM4beL/d7Phl+yuYBuWs1LZwRkxDztLkVySxLQwL5VTDuV3NHT2/uHSIsaxHM
r7xlDjyzeATSTAdxdRLDwZsVmboqf5Mbn0fzMJiFt3YL41mhAkEA3xPCwuLvCupc
hJ3QIBc55rirYw9CGS4NAuH2PSgbev2i/RvdA5hBC/IS2bN8NGxniFLXRO+/f7E1
usVp5ZIlSQJBAOzd0yiny0RDWEizpDup+V1O+Jp+e8CJjaH+UWod0+pzISpiHPza
KRAc3ezYe6uo7wDYjnb8kvOUhsilpfQ2TyUCQQCdN2QPzbgCzWEe5coEk9nuzT+c
tOg0rsvkuDO+rkGP0KnKEJUXL3rIXHcEjwZ+O9hLr3af0wf3ioD/fJpBfVphAkEA
kZBE2yA674l/cLZNQIlVgL0uVCtUu98MljfnKpKID/WOtTA0ZkNfptJGo+3qGnUn
49oxuve/C0gEiLwbv3e8rQJAN3EOF0pridWcKw5l06pG8nxzXJEWzfus0FX7qfdy
RGGaehQAV4nqic/i88MivONjUb4+cSQbY8/Qq9xolxv++A==
-----END RSA PRIVATE KEY-----

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDOZ4ObgkZaH3ZexNj9WwAnXD4n
DPBxPdyCSSehXvaM9ytSHpdPRefVtRysq1J866DgzXA+mUUHXEzRfvRQHqZrCenq
gsb2FGnCA7SkbLOp5c92ZLPiDaET0/rZ7gkUCLZj1cRxXF8ZLyXgN7T8x7sAXyLa
+tK0rt16UgOQuQbqjQIDAQAB
-----END PUBLIC KEY-----

当然每次运行的结果都不一定，公钥是公开的，任何人都可以看到，但是私钥一定要保存好，否则一旦泄露，意味着你的信息也不安全了。

加密与解密

通常通信的时候，发送者使用接受者的公钥加密，接受者使用接受者私钥解密。简而言之，Master给Ghost通信，需要加密内容，那么Ghost会生成一个秘钥对，Ghost的公钥ghost-public.pem和私钥ghost-private.pem 。Ghost 把公钥公开给发送者，任何人都可以用来加密，然后Master使用ghost-public.pem进行加密，然后把内容发给Ghost，Ghost再使用ghost-private.pem进行解密。

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
import base64


def encrypt(text):
    with open('ghost-public.pem') as f:
        rsa_key = RSA.importKey(f.read())
        cipher = PKCS1_OAEP.new(rsa_key)
        encrypt_text = base64.b64encode(cipher.encrypt(text.encode("utf-8")))
        return encrypt_text.decode("utf-8")

def decrypt(encrypt_text):
    with open('ghost-private.pem') as f:
        rsa_key = RSA.importKey(f.read())
        cipher = PKCS1_OAEP.new(rsa_key)
        text = cipher.decrypt(base64.b64decode(encrypt_text))
        return text.decode("utf-8")

if __name__ == "__main__":
    text = 'hello ghost, this is a plian text'
    encrypt_text = encrypt(text)
    print(encrypt_text)
    decrypt_text = decrypt(encrypt_text)
    print(decrypt_text)

注意：

• 在使用RSA加密时，推荐使用PKCS1_OAE，PKCS1_V1_5可用于兼容老代码，但已不推荐使用。
• RSA可以加密的单段数据长度受key的长度所限制，大量数据需分段加密。

根据RFC 3447描述，若使用PKCS1_OAEP加密，单段数据最大长度mLen <= k – 2hLen -2，若采用PKCS1_V1_5加密，则能够加密的明文最大mLen <= k – 11。我们来计算下采用PKCS1_OAEP时，能加密的字符串的最大长度多少。

mLen <= k – 2hLen – 2 中：

• mLen：需要加密的字符串的长度
• k：RSA key的位数（2048或1024）
• hLen：使用的hash算法所输出的字节数，若未指定，则默认为SHA1，hLen = 40。

所以当key长度为1024时，支持的最大长度为 1024/8-2*20-2=86，当key长度为2048时，支持的最大长度为2048/8-2*20-2=214

签名与验签

当然，对于窃听者，有时候也可以对伪造Master给Ghost发送内容。为此出现了数字签名。也就是Master给Ghost发送消息的时候，先对消息进行签名，表明自己的身份，并且这个签名无法伪造。具体过程即Master使用自己的私钥对内容签名，然后Ghost使用Master的公钥进行验签。

from Crypto.Signature import PKCS1_PSS
from Crypto.Hash import SHA
from Crypto.PublicKey import RSA
import base64

def get_signature(message):
    with open('master-private.pem') as f:
        rsa_key = RSA.importKey(f.read())
        digest = SHA.new()
        digest.update(message.encode("utf-8"))
        signer = PKCS1_PSS.new(rsa_key)
        signature = base64.b64encode(signer.sign(digest))
        return signature.decode("utf-8")

def verify_signature(message,signature):
    with open('master-public.pem') as f:
        rsa_key = RSA.importKey(f.read())
        verifier = PKCS1_PSS.new(rsa_key)
        digest = SHA.new()
        digest.update(message.encode("utf-8"))
        is_verify = verifier.verify(digest, base64.b64decode(signature))
        return is_verify

if __name__ == "__main__":
    message = 'To be signed'
    signature = get_signature(message)
    print(signature)
    print(verify_signature(message,signature))

其中签名算法有PKCS1_PSS和PKCS1_v1_5

参考链接：https://www.dlitz.net/software/pycrypto/api/current/

总结

破解加密的难度除了跟加密方法有关，还跟密钥长度以及加密模式有很大的关系，就拿AES来说，有AES128和AES256（代表密钥长度），显然AES256的安全性能比AES128更高，而AES又要四种模式：ECB、CBC、CFB、OFB（代表加密模式）。RSA1024是属于非对称加密，是基于大整数因式分解难度，也就是两个质数相乘很容易，但是找一个大数的质因子非常困难。量子计算机时代，RSA有一定的破绽，因为利用shro’s algorithm，量子计算机穷举计算质因子速度可以提高N个数量级，能够在有限的时间内破解RSA密钥，具体可以参考：超链接。

AES作为对称加密技术，加密速度很快。现在高端一点的CPU都带有AES-NI指令，可以极快的完成加密和解密。AES256目前没有明显的漏洞，唯一的问题就是如何安全的分发密钥。现在大部分的加密解密都是同时应用RSA和AES，发挥各自的优势，使用RSA进行密钥分发、协商，使用AES进行业务数据的加解密。