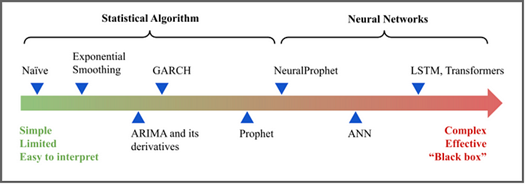
NeuralProphet 产生背景
大多数时间序列问题需要易于理解的预测。同时,需要有效的预测。这两个愿望导致了一种权衡:可解释性与准确率。准确率的显著提高通常归因于更复杂的模型。然而,复杂性与可解释性存在天然的矛盾。
简而言之,存在两类模型:
- 统计算法(ARIMA、GARCH…)可以在知道理论的情况下进行数学解释
- 神经网络模型,虽然更加复杂,但已经证明了它们的性能
最初,Facebook 与 Prophet 的意愿是提供一个易于使用、可调整和可解释的工具来预测时间序列。然而,有一个问题依然存在:准确性不佳。为了解决这个问题,NeuralProphet 应运而生。
简而言之,NeuralProphet = 神经网络 + Prophet
因此,目的是通过在 Prophet(一种统计算法)中包含神经网络来结合前两个类别。目的:提高准确性,同时限制可解释性的损失。
这个介绍部分可以通过下图来大致描述:
NeuralProphet 简介
最初的Facebook Prophet 算法是非常轻量级但有效的时间序列预测模型。它易于使用和解释,描述很少与时间序列建模相关联。根据原始论文,该模型之所以成功,是因为研究人员将时间序列预测重新定义为曲线拟合问题,而不是自回归问题。许多先前的模型,例如 ARIMA,滞后和拟合数据,而不是试图找到我们趋势的函数形式。该模型具有三个主要组成部分。T(t) 对应于我们的时间序列在去除季节性后的趋势。S(t) 对应于我们的季节性,无论是每周、每月还是每年。最后,E(t) 对应于预先指定的事件和假期。这些组件中的每一个都有一个拟合过程,一旦拟合,它们通常会结合起来产生可靠的预测。
2020 年,斯坦福大学和 Facebook 的研究人员对 Prophet 算法进行了重组,以包含深度学习组件。主要卖点是准确度提高了 55-92%。该模型的深度学习部分建立在 PyTorch 之上,因此它们很容易扩展。运行时间平均增加了约 4 倍,但时间序列预测很少是实时的,因此运行时间不是主要问题。
如果您需要可解释但功能强大的时间序列预测,NeuralProphet 可能是您的最佳选择。
NeuralProphet 是一个基于 PyTorch 实现的客户友好型时间序列预测工具,延续了 Facebook 开源预测工具 Prophet 的主要功能。NeuralProphet 是在一个完全模块化的架构中开发的,这使得它可以在未来增加额外组件,可扩展性很强。项目意在保留 Prophet 的原始特性,如 Classic AR 模型可解释性、可配置性,并使用了 PyTorch 后台进行优化,如 Gradient Descent,另外还引入了 AR-Net 建模时间序列自相关、自己设置损失和指标、具备前馈神经网络的可配置非线性层等等特性。
NeuralProphet 是升级版的 Prophet。NeuralProphet 模型集成了 Prophet 的所有优点,不仅具有不错的可解释性,还有优于 Prophet 的预测性能。
- 使用 PyTorch 作为后端进行优化的梯度下降法。
- 使用 AR-Net 对时间序列的自相关进行建模。
- 使用 separate 前馈神经网络对滞后回归者进行建模。
- 可配置的 FFNNs 非线性深层。
- 可调整到特定的预测范围(大于 1)。
- 自定义损失和指标。
虽然官方 PPT 写了很多改变,但是其实就是基于两个”巨变”。
- 分解的分量增加了一个重量级的 AR(自回归),这个是超级重量级的。
- AR 模型本身在经典时序分析里面就独当一面,到了 NeuralProphet 里面做为辅助,它对于精度的提高是神级的。
- 相比于传统的 AR 模型,AR 模型借助于神经网络,拟合的更加快捷和精确。
- 对于 AR 模型也添加了正则项(参数为 ar_sparsity)。通过正则加持,AR 模型可以看的更远,因为你有能力使用更多的历史数据而不用担心求解。
- Pytorch 作为 backend。
- NeuralProphet 把所有的分量都用 pytorch 写了。
- 趋势项,周期项变化不大,因为他们的算法还是和 Prophet 一致。
- AR 项,外部回归项变化很大,因为有了 Pytorch 的加持,意味着你不用再局限于线性回归。
- 从源码看,NeuralProphet 采用 Relu 非线性化了。
- 神经网络适合魔改,看着结果不顺眼,改改层数,说不定就顺眼了。
NeuralProphet 原理
NeuralProphet 是一个可分解的时间序列模型,和 Prophet 相比,类似的组成部分有趋势(trend)、季节性(seasonality)、自回归(auto-regression)、特殊事件(special events),不同之处在于引入了未来回归项(future regressors)和滞后回归项(lagged regressors)。
未来回归项(future-known regressors)是指在预测期有已知未来值的外部变量,而滞后回归项(lagged covariates)是指那些只有观察期值的外部变量。趋势 trend 可以通过设置变化点来建立线性或者组合多个线性趋势的模型。季节性 seasonality 使用傅里叶项建模,因而可以解决高频率数据的多种季节性。自回归项(auto-regression)使用 AR-Net 的实现来解决,这是一个用于时间序列的自回归前馈神经网络(Auto-Regressive Feed-Forward Neural Network)。滞后回归项也使用单独的前馈神经网络进行建模。未来回归项和特殊事件都是作为模型的协变量,只要 single weight 进行建模。
NeuralProphet 模块组件
NeuralProphet 模型模型由多个模块组成,每个模块都有各自的输入和建模过程。每个模块都有自己的个人输入和建模过程。但是,所有模块都必须产生 h 个输出,其中 h 定义了一次预测未来的步数。
$$\hat{y_t}=T(t)+S(t)+E(t)+F(t)+A(t)+L(t)$$
其中:
- T(t) = 时间 t 的趋势
- S(t) = 时间 t 的季节性影响
- E(t) = 时间 t 的事件和假日效应
- F(t) = 未来已知外生变量在时间 t 的回归效应
- A(t) = 基于过去观察的时间 t 的自回归效应
- L(t) = t 时刻外生变量滞后观测的回归效应
所有模型组件模块都可以单独配置和组合以组成模型。如果所有模块都关闭,则仅安装一个静态偏移参数作为趋势分量。默认情况下,仅激活 trend 和 seasonality 模块。
Trend
趋势与之前的 Prophet 模型没有变化。简而言之,我们希望使用指数或线性增长函数来模拟趋势。使用逻辑增长是一种非常传统且广为接受的解决方案,但是原始 Prophet 模型的创新之处在于它允许函数的参数发生变化。这些变化点由模型动态确定,并为其他静态增长率和偏移参数提供了更大的自由度。
建模趋势的经典方法是将其建模为偏移量 m 和增长率 k。$t_1$ 时刻的趋势效应由增长率乘以从偏移量 m 顶部的起点 $t_0$ 开始的时间差。
$$T(t_1)=T(t_0)Z+k\cdot\Delta_t=m+k\cdot(t_1-t_0)$$
Seasonality季节性被定义为以特定的定期间隔发生的变化。众所周知,它很难解释,因为它可以采用多种形式。该模型的最初开发人员提出了另一个好主意——他们没有尝试使用自回归(即滞后数据)对季节性进行建模,而是尝试对季节性曲线进行建模。这就是傅立叶级数的用武之地。傅立叶级数只是一堆加在一起的正弦曲线,可用于拟合任何曲线。一旦我们有了数据的每日、每周、每月等季节性的函数形式,我们就可以简单地将这些术语添加到我们的模型中并准确预测未来的季节性。
类似 Prophet,NeuralProphet 也使用傅立叶项(Fourier terms)来处理 Seasonality。傅立叶项定义为正弦、余弦对并允许对多个季节性以及具有非整数周期的季节性进行建模。每个季节性可以定义为多个傅里叶项。
$$S_p(t)=\sum_{j=1}^{k}(a_j\cdot\cos(\frac{2\pi j t}{p})+b_j\cdot\sin(\frac{2\pi j t}{p}))$$
其中 k 具有周期性 p 的季节性的傅立叶的数量。每一个季节性对应 2k 个系数。在 t 时刻,模型涉及的所有季节性效应可以表示为:
$$s(t)=\sum_{p\in\mathbb{P}}S^*_p(t)$$
每个季节周期性可以单独表示为 additive 或者 multiplicative 的形式:
$$S^*_p(t)=\left\{\begin{matrix}S^{\dagger}_p(t)=T(t)\cdot S_p(t)& if\ S_p\ is\ multiplicative\\S_p(t)&otherwise\end{matrix}\right.$$
NeuralProphet 根据数据频率和长度自动激活每日、每周或每年的季节性。既周期大于 2 个季节性,激活对应季节性。默认每个季节性的傅立叶项数为:年:k=6,p=365.25,周:k=3,p=7,日:p=1,k=6。
Events and Holidays
对于初始 Prophet 模型中的最后一项,用于处理事件。季节性和事件的处理方式几乎相同–使用傅立叶级数。然而,我们希望傅立叶变换不是平滑曲线,而是在给定特定假期时产生非常尖的曲线。而且,由于底层函数是正弦函数,它们很容易扩展到未来。
$$E(t)=\sum_{e\in\mathbb{E}}E_e^{\star}(t)$$
其中,
$$E_e(t)=z_e e(t)$$
$$E_e^{\star}(t)=\begin{cases}E_e^{\dagger}(t)=T(t)\cdot E_e(t),&\text{if}f\text{ is multiplicative}\\E_e(t),&\text{otherwise}\end{cases}$$
Auto-Regression
自回归是回顾先前值并将其用作未来值的预测器的概念。最初的先知模型之所以如此有效,是因为它偏离了这一理念,但是为了利用深度学习,我们必须回归。自回归项使用滞后值来预测未来值。
$$y_t=c+\sum_{i=1}^{i=p}\theta_i\cdot y_{t-i}+e_t$$
$$A^t(t),A^t(t+1),…,A^t(t+h-1)=\text{AR-NET}(y_{t-1},y_{t-2},…,y_{t-p})$$
对 NeuralProphet 对象的 n_lags 参数设置一个适当的值,就可以在 NeuralProphet 中启用 AR-Net。
例如,将 5 个滞后期输入 AR-Net,并接收 3 个步骤作为预测。
m = NeuralProphet(
n_forecasts=3,
n_lags=5,
yearly_seasonality=False,
weekly_seasonality=False,
daily_seasonality=False,
)
- num_hidden_layers 参数:增加 AR-Net 的复杂度
- ar_sparsity 参数:为 AR-Net 加入正则约束
- highlight_nth_step_ahead_of_each_forecast 参数:突出特定的预测步骤,用法:
m.highlight_nth_step_ahead_of_each_forecast(step_number=m.n_forecasts)
Lagged Regressors
Prophet 和 NeuralProphet 模型的强大方面之一是它们允许协变量。大多数时间序列预测模型都是单变量的,尽管它们有时会提供多变量版本——ARIMA 与 MARIMA。
在处理带有时间序列预测的协变量时,我们需要确保这些协变量会提前 n 个时间段出现,否则我们的模型将无法预测。我们可以通过将当前协变量滞后 n 个时间段来做到这一点,这由 L(t) 项建模,或者对这些协变量进行预测,由 F(t) 项建模。
滞后回归用于为我们的时间序列预测目标加入其他观察变量。在 t 时刻,我们只知道 t-1 时刻(包括 t-1)前的观察值。
$$L(t)=\sum_{x\in\mathbb{X}}L_x(x_{t-1},x_{t-2},…x_{t-p})$$
只有在启用 AR-Net 的情况下,才会支持 LaggedRegressor
NeuralProphet 通过调用 add_lagged_regressor 函数并给出必要的设置,将 LaggedRegressor 用于 NeuralProphet 对象中。
假如有一个名为 A 的滞后回归项,通过 add_lagged_regressor 注册它到 NeuralProphet
m = m.add_lagged_regressor(names=’A’)
Future Regressors
未来回归器是指具有已知未来值的外部变量。从这个意义上说,未来回归者的功能如果和特殊事件非常相似。这些回归器的过去值对应于训练 timestamps,必须与训练数据本身一起提供。
对于 future regressors,在 t 时刻,过去和未来的回归因子(regressor)都是知道的。
$$F(t)=\sum_{f\in\mathbb{F}}F_f^{\star}(t)$$
其中:
$$F_f(t)=d_f f(t)$$
$$F_f^{\star}(t)=\begin{cases}F_f^{\dagger}(t)=T(t)\cdot F_f(t),&\text{if}f\text{ is multiplicative}\\F_f(t),&\text{otherwise}\end{cases}$$
NeuralProphet 数据预处理
Missing Data
当没有滞后变量的时候,直接丢掉缺失值就好。有滞后变量的情况下,每个缺失值会导致 h+p 被丢弃,因此引入数据插值机制;如果不特别指定的话,缺失值用 0 填充。
数据插值:当 Auto-regression 或者 lagged regressor 使用的时候,主要采取三个步骤
- 对于不超过 10 个值的缺失,使用前后已知的值线性插值;
- 对于小于 20 个值的缺失,使用一个滑动窗口大小为 30 的计算平均值;
- 如果超过连续 30 个值缺失的话,不插值,直接丢弃这部分值
Data Normalization
对于观察到的时间序列值,用户可以指定是否希望将这些值标准化。默认情况下,y 值将被最小-最大归一化。如果用户特别将 normalize_y 参数设置为 true,则数据将进行 z-score 归一化。对协变量也可以进行归一化处理。协变量归一化的默认模式是 auto。在这种模式下,除了事件等 binary features 外,所有其他特征都进行 z-score 归一化。
用户可以设定归一化的参数,如果不设定,对于二值化数值使用 minmax,其他默认使用 soft。

NeuralProphet 模型训练
Prophet 使用 Stan 实现的 L-BFGS 拟合模型,NeuralProphet 依赖 PyTorch 实现的 SGD 拟合模型;
Loss FunctionNeuralProphet 默认使用 Huber loss,即 smooth L1-loss,如下
$$L_{\text{huber}}(y,\hat{y})=\begin{cases}\frac{1}{2\beta}(y-\hat{y})^2,&\text{for}|y-\hat{y}|<\beta\\|y-\hat{y}|-\frac{\beta}{2},&\text{otherwise}\end{cases}$$ 对于给定的阈值$\beta$, 低于阈值$\beta$,损失函数变为 mean squared error (MSE);高于阈值$\beta$,损失函数变为 mean absolute error (MAE)。用户可以设定 MSE,MAE 或者其他 PyTorch 实现的函数; Regularization
NeuralProphet 使用权重绝对值的缩放和对数变换偏移作为一般正则化函数。
其中$ϵ\epsilon\in(0,\infty)$为偏移的倒数,$\alpha\in(0,\infty)$为对数变换的比例。$\epsilon$控制权重参数的稀疏程度,$\alpha$控制权重值的大小;
默认情况下,设置$\epsilon=1,$ $\alpha=1$
Optimizer
默认使用 AdamW
AdamW(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0.0001, maximize=False, capturable=False)
也可以选用 SGD
SGD(params, lr=0.01, momentum=0.9, dampening=0, weight_decay=0.001, nesterov=False)
同时也可以使用 PyTorch 支持的其他 optimizer。
Learning Rate
通过测试的方式来估计一个学习率,针对特定的数据集大小,测试 100+log10(10+T)*50) 次, 测试区间从$\eta=1e-7$到$\eta=1e+2$之间。为了稳定性,分别测试三次求平均:
$$\eta^{\star}=\frac{1}{3}(\log_{10}(\eta_1)+\log_{10}(\eta_2)+\log_{10}(\eta_3))$$
$$\eta=10^{\eta^{\star}}$$
Batch Size
如果未指定,根据数据量 T 来决定,
$$B^{\star}=2^{2+\left\lfloor\log_{10}(T)\right\rfloor}$$
$$B =\min(T,\max(16,\min(256,B^{\star})))$$
Epochs
如果未指定,根据数据量 T 来决定,
$$N_{\text{epoch}}^{\star}=\frac{1000\cdot2^{\frac{5}{2}\cdot\log_{10}(T)}}{T}$$
$$N_{\text{epoch}}=\min(500,\max(50,\lfloor N_{\text{epoch}}^{\star}\rfloor))$$
Scheduler
采用 1cycle policy,学习率在最初的 30% 训练时间内从$\frac{\eta}{100}$上升到$\eta$,接着 cosine 曲线下降到$\frac{\eta}{5000}$,直到训练结束。
NeuralProphet 的使用
NeuralProphet 的使用与 Prophet 类似。
# 安装 ## pip install neuralprophet # 使用 from neuralprophet import NeuralProphet m = NeuralProphet() metrics = m.fit(df) forecast = m.predict(df) # 可视化结果: fig_forecast = m.plot(forecast) fig_components = m.plot_components(forecast) fig_model = m.plot_parameters() # 预测: m = NeuralProphet().fit(df, freq="D") df_future = m.make_future_dataframe(df, periods=30) forecast = m.predict(df_future) fig_forecast = m.plot(forecast)
超参数说明
class neuralprophet.forecaster.NeuralProphet(growth: Literal['off', 'linear', 'discontinuous'] = 'linear', changepoints: Optional[list] = None, n_changepoints: int = 10, changepoints_range: float = 0.8, trend_reg: float = 0, trend_reg_threshold: Optional[Union[bool, float]] = False, trend_global_local: str = 'global', yearly_seasonality: Union[Literal['auto'], bool, int] = 'auto', weekly_seasonality: Union[Literal['auto'], bool, int] = 'auto', daily_seasonality: Union[Literal['auto'], bool, int] = 'auto', seasonality_mode: Literal['additive', 'multiplicative'] = 'additive', seasonality_reg: float = 0, season_global_local: Literal['global', 'local'] = 'global', n_forecasts: int = 1, n_lags: int = 0, ar_layers: Optional[list] = [], ar_reg: Optional[float] = None, lagged_reg_layers: Optional[list] = [], learning_rate: Optional[float] = None, epochs: Optional[int] = None, batch_size: Optional[int] = None, loss_func: Union[str, torch.nn.modules.loss._Loss, Callable] = 'Huber', optimizer: Union[str, Type[torch.optim.optimizer.Optimizer]] = 'AdamW', newer_samples_weight: float = 2, newer_samples_start: float = 0.0, quantiles: List[float] = [], impute_missing: bool = True, impute_linear: int = 10, impute_rolling: int = 10, drop_missing: bool = False, collect_metrics: Union[List[str], bool, Dict[str, torchmetrics.metric.Metric]] = True, normalize: Literal['auto', 'soft', 'soft1', 'minmax', 'standardize', 'off'] = 'auto', global_normalization: bool = False, global_time_normalization: bool = True, unknown_data_normalization: bool = False, accelerator: Optional[str] = None, trainer_config: dict = {}, prediction_frequency: Optional[dict] = None)
超参数说明:
| Parameter | Default Value | 说明 |
| growth | linear | 传 off 代表没有趋势 |
| changepoints | None | 手动设置拐点 | 5 | 控制潜在拐点的数量 |
| changepoints_range | 0.8 | 默认值0.8,表示后20%的训练数据无changepoints |
| trend_reg | 0 | 趋势正则项 |
| trend_reg_threshold | False | 允许趋势在没有规则化的情况下发生变化。 |
| trend_global_local | global | 存在多个时间序列时的趋势建模策略。 |
| yearly_seasonality | auto | 默认6 |
| weekly_seasonality | auto | 默认4 |
| daily_seasonality | auto | 默认6 |
| seasonality_mode | additive | additive,multiplicative |
| seasonality_reg | 0 | 值越大正则约束越大 |
| season_global_local | global | global |
| n_lags | 0 | 定义是否使用AR-Net,n_lags决定AR-Net回看步数,建议取值大于n_forecasts |
| ar_reg | 可选 | 在AR系数中引入多少稀疏性 |
| ar_layers | 可选 | AR网络的隐藏层维度 |
| n_forecasts | 1 | 预测范围,1意味着将来预测一步 |
| lagged_reg_layers | 可选 | CovarNet的隐藏层维度 |
| learning_rate | None | 如果未指定,自动调整 |
| epochs | None | 如果未指定,根据数据大小设定 |
| batch_size | None | |
| newer_samples_weight | 2.0 | 设置模型拟合向最近观测值倾斜的因子。 |
| newer_samples_start | 0 | 将“较新”样本的开头设置为训练数据的一部分。 |
| loss_func | Huber | Huber,MSE,MAE或torch.nn.functional.loss |
| collect_metrics | True | 默认计算mae和rmse |
| quantiles | None | 介于(0,1)之间的浮点值列表,表示要估计的分位数集。 |
| impute_missing | True | 是否自动估算缺失的日期/值 |
| impute_linear | 10 | 要线性估算的缺失日期/值的最大数量 |
| impute_rolling | 10 | 使用滚动平均值估算的最大缺失日期/数值 |
| drop_missing | False | 是否自动从数据中删除丢失的样本 |
| normalize | soft | 要应用于时间序列的规范化类型。 |
| global_normalization | False | 激活全局规范化 |
| global_time_normalization | True | 指定全局时间规范化 |
| unknown_data_normalization | False | 指定未知数据规范化 |
| accelerator | auto | 使用“自动”可自动选择可用的加速器。 |
| trainer_config | 附加训练器配置参数词典。 | |
| prediction_frequency | 应进行预测的周期性间隔。 |
NeuralProphet实战:基于Optuna的超参数优化
NeuralProphet主要超参介绍
- 趋势相关
- growth:趋势为线性还是没有趋势,NeuralProphet提供了一个新颖的增长方式discontinuous,允许趋势中断与跳跃,也就是会更灵活(与过拟合)
- changepoints:变更点列表,一般让NeuralProphet自己找
- n_changepoints:变更点个数
- changepoints_range:变更点探测的区间,默认为8,这个一般影响较大
- trend_reg:趋势项的正则(限制),也就是趋势项的灵活程度,这就是文中开头所说的regulation之一,影响很大
- 季节相关
- yearly_seasonality/weekly_seasonality/daily_seasonality:是否自动探测这三个周期的季节分量,NeuralProphet会根据数据集的长度,分辨率来自动设置。我一般会禁用掉,然后自己添加周期,并且调整他们的参数:傅里叶级数
- seasonality_mode:additive还是multiplicative,一般来说multiplicative会更灵活
- seasonality_reg:季节项的正则限制,也是影响很大
- AR相关
- n_lags:滞后的阶数,如果是多步预测(n_forecasts>1),需要大于n_forecasts
- ar_reg:AR项的正则
- 神经网络结构
- ar_layers:层数,也是超参数
- 拟合参数
- learning_rate:学习率
- epochs:epochs拟合次数
- batch_size:每次拟合的batch
直接上代码:
```python
import pandas as pd
from neuralprophet import NeuralProphet, set_log_level
import optuna
set_log_level("ERROR")
df = pd.read_csv('data/data.csv')
df['ds'] = pd.to_datetime(df['ds'])
events = pd.read_csv("data/holidays-events.csv")
# 定义NeuralProphet模型
def objective(trial):
# 定义模型参数空间
newer_samples_weight = trial.suggest_int('newer_samples_weight', 0, 100)
newer_samples_start = trial.suggest_float('newer_samples_start', 0.001, 0.999)
seasonality_reg = trial.suggest_float('seasonality_reg', 0.1, 500)
seasonality_mode = trial.suggest_categorical('seasonality_mode', ['additive', 'multiplicative'])
yearly_seasonality = trial.suggest_int('yearly_seasonality', 1, 10)
weekly_seasonality = trial.suggest_int('weekly_seasonality', 1, 10)
epochs = trial.suggest_int('epochs', 2, 30)
learning_rate = trial.suggest_float('learning_rate', 0.001, 0.1, log=True)
changepoints_range = trial.suggest_float('changepoints_range', 0.6, 0.9)
n_changepoints = trial.suggest_int('n_changepoints', 4, 10)
trend_reg = trial.suggest_float('trend_reg', 0.001, 1, log=True)
n_lags = trial.suggest_int('n_lags', 10, 30)
n_forecasts = trial.suggest_int('n_forecasts', 10, 30)
m = NeuralProphet(
newer_samples_weight=newer_samples_weight,
newer_samples_start=newer_samples_start,
yearly_seasonality=yearly_seasonality,
weekly_seasonality=weekly_seasonality,
seasonality_reg=seasonality_reg,
seasonality_mode=seasonality_mode,
learning_rate=learning_rate,
epochs=epochs,
changepoints_range=changepoints_range,
n_changepoints=n_changepoints,
trend_reg=trend_reg,
n_lags=n_lags,
n_forecasts=n_forecasts,
loss_func='MSE',
collect_metrics=['rmse']
)
for e in events['event'].unique():
m.add_events(e, mode='multiplicative')
df_with_events = m.create_df_with_events(df, events)
df_train, df_val = m.split_df(df_with_events, freq="D", valid_p=0.05)
metrics = m.fit(df_train, freq="D", validation_df=df_val, metrics=True, progress=False)
return metrics['RMSE_val'].min()
# 定义Optuna study对象
study = optuna.create_study(direction='minimize')
# 运行参数搜索
study.optimize(objective, n_trials=50)
# 打印最佳参数和目标值
print('Best parameter:', study.best_params)
print('Best target value:', study.best_value)
最终输出的结果为:
Best parameter: {'newer_samples_weight': 26, 'newer_samples_start': 0.6024308578115192, 'seasonality_reg': 306.3632013108877, 'seasonality_mode': 'multiplicative', 'yearly_seasonality': 9, 'weekly_seasonality': 4, 'epochs': 28, 'learning_rate': 0.09906363251832066, 'changepoints_range': 0.6319992574004804, 'n_changepoints': 9, 'trend_reg': 0.16600258440062496, 'n_lags': 24, 'n_forecasts': 12}
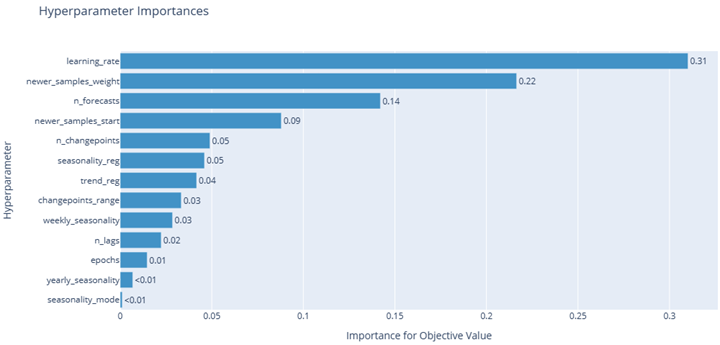
fig1 = optuna.visualization.plot_param_importances(study)
fig1.show()
fig2 = optuna.visualization.plot_optimization_history(study)
fig2.show()
fig3 = optuna.visualization.plot_parallel_coordinate(study)
fig3.show()
基于训练好的超参数使用模型:
import pandas as pd
from neuralprophet import NeuralProphet, set_log_level
set_log_level("ERROR")
df = pd.read_csv('data/data.csv')
df['ds'] = pd.to_datetime(df['ds'])
events = pd.read_csv("data/holidays-events.csv")
para = {'newer_samples_weight': 26,
'newer_samples_start': 0.6024308578115192,
'seasonality_reg': 306.3632013108877,
'seasonality_mode': 'multiplicative',
'yearly_seasonality': 9,
'weekly_seasonality': 4,
'epochs': 28,
'learning_rate': 0.09906363251832066,
'changepoints_range': 0.6319992574004804,
'n_changepoints': 9,
'trend_reg': 0.16600258440062496,
'n_lags': 24,
'n_forecasts': 12}
m = NeuralProphet(**para)
for e in events['event'].unique():
m.add_events(e, mode='multiplicative')
df_with_events = m.create_df_with_events(df, events)
metrics = m.fit(df_with_events)
forecast = m.predict(df_with_events)
fig1 = m.plot(forecast)
fig2 = m.plot_components(forecast)
fig3 = m.plot_parameters()
fig1.show()
fig2.show()
fig3.show()
参考链接: