Prophet简介
时间序列(Time Series Analysis)作为计量经济学的三大数据形态之一,比较主流的观点认为,时间序列受四种成分影响:
- 趋势:宏观、长期、持续性的作用力
- 周期:比如商品价格在较短时间内,围绕某个均值上下波动;
- 季节:变化规律相对固定,并呈现某种周期特征。”季节”不一定按年计。每周、每天的不同时段的规律,也可称作季节性。
- 随机:随机的不确定性,也是人们常说的随机过程(Stochastic Process)。
这四种成分对时间序列的影响,常归纳为累积和相乘两种。累积意味着四种成分相互叠加,它们之间相对独立,相互影响较小。而相乘意味着它们相互影响更为明显。
实践中最常见的分析模型包括三类:自回归、移动平均和整合模型。他们相互结合,又产生了ARIMA(Auto Regression Integreated Moving Average)等模型,但是由于ARIMA使用起来非常的麻烦,所以Facebook推出了使用方便同时能获得高质量预测结果的Prophet。Facebook用它来进行容量安排和目标设置等工作,以便有效地分配稀有资源,以及评测和考核结果。并不是所有问题都可以用同样的程序解决。Prophet所针对的,是Facebook的商业预测任务,这些任务一般具有以下特征:
- 观察值是按每小时或每天或每周或每月给出的一段历史数据
- 多尺度的周期性:一周七天,一个月30天,12个月等等
- 提前已知的一些重要假期:各种法定节日或传统节日
- 数据中存在缺失值或异常值
- 历史趋势的变化
- 趋势是非线性变化,达到自然极限或趋于饱和
Prophet通过将全自动预测与在线学习相结合从而保证了该工具能够解决大多数商业业务问题,Prophet工作流程如下图所示:
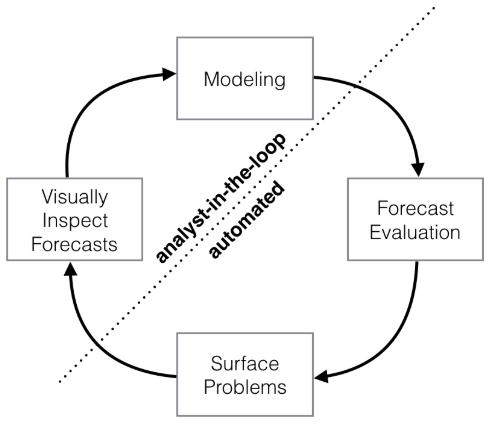
上图是prophet的整体框架,整个过程分为四部分:Modeling、Forecast Evaluation、Surface Problems以及Visually Inspect Forecasts。从整体上看,这是一个循环结构,而这个结构又可以根据虚线分为分析师操纵部分与自动化部分,因此,整个过程就是分析师与自动化过程相结合的循环体系,也是一种将问题背景知识与统计分析融合起来的过程,这种结合大大的增加了模型的适用范围,提高了模型的准确性。按照上述的四个部分,prophet的预测过程为:
- Modeling:建立时间序列模型。分析师根据预测问题的背景选择一个合适的模型。
- Forecast Evaluation:模型评估。根据模型对历史数据进行仿真,在模型的参数不确定的情况下,我们可以进行多种尝试,并根据对应的仿真效果评估哪种模型更适合。
- Surface Problems:呈现问题。如果尝试了多种参数后,模型的整体表现依然不理想,这个时候可以将误差较大的潜在原因呈现给分析师。
- Visually Inspect Forecasts:以可视化的方式反馈整个预测结果。当问题反馈给分析师后,分析师考虑是否进一步调整和构建模型。
相比于目前开源的一些预测工具,Prophet主要有以下两点优势:
- Prophet能够让你更方便直接地创建一个预测任务,而其他的一些工具包(ARMA,指数平滑)等,这些工具每个有自己的优缺点及参数,即使是优秀的数据分析师想要从众多的模型中选择合适的模型及相应的参数也是够让他头皮发麻的。
- Prophet是为非专家们”量身定制”的。为什么这么说呢?你利用Prophet可以直接通过修改季节参数来拟合季节性,修改趋势参数来拟合趋势信息,指定假期来拟合假期信息等等。
Prophet实例解析
Prophet遵循sklearn模型API。我们可以创建一个prophet类的实例,然后调用它的fit和predict方法。Prophet的输入必须包含两列数据:ds和y,其中ds是时间戳列,必须是时间信息;y列必须是数值,代表我们需要预测的信息。我们使用官方示例中的数据进行讲解。
示例代码:
import pandas as pd
from fbprophet import Prophet
df = pd.read_csv('example_wp_log_peyton_manning.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)
forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail()
fig1 = m.plot(forecast)
fig2 = m.plot_components(forecast)
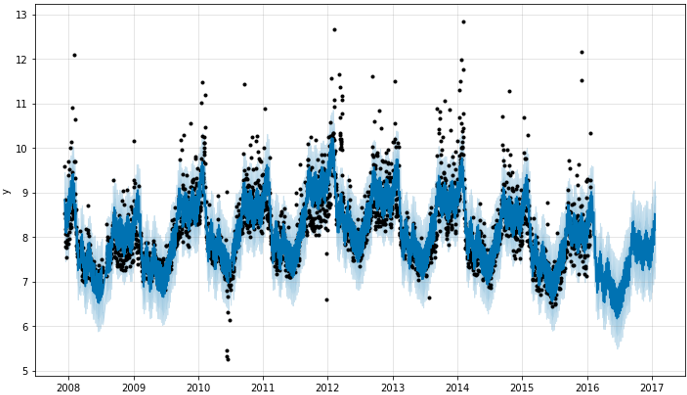
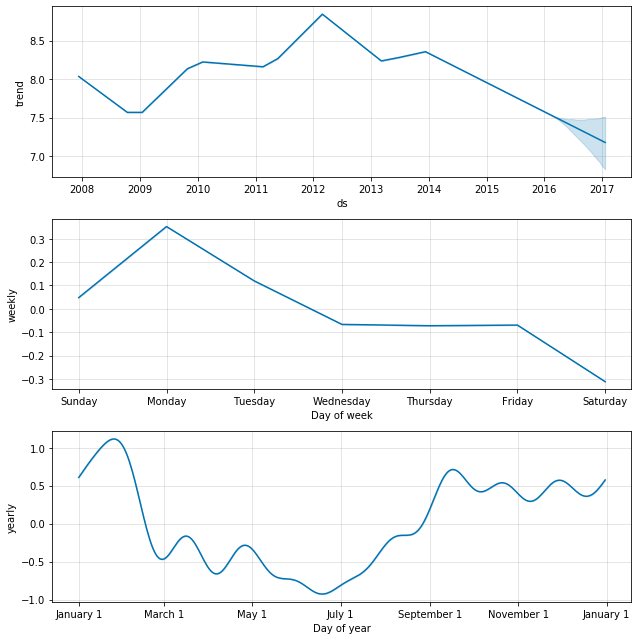
Prophet的官网上本身没有对API的进一步说明。我们只能从代码入手:
class Prophet(object):
"""Prophet forecaster.
Parameters
----------
growth: String 'linear' or 'logistic' to specify a linear or logistic
trend.
changepoints: List of dates at which to include potential changepoints. If
not specified, potential changepoints are selected automatically.
n_changepoints: Number of potential changepoints to include. Not used
if input `changepoints` is supplied. If `changepoints` is not supplied,
then n_changepoints potential changepoints are selected uniformly from
the first `changepoint_range` proportion of the history.
changepoint_range: Proportion of history in which trend changepoints will
be estimated. Defaults to 0.8 for the first 80%. Not used if
`changepoints` is specified.
Not used if input `changepoints` is supplied.
yearly_seasonality: Fit yearly seasonality.
Can be 'auto', True, False, or a number of Fourier terms to generate.
weekly_seasonality: Fit weekly seasonality.
Can be 'auto', True, False, or a number of Fourier terms to generate.
daily_seasonality: Fit daily seasonality.
Can be 'auto', True, False, or a number of Fourier terms to generate.
holidays: pd.DataFrame with columns holiday (string) and ds (date type)
and optionally columns lower_window and upper_window which specify a
range of days around the date to be included as holidays.
lower_window=-2 will include 2 days prior to the date as holidays. Also
optionally can have a column prior_scale specifying the prior scale for
that holiday.
seasonality_mode: 'additive' (default) or 'multiplicative'.
seasonality_prior_scale: Parameter modulating the strength of the
seasonality model. Larger values allow the model to fit larger seasonal
fluctuations, smaller values dampen the seasonality. Can be specified
for individual seasonalities using add_seasonality.
holidays_prior_scale: Parameter modulating the strength of the holiday
components model, unless overridden in the holidays input.
changepoint_prior_scale: Parameter modulating the flexibility of the
automatic changepoint selection. Large values will allow many
changepoints, small values will allow few changepoints.
mcmc_samples: Integer, if greater than 0, will do full Bayesian inference
with the specified number of MCMC samples. If 0, will do MAP
estimation.
interval_width: Float, width of the uncertainty intervals provided
for the forecast. If mcmc_samples=0, this will be only the uncertainty
in the trend using the MAP estimate of the extrapolated generative
model. If mcmc.samples>0, this will be integrated over all model
parameters, which will include uncertainty in seasonality.
uncertainty_samples: Number of simulated draws used to estimate
uncertainty intervals.
"""
def __init__(
self,
growth='linear',
changepoints=None,
n_changepoints=25,
changepoint_range=0.8,
yearly_seasonality='auto',
weekly_seasonality='auto',
daily_seasonality='auto',
holidays=None,
seasonality_mode='additive',
seasonality_prior_scale=10.0,
holidays_prior_scale=10.0,
changepoint_prior_scale=0.05,
mcmc_samples=0,
interval_width=0.80,
uncertainty_samples=1000,
):
Prophet()参数说明:
- growth: 字符串‘linear’或‘logistic’,表示线性或者逻辑增长趋势。
- changepoints: 日期型向量,指定潜在拐点,如果不指定,将会自动选择潜在拐点。例如:changepoints=[‘2014-01-01’]指定2014-01-01这一天是潜在的changepoints。
- n_changepoints: 表示changepoints的数量大小,如果changepoints指定,该传入参数将不会被使用。如果changepoints不指定,将会从输入的历史数据前80%中选取25个(个数由n_changepoints传入参数决定)潜在改变点。
- changepoint_range: 估计趋势变化点的历史比例。如果指定了`changepoints`,则不使用。
- yearly_seasonality: 指定是否分析数据的年季节性,如果为True,默认取傅里叶项为10,最后会输出,yearly_trend,yearly_upper,yearly_lower等数据。
- weekly_seasonality: 指定是否分析数据的周季节性,如果为True,默认取傅里叶项为10,最后会输出,weekly_trend,weekly_upper,weekly_lower等数据。
- daily_seasonality: 指定是否分析数据的天季节性,如果为True,默认取傅里叶项为10,最后会输出,daily_trend,daily_upper,daily_lower等数据。
- holidays: 传入dataframe格式的数据。这个数据包含有holiday列(string)和ds(date类型)和可选列lower_window和upper_window来指定该日期的lower_window或者upper_window范围内都被列为假期。lower_window=-2将包括前2天的日期作为假期。(默认None)
- seasonality_mode: ‘additive'(default) or ‘multiplicative’。季节模型。
- seasonality_prior_scale: 调节季节性组件的强度。值越大,模型将适应更强的季节性波动,值越小,越抑制季节性波动。
- holidays_prior_scale: 调节节假日模型组件的强度。值越大,该节假日对模型的影响越大,值越小,节假日的影响越小。
- mcmc_samples: mcmc采样,用于获得预测未来的不确定性。若大于0,将做mcmc样本的全贝叶斯推理,如果为0,将做最大后验估计。
- interval_width: 衡量未来时间内趋势改变的程度。表示预测未来时使用的趋势间隔出现的频率和幅度与历史数据的相似度,值越大越相似。当mcmc_samples=0时,该参数仅用于增长趋势模型的改变程度,当mcmc_samples>0时,该参数也包括了季节性趋势改变的程度。
- uncertainty_samples: 用于估计不确定性区间的模拟抽取数
changepoint_prior_scale: 增长趋势模型的灵活度。调节“changepoint”选择的灵活度,值越大选择的“changepoint”越多,使模型对历史数据的拟合程度变强,然而也增加了过拟合的风险。
def make_future_dataframe(self, periods, freq='D', include_history=True): """Simulate the trend using the extrapolated generative model. Parameters ---------- periods: Int number of periods to forecast forward. freq: Any valid frequency for pd.date_range, such as 'D' or 'M'. include_history: Boolean to include the historical dates in the data frame for predictions. Returns ------- pd.Dataframe that extends forward from the end of self.history for the requested number of periods. """
make_future_dataframe()参数说明:
- periods: 向前预测步数
- freq: 预测单位小时为’H’,天为’D’,月为’M’
- include_history: 是否包含历史数据的预测
Prophet的算法实现
在时间序列分析领域,有一种常见的分析方法叫做时间序列的分解(Decomposition of Time Series),它把时间序列$y_t$分成几个部分,分别是季节项$S_t$,趋势项$T_t$,剩余项$R_t$。也就是说对所有的$t\geq0$,都有$y_t=S_t+T_t+R_t$。除了加法的形式,还有乘法的形式,也就是:$y_t=S_t\times T_t\times R_t$。
以上式子等价于$\ln y_t=\ln S_t\times \ln T_t\times \ln R_t$。所以,有的时候在预测模型的时候,会先取对数,然后再进行时间序列的分解,就能得到乘法的形式。在fbprophet算法中,作者们基于这种方法进行了必要的改进和优化。
一般来说,在实际生活和生产环节中,除了季节项,趋势项,剩余项之外,通常还有节假日的效应。所以,在prophet算法里面,作者同时考虑了以上四项,也就是:
$$y(t)=g(t)+s(t)+h(t)+\epsilon_t$$
- g(t):表示趋势项,它表示时间序列在非周期上面的变化趋势。
- s(t):表示周期项,或者称为季节项,一般来说是以周或者年为单位。
- h(t):表示节假日项,表示在当天是否存在节假日。
- $\epsilon_t$:表示误差项或者称为剩余项。
Prophet算法就是通过拟合这几项,然后最后把它们累加起来就得到了时间序列的预测值。
趋势项$g(t)$
在Prophet算法里面,趋势项有两个重要的函数,一个是基于逻辑回归函数(logistic function)的,另一个是基于分段线性函数(piecewise linear function)的。
逻辑回归的趋势项
说起逻辑回归,一般会想起这样的形式:$\sigma(x)=\frac{1}{1+e^{-x}}$,它的导数是${\sigma}'(x)=\sigma(x)\cdot(1-\sigma(x))$,并且$\lim_{x\to\infty}\sigma(x)=1,\lim_{x\to-\infty}\sigma(x)=0$,如果增加一些参数的话,那么逻辑回归就可以改写成:
$$f(x)=\frac{C}{1+e^{-k(x-m)}}$$
这里的$C$称为曲线的最大渐近值,$k$表示曲线的增长率,$m$表示曲线的中点。当$C=1,k=1,m=0$时,恰好就是大家常见的sigmoid函数的形式。
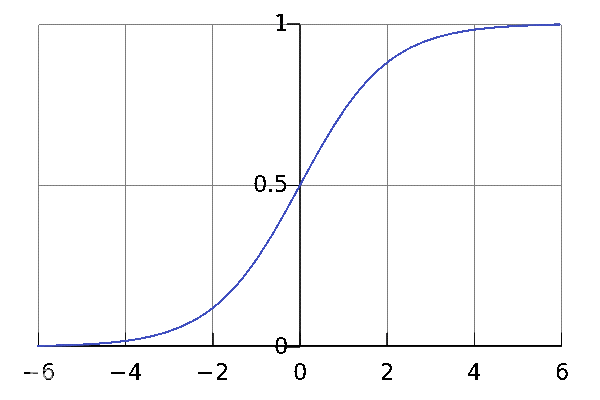
从sigmoid的函数表达式来看,它满足以下的微分方程:${y}’=y(1-y)$。那么,如果使用分离变量法来求解微分方程${y}’=y(1-y)$就可以得到:
$$\frac{y^{\prime}}{y}+\frac{y^{\prime}}{1-y}=1\Rightarrow\ln\frac{y}{1-y}=1\Rightarrow y=1/\left(1+Ke^{-x}\right)$$
但是在现实环境中,函数$f(x)=\frac{C}{1+e^{-k(x-m)}}$的三个参数$C,k,m$不可能都是常数,而很有可能是随着时间的迁移而变化的,因此,在Prophet里面,作者考虑把这三个参数全部换成了随着时间而变化的函数,也就是$C=C(t),k=k(t),m=m(t)$。除此之外,在现实的时间序列中,曲线的走势肯定不会一直保持不变,在某些特定的时候或者有着某种潜在的周期曲线会发生变化,这种时候,就有学者会去研究变点(拐点)检测,也就是所谓changepoint detection。例如下面的这幅图的$t_1^*,t_2^*$就是时间序列的两个变点。
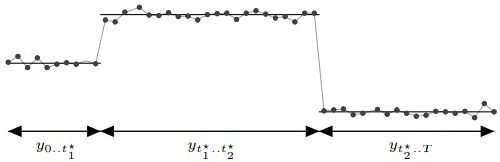 在Prophet里面,是需要设置变点的位置的,而每一段的趋势和走势也是会根据变点的情况而改变的。在程序里面有两种方法,一种是通过人工指定的方式指定变点的位置;另外一种是通过算法来自动选择。在默认的函数里面,Prophet会选择n_changepoints=25个变点,然后设置变点的范围是前80%(changepoint_range),也就是在时间序列的前80%的区间内会设置变点。通过forecaster.py里面的set_changepoints函数可以知道,首先要看一些边界条件是否合理,例如时间序列的点数是否少于n_changepoints等内容;其次如果边界条件符合,那变点的位置就是均匀分布的,这一点可以通过np.linspace这个函数看出来。
在Prophet里面,是需要设置变点的位置的,而每一段的趋势和走势也是会根据变点的情况而改变的。在程序里面有两种方法,一种是通过人工指定的方式指定变点的位置;另外一种是通过算法来自动选择。在默认的函数里面,Prophet会选择n_changepoints=25个变点,然后设置变点的范围是前80%(changepoint_range),也就是在时间序列的前80%的区间内会设置变点。通过forecaster.py里面的set_changepoints函数可以知道,首先要看一些边界条件是否合理,例如时间序列的点数是否少于n_changepoints等内容;其次如果边界条件符合,那变点的位置就是均匀分布的,这一点可以通过np.linspace这个函数看出来。
下面假设已经放置了$S$个变点了,并且变点的位置是在时间戳$s_j, 1\leq j \leq S$上,那么在这些时间戳上,我们就需要给出增长率的变化,也就是在时间戳$s_j$上发生的change in rate。可以假设有这样一个向量:$\delta\in\mathbb{R}^{S}$其中$\delta_j$表示在时间戳$s_j$上的增长率的变化量。如果一开始的增长率我们使用$k$来代替的话,那么在时间戳$t$上的增长率就是$k+\sum_{j:t>s_j}\delta_j$,通过一个指示函数$a(t)\in\{0,1\}^S$就是:
$$a_{j}(t)=\left\{\begin{array}{ll}{1,}&{\text{if }t\geq s_{j}}\\{0,}&{\text{otherwise}}\end{array}\right.$$
那么在时间戳$t$上面的增长率就是$k+s^T\delta$。一旦变化量$k$确定了,另外一个参数$m$也要随之确定。在这里需要把线段的边界处理好,因此通过数学计算可以得到:
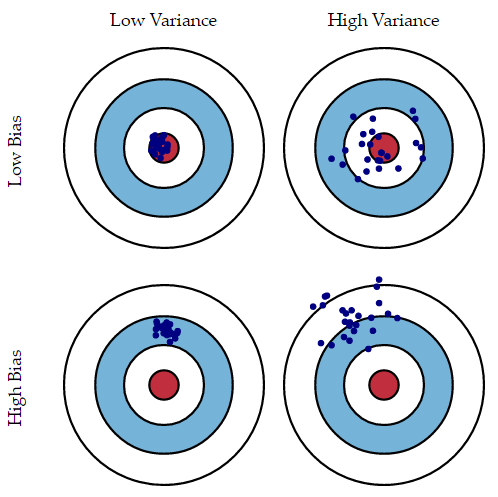
$$\gamma_{j}=\left(s_{j}-m-\sum_{\ell 分段线性的趋势项 众所周知,线性函数指的是$y=kx+b$而分段线性函数指的是在每一个子区间上,函数都是线性函数,但是在整段区间上,函数并不完全是线性的。正如下图所示,分段线性函数就是一个折线的形状。 因此,基于分段线性函数的模型如: $$g(t)=(k+a(t)\delta)\cdot t+(m+a(t)^T\gamma)$$ 其中$k$表示增长率(growth rate),$\delta$表示增长率的变化量,$m$表示offset parameter。而这两种方法(分段线性函数与逻辑回归函数)最大的区别就是$\gamma$的设置不一样,在分段线性函数中,$\gamma=(\gamma_1,…,\gamma_S)^T,\delta_j=-s_j\delta_j$。注意:这与之前逻辑回归函数中的设置是不一样的。 growth=’linear’和growth=’logistic’该如何选择? 具体选择要看你预测模型的业务背景,如果是做一些类似市场份额的预测,因为存在着总量天花板(比如因为人口、环境的限制,不可能一直快速增长,总会到达一个饱和点),可以选择logistic;一般情况下都是使用linear,prophet默认应该也是选择的linear。 变点(拐点)的选择(Changepoint Selection) 另一个要回答的问题是时间序列是否会因为其他现象发生潜在变化,例如新产品发布、不可预见的灾难等。这种情况下,增长率是会改变的。这些突变点是自动选择的,然而有需要的时候也可以手动输入突变点。Prophet中默认设置的拐点是25个,并且均匀地分布在前80%的时间序列里。然后会用稀疏先验(Sparse Prior, L1范数)选出尽量少的几个点建模。采用L1范数的主要问题是过拟合(Overfitting)。 在介绍变点之前,先要介绍一下Laplace分布,它的概率密度函数为: $$f(x|\mu,b)=\frac{\exp(-\frac{|x-\mu|}{b})}{2b}$$ 其中$\mu$表示位置参数,$b>0$表示尺度参数。Laplace分布与正态分布有一定的差异。 在Prophet算法中,是需要给出变点的位置、个数、以及增长的变化率的。因此,有三个比较重要的指标,那就是 在整个开源框架里面,在默认的场景下,变点的选择是基于时间序列的前80%的历史数据,然后通过等分的方法找到25个变点(changepoints),而变点的增长率是满足Laplace分布$\delta_{j}\sim\text{Laplace}(0,0.05)$的。因此,当$\tau$趋近于零的时候,$\delta_{j}$也是趋向于零的,此时的增长函数将变成全段的逻辑回归函数或者线性函数。这一点从$g(t)$的定义可以轻易地看出。 对未来的预估(Trend Forecast Uncertainty) 从历史上长度为$T$的数据中,我们可以选择出$S$个变点,它们所对应的增长率的变化量是$\delta_{j}\sim\text{Laplace}(0,\tau)$。此时我们需要预测未来,因此也需要设置相应的变点的位置,从代码中看,在forecaster.py的sample_predictive_trend函数中,通过Poisson分布等概率分布方法找到新增的changepoint_ts_new的位置,然后与changepoint_t拼接在一起就得到了整段序列的changepoint_ts。 第一行代码的1保证了 changepoint_ts_new 里面的元素都大于 change_ts 里面的元素。除了变点的位置之外,也需要考虑 $\delta$ 的情况。这里令 $\lambda=\sum_{j=1}^{S}\frac{\left|\delta_j\right|}{S}$,于是新的增长率的变化量就是按照下面的规则来选择的:当 $J>T$ 时: $$\delta_{j}=\{\begin{array}{l}{0,\text{with probability }(T-S)/T}\\{\sim\text{Laplace}(0,\lambda),\text{with probability }S/T}\end{array}$$ 几乎所有的时间序列预测模型都会考虑这个因素,因为时间序列通常会随着天、周、月、年等季节性的变化而呈现季节性的变化,也称为周期性的变化。对于周期函数而言,大家能够马上联想到的就是正弦余弦函数。而在数学分析中,区间内的周期性函数是可以通过正弦和余弦的函数来表示的:假设 $f(x)$ 是以 $2\pi$ 为周期的函数,那么它的傅立叶级数就是 $a_0+\sum_{n=1}^{\infty}(a_n\cos(nx)+b_n\sin(nx))$。 在论文中,作者使用傅立叶级数来模拟时间序列的周期性。假设 $P$ 表示时间序列的周期,$P=365.25$ 表示以年为周期,$P=7$ 表示以周为周期。它的傅立叶级数的形式都是: $$s(t)=\sum_{n=1}^{N}(a_{n}\cos(\frac{2\pi nt}{P})+b_{n}\sin(\frac{2\pi nt}{P}))$$ 就作者的经验而言,对于以年为周期的序列($P=365.25$)而言,$N=10$;对于以周为周期的序列($P=7$)而言,$N=3$。这里的参数可以形成列向量:$\beta=(a_1,b_1,…,a_N,b_N)^T$。 当 $N=10$ 时,$X(t)=[\cos(\frac{2\pi (1)t}{365.25}),…,\sin(\frac{2\pi (10)t)}{365.25})]$ 当 $N=3$ 时,$X(t)=[\cos(\frac{2\pi (1)t}{7}),…,\sin(\frac{2\pi (3)t)}{7})]$ 因此,时间序列的季节项就是:$s(t)=X(t)\beta$ 而 $\beta$ 的初始化是 $\beta\sim\mathrm{Normal}(0,\sigma^{2})$。这里的 $\sigma$ 是通过 seasonality_prior_scal 来控制的,也就是说 $\sigma= \text{seasonality\_prior\_scale}$。这个值越大,表示季节的效应越明显;这个值越小,表示季节的效应越不明显。同时,在代码里面,seasonality_mode 也对应着两种模式,分别是加法和乘法,默认是加法的形式。在开源代码中,$X_t$ 函数是通过 fourier_series 来构建的。 在现实环境中,除了周末,同样有很多节假日,而且不同的国家有着不同的假期。在 Prophet 里面,通过维基百科里面对各个国家的节假日的描述,hdays.py 收集了各个国家的特殊节假日。除了节假日之外,用户还可以根据自身的情况来设置必要的假期,例如 TheSuperBowl,双十一等。 由于每个节假日对时间序列的影响程度不一样,例如春节,国庆节则是七天的假期,对于劳动节等假期来说则假日较短。因此,不同的节假日可以看成相互独立的模型,并且可以为不同的节假日设置不同的前后窗口值,表示该节假日会影响前后一段时间的时间序列。用数学语言来说,对与第 $i$ 个节假日来说,$D_i$ 表示该节假日的前后一段时间。为了表示节假日效应,我们需要一个相应的指示函数(indicator function),同时需要一个参数 $\kappa_{i}$ 来表示节假日的影响范围。假设我们有 $L$ 个节假日,那么 $h(t)=Z(t)\kappa=\sum_{i=1}^{L}\kappa_{i}\cdot1_{\{t\in D_{i}\}}$。其中 $Z(t)=(1_{\{t\in D_{1}\}},\cdots,1_{\{t\in D_{L}\}}),\kappa=(\kappa_{1},\cdots,\kappa_{L})^{T}$, 其中 $\kappa\sim\text{Normal}(0,v^{2})$ 并且该正态分布是受到 $v=\text{holidays\_prior\_scale}$ 这个指标影响的。默认值是 10,当值越大时,表示节假日对模型的影响越大;当值越小时,表示节假日对模型的效果越小。用户可以根据自己的情况自行调整。 按照以上的解释,我们的时间序列已经可以通过增长项,季节项,节假日项来构建了,i.e. $$y(t)=g(t)+s(t)+h(t)+\epsilon_t$$ 下一步我们只需要拟合函数就可以了,在 Prophet 里面,作者使用了 pyStan 这个开源工具中的 L-BFGS 方法来进行函数的拟合。 本质上讲,Prophet 是由四个组件组成的自加性回归模型: Prophet 其中最重要的思想就是曲线拟合,这与传统的时序预测算法有很大的不同。 统计模型的一个重要的特点在于,包含有随机误差,而且对随机误差有完整的解释体系。预测结果常常是这样的:“下周 xx 销售额 1000 到 1100 万元之间的概率是 90%”。预测结果实际上是出现在某个置信空间(Confidence interval)的概率。预测“准不准”是暂时、局部的——持续几小时还是几个月?不准的时候,会不会偏离得很离谱? 实际上,预测误差是由三个变量组成:偏差(bias)、方差(variance)和自带误差。 言归正传,Prophet 认为置信区间的不确定性来自于:趋势、季节性(含年月日等周期)和其他观测噪声。 趋势中的不确定性 预测中,不确定性最大的来源就在于未来趋势改变的不确定性。在之前教程中的时间序列实例中,我们可以发现历史数据具有明显的趋势性。Prophet 能够监测并去拟合它,但是我们期望得到的趋势改变究竟会如何走向呢?或许这是无解的,因此我们尽可能地做出最合理的推断,假定“未来将会和历史具有相似的趋势”。尤其重要的是,我们假定未来趋势的平均变动频率和幅度和我们观测到的历史值是一样的,从而预测趋势的变化并通过计算,最终得到预测区间。这种衡量不确定性的方法具有以下性质:变化速率灵活性更大时,预测的不确定性也会随之增大。原因在于如果将历史数据中更多的变化速率加入了模型,也就代表我们认为未来也会变化得更多,就会使得预测区间成为反映过拟合的标志。预测区间的宽度(默认下,是 80%)可以通过设置 interval_width 参数来控制: 季节效应估计中的不确定性 默认情况下,Prophet 只会返回趋势中的不确定性和观测值噪声的影响。你必须使用贝叶斯取样的方法来得到季节效应的不确定性,可通过设置 mcmc.samples 参数(默认下取 0)来实现。 上述代码将最大后验估计(MAP)修改为马尔科夫蒙特卡洛取样(MCMC)。执行后可通过绘图的方式直观的观测到季节效应的不确定性。 观测值的噪声影响处理异常值最好的方法是移除它们,而Prophet能够处理缺失数据的。如果在历史数据中某行的值为空(NA),但是在待预测日期数据框future中仍保留这个日期,那么Prophet依旧可以给出该行的预测值。 fbprophet为Prophet在Python环境下的包,想要使用fbprohhet并没有想象中的那么简单,特别是在Windows系统上可能发生错误。主要原因是fbprophet基于pystan,pystan基于cython。问题会卡在pystan的安装上。 即正确的安装流程为: 在安装pystan时会报如下错误:WARNING: pystan: MSVC compiler is not supported 。具体原因可在官方说明中找到: PyStan is partially supported under Windows with the following caveats: Python 2.7: Doesn’t support parallel sampling. When drawing samples n_jobs=1 must be used) Python 3.5 or higher: Parallel sampling is supported MSVC compiler is not supported. PyStan requires a working C++ compiler. Configuring such a compiler is typically the most challenging step in getting PyStan running. PyStan is tested against the MingW-w64 compiler which works on both Python versions (2.7, 3.x) and supports x86 and x64. Due to problems with MSVC template deduction, functions with Eigen library are failing. Until this and other bugs are fixed no support is provided for Windows+MSVC. Currently, no fix is known for this problem, other than to change the compiler to GCC or clang-cl. 解决方案为:将Python编译环境更改为MingW-w64。 完后后再执行安装即可。如果是Anaconda环境,除了上述步骤外,还需执行: Linux下报ModuleNotFoundError: No module named ‘pystan’的解决方案: update:无需安装编译器 参考链接: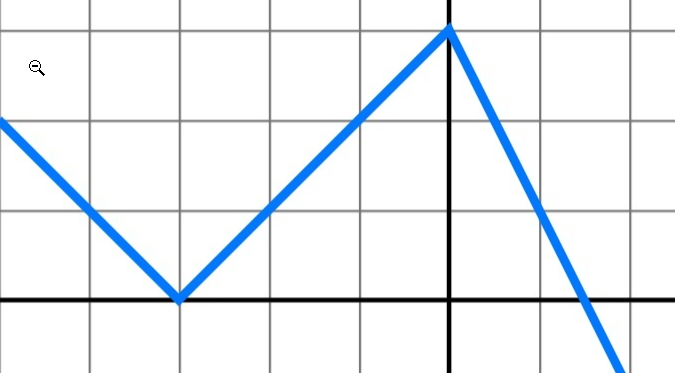
changepoint_ts_new = 1 + np.random.rand(n_changes) * (T - 1)
changepoint_ts = np.concatenate((self.changepoints_t, changepoint_ts_new))
周期(季节)项 $s(t)$
节假日项 $h(t)$
模型拟合(Model Fitting)

Prophet 的置信区间
my_model = Prophet(interval_width=0.95) # 设置置信空间为 95%(如果不设置的话默认 80%)
my_model.fit(data)
my_model = Prophet(interval_width=0.95, mcmc_samples=500)
my_model.fit(data)
Prophet的安装
pip install cython
pip install pystan
pip install fbprophet
[build]
compiler=mingw32
conda update conda
conda install libpython m2w64-toolchain -c msys2
pip uninstall pystan
pip install pystan~=2.14
pip install fbprophet
pip install pystan==2.17.1.0
pip install fbprophet==0.6
pip install --upgrade fbprophet
Prophet调参经验



