超参数调优之贝叶斯优化

超参数优化简介

目前人工智能和深度学习越趋普及，大家可以使用开源的Scikit-Learn、TensorFlow来实现机器学习模型。对于各种模型而言，或多或少都具有要调节的超参数。相同的模型应用在不同的数据集上，如何选择一组最优超参数至关重要，很大程度上决定了模型的性能。超参数是在建立模型时用来控制算法行为的参数，这些参数不能从正常的训练过程中学习，他们需要在训练模型之前被分配。

机器学习中的超参数优化旨在寻找使得机器学习算法在验证数据集上表现性能最佳的超参数。超参数与一般模型参数不同，超参数是在训练前提前设置的。举例来说，随机森林算法中树的数量就是一个超参数，而神经网络中的权值则不是超参数。

超参数优化找到一组超参数，这些超参数返回一个优化模型，该模型减少了预定义的损失函数，进而提高了给定独立数据的预测或者分类精度。

常见调参方法

• Heuristic Tuning手动调参
  • 经验法，耗时长。
  • 老人看经验、新人看运气
• Grid Search网格搜索/穷举搜索
  • 搜索整个超参数空间，在高维空间容易遇到维度灾难，不实用。
  • 网格搜索是一种昂贵的方法。假设我们有n个超参数，每个超参数有两个值，那么配置总数就是2的N次方。因此，仅在少量配置上进行网格搜索是可行的。
  • 网格搜索可以并行化，使得网格搜索在足够的计算能力下更加可行。
  • 每次trial之间是相互独立的，不能利用先验知识选择下一组超参数。
• Random Search随机搜索
  • 稀疏的简单抽样，试验之间是相互独立的，不能利用先验知识选择下一组超参数。
  • 超参通过并行选择，但试验次数要少得多，而性能却相当。一些超参可能会产生良好的性能，另一些不会。
• Automatic Hyperparameter Tuning自动超参数调优
  • 自动超参数调整形成了关于超参数设置和模型性能之间关系的知识，能利用先验知识选择下一组超参数。
  • 首先在多个配置中收集性能，然后进行一些推断并确定接下来要尝试的配置。目的是在找到最佳状态时尽量减少试验次数。
  • 这个过程本质上是顺序的，不容易并行化。
  • 调整超参数的大多数方法都属于基于顺序模型的全局优化（SMBO）。这些方法使用代理函数来逼近真正的黑盒函数。SMBO的内部循环是对该替代品的优化，或者对代理进行某种转换。最大化此代理的配置将是下一个应该尝试的配置。SMBO算法在优化替代品的标准以及他们根据观察历史对替代品进行建模的方式上有所不同。最近在文献中提出了几种用于超参数的SMBO方法：
  • Bayesian Optimization。使用高斯过程对代理进行建模，通常优化 Expected Improvement(EI)，这是新试验将在当前最佳观察上改进的预期概率。高斯过程是函数的分布。来自高斯过程的样本是整个函数。训练高斯过程涉及将此分布拟合到给定数据，以便生成接近观察数据的函数。使用高斯过程，可以计算搜索空间中任何点的EI。接下来将尝试给出最高的EI。贝叶斯优化通常为连续超参数（例如learning rate, regularization coefficient…）提供 non-trivial/off-the-grid 值，并且在一些好的数据集上击败人类表现。Spearmint是一个众所周知的贝叶斯优化实现。
  • SMAC。使用随机森林对目标函数进行建模，从随机森林认为最优的区域（高EI）中抽取下一个点。
  • TPE。是SMAC的改进版本，其中两个分离的模型用于模拟后验。众所周知的TPE实现是hyperopt。

先前写过一篇《算法模型自动超参数优化方法》，但是感觉介绍的还不够详细，特此再梳理一遍。

网格搜索（Grid Search）

网格搜索是一种基本并使用最广泛，也是最自然的超参数调整技术，它类似于手动调优。为网格中指定的所有给定超参数值的每种组合建立模型，并评估和选择最佳模型。例如，一种模型有两个超参数 k_value =[2,3,4,5,6,7,8,9,10] 和 algorithm = [‘auto’, ’ball_tree’, ’kd_tree’, ’brute’]，在这种情况下，网格搜索总共构建了 9 * 4 = 36 ​个不同的模型

动画演示：

网格搜索的缺点就是计算量大。我们试想一下，当需要调节的超参数很多，每一种超参数有许多备选值，那么组合起来运行的时间就是天文数字。另外，在深度学习流行的年代，该方法并不适用，因为深度学习本身运行所需时间就长，一般试不了多少个参数组合。

随机搜索（Random Search）

有没有什么方法能较好地替代网格搜索吗？随机搜索自然被提出来了。使用随机搜索代替网格搜索的动机是，在许多情况下，所有的超参数可能并非同等重要。随机搜索从超参数空间中随机选择参数组合，参数按​ n_iter 给定的迭代次数进行选择。随机搜索已经被实践证明比网格搜索得到的结果更好。

动画演示：

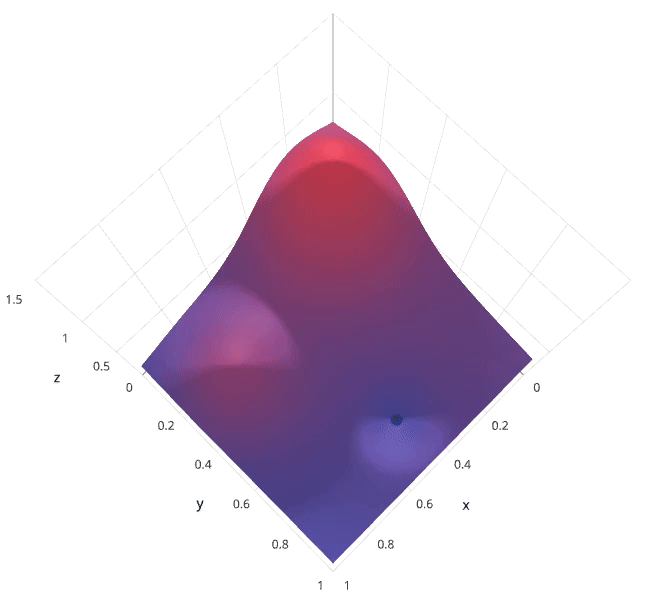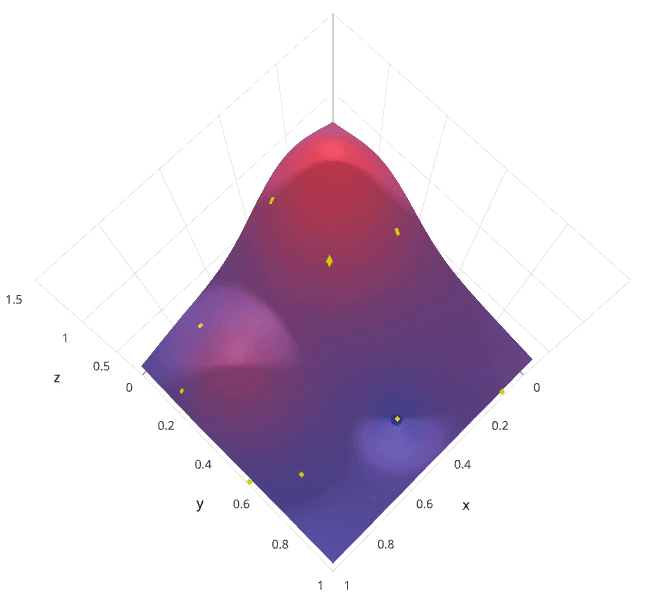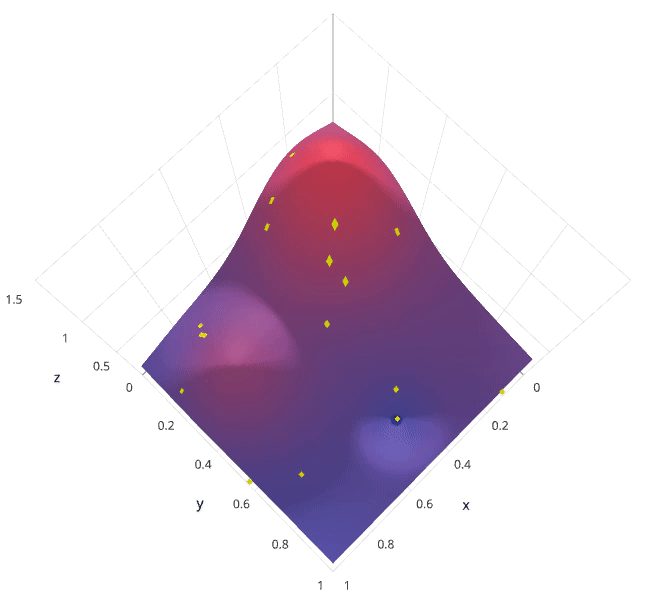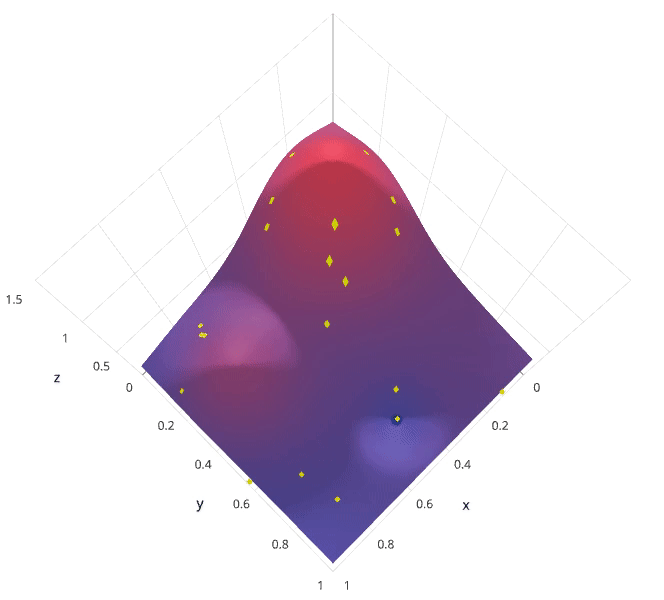
随机搜索的缺点在于，不能保证我们能够找到全局最小值，当迭代次数较少时，局部最小值可能也不会得到。实际应用过程中，应保证一定的迭代次数，可以在整个超参空间上进行搜索。

贝叶斯优化

贝叶斯优化用于机器学习调参由 J. Snoek(2012) 提出，主要思想是，给定优化的目标函数(广义的函数，只需指定输入和输出即可，无需知道内部结构以及数学性质)，通过不断地添加样本点来更新目标函数的后验分布，即高斯过程，直到后验分布基本贴合于真实分布。简单的说，就是考虑了上一次参数的信息，从而更好的调整当前的参数。sequential model-based optimization(SMBO)是贝叶斯优化的最简形式。

动画演示：

它与常规的网格搜索或者随机搜索的区别是：

• 贝叶斯调参采用高斯过程，考虑之前的参数信息，不断地更新先验；网格搜索未考虑之前的参数信息
• 贝叶斯调参迭补补代次数少，速度快；网格搜索速度慢,参数多时易导致维度爆炸
• 贝叶斯调参针对非凸问题依然稳健；网格搜索针对非凸问题易得到局部最优

下图是贝叶斯优化流程框架：

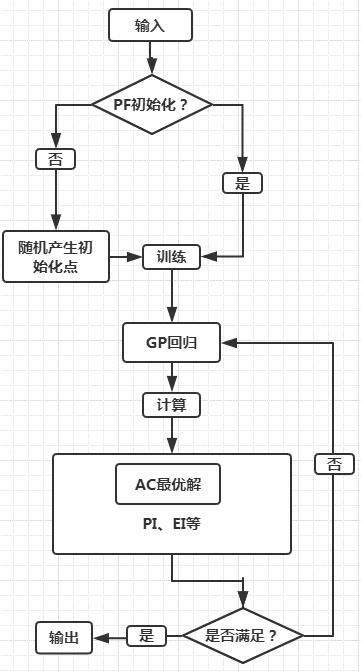
上图描述了贝叶斯优化的大致流程，从图中我们可以知道该优化方法最为重要的两个组件 PF（先验函数，模型是否初始化）、AC（采集函数）：

• PF(Priori Function)若模型分布已知，则可以根据经验选择最优的模型；若未知，则可以采用基于高斯过程的核函数作为黑盒函数自己学习
• AC(Acquisition function)用于找到目标函数下的极大值点（这个点代表着我们模型中需要实验的参数），然后使用这个极大值点投入我们的机器学习或者深度学习模型预测出一个结果，并将这个结果更新到我们的上一步里面的那个高斯分布模型里。不断迭代知道找到一组合适的参数或达到最大迭代次数。

经过多次迭代计算后，基于高斯过程本身具有易陷入局部最优的缺点，我们需要用 AC 来寻找下一个较优的点，那么这就涉及到该步骤的开发和探索之间的权衡：

• 开发：目的是根据后验分布在更好的区域进行采样，均值越大越好
• 探索：目的是在未取样的区域采样，方差越大越好

介绍贝叶斯优化调参，必须要从两个部分讲起：

• 高斯过程，用以拟合优化目标函数
• 贝叶斯优化，包括了“开采”和“勘探”，用以花最少的代价找到最优值

高斯过程

高斯过程可以用于非线性回归、非线性分类、参数寻优等等。以往的建模需要对 $p(y|X)$建模，当用于预测时，则是

$$p(y_{N+1} | X_{N+1})$$

而高斯过程则， 还考虑了 $y_N$和$y_{N+1}$之间的关系，即：

$$p(y_{N+1} | X_{N+1}, y_{N})$$

高斯过程通过假设 Y 值服从联合正态分布，来考虑 $y_N$和$y_{N+1}$之间的关系，因此需要给定参数包括：均值向量和协方差矩阵，即：

$$\begin{bmatrix}y_1 \\y_2 \\… \\y_n \\ \end{bmatrix} \sim N( \mathbf{0}, \begin{bmatrix} k(x_1, x_1) , k(x_1, x_2), …, k(x_1, x_n) \\ k(x_2, x_1) , k(x_2, x_2), …, k(x_2, x_n) \\ … \\ k(x_n, x_1) , k(x_n, x_2), …, k(x_n, x_n) \end{bmatrix} )$$

其中协方差矩阵又叫做 核矩阵, 记为 K ，仅和特征 x 有关，和 y 无关。

高斯过程的思想是： 假设 $Y$服从高维正态分布（先验），而根据训练集可以得到最优的核矩阵 ，从而得到后验以估计测试集$ Y∗$

我们有后验：

$$p(y_*| \mathbf{y} \sim N(K_* K^{-1} \mathbf{y}, ~  K_{**} – K_* K^{-1} K_*^T)$$

其中，$K_*$为训练集的核向量，有如下关系：

$$\begin{bmatrix}
\mathbf{y} \\
y_*
\end{bmatrix} \sim
N(\mathbf{0}, \begin{bmatrix}
K, K_*^T \\
K_*, K_{**} \\
\end{bmatrix})$$

可以发现，在后验公式中，只有均值和训练集 Y 有关，方差则仅仅和核矩阵，也就是训练集和测试集的 X有关，与训练集 Y无关

高斯过程的估计（训练）方法

假设使用平方指数核(Squared Exponential Kernel)，那么有：

$$k(x_1, x_2) = \sigma^2_f exp(\frac{-(x_1 – x_2)^2}{2 l^2})$$

那么所需要的确定的超参数$\theta = [\sigma^2_f, l]$ ，由于 Y服从多维正态分布，因此似然函数为：

$$L = log p(y| x, \theta) = – \frac{1}{2} log|\mathbf{K}| – \frac{1}{2} (y – \mu)^T \mathbf{K}^{-1} (y – \mu) – n*log(2\pi)/2$$

由于 K是由 θ 决定的，所以通过梯度下降即可求出超参数 θ，而根据核矩阵的计算方式也可以进行预测。

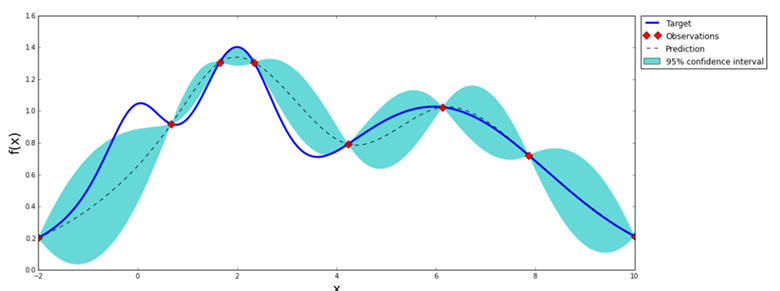
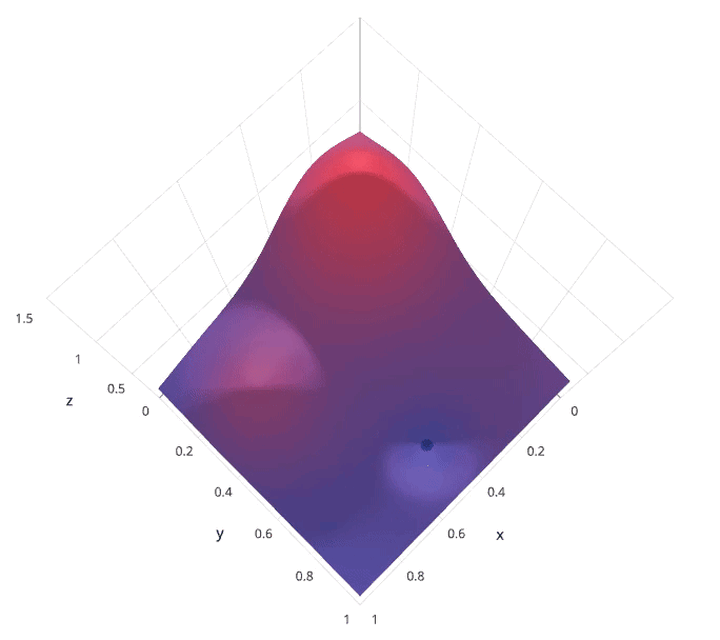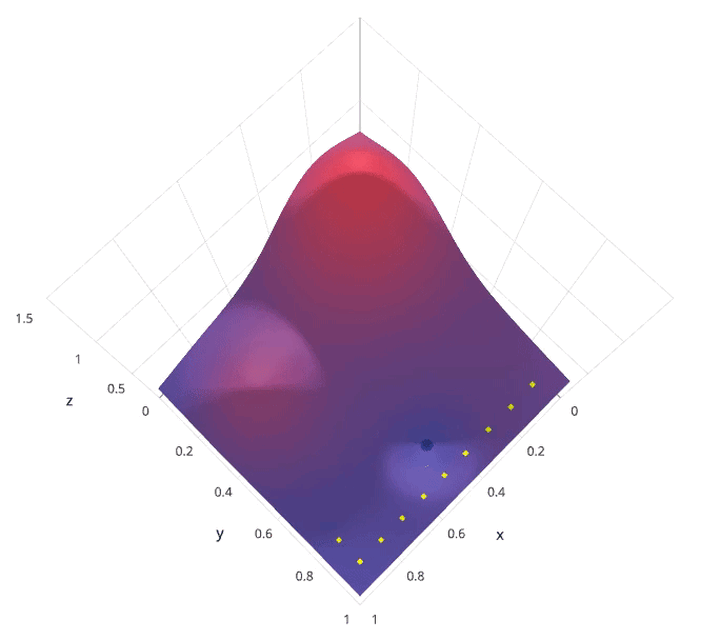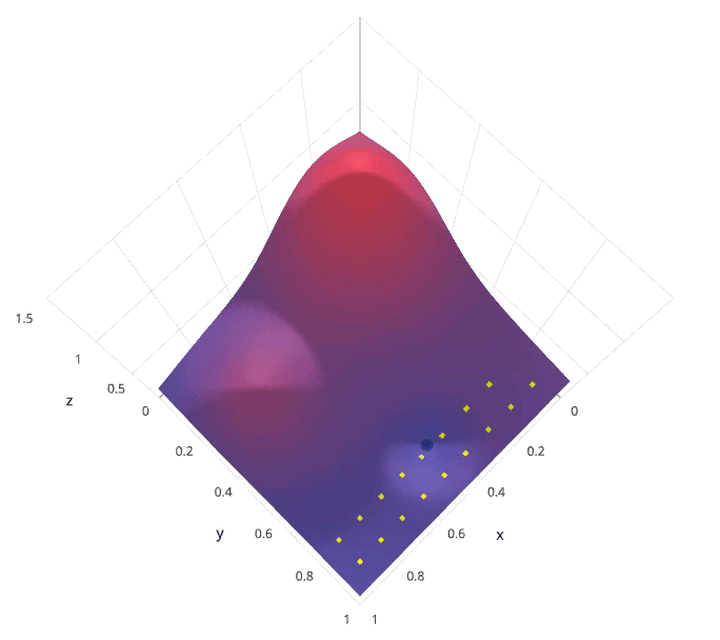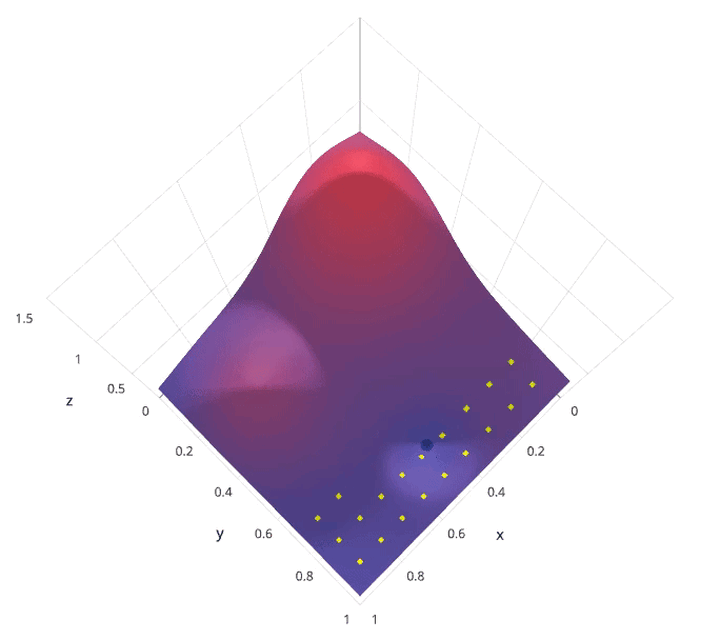
上图是一张高斯分布拟合函数的示意图，可以看到，它只需要九个点，就可以大致拟合出整个函数形状。

贝叶斯优化理论

贝叶斯优化是一种逼近思想，当计算非常复杂、迭代次数较高时能起到很好的效果，多用于超参数确定

基本思想

基于数据使用贝叶斯定理估计目标函数的后验分布，然后再根据分布选择下一个采样的超参数组合。它充分利用了前一个采样点的信息，其优化的工作方式是通过对目标函数形状的学习，并找到使结果向全局最大提升的参数

高斯过程用于在贝叶斯优化中对目标函数建模，得到其后验分布

通过高斯过程建模之后，我们尝试抽样进行样本计算，而贝叶斯优化很容易在局部最优解上不断采样，这就涉及到了开发和探索之间的权衡。

• 开发 (exploitation)： 根据后验分布，在最可能出现全局最优解的区域进行采样, 开发高意味着均值高
• 探索 (exploration): 在还未取样的区域获取采样点， 探索高意味着方差高

而如何高效的采样，即开发和探索，我们需要用到 Acquisition Function, 它是用来寻找下一个 x 的函数。

Acquistion Function

一般形式的Acquisition Funtion是关于x的函数，映射到实数空间R，表示改点的目标函数值能够比当前最优值大多少的概率，目前主要有以下几种主流的Acquisition Function

POI(probability of improvement)

$$POI(X) = P(f(X) \ge f(X^+) + \xi) = \Phi(\frac{\mu(x) – f(X^+) – \xi}{\sigma(x)})$$

其中， $f(X)$为X的目标函数值， $f(X^+)$为 到目前为止 最优的X的目标函数值， $\mu(x), \sigma(x)$ 分别是高斯过程所得到的目标函数的均值和方差，即  $f(X)$的后验分布。$\xi$为trade-off系数,如果没有该系数，POI函数会倾向于取在$ X^+$周围的点，即倾向于exploit而不是explore，因此加入该项进行权衡。

而我们要做的，就是尝试新的X，使得 $POI(X) $最大，则采取该X（因为$f(X)$的计算代价非常大），通常我们使用 蒙特卡洛模拟 的方法进行。

详细情况见下图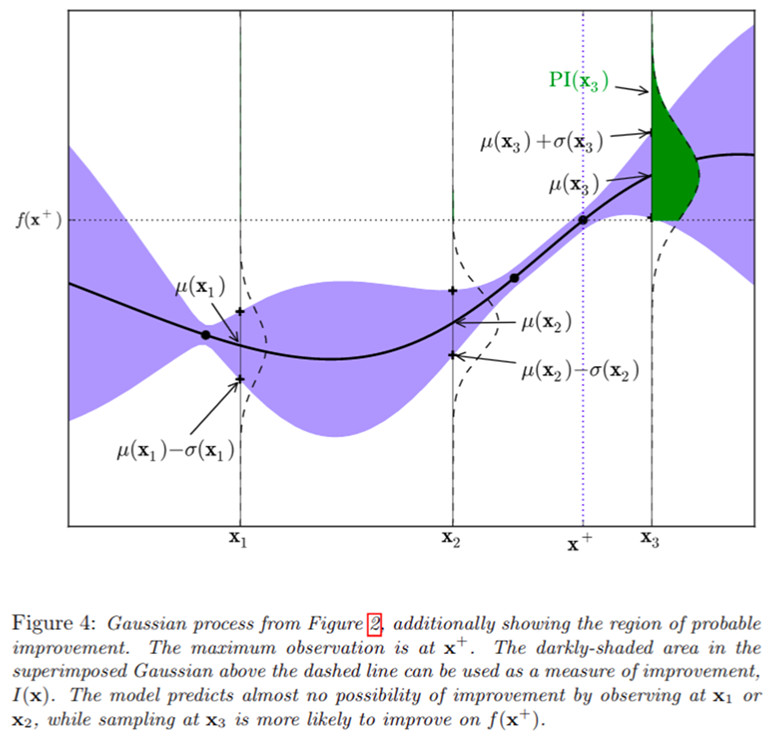

Expected Improvement

POI是一个概率函数，因此只考虑了$f(x)$ 比$ f(x^+)$大的概率，而EI则是一个期望函数，因此考虑了 $f(x)$ 比$ f(x^+)$ 大多少。我们通过下式获取x

$$x = argmax_x \ \  E(\max\{0, f_{t+1}(x) – f(X^+)\}| D_t)$$

其中$ D_t $为前t个样本，在正态分布的假定下，最终得到:

$$EI(x) = \begin{cases}(\mu(x) – f(x^+)) \Phi(Z) + \sigma(x) \phi(Z), if \ \sigma(x) > 0 \\ 0, if \ \sigma(x) = 0 \end{cases}$$

其中 $$Z= \frac{\mu(x) – f(x^+)}{\sigma(x)}$$

Confidence bound criteria

$$LCB(x) = \mu(x) – \kappa \sigma(x)$$

$$UCB(x) = \mu(x) + \kappa \sigma(x)$$

超参数调优工具介绍

BayesianOptimization

Bayesian Optimization 包是一个 Python 库，提供了基于高斯过程的贝叶斯优化算法的实现。

使用 Bayesian Optimization 包的步骤如下：

定义目标函数

首先需要定义一个目标函数，该函数可能是一个黑箱函数，可以是连续或离散的，并且可能存在噪声。该函数必须是一个接受一组输入参数并返回一个标量输出值的函数。

def target_function(x, y):
    return -x**2 - (y-1)**2 + 1

定义搜索空间

然后需要定义搜索空间，即要优化的参数的范围和类型。可以使用 bounds 参数来定义连续参数的范围，或使用 categories 参数来定义分类变量的集合。例如，在下面这个例子中，我们定义了两个连续的参数 x 和 y 的范围均为 [−10,10][-10, 10][−10,10]：

from bayes_opt import BayesianOptimization

pbounds = {'x': (-10, 10), 'y': (-10, 10)}

初始化贝叶斯优化器

接下来，需要初始化贝叶斯优化器。可以通过传递目标函数、搜索空间、以及其他可选参数（如高斯过程模型的超参数）来构造 BayesianOptimization 类。例如：

optimizer = BayesianOptimization(
    f=target_function,
    pbounds=pbounds,
    random_state=42
)

进行优化

最后，可以调用 maximize() 方法来进行迭代优化。在每次迭代中，maximize() 方法使用当前的高斯过程模型来选择下一个样本点并计算其函数值，然后更新模型以反映新的数据点。可以通过设置 n_iter 参数来指定迭代次数，或通过设置 acq 参数来选择不同的采样策略。例如：

optimizer.maximize(n_iter=10, init_points=2, acq='ei')
print(optimizer.max)

其中，n_iter 是迭代次数，init_points 是初始采样点数量，acq 是采样策略，optimizer.max 返回找到的最佳解决方案及其函数值。

这是一个简单的例子，实际上 Bayesian Optimization 还包括许多其他参数和功能，包括调整高斯过程模型的参数、处理噪声等。

Optuna

Optuna是一个用于超参数优化的Python库，它通过使用贝叶斯优化和多点采样等技术，可以高效地搜索超参数空间。Optuna提供了许多高级功能，如并行化、分布式优化和自定义试验设计，使其成为一个非常强大和灵活的工具。

Optuna的核心思想是使用贝叶斯优化来选择下一组超参数，以最小化或最大化目标函数（通常是验证集损失或精度）。在每次迭代中，Optuna会基于当前已知的超参数值来预测下一个最有可能获得最佳结果的超参数值，并进行评估。这些新的观察结果将被添加到已知数据集中，以更新模型并继续优化。Optuna还支持多种用于探索和开发权衡的采样策略，如随机采样、TPE和CMA-ES等。

在Optuna中，我们需要定义三个主要部分：搜索空间、目标函数和试验。以下是关于Optuna的每个部分的更详细介绍：

搜索空间

搜索空间指定了我们要优化的超参数范围和类型。Optuna支持多种不同的参数类型，包括离散参数、连续参数和条件参数。我们可以使用Trial对象的suggest_*()方法来从搜索空间中抽样下一组超参数。例如，以下代码定义了一个搜索空间，其中包含两个连续参数和一个整数参数：

import optuna

def objective(trial):
    x = trial.suggest_uniform('x', -10, 10)
    y = trial.suggest_loguniform('y', 1e-8, 1.0)
    z = trial.suggest_int('z', 0, 10)
    return x**2 + y**2 + z**2

study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)

在此示例中，我们使用了Uniform分布和LogUniform分布来定义两个连续参数，使用IntUniform分布来定义一个整数参数。我们还创建了一个optuna.Study对象，用于记录每次试验的结果，并使用create_study()函数初始化该对象。

目标函数

目标函数是我们要优化的主要函数，它接受超参数作为输入，并返回一个标量值作为输出。Optuna的优化过程旨在最小化或最大化目标函数的输出。在每次试验中，Optuna会根据当前的超参数值调用目标函数，然后将输出传递给贝叶斯优化算法以更新超参数的建议。通常，目标函数包括以下步骤：

• 加载数据和定义模型
• 调整超参数
• 训练模型并计算验证集上的性能指标

例如，以下代码定义了一个简单的目标函数，该函数通过运行XGBoost模型来预测波士顿房价，并返回验证集上的均方误差。

import 	
import numpy as np
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from xgboost import XGBRegressor

def objective(trial):
    # Load data
    data = load_boston()
    X = data.data
    y = data.target
    
    # Define model
    model = XGBRegressor(
        learning_rate=trial.suggest_loguniform('learning_rate', 1e-5, 1),
        max_depth=trial.suggest_int('max_depth', 3, 9),
        n_estimators=trial.suggest_int('n_estimators', 50, 200)
    )
    
    # Evaluate model performance
    score = -np.mean(cross_val_score(model, X, y, cv=5, scoring='neg_mean_squared_error'))
    
    return score

study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)

print(study.best_params)

在此示例中，我们使用了optuna.Study对象来记录每次试验的结果，并使用optimize()函数运行优化过程。我们还使用了loguniform()和int()方法来定义连续和整数参数。最后，我们打印了找到的最佳超参数。

试验

试验指定了我们要执行的一组相关的试验。在Optuna中，我们可以通过定义Trial对象来实现试验。每个Trial对象表示一组正在执行的试验，并且会记录每个试验的超参数和结果。我们可以使用Trial对象的suggest_*()方法来从搜索空间中采样下一组超参数，并使用report()方法来报告试验结果。例如，以下代码定义了一个简单的试验，该试验使用了Uniform分布和LogUniform分布来定义两个连续参数：

import optuna

def objective(trial):
    x = trial.suggest_uniform('x', -10, 10)
    y = trial.suggest_loguniform('y', 1e-8, 1.0)
    return x**2 + y**2

with optuna.logging.disabled():
    study = optuna.create_study(direction='minimize')

for i in range(100):
    trial = study.ask()
    value = objective(trial)
    study.tell(trial, value)

在此示例中，我们使用了ask() 和 tell() 方法来执行试验。在每次循环中，我们调用ask()方法来获取下一组超参数，并使用objective()函数来计算目标函数的输出。然后，我们使用tell()方法将超参数和目标函数的输出报告给Trial对象，以便Optuna可以更新其内部模型并继续优化。

总的来说，Optuna提供了一个高效、灵活和可扩展的框架来搜索超参数空间。Optuna不仅支持各种类型的超参数和采样策略，还提供了诸如并行化、分布式优化和自定义试验设计等高级功能，以满足各种应用场景的需求。

Hyperopt

Hyperopt是一个用于优化超参数的Python库，它提供了一种基于贝叶斯优化的高效方式来搜索超参数空间，并且具有良好的可扩展性和可配置性。Hyperopt使用TPE算法（Tree-structured Parzen Estimator）对参数进行采样，然后使用高斯过程模型来建立模型并预测下一组参数，以最小化损失函数或最大化目标函数。在Hyperopt中，我们需要定义三个部分：搜索空间、目标函数和优化算法。

搜索空间

搜索空间指定了我们要优化的超参数范围和类型。Hyperopt的搜索空间支持以下类型：

• 离散参数，使用choice()函数定义
• 连续参数，使用uniform() 或 hp.quniform() 函数定义
• 对数尺度的连续参数，使用loguniform() 或 hp.qloguniform() 函数定义

例如，以下代码定义了一个搜索空间，其中包含两个离散参数和一个连续参数。

from hyperopt import hp

space = {
    'learning_rate': hp.loguniform('learning_rate', -5, 0),
    'max_depth': hp.choice('max_depth', [3, 5, 7]),
    'n_estimators': hp.quniform('n_estimators', 50, 200, 10)
}

目标函数

目标函数是我们要优化的主要函数，它接受超参数作为输入，并返回一个标量值作为输出。在每次迭代中，Hyperopt会根据当前的超参数值调用目标函数，然后将输出传递给优化算法以更新超参数的建议。通常，目标函数中包括以下步骤：

• 定义数据预处理和模型训练过程
• 调整超参数
• 评估模型性能

例如，以下代码定义了一个简单的目标函数，该函数通过运行XGBoost模型来预测波士顿房价，并返回验证集上的均方误差。

import numpy as np
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from xgboost import XGBRegressor

def objective(args):
    # Load data
    data = load_boston()
    X = data.data
    y = data.target
    
    # Define model
    model = XGBRegressor(
        learning_rate=args['learning_rate'],
        max_depth=args['max_depth'],
        n_estimators=int(args['n_estimators'])
    )
    
    # Evaluate model performance
    score = -np.mean(cross_val_score(model, X, y, cv=5, scoring='neg_mean_squared_error'))
    
    return score

优化算法

Hyperopt提供了多种优化算法，包括随机搜索、TPE和随机森林。在Hyperopt中，我们可以使用fmin()函数来指定优化算法和其他超参数，并运行优化过程。以下是一个示例：

from hyperopt import fmin, tpe, Trials

trials = Trials()

best = fmin(
    fn=objective,
    space=space,
    algo=tpe.suggest,
    max_evals=100,
    trials=trials
)

print(best)

在此示例中，我们使用了TPE算法，并设置最大评估次数为100。我们还使用Trials对象来记录每次评估的超参数和结果，以便我们可以查看优化的进展情况。

在Hyperopt运行完毕后，我们可以使用best变量来获取最佳超参数组合及其相应的得分。

Optuna和Hyperopt的比较

Optuna的优点：

• 可以使用多种优化算法，例如TPE、Grid Search等。
• 支持并行计算，可以利用多核CPU或集群进行计算。
• 具有可视化界面，可帮助用户理解和分析超参数调整结果。
• 灵活的API使得很容易将其与各种深度学习框架集成。

Hyperopt的优点：

• 使用贝叶斯优化，能够更有效地搜索超参数空间。
• 有一个可扩展的系统，可以自定义建模方式、搜索策略等。
• 自适应优化方法，可以在不同的搜索步骤中推荐不同的参数组合。
• 总的来说，Optuna更适合初学者和非专业人士，因为它具有较低的学习曲线和易于使用的API。而Hyperopt更适合机器学习专家和研究人员，因为它提供了更大的灵活性和自定义选项。

Google Vizier

Google Vizier是谷歌开发的一种超参数优化平台，它提供了一种可扩展、自动化和分布式的方法来优化机器学习模型的性能。Vizier使用贝叶斯优化算法和多点采样等技术来搜索超参数空间，并提供了一组丰富的工具和API来帮助用户设计、运行和监控试验。

Vizier是一个通用平台，适用于任何需要进行超参数优化的应用场景。它可以处理各种类型的超参数，如连续参数、离散参数和条件参数，并提供了各种采样策略，如随机采样、TPE和CMA-ES等。此外，Vizier还支持并行化、分布式优化和自定义试验设计等高级功能，以满足不同的应用需求。

使用Vizier进行超参数优化的基本步骤如下：

定义目标函数

首先要定义一个目标函数，该函数接受超参数作为输入，并返回一个标量值作为输出。在每次迭代中，Vizier会根据当前的超参数值调用目标函数，然后将输出传递给优化算法以更新超参数的建议。目标函数可以是任何机器学习模型的性能指标，如验证集损失或精度等。

创建试验对象

接下来，需要创建一个试验对象并设置超参数空间、优化算法和其他参数。试验对象是一个抽象层，用于管理超参数优化过程中的所有实例。在Vizier中，每个试验包含一个或多个实例，每个实例都表示一个正在执行的试验。

from google.cloud import vizier

client = vizier.Client()

experiment = client.create_experiment('my-experiment')
instance = experiment.create_instance()

定义搜索空间

然后需要定义超参数的搜索空间。Vizier支持多种类型的超参数，如连续参数、离散参数和条件参数。可以使用add_parameter()方法来向实例添加超参数，并使用ParameterType枚举类来指定超参数的类型。

from google.cloud.vizier.parameter import *

instance.add_parameter(
    Parameter(
        'learning_rate',
        ParameterType.FLOAT,
        FloatRange(min_value=0.01, max_value=0.1)
    )
)

instance.add_parameter(
    Parameter(
        'num_layers',
        ParameterType.INTEGER,
        DiscreteRange(min_value=1, max_value=5)
    )
)

instance.add_parameter(
    Parameter(
        'activation',
        ParameterType.CATEGORICAL,
        CategoricalRange(['relu', 'sigmoid', 'tanh'])
    )
)

运行试验

最后，可以运行试验并监视其进展情况。Vizier提供了丰富的工具和API来帮助用户监视试验，并显示结果和日志信息。可以使用run_trial()方法来执行单个试验，并使用get_trials()方法来获取所有试验的结果。

trial = instance.run_trial({
    'learning_rate': 0.05,
    'num_layers': 3,
    'activation': 'relu'
})

trials = instance.get_trials()
print(trials)

在此示例中，我们使用run_trial()方法来执行单个试验，并使用字典参数指定超参数值。然后，我们使用get_trials()方法来获取所有试验的结果，并打印出结果。

总的来说，Vizier是一个高效、灵活和可扩展的平台，用于自动化超参数优化和机器学习模型选择。它提供了一组强大的工具和API，使用户可以轻松地设计、运行和监视试验，并找到最佳的超参数组合来最小化或最大化目标函数。

Microsoft NNI

Microsoft NNI是一种用于自动机器学习的工具包，它可以帮助用户高效地搜索超参数空间、调整模型架构和选择最佳模型等。NNI使用了多种优化算法，如贝叶斯优化、网格搜索和随机搜索等，以及各种集成方法，如模型融合和组合等，来进行超参数优化和模型选择。

NNI的核心思想是通过使用自动机器学习技术来加速模型开发和部署过程。在每次迭代中，NNI会根据当前的超参数值、模型架构和训练数据来计算目标函数的输出，并使用优化算法来更新超参数和模型架构。此外，NNI还提供了丰富的可视化工具和API来帮助用户分析和理解优化过程的结果。

使用NNI进行自动机器学习的基本步骤如下：

定义搜索空间

首先要定义超参数和模型架构的搜索空间。NNI支持多种类型的超参数和模型架构，如连续参数、离散参数、整数参数、层级结构和神经元个数等。可以使用JSON格式的配置文件来定义搜索空间，并将其传递给NNI的命令行接口进行使用。

{
    "authorName": "YourName",
    "experimentName": "ExampleExperiment",
    "trialConcurrency": 2,
    "maxTrialNum": 10,
    "trainingServicePlatform": "local",
    "searchSpace": {
        "lr": {
            "_type": "uniform",
            "_value": [0.01, 0.1]
        },
        "batch_size": {
            "_type": "choice",
            "_value": [32, 64, 128]
        },
        "hidden_size": {
            "_type": "choice",
            "_value": [16, 32, 64]
        }
    },
    "trial": {
        "command": "python mnist.py --lr {lr} --batch-size {batch_size} --hidden-size {hidden_size}",
        "codeDir": "."
    }
}

在此示例中，我们使用了_uniform_ 和 choice 等不同的采样方法来定义三个超参数的搜索空间。

运行实验

然后可以运行实验并监视其进展情况。可以使用CLI命令行接口来启动和停止实验，并使用WebUI界面来查看实验结果和日志信息。在每次迭代中，NNI会根据当前的超参数和模型架构执行训练任务，并记录结果和日志。可以使用nnictl命令行工具来管理实验。

nnictl create --config nni.json

分析结果

最后，可以使用NNI提供的可视化工具和API来分析和理解实验结果。NNI提供了丰富的可视化工具，如超参数重要性图、误差曲线、特征重要性图和混淆矩阵等，以便用户更好地理解实验结果。此外，NNI还提供了API来获取和处理实验结果，并支持与其他Python库进行交互。

总的来说，NNI是一个强大、灵活和易于使用的自动机器学习工具包。它提供了多种优化算法、集成方法和可视化工具，使用户可以轻松地搜索超参数空间、调整模型架构和选择最佳模型。NNI的大量功能和广泛的应用场景使其成为一个非常有价值的工具包，可以帮助用户提高机器学习的效率和性能。

其他推荐

除了之前提到的Optuna、Hyperopt、Google Vizier和Microsoft NNI，还有一些其他自动调参的包：

• Scikit-optimize：Scikit-optimize是一个Python库，提供了贝叶斯优化、随机搜索和组合优化等多种超参数优化算法。它具有简单易用、易于扩展和高效处理噪声等特点。
• GPyOpt：GPyOpt是一个基于Gaussian Process模型的Python库，提供了贝叶斯优化、随机搜索和L-BFGS等多种超参数优化算法。它具有灵活性强、可扩展性好和自适应能力等特点。
• HpBandSter：HpBandSter是一个面向分布式超参数优化的Python库，提供了贝叶斯优化、TPE和随机搜索等多种超参数优化算法。它可以在多个计算节点上运行，并提供了丰富的可视化工具来帮助用户监视实验进展。
• Keras Tuner：Keras Tuner是一个专门针对Keras模型的自动调参库，它提供了贝叶斯优化、随机搜索和网格搜索等多种超参数优化算法。它可以与Keras模型直接集成，并支持GPU加速和分布式计算等功能。

总的来说，这些自动调参的包都提供了一些常见的超参数优化算法，并且都具有一定的灵活性和可扩展性，可以根据不同的应用场景进行选择和使用。

自动化调参实例

使用Hyperopt优化LightGBM超参数

Hyperopt中集成了包括随机搜索、模拟退火和TPE（Tree-structured Parzen Estimator Approach）等多种优化算法。相比于Bayes_opt，Hyperopt的是更先进、更现代、维护更好的优化器，也是我们最常用来实现TPE方法的优化器。在实际使用中，相比基于高斯过程的贝叶斯优化，基于高斯混合模型的TPE在大多数情况下以更高效率获得更优结果，该方法目前也被广泛应用于AutoML领域中。TPE算法原理可以参阅原论文Multiobjective tree-structured parzen estimator for computationally expensive optimization problems，在这里我们将重点介绍关于Hyperopt中使用TPE进行超参数搜索的过程。

import numpy as np
from sklearn.model_selection import train_test_split
from hyperopt import hp, fmin, tpe, Trials, STATUS_OK
import lightgbm as lgb

X = data.iloc[:, :-1]
y = data.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.2)


def objective(params):
    # 将超参数转换为LGBM参数
    lgb_params = {
        'boosting_type': 'gbdt',
        'objective': 'binary',
        "metric": "binary_logloss",
        "verbose": -1,
        "is_unbalance": True,
        'num_leaves': int(params['num_leaves']),
        'max_depth': int(params['max_depth']),
        'lambda_l1': params['lambda_l1'],
        'lambda_l2': params['lambda_l2'],
        'learning_rate': params['learning_rate'],
        'feature_fraction': params['feature_fraction'],
        'bagging_fraction': params['bagging_fraction'],
        'bagging_freq': params['bagging_freq'],
        'min_gain_to_split': params['min_gain_to_split'],
        'num_iterations': params['num_iterations']
    }

    # 定义LGBM模型，并指定类别型特征
    model = lgb.LGBMClassifier(**lgb_params)

    # 进行5折交叉验证
    cv_results = lgb.cv(
        params=lgb_params,
        train_set=train_set,
        num_boost_round=1000,
        nfold=5,
        early_stopping_rounds=50,
        stratified=True,
        verbose_eval=False,
        seed=42)

    # 计算平均精度
    mean_binary_logloss = cv_results['binary_logloss-mean'][-1]

    # 返回结果（需要最小化的是1 - AUC）
    return {'loss': mean_binary_logloss, 'status': STATUS_OK}


space = {
    'num_leaves': hp.quniform('num_leaves', 20, 300, 1),
    'max_depth': hp.quniform('max_depth', 3, 11, 1),
    'lambda_l1': hp.uniform('lambda_l1', 0, 1),
    'lambda_l2': hp.uniform('lambda_l2', 0, 1),
    'learning_rate': hp.loguniform('learning_rate', -5, 0),
    "feature_fraction": hp.uniform("feature_fraction", 0.5, 1.0),
    "bagging_fraction": hp.uniform("bagging_fraction", 0.5, 1.0),
    "bagging_freq": hp.choice("bagging_freq", range(1, 20)),
    "min_gain_to_split": hp.uniform("min_gain_to_split", 0.0, 1.0),
    'num_iterations': hp.choice('num_iterations', range(100, 1000))
}

# 准备数据集
train_set = lgb.Dataset(X_train, y_train)

# 定义搜索算法
tpe_algorithm = tpe.suggest
trials = Trials()

# 运行超参数优化
best_params = fmin(
    fn=objective,
    space=space,
    algo=tpe_algorithm,
    max_evals=50,
    trials=trials,
    rstate=np.random.default_rng(42)
)

print(best_params)

定义目标函数

在定义目标函数f(x)时，我们需要严格遵守需要使用的当下优化库的基本规则。与Bayes_opt一样，Hyperopt也有一些特定的规则会限制我们的定义方式，主要包括：

• 目标函数的输入必须是符合hyperopt规定的字典，不能是类似于sklearn的参数空间字典、不能是参数本身，更不能是数据、算法等超参数以外的元素。因此在自定义目标函数时，我们需要让超参数空间字典作为目标函数的输入。
• Hyperopt只支持寻找f(x)的最小值，不支持寻找最大值，因此当我们定义的目标函数是某种正面的评估指标时（如准确率，auc），我们需要对该评估指标取负。如果我们定义的目标函数是负损失，也需要对负损失取绝对值。当且仅当我们定义的目标函数是普通损失时，我们才不需要改变输出。

定义参数空间

在任意超参数优化器中，优化器会将参数空格中的超参数组合作为备选组合，一组一组输入到算法中进行训练。在贝叶斯优化中，超参数组合会被输入我们定义好的目标函数f(x)中。

在hyperopt中，我们使用特殊的字典形式来定义参数空间，其中键值对上的键可以任意设置，只要与目标函数中索引参数的键一致即可，键值对的值则是hyperopt独有的hp函数，包括了：

• choice(label, options)：从一组离散选项中选择一个。例如，以下代码定义了一个名为’method’的超参数，其可选项为’sgd’和’adam’。
• uniform(label, low, high)：在指定的连续区间内均匀分布采样。例如，以下代码定义了一个名为’learning_rate’的超参数，在区间[0.001, 1]中均匀分布采样。
• loguniform(label, low, high)：在指定的对数区间内均匀分布采样。例如，以下代码定义了一个名为’batch_size’的超参数，在区间[32, 1024]的对数空间内均匀分布采样。
• quniform(label, low, high, q)：在指定的离散区间内等间隔采样。例如，以下代码定义了一个名为’num_layers’的超参数，在区间[1, 10]内以步长为2进行均匀采样。
• qloguniform(label, low, high, q)：在指定的对数区间内以指定的步长进行等间隔采样。例如，以下代码定义了一个名为’hidden_size’的超参数，在区间[16, 256]的对数空间内以步长为16进行等比采样。

总的来说，Hyperopt提供了多种不同类型的超参数定义方式，可以根据不同的应用需求进行选择和使用。

示例：

space = {
    'method': hp.choice('method', ['sgd', 'adam']),
    'learning_rate': hp.uniform('learning_rate', 0.001, 1),
    'batch_size': hp.loguniform('batch_size', 5, 10),
    'num_layers': hp.quniform('num_layers', 1, 10, 2),
    'hidden_size': hp.qloguniform('hidden_size', 4, 8, 1)
}

在hyperopt的说明当中，并未明确参数取值范围空间的开闭，根据实验，如无特殊说明，hp中的参数空间定义方法应当都为前闭后开区间。

由于hp.choice最终会返回最优参数的索引，容易与数值型参数的具体值混淆，所以最好使用hp.quniform()函数，而hp.randint又只能够支持从0开始进行计数，因此我们常常会使用quniform获得均匀分布的浮点数来替代整数。对于需要取整数的参数值，如果采用quniform方式构筑参数空间，则需要在目标函数中使用int函数限定输入类型。例如，在范围[0,5]中取值时，可以取出[0.0, 1.0, 2.0, 3.0,…]这种均匀浮点数，在输入目标函数时，则必须确保参数值前存在int函数。当然，如果使用hp.choice则不会存在该问题。

定义优化目标函数的具体流程

有了目标函数和参数空间，接下来我们就可以进行优化了。在Hyperopt中，我们用于优化的基础功能叫做fmin，fmin用于求解最小值。

在fmin中，我们可以自定义使用的代理模型（参数algo），一般来说我们有tpe.suggest以及rand.suggest两种选项，前者指代TPE方法，后者指代随机网格搜索方法。tpe.suggest代表使用TPE的默认参数，当然我们还可以通过partial功能来修改算法涉及到的具体参数，包括模型具体使用了多少个初始观测值（参数n_start_jobs），以及在计算采集函数值时究竟考虑多少个样本（参数n_EI_candidates）。

除此之外，Hyperopt当中还有两个值得注意的功能，一个记录整个迭代过程的trials，另一个是提前停止参数early_stop_fn。提前停止参数early_stop_fn中我们一般输入从hyperopt库导入的方法no_progress_loss()，这个方法中可以输入具体的数字n，表示当损失连续n次没有下降时，让算法提前停止。由于贝叶斯方法的随机性较高，当样本量不足时需要多次迭代才能够找到最优解，因此一般no_progress_loss()中的数值不会设置得太高。

其中，trials直译为“实验”或“测试”，表示我们不断尝试的每一种参数组合，这个参数中我们一般输入从hyperopt库中导入的方法Trials()，当优化完成之后，我们可以从保存好的trials中查看损失、参数等各种中间信息。

执行实际优化流程

由于具有提前停止功能，因此基于TPE的hyperopt优化可能在我们设置的迭代次数被达到之前就停止，也因此hyperopt迭代到实际最优值所需的迭代次数可能更少。同时，TPE方法相比于高斯过程计算会更加迅速，即便运行同样的迭代次数，hyperopt也是更有优势的。

不过HyperOpt的缺点也很明显，那就是代码精密度要求较高、灵活性较差，略微的改动就可能让代码疯狂报错难以跑通。同时，HyperOpt所支持的优化算法也不够多，如果我们专注地使用TPE方法，则掌握HyperOpt即可，如果我们希望拥有丰富的HPO手段，则可以更深入地接触Optuna库。

使用Optuna优化Facebook Prophet超参数

Optuna是目前为止最为成熟、拓展性最强的超参数优化框架，与古旧的bayes_opt相比，Optuna明显是专门为机器学习和深度学习所设计。为了满足机器学习开发者的需求，Optuna拥有强大且固定的API，因此Optuna代码简单，编写高度模块化，是我们介绍的库中代码最为简练的库，有点kears的意思了。Optuna的优势在于，它可以无缝衔接到PyTorch、Tensorflow等深度学习框架上，也可以与sklearn的优化库scikit-optimize结合使用，因此Optuna可以被用于各种各样的优化场景。

import pandas as pd
from prophet import Prophet
from prophet.diagnostics import cross_validation
from prophet.diagnostics import performance_metrics
import numpy as np
import optuna

df_past = pd.read_excel("data/h.xlsx")
df_past['ds'] = pd.to_datetime(df_past['ds'])
holidays = pd.read_csv("holidays.csv")


def prophet_objective(trial, df_past):
    changepoint_prior_scale = trial.suggest_float('changepoint_prior_scale', 0.01, 0.2)
    changepoint_range = trial.suggest_float('changepoint_range', 0.50, 0.95)
    yearly_seasonality = trial.suggest_float('yearly_seasonality', 0.01, 10, log=True)
    weekly_seasonality = trial.suggest_float('weekly_seasonality', 0.01, 10, log=True)
    holidays_prior_scale = trial.suggest_float('holidays_prior_scale', 0.01, 10, log=True)
    
    holidays_subset = holidays.copy()
    
    m = Prophet(
        seasonality_mode="multiplicative",
        changepoint_prior_scale=changepoint_prior_scale,
        changepoint_range=changepoint_range,
        yearly_seasonality=yearly_seasonality,
        weekly_seasonality=weekly_seasonality,
        holidays_prior_scale=holidays_prior_scale,
        holidays=holidays_subset,
        uncertainty_samples=0
    )
    
    m.fit(df_past)
    
    df_cv = cross_validation(m, initial='540 days', period='1 days', horizon='1 days')
    df_p = performance_metrics(df_cv, rolling_window=1)
    
    mape = np.mean(df_p.mape)
    
    return mape


study = optuna.create_study(direction="minimize")
study.optimize(lambda trial: prophet_objective(trial, df_past),
               n_trials=50, n_jobs=8)
print(study.best_params)

定义目标函数与参数空间

Optuna的目标函数相当特别。在其他优化库中，我们需要单独输入参数或参数空间，优化器会在具体优化过程中将参数空间一一放入我们的目标函数进行优化，但在Optuna中，我们并不需要将参数或参数空间输入目标函数，而是需要直接在目标函数中定义参数空间。特别的是，Optuna优化器会生成一个指代备选参数的变量trial，该变量无法被用户获取或打开，但该变量在优化器中生存，并被输入目标函数。在目标函数中，我们可以通过变量trail所携带的方法来构造参数空间。

Y在Optuna中，suggest_*()方法是用于指定下一个采样点的值的函数。不同类型的提示函数可以根据超参数的类型进行选择和使用。以下是一些常见类型的suggest_*()方法及其使用方法：

• suggest_categorical(name, choices)：从枚举值中随机取一个值
• suggest_uniform(name, low, high)：随机一个小数，范围为[low,high)。
• suggest_discrete_uniform(name, low, high, q)：随机离散化取值，随机中low,low+q,low+2q,…,low+nq<high中获取一个值。
• suggest_loguniform(name, low, high)：以log分布，随机一个小数
• suggest_float(name, low, high, *[, step, log])：随机一个小数，功能包含了suggest_uniform、suggest_discrete_uniform、suggest_loguniform
• suggest_int(name, low, high[, step, log])：随机一个整数，同上

定义优化目标函数的具体流程

在HyperOpt当中我们可以调整参数algo来自定义用于执行贝叶斯优化的具体算法，在Optuna中我们也可以。大部分备选的算法都集中在Optuna的模块sampler中，包括我们熟悉的TPE优化、随机网格搜索以及其他各类更加高级的贝叶斯过程，对于Optuna.sampler中调出的类，我们也可以直接输入参数来设置初始观测值的数量、以及每次计算采集函数时所考虑的观测值量。在Optuna库中并没有集成实现高斯过程的方法，但我们可以从scikit-optimize里面导入高斯过程来作为optuna中的algo设置，而具体的高斯过程相关的参数则可以通过如下方法进行设置：

def optimizer_optuna(n_trials, algo):
    
    # 定义使用TPE或者高斯过程（GP）
    if algo == "TPE":
        algo = optuna.samplers.TPESampler(n_startup_trials = 10, n_ei_candidates = 24) # n_startup_trials：初始观测点个数；n_ei_candidates：期望增量；这里都是默认值
    elif algo == "GP":
        # Optuna没有内置高斯过程类，使用Optuna库的integration模块，有很多与其他模块相结合的工具，例如这里的SkoptSampler
        from optuna.integration import SkoptSampler
        import skopt
        algo = SkoptSampler(skopt_kwargs={'base_estimator':'GP', # 选择高斯过程
                                          'n_initial_points':10, # 初始观测点10个
                                          'acq_func':'EI'}       # 选择的采集函数为期望增量（EI）
                           )
    
    # 实际优化过程，首先实例化优化器
    study = optuna.create_study(sampler = algo         # 要使用的具体算法，sampler表示抽样器
                                , direction="minimize" # 优化的方向，可以填写minimize或maximize确立找最小值还是最大值
                               )
    # 开始优化，n_trials为允许的最大迭代次数
    # 由于参数空间已经在目标函数中定义好，因此这里不需要输入参数空间
    study.optimize(optuna_objective         # 目标函数
                   , n_trials=n_trials      # 最大迭代次数（包括最初的观测值的）
                   , show_progress_bar=True # 是否展示进度条
                  )
    
    # 可直接从优化好的对象study中调用优化的结果
    # 打印最佳参数与最佳损失值
    print("\n","\n","best params: ", study.best_trial.params,
          "\n","\n","best score: ", study.best_trial.values,
          "\n")
    
return study.best_trial.params, study.best_trial.values

执行实际优化流程

Optuna库虽然是当今最为成熟的HPO方法之一，但当参数空间较小时，Optuna库在迭代中容易出现抽样BUG，即Optuna会持续抽到曾经被抽到过的参数组合，并且持续报警告说”算法已在这个参数组合上检验过目标函数了”。在实际迭代过程中，一旦出现这个Bug，那当下的迭代就无用了，因为已经检验过的观测值不会对优化有任何的帮助，因此对损失的优化将会停止。如果出现该BUG，则可以增大参数空间的范围或密度。或者使用如下的代码令警告关闭：

# 屏蔽警告
import warnings
warnings.filterwarnings('ignore', message='The objective has been evaluated at this point before.')

optuna.logging.set_verbosity(optuna.logging.ERROR)     # 关闭自动打印的info，只显示进度条
#optuna.logging.set_verbosity(optuna.logging.INFO)

基于高斯过程的贝叶斯优化是比基于TPE的贝叶斯优化运行更加缓慢的，不过在TPE模式下，其运行速度与HyperOpt的运行速度高度接近。

参考链接：

• 超参数优化 – 贝叶斯优化方法
• 【机器学习】Optuna vs Hyperopt 超参数优化哪家强？
• 深度学习-超参数优化