k-medoids算法概述
k-medoids 是一种基于中心的聚类算法,是 k-means 算法的改进版本。与 k-means 使用簇内数据点的均值作为中心点不同,k-medoids 使用实际数据点作为中心点(称为 medoid)。
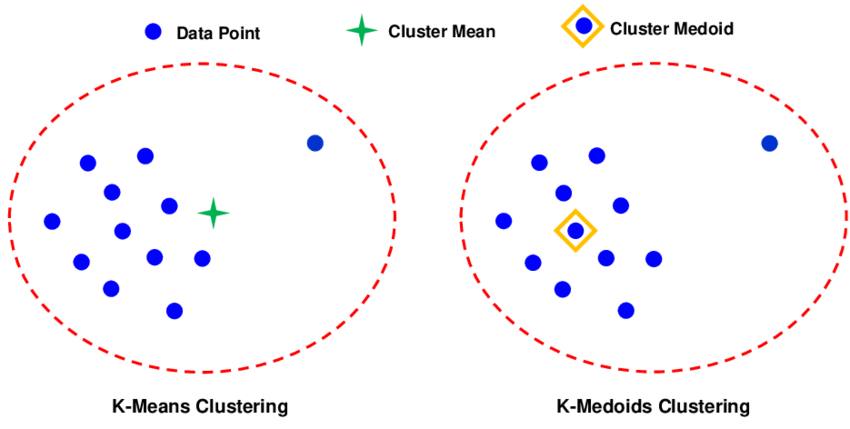
与 k-means 的对比
| 特性 | k-medoids | k-means |
| 中心点 | 实际数据点 | 计算出的均值点 |
| 对异常值 | 鲁棒性较好 | 非常敏感 |
| 距离度量 | 可处理任意距离度量 | 主要使用欧氏距离 |
| 时间复杂度 | 较高 | 较低 |
| 适用数据 | 任意类型(需距离度量) | 数值型数据 |
k-medoids算法原理
基本理念
k-medoids 算法是一种基于实际数据点作为聚类中心的划分聚类方法。与 k-means 使用均值点(可能不是实际数据点)不同,k-medoids 选择实际存在的数据点作为每个簇的代表点(medoid),这使得算法对异常值和噪声具有更强的鲁棒性。
算法目标
找到 k 个中心点(medoids),使得所有数据点到其最近中心点的距离总和最小化,数学表达为:
其中:
- 是数据集
- 是中心点集合
- 是距离函数
- 表示选择 k 个中心点
算法工作流程
k-medoids 算法的核心是 PAM(Partitioning Around Medoids)算法,其流程如下:
输入:数据集 D,聚类数 k,最大迭代次数 T
输出:k 个中心点,k 个簇
过程:
1. 初始化:随机选择 k 个数据点作为初始中心点
2. 分配:将每个数据点分配给距离最近的中心点
3. 迭代优化:
repeat
对于每个中心点 m_j
对于每个非中心点 o
计算用 o 替换 m_j 的总代价 TC(j, o)
找到最小代价的替换 (j*, o*)
if TC(j*, o*) < 0 then
执行替换:m_j* = o*
重新分配数据点
until 没有负代价的替换 或 达到最大迭代次数
4. 返回聚类结果
代价计算机制
代价计算是 k-medoids 算法的核心,用于评估中心点替换的质量。总代价计算公式为:
$$TC(j, o) = \sum_{x \in D} C_{j,o}(x)$$
其中$C_{j,o}(x)$是点 x 在中心点 j 被 o 替换后的重新分配代价。
四种情况分析
设当前中心点集合为$M = \{m_1, m_2, …, m_k\}$,考虑用非中心点o替换中心点$m_j$。对于任意点 x,有以下四种情况:
- 情况 1:x 当前归属于$m_j$,且替换后仍选择 o 作为最近中心。$C_{j,o}(x) = d(x, o) – d(x, m_j)$,解释:x 原本属于中心$m_j$的簇,替换后,o 成为其新的最近中心点。
- 情况 2:x 当前归属于$m_j$,但替换后选择其他中心$m_i(i \neq j)$作为最近中心,设$m_{second}$是 x 的第二近中心点(除$m_j$外):$C_{j,o}(x) = d(x, m_{second}) – d(x, m_j)$,解释:替换后,x 发现 o 不是最近的,但原来第二近的中心 m_{second} 现在是最近的。
- 情况 3:x 当前不归属于$m_j$,且替换后仍选择原来的中心,$C_{j,o}(x) = 0$,解释:替换操作不影响 x 的簇归属。
- 情况 4:x 当前不归属于$m_j$,但替换后选择o作为最近中心,设x当前最近中心为$m_{curr}$:$C_{j,o}(x) = d(x, o) – d(x, m_{curr})$,解释:x 原本属于其他簇,但替换后发现o比原来的中心更近。
收敛性原理
k-medoids 算法在每次迭代中都会尝试降低目标函数值:$J^{(t+1)} \leq J^{(t)}$,其中$J^{(t)} = \sum_{x \in D} \min_{m \in M^{(t)}} d(x, m)$ 是第 t 次迭代的目标函数值。
收敛证明:
- 有下界:目标函数$J \geq 0$(距离非负)
- 严格递减:只有当$TC(j, o) < 0$时才执行替换
- 有限性:可能的中心点组合有限($C_n^k$种)
因此,算法必然在有限步内收敛到局部最优解。
鲁棒性原理
k-medoids 对异常值鲁棒的关键在于中心点选择机制:
- k-means:中心是簇内点的均值,受异常值影响大
- k-medoids:中心是实际数据点,相当于”中值”点
设簇 C 包含 n 个点,其中包含异常值 o。
- 均值:$\mu = \frac{1}{n}\sum_{x \in C} x$,受 o 影响大
- medoid:$m = \arg\min_{x \in C} \sum_{y \in C} d(x, y)$,对单个异常值不敏感
距离度量的影响
k-medoids 可以使用任意距离度量,而 k-means 通常需要欧氏距离(保证均值是最优中心)。
复杂度分析原理
PAM 算法的时间复杂度推导:
- 初始化:O(k)
- 分配阶段:O(nk)
- 代价计算:
- 每个中心点:O(n-k) 个候选
- 每个候选:计算 n 个点的代价
- 每次迭代:O(k(n-k)n)
- 总复杂度:O(t \cdot k(n-k)n),其中 t 是迭代次数
优化策略
实际实现中的优化:
- 缓存距离:预先计算和存储距离
- 增量计算:只计算受影响的点
- 提前终止:当代价不再显著下降时终止
参数选择原理
- k 值确定:
- 肘部法则:J(k) 的拐点
- 轮廓系数:度量簇内紧密度和簇间分离度
- 距离选择:
- 数值数据:欧氏距离、曼哈顿距离
- 文本数据:余弦距离、Jaccard距离
- 时间序列:DTW距离
k-medoids算法实现
import numpy as np
from scipy.spatial.distance import cdist
def k_medoids(X, k, max_iter=100):
# 1. 初始化:随机选择k个点作为初始中心点
n_samples = X.shape[0]
medoid_indices = np.random.choice(n_samples, size=k, replace=False)
medoids = X[medoid_indices]
for iteration in range(max_iter):
# 2. 分配阶段:计算每个点到各中心点的距离,分配到最近的中心点所在的簇
distances = cdist(X, medoids, metric='euclidean') # 可以使用其他距离度量
labels = np.argmin(distances, axis=1)
# 3. 更新阶段:尝试在每个簇内交换中心点,寻找能降低总距离的交换
new_medoids = medoids.copy()
total_cost_changed = False
# 遍历每个簇
for cluster_idx in range(k):
cluster_points = X[labels == cluster_idx] # 当前簇的所有点
current_medoid = medoids[cluster_idx] # 当前簇的中心点
# 计算当前簇内所有点到当前中心点的距离总和
current_cost = np.sum(cdist(cluster_points, [current_medoid], metric='euclidean'))
# 尝试将中心点替换为簇内其他点,计算替换后的成本
best_cost = current_cost
best_candidate = current_medoid
for candidate_point in cluster_points:
if np.array_equal(candidate_point, current_medoid):
continue # 跳过当前中心点本身
# 计算用候选点作为新中心点时,簇内所有点到新中心点的距离总和
candidate_cost = np.sum(cdist(cluster_points, [candidate_point], metric='euclidean'))
if candidate_cost < best_cost:
best_cost = candidate_cost
best_candidate = candidate_point
# 如果找到了更好的中心点,则更新
if not np.array_equal(best_candidate, current_medoid):
new_medoids[cluster_idx] = best_candidate
total_cost_changed = True
medoids = new_medoids
# 4. 终止检查:如果中心点没有变化,则提前终止迭代
if not total_cost_changed:
break
# 最终分配一次标签
distances = cdist(X, medoids, metric='euclidean')
labels = np.argmin(distances, axis=1)
return medoids, labels
k-medoids 变体算法
CLARA 算法 (Clustering LARge Applications)
核心思想
CLARA 通过抽样来处理大规模数据集,在随机样本上运行 PAM 算法,然后将结果应用到整个数据集。
算法原理
理论基础:如果样本能代表整个数据集,则在样本上找到的最优 medoids 在整个数据集上也会接近最优。
数学表达:设数据集$D$有$n$个点,从中随机抽取$s$个点的样本$S$。在$S$上运行PAM得到medoids集合$M_S$,然后计算在整个数据集$D$上的质量:$J_D(M_S) = \sum_{x \in D} \min_{m \in M_S} d(x, m)$
算法步骤
输入:数据集 D,聚类数 k,样本大小 s,样本数 t 输出:k 个中心点 1. 初始化最佳中心点集合 M* 和最佳代价 J* = ∞ 2. 重复 t 次: a. 从 D 中随机抽取大小为 s 的样本 S b. 在 S 上运行 PAM 算法,得到 medoids 集合 M_S c. 计算 M_S 在整个数据集 D 上的代价 J_D(M_S) d. 如果 J_D(M_S) < J*,则更新 J* = J_D(M_S) 和 M* = M_S 3. 返回 M*
参数选择
- 样本大小:经验公式 $s = 40 + 2k$
- 样本数 t:通常 5-10
- 样本质量:样本应保持原始数据的分布特征
优缺点
- 优点:
- 处理大规模数据集
- 时间复杂度:$O(ks^2 + k(n-k))$,其中 $s << n$
- 缺点:
- 样本的代表性影响结果质量
- 不保证全局最优
- 对非均匀分布的数据效果差
CLARANS 算法 (Clustering Large Applications based on RANdomized Search)
核心思想
CLARANS 将 k-medoids 问题视为图搜索问题,通过随机搜索在解空间中找到近似最优解。
算法原理
搜索空间图定义:
- 节点:所有可能的 k-medoids 集合
- 边:两个节点可以通过交换一个 medoid 得到
例如,节点 $M = \{m_1, m_2, …, m_k\}$ 的邻居是所有通过以下操作得到的集合:$M’ = M \setminus \{m_i\} \cup \{x\}, \quad x \in D \setminus M$
这样的邻居节点有 $k \times (n-k)$ 个。
算法步骤
输入:数据集 D,聚类数 k,maxneighbor,numlocal
输出:k 个中心点
1. 初始化 bestnode = null, bestcost = ∞
2. 重复 numlocal 次(重启次数):
a. 随机选择一个当前节点 current
b. 计数器 i = 1
c. 重复:
i. 从 current 的邻居中随机选择一个邻居节点 neighbor
ii. 计算两个节点的代价差 Δ = cost(neighbor) - cost(current)
iii. 如果 Δ < 0:
current = neighbor
i = 1
否则:
i = i + 1
iv. 直到 i > maxneighbor
d. 如果 cost(current) < bestcost:
bestnode = current, bestcost = cost(current)
3. 返回 bestnode
参数说明
| 参数 | 含义 | 推荐值 |
| numlocal | 重启次数 | 2-5 |
| maxneighbor | 连续失败的随机邻居数 | 0.01-0.025 × k(n-k) |
优缺点
- 优点:
- 搜索效率高于穷举
- 可以处理大规模数据
- 结果质量通常优于 CLARA
- 缺点:
- 结果具有随机性
- 参数需要调优
- 不保证找到全局最优
FastPAM 算法
核心思想
FastPAM 通过优化代价计算来提高 PAM 的效率,减少不必要的计算。
关键技术
增量代价计算:维护两个矩阵,避免重复计算距离
- 距离矩阵:$D_{n \times n}$,$D[i][j] = d(x_i, x_j)$
- 最近距离矩阵:$C_{n \times 2}$,存储每个点到:
- 最近 medoid 的距离
- 第二近 medoid 的距离
代价更新公式:对于替换操作 $m \rightarrow x$,点 $p$ 的代价:
$$\Delta(p, m, x) = \begin{cases} \min(d(p, x), C[p][2]) – C[p][1] & \text{如果 } C[p][1] = d(p, m) \\ \min(d(p, x) – C[p][1], 0) & \text{否则} \end{cases}$$
算法步骤
输入:数据集 D,聚类数 k
输出:k 个中心点
1. 初始化:随机选择 k 个 medoids
2. 计算距离矩阵 D
3. 初始化最近距离矩阵 C
4. repeat
对于每个 medoid m:
对于每个非 medoid 点 x:
计算交换代价 Δ(m, x) = Σ Δ(p, m, x)
找到最小代价的交换 (m*, x*)
if Δ(m*, x*) < 0 then
执行交换
更新距离矩阵 C
until 没有负代价的交换
5. 返回 medoids
性能分析
- 时间复杂度:$O(n^2)$,但常数因子较小
- 空间复杂度:$O(n^2)$
- 实践中比原始 PAM 快 10-100 倍
模糊 k-medoids 算法
核心思想
允许每个点以隶属度属于多个簇,更适合重叠簇的情况。
数学模型
目标函数:$J = \sum_{i=1}^n \sum_{j=1}^k u_{ij}^m d(x_i, m_j)$
约束条件:
- $\sum_{j=1}^k u_{ij} = 1, \quad \forall i$
- $u_{ij} \in [0, 1], \quad \forall i,j$
- $\sum_{i=1}^n u_{ij} > 0, \quad \forall j$
其中 $m > 1$ 是模糊化参数。
算法步骤
输入:数据集 D,聚类数 k,模糊参数 m,最大迭代次数 T
输出:隶属度矩阵 U,中心点 M
1. 随机初始化隶属度矩阵 U
2. 计算初始中心点 M:对于每个簇 j
m_j = argmin_{x \in D} Σ_{i=1}^n u_{ij}^m d(x_i, x)
3. repeat
a. 更新隶属度:
u_{ij} = [Σ_{l=1}^k (d(x_i, m_j)/d(x_i, m_l))^{2/(m-1)}]^{-1}
b. 更新中心点:
对于每个簇 j,找到最小化 Σ u_{ij}^m d(x_i, x) 的点
c. 计算目标函数 J
until |J_{new} - J_{old}| < ε 或达到最大迭代次数
4. 返回 U, M
参数说明:
- 模糊参数 m:控制模糊程度,通常5-3.0
- 收敛阈值 ε:通常001-0.0001
核 k-medoids 算法
核心思想
通过核方法将数据映射到高维特征空间,处理非线性可分的数据。
数学模型
核技巧:不需要显式计算映射 $\phi(x)$,只需核函数 $k(x, y) = \phi(x)^T \phi(y)$
特征空间距离:$d_{\mathcal{H}}^2(x, y) = \|\phi(x) – \phi(y)\|^2 = k(x, x) + k(y, y) – 2k(x, y)$
目标函数:$J = \sum_{i=1}^n \min_{j=1}^k d_{\mathcal{H}}^2(x_i, m_j)$
常用核函数
- 高斯核:$k(x, y) = \exp\left(-\frac{\|x-y\|^2}{2\sigma^2}\right)$
- 多项式核:$k(x, y) = (x^Ty + c)^d$
- Sigmoid 核:$k(x, y) = \tanh(\alpha x^Ty + c)$
算法步骤
输入:数据集 D,聚类数 k,核函数 k(·,·)
输出:k 个中心点
1. 计算核矩阵 K,其中 K[i][j] = k(x_i, x_j)
2. 随机选择 k 个初始中心点
3. repeat
分配阶段:使用特征空间距离分配点到最近中心
更新阶段:对每个簇,找到最小化 Σ d_H^2(x, m) 的点作为新中心
until 收敛
4. 返回中心点
增量 k-medoids 算法
核心思想
处理动态变化的数据集,当新数据到达时,无需重新计算整个聚类。
关键技术
增量更新策略:
- 新点插入:
- 计算新点到所有 medoids 的距离
- 分配到最近 medoid 的簇
- 如果必要,更新 medoid
- 旧点删除:
- 如果删除的点是 medoid,需要重新选择
- 否则,只需从簇中移除
- 批量更新:累积一定数量的变化后批量更新
更新规则
设当前 medoids 为 $M = \{m_1, …, m_k\}$,新点 $x_{new}$ 插入。
插入算法:
1. 找到最近 medoid:m_j = argmin_{m∈M} d(x_new, m)
2. 将 x_new 分配到簇 C_j
3. 更新 medoid m_j:m_j' = argmin_{x∈C_j∪{x_new}} Σ_{y∈C_j∪{x_new}} d(x, y)
4. 如果 m_j' ≠ m_j,则更新 m_j = m_j'
并行 k-medoids 算法
核心思想
利用并行计算加速 k-medoids,特别是代价计算步骤。
并行策略
- 数据并行:
- 将数据分块到不同处理器
- 每个处理器计算局部代价
- 汇总得到全局代价
- 任务并行:
- 并行计算不同交换操作的代价
- 选择最优交换
MapReduce 实现
# Map 阶段:计算局部代价
def map_function(point, medoids):
# 计算点到各 medoids 的距离
# 返回 (medoid_id, (point, min_distance, second_min_distance))
# Reduce 阶段:汇总代价
def reduce_function(medoid_id, points_info):
# 计算替换每个非 medoid 点的代价
# 返回最小代价的交换
层次 k-medoids 算法
核心思想
结合层次聚类和 k-medoids 的优点,生成层次结构的聚类。
算法类型
- 自底向上(凝聚):
- 从每个点作为一个簇开始
- 逐步合并最相似的簇
- 使用 k-medoids 选择代表点
- 自顶向下(分裂):
- 从所有点作为一个簇开始
- 逐步分裂为更小的簇
- 使用 k-medoids 找到分裂点
凝聚层次 k-medoids
输入:数据集 D 输出:层次聚类树 1. 初始化:每个点作为一个簇,medoid 是自身 2. 重复: a. 找到距离最近的两个簇 C_i 和 C_j b. 合并 C_i 和 C_j 为 C_new c. 在 C_new 上运行 k-medoids (k=1) 找到 medoid d. 更新距离矩阵 until 只剩下一个簇 3. 返回层次树
鲁棒 k-medoids 算法
核心思想
增强对噪声和异常值的鲁棒性。
改进方法
- 加权距离:给疑似噪声点较小权重 $d_w(x, y) = w(x)w(y)d(x, y)$
- 截断距离:使用 Huber 损失函数
$$d_{\text{huber}}(x, y) = \begin{cases} \frac{1}{2}d(x, y)^2 & \text{if } d(x, y) \leq \delta \\ \delta(d(x, y) – \frac{1}{2}\delta) & \text{otherwise} \end{cases}$$
- 软分配:结合模糊聚类思想
约束 k-medoids 算法
核心思想
加入用户定义的约束,如必须连接(must-link)和不能连接(cannot-link)。
约束类型
- Must-link 约束:$(x_i, x_j)$ 必须在同一簇
- Cannot-link 约束:$(x_i, x_j)$ 必须在不同簇
带约束的 PAM
修改代价计算:
如果交换违反约束,设置代价为无穷大
在分配阶段强制执行约束
使用约束指导初始化
密度敏感 k-medoids 算法
核心思想
考虑数据密度分布,在密集区域选择更多 medoids。
密度估计
使用核密度估计:$\hat{f}(x) = \frac{1}{n} \sum_{i=1}^n K_h(x – x_i)$
密度加权的 k-medoids
目标函数:$J = \sum_{i=1}^n f(x_i) \min_{j=1}^k d(x_i, m_j)$
其中 $f(x_i)$ 是点 $x_i$ 的密度。
评估与选择
变体算法比较
| 算法 | 时间复杂度 | 空间复杂度 | 适用场景 | 优点 | 缺点 |
| PAM | $O(k(n-k)^2t)$ | $O(n^2)$ | 小规模数据 | 精确 | 慢,内存消耗大 |
| CLARA | $O(ks^2 + k(n-k))$ | $O(s^2+n)$ | 大规模数据 | 可扩展 | 依赖样本质量 |
| CLARANS | $O(n^2t)$ | $O(n^2)$ | 中大规模数据 | 效率质量平衡 | 参数敏感 |
| FastPAM | $O(n^2)$ | $O(n^2)$ | 中小规模数据 | 比 PAM 快 | 仍需存储距离矩阵 |
| 模糊k-medoids | $O(kn^2t)$ | $O(nk)$ | 重叠簇 | 软分配 | 计算复杂 |
| 核k-medoids | $O(n^2)$ | $O(n^2)$ | 非线性数据 | 处理复杂结构 | 核参数选择 |
选择指南
- 数据规模:
- $n < 1000$:PAM 或 FastPAM
- $1000 < n < 10000$:CLARANS
- $n > 10000$:CLARA
- 数据结构:
- 线性可分:标准 k-medoids
- 非线性:核 k-medoids
- 重叠簇:模糊 k-medoids
- 计算资源:
- 内存充足:PAM
- 内存有限:CLARA
- 并行环境:并行 k-medoids
- 数据动态性:
- 静态数据:标准变体
- 动态数据:增量 k-medoids
k-medoids 的各种变体算法针对不同场景和需求进行了优化。选择合适的变体需要考虑数据规模、结构、计算资源和特定需求。实践中,建议:
- 从小规模数据开始,使用 PAM 理解数据特性
- 对于大规模数据,优先尝试 CLARANS
- 如果数据有特殊结构,选择相应的变体
- 通过交叉验证调整参数
- 结合多种评估指标选择最佳结果
这些变体算法扩展了 k-medoids 的应用范围,使其能够处理从传统数值数据到复杂结构数据的各种聚类问题。