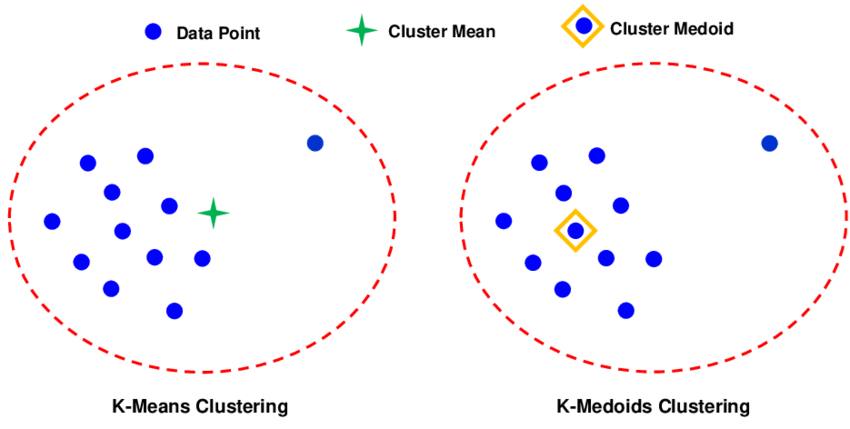
ROCK算法概述
ROCK产生背景
传统聚类算法的局限性
20世纪90年代末,随着电子商务、市场篮子分析和生物信息学等领域的快速发展,分类属性和布尔型数据的聚类需求日益凸显。传统聚类方法面临两大挑战:
- 距离度量的不适应性:经典的K-means、层次聚类等算法主要基于欧氏距离、曼哈顿距离等数值型距离度量,这些度量对分类数据效果不佳。例如,在购物篮分析中,商品是离散的分类属性,传统距离难以准确衡量交易记录间的相似性。
- 聚类结构的复杂性:在分类数据中,自然形成的簇往往具有复杂的结构,不是简单的球形凸集。传统基于距离的方法难以识别这些非球形、边界模糊的聚类结构。
现实应用的需求驱动
- 市场篮子分析:零售商需要从海量交易数据中发现商品之间的关联模式,识别有意义的顾客群体
- 文档聚类:在信息检索中,需要将文档按主题自动分组,文档通常表示为关键词的集合
- 生物信息学:基因表达数据通常包含大量分类属性,需要有效的聚类方法进行分析
- 社交网络分析:用户兴趣通常表示为离散标签集合,需要基于社区结构进行聚类
ROCK的诞生
为了解决这些问题,Sudipto Guha、Rajeev Rastogi和Kyuseok Shim于1999年提出了ROCK算法(Robust Clustering using LinKs)。该算法发表在数据库领域的顶级会议VLDB上,迅速成为分类数据聚类的经典方法之一。ROCK的核心创新在于:
- 用连接(链接数)替代传统距离作为相似性度量
- 专门针对分类属性和布尔型数据设计
- 能够识别任意形状的聚类结构
ROCK的核心思想与实现逻辑
核心思想:从二元关系到社区结构
ROCK的基本理念是:判断两个数据对象是否属于同一聚类,不应仅仅基于它们直接的相似性,而应考察它们共享邻居的程度。这种思想源自社会网络分析中的”结构等价”概念:
两个人如果拥有大量共同的朋友,即使他们之间没有直接联系,也很可能属于同一个社交圈子。
三个关键概念
- 邻居(Neighbors)
- 定义:如果两个数据点之间的相似度(通常使用Jaccard系数)超过预设阈值θ,则称它们互为邻居
- 作用:定义了数据间的直接关系,形成初步的局部连接
- 连接(Links)
- 定义:两个点之间的连接数是指它们共同邻居的数量
- 数学表达:link(i, j) = |{k | sim(i, k) ≥ θ 且 sim(j, k) ≥ θ}|
- 本质:衡量两个点所属”社区”的重叠程度,是一种全局性的结构相似性度量
- 邻域(Neighborhoods)
- 通过连接关系,每个点不仅与其直接邻居相连,还通过共享邻居间接相连
- 这种连接网络形成了一个图结构,自然的聚类对应于图中的密集子图
实现逻辑流程
输入:数据集S,相似度阈值θ,目标聚类数k
输出:k个聚类
1. 初始化阶段
- 将每个数据点视为独立簇
- 计算所有点对的相似度
- 识别邻居关系(sim ≥ θ的点对)
2. 连接计算阶段
- 为每对点计算连接数(共同邻居数)
- 构建连接矩阵
3. 层次合并阶段
- 计算每对簇的Goodness值:
goodness = 跨簇连接总数 / 期望连接增量
- 选择Goodness值最大的簇对合并
- 更新连接矩阵
- 重复直到剩下k个簇
算法设计的精妙之处
- 多层级信息利用:同时考虑局部相似性(邻居)和全局结构(连接)
- 抗噪能力:通过连接数过滤偶然的相似性,增强聚类鲁棒性
- 自适应归一化:Goodness函数中的分母项防止算法偏向于合并大簇
- 层次结构保持:凝聚式合并产生层次聚类树,便于多粒度分析
ROCK与其他层次聚类方法的对比
层次聚类方法分类
层次聚类 ├── 凝聚式(自底向上) │ ├── 传统方法:AGNES(基于距离) │ ├── 基于图的方法:ROCK、Chameleon │ └── 基于密度的:CURE │ └── 分裂式(自顶向下):DIANA
详细对比分析
| 特征维度 | ROCK | 传统凝聚层次聚类(AGNES) | CURE | Chameleon |
| 适用数据类型 | 分类/布尔型 | 数值型为主 | 数值型 | 数值型为主 |
| 相似性度量 | 连接数(基于Jaccard相似度) | 欧氏距离、曼哈顿距离等 | 距离(支持多种) | 相对互连性和相对接近性 |
| 核心思想 | 基于共享邻居的连接强度 | 基于点对距离的最小/平均/最大值 | 代表点和收缩因子 | 图的k最近邻划分 |
| 时间复杂度 | O(n² + nm_m*m_a + n²logn) | O(n³)朴素,优化后O(n²logn) | O(n²logn) | O(n²) |
| 空间复杂度 | O(n*m_m)稀疏存储 | O(n²)距离矩阵 | O(n) | O(k*n) |
| 聚类形状适应性 | 任意形状(基于图连接) | 球形凸集为主 | 任意形状 | 任意形状 |
| 噪声处理能力 | 较强(连接过滤噪声) | 较弱 | 较强(收缩远离异常) | 中等 |
| 参数敏感性 | 对阈值θ敏感 | 对距离度量敏感 | 对收缩因子敏感 | 对k和阈值敏感 |
| 主要优点 | 1. 专为分类数据设计 2. 发现任意形状聚类 3. 理论基础坚实 |
1. 简单直观 2. 确定性结果 3. 可视化效果好 |
1. 抗噪声 2. 任意形状聚类 3. 可伸缩性好 |
1. 动态建模 2. 自适应聚类 3. 效果好 |
| 主要缺点 | 1. 参数θ难以确定 2. 计算开销较大 3. 仅适用离散数据 |
1. 计算复杂度高 2. 不能撤销合并 3. 球形偏好 |
1. 收缩因子敏感 2. 需要预设聚类数 3. 时间复杂度较高 |
1. 参数较多 2. 计算复杂 3. 理论基础较弱 |
关键技术差异详解
相似性度量演进
距离度量 → 连接度量 → 相对度量 → 密度度量 ↓ ↓ ↓ ↓ AGNES ROCK Chameleon DBSCAN
- AGNES的距离链路准则
- 单链接:合并距离最近的两个簇
- 全链接:合并使得合并后簇内最远点对距离最小的簇
- 平均链接:合并使得平均距离最小的簇
- 缺点:对噪声敏感,容易形成链状聚类
- ROCK的连接度量
- 优点:考虑全局结构,抗噪能力强
- 缺点:计算复杂度高,参数敏感
- CURE的代表点策略
- 每个簇用多个代表点表示
- 通过收缩因子控制代表点位置
- 优点:识别任意形状,抗噪
- 缺点:参数调整复杂
- Chameleon的动态建模
- 基于k最近邻图划分
- 考虑簇间互连性和接近性
- 优点:自适应性强
- 缺点:计算复杂度高
应用场景对比
| 应用场景 | 推荐算法 | 理由 |
| 购物篮分析/市场篮子 | ROCK | 直接处理集合数据,连接概念贴合购买模式 |
| 客户细分(数值特征) | AGNES/CURE | 数值特征适用,距离度量直观 |
| 社交网络社区发现 | ROCK/Chameleon | 图结构数据,连接/互连性概念自然 |
| 文本聚类(词袋模型) | ROCK/LDA-based | 分类属性(词语),连接捕捉主题关联 |
| 空间数据聚类(GIS) | CURE/Chameleon | 空间坐标数值型,需要形状适应性 |
| 异常检测 | DBSCAN/CURE | 密度/距离基础,识别噪声点 |
| 大规模数值数据 | BIRCH/Agglomerative | 可伸缩性要求高 |
总结:ROCK的独特定位
ROCK在层次聚类算法家族中占据独特地位:
- 数据类型专业化:专门针对分类/布尔型数据优化,填补了传统方法在这一领域的空白
- 结构相似性导向:引入连接概念,从二元关系到社区结构的转变是重要的方法论创新
- 鲁棒性设计:通过Goodness函数的归一化项平衡簇大小偏差,增强算法稳定性
- 理论基础坚实:基于随机图模型的理论推导,为参数设置提供指导
虽然ROCK在计算效率和参数敏感性方面存在局限,但它在处理特定类型数据时的优势使其在聚类算法家族中具有不可替代的价值。后续发展的许多算法(如SNN、Jaccard图聚类等)都借鉴了ROCK的连接思想,进一步验证了其核心概念的前瞻性和实用性。
ROCK算法原理
数学基础与符号定义
基本符号
- 数据集:$S = \{s_1, s_2, …, s_n\}$,包含 $n$ 个数据点
- 每个数据点:$s_i = \{a_{i1}, a_{i2}, …, a_{im}\}$,是 $m$ 个属性的集合
- 阈值:$\theta \in (0, 1]$,相似度阈值
- 目标簇数:$k$
相似性度量函数
对于任意两个点 $s_i$ 和 $s_j$,ROCK通常使用Jaccard相似度:
$$\text{sim}(s_i, s_j) = \frac{|s_i \cap s_j|}{|s_i \cup s_j|}$$
Jaccard相似度的取值在0到1之间,适用于分类属性数据。
核心概念的形式化定义
邻居关系
两点 $s_i$ 和 $s_j$ 是邻居当且仅当:$\text{sim}(s_i, s_j) \geq \theta$
连接数
点 $s_i$ 和 $s_j$ 之间的连接数定义为:$\text{link}(s_i, s_j) = |\{s_k \in S : \text{sim}(s_i, s_k) \geq \theta \ \text{and} \ \text{sim}(s_j, s_k) \geq \theta\}|$
簇间连接
对于两个簇 $C_i$ 和 $C_j$,它们之间的总连接数为:$\text{link}(C_i, C_j) = \sum_{p \in C_i} \sum_{q \in C_j} \text{link}(p, q)$
Goodness函数的数学推导
随机图模型基础
ROCK算法的理论基础是**随机图模型**。假设一个簇是一个随机图:
- 每个点对的连接概率为 $t$(与 $\theta$ 相关)
- 在大小为 $n$ 的簇中,期望的连接数为 $n^{1+2f(\theta)}$
Goodness函数定义
簇 $C_i$ 和 $C_j$ 的Goodness函数定义为:
$$g(C_i, C_j) = \frac{\text{link}(C_i, C_j)}{(n_i + n_j)^{1+2f(\theta)} – n_i^{1+2f(\theta)} – n_j^{1+2f(\theta)}}$$
其中:
- $n_i = |C_i|$,$n_j = |C_j|$
- $f(\theta)$ 是依赖于 $\theta$ 的函数
$f(\theta)$ 函数的推导
根据ROCK原论文,$f(\theta)$ 的设定基于以下观察:
- 在一个随机图中,如果每对点以概率 $t$ 相连
- 则连接数的期望与 $n^{1+2f}$ 成正比
- 其中 $f$ 与 $\theta$ 相关,通常取 $f(\theta) = \frac{1 – \theta}{1 + \theta}$
推导过程:
- 两点为邻居的概率:$P(\text{sim} \geq \theta) = t$
- 三点构成三角形的概率:$t^3$
- 在随机假设下,连接数期望为 $\binom{n}{2}t^2$
- 但实际簇中,由于同质性,连接密度更高
- 通过调整指数 $f(\theta)$ 来匹配实际观测
Goodness函数的直观解释
分子 $\text{link}(C_i, C_j)$ 是实际观测到的连接数,衡量两簇间的紧密程度。
分母 $(n_i + n_j)^{1+2f} – n_i^{1+2f} – n_j^{1+2f}$ 是合并的”代价”:
- 如果合并是随机的,期望连接数增长符合此分母形式
- 实际连接数远超此期望,说明合并有意义
- 分母防止算法偏好合并大簇(大簇自然有更多连接)
层次合并的数学证明
引理1:连接的传递性
如果 $\text{link}(s_i, s_j) > 0$ 且 $\text{link}(s_j, s_k) > 0$,则 $\text{link}(s_i, s_k) > 0$ 的概率很高。
证明:由于连接基于共同邻居,如果 $s_i$ 和 $s_j$ 有共同邻居,$s_j$ 和 $s_k$ 有共同邻居,则 $s_i$ 和 $s_k$ 很可能通过 $s_j$ 间接连接。
定理1:Goodness函数的单调性
在合理的 $\theta$ 下,同一自然簇内点对的Goodness值高于不同簇点对的Goodness值。
证明思路:
- 同一簇内点对共享更多邻居
- 因此分子 $\text{link}(C_i, C_j)$ 更大
- 分母增长相对较慢
- 故Goodness值更大
定理2:算法收敛性
ROCK算法在有限步内收敛到k个簇。
证明:
- 初始状态有 $n$ 个簇
- 每次合并减少1个簇
- 最多进行 $n-k$ 次合并
- 每次合并都选择Goodness最大的簇对
- 当簇数达到k时算法终止
算法复杂度的理论分析
时间复杂度
- 相似度计算:$O(n^2 \cdot m)$
- $n$ 个点,$m$ 个属性
- 每对点需要 $O(m)$ 时间计算Jaccard相似度
- 邻居识别:$O(n^2)$
- 比较每对相似度与 $\theta$
- 连接数计算:$O(n^2 \cdot \bar{n}_n)$
- $\bar{n}_n$ 是平均邻居数
- 对于每对点,计算共同邻居数
- 层次合并:$O(n^2 \log n)$
- 每次合并需重新计算Goodness
- 共 $n-k$ 次合并
- 每次需检查 $O(n^2)$ 对(优化后可减少)
总时间复杂度:$O(n^2 \cdot (m + \bar{n}_n + \log n))$
空间复杂度
- 相似度矩阵:$O(n^2)$(可优化为稀疏存储)
- 连接矩阵:$O(n^2)$
- 邻居列表:$O(n \cdot \bar{n}_n)$
总空间复杂度:$O(n^2)$ 最坏情况,实际通常 $O(n \cdot \bar{n}_n)$
参数选择的数学指导
$\theta$ 选择的数学原理
$\theta$ 的选择基于数据集的相似度分布:
设相似度随机变量为 $X$,其概率密度函数为 $f_X(x)$。
理想 $\theta$ 应满足:
- 簇内相似度 $P(X \geq \theta | \text{same cluster})$ 较大
- 簇间相似度 $P(X \geq \theta | \text{different cluster})$ 较小
实际中选择 $\theta$ 的方法:
- 计算所有点对相似度的直方图
- 寻找双峰分布的谷底
- 或通过最大似然估计
目标簇数 $k$ 的确定
可以使用聚类有效性指标:
- Calinski-Harabasz指数:
$$CH(k) = \frac{\text{tr}(B)/(k-1)}{\text{tr}(W)/(n-k)}$$
其中 $B$ 是簇间散度,$W$ 是簇内散度
- 轮廓系数:
$$s(i) = \frac{b(i) – a(i)}{\max\{a(i), b(i)\}}$$
其中 $a(i)$ 是 $i$ 到同簇其他点的平均距离,$b(i)$ 是 $i$ 到最近其他簇的最小平均距离
ROCK算法实现(Python)
完整的Python实现
import numpy as np
from typing import List, Set, Tuple, Dict
from collections import defaultdict
from scipy.sparse import lil_matrix, csr_matrix
import heapq
import math
class ROCKClustering:
"""ROCK聚类算法的完整实现"""
def __init__(self, theta: float = 0.5, k: int = None,
f_theta_func: str = 'default'):
"""
初始化ROCK聚类器
参数:
----------
theta : float
相似度阈值,范围(0, 1]
k : int, optional
目标聚类数,如果不指定,算法会一直合并直到只剩下1个簇
f_theta_func : str
f(theta)函数的计算方式,可选['default', 'log', 'linear']
"""
self.theta = theta
self.k = k
self.f_theta_func = f_theta_func
self.clusters_ = None
self.history_ = [] # 保存合并历史
def _jaccard_similarity(self, set1: Set, set2: Set) -> float:
"""计算两个集合的Jaccard相似度"""
if not set1 or not set2:
return 0.0
intersection = len(set1.intersection(set2))
union = len(set1.union(set2))
return intersection / union if union > 0 else 0.0
def _compute_f_theta(self) -> float:
"""计算f(theta)函数"""
if self.f_theta_func == 'default':
# 原始ROCK论文中的公式
return (1 - self.theta) / (1 + self.theta)
elif self.f_theta_func == 'log':
# 对数变体,对高维数据更稳定
return np.log(1 + (1 - self.theta) / (1 + self.theta))
elif self.f_theta_func == 'linear':
# 线性变体,简化计算
return 1 - self.theta
else:
raise ValueError(f"Unknown f_theta_func: {self.f_theta_func}")
def _compute_similarity_matrix(self, data: List[Set]) -> np.ndarray:
"""计算相似度矩阵(优化版本)"""
n = len(data)
# 使用稀疏矩阵存储相似度,只存储≥theta的值
sim_matrix = lil_matrix((n, n), dtype=np.float32)
for i in range(n):
for j in range(i+1, n):
sim = self._jaccard_similarity(data[i], data[j])
if sim >= self.theta:
sim_matrix[i, j] = sim
sim_matrix[j, i] = sim
return sim_matrix.tocsr()
def _build_neighbor_lists(self, sim_matrix: csr_matrix) -> List[List[int]]:
"""构建邻居列表"""
n = sim_matrix.shape[0]
neighbors = []
for i in range(n):
# 获取第i行的非零元素索引(相似度≥theta的点)
row = sim_matrix.getrow(i)
neighbor_indices = row.nonzero()[1].tolist()
# 移除自身(如果存在)
if i in neighbor_indices:
neighbor_indices.remove(i)
neighbors.append(neighbor_indices)
return neighbors
def _compute_link_matrix(self, neighbors: List[List[int]]) -> csr_matrix:
"""高效计算连接矩阵"""
n = len(neighbors)
# 使用稀疏矩阵存储连接数
link_matrix = lil_matrix((n, n), dtype=np.int32)
# 将邻居列表转换为集合,便于快速求交
neighbor_sets = [set(nb) for nb in neighbors]
for i in range(n):
for j in range(i+1, n):
# 计算共同邻居数
common = len(neighbor_sets[i].intersection(neighbor_sets[j]))
if common > 0:
link_matrix[i, j] = common
link_matrix[j, i] = common
return link_matrix.tocsr()
def _compute_goodness(self, cluster_i: Set[int], cluster_j: Set[int],
link_matrix: csr_matrix, f_theta: float) -> float:
"""计算两个簇合并的goodness值"""
ni = len(cluster_i)
nj = len(cluster_j)
if ni == 0 or nj == 0:
return 0.0
# 计算总连接数
total_links = 0
for p in cluster_i:
for q in cluster_j:
total_links += link_matrix[p, q]
# 计算分母
denominator = ((ni + nj) ** (1 + 2 * f_theta)
- ni ** (1 + 2 * f_theta)
- nj ** (1 + 2 * f_theta))
if denominator <= 0:
return 0.0
return total_links / denominator
def _initialize_priority_queue(self, clusters: List[Set[int]],
link_matrix: csr_matrix, f_theta: float):
"""初始化优先队列(最大堆)"""
heap = []
n_clusters = len(clusters)
for i in range(n_clusters):
for j in range(i+1, n_clusters):
goodness = self._compute_goodness(
clusters[i], clusters[j], link_matrix, f_theta
)
if goodness > 0:
# 使用负值实现最大堆
heapq.heappush(heap, (-goodness, i, j, clusters[i], clusters[j]))
return heap
def fit(self, data: List[Set]) -> 'ROCKClustering':
"""
执行ROCK聚类
参数:
----------
data : List[Set]
输入数据,每个元素是一个属性集合
返回:
----------
self : 返回聚类器实例
"""
n = len(data)
if n == 0:
self.clusters_ = []
return self
# 步骤1: 计算相似度矩阵
print("步骤1: 计算相似度矩阵...")
sim_matrix = self._compute_similarity_matrix(data)
# 步骤2: 构建邻居列表
print("步骤2: 构建邻居列表...")
neighbors = self._build_neighbor_lists(sim_matrix)
# 步骤3: 计算连接矩阵
print("步骤3: 计算连接矩阵...")
link_matrix = self._compute_link_matrix(neighbors)
# 步骤4: 计算f(theta)
f_theta = self._compute_f_theta()
# 步骤5: 初始化簇(每个点一个簇)
clusters = [{i} for i in range(n)]
cluster_map = {i: i for i in range(n)} # 点->簇的映射
# 步骤6: 初始化优先队列
print("步骤4: 初始化优先队列...")
heap = self._initialize_priority_queue(clusters, link_matrix, f_theta)
# 步骤7: 层次合并
print("步骤5: 开始层次合并...")
merge_step = 0
while len(clusters) > 1:
# 如果指定了k,且当前簇数≤k,则停止
if self.k is not None and len(clusters) <= self.k:
break
# 从堆中获取goodness最大的簇对
if not heap:
break
neg_goodness, i, j, cluster_i, cluster_j = heapq.heappop(heap)
goodness = -neg_goodness
# 检查簇是否仍然存在且未改变
if (i >= len(clusters) or j >= len(clusters) or
clusters[i] != cluster_i or clusters[j] != cluster_j):
# 簇已发生变化,跳过
continue
# 合并簇i和j
new_cluster = clusters[i].union(clusters[j])
# 记录合并历史
self.history_.append({
'step': merge_step,
'merged': (i, j),
'goodness': goodness,
'size_i': len(clusters[i]),
'size_j': len(clusters[j]),
'new_size': len(new_cluster)
})
# 确定要保留的索引(保留较小的索引)
keep_idx, remove_idx = (i, j) if i < j else (j, i)
# 更新cluster_map
for point in clusters[remove_idx]:
cluster_map[point] = keep_idx
# 创建新簇列表
new_clusters = []
for idx, cluster in enumerate(clusters):
if idx == remove_idx:
continue
elif idx == keep_idx:
new_clusters.append(new_cluster)
else:
new_clusters.append(cluster)
clusters = new_clusters
# 更新堆:移除涉及被删除簇的条目,添加新簇与其他簇的条目
new_heap = []
while heap:
neg_g, idx_i, idx_j, cl_i, cl_j = heapq.heappop(heap)
# 调整索引:删除的簇之后的索引减1
if idx_i > remove_idx:
idx_i -= 1
if idx_j > remove_idx:
idx_j -= 1
# 检查条目是否仍然有效
valid = True
for idx, cl in [(idx_i, cl_i), (idx_j, cl_j)]:
if idx >= len(clusters) or clusters[idx] != cl:
valid = False
break
if valid:
heapq.heappush(new_heap, (neg_g, idx_i, idx_j, cl_i, cl_j))
heap = new_heap
# 添加新簇与其他簇的goodness
new_idx = keep_idx
for other_idx, other_cluster in enumerate(clusters):
if other_idx == new_idx:
continue
goodness = self._compute_goodness(
clusters[new_idx], other_cluster, link_matrix, f_theta
)
if goodness > 0:
# 确保索引顺序:小的在前
i, j = (new_idx, other_idx) if new_idx < other_idx else (other_idx, new_idx)
heapq.heappush(heap, (
-goodness, i, j, clusters[i], clusters[j]
))
merge_step += 1
if merge_step % 10 == 0:
print(f" 已合并 {merge_step} 次,当前簇数: {len(clusters)}")
self.clusters_ = clusters
self.cluster_labels_ = np.zeros(n, dtype=int)
for label, cluster in enumerate(clusters):
for point in cluster:
self.cluster_labels_[point] = label
print(f"聚类完成!最终得到 {len(clusters)} 个簇")
return self
def fit_predict(self, data: List[Set]) -> np.ndarray:
"""执行聚类并返回标签"""
self.fit(data)
return self.cluster_labels_
def get_cluster_summary(self) -> Dict:
"""获取聚类结果摘要"""
if self.clusters_ is None:
raise ValueError("请先调用fit方法进行聚类")
summary = {
'n_clusters': len(self.clusters_),
'cluster_sizes': [len(c) for c in self.clusters_],
'total_points': sum(len(c) for c in self.clusters_)
}
# 计算簇大小统计
sizes = summary['cluster_sizes']
if sizes:
summary['min_size'] = min(sizes)
summary['max_size'] = max(sizes)
summary['avg_size'] = sum(sizes) / len(sizes)
summary['std_size'] = np.std(sizes)
return summary
def plot_dendrogram(self, max_depth: int = 20):
"""绘制树状图(简化版)"""
import matplotlib.pyplot as plt
if not self.history_:
print("没有合并历史记录")
return
# 只显示最后max_depth次合并
history = self.history_[-max_depth:] if len(self.history_) > max_depth else self.history_
steps = [h['step'] for h in history]
goodness_values = [h['goodness'] for h in history]
sizes = [h['new_size'] for h in history]
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
# 左侧:合并goodness
ax1 = axes[0]
ax1.plot(steps, goodness_values, 'b-', marker='o')
ax1.set_xlabel('合并步骤')
ax1.set_ylabel('Goodness值')
ax1.set_title('合并Goodness变化')
ax1.grid(True, alpha=0.3)
# 右侧:簇大小
ax2 = axes[1]
ax2.plot(steps, sizes, 'r-', marker='s')
ax2.set_xlabel('合并步骤')
ax2.set_ylabel('新簇大小')
ax2.set_title('合并后簇大小变化')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
优化版本:使用更高效的数据结构
class OptimizedROCK(ROCKClustering):
"""优化的ROCK实现,使用更高效的数据结构和算法"""
def __init__(self, theta: float = 0.5, k: int = None,
use_minhash: bool = False, minhash_perm: int = 128):
"""
优化版ROCK
参数:
----------
use_minhash : bool
是否使用MinHash近似计算Jaccard相似度
minhash_perm : int
MinHash的排列数
"""
super().__init__(theta, k)
self.use_minhash = use_minhash
self.minhash_perm = minhash_perm
def _compute_minhash_signatures(self, data: List[Set]) -> np.ndarray:
"""计算MinHash签名矩阵"""
import mmh3
import random
n = len(data)
# 获取所有元素
all_elements = set()
for d in data:
all_elements.update(d)
element_list = list(all_elements)
# 生成随机哈希函数
random.seed(42)
hash_funcs = []
for _ in range(self.minhash_perm):
a = random.randint(1, 2**32 - 1)
b = random.randint(1, 2**32 - 1)
hash_funcs.append(lambda x, a=a, b=b: (a * mmh3.hash(str(x)) + b) % (2**32))
# 计算MinHash签名
signatures = np.full((n, self.minhash_perm), np.inf)
for i, d in enumerate(data):
for element in d:
for p, hash_func in enumerate(hash_funcs):
h = hash_func(element)
if h < signatures[i, p]:
signatures[i, p] = h
return signatures
def _minhash_similarity(self, sig1: np.ndarray, sig2: np.ndarray) -> float:
"""基于MinHash签名估计Jaccard相似度"""
matches = np.sum(sig1 == sig2)
return matches / len(sig1)
def _compute_similarity_matrix_fast(self, data: List[Set]) -> csr_matrix:
"""快速计算相似度矩阵(使用MinHash近似)"""
n = len(data)
if self.use_minhash and len(data) > 100:
# 使用MinHash近似
print("使用MinHash近似计算相似度...")
signatures = self._compute_minhash_signatures(data)
sim_matrix = lil_matrix((n, n), dtype=np.float32)
for i in range(n):
for j in range(i+1, n):
sim = self._minhash_similarity(signatures[i], signatures[j])
if sim >= self.theta:
sim_matrix[i, j] = sim
sim_matrix[j, i] = sim
else:
# 使用精确计算
sim_matrix = super()._compute_similarity_matrix(data)
return sim_matrix.tocsr()
def _compute_link_matrix_fast(self, neighbors: List[List[int]]) -> csr_matrix:
"""快速计算连接矩阵(使用倒排索引)"""
n = len(neighbors)
# 构建倒排索引:点 -> 包含该点的邻居列表
inverted_index = defaultdict(list)
for i, nb_list in enumerate(neighbors):
for neighbor in nb_list:
inverted_index[neighbor].append(i)
# 使用稀疏矩阵存储连接
link_matrix = lil_matrix((n, n), dtype=np.int32)
# 对每个点,其邻居之间相互连接
for i in range(n):
nb_set = set(neighbors[i])
for j in nb_set:
if j > i: # 只计算上三角
# 计算共同邻居数
common = len(nb_set.intersection(set(neighbors[j])))
if common > 0:
link_matrix[i, j] = common
link_matrix[j, i] = common
return link_matrix.tocsr()
def fit_fast(self, data: List[Set]) -> 'OptimizedROCK':
"""快速拟合(使用优化方法)"""
print("快速ROCK聚类开始...")
n = len(data)
if n == 0:
self.clusters_ = []
return self
# 步骤1: 快速计算相似度矩阵
print("步骤1: 计算相似度矩阵(快速)...")
sim_matrix = self._compute_similarity_matrix_fast(data)
# 步骤2: 构建邻居列表
print("步骤2: 构建邻居列表...")
neighbors = self._build_neighbor_lists(sim_matrix)
# 步骤3: 快速计算连接矩阵
print("步骤3: 计算连接矩阵(快速)...")
link_matrix = self._compute_link_matrix_fast(neighbors)
# 步骤4: 计算f(theta)
f_theta = self._compute_f_theta()
# 步骤5-7: 层次合并(使用并查集优化)
self._hierarchical_merge_fast(data, neighbors, link_matrix, f_theta)
return self
def _hierarchical_merge_fast(self, data: List[Set], neighbors: List[List[int]],
link_matrix: csr_matrix, f_theta: float):
"""快速层次合并(使用并查集)"""
n = len(data)
# 初始化并查集
parent = list(range(n))
rank = [0] * n
cluster_sets = [{i} for i in range(n)]
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
# 计算所有点对之间的goodness
goodness_heap = []
for i in range(n):
for j in range(i+1, n):
goodness = self._compute_goodness(
{i}, {j}, link_matrix, f_theta
)
if goodness > 0:
heapq.heappush(goodness_heap, (-goodness, i, j))
# 合并循环
n_clusters = n
merge_step = 0
while goodness_heap and (self.k is None or n_clusters > self.k):
neg_goodness, i, j = heapq.heappop(goodness_heap)
goodness = -neg_goodness
root_i, root_j = find(i), find(j)
if root_i == root_j:
continue # 已经在同一簇
# 合并簇
if rank[root_i] < rank[root_j]:
root_i, root_j = root_j, root_i
parent[root_j] = root_i
if rank[root_i] == rank[root_j]:
rank[root_i] += 1
# 更新簇集合
cluster_sets[root_i].update(cluster_sets[root_j])
cluster_sets[root_j] = set()
n_clusters -= 1
merge_step += 1
# 记录合并
self.history_.append({
'step': merge_step,
'merged': (i, j),
'goodness': goodness,
'new_size': len(cluster_sets[root_i])
})
if merge_step % 20 == 0:
print(f" 已合并 {merge_step} 次,当前簇数: {n_clusters}")
# 提取最终簇
final_clusters = []
cluster_labels = np.zeros(n, dtype=int)
cluster_id = 0
for i in range(n):
if parent[i] == i: # 是根节点
if cluster_sets[i]: # 非空簇
final_clusters.append(cluster_sets[i])
for point in cluster_sets[i]:
cluster_labels[point] = cluster_id
cluster_id += 1
self.clusters_ = final_clusters
self.cluster_labels_ = cluster_labels
print(f"聚类完成!最终得到 {len(final_clusters)} 个簇")
使用示例和测试
def test_rock_algorithm():
"""测试ROCK算法"""
# 创建示例数据(交易数据)
transactions = [
{"牛奶", "面包", "黄油"},
{"牛奶", "面包", "尿布"},
{"牛奶", "尿布", "啤酒"},
{"面包", "黄油", "尿布"},
{"啤酒", "尿布"},
{"面包", "啤酒", "黄油"},
{"牛奶", "面包", "尿布", "黄油"},
{"牛奶", "面包", "啤酒"},
{"面包", "尿布", "啤酒"},
{"牛奶", "尿布", "啤酒", "黄油"},
{"咖啡", "糖", "牛奶"},
{"咖啡", "饼干", "糖"},
{"咖啡", "糖", "茶"},
{"饼干", "茶", "牛奶"},
{"咖啡", "牛奶", "饼干"}
]
print("=" * 60)
print("ROCK聚类算法测试")
print("=" * 60)
# 测试1: 基本ROCK
print("\n1. 基本ROCK算法")
rock = ROCKClustering(theta=0.3, k=3)
labels = rock.fit_predict(transactions)
# 显示结果
print(f"\n聚类结果 (θ={rock.theta}, k={rock.k}):")
for i, cluster in enumerate(rock.clusters_):
print(f" 簇{i} (大小: {len(cluster)}):")
for point_idx in cluster:
print(f" 交易{point_idx}: {transactions[point_idx]}")
# 显示摘要
summary = rock.get_cluster_summary()
print(f"\n聚类摘要:")
print(f" 总簇数: {summary['n_clusters']}")
print(f" 总点数: {summary['total_points']}")
print(f" 簇大小: 最小={summary['min_size']}, 最大={summary['max_size']}, "
f"平均={summary['avg_size']:.2f}, 标准差={summary['std_size']:.2f}")
# 测试2: 优化版ROCK
print("\n" + "=" * 60)
print("2. 优化版ROCK算法(使用MinHash)")
print("=" * 60)
opt_rock = OptimizedROCK(theta=0.3, k=3, use_minhash=True, minhash_perm=64)
opt_labels = opt_rock.fit_fast(transactions)
print(f"\n优化版聚类结果:")
for i, cluster in enumerate(opt_rock.clusters_):
print(f" 簇{i} (大小: {len(cluster)}): {list(cluster)}")
# 测试3: 参数敏感性分析
print("\n" + "=" * 60)
print("3. 参数敏感性分析")
print("=" * 60)
thetas = [0.2, 0.3, 0.4, 0.5]
k_values = [2, 3, 4]
for theta in thetas:
for k in k_values:
test_rock = ROCKClustering(theta=theta, k=k)
test_rock.fit(transactions[:10]) # 使用子集加速
summary = test_rock.get_cluster_summary()
print(f"θ={theta:.1f}, k={k}: {summary['n_clusters']}个簇, "
f"大小范围[{summary['min_size']}-{summary['max_size']}]")
return rock, opt_rock
# 运行测试
if __name__ == "__main__":
basic_rock, optimized_rock = test_rock_algorithm()
# 绘制树状图
print("\n绘制合并历史树状图...")
basic_rock.plot_dendrogram(max_depth=15)
性能优化技巧
相似度计算优化
def compute_jaccard_fast(set1: Set, set2: Set) -> float:
"""快速计算Jaccard相似度"""
if not set1 or not set2:
return 0.0
# 假设集合较小,直接求交集
if len(set1) > len(set2):
set1, set2 = set2, set1
intersection = sum(1 for x in set1 if x in set2)
union = len(set1) + len(set2) - intersection
return intersection / union
连接矩阵计算的批量处理
def compute_links_batch(neighbors: List[List[int]], batch_size: int = 1000) -> csr_matrix:
"""批量计算连接矩阵,减少内存使用"""
n = len(neighbors)
link_matrix = lil_matrix((n, n), dtype=np.int32)
# 转换为集合数组
neighbor_sets = [set(nb) for nb in neighbors]
# 分批处理
for i_start in range(0, n, batch_size):
i_end = min(i_start + batch_size, n)
for i in range(i_start, i_end):
nb_set_i = neighbor_sets[i]
for j in range(i+1, n):
# 批量计算共同邻居
common = len(nb_set_i.intersection(neighbor_sets[j]))
if common > 0:
link_matrix[i, j] = common
link_matrix[j, i] = common
return link_matrix.tocsr()
并行计算支持
from concurrent.futures import ProcessPoolExecutor
import multiprocessing as mp
def compute_similarity_parallel(data: List[Set], theta: float, n_workers: int = None) -> csr_matrix:
"""并行计算相似度矩阵"""
n = len(data)
if n_workers is None:
n_workers = mp.cpu_count()
# 准备参数
params = [(i, j, data[i], data[j], theta)
for i in range(n) for j in range(i+1, n)]
def compute_pair(args):
i, j, set1, set2, theta_val = args
sim = len(set1 & set2) / len(set1 | set2) if (set1 and set2) else 0.0
return (i, j, sim) if sim >= theta_val else None
# 并行计算
sim_matrix = lil_matrix((n, n), dtype=np.float32)
with ProcessPoolExecutor(max_workers=n_workers) as executor:
results = executor.map(compute_pair, params)
for result in results:
if result:
i, j, sim = result
sim_matrix[i, j] = sim
sim_matrix[j, i] = sim
return sim_matrix.tocsr()
评估指标实现
def evaluate_clustering(data: List[Set], labels: np.ndarray,
metric: str = 'silhouette') -> float:
"""
评估聚类结果
参数:
----------
data : 原始数据
labels : 聚类标签
metric : 评估指标 ['silhouette', 'davies_bouldin', 'calinski_harabasz']
返回:
----------
score : 评估分数
"""
from sklearn.metrics import silhouette_score, davies_bouldin_score, calinski_harabasz_score
from sklearn.preprocessing import MultiLabelBinarizer
# 将集合数据转换为二进制矩阵
mlb = MultiLabelBinarizer()
X = mlb.fit_transform(data)
if metric == 'silhouette':
if len(set(labels)) <= 1:
return -1.0
return silhouette_score(X, labels, metric='jaccard')
elif metric == 'davies_bouldin':
if len(set(labels)) <= 1:
return float('inf')
return davies_bouldin_score(X, labels)
elif metric == 'calinski_harabasz':
if len(set(labels)) <= 1:
return 0.0
return calinski_harabasz_score(X, labels)
else:
raise ValueError(f"不支持的评估指标: {metric}")
def find_best_theta(data: List[Set], theta_range: Tuple[float, float, float] = (0.1, 0.9, 0.1),
k_range: Tuple[int, int] = (2, 10)):
"""自动寻找最佳参数"""
best_score = -float('inf')
best_params = None
best_labels = None
thetas = np.arange(theta_range[0], theta_range[1], theta_range[2])
for theta in thetas:
for k in range(k_range[0], k_range[1] + 1):
try:
rock = ROCKClustering(theta=theta, k=k)
labels = rock.fit_predict(data)
if len(set(labels)) <= 1:
continue
# 使用轮廓系数评估
score = evaluate_clustering(data, labels, 'silhouette')
if score > best_score:
best_score = score
best_params = {'theta': theta, 'k': k}
best_labels = labels
except Exception as e:
print(f"参数 theta={theta}, k={k} 时出错: {e}")
continue
print(f"最佳参数: {best_params}, 轮廓系数: {best_score:.4f}")
return best_params, best_labels
这个完整的Python实现包含了ROCK算法的所有关键组件,包括基本实现、优化版本、评估指标和参数调优工具。在实际使用中,可以根据数据规模选择合适的实现版本。