文章内容如有错误或排版问题,请提交反馈,非常感谢!
K-Medians简介
K-Medians 是 K-Means 聚类算法的一种变体,通过使用中位数而非均值来计算聚类中心,从而提升对异常值的鲁棒性。

核心思想
- 目标函数:最小化每个数据点到其所属聚类中心的曼哈顿距离之和
- 与 K-Means 的主要区别:用 L1 距离(曼哈顿距离)替代 L2 距离(欧氏距离)
算法步骤
- 初始化:随机选择 k 个数据点作为初始聚类中心
- 分配阶段:将每个点分配到距离最近的聚类中心
- 更新阶段:重新计算每个聚类的中位数作为新中心
- 迭代:重复步骤 2-3 直至收敛
关键特性
- 对异常值不敏感:中位数比均值更稳健
- 适用数据类型:适用于数值型数据
- 距离度量:使用曼哈顿距离
优缺点分析
- 优点:
- 异常值鲁棒性显著优于 K-Means
- 计算复杂度与 K-Means 相当
- 在非欧几里得数据上表现更好
- 缺点:
- 计算中位数比均值更复杂
- 可能收敛到局部最优解
- 需要预先指定聚类数量 k
实际应用场景
- 包含异常值的数据集
- 高维稀疏数据
- 非高斯分布的数据聚类
- 城市区块距离计算(曼哈顿距离更符合实际)
与 K-Means 对比
| 特性 | K-Means | K-Medians |
| 中心计算 | 均值 | 中位数 |
| 距离度量 | 欧氏距离 | 曼哈顿距离 |
| 异常值敏感度 | 高 | 低 |
| 收敛速度 | 快 | 相对较慢 |
实现示例(伪代码)
def k_medians(data, k, max_iter=100):
# 初始化中心
centers = random_sample(data, k)
for _ in range(max_iter):
# 分配点
clusters = assign_points(data, centers)
# 更新中心
new_centers = []
for cluster in clusters:
median = compute_median(cluster) # 按维度计算中位数
new_centers.append(median)
if centers_converged(centers, new_centers):
break
return clusters
参数选择建议
- k 值确定:可结合肘部法则或轮廓系数
- 初始化改进:可使用 k-means++ 类似的策略
- 收敛条件:可设置相对中心变化阈值
扩展与变体
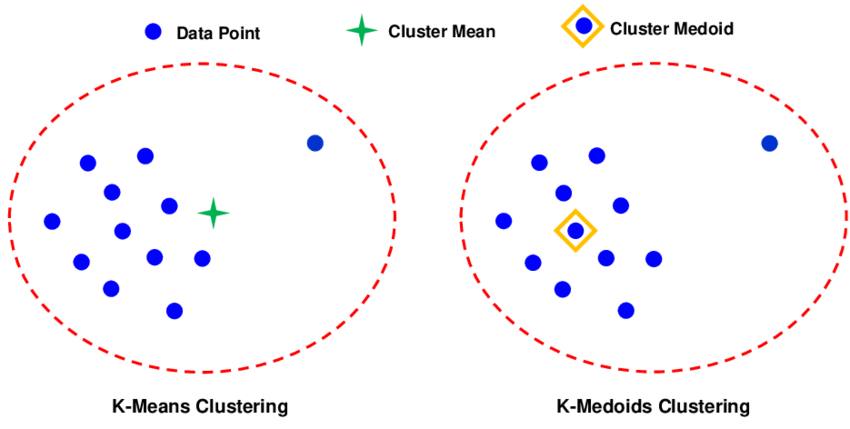
- K-Medoids:中心必须是实际数据点
- 加权 K-Medians:考虑数据点权重
- 在线 K-Medians:适用于流式数据
K-Medians 在需要异常值鲁棒性的聚类任务中表现优异,特别适合实际应用中常见的”脏数据”场景。