CURE(Clustering Using Representatives)是一种针对大型数据库的高效的聚类算法。基于层次的传统的聚类算法得到的是球状的,相等大小的聚类,对异常数据比较脆弱。CURE采用了用多个点代表一个簇的方法,可以较好的处理以上问题。并且在处理大数据量的时候采用了随机取样,分区的方法,来提高其效率,使得其可以高效的处理大量数据。先看一下基于层次聚类算法的缺陷:

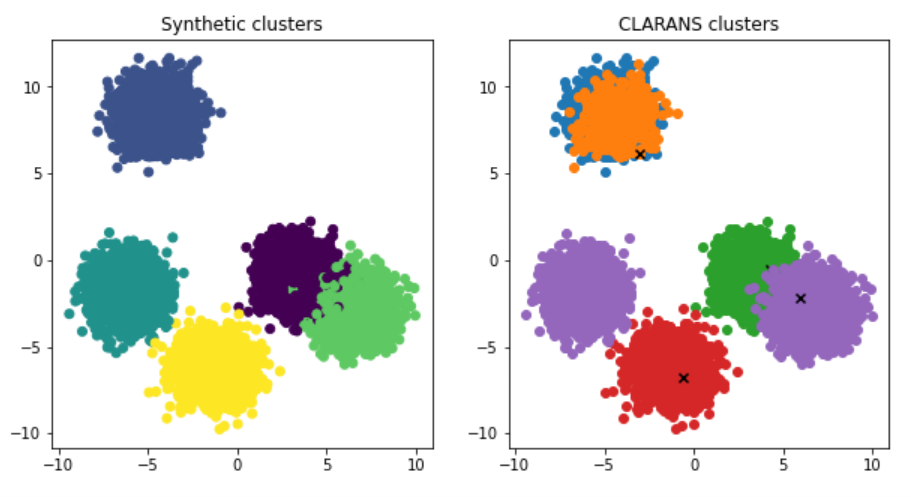
如上图所示,基于层级的聚类算法比如Hierarchical K-means聚类算法,不能够很好地区分尺寸差距大的簇,原因是K-means算法基于“质心”加一定“半径”对数据进行划分,导致最后聚类的簇近似“圆形”。
再看一下其他聚类算法在聚类结果上可能存在的问题:
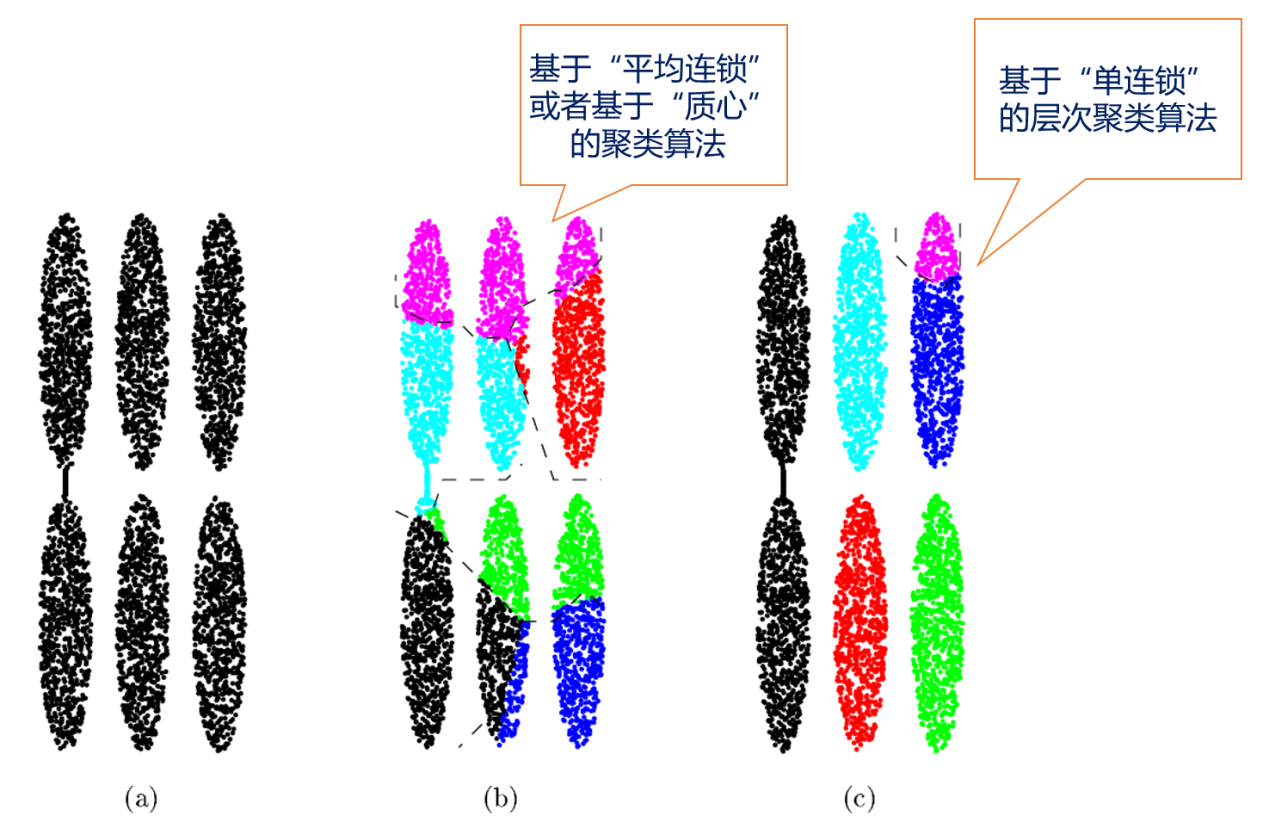
上面(b)图使用的是基于“平均连锁”或者基于“质心”的簇间距离计算方式得到的聚类结果,可以看出,聚类结果同基于划分的聚类算法相似、最后聚类的结果呈“圆形”,不能够准确地识别条形的数据;(c)图使用的是基于“单连锁”的簇间距离计算策略,由“单连锁”的定义可知,对于(c)图中最左边两个由一条细线相连的两个簇,会被聚类成一个簇,这也不是我们想要的。
CURE算法核心的思想是使用一定数量的“分散的”点(scattered points)来代表一个簇(cluster),而不像是其他层次聚类算法中,只使用一个点,使得CURE算法有如下优势:
- 准确地识别任意形状的簇;
- 准确地识别尺寸差距大的簇;
- 很好地处理“噪点”
所以,CURE算法很好地解决了上面提到的聚类结果的缺陷。
CURE算法流程
CURE的算法在开始时,每个点都是一个簇,然后将距离最近的簇结合,一直到簇的个数为要求的K。它是一种分裂的层次聚类。算法分为以下6步:
- 从源数据对象中抽取一个随机样本S。
- 将样本S分割为一组划分。
- 对划分局部的聚类。
- 通过随机取样提出孤立点。如果一个簇增长得太慢,就去掉它。
- 对局部的簇进行聚类。
- 用相应的簇标签标记数据。
CURE算法主流程如下:

首先从原始数据集中随机抽取一部分样本点作为子集,再对该子集进行划分,在这些划分后的集合上运行CURE聚类算法得到每个集合的簇,并删除其中的离群点,然后对这些簇进一步进行CURE层次聚类,并删除其中的离群点,最后对磁盘中剩余的数据集样本点进行划分。
CURE算法设计
1)基本聚类算法
procedure cluster(S,k)/*将数据集S聚类成为k个簇*/
begin
T:=build_kd_tree(S)/*对应数据集S建立一个K-D Tree T*/
Q:=build_heap(S)/*对应数据集S建立一个堆Q*/
while size(Q)>k do{/*聚类直至簇的个数为k*/
u:=extract_min(Q)/*找到最近的两个簇u,v*/
v:=u.cloest
delete(Q,v)
w:=merge(u,v)/*将u,v合并为簇w*/
delete_rep(T,u);delete_rep(T,v);insert_rep(T,w)
w.cloest:=x/*x is an arbitrary cluster in Q*/
foreach x∈Q do{/*调节因合并带来的T和Q的变化*/
if(dist(w,x)<dist(w,w.cloest))
w.cloest:=x
if x.cloest is either u or v{
if dist(x,x.cloest)<dist(x.w)
x.cloest:=cloest_cluster(T,x,dist(x,w))
else
x.cloest:=w
relocate(Q,x)
}
else if dist(x,x.cloest)>dist(x,w){
x.cloest:=w
relocate(Q,x)
}
}
insert(Q,w)
}
End
此程序段用到的数据结构有Heap和KDTree。为了合并距离最短的两个聚类,需要构建一个KDTree来找到空间中的一聚类最近的一个聚类,之后把DTree中的聚类按照其与最近的聚类的距离进行排序(用的是堆排序),找到最近的两个的聚类,将它们合并(对应函数merge())。
2)Merge算法
procedure merge(u,v)/*合并两个簇,并确定新簇的中心点和代表点*/
begin
w:=u∪v
w.mean:=(|u|u.mean+|v|v.mean)/(|u|+|v|)/*求新簇w的中心点*/
tmpSet:=Ø/*用来存c个代表点的集合*/
for i:=1 to c do{/*选出c个代表点*/
maxDist:=0
if i=1
minDist:=dist(p,w.mean)
else
minDist:=min{dist(p,q):q∈tmpSet}
if(minDist>=maxDist){
maxDist:=minDist
maxPoint:=p
}
}
tmpSet:=tmpSet∪{maxPoint}
}
foreach point p in tmpSet do/*按照收缩因子α处理代表点*/
w.rep:=w.rep∪{p+α*(w.mean–p)}
return w
end
此程序段同时描述了如何选取代表点:对每个簇选择c个分布较好的点,通过系数$\alpha$向中心收缩,其中$0<\alpha<1$。$\alpha$小,收缩小,可以区分拉长的簇;$\alpha$大,靠近中心点,得到的簇更紧凑。显然,如果$\alpha=1$,聚类w的代表点就是w.mean,即其中心点,此时类似于Centroid-base approach,即中心点代表簇,当$\alpha=0$,此时类似于All-points approach,即所有点代表簇。簇之间的距离定义为:两个簇的代表点之间的最小距离,即:
$$dist(u,v)=\min dist(p,q)$$
点到簇的距离与此类似,是该点到最近的簇的代表点的距离。c个代表点体现了簇的物理几何形状;向中心收缩可以降低异常点的影响。两个簇组合后的新簇,则重新选择c个点作为簇的代表。
3)数据取样在对大规模数据库进行聚类分析时,数据取样是一种常用的提高聚类效率的方法,即对整个数据库进行数据取样,然后对取样数据库进行聚类分析,而对未被取样的数据进行聚类标注。这样,对大规模数据库的聚类分析就转化为对较小规模的取样数据库的聚类分析。由于没有考虑到整个数据库的数据,聚类质量必然会受到影响。但是,只要取样均匀且取样率适当,则取样数据库也可以较好地反映整个数据库状况,从而在保证聚类质量的同时提高聚类效率。
定理1:对一个簇u,如果取样大小s满足:
$$s \geq fN + \frac{N}{|u|} \log(\frac{1}{\delta}) + \frac{N}{|u|} \sqrt{(\log(\frac{1}{\delta}))^2 + 2f|u| \log(\frac{1}{\delta})}$$
那么,样本中属于簇u的点的个数小于f|u|的概率小于$\delta$,$0<= \delta<= 1$。因此,采用chernoff bounds来确定的最小的取样数据量: $$s_{min} = \zeta k \rho + k \rho \log(\frac{1}{\delta}) + \sqrt{\log(\frac{1}{\delta})^2 + 2 \zeta \log(\frac{1}{\delta})}$$ 这就表示着如果我们只关心数据点数目大于的聚类,且最小的聚类至少有$\zeta$个数据点,那么我们只需要一个独立于原始数据点个数的取样数目。 4) 分区方法-减少输入数据,保证内存中存放所有聚类的代表点
分区过程如下:将所有样本分成p个分区,每个分区大小n/p。每个分区内作聚类,直到分区内的簇的个数为n/pq, q > 1。或者指定一个距离阈值,当最近簇距离大于阈值,则停止。在CURE算法中,
- First pass每个分区:$O(\frac{n^2}{p^2}(\frac{q-1}{q}) \log \frac{n}{p})$
- Second pass总聚类: $O(\frac{n^2}{p^2} \log \frac{n}{p})$
p, q的最好选值:使n/pq为k的2~3倍。其优点是:减少执行时间;减少输入数据,保证可以在内存中存放所有聚类的代表点。
5) 标记数据所属的簇
因为CURE用c个点来代表一个聚类,因此在聚类完成后,对未参加聚类的数据或新增的数据进行标注从而计算聚类的可信度时,其可以准确的识别非球状数据集,使得标注更加准确。
6) 异常点的处理
在进行随机采样时,会过滤掉大部分的离群点,此外,在随机采样得到的数据集中存在的少量离群点由于分布在整个原始数据空间,因而被随机采样进一步隔离了。在进行CURE凝聚层次聚类时,需要将每个点单独初始化为一个簇,并将距离最近的点合并为一个簇,由于离群点往往距离样本中的其它点很远,因此他所代表的簇增长的最为缓慢,以至于簇的大小远远小于正常的簇。
以上述讨论作为契机,我们将层次聚类中的离群点识别分为两个阶段,第一个阶段是在聚类算法执行到某一阶段(或称当前的簇总数减小到某个值)时,根据簇的增长速度和簇的大小对离群点进行一次识别,需要注意的是,如果这个阶段选择的较早(即簇总数依旧很大)的话,会将一部分本应被合并的簇识别为离群点,如果这个阶段选择的较晚(即簇总数过少)的话,离群点很可能在被识别之前就已经合并到某些簇中,因此原文推荐当前簇的总数为数据集大小的1/3时,进行离群点的识别。第一阶段有一个很明显的问题,就是当随机采样到的离群点分布的比较近时(即使可能性比较小),这些点会被合并为一个簇,而导致无法将他们识别出来,这时就需要第二阶段的来进行处理。由于离群点占的比重很小,而在层次聚类的最后几步中,每个正常簇的粒度都是非常高的,因此很容易将他们识别出来,一般当簇的总数缩减到大约为k时,进行第二阶段的识别。
数据取样算法
在对大规模数据库进行聚类分析时,数据取样是一种常用的提高聚类效率的方法,即对整个数据库进行数据取样,然后对取样数据库进行聚类分析,而对未被取样的数据进行聚类标注。这样,对大规模数据库的聚类分析就转化为对较小规模的取样数据库的聚类分析。由于没有考虑到整个数据库的数据,聚类质量必然会受到影响。但是,只要取样均匀且取样率适当,则取样数据库也可以较好地反映整个数据库状况,从而在保证聚类质量的同时提高聚类效率。与以前的基于取样的聚类算法相比。
取样算法:这种算法只需扫描一遍被取样数据库,而且使用恒定的内存空间,便可以从N个记录中随机取出n个取样记录。其基本思想是:从第N-n+1条记录开始,做下列操作。设当前处理的是第t个记录(n+1 ≤ t ≤ N),u是产生的一个随机数(u ∈ [0, t-1]),若u< n,则把第u个记录替换成第t个记录。可以证明该算法能够得到均匀的取样结果。确定取样率很重要。为保证聚类质量,取样数据库应该能够有效地代表原数据库。若取样率太低,取样数据库必然会丢失原数据库的某些特质,导致聚类效果失真。
CURE算法Python实现
#-*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import scipy.spatial.distance as distance
from sklearn import metrics
from sklearn.datasets import make_blobs
# Returns the distance between two vectors
def dist(vecA, vecB):
return np.sqrt(np.power(vecA - vecB, 2).sum())
# This class describes the data structure and method of operation for CURE clustering.
class CureCluster:
def __init__(self, id__, center__):
self.points = center__
self.rep_points = center__
self.center = center__
self.index = [id__]
def __repr__(self):
return "Cluster" + "Size:" + str(len(self.points))
# Computes and stores the centroid of this cluster, based on its points
def compute_centroid(self, clust):
total_points_1 = len(self.index)
total_points_2 = len(clust.index)
self.center = (self.center * total_points_1 + clust.center * total_points_2) / (total_points_1 + total_points_2)
# Computes and stores representative points for this cluster
def generate_rep_points(self, num_rep_points, alpha):
temp_set = None
for i in range(1, num_rep_points + 1):
max_dist = 0
max_point = None
for p in range(0, len(self.index)):
if i == 1:
min_dist = dist(self.points[p, :], self.center)
else:
X = np.vstack([temp_set, self.points[p, :]])
tmp_dist = distance.pdist(X)
min_dist = tmp_dist.min()
if min_dist >= max_dist:
max_dist = min_dist
max_point = self.points[p, :]
if temp_set is None:
temp_set = max_point
else:
temp_set = np.vstack((temp_set, max_point))
for j in range(len(temp_set)):
if self.rep_points is None:
self.rep_points = temp_set[j, :] + alpha * (self.center - temp_set[j, :])
else:
self.rep_points = np.vstack((self.rep_points, temp_set[j, :] + alpha * (self.center - temp_set[j, :])))
# Computes and stores distance between this cluster and the other one.
def dist_rep(self, clust):
dist_rep = float('inf')
for repA in self.rep_points:
if type(clust.rep_points[0]) != list:
repB = clust.rep_points
dist_temp = dist(repA, repB)
if dist_temp< dist_rep:
dist_rep = dist_temp
else:
for repB in clust.rep_points:
dist_temp = dist(repA, repB)
if dist_temp< dist_rep:
dist_rep = dist_temp
return dist_rep
# Merges this cluster with the given cluster, recomputing the centroid and the representative points.
def merge_with_cluster(self, clust, num_rep_points, alpha):
self.compute_centroid(clust)
self.points = np.vstack((self.points, clust.points))
self.index = np.append(self.index, clust.index)
self.rep_points = None
self.generate_rep_points(num_rep_points, alpha)
# Describe the process of the CURE algorithm
def run_CURE(data, num_rep_points, alpha, num_des_cluster):
# Initialization
clusters = []
num_cluster = len(data)
num_Pts = len(data)
dist_cluster = np.ones([len(data), len(data)])
dist_cluster = dist_cluster * float('inf')
for id_point in range(len(data)):
new_clust = CureCluster(id_point, data[id_point, :])
clusters.append(new_clust)
for row in range(0, num_Pts):
for col in range(0, row):
dist_cluster[row][col] = dist(clusters[row].center, clusters[col].center)
while num_cluster > num_des_cluster:
if np.mod(num_cluster, 50) == 0:
print('Cluster count:', num_cluster)
# Find a pair of closet clusters
min_index = np.where(dist_cluster == np.min(dist_cluster))
min_index1 = min_index[0][0]
min_index2 = min_index[1][0]
# Merge
clusters[min_index1].merge_with_cluster(clusters[min_index2], num_rep_points, alpha)
# Update the distCluster matrix
for i in range(0, min_index1):
dist_cluster[min_index1, i] = clusters[min_index1].dist_rep(clusters[i])
for i in range(min_index1 + 1, num_cluster):
dist_cluster[i, min_index1] = clusters[min_index1].dist_rep(clusters[i])
# Delete the merged cluster and its disCluster vector.
dist_cluster = np.delete(dist_cluster, min_index2, axis=0)
dist_cluster = np.delete(dist_cluster, min_index2, axis=1)
del clusters[min_index2]
num_cluster = num_cluster - 1
print('Cluster count:', num_cluster)
# Generate sample labels
label = [0] * num_Pts
for i in range(0, len(clusters)):
for j in range(0, len(clusters[i].index)):
label[clusters[i].index[j]] = i + 1
return label
if __name__ == "__main__":
centers = [[1, 1], [-1, -1], [1, -1]]
data, Label_true = make_blobs(n_samples=750, centers=centers,
cluster_std=0.4, random_state=0)num_rep_points = 5 # The number of representative points
alpha = 0.1 # Shrink factor
num_des_cluster = 3 # Desired cluster number
Label_pre = run_CURE(data, num_rep_points, alpha, num_des_cluster)
nmi = metrics.v_measure_score(Label_true, Label_pre)
print("NMI =", nmi)
scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange', 'brown', 'cyan', 'brown',
'chocolate', 'darkgreen', 'darkblue', 'azure', 'bisque']
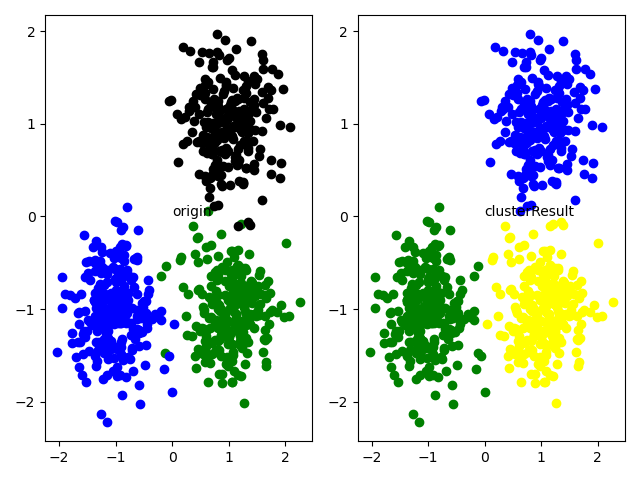
plt.subplot(121)
for i in range(data.shape[0]):
color = scatterColors[Label_true[i]]
plt.scatter(data[i, 0], data[i, 1], marker='o', c=color)
plt.text(0, 0, "origin")
plt.subplot(122)
for i in range(data.shape[0]):
color = scatterColors[Label_pre[i]]
plt.scatter(data[i, 0], data[i, 1], marker='o', c=color)
plt.text(0, 0, "clusterResult")
plt.show()
参考链接: