FastText简介
fastText是Facebook于2016年开源的一个词向量计算和文本分类工具,在文本分类任务中,fastText(浅层网络)往往能取得和深度网络相媲美的精度,却在训练时间上比深度网络快许多数量级。在标准的多核CPU上,能够训练10亿词级别语料库的词向量在10分钟之内,能够分类有着30万多类别的50多万句子在1分钟之内。
该工具的理论基础是以下两篇论文:
- Enriching Word Vectors with Subword Information:这篇论文提出了用word n-gram的向量之和来代替简单的词向量的方法,以解决简单word2vec无法处理同一词的不同形态的问题。fastText中提供了maxn这个参数来确定word n-gram的n的大小。
- Bag of Tricks for Efficient Text Classification:这篇论文提出了fastText算法,该算法实际上是将目前用来算word2vec的网络架构做了个小修改,原先使用一个词的上下文的所有词向量之和来预测词本身(CBOW模型),现在改为用一段短文本的词向量之和来对文本进行分类。
词向量背景
假设我们需要在机器学习的模型中使用以下单词,首先需要做的是将他们转化为向量。
Ronaldo, Messi, Dicaprio(罗纳尔多,梅西,莱昂纳多·迪卡普里奥)
一个简单的想法是对单词进行一次热编码:
| Ronaldo | Messi | Dicaprio | |
| Ronaldo | 1 | 0 | 0 |
| Messi | 0 | 1 | 0 |
| Dicaprio | 0 | 0 | 1 |
我们可以看到这种稀疏表示没有捕捉到单词之间的任何关系,而且每个单词都是相互隔离的。我们知道罗纳尔多和梅西是足球运动员,而迪卡普里奥是演员。让我们利用我们的世界知识,创建手动功能来更好地表示单词。
| isFootballer | isActor | |
| Ronaldo | 1 | 0 |
| Messi | 1 | 0 |
| Dicaprio | 0 | 1 |
这比前一个热编码要好,因为相关项在空间上更接近。

我们可以继续添加更多的方面作为维度,以获得更细致的表示:
| isFootballer | isActor | Popularity | Gender | Height | Weight | … | |
| Ronaldo | 1 | 0 | … | … | … | … | … |
| Messi | 1 | 0 | … | … | … | … | … |
| Dicaprio | 0 | 1 | … | … | … | … | … |
但对每个单词进行这样的标注是行不通的。我们能否通过神经网络对大量的文本进行学习来生成我们的词汇表?
Word2Vec简介
2013年,Mikolov等人介绍了一种从大量非结构化文本数据中学习单词向量表示的有效方法。由于相似的词出现在相似的语境中,Mikolov等人利用这一洞察,提出了两个表征学习任务。
第一个被称为“Continuous Bag of Words”,即通过周边单词预测中间的单词:
第二个被称为“Skip-gram”,即通过给定一个中间的单词预测周边单词:
通过以上学习获得词向量由一些有趣的特征,比如对词向量进行算术运算似乎可以保留一定的含义:

Word2Vec的局限
虽然Word2Vec是NLP的游戏规则改变者,但我们将看到仍有一些改进的空间:
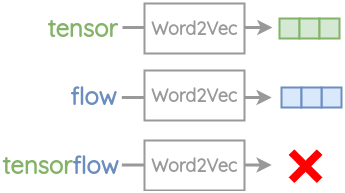
1、词汇表外(OOV)单词在Word2Vec中,为每个单词创建一个嵌入。因此,它不能处理任何它在训练中没有遇到的单词。
例如“tensor”和“flow”出现在Word2Vec的词汇表中。但如果你想把复合词“tensorflow”进行embedding,你会得到一个“out of vocabulary error”错误。
2、单词形态:对于词根相同的单词,比如“eat”和“eaten”,Word2Vec不做任何参数共享。每一个单词都是根据它出现的上下文来学习的。因此,可以利用单词的内部结构来提高处理效率。

FastText的改进
为了解决上述挑战,Bojanowski等人提出了一种新的嵌入方法FastText。他们的主要见解是使用单词的内部结构来改进从skipgram方法获得的向量表示。对skipgram方法的修改如下:
1、子词生成:针对一个单词,我们获取长度3-6个字符的n-gram。
我们取一个单词并加上尖括号来表示单词的开头和结尾:

然后,我们生成长度为n的字符n-gram。例如,对于单词“eating”,可以通过从角括号的开始滑动一个3个字符的窗口直到到达结束角括号来生成长度为3的字符n-gram。
![]()
最后,我们得到一个单词的字符n-gram列表:

不同长度字符n-gram的示例如下:
| Word | Length(n) | Character n-grams |
| eating | 3 | <ea,eat,ati,tin,ing,ng> |
| eating | 4 | <eat,eati,atin,ting,ing> |
| eating | 5 | <eati,eatin,ating,ting> |
| eating | 6 | <eatin,eating,ating> |
由于可能有大量的唯一n-gram,所以使用hash来绑定内存需求。
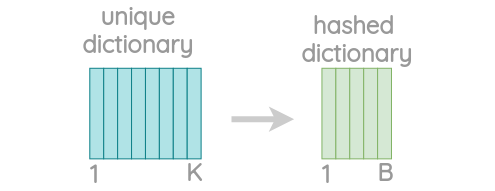
每个字符n-gram被散列为1到B之间的整数。尽管这可能会导致冲突,但它有助于控制词汇表的大小。这里使用的是FNV-1a型Fowler-Noll-Vo hashing函数将字符序列哈希为整数值。

2、包含负采样的Skip-gram
为了更好的理解,比如,我们有一个中间包含“eating”的句子,需要预测上下文单词“am”和“food”。
![]()
首先,计算中心字的嵌入量是通过取n-gram字符和整个单词本身的向量和来计算的:

对于实际的上下文词,我们直接从嵌入表中提取其词向量,而不添加字符n-gram。

现在,我们随机收集负样本,概率与单峰频率的平方根成比例。对于一个实际的语境词,随机抽取5个负样本。

我们取中心词和实际语境词之间的点积,并应用sigmoid函数得到0到1之间的匹配分数。
基于这个损失,我们用SGD优化器更新嵌入向量,使实际上下文词更接近中心词,但增加了与负样本的距离。

FastText总结
1、对于像捷克语和德语这样形态丰富的语言,FastText可以显著提高句法单词类比任务的性能。

| word2vec-skipgram | word2vec-cbow | fasttext | |
| Czech | 52.8 | 55.0 | 77.8 |
| German | 44.5 | 45.0 | 56.4 |
| English | 70.1 | 69.9 | 74.9 |
| Italian | 51.5 | 51.8 | 62.7 |
2、与Word2Vec相比,FastText在语义类比任务上的性能有所下降。
| word2vec-skipgram | word2vec-cbow | fasttext | |
| Czech | 25.7 | 27.6 | 27.5 |
| German | 66.5 | 66.8 | 62.3 |
| English | 78.5 | 78.2 | 77.8 |
| Italian | 52.3 | 54.7 | 52.3 |
3、由于增加了n-grams的开销,FastText的训练速度比普通skipgram慢5倍
4、将子词信息与字符n-grams结合使用,在单词相似性任务中比CBOW和skip-gram基线具有更好的性能。用子词求和来表示单词外的单词比指定空向量具有更好的性能。
| skipgram | cbow | fasttext(null OOV) | fasttext(char-ngrams for OOV) | ||
| Arabic | WS353 | 51 | 52 | 54 | 55 |
| GUR350 | 61 | 62 | 64 | 70 | |
| German | GUR65 | 78 | 78 | 81 | 81 |
| ZG222 | 35 | 38 | 41 | 44 | |
| English | RW | 43 | 43 | 46 | 47 |
| WS353 | 72 | 73 | 71 | 71 | |
| Spanish | WS353 | 57 | 58 | 58 | 59 |
| French | RG65 | 70 | 69 | 75 | 75 |
| Romanian | WS353 | 48 | 52 | 51 | 54 |
| Russian | HJ | 69 | 60 | 60 | 66 |
FastText与Word2Vec
fastText的其中的一个作者是Thomas Mikolov。也正是这个人在谷歌的时候,带领团队在2012年提出了word2vec代替了one-hot编码,将词表示为一个低维连续嵌入,极大促进了NLP的发展。14年她去了脸书,然后提出了word2vec的改进版:fasttext。所以fastText和word2vec在结构上很相似。
相同之处:
- 图模型结构很像,都是采用embedding向量的形式,得到word的隐向量表达。
- 采用很多相似的优化方法,比如使用Hierarchical softmax优化训练和预测中的打分速度。
- 训练词向量时,两者都是无监督算法。输入层是context window内的term。输出层对应的是每一个term,计算某term的概率最大;
- 在使用层次softmax的时候,huffman树叶子节点处是训练语料里所有词的向量。
不同之处:
- 模型的输出层:word2vec的输出层,对应的是每一个term,计算某term的概率最大;而fasttext的输出层对应的是分类的label。不过不管输出层对应的是什么内容,其对应的vector都不会被保留和使用;
- 模型的输入层:word2vec的输入层,是context window内的term;而fasttext对应的整个sentence的内容,包括term,也包括n-gram的内容;
- 两者本质的不同,体现在Hierarchical softmax的使用。
- Wordvec的目的是得到词向量,该词向量最终是在输入层得到,输出层对应的Hierarchical softmax也会生成一系列的向量,但最终都被抛弃,不会使用。
- fasttext则充分利用了Hierarchical softmax的分类功能,遍历分类树的所有叶节点,找到概率最大的label(一个或者N个)
FastText的优点:
- 适合大型数据+高效的训练速度:能够训练模型“在使用标准多核 CPU 的情况下 10 分钟内处理超过 10 亿个词汇”,特别是与深度模型对比,fastText 能将训练时间由数天缩短到几秒钟。使用一个标准多核 CPU,得到了在 10 分钟内训练完超过 10 亿词汇量模型的结果。此外,FastText 还能在五分钟内将 50 万个句子分成超过 30 万个类别。
- 支持多语言表达:利用其语言形态结构,FastText 能够被设计用来支持包括英语、德语、西班牙语、法语以及捷克语等多种语言。它还使用了一种简单高效的纳入子字信息的方式,在用于像捷克语这样词态丰富的语言时,这种方式表现得非常好,这也证明了精心设计的字符 n-gram 特征是丰富词汇表征的重要来源。FastText 的性能要比时下流行的 word2vec 工具明显好上不少,也比其他目前最先进的词态词汇表征要好。
- FastText 专注于文本分类,在许多标准问题上实现当下最好的表现(例如文本倾向性分析或标签预测)。
- 比 word2vec 更考虑了相似性,比如 FastText 的词嵌入学习能够考虑 english-born 和 british-born 之间有相同的后缀,但 word2vec 却不能。
FastText 实现细节
模型架构
FastText 的架构和 word2vec 中的 CBOW 的架构类似,因为它们的作者 Tomas Mikolov,而且确实 FastText 也算是 word2vec 所衍生出来的。
CBOW 的架构
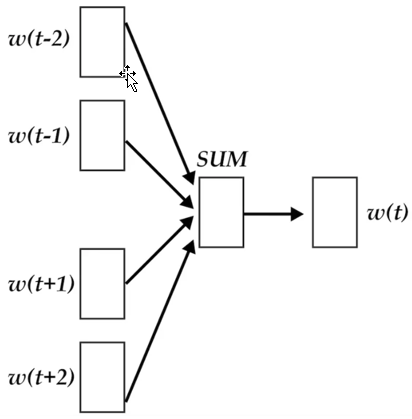
输入的是 $w(t)$ 的上下文 2d 个词,经过隐藏层后,输出的是 $w(t)$。word2vec 将上下文关系转化为多分类任务,进而训练逻辑回归模型,这里的类别数量是 $|V|$ 词库大小。通常的文本数据中,词库少则数万,多则百万,在训练中直接训练多分类逻辑回归并不现实。word2vec 中提供了两种针对大规模多分类问题的优化手段,negative sampling 和 hierarchical softmax。在优化中,negative sampling 只更新少量负面类,从而减轻了计算量。hierarchical softmax 将词库表示成前缀树,从树根到叶子的路径可以表示为一系列二分类器,一次多分类计算的复杂度从 $|V|$ 降低到了树的高度。
fastText 模型架构
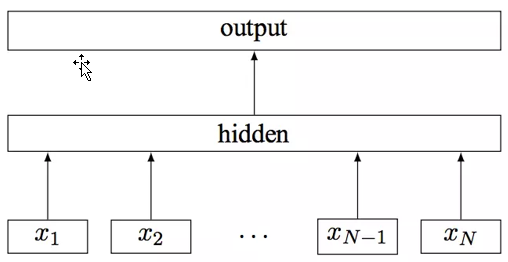
其中 $x_1, x_2, …, x_{N-1}, x_N$ 表示一个文本中的 n-gram 向量,每个特征是词向量的平均值。这和前文中提到的 cbow 相似,cbow 用上下文去预测中心词,而此处用全部的 n-gram 去预测指定类别。注意:此架构图没有展示词向量的训练过程。可以看到,和 CBOW 一样,fastText 模型也只有三层:输入层、隐含层、输出层(Hierarchical Softmax),输入都是多个经向量表示的单词,输出都是一个特定的 target,隐含层都是对多个词向量的叠加平均。
fastText 与 CBOW 的不同点:
- CBOW 的输入是目标单词的上下文,fastText 的输入是多个单词及其 n-gram 特征,这些特征用来表示单个文档
- CBOW 的输入单词被 one-hot 编码过,fastText 的输入特征是被 embedding 过
- CBOW 的输出是目标词汇,fastText 的输出是文档对应的类标
值得注意的是,fastText 在输入时,将单词的字符级别的 n-gram 向量作为额外的特征;在输出时,fastText 采用了分层 Softmax,大大降低了模型训练时间。
Hierarchical softmax
Softmax 回归(Softmax Regression)又被称作多项逻辑回归(multinomial logistic regression),它是逻辑回归在处理多类别任务上的推广。
在逻辑回归中,我们有 m 个被标注的样本:$\{(x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)})\}$,其中 $x^{(i)} \in R^n$。因为类标是二元的,所以我们有 $y^{(i)} \in \{0, 1\}$。我们的假设(hypothesis)有如下形式:$h_{\theta}(x) = \frac{1}{1 + e^{-\theta^{T}x}}$
代价函数(cost function)如下:
$$J(\theta) = -[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}(x^{(i)}) + (1 – y^{(i)}) \log (1 – h_{\theta}(x^{(i)}))]$$
在 Softmax 回归中,类标是大于 2 的,因此在我们的训练集 $\{(x^{(1)}, y^{(1)}), \ldots, t(x^{(m)}, y^{(m)})\}$ 中,。给定一个测试输入 x,我们的假设应该输出一个 K 维的向量,向量内每个元素的值表示 x 属于当前类别的概率。具体地,假设 $h_{\theta}$ 形式如下:
$$h_{\theta}(x) = [\begin{array}{c}{P(y=1|x;\theta)}\\{P(y=2|x;\theta)}\\{\vdots}\\{P(y=K|x;\theta)}\end{array}] = \frac{1}{\sum_{j=1}^{K} e^{\theta(j)^{T}x}} [\begin{array}{c}{e^{\theta^{(1)}x}x}\\{e^{\theta(2)^{T}x}}\\{\vdots}\\{e^{\theta^{(K)^{T}}x}}\end{array}]$$
代价函数如下:
$$J(\theta) = -[\sum_{i=1}^{m} \sum_{k=1}^{K} 1\{y^{(i)} = k\} \log \frac{e^{\theta^{(k)T}x^{(i)}}}{\sum_{j=1}^{K} e^{\theta(j)T_{x^{(i)}}}}]$$
其中 $1\{\cdot\}$ 是指示函数,即 $1\{true\} = 1, 1\{false\} = 0$
既然我们说 Softmax 回归是逻辑回归的推广,那我们是否能够在代价函数上推导出它们的一致性呢?当然可以,于是:
$$\begin{aligned}J(\theta) &= -[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}(x^{(i)}) + (1 – y^{(i)}) \log (1 – h_{\theta}(x^{(i)}))]\\&= -\sum_{i=1}^{m} \sum_{k=0}^{1} 1\{y^{(i)} = k\} \log P(y^{(i)} = k|x^{(i)}; \theta)\\&= -\sum_{i=1}^{m} \sum_{k=0}^{1} 1\{y^{(i)} = k\} \log \frac{e^{\theta^{(k)T}x^{(i)}}}{\sum_{j=1}^{K} e^{\theta(j)T_{x}(i)}}\end{aligned}$$
可以看到,逻辑回归是 softmax 回归在 K=2 时的特例。你可能也发现了,标准的 Softmax 回归中,要计算 y=j 时的 Softmax 概率:$P(y=j)$,我们需要对所有的 K 个概率做归一化,这在 $|y|$ 很大时非常耗时。于是,分层 Softmax 诞生了,它的基本思想是使用树的层级结构替代扁平化的标准 Softmax,使得在计算 $P(y=j)$ 时,只需计算一条路径上的所有节点的概率值,无需在意其它的节点。
下图是一个分层 Softmax 示例:
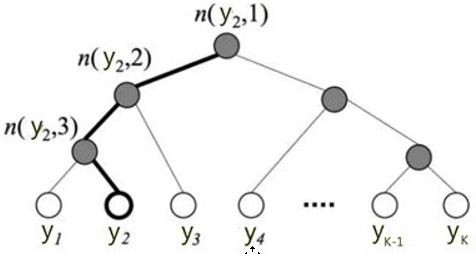 树的结构是根据类标的频数构造的霍夫曼树。K个不同的类标组成所有的叶子节点,K-1个内部节点作为内部参数,从根节点到某个叶子节点经过的节点和边形成一条路径,路径长度被表示为$L(y_j)$。于是$P(y_j)$就可以被写成:
树的结构是根据类标的频数构造的霍夫曼树。K个不同的类标组成所有的叶子节点,K-1个内部节点作为内部参数,从根节点到某个叶子节点经过的节点和边形成一条路径,路径长度被表示为$L(y_j)$。于是$P(y_j)$就可以被写成:
$$\mathrm{P}(y_{j})=\prod_{i=1}^{L(y_{j})-1}\sigma(\left\|n(y_{j},l+1)=LC(n(y_{j},l))\right\|\cdot\theta_{n(y_{j},l)}^{T}X)$$
其中:$\sigma(\cdot)$表示sigmoid函数;$LC(n)$表示n节点的左孩子;$\left\|x\right\|$是一个特殊的函数,被定义为:$\left\|x\right\|=\{\begin{aligned}1&\text{if}x==\text{true}\\-1&\text{otherwise}\end{aligned}$;$\theta_{n(y_{j},l)}$是中间节点$n(y_{j},l)$的参数;X是Softmax层的输入。
上图中,高亮的节点和边是从根节点到$y_2$的路径,路径长度$L(y_2)=4$,$P(y_2)$可以被表示为:
$$\begin{aligned}\mathrm{P}(y_{2})&=\mathrm{P}(n(y_{2},1),\text{left})\cdot\mathrm{P}(n(y_{2},2),\text{left})\cdot\mathrm{P}(n(y_{2},3),\text{right})\\&=\sigma(\theta_{n(y_{2},1)}^{T}X)\cdot\sigma(\theta_{n(y_{2},2)}^{T}X)\cdot\sigma(-\theta_{n(y_{2},3)}^{T}X)\end{aligned}$$
于是,从根节点走到叶子节点$y_2$,实际上是在做了3次二分类的逻辑回归。通过分层的Softmax,计算复杂度一下从$|K|$降低到$\log|K|$。
N-gram
word2vec把语料库中的每个单词当成原子的,它会为每个单词生成一个向量。这忽略了单词内部的形态特征,比如:”book”和”books”,”apple”和”apples”,这两个例子中,两个单词都有较多公共字符,即它们的内部形态类似,但是在传统的word2vec中,这种单词内部形态信息因为它们被转换成不同的id丢失了。
为了克服这个问题,fastText使用了字符级别的n-grams来表示一个单词。对于单词”apple”,假设n的取值为3,则它的trigram有
"<ap","app","ppl","ple","le>"
其中,<表示前缀,>表示后缀。于是,我们可以用这些trigram来表示”apple”这个单词,进一步,我们可以用这5个trigram的向量叠加来表示”apple”的词向量。
这带来两点好处:
- 对于低频词生成的词向量效果会更好。因为它们的n-gram可以和其它词共享。
- 对于训练词库之外的单词,仍然可以构建它们的词向量。我们可以叠加它们的字符级n-gram向量。
FastText的优化
子空间量化
product quantization是一种保存数据间距离的压缩技术。PQ用一个码本来近似数据,与传统的kmeans训练码本不同的是,PQ将数据空间划分为k个子空间,并分别用kmeans学习子空间码本。数据的近似和重建均在子空间完成,最终拼接成结果。在fasttext中,子空间码本大小为256,可以用1byte表示。子空间的数量在[2,d/2]间取值。除了用PQ对数据进行量化压缩,fasttext还提供了对分类系数的PQ量化选项。PQ的优化能够在不影响分类其表现的情况下,将分类模型压缩为原大小的$\frac{1}{10}$。
裁剪字典内容
fasttext提供了一个诱导式裁剪字典的算法,保证裁剪后的字典内容覆盖了所有的文章。具体而言,fasttext存有一个保留字典,并在线处理文章,如果新的文章没有被保留字典涵盖,则从该文章中提取一个norm最大的词和其子串加入字典中。字典裁剪能够有效将模型的数量减少,甚至到原有的$\frac{1}{100}$。
FastText的使用
使用FastText训练词向量
# -*- coding: utf-8 -*-
import jieba
import os
import fasttext
def get_data():
# 清华大学的新闻分类文本数据集下载:https://thunlp.oss-cn-qingdao.aliyuncs.com/THUCNews.zip
data_dir = 'D:\\迅雷下载\\THUCNews\\THUCNews\\财经'
with open("finance_news_cut.txt", "w", encoding='utf-8') as f:
for file_name in os.listdir(data_dir):
print(file_name)
file_path = data_dir + os.sep + file_name
with open(file_path, 'r', encoding='utf-8') as fr:
text = fr.read()
seg_text = jieba.cut(text.replace("\t", "").replace("\n", ""))
outline = "".join(seg_text)
f.write(outline)
f.flush()
def train_model():
model = fasttext.train_unsupervised('finance_news_cut.txt')
model.save_model("news_fasttext.model.bin")
def test_model():
model = fasttext.load_model('news_fasttext.model.bin')
print(model.words)
print(model.get_word_vector("股票"))
print(model.get_nearest_neighbors('股票'))
if __name__ == "__main__":
pass
# get_data()
# train_model()
test_model()
备注:不要使用pip install FastText 进行安装,否则会出现如下报错:
AttributeError: ‘_FastText’ object has no attribute ‘get_nearest_neighbors’
安装流程:
git clone https://github.com/facebookresearch/fastText.git cd fastText pip install .
使用FastText进行文本分类
#-*- coding: utf-8 -*-
import jieba
import os
import fasttext
def get_data():
# 清华大学的新闻分类文本数据集下载:https://thunlp.oss-cn-qingdao.aliyuncs.com/THUCNews.zip
data_dir = 'D:\\迅雷下载\\THUCNews\\THUCNews'
# 生成训练数据&测试数据
with open("news_fasttext_train.txt", "w", encoding='utf-8') as train_f, open("news_fasttext_test.txt", "w",
encoding='utf-8') as test_f:
for category in os.listdir(data_dir):
print(category)
category_path = data_dir + os.sep + category
count = 0
for file_name in os.listdir(category_path):
file_path = data_dir + os.sep + category + os.sep + file_name
with open(file_path, 'r', encoding='utf-8') as fr:
count += 1
text = fr.read()
seg_text = jieba.cut(text.replace("\t", "").replace("\n", ""))
outline = "".join(seg_text)
outline = outline + "\t__label__" + category + "\n"
print(count)
if count < 10000:
train_f.write(outline)
train_f.flush()
continue
elif count < 20000:
test_f.write(outline)
test_f.flush()
continue
else:
break
def train_model():
model = fasttext.train_supervised("news_fasttext_train.txt", label_prefix="__label__")
model.save_model("news_fasttext.model.bin")
def test_model():
model = fasttext.load_model('news_fasttext.model.bin')
result = model.test("news_fasttext_test.txt")
print('precision:', result[1])
# fasttext只提供全部结果的p值和r值,想要统计不同分类的结果,就需要自己写代码来实现了。
labels_right = []
texts = []
with open("news_fasttext_test.txt", encoding='utf-8') as fr:
for line in fr:
line = line.rstrip()
labels_right.append(line.split("\t")[1].replace("__label__", ""))
texts.append(line.split("\t")[0])
labels_predict = [term[0] for term in model.predict(texts)[0]] # 预测输出结果为二维形式
text_labels = list(set(labels_right))
text_predict_labels = list(set(labels_predict))
A = dict.fromkeys(text_labels, 0) # 预测正确的各个类的数目
B = dict.fromkeys(text_labels, 0) # 测试数据集中各个类的数目
C = dict.fromkeys(text_predict_labels, 0) # 预测结果中各个类的数目
for i in range(0, len(labels_right)):
B[labels_right[i]] += 1
C[labels_predict[i]] += 1
if labels_right[i] == labels_predict[i].replace('__label__', ''):
A[labels_right[i]] += 1
# 计算准确率,召回率,F值
for key in B:
try:
r = float(A[key]) / float(B[key])
p = float(A[key]) / float(C['__label__' + key])
f = p * r * 2 / (p + r)
print("%s:\tp:%f\tr:%f\tf:%f" % (key, p, r, f))
except:
print("error:", key, "right:", A.get(key, 0), "real:", B.get(key, 0), "predict:", C.get(key, 0))
if __name__ == "__main__":
pass
get_data()
# train_model()
# test_model()
另外,还可以使用gensim来使用FastText,如:from gensim.models import FastText
也可以下载基于Wikipedia预先生成的157语言的词向量使用:https://fasttext.cc/docs/en/crawl-vectors.html
参考链接: