CLARANS简介
CLARANS(Clustering Large Applications based on RANdomized Search,基于随机搜索的大规模应用聚类)是一种经典的聚类算法,由Raymond T. Ng和Jiawei Han于1994年提出。它旨在解决当时主流聚类算法(如K-means)在处理大规模数据集和发现任意形状簇方面的两大核心挑战。
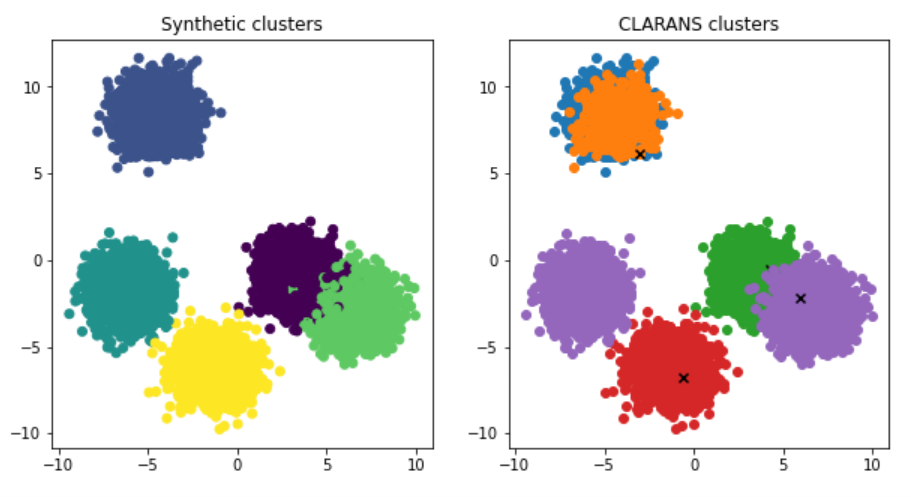
本质上,CLARANS是 K-medoids(或PAM)算法 的一个高效、随机化的改进版本,特别适用于空间数据挖掘。
核心思想与设计动机
CLARANS的核心思想是:将寻找最优聚类中心点(Medoids)的过程,视作在一个巨大的“邻居图”上进行一次受限制的、随机化的局部搜索,通过多次重启来逼近全局最优解。
为了更透彻地理解,我们将其拆解为以下几个层次:
根本动机:解决前辈算法的致命缺陷
CLARANS并非凭空诞生,它的设计直接针对当时两个主流划分算法 PAM 和 CLARA 的痛点:
- 对 PAM 的改进:
- PAM(K-medoids)的问题: 采用贪心交换策略,质量高,能准确找到局部最优解。但其计算复杂度为 O(k(n-k)²),这意味着它对数据量 n极其敏感,几乎无法用于大规模数据集。
- CLARANS的洞察:“我们真的需要检查每一个可能的交换吗?”答案是否定的。很多交换方向是低效或无效的。因此,CLARANS放弃穷举检查,改用随机抽样检查。
- 对 CLARA 的改进:
- CLARA 的问题:为了处理大数据,它对数据本身进行采样,然后对样本使用PAM。这带来了一个根本性问题:如果采样不能代表原始数据的整体结构(尤其是当簇的大小、密度不均时),那么在样本上找到的“最优”中心点,对于全体数据来说往往是次优的。
- CLARANS的洞察:“与其对固定不变的数据进行采样,不如对‘解的空间’进行动态采样。”它始终在整个数据集上评估解的质量,但只在解的搜索空间中随机游走,从而避免了CLARA的“代表性偏差”。
核心思想一:将解空间构建为“邻居图”
这是CLARANS最精妙的概念建模。
- 什么是“节点”?每个节点代表一个可能的k-medoids集合,即一组k个实际数据点作为中心点的方案。这是一个候选解。
- 什么是“边”?如果两个节点(两个k-medoids集合)可以通过交换一个中心点(例如,用集合外的某个点替换集合内的一个点)来相互转换,那么它们之间就有一条边相连。这两个节点互为“邻居”。
- 这个图有什么特点?
- 巨大无比: 节点数量是组合数 C(n, k),对于大规模数据,这是一个天文数字。
- 每个节点的度(邻居数)很高: 每个节点有 k * (n-k)个邻居。
这个建模的意义在于: 寻找最佳聚类方案的问题,被转化成了在这个巨大图上寻找成本最低(即目标函数值最小)的节点的优化问题。
核心思想二:受限的随机化局部搜索
面对这个巨大且复杂的图,如何进行高效搜索?CLARANS采用了两种关键策略:
- 随机化:
- 起点随机: 每次搜索从一个随机节点(随机选择的k个中心点)开始。
- 探索随机: 在当前节点,随机选择一个邻居进行考察,而不是按固定顺序检查。
- 作用: 这赋予了算法跳出局部最优的能力,并通过多次重启增加找到更好解的概率。
- 受限搜索(最核心的控制参数 maxNeighbor):
- 关键问题: 在图的某个节点(山顶或山谷),如果盲目地一直随机尝试邻居,可能会浪费大量时间在“坏方向”上。
- CLARANS的策略: 它为搜索设置了一个耐心限制 maxNeighbor。在当前节点,算法会连续随机尝试最多 maxNeighbor个邻居:
- 如果发现一个更好(成本更低)的邻居,就立即“走”过去,并重置计数器,开始新的探索(这相当于下山)。
- 如果连续尝试了 maxNeighbor个邻居都没有改善,算法就认为当前节点是一个局部最优解(已经身处一个“洼地”),并停止本次搜索。
- 哲学: maxNeighbor平衡了 “探索深度” 和 “搜索效率”。值太小,容易在平缓区域过早放弃;值太大,则可能在不值得的坏节点上浪费过多时间。
核心思想三:多次重启,择优录用
- 为什么要多次重启(参数 numLocal)?由于搜索是局部且随机的,单次搜索很可能终止于一个普通的局部最优解,而非全局最优解。
- CLARANS的策略:它独立地执行 numLocal次上述的“随机化局部搜索”。每次从一个全新的随机起点开始,找到一个新的局部最优解。最后,从这 numLocal个局部最优解中,选出成本最低的那个作为最终答案。
- 本质: 这是一种朴素而有效的集成思想。通过增加对解空间的采样次数,来提高捕获全局最优解或接近全局最优解的概率。
设计动机总结
CLARANS的设计动机,源于在 “聚类质量”、“计算效率” 和“对大数据及复杂形状的适应性” 三者之间寻求一个实用的工程平衡点。
它继承了PAM基于Medoid的鲁棒性和任意度量能力,摒弃了其穷举搜索的低效性。
它借鉴了CLARA的采样思想,但将其从数据采样升维到解空间采样,保证了搜索的全局视野。
最终,CLARANS通过“邻居图”的抽象、 “受限随机游走”的搜索机制、以及“多次重启择优”的集成策略,成功地将一个NP难组合优化问题,转化为一个可通过参数控制、在实践中高效可解的启发式算法。 这正是它经典且巧妙之处。
CLARANS的优缺点
优点
- 对噪声和异常值鲁棒性强
- 核心原因: 使用实际数据点作为簇中心点。一个异常值最多影响它所在的一个簇,而不会像K-means的“均值”那样将整个簇的中心拖偏。这使得聚类结果更稳定。
- 不依赖于数据的几何形状或均值概念
- 核心原因: 只需定义任意两个对象之间的相异性度量(如编辑距离、语义相似度、交通时间),无需在向量空间中计算均值。因此,它能处理K-means无法处理的复杂数据类型和任意形状的簇。
- 搜索效率比PAM有质的提升
- 核心原因: 通过引入 maxNeighbor参数,避免了PAM算法的穷举交换测试,将计算复杂度从 O(k(n-k)²)降低到可控水平,使其能够应用于大规模数据集。
- 比CLARA的采样策略更可靠
- 核心原因: CLARANS始终在整个数据集上评估解的质量,避免了CLARA因数据采样偏差导致的次优解。它的随机化是对解空间的采样,而非对数据的采样。
- 原理清晰,易于理解和实现
- 核心原因: 基于图搜索和局部优化的思想非常直观,代码实现比许多复杂模型(如深度聚类)更简单。
缺点
- 计算复杂度依然较高
- 核心原因: 虽然比PAM快,但每次评估成本都需要计算所有点到k个中心点的距离,其时间复杂度通常被认为是 O(n²) 级别。对于超大规模数据集(如千万级以上),运行时间仍可能不可接受。
- 对参数 (maxNeighbor, numLocal) 敏感
- 核心原因: 算法性能高度依赖这两个参数。maxNeighbor太小会导致搜索不充分,陷入较差局部最优;太大会显著增加计算量。numLocal同样需要权衡效果与时间。调参需要经验和实验。
- 需要预先指定簇的数量 k
- 核心原因: 与K-means一样,k值的选择是一个难题,需要领域知识或使用肘部法则、轮廓系数等方法辅助确定,增加了使用成本。
- 可能无法找到全局最优解
- 核心原因: 作为一种启发式随机搜索算法,它只能保证找到高质量的局部最优解,无法保证是全局最优。虽然多次重启提高了概率,但并非绝对。
- 对初始随机种子敏感
- 核心原因: 随机化的起点意味着多次运行的结果可能有细微差异,这在需要完全确定性的场景中是一个缺点。
CLARANS的典型应用场景
CLARANS特别适用于同时满足以下 “三重特性” 的问题:
- 数据存在噪声或异常值。
- 数据间的“距离”不能用简单的欧氏距离衡量,或簇的形状复杂。
- 数据规模处于“中等至大型”,而非“超大规模”。
具体领域示例:
- 空间数据挖掘与地理信息系统
- 场景: 根据地理位置对商店、加油站、故障设备进行聚类,以规划物流或部署维护团队。
- 为何适用: 使用实际坐标点(经纬度)作为中心点很合理;距离通常采用球面距离(如Haversine公式),而非欧氏距离;城市中的店铺分布可能形成不规则形状的簇。
- 生物信息学与计算生物学
- 场景: 基于基因序列的相似性(如编辑距离、BLAST得分)对基因或蛋白质进行聚类,以发现功能相似的家族。
- 为何适用: 序列数据无法计算均值;相似性度量复杂;数据可能存在测序错误(噪声)。
- 图像分析与计算机视觉
- 场景: 在颜色、纹理等特征空间中对图像区域进行分割。
- 为何适用: 可以使用各种特征距离度量;图像中物体区域可能是不规则形状;对分割边界的噪声点不敏感。
- 社交网络与图数据分析
- 场景: 基于节点间的结构距离(如最短路径长度、Jaccard系数)发现社区结构。
- 为何适用: 图数据无法定义均值;社区结构复杂;离群节点(与所有社区联系都弱)应被妥善处理。
- 市场研究与客户细分
- 场景: 基于多维度行为数据(购买记录、浏览时长等)对客户进行分群,其中使用自定义的混合距离函数。
- 为何适用: 客户行为数据常包含异常值(如“羊毛党”);细分群体可能具有非球形的复杂特征分布。
总结与选型建议
CLARANS是“稳健性”和“通用性”的折衷之选。
- 当你需要比K-means更鲁棒、更通用的聚类能力,且数据量尚未达到PB级别时,CLARANS是一个强有力的候选。
- 当计算资源极其有限,或数据规模达到海量级别时,应考虑更现代、更高效的算法,如:
- 追求速度与规模:改进的K-means变种(如Mini-Batch K-means)、或基于密度的算法如 HDBSCAN(自带噪声识别,无需指定k)。
- 追求任意形状和自动确定簇数:DBSCAN 或 HDBSCAN。
- 超大规模数据:需要依赖于分布式计算框架(如Spark MLlib)中的聚类实现。
核心定位: CLARANS在算法演进史上,是一座连接经典精确算法与现代高效启发式算法的桥梁。它解决了其前辈(PAM, CLARA)的关键痛点,为2000年代前后的空间数据挖掘提供了可靠的解决方案。在今天,它依然是一个在特定约束下(中等数据、需鲁棒性、复杂度量)值得考虑的经典工具。
CLARANS算法实现
CLARANS算法详细步骤
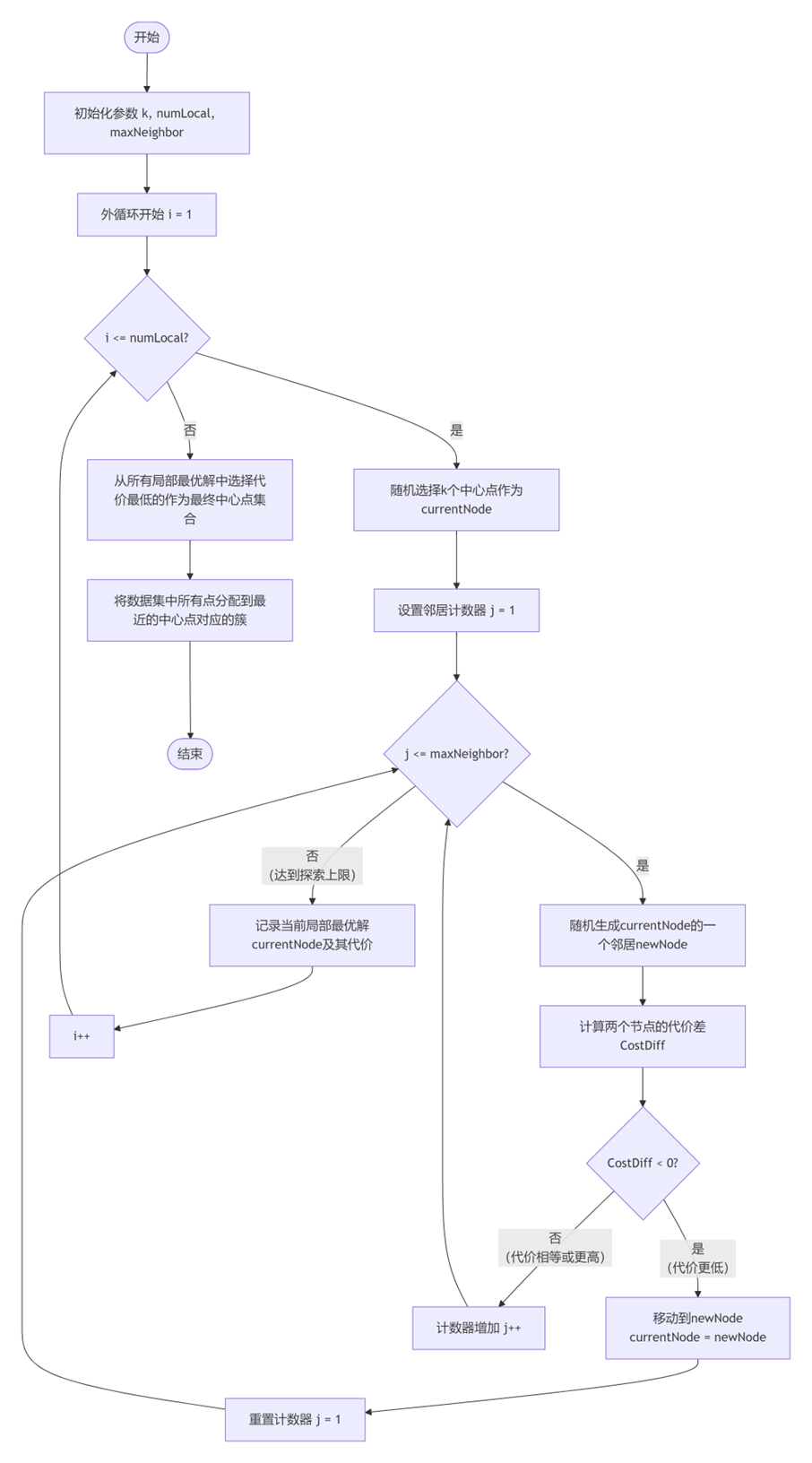
算法输入参数
- k:要聚类的簇数量
- numlocal:尝试的局部最优解数量
- maxneighbor:每个节点探索的邻居数量上限
- data:包含n个数据点的数据集
- distance_func:计算两点间距离的函数
步骤1:初始化
- 设置 i = 1(当前局部搜索次数)
- 初始化 best_solution = None和 best_cost = float(‘inf’)
步骤2:外循环 – 多次局部搜索
对于 i从 1 到 numlocal执行:
- 随机选择初始中心点:从n个数据点中随机选择k个点作为初始中心点集合,称为 current_node
- 计算当前代价:current_cost = 计算所有点到最近中心点的总距离
- 设置邻居计数器:j = 1
步骤3:内循环 – 局部优化
当 j <= maxneighbor时执行:
- 生成随机邻居:
- 随机选择一个非中心点 P_random
- 随机选择一个当前中心点 P_medoid
- 用 P_random替换 P_medoid得到新中心点集合 new_node
- 计算新代价:new_cost = 使用new_node时所有点到最近中心点的总距离
- 判断与移动:
- 如果 new_cost < current_cost:
- 接受移动:current_node = new_node, current_cost = new_cost
- 重置计数器:j = 1
- 否则:
- 拒绝移动:j = j + 1
- 如果 new_cost < current_cost:
步骤4:记录局部最优解
- 当内循环结束后,current_node是局部最优解
- 如果 current_cost < best_cost,则更新:best_cost = current_cost, best_solution = current_node
步骤5:最终分配
- 使用最终的中心点集合 best_solution
- 将每个数据点分配到距离最近的中心点所在的簇
Python实现代码
import numpy as np
import random
from sklearn.datasets import make_blobs
from sklearn.metrics import pairwise_distances
import matplotlib.pyplot as plt
from typing import List, Tuple, Callable, Any
import time
class CLARANS:
"""
CLARANS聚类算法实现
参数:
-----------
n_clusters : int, default=3
聚类数量
numlocal : int, default=5
局部最优解尝试次数
maxneighbor : int or float, default=0.025
每个节点探索的邻居数量上限
如果是浮点数,表示总可能邻居数的百分比
distance_metric : str, default='euclidean'
距离度量,可选: 'euclidean', 'manhattan', 'cosine'
random_state : int, default=42
随机种子
"""
def __init__(self, n_clusters=3, numlocal=5, maxneighbor=0.025,
distance_metric='euclidean', random_state=42):
self.n_clusters = n_clusters
self.numlocal = numlocal
self.maxneighbor = maxneighbor
self.distance_metric = distance_metric
self.random_state = random_state
self.medoids = None
self.labels_ = None
self.cost_ = None
np.random.seed(random_state)
random.seed(random_state)
def _compute_distance_matrix(self, X: np.ndarray) -> np.ndarray:
"""计算距离矩阵"""
return pairwise_distances(X, metric=self.distance_metric)
def _compute_cost(self, distance_matrix: np.ndarray, medoids: List[int]) -> float:
"""计算给定中心点集合的代价(总距离和)"""
# 选择每个点到最近中心点的距离
medoid_distances = distance_matrix[:, medoids]
min_distances = np.min(medoid_distances, axis=1)
return np.sum(min_distances)
def _get_random_neighbor(self, medoids: List[int], n_points: int) -> Tuple[List[int], int, int]:
"""随机生成一个邻居:替换一个中心点"""
# 深拷贝当前中心点列表
new_medoids = medoids.copy()
# 当前非中心点的索引
non_medoids = [i for i in range(n_points) if i not in medoids]
if not non_medoids:
return medoids, -1, -1
# 随机选择一个非中心点和一个中心点进行替换
random_non_medoid = random.choice(non_medoids)
random_medoid = random.choice(range(len(medoids)))
# 执行替换
replaced_medoid = new_medoids[random_medoid]
new_medoids[random_medoid] = random_non_medoid
return new_medoids, replaced_medoid, random_non_medoid
def _find_closest_medoid(self, distance_matrix: np.ndarray, medoids: List[int]) -> np.ndarray:
"""为每个点找到最近的中心点索引"""
medoid_distances = distance_matrix[:, medoids]
closest_medoid_indices = np.argmin(medoid_distances, axis=1)
return closest_medoid_indices
def _assign_clusters(self, distance_matrix: np.ndarray, medoids: List[int]) -> np.ndarray:
"""分配每个点到最近的中心点对应的簇"""
closest_medoid_indices = self._find_closest_medoid(distance_matrix, medoids)
# 将中心点索引映射到簇标签
cluster_labels = np.zeros(distance_matrix.shape[0], dtype=int)
for i, medoid_idx in enumerate(medoids):
# 找到以这个中心点为最近中心点的所有点
mask = closest_medoid_indices == i
cluster_labels[mask] = i
return cluster_labels
def fit(self, X: np.ndarray) -> 'CLARANS':
"""
在数据X上拟合CLARANS模型
参数:
----------
X : array-like, shape (n_samples, n_features)
输入数据
返回:
-------
self : CLARANS
拟合后的模型
"""
n_samples = X.shape[0]
# 计算距离矩阵
distance_matrix = self._compute_distance_matrix(X)
# 如果maxneighbor是浮点数,则计算为百分比
if isinstance(self.maxneighbor, float):
maxneighbor = int(self.maxneighbor * self.n_clusters * (n_samples - self.n_clusters))
else:
maxneighbor = self.maxneighbor
# 确保maxneighbor至少为1
maxneighbor = max(1, maxneighbor)
best_cost = float('inf')
best_medoids = None
# 记录每次迭代的成本用于可视化
self.cost_history_ = []
# 外循环:尝试多个局部最优解
for local_idx in range(self.numlocal):
# 步骤A: 随机选择初始中心点
all_indices = list(range(n_samples))
current_medoids = random.sample(all_indices, self.n_clusters)
# 计算当前代价
current_cost = self._compute_cost(distance_matrix, current_medoids)
# 内循环:局部搜索
neighbor_count = 0
while neighbor_count < maxneighbor:
# 步骤B: 生成随机邻居
new_medoids, old_medoid, new_medoid = self._get_random_neighbor(
current_medoids, n_samples
)
# 步骤C: 计算新代价
new_cost = self._compute_cost(distance_matrix, new_medoids)
# 步骤D: 判断与移动
if new_cost < current_cost:
# 接受移动
current_medoids = new_medoids
current_cost = new_cost
neighbor_count = 0 # 重置计数器
else:
neighbor_count += 1
# 记录成本历史
self.cost_history_.append(current_cost)
# 记录当前局部最优解
if current_cost < best_cost:
best_cost = current_cost
best_medoids = current_medoids.copy()
print(f"局部搜索 {local_idx+1}/{self.numlocal} 完成,当前最佳成本: {best_cost:.4f}")
# 保存结果
self.medoids = best_medoids
self.cost_ = best_cost
self.labels_ = self._assign_clusters(distance_matrix, best_medoids)
self.cluster_centers_ = X[best_medoids]
return self
def predict(self, X: np.ndarray) -> np.ndarray:
"""
预测X中每个样本的簇标签
参数:
----------
X : array-like, shape (n_samples, n_features)
要预测的数据
返回:
-------
labels : array, shape (n_samples,)
每个样本的簇标签
"""
if self.medoids is None:
raise ValueError("模型尚未拟合,请先调用fit方法")
distance_matrix = self._compute_distance_matrix(X)
# 计算每个点到各个中心点的距离
medoid_distances = distance_matrix[:, self.medoids]
# 为每个点找到最近的中心点
closest_medoid_indices = np.argmin(medoid_distances, axis=1)
return closest_medoid_indices
def fit_predict(self, X: np.ndarray) -> np.ndarray:
"""拟合模型并返回簇标签"""
self.fit(X)
return self.labels_
# 三、使用示例和可视化
def generate_sample_data(n_samples=300, centers=4, random_state=42):
"""生成示例数据"""
X, y_true = make_blobs(
n_samples=n_samples,
centers=centers,
cluster_std=0.7,
random_state=random_state
)
return X, y_true
def plot_clustering_results(X, y_pred, medoids, title="CLARANS聚类结果"):
"""可视化聚类结果"""
plt.figure(figsize=(12, 5))
# 绘制原始数据
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c='gray', alpha=0.6, s=30)
plt.title("原始数据")
plt.xlabel("特征1")
plt.ylabel("特征2")
# 绘制聚类结果
plt.subplot(1, 2, 2)
scatter = plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='tab20', s=30, alpha=0.7)
# 标记中心点
plt.scatter(
X[medoids, 0], X[medoids, 1],
c='red', marker='X', s=200,
edgecolors='black', linewidth=2,
label='中心点'
)
plt.title(title)
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.colorbar(scatter, label='簇标签')
plt.tight_layout()
plt.show()
def plot_cost_history(cost_history, title="CLARANS代价变化历史"):
"""可视化代价变化历史"""
plt.figure(figsize=(10, 5))
plt.plot(cost_history, linewidth=1)
plt.title(title)
plt.xlabel("迭代次数")
plt.ylabel("总代价(距离和)")
plt.grid(True, alpha=0.3)
plt.show()
def evaluate_clustering(X, y_true, y_pred):
"""评估聚类结果"""
from sklearn.metrics import adjusted_rand_score, silhouette_score
ari = adjusted_rand_score(y_true, y_pred)
silhouette = silhouette_score(X, y_pred)
print(f"调整兰德指数 (ARI): {ari:.4f}")
print(f"轮廓系数: {silhouette:.4f}")
return ari, silhouette
# 四、完整示例
def main():
"""CLARANS算法完整示例"""
# 1. 生成示例数据
print("生成示例数据...")
X, y_true = generate_sample_data(n_samples=300, centers=4)
print(f"数据形状: {X.shape}")
# 2. 创建并训练CLARANS模型
print("\n训练CLARANS模型...")
start_time = time.time()
# 创建模型
clarans = CLARANS(
n_clusters=4, # 簇数量
numlocal=5, # 尝试5个不同的局部最优解
maxneighbor=0.025, # 探索每个节点2.5%的邻居
distance_metric='euclidean',
random_state=42
)
# 训练模型
y_pred = clarans.fit_predict(X)
end_time = time.time()
print(f"训练时间: {end_time - start_time:.2f}秒")
print(f"最终代价: {clarans.cost_:.4f}")
print(f"中心点索引: {clarans.medoids}")
# 3. 可视化结果
plot_clustering_results(X, y_pred, clarans.medoids, "CLARANS聚类结果")
plot_cost_history(clarans.cost_history_, "代价变化历史")
# 4. 评估聚类结果
print("\n聚类评估:")
evaluate_clustering(X, y_true, y_pred)
# 5. 对比K-means
print("\n与K-means对比:")
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4, random_state=42, n_init=10)
y_kmeans = kmeans.fit_predict(X)
# 可视化K-means结果
plt.figure(figsize=(6, 5))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='tab20', s=30, alpha=0.7)
plt.scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
c='red', marker='X', s=200, edgecolors='black', linewidth=2,
label='K-means中心'
)
plt.title("K-means聚类结果")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.colorbar(label='簇标签')
plt.tight_layout()
plt.show()
# 评估K-means
evaluate_clustering(X, y_true, y_kmeans)
# 五、优化版本:增量计算代价
class OptimizedCLARANS(CLARANS):
"""优化版CLARANS,使用增量计算提高效率"""
def _compute_cost_incremental(self, distance_matrix: np.ndarray,
medoids: List[int],
old_medoid: int,
new_medoid: int) -> float:
"""
增量计算替换中心点后的代价变化
这比重新计算整个数据集的代价要快得多
"""
# 获取当前中心点到所有点的距离
medoid_distances = distance_matrix[:, medoids]
current_min_distances = np.min(medoid_distances, axis=1)
# 计算新中心点的影响
new_distances = distance_matrix[:, new_medoid]
# 找到受影响的点(新距离比当前最小距离小的点)
affected_mask = new_distances < current_min_distances
if not np.any(affected_mask):
return np.sum(current_min_distances)
# 计算新代价
new_min_distances = current_min_distances.copy()
new_min_distances[affected_mask] = new_distances[affected_mask]
return np.sum(new_min_distances)
def fit(self, X: np.ndarray) -> 'OptimizedCLARANS':
"""优化的fit方法"""
n_samples = X.shape[0]
# 计算距离矩阵
distance_matrix = self._compute_distance_matrix(X)
# 设置maxneighbor
if isinstance(self.maxneighbor, float):
maxneighbor = int(self.maxneighbor * self.n_clusters * (n_samples - self.n_clusters))
else:
maxneighbor = self.maxneighbor
maxneighbor = max(1, maxneighbor)
best_cost = float('inf')
best_medoids = None
self.cost_history_ = []
# 外循环
for local_idx in range(self.numlocal):
# 随机选择初始中心点
all_indices = list(range(n_samples))
current_medoids = random.sample(all_indices, self.n_clusters)
current_cost = self._compute_cost(distance_matrix, current_medoids)
neighbor_count = 0
# 内循环
while neighbor_count < maxneighbor:
# 生成随机邻居
new_medoids, old_medoid_idx, new_medoid = self._get_random_neighbor(
current_medoids, n_samples
)
if old_medoid_idx == -1: # 没有有效的邻居
break
# 增量计算新代价
new_cost = self._compute_cost_incremental(
distance_matrix, new_medoids,
current_medoids[old_medoid_idx], new_medoid
)
# 判断是否接受移动
if new_cost < current_cost:
current_medoids = new_medoids
current_cost = new_cost
neighbor_count = 0
else:
neighbor_count += 1
self.cost_history_.append(current_cost)
# 更新最佳解
if current_cost < best_cost:
best_cost = current_cost
best_medoids = current_medoids.copy()
print(f"局部搜索 {local_idx+1}/{self.numlocal} 完成,当前最佳成本: {best_cost:.4f}")
# 保存结果
self.medoids = best_medoids
self.cost_ = best_cost
self.labels_ = self._assign_clusters(distance_matrix, best_medoids)
self.cluster_centers_ = X[best_medoids]
return self
# 六、性能对比
def compare_performance():
"""对比原始版本和优化版本的性能"""
print("性能对比测试...")
X, _ = generate_sample_data(n_samples=1000, centers=5)
# 测试原始版本
print("\n1. 原始CLARANS:")
start_time = time.time()
clarans_original = CLARANS(n_clusters=5, numlocal=3, maxneighbor=0.01)
clarans_original.fit(X)
original_time = time.time() - start_time
print(f" 时间: {original_time:.2f}秒")
print(f" 最终代价: {clarans_original.cost_:.4f}")
# 测试优化版本
print("\n2. 优化版CLARANS:")
start_time = time.time()
clarans_optimized = OptimizedCLARANS(n_clusters=5, numlocal=3, maxneighbor=0.01)
clarans_optimized.fit(X)
optimized_time = time.time() - start_time
print(f" 时间: {optimized_time:.2f}秒")
print(f" 最终代价: {clarans_optimized.cost_:.4f}")
print(f"\n优化版本加速: {original_time/optimized_time:.2f}倍")
# 可视化优化版本的结果
plot_clustering_results(
X, clarans_optimized.labels_, clarans_optimized.medoids,
"优化版CLARANS聚类结果"
)
# 执行主程序
if __name__ == "__main__":
print("=" * 50)
print("CLARANS算法实现与示例")
print("=" * 50)
# 运行主示例
main()
# 运行性能对比
compare_performance()
print("\n" + "=" * 50)
print("程序执行完毕")
print("=" * 50)