贝叶斯估计中C值的确定方法

什么是C值？

想象一下你要估计一个网约车司机的完单率（比如接单后成功完成的比例）。你有两种信息：

• 样本信息：这个司机实际接了多少单，完成了多少单
• 先验信息：所有司机的平均完单率是多少

C值就是用来平衡这两种信息的”调节器”。C值越大，表示你更相信先验信息；C值越小，表示你更相信样本数据。

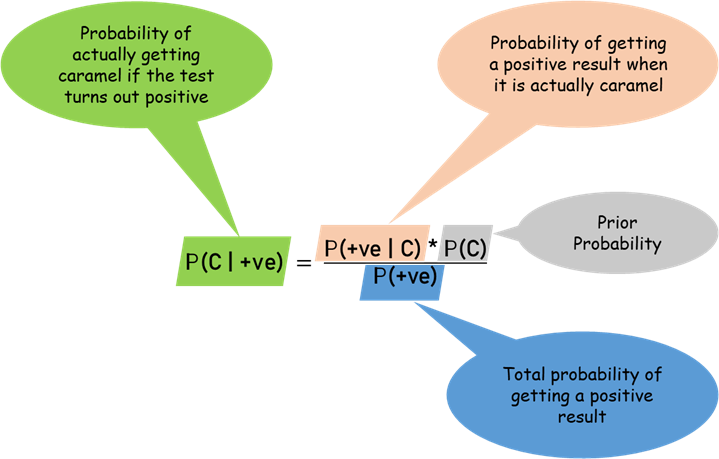
计算公式很简单：

最终估计 = (样本量/(样本量+C)) × 样本均值 + (C/(样本量+C)) × 先验均值

方法1：基于经验快速设定（最简单）

直接问业务专家两个问题：

• “你觉得平均完单率大概是多少？” → 得到先验均值
• “你觉得看多少数据才比较可靠？” → 得到C值

prior_mean = 0.25  # 专家认为平均完单率
equivalent_samples = 10  # 专家认为看10个样本才可靠

df['finish_rate'] = df['finish_count'] / df['decision_count']
df['bayes_estimate_method1'] = (
        (df['decision_count'] / (df['decision_count'] + equivalent_samples)) * df['finish_rate'] +
        (equivalent_samples / (df['decision_count'] + equivalent_samples)) * prior_mean
    )
print(df.head())

方法2：用历史数据找最优C值

如果有历史数据，可以让数据自己说话，找到最好的C值。

def method2_grid_search(df, train_ratio=0.7):
    """
    方法2：用历史数据网格搜索最优C值
    """
    # 随机划分训练集和测试集
    np.random.seed(42)
    train_indices = np.random.choice(
        df.index,
        size=int(len(df) * train_ratio),
        replace=False
    )
    test_indices = df.index[~df.index.isin(train_indices)]

    train_df = df.loc[train_indices]
    test_df = df.loc[test_indices]

    # 计算训练集整体平均
    train_global_mean = train_df['finish_count'].sum() / train_df['decision_count'].sum()

    # 网格搜索C值
    C_candidates = [1, 2, 3, 5, 8, 13, 21, 34]
    best_C = None
    best_score = float('inf')

    for C in C_candidates:
        predictions = []
        actuals = []

        for _, row in test_df.iterrows():
            # 贝叶斯估计
            alpha = train_global_mean * C + row['finish_count']
            beta_param = (1 - train_global_mean) * C + (row['decision_count'] - row['finish_count'])

            # 预测完单率
            pred_rate = alpha / (alpha + beta_param)
            predictions.append(pred_rate)
            actuals.append(row['finish_rate'])

        # 计算RMSE
        rmse = np.sqrt(np.mean((np.array(predictions) - np.array(actuals)) ** 2))

        if rmse < best_score:
            best_score = rmse
            best_C = C

    # 用最佳C值估计所有司机
    global_mean = df['finish_count'].sum() / df['decision_count'].sum()
    df['bayes_estimate_method2'] = (
            (df['decision_count'] / (df['decision_count'] + best_C)) * df['finish_rate'] +
            (best_C / (df['decision_count'] + best_C)) * global_mean
    )

    return best_C, best_score, df['bayes_estimate_method2']


best_C2, best_score2, bayes_estimates2 = method2_grid_search(df)
print(f"\n方法2结果:")
print(f"最优C值: {best_C2}, 最小RMSE: {best_score2:.4f}")

方法3：让数据自己学习C值（经验贝叶斯）

这种方法更聪明：它认为所有司机的真实能力都来自同一个分布，然后从这个分布中学习C值。

from scipy.optimize import minimize
from scipy.special import betaln

def method3_empirical_bayes(df):
    """
    方法3：经验贝叶斯法，从数据中学习C值
    """
    def negative_log_likelihood(params):
        m, C = params
        alpha = m * C
        beta_param = (1 - m) * C

        total_ll = 0
        for _, row in df.iterrows():
            k = row['finish_count']
            n = row['decision_count']

            # 贝塔-二项分布的对数似然
            ll = (betaln(k + alpha, n - k + beta_param)
                  - betaln(alpha, beta_param))
            total_ll += ll

        return -total_ll  # 最小化负对数似然

    # 初始值
    init_m = df['finish_count'].sum() / df['decision_count'].sum()
    init_C = 10

    # 约束条件
    bounds = [(0.001, 0.999), (0.1, 100)]

    result = minimize(negative_log_likelihood, [init_m, init_C], bounds=bounds)
    m_opt, C_opt = result.x

    # 用估计的参数计算贝叶斯估计
    df['bayes_estimate_method3'] = (
        (df['decision_count'] / (df['decision_count'] + C_opt)) * df['finish_rate'] +
        (C_opt / (df['decision_count'] + C_opt)) * m_opt
    )

    return m_opt, C_opt, df['bayes_estimate_method3']

m_opt, C_opt, bayes_estimates3 = method3_empirical_bayes(df)
print(f"\n方法3结果:")
print(f"估计的先验均值: {m_opt:.4f}")
print(f"估计的C值: {C_opt:.2f}")

方法4：通过模拟测试不同C值

创建一个虚拟世界来测试各种C值的表现。

def method4_simulation_validation(df, n_simulations=1000):
    """
    方法4：通过模拟验证不同C值的表现
    """
    # 从数据中估计超参数
    total_decisions = df['decision_count'].sum()
    total_finishes = df['finish_count'].sum()
    global_mean = total_finishes / total_decisions

    # 模拟不同的C值
    C_values = [1, 2, 3, 5, 8, 13, 21]
    results = []

    for C in C_values:
        mse_list = []

        for _ in range(n_simulations):
            # 为每个司机生成模拟真实完单率
            np.random.seed(_)

            # 使用当前C值计算每个司机的贝叶斯估计
            estimates = []
            true_rates = []

            for _, row in df.iterrows():
                # 生成模拟的真实完单率（基于当前观察和先验）
                alpha_post = global_mean * C + row['finish_count']
                beta_post = (1 - global_mean) * C + (row['decision_count'] - row['finish_count'])

                # 从后验分布中采样真实完单率
                true_rate = np.random.beta(alpha_post, beta_post)
                true_rates.append(true_rate)

                # 计算贝叶斯估计
                bayes_estimate = alpha_post / (alpha_post + beta_post)
                estimates.append(bayes_estimate)

            # 计算MSE
            mse = np.mean((np.array(estimates) - np.array(true_rates)) ** 2)
            mse_list.append(mse)

        avg_mse = np.mean(mse_list)
        results.append({
            'C': C,
            'avg_mse': avg_mse,
            'bayes_estimates': estimates
        })

    # 找到最优C值
    best_result = min(results, key=lambda x: x['avg_mse'])
    best_C4 = best_result['C']

    # 用最优C值计算最终估计
    df['bayes_estimate_method4'] = (
            (df['decision_count'] / (df['decision_count'] + best_C4)) * df['finish_rate'] +
            (best_C4 / (df['decision_count'] + best_C4)) * global_mean
    )

    return best_C4, results, df['bayes_estimate_method4']


best_C4, sim_results, bayes_estimates4 = method4_simulation_validation(df, n_simulations=100)
print(f"\n方法4结果:")
print(f"模拟验证最优C值: {best_C4}")
print("\n不同C值的平均MSE:")
for res in sim_results:
    print(f"  C={res['C']:2d}: MSE={res['avg_mse']:.6f}")

方法5：完整的贝叶斯方法（最复杂但最准确）

把C值也当作需要估计的参数，用MCMC方法一起估计。

"""
方法5：使用PyMC5实现分层贝叶斯模型（Plotly可视化版本）
"""
print("正在使用PyMC5运行分层贝叶斯模型...")
print(f"数据量: {len(df)} 个司机")
print(f"总决策次数: {df['decision_count'].sum()}")
print(f"总完成次数: {df['finish_count'].sum()}")

# 准备数据
n_drivers = len(df)
n = df['decision_count'].values.astype(int)
y = df['finish_count'].values.astype(int)

# 打印数据摘要
print(f"样本量范围: {n.min()} - {n.max()}")

# 构建PyMC5模型
with pm.Model() as hierarchical_model:
    # 超先验 - 全局参数
    mu = pm.Beta('mu', alpha=2, beta=2)  # 全局平均完单率
    kappa = pm.Gamma('kappa', alpha=2, beta=0.1)  # 精度参数

    # 个体司机的真实完单率
    theta = pm.Beta('theta',
                   alpha=mu * kappa,
                   beta=(1 - mu) * kappa,
                   shape=n_drivers)

    # 观测模型
    obs = pm.Binomial('obs', n=n, p=theta, observed=y)

    # 采样
    print("开始MCMC采样...")
    idata = pm.sample(
        draws=1000,
        tune=1000,
        cores=1,
        progressbar=True,
        random_seed=42
    )

print("采样完成!")

# 提取后验均值
mu_estimate = idata.posterior['mu'].mean().item()
kappa_estimate = idata.posterior['kappa'].mean().item()
theta_estimates = idata.posterior['theta'].mean(dim=['chain', 'draw']).values

df['bayes_estimate_method5'] = theta_estimates

# 计算95%可信区间
theta_hdi = az.hdi(idata, var_names=['theta'])['theta'].values
df['method5_lower'] = theta_hdi[:, 0]
df['method5_upper'] = theta_hdi[:, 1]
print(mu_estimate)
print(kappa_estimate)

数据可视化

贝叶斯收缩效果

import plotly.graph_objects as go
import pandas as pd

# 1. 原始完单率 vs 贝叶斯估计
fig1 = go.Figure()

# 添加原始数据点
fig1.add_trace(go.Scatter(
    x=df['finish_rate'],
    y=df['bayes_estimate_method5'],
    mode='markers',
    marker=dict(
        size=8,
        color=df['decision_count'],
        colorscale='Viridis',
        showscale=True,
        colorbar=dict(title="样本量", x=1)
    ),
    text=[f"司机: {row.plate_number}<br>样本量: {row.decision_count}<br>原始: {row.finish_rate:.3f}<br>贝叶斯: {row.bayes_estimate_method5:.3f}"
          for row in df.itertuples()],
    hovertemplate='<b>%{text}</b><extra></extra>',
))

# 添加对角线
fig1.add_trace(go.Scatter(
    x=[df['finish_rate'].min(), df['finish_rate'].max()],
    y=[df['finish_rate'].min(), df['finish_rate'].max()],
    mode='lines',
    line=dict(dash='dash', color='red', width=2),
    name='y=x (无调整)'
))

# 添加总体均值线
fig1.add_hline(
    y=mu_est,
    line_dash="dot",
    line_color="orange",
    annotation_text=f"总体均值 μ={mu_est:.3f}",
    annotation_position="top left"
)

# 更新布局
fig1.update_layout(
    title=dict(
        text=f"贝叶斯收缩效果 (μ={mu_est:.3f}, κ={kappa_est:.1f})",
        x=0.5,
        font=dict(size=16)
    ),
    xaxis_title="原始完单率",
    yaxis_title="贝叶斯估计",
    width=800,
    height=600,
    showlegend=True,
    margin=dict(l=50, r=50, t=80, b=50),
    # 调整图例位置
    legend=dict(
        x=0.02,  # 水平位置 (0-1，0为最左侧)
        y=0.98,  # 垂直位置 (0-1，1为最顶部)
        xanchor="left",  # 水平锚点
        yanchor="top",   # 垂直锚点
        bgcolor="rgba(0, 0, 0, 0.8)",  # 半透明背景
        bordercolor="Black",
        borderwidth=1
    )
)

fig1.show()

• 横轴：原始完单率（基于样本的直接计算）
• 纵轴：贝叶斯估计（收缩后的后验估计）
• 点颜色：样本量（颜色越深，样本量越大）
• 红色虚线：y=x 参考线（表示无调整）

解读要点：

• 点偏离对角线的程度代表收缩强度。偏离越大，收缩越明显。
• 通常，样本量小的点（浅色）更可能偏离对角线，被拉向总体均值；样本量大的点（深色）更靠近对角线，即数据本身更可靠，收缩程度低。
• 整体上，点应大致围绕对角线分布，但小样本点会向中心收缩，形成“收缩 toward the mean”的模式。

调整幅度 vs 样本量

# 2. 调整幅度 vs 样本量
fig2 = go.Figure()

# 计算调整幅度
adjustment = df['bayes_estimate_method5'] - df['finish_rate']

# 添加散点
fig2.add_trace(go.Scatter(
    x=df['decision_count'],
    y=adjustment,
    mode='markers',
    marker=dict(
        size=8,
        color=adjustment,
        colorscale='RdBu',
        colorbar=dict(title="调整方向", x=1.02),
        showscale=True
    ),
    text=[f"司机: {row.plate_number}<br>样本量: {row.decision_count}<br>原始: {row.finish_rate:.3f}<br>调整: {adj:.3f}"
          for row, adj in zip(df.itertuples(), adjustment)],
    hovertemplate='<b>%{text}</b><extra></extra>',
    name='调整幅度'
))

# 添加参考线
fig2.add_hline(
    y=0,
    line_dash="dash",
    line_color="red",
    annotation_text="无调整线",
    annotation_position="top right"
)

if len(df) > 5:
    # 按样本量排序
    sorted_idx = np.argsort(df['decision_count'])
    x_sorted = df['decision_count'].iloc[sorted_idx].values
    y_sorted = adjustment.iloc[sorted_idx].values

    # 计算移动平均
    window = max(3, len(df) // 10)  # 自适应窗口
    y_smooth = np.convolve(y_sorted, np.ones(window)/window, mode='valid')
    x_smooth = x_sorted[window//2: len(x_sorted)-window//2]

    fig2.add_trace(go.Scatter(
        x=x_smooth,
        y=y_smooth,
        mode='lines',
        line=dict(color='green', width=3),
        name='趋势线'
    ))

fig2.update_layout(
    title=dict(
        text="调整幅度 vs 样本量",
        x=0.5,
        font=dict(size=16)
    ),
    xaxis_title="样本量",
    yaxis_title="调整幅度 (贝叶斯估计 - 原始值)",
    width=800,
    height=600,
    showlegend=True,
    margin=dict(l=50, r=50, t=80, b=50),
    legend=dict(
        x=0.02,  # 水平位置 (0-1，0为最左侧)
        y=0.98,  # 垂直位置 (0-1，1为最顶部)
        xanchor="left",  # 水平锚点
        yanchor="top",   # 垂直锚点
        bgcolor="rgba(0, 0, 0, 0.8)",  # 半透明背景
        bordercolor="Black",
        borderwidth=1
    )
)

fig2.show()

• 横轴：样本量
• 纵轴：调整幅度（贝叶斯估计 − 原始完单率）
• 红色虚线：y=0（无调整）

解读要点：

• 调整幅度可正可负，正表示向上调整（原始值低估），负表示向下调整（原始值高估）。
• 理想情况下，小样本点的调整幅度绝对值较大，大样本点的调整幅度接近零。
• 如果点的分布呈现“漏斗形”（小样本点分散，大样本点集中 near zero），则符合预期，说明模型合理地对不确定性高的估计进行了更强收缩。

收缩强度 vs 样本量

# 3. 收缩强度 vs 样本量
fig3 = go.Figure()

# 计算收缩强度
shrinkage = kappa_est / (kappa_est + df['decision_count'])

# 添加散点
fig3.add_trace(go.Scatter(
    x=df['decision_count'],
    y=shrinkage,
    mode='markers',
    marker=dict(
        size=8,
        color='lightblue',
        line=dict(width=1, color='darkblue')
    ),
    text=[f"司机: {row.plate_number}<br>样本量: {row.decision_count}<br>收缩强度: {s:.3f}"
          for row, s in zip(df.itertuples(), shrinkage)],
    hovertemplate='<b>%{text}</b><extra></extra>',
    name='司机收缩强度'
))

# 添加理论收缩曲线
x_theory = np.linspace(df['decision_count'].min(), df['decision_count'].max(), 100)
y_theory = kappa_est / (kappa_est + x_theory)

fig3.add_trace(go.Scatter(
    x=x_theory,
    y=y_theory,
    mode='lines',
    line=dict(color='red', width=3, dash='dash'),
    name=f'理论收缩曲线 κ={kappa_est:.1f}'
))

# 添加说明文本
if len(df) > 0:
    max_sample = df['decision_count'].max()
    min_shrinkage = shrinkage.min()
    max_shrinkage = shrinkage.max()

    fig3.add_annotation(
        x=max_sample * 0.7,
        y=0.8,
        text=f"收缩强度 = κ/(κ+n)<br>κ={kappa_est:.1f}",
        showarrow=False,
        font=dict(size=12)
    )

fig3.update_layout(
    title=dict(
        text="收缩强度 vs 样本量",
        x=0.5,
        font=dict(size=16)
    ),
    xaxis_title="样本量 (n)",
    yaxis_title="收缩强度 (κ/(κ+n))",
    yaxis_range=[0, 1],
    width=800,
    height=600,
    showlegend=True,
    margin=dict(l=50, r=50, t=80, b=50)
)

fig3.show()

• 横轴：样本量
• 纵轴：收缩强度（公式为 $\kappa / (\kappa + n)$）
• 点的位置：沿曲线$y = \frac{\kappa}{\kappa + n}$分布

解读要点：

• 收缩强度表示先验权重，取值范围 0~1。值越大，表示后验越依赖先验（收缩越强）。
• 曲线单调递减：样本量越大，收缩强度越小（后验更依赖数据）。
• 该图是理论曲线，验证模型是否按预期工作。实际收缩程度应与该曲线一致。

先验与后验分布

# 4. 先验与后验分布对比
fig4 = go.Figure()

# 生成x轴范围
x = np.linspace(0, 1, 200)

# 先验分布 (Beta分布)
prior_pdf = beta.pdf(x, mu_est * kappa_est, (1 - mu_est) * kappa_est)

fig4.add_trace(go.Scatter(
    x=x,
    y=prior_pdf,
    mode='lines',
    line=dict(color='red', width=3),
    fill='tozeroy',
    fillcolor='rgba(255, 0, 0, 0.2)',
    name=f'先验分布 Beta({mu_est*kappa_est:.1f}, {(1-mu_est)*kappa_est:.1f})'
))

# 后验分布 (核密度估计)
if len(df) > 1:
    posterior_rates = df['bayes_estimate_method5'].values
    kde = gaussian_kde(posterior_rates)
    posterior_pdf = kde(x)

    fig4.add_trace(go.Scatter(
        x=x,
        y=posterior_pdf,
        mode='lines',
        line=dict(color='green', width=3),
        fill='tozeroy',
        fillcolor='rgba(0, 255, 0, 0.2)',
        name='后验分布 (核密度估计)'
    ))

# 添加原始数据分布
fig4.add_trace(go.Histogram(
    x=df['finish_rate'],
    histnorm='probability density',
    opacity=0.5,
    marker_color='blue',
    name='原始数据分布',
    nbinsx=20
))

# 添加总体均值线
fig4.add_vline(
    x=mu_est,
    line_dash="dash",
    line_color="orange",
    annotation_text=f"μ={mu_est:.3f}",
    annotation_position="top right"
)

# 计算并显示关键统计量
if len(df) > 0:
    prior_mean = mu_est
    prior_std = np.sqrt(mu_est * (1 - mu_est) / (kappa_est + 1))
    posterior_mean = df['bayes_estimate_method5'].mean()
    posterior_std = df['bayes_estimate_method5'].std()
    original_mean = df['finish_rate'].mean()
    original_std = df['finish_rate'].std()

fig4.update_layout(
    title=dict(
        text="先验、后验与原始数据分布对比",
        x=0.5,
        font=dict(size=16)
    ),
    xaxis_title="完单率",
    yaxis_title="密度",
    xaxis_range=[0, 1],
    width=800,
    height=600,
    showlegend=True,
    margin=dict(l=50, r=50, t=80, b=50),
    barmode='overlay'
)

fig4.update_traces(opacity=0.6, selector=dict(type='histogram'))
fig4.show()

• 红色曲线：先验分布（Beta 分布，参数由估计的超参数$\mu$和$\kappa$决定）
• 绿色曲线：后验分布（各司机贝叶斯估计的核密度估计）
• 横轴：完单率，纵轴：密度

解读要点：

• 先验分布代表观察数据前的信念，后验分布代表结合数据后的整体估计分布。
• 对比两者可看出数据带来的信息更新：
  • 若后验更窄，表示数据降低了不确定性。
  • 若后验位置偏移，表示数据系统性改变了先验的认知。
• 理想情况下，后验应比先验更集中，且可能偏移，反映数据的实际模式。