文章内容如有错误或排版问题,请提交反馈,非常感谢!
BANG算法概述
BANG算法是21世纪初提出的一种用于空间数据聚类的算法,它结合了网格划分和层次聚类的思想,旨在高效地发现数据集中任意形状、不同密度的聚类,并且能够识别嵌套的聚类结构。
BANG算法是一种巧妙的混合方法,它通过平衡网格获得了计算效率,通过构建密度主导的层次结构获得了处理任意形状、变密度和嵌套聚类的能力。尽管在高维数据上受限,但它为空间数据聚类提供了一个强大而直观的框架,在特定领域(尤其是地球科学、遥感等)中,仍然是比DBSCAN和OPTICS等算法更具结构性优势的选择。后续许多基于网格和密度的聚类算法(如STING, CLIQUE等)都受到了它的启发。
BANG产生背景
BANG(Balanced and Nested Grid)算法产生于上世纪90年代末,是为了解决传统聚类算法的几个关键痛点而设计的:
传统聚类算法的局限性
| 算法类型 | 主要问题 | 实际影响 |
| 划分式聚类 (K-means) | 需要预设簇数,只能发现凸形簇 | 无法处理复杂形状的聚类结构 |
| 层次聚类 | 计算复杂度高(O(n²)),不可逆 | 难以处理大规模数据集 |
| DBSCAN | 全局参数敏感,高维数据效果差 | 难以适应密度变化的数据集 |
现实需求驱动
- 空间数据爆炸:GIS、遥感图像、天文观测产生海量空间数据
- 形状多样性:现实中的聚类往往具有复杂、非凸的形状
- 效率要求:需要处理大规模数据集的计算效率
- 自动化需求:希望减少人工参数调优的依赖
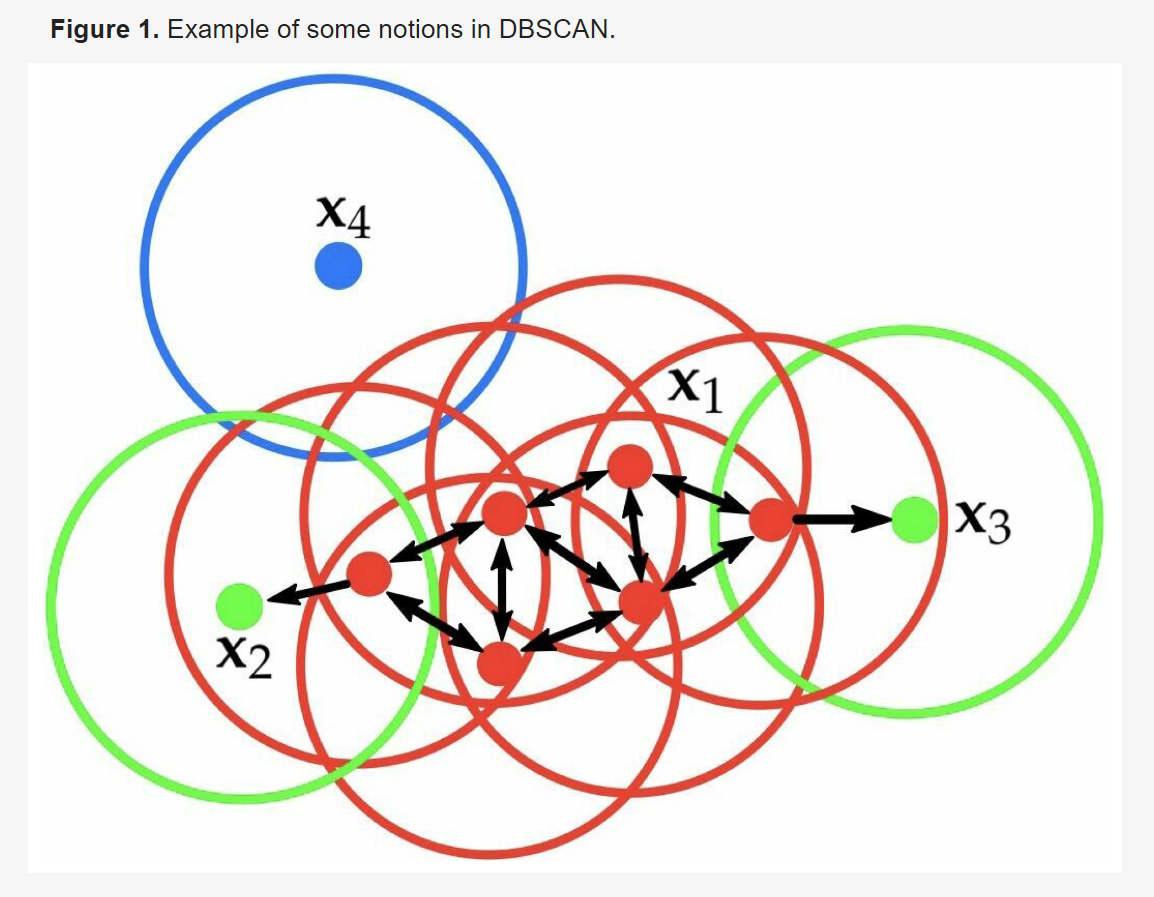
技术演变路径
网格化方法 (STING, CLIQUE)
↓
基于密度的聚类 (DBSCAN)
↓
网格+密度结合 (BANG) ← 1998年由M. Ester等人提出
↓
层次化+密度+网格的融合
核心思想与动机
在聚类分析中,传统的算法(如K-means)难以识别非凸形状,而基于密度的算法(如DBSCAN)虽然能识别任意形状,但对全局参数敏感,且在数据密度差异较大时表现不佳。BANG算法的设计目标就是解决这些问题,其核心思想是:
- 网格化:将数据空间划分为大小相等的网格单元。
- 基于网格的密度估计:通过统计落入每个网格单元的数据点数量来计算该单元的“密度”。
- 构建密度依赖的层次结构:根据相邻网格单元的密度关系,构建一个层次树(Dendrogram)。这棵树反映了从高密度区域到低密度区域的连接关系。
- 提取聚类:通过一个密度阈值在层次树上进行“切割”,低于该阈值的连接被切断,从而形成不同的聚类。由于是层次结构,它可以自然地揭示出嵌套的聚类(即一个大的聚类内部包含若干小的子聚类)。
关键概念与步骤详解
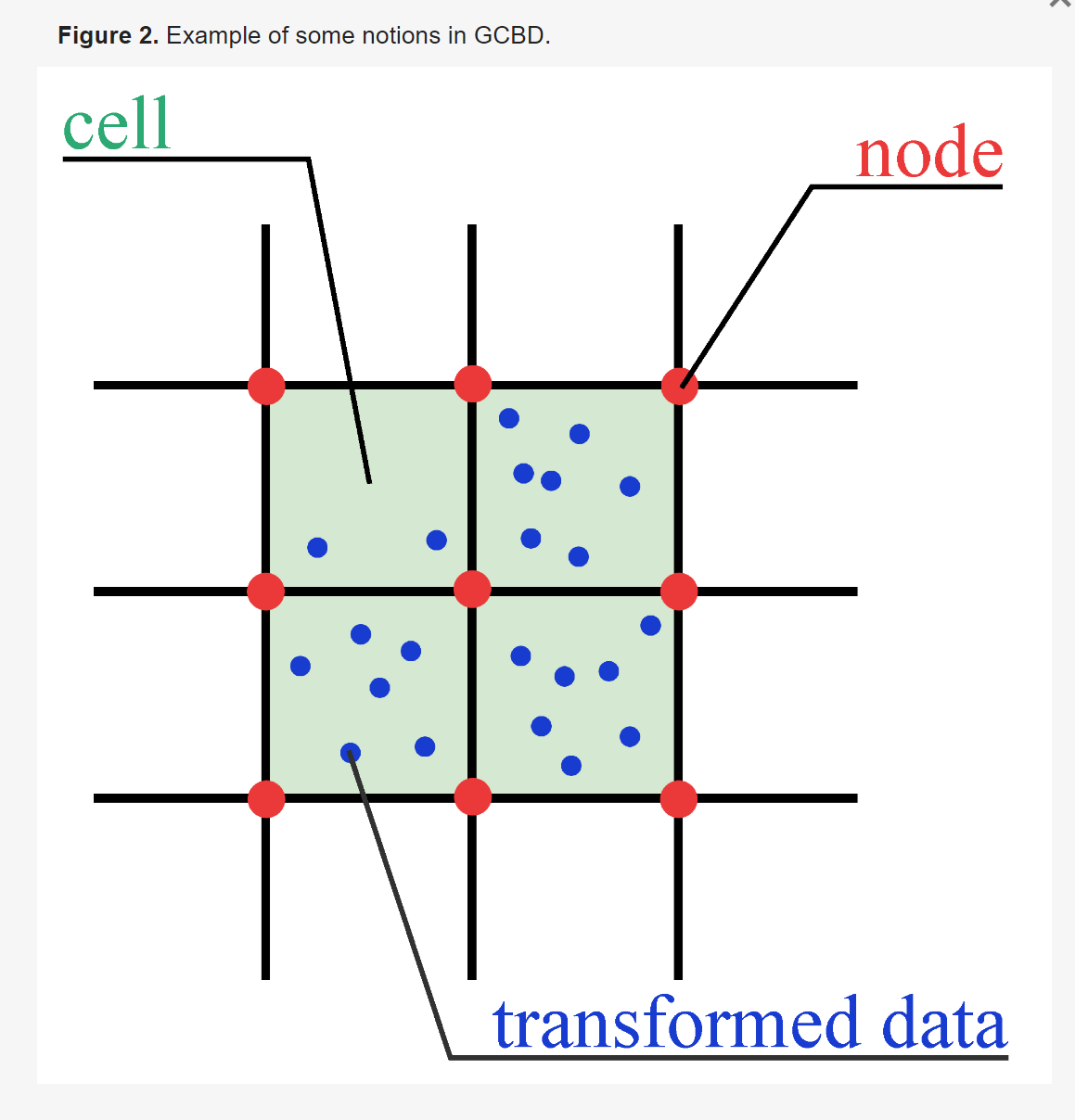
空间划分与网格结构
- BANG使用一个固定的、平衡的(即大小相等)的网格来覆盖整个数据空间。这个网格可以是二维的(用于空间数据),也可以扩展到更高维。
- 每个网格单元有三个关键属性:
- 空间位置:由其坐标确定。
- 密度:落入该单元的数据点数目。
- 状态:被标记为“稠密”或“稀疏”(根据一个预设的密度阈值)。
密度估计与邻域关系
- 密度直接在网格单元上计算,计算复杂度与数据点的关系较小,主要与网格数量有关,因此在大数据集上效率很高。
- 算法定义网格单元之间的邻接关系(如4邻域或8邻域)。聚类将通过连接相邻的“稠密”单元来形成。
核心创新:BANG 结构(BANG-Structure)
这是算法的核心数据结构,它是一个有向图,节点是网格单元。它的构建基于一个核心观察:在自然聚类中,密度通常从聚类中心向边缘递减。
- 主导关系:对于一对相邻的单元A和B,如果A的密度 大于 B的密度,则定义一条从A指向B的边,表示A在密度上“主导”B。
- 构建过程:算法遍历所有网格单元,为每个单元找到其所有密度更低的邻居,并建立“主导”边。最终形成一个以最高密度单元为根、指向低密度区域的有向无环图(DAG),也被称为“等高线树”或“层次树”的变体。
聚类提取过程
- 选择起始点(根节点):通常从密度最高的网格单元开始。
- 区域生长:沿着BANG结构中的边,从根节点出发,访问所有它“主导”的单元。这个生长过程会持续到遇到以下情况:
- 遇到一个“稀疏”单元(密度低于阈值)。
- 遇到一个已经被其他聚类占用的单元。
- 形成一个聚类:所有被访问到的连通“稠密”单元集合就形成了一个聚类。
- 迭代:从未被访问过的、剩余的最高密度单元开始,重复上述过程,直到所有“稠密”单元都被访问,最终得到所有聚类。
- 嵌套结构:由于BANG结构是层次的,通过设置不同的密度阈值进行切割,可以揭示不同层次的聚类。例如,一个高阈值可以识别出核心的高密度子聚类,而一个低阈值可以识别出包含这些子聚类的更大的父聚类。
与经典算法的对比
| 特性 | BANG 算法 | DBSCAN | K-means |
| 聚类形状 | 任意形状 | 任意形状 | 凸形(球形) |
| 处理密度变化 | 优秀,能识别不同密度区域 | 较差,全局参数对不同密度敏感 | 假设均匀分布 |
| 嵌套/层次结构 | 支持,是其核心能力 | 不支持 | 不支持 |
| 噪声处理 | 支持(稀疏单元视为噪声) | 支持 | 不支持 |
| 参数敏感性 | 对网格大小和密度阈值敏感 | 对邻域半径和最小点数敏感 | 对K值(聚类数)和初始点敏感 |
| 效率 | 高(基于网格,与点数线性相关) | 中等(需要邻近查询) | 高(迭代优化) |
| 主要思想 | 网格密度 + 层次主导关系 | 基于密度的区域生长 | 最小化类内距离 |
优点
- 识别复杂结构:能有效发现任意形状和嵌套的聚类。
- 对密度变化鲁棒:通过局部密度关系和层次结构,能同时处理高密度和低密度区域。
- 高效率:网格化预处理使密度计算和邻居查找非常快,适合处理大规模空间数据集。
- 提供多粒度视图:通过改变密度阈值,可以获得不同层次的聚类结果,有助于多尺度数据分析。
缺点
- 参数选择:网格大小和密度阈值对结果影响很大,需要仔细调整。
- 网格边界效应:聚类边界可能被网格的硬边界“锯齿化”,不够平滑。
- 维数灾难:在高维空间中,网格数量会呈指数级增长,导致内存消耗巨大,效率急剧下降(这是所有基于网格方法的通病)。
- 对数据分布假设:它假设聚类内部密度从中心向外单调递减,这在某些真实场景中可能不成立。
其他密度聚类的对比
| 特性维度 | BANG | DBSCAN | OPTICS | DENCLUE |
| 理论基础 | 网格+密度+层次 | 核心点+密度可达 | 可达性排序 | 核密度估计 |
| 簇形状 | 任意形状 | 任意形状 | 任意形状 | 任意形状 |
| 参数需求 | 网格大小、密度阈值 | ε, MinPts | ε, MinPts | 核半径、噪声阈值 |
| 计算复杂度 | O(n+k) | O(n log n) | O(n log n) | O(n log n) |
| 内存占用 | 中 | 低 | 高 | 高 |
| 噪声处理 | 好 | 好 | 好 | 中等 |
| 层次输出 | 支持 | 不支持 | 支持 | 不支持 |
| 高维性能 | 较好 | 差 | 中等 | 好 |
| 边界处理 | 网格边界 | 精确边界 | 精确边界 | 模糊边界 |
BANG的核心思想与实现逻辑
核心设计理念
BANG算法的核心是”用网格的规整性简化密度计算,用层次的灵活性捕捉多尺度结构”。
三大支柱:
- 网格划分:将连续空间离散化为规整网格
- 密度估计:基于网格单元统计局部密度
- 层次合并:自底向上构建聚类层次
实现逻辑流程
输入:数据集D,网格分辨率r,密度阈值τ
输出:聚类结果C
1. 空间划分阶段
for 每个维度i in d:
计算[min_i, max_i]的数据范围
划分区间为n_i = ⌈(max_i-min_i)/r⌉个单元
2. 密度计算阶段
初始化网格单元统计:
grid[cell].count = 0
grid[cell].density = 0
for 每个数据点p in D:
计算p所在的网格单元c
c.count += 1
for 每个网格单元c:
c.density = c.count / cell_volume
标记高密度单元:if c.density > τ then c.isHigh = true
3. 层次聚类阶段
level = 0
while 存在可合并的相邻高密度单元:
在当前层level:
for 每个高密度单元u:
for 每个与u相邻的高密度单元v:
if 密度相似(u, v) and 空间邻接(u, v):
合并u和v到同一簇
// 构建下一层粗粒度网格
构建level+1层网格:
每个2^d个细粒度单元合并为一个粗粒度单元
计算粗粒度单元密度 = 子单元平均密度
level += 1
4. 结果提取阶段
从层次结构中选取"最优"层次:
基于簇内紧密性、簇间分离性
将低密度单元分配给最近的高密度簇
过滤掉过小的簇(噪声处理)
5. 返回聚类结果
关键创新点
- 平衡网格结构
- 通过规则划分避免计算复杂度爆炸
- 支持多分辨率分析
- 嵌套网格层次
细粒度层(Level 0):单元小,分辨率高
↓
中间层(Level 1):2×2单元合并
↓
粗粒度层(Level 2):4×4单元合并
↓
... 形成金字塔结构
- 密度导向合并策略
- 基于局部密度而非全局距离
- 支持密度变化的簇发现
BANG算法Python实现
import numpy as np
from collections import defaultdict, deque
import matplotlib.pyplot as plt
from typing import List, Tuple, Dict, Set, Optional
from sklearn.datasets import make_blobs, make_moons, make_circles
import warnings
warnings.filterwarnings('ignore')
class BANGClustering:
"""
BANG (Balanced and Nested Grid) 聚类算法实现
算法特点:
1. 基于网格划分,计算效率高
2. 能识别任意形状的聚类
3. 能处理不同密度的数据集
4. 可发现嵌套聚类结构
"""
def __init__(self, grid_size: int = 20, density_threshold: int = 3,
min_cluster_size: int = 5, nested_levels: int = 1):
"""
初始化BANG聚类算法
参数:
grid_size: 网格划分的粒度
density_threshold: 密度阈值,超过此值的网格单元被认为是稠密的
min_cluster_size: 最小聚类尺寸(网格单元数)
nested_levels: 嵌套层次数(>1时可发现嵌套聚类)
"""
self.grid_size = grid_size
self.density_threshold = density_threshold
self.min_cluster_size = min_cluster_size
self.nested_levels = nested_levels
# 内部状态变量
self.grid_ = None
self.densities_ = None
self.grid_labels_ = None
self.labels_ = None
self.hierarchy_ = None
def _create_grid(self, X: np.ndarray) -> np.ndarray:
"""
创建均匀网格并统计每个网格的点数
参数:
X: 输入数据,形状为(n_samples, n_features)
返回:
grid: 网格密度矩阵
"""
n_samples, n_features = X.shape
grid = np.zeros((self.grid_size,) * n_features, dtype=int)
# 数据归一化到[0, 1]区间
X_min = X.min(axis=0)
X_max = X.max(axis=0)
X_norm = (X - X_min) / (X_max - X_min + 1e-10)
# 计算每个点所在的网格索引
grid_indices = (X_norm * (self.grid_size - 1)).astype(int)
# 统计每个网格的点数
for idx in grid_indices:
if n_features == 1:
grid[tuple([idx])] += 1
else:
grid[tuple(idx)] += 1
return grid, X_norm, grid_indices
def _get_neighbors(self, idx: Tuple, grid_shape: Tuple) -> List[Tuple]:
"""
获取网格单元的所有邻接单元(8邻域)
参数:
idx: 当前网格单元的索引
grid_shape: 网格的形状
返回:
邻居索引列表
"""
neighbors = []
dim = len(idx)
# 生成所有可能的邻居偏移
offsets = []
if dim == 1:
offsets = [(-1,), (1,)]
elif dim == 2:
offsets = [(dx, dy) for dx in [-1, 0, 1] for dy in [-1, 0, 1] if not (dx == 0 and dy == 0)]
# 添加有效邻居
for offset in offsets:
neighbor_idx = tuple(idx[i] + offset[i] for i in range(dim))
# 检查索引是否在网格范围内
if all(0 <= neighbor_idx[i] < grid_shape[i] for i in range(dim)):
neighbors.append(neighbor_idx)
return neighbors
def _build_dominance_graph(self, grid: np.ndarray) -> Dict[Tuple, List[Tuple]]:
"""
构建主导关系图(核心BANG结构)
参数:
grid: 网格密度矩阵
返回:
主导关系图,键为网格单元,值为被其主导的邻居列表
"""
dominance_graph = defaultdict(list)
grid_shape = grid.shape
dim = len(grid_shape)
# 遍历所有网格单元
if dim == 1:
indices = [(i,) for i in range(grid_shape[0])]
elif dim == 2:
indices = [(i, j) for i in range(grid_shape[0]) for j in range(grid_shape[1])]
else:
raise ValueError("只支持1D或2D数据")
for idx in indices:
current_density = grid[idx]
# 获取所有邻居
neighbors = self._get_neighbors(idx, grid_shape)
# 建立主导关系
for neighbor_idx in neighbors:
neighbor_density = grid[neighbor_idx]
# 如果当前单元密度大于邻居,则建立主导关系
if current_density > neighbor_density:
dominance_graph[idx].append(neighbor_idx)
return dominance_graph
def _find_clusters(self, grid: np.ndarray, dominance_graph: Dict) -> np.ndarray:
"""
从主导关系图中提取聚类
参数:
grid: 网格密度矩阵
dominance_graph: 主导关系图
返回:
网格标签矩阵
"""
grid_shape = grid.shape
grid_labels = -np.ones(grid_shape, dtype=int) # -1表示未访问或噪声
visited = set()
cluster_id = 0
# 按密度从高到低排序网格单元
dim = len(grid_shape)
if dim == 1:
all_cells = [(i,) for i in range(grid_shape[0])]
elif dim == 2:
all_cells = [(i, j) for i in range(grid_shape[0]) for j in range(grid_shape[1])]
# 按密度降序排序
all_cells.sort(key=lambda idx: grid[idx], reverse=True)
for start_cell in all_cells:
# 如果已经访问过或密度低于阈值,跳过
if start_cell in visited or grid[start_cell] < self.density_threshold:
continue
# 使用BFS从高密度单元开始生长聚类
queue = deque([start_cell])
cluster_cells = []
while queue:
cell = queue.popleft()
if cell in visited:
continue
visited.add(cell)
cluster_cells.append(cell)
# 将当前单元的主导邻居加入队列
for neighbor in dominance_graph.get(cell, []):
if neighbor not in visited and grid[neighbor] >= self.density_threshold:
queue.append(neighbor)
# 如果聚类足够大,分配聚类标签
if len(cluster_cells) >= self.min_cluster_size:
for cell in cluster_cells:
grid_labels[cell] = cluster_id
cluster_id += 1
return grid_labels
def _find_nested_clusters(self, grid: np.ndarray, dominance_graph: Dict) -> Dict[int, List[Set]]:
"""
发现嵌套聚类结构
参数:
grid: 网格密度矩阵
dominance_graph: 主导关系图
返回:
层次聚类结构字典
"""
hierarchy = defaultdict(list)
# 使用不同的密度阈值发现不同层次的聚类
for level in range(self.nested_levels):
# 调整密度阈值
level_threshold = self.density_threshold * (level + 1)
# 临时修改阈值并运行聚类
original_threshold = self.density_threshold
self.density_threshold = level_threshold
# 获取当前层次的聚类
level_labels = self._find_clusters(grid, dominance_graph)
# 将每个聚类的网格单元集合存储到层次结构中
unique_labels = np.unique(level_labels)
for label in unique_labels:
if label != -1: # 忽略噪声
# 获取属于该聚类的所有网格单元
cluster_cells = set(zip(*np.where(level_labels == label)))
if len(cluster_cells) >= self.min_cluster_size:
hierarchy[level].append(cluster_cells)
# 恢复原始阈值
self.density_threshold = original_threshold
return hierarchy
def fit_predict(self, X: np.ndarray) -> np.ndarray:
"""
执行聚类并返回每个点的标签
参数:
X: 输入数据,形状为(n_samples, n_features)
返回:
每个数据点的聚类标签
"""
# 1. 创建网格
self.grid_, X_norm, grid_indices = self._create_grid(X)
# 2. 构建主导关系图
self.dominance_graph_ = self._build_dominance_graph(self.grid_)
# 3. 发现聚类
if self.nested_levels > 1:
# 发现嵌套聚类
self.hierarchy_ = self._find_nested_clusters(self.grid_, self.dominance_graph_)
# 使用最精细层次的聚类
if self.hierarchy_:
finest_level = min(self.hierarchy_.keys())
# 将层次聚类结果转换为网格标签
self.grid_labels_ = -np.ones(self.grid_.shape, dtype=int)
for cluster_id, cluster_cells in enumerate(self.hierarchy_[finest_level]):
for cell in cluster_cells:
self.grid_labels_[cell] = cluster_id
else:
self.grid_labels_ = -np.ones(self.grid_.shape, dtype=int)
else:
# 单层次聚类
self.grid_labels_ = self._find_clusters(self.grid_, self.dominance_graph_)
# 4. 将网格标签映射回数据点
self.labels_ = np.full(X.shape[0], -1, dtype=int)
for i, idx in enumerate(grid_indices):
grid_label = self.grid_labels_[tuple(idx)]
if grid_label != -1:
self.labels_[i] = grid_label
return self.labels_
def visualize_grid(self, X: np.ndarray, show_points: bool = True):
"""
可视化网格划分和密度
参数:
X: 原始数据
show_points: 是否显示数据点
"""
if X.shape[1] != 2:
print("只能可视化2D数据")
return
plt.figure(figsize=(15, 5))
# 1. 原始数据
plt.subplot(131)
plt.scatter(X[:, 0], X[:, 1], s=20, alpha=0.6, c='gray')
plt.title("原始数据")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
# 2. 网格划分
plt.subplot(132)
# 创建网格
x_min, x_max = X[:, 0].min(), X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()
x_edges = np.linspace(x_min, x_max, self.grid_size + 1)
y_edges = np.linspace(y_min, y_max, self.grid_size + 1)
# 绘制网格
for i in range(self.grid_size + 1):
plt.axvline(x=x_edges[i], color='gray', alpha=0.3, linestyle='-', linewidth=0.5)
plt.axhline(y=y_edges[i], color='gray', alpha=0.3, linestyle='-', linewidth=0.5)
# 绘制数据点
if show_points:
plt.scatter(X[:, 0], X[:, 1], s=20, alpha=0.6, c='blue')
# 高亮稠密网格
for i in range(self.grid_size):
for j in range(self.grid_size):
density = self.grid_[i, j]
if density >= self.density_threshold:
plt.gca().add_patch(plt.Rectangle(
(x_edges[i], y_edges[j]),
x_edges[i+1]-x_edges[i],
y_edges[j+1]-y_edges[j],
alpha=density/self.grid_.max()*0.7,
facecolor='red',
edgecolor='red'
))
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.title("网格划分与稠密单元")
plt.xlabel("特征1")
plt.ylabel("特征2")
# 3. 聚类结果
plt.subplot(133)
if self.labels_ is not None:
unique_labels = np.unique(self.labels_)
colors = plt.cm.tab20(np.linspace(0, 1, len(unique_labels)))
for label, color in zip(unique_labels, colors):
if label == -1:
# 噪声点
mask = self.labels_ == label
plt.scatter(X[mask, 0], X[mask, 1], s=20, alpha=0.5, c='gray', label='噪声')
else:
mask = self.labels_ == label
plt.scatter(X[mask, 0], X[mask, 1], s=30, alpha=0.7, c=color, label=f'聚类{label}')
plt.title("BANG聚类结果")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.show()
def visualize_density(self):
"""可视化网格密度"""
if self.grid_ is None or len(self.grid_.shape) != 2:
print("只能可视化2D网格密度")
return
plt.figure(figsize=(8, 6))
plt.imshow(self.grid_, cmap='hot', interpolation='nearest', aspect='auto')
plt.colorbar(label='点密度')
plt.title("网格密度热图")
plt.xlabel("X网格坐标")
plt.ylabel("Y网格坐标")
plt.grid(True, alpha=0.3)
plt.show()
def get_cluster_info(self) -> Dict:
"""
获取聚类统计信息
返回:
包含聚类信息的字典
"""
if self.labels_ is None:
return {}
unique_labels, counts = np.unique(self.labels_[self.labels_ != -1], return_counts=True)
info = {
"n_clusters": len(unique_labels),
"cluster_sizes": dict(zip(unique_labels, counts)),
"noise_points": np.sum(self.labels_ == -1),
"total_points": len(self.labels_)
}
return info
# 示例1:测试BANG算法在不同数据集上的表现
def test_bang_on_synthetic_datasets():
"""在合成数据集上测试BANG算法"""
# 创建测试数据集
np.random.seed(42)
# 数据集1:圆形嵌套数据集
X1, _ = make_circles(n_samples=500, factor=0.5, noise=0.05, random_state=42)
# 数据集2:不同密度的混合数据集
X2_1, _ = make_blobs(n_samples=300, centers=[(0, 0)], cluster_std=0.3, random_state=42)
X2_2, _ = make_blobs(n_samples=100, centers=[(2, 2)], cluster_std=0.1, random_state=42)
X2_3, _ = make_blobs(n_samples=100, centers=[(-2, 2)], cluster_std=0.5, random_state=42)
X2 = np.vstack([X2_1, X2_2, X2_3])
# 数据集3:月牙形数据集
X3, _ = make_moons(n_samples=500, noise=0.1, random_state=42)
datasets = [
("嵌套圆形", X1),
("变密度", X2),
("月牙形", X3)
]
# 对每个数据集应用BANG聚类
for dataset_name, X in datasets:
print(f"\n{'='*50}")
print(f"数据集: {dataset_name}")
print(f"{'='*50}")
# 创建BANG聚类器
bang = BANGClustering(
grid_size=30,
density_threshold=5,
min_cluster_size=10,
nested_levels=2
)
# 执行聚类
labels = bang.fit_predict(X)
# 获取聚类信息
info = bang.get_cluster_info()
print(f"发现聚类数: {info['n_clusters']}")
print(f"聚类大小: {info['cluster_sizes']}")
print(f"噪声点数: {info['noise_points']}")
# 可视化
bang.visualize_grid(X, show_points=True)
# 可视化密度
bang.visualize_density()
# 示例2:嵌套聚类的演示
def demonstrate_nested_clustering():
"""演示嵌套聚类发现"""
# 创建具有嵌套结构的数据
np.random.seed(123)
# 外部大聚类
outer_cluster = np.random.randn(500, 2) * 2
# 内部嵌套的两个聚类
inner_cluster1 = np.random.randn(150, 2) * 0.5 + np.array([1.5, 1.5])
inner_cluster2 = np.random.randn(150, 2) * 0.5 + np.array([-1.5, -1.5])
# 合并数据
X = np.vstack([outer_cluster, inner_cluster1, inner_cluster2])
print("\n" + "="*60)
print("嵌套聚类演示")
print("="*60)
# 使用不同参数发现不同层次的聚类
plt.figure(figsize=(15, 4))
for i, (density_threshold, title) in enumerate([
(3, "高密度阈值: 发现内部密集子聚类"),
(1, "低密度阈值: 发现外部大聚类")
]):
# 创建BANG聚类器
bang = BANGClustering(
grid_size=25,
density_threshold=density_threshold,
min_cluster_size=8
)
# 执行聚类
labels = bang.fit_predict(X)
# 可视化
plt.subplot(1, 3, i+1)
unique_labels = np.unique(labels)
colors = plt.cm.tab20(np.linspace(0, 1, len(unique_labels)))
for label, color in zip(unique_labels, colors):
if label == -1:
plt.scatter(X[labels==label, 0], X[labels==label, 1],
s=20, alpha=0.3, c='gray', label='噪声')
else:
plt.scatter(X[labels==label, 0], X[labels==label, 1],
s=30, alpha=0.7, c=color, label=f'聚类{label}')
plt.title(title)
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
# 使用嵌套层次发现
plt.subplot(1, 3, 3)
bang_nested = BANGClustering(
grid_size=25,
density_threshold=2,
min_cluster_size=8,
nested_levels=2
)
labels_nested = bang_nested.fit_predict(X)
# 由于简化实现,我们手动展示多级聚类
# 这里我们展示如何结合不同阈值的结果
from matplotlib.patches import Ellipse
# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], s=20, alpha=0.5, c='blue')
# 添加聚类边界示意
from matplotlib.patches import Ellipse, Circle
# 外部大聚类示意
ellipse_outer = Ellipse(xy=(0, 0), width=12, height=12,
edgecolor='red', facecolor='none',
linewidth=2, linestyle='--', alpha=0.7, label='外部聚类')
plt.gca().add_patch(ellipse_outer)
# 内部子聚类示意
circle_inner1 = Circle(xy=(1.5, 1.5), radius=1.5,
edgecolor='green', facecolor='none',
linewidth=2, alpha=0.7, label='子聚类1')
circle_inner2 = Circle(xy=(-1.5, -1.5), radius=1.5,
edgecolor='orange', facecolor='none',
linewidth=2, alpha=0.7, label='子聚类2')
plt.gca().add_patch(circle_inner1)
plt.gca().add_patch(circle_inner2)
plt.title("嵌套聚类结构示意")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.xlim(-8, 8)
plt.ylim(-8, 8)
plt.tight_layout()
plt.show()
# 示例3:与DBSCAN算法对比
def compare_with_dbscan():
"""对比BANG和DBSCAN算法"""
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
# 创建具有不同密度和形状的数据
np.random.seed(42)
# 密集的小聚类
cluster1 = np.random.randn(100, 2) * 0.3 + np.array([2, 2])
# 稀疏的大聚类
cluster2 = np.random.randn(300, 2) * 1.5 + np.array([-2, -2])
# 月牙形聚类
from sklearn.datasets import make_moons
cluster3, _ = make_moons(n_samples=200, noise=0.1, random_state=42)
cluster3 = cluster3 * 2 - np.array([1, 0.5])
X = np.vstack([cluster1, cluster2, cluster3])
# 标准化数据(DBSCAN对尺度敏感)
X_scaled = StandardScaler().fit_transform(X)
print("\n" + "="*60)
print("BANG vs DBSCAN 对比")
print("="*60)
plt.figure(figsize=(15, 5))
# 原始数据
plt.subplot(131)
plt.scatter(X[:, 0], X[:, 1], s=20, alpha=0.6, c='gray')
plt.title("原始数据 (不同密度和形状)")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
# BANG聚类结果
plt.subplot(132)
bang = BANGClustering(
grid_size=25,
density_threshold=4,
min_cluster_size=10
)
bang_labels = bang.fit_predict(X_scaled)
unique_labels = np.unique(bang_labels)
colors = plt.cm.tab20(np.linspace(0, 1, len(unique_labels)))
for label, color in zip(unique_labels, colors):
if label == -1:
plt.scatter(X[bang_labels==label, 0], X[bang_labels==label, 1],
s=20, alpha=0.3, c='gray', label='噪声')
else:
plt.scatter(X[bang_labels==label, 0], X[bang_labels==label, 1],
s=30, alpha=0.7, c=color, label=f'聚类{label}')
plt.title("BANG聚类结果")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
# DBSCAN聚类结果
plt.subplot(133)
dbscan = DBSCAN(eps=0.3, min_samples=10)
dbscan_labels = dbscan.fit_predict(X_scaled)
unique_labels = np.unique(dbscan_labels)
colors = plt.cm.tab20(np.linspace(0, 1, len(unique_labels)))
for label, color in zip(unique_labels, colors):
if label == -1:
plt.scatter(X[dbscan_labels==label, 0], X[dbscan_labels==label, 1],
s=20, alpha=0.3, c='gray', label='噪声')
else:
plt.scatter(X[dbscan_labels==label, 0], X[dbscan_labels==label, 1],
s=30, alpha=0.7, c=color, label=f'聚类{label}')
plt.title("DBSCAN聚类结果 (eps=0.3, min_samples=10)")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.grid(True, alpha=0.3)
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.show()
# 输出性能对比
print("\n性能对比:")
print(f"BANG - 聚类数: {len(np.unique(bang_labels))-1}, 噪声点: {np.sum(bang_labels==-1)}")
print(f"DBSCAN - 聚类数: {len(np.unique(dbscan_labels))-1}, 噪声点: {np.sum(dbscan_labels==-1)}")
# 主程序
if __name__ == "__main__":
# 运行所有示例
print("BANG聚类算法Python实现演示")
print("="*60)
# 示例1:测试BANG算法在不同数据集上的表现
test_bang_on_synthetic_datasets()
# 示例2:嵌套聚类的演示
demonstrate_nested_clustering()
# 示例3:与DBSCAN算法对比
compare_with_dbscan()
# 参数调优示例
print("\n" + "="*60)
print("BANG参数调优提示")
print("="*60)
print("""
关键参数说明:
1. grid_size: 网格大小
- 值太小 -> 网格粗糙,可能丢失细节
- 值太大 -> 计算成本高,可能过拟合
2. density_threshold: 密度阈值
- 值太小 -> 将噪声识别为聚类
- 值太大 -> 可能分裂真正的聚类
3. min_cluster_size: 最小聚类尺寸
- 过滤掉小的噪声聚类
4. nested_levels: 嵌套层次
- >1时可发现多尺度聚类结构
调优建议:
1. 从较小的grid_size开始,逐渐增加直到结果稳定
2. 观察网格密度分布,选择适当的密度阈值
3. 使用可视化工具理解聚类结果
4. 对嵌套数据,尝试多个密度阈值
""")