Statsmodels 和 Scikit-learn 是两个不同的 Python 库,它们都提供了用于线性回归的工具。Statsmodels 中支持的线性回归模型列表:
- OLS 回归:OLS 代表“普通最小二乘回归”,它是一种最常见且最简单的线性回归模型。
- WLS 回归:WLS 代表“加权最小二乘回归”,它在处理异方差性(即误差项方差不相等)时比 OLS 回归更为有效。
- GLS 回归:GLS 代表“广义最小二乘回归”,它可以处理异方差性和相关性。
- GLSAR 回归:GLSAR 代表“广义最小二乘回归自回归误差模型”,它可以用于处理自相关误差。
- WLSIV 回归:WLSIV 代表“两阶段最小二乘回归”,它应用于当某些解释变量存在内生性时,可以采用这种回归方法来控制内生性。
- 交互作用回归:它可用于模拟两个或多个自变量之间的交互作用。
- 多项式回归:它添加了自变量的高次幂项以建立非线性关系。
- 岭回归:岭回归是一种正则化线性回归方法,旨在减少过拟合问题。
- Lasso 回归:Lasso 回归也是一种正则化线性回归方法,但与岭回归不同,它倾向于将一些系数缩小到零,从而实现特征选择。
- ElasticNet 回归:ElasticNet 回归是岭回归和 Lasso 回归的组合。
由于 OLS 回归是最常用的,所以今天的这篇文章主要围绕 OLS 回归展开。OLS 回归是一种最小二乘法线性回归模型,其中 OLS 代表“普通最小二乘回归”(Ordinary Least Squares Regression)。在 OLS 回归中,我们尝试将一个因变量 Y 与一个或多个自变量 X 之间的关系建模为线性函数,并使用最小二乘法拟合一条直线来描述它们之间的关系。为了找到最佳的拟合线,我们需要找到通过数据点的直线,使得所有点到该直线的距离之和最小。这就是所谓的“最小二乘法”。通过 OLS 回归可以计算出每个自变量对因变量的影响大小,并且给出一个可靠的度量标准来评估整个模型的拟合程度。
下面是 Statsmodels OLS 线性回归和 Scikit-learn 中的线性回归的区别:
- API 风格:statsmodels 和 Scikit-learn 的 API 有所不同,这意味着在使用它们时需要编写不同的代码。例如,statsmodels 的 OLS 使用类似 R 语言的 formula 语法,而 Scikit-learn 的线性回归则需要通过 X 和 y 参数传递数据。
- 推断统计:statsmodels 的 OLS 回归提供了更多的统计信息,并可以执行各种假设检验、置信区间等推断统计操作。相反,Scikit-learn 的线性回归主要专注于预测目标变量,其输出只包括系数和截距等基本信息。
- 数据处理:在数据预处理方面,Scikit-learn 提供了许多常见的数据清洗和转换工具,例如填充缺失值、标准化数据等。在另一方面,statsmodels 主要专注于对模型进行拟合和统计分析。
- 应用场景:由于针对的应用场景不同,建议根据实际需求选择合适的工具。如果主要关注的是推断统计,则建议使用 statsmodels 的 OLS 回归;如果主要关注预测目标变量,则建议使用 Scikit-learn 的线性回归模型。
在机器学习中的线性回归,一般都会使用 scikit-learn 中的 linear_model 这个模块,用 linear_model 的好处是速度快、结果简单易懂,但它的使用是有条件的,就是使用者在明确该模型是线性模型的情况下才能用,否则生成的结果很可能是错误的。如果不知道该模型是否是线性模型的情况下可以使用 statsmodels,statsmodels 是 python 中专门用于统计学分析的包,它能够帮我们在模型未知的情况下来检验模型的线性显著性。
Statsmodels 中 OLS 的使用
使用示例:
import pandas as pd
from statsmodels.formula.api import ols
data = pd.read_csv('data.csv')
model = ols("y ~ x", data=data).fit()
print(model.summary())
输出内容为:
OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.568 Model: OLS Adj. R-squared: 0.563 Method: Least Squares F-statistic: 101.4 Date: Wed, 08 Nov 2023 Prob (F-statistic): 1.07e-15 Time: 13:58:37 Log-Likelihood: 249.14 No. Observations: 79 AIC: -494.3 Df Residuals: 77 BIC: -489.5 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 0.1589 0.004 45.367 0.000 0.152 0.166 x 0.0872 0.009 10.069 0.000 0.070 0.104 ============================================================================== Omnibus: 2.226 Durbin-Watson: 0.941 Prob(Omnibus): 0.329 Jarque-Bera (JB): 1.549 Skew: 0.296 Prob(JB): 0.461 Kurtosis: 3.348 Cond. No. 8.44 ============================================================================== Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
OLS Regression Results 的解读
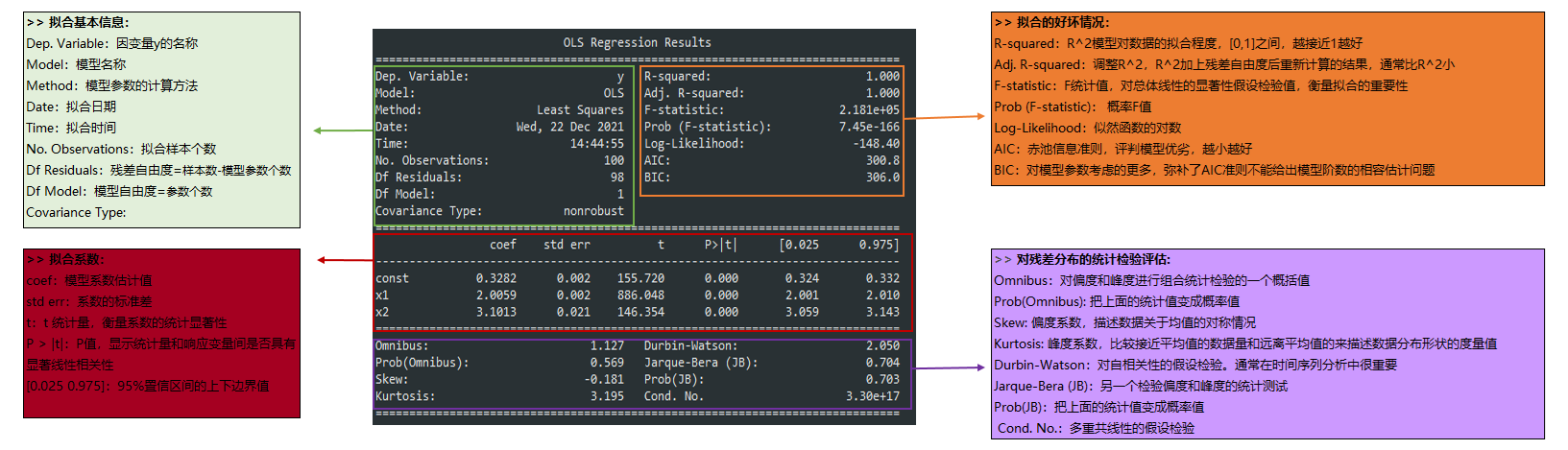
Summary 内容较多,其中重点考虑参数 R-squared、Prob(F-statistic) 以及 P>|t| 的两个值,通过这 4 个参数就能判断的模型是否是线性显著的,同时知道显著的程度如何。
- R-squared:决定系数,其值=SSR/SST,SSR 是 Sum of Squares for Regression,SST 是 Sum of Squares for Total,这个值范围在[0,1],其值越接近 1,说明回归效果越好。
- F-statistic:这就是我们经常用到的 F 检验,这个值越大越能推翻原假设,本例中其值为 4,这个值过大,说明我们的模型是线性模型,原假设是“我们的模型不是线性模型”。如果显著性水平为 0.05,则当自由度为 1 时,F 检验临界值分别为 3.84。
- Prob(F-statistic):这就是上面 F-statistic 的概率,这个值越小越能拒绝原假设,本例中为 25e-08,该值非常小了,足以证明我们的模型是线性显著的。
- P>|t|:统计检验中的 P 值,这个值越小越能拒绝原假设。P 值的临界值取决于显著性水平,通常在统计假设检验中使用 05 或 0.01 作为显著性水平。这意味着如果 P 值小于 0.05(或 0.01),我们可以在 95%(或 99%)的置信水平下拒绝原假设,并得出结论表明结果是显著的。
单独输出相关结果:
coef_df = pd.DataFrame({"params": model.params, # 回归系数
"stderr": model.bse, # 回归系数标准差
"t": round(model.tvalues, 3), # 回归系数T值
"p-values": round(model.pvalues, 3) # 回归系数P值
})
coef_df[['coef_0.025', 'coef_0.975']] = model.conf_int() # 回归系数置信区间默认5%,括号中可填具体数字比如0.05, 0.1
coef_df
| params | stderr | t | p-values | coef_0.025 | coef_0.975 | |
| Intercept | 0.158931 | 0.003503 | 45.367 | 0.0 | 0.151955 | 0.165907 |
| x | 0.087192 | 0.008660 | 10.069 | 0.0 | 0.069948 | 0.104435 |
线性回归图像
Statsmodels的plot_regress_exog函数来帮助我们理解我们的模型。根据一个回归因子绘制回归结果。在一个2*2的图中绘制了四幅图:”endog vs exog”,”残差 vs exog”,”拟合 vs exog”和”拟合+残差 vs exog”
import matplotlib.pyplot as plt import statsmodels.api as sm fig = plt.figure(figsize=(15, 8)) fig = sm.graphics.plot_regress_exog(model, "x", fig=fig)
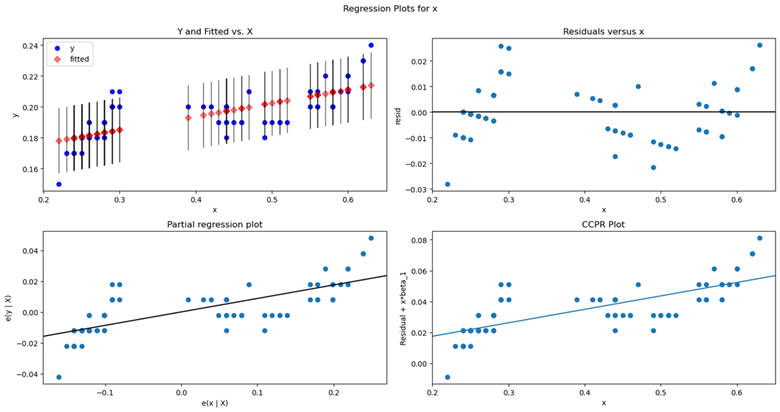
获取置信空间
下面做图画出拟合线「绿色标记」,样本数据中的观测值「蓝色圆点」,置信区间「红色标记」。
from statsmodels.sandbox.regression.predstd import wls_prediction_std
# wls_prediction_std(model)返回三个值, 标准差,置信区间下限,置信区间上限
_, confidence_interval_lower, confidence_interval_upper = wls_prediction_std(model)
x = data['x']
y = data['y']
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(x, y, 'bo', label="data")
ax.plot(x, model.fittedvalues, 'g--.', label="OLS")
ax.plot(x, confidence_interval_upper, 'r--')
ax.plot(x, confidence_interval_lower, 'r--')
ax.set_title('Simple Linear Regression')
ax.grid()
ax.legend(loc='best')
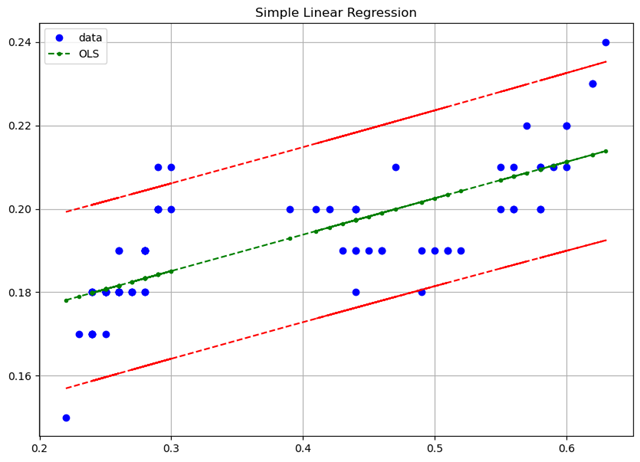
其他更为复杂的使用:
# 多元线性模型构建
stock_models = ols("close ~ open + high + low + volume", data=data).fit()
# 用ols做非线性回归
lm_s = smf.ols(formula='y ~ np.sin(x) + x', data=df).fit()
# ridge
ols('y ~ x1 + x2', data=df).fit_regularized(alpha=1, L1_wt=1)
# C指的是Categorical variables
res = smf.ols(formula='Lottery ~ Literacy + Wealth + C(Region)', data=df).fit()
# -1指的是使Intercept=0
res = smf.ols(formula='Lottery ~ Literacy + Wealth + C(Region) - 1', data=df).fit()
# “:” adds a new column to the design matrix with the product of the other two columns. “
# *” will also include the individual columns that were multiplied together:
# 所以'Lottery ~ Literacy * Wealth - 1'相当于'Lottery ~ Literacy + Wealth + Literacy:Wealth - 1'
res1 = smf.ols(formula='Lottery ~ Literacy:Wealth - 1', data=df).fit()
res2 = smf.ols(formula='Lottery ~ Literacy * Wealth - 1', data=df).fit()