在前面的文章中介绍了基本的线性回归模型 属于全局的模型(除局部加权线性回归外),在线性回归模型中,其前提是假设全局的数据之间是线性的,通过拟合所有的样本点,训练得到最终的模型。然而现实中的很多问题是非线性的,当处理这类复杂的数据的回归问题时,特征之间的关系并不是简单的线性关系,此时,不可能利用全局的线性回归模型拟合这类数据。
CART树回归算法属于一种局部的回归算法,通过将全局的数据集划分成多份容易建模的数据集,这样在每一个局部的数据集上进行局部的回归建模。
复杂的回归问题
线性回归模型
在基本的线性回归算法中,样本的特征与样本的标签之间存在线性相关关系,但是,对于样本特征与样本标签存在非线性的关系时,如图所示:
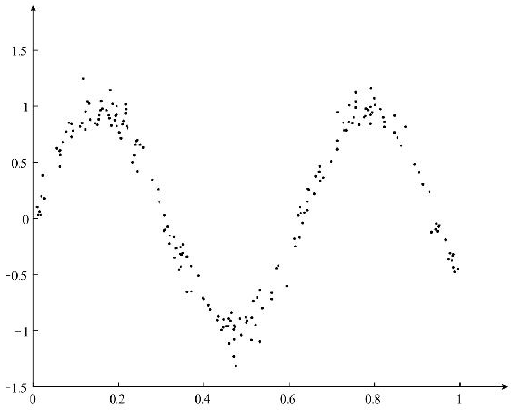
对于上图所示的非线性的回归问题,利用简单的线性回归求解的结果如图所示:
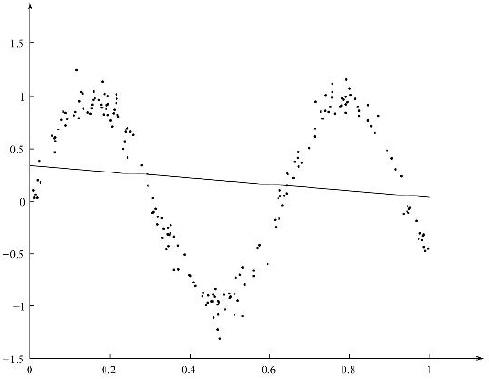
局部加权线性回归
为了能够实现对非线性数据的拟合,可以使用局部加权线性回归,局部加权线性回归的求解结果如图所示:
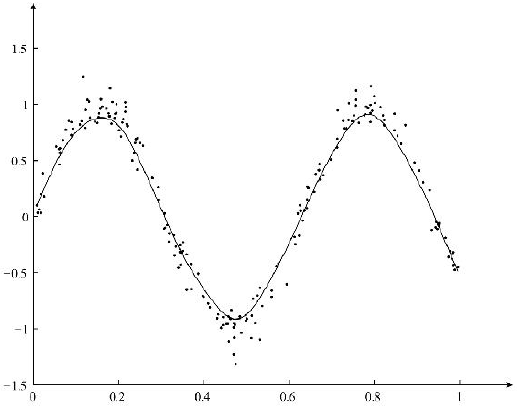
局部加权线性回归能够对非线性的数据实现较好拟合,与简单的线性回归算法相比,局部线性加权回归算法是局部的线性模型,而简单的线性回归模型是全局的模型,利用局部的模型能够较好拟合出局部的数据。虽然基于局部加权线性回归模型能够较好拟合非线性数据,但是局部加权线性回归模型属于非参学习算法,在每次对数据进行预测时,需要利用数据重新训练模型的参数,当数据量较大时,这样的计算是非常耗费时间的。
CART算法
基于树的回归算法也是一类基于局部的回归算法,通过将数据集切分成多份,在每一份数据中单独建模。与局部加权线性回归不同的是,基于树回归的算法是一种基于参数的学习算法,利用训练数据训练完模型后,参数一旦确定,无需再改变。
分类回归树(Classification And Regression Tree,CART)算法是使用较多的一种树模型,CART算法可以处理分类问题,也可以处理回归问题。在决策树算法 文章中,我们介绍了如何利用CART算法处理分类问题,在本文中,我们着重介绍如何利用CART算法处理回归问题。CART算法中的树采用一种二分递归分割的技术,即将当前的样本集分为左子树和右子树两个子样本集,使得生成的每个非叶子节点都有两个分支。因此,CART算法生成的决策树是非典型的二叉树。利用CART算法处理回归问题的主要步骤:①CART回归树的生成;②CART回归树的剪枝。
CART回归树生成
CART回归树的划分
CART分类树算法中,利用Gini指数作为划分树的指标,通过样本中的特征,对样本进行划分,直到所有的叶节点中的所有样本都为同一个类别为止。但是在CART回归树中,样本的标签是一系列的连续值的集合,不能再使用Gini指数作为划分树的指标。但是,我们注意到,Gini指数表示的是数据的混乱程度,对于连续数据,当数据分布比较分散时,各个数据与平均数的差的平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。方差越大,数据的波动越大;方差越小,数据的波动就越小。因此,对于连续的数据,可以使用样本与平均值的差的平方和作为划分回归树的指标:
$$m\cdots^2=\sum_{i=1}^{m}(y^{(i)}-\bar{y})^2$$
其中$y^{(i)}$为第i个样本的标签,$\bar{y}$为m个样本标签的均值。公式用Python表示为:
import numpy as np def err_cnt(dataSet): '''回归树的划分指标 input:dataSet(list):训练数据 output:m*s^2(float):总方差 ''' data = np.mat(dataSet) return np.var(data[:,-1]) * np.shape(data)[0]
err_cnt函数用于计算当前节点的总方差。有了划分的标准,那么,应该如何对样本进行划分呢?与CART分类树中的方法一样,我们根据每一维特征中的每一个取值,尝试将样本划分到树节点的左右子树中,如取得样本特征中的第j维特征中值x作为划分的值,如果一个样本在第j维处的值大于或者等于x,则将其划分到右子树中,否则划分到左子树中。划分过程程序如下:
def split_tree(data, fea, value): '''根据特征fea中的值value将数据集data划分成左右子树 input:data(list):训练样本 fea(float):需要划分的特征index value(float):指定的划分的值 output:(set_1, set_2)(tuple):左右子树的聚合 ''' set_1 = [] #右子树的集合 set_2 = [] #左子树的集合 for x in data: if x[fea] >= value: set_1.append(x) else: set_2.append(x) return (set_1, set_2)
split_tree函数根据fea位置处的特征,按照值value将样本划分到左右子树中,当样本在fea处的值大于或者等于value时,将其划分到右子树中,否则将其划分到左子树中。
CART回归树的构建
CART分类树的构建过程如下所示:
- 对于当前训练数据集,遍历所有属性及其所有可能的切分点,寻找最佳切分属性及其最佳切分点,使得切分之后的基尼指数最小,利用该最佳属性及其最佳切分点将训练数据集切分成两个子集,分别对应着判别结果是左子树和判别结果是右子树。
- 对第一步中生成的两个数据子集递归地调用第一步,直至满足停止条件。
- 生成CART决策树
为了能构建CART回归树算法,首先,需要为CART回归树中节点设置一个结构,其具体的实现:
class node: '''树的节点的类 ''' def __init__(self, fea=-1, value=None, results=None, right=None, left=None): self.fea = fea #用于切分数据集的属性的列索引值 self.value = value #设置划分的值 self.results = results #存储叶节点的值 self.right = right #右子树 self.left = left #左子树
def build_tree(data, min_sample, min_err):
”’构建树
input:data(list):训练样本
min_sample(int):叶子节点中最少的样本数
min_err(float):最小的error
output:node:树的根结点
”’
#构建决策树,函数返回该决策树的根节点
if len(data) <= min_sample:
return node(results=leaf(data))
#1、初始化
best_err = err_cnt(data)
bestCriteria = None #存储最佳切分属性以及最佳切分点
bestSets = None #存储切分后的两个数据集
#2、开始构建CART回归树
feature_num = len(data[0]) - 1
for fea in range(0, feature_num):
feature_values = {}
for sample in data:
feature_values[sample[fea]] = 1
for value in feature_values.keys():
#2.1、尝试划分
(set_1, set_2) = split_tree(data, fea, value)
if len(set_1) < 2 or len(set_2) < 2:
continue
#2.2、计算划分后的error值
now_err = err_cnt(set_1) + err_cnt(set_2)
#2.3、更新最优划分
if now_err< best_err and len(set_1) > 0 and len(set_2) > 0:
best_err = now_err
bestCriteria = (fea, value)
bestSets = (set_1, set_2)
#3、判断划分是否结束
if best_err > min_err:
right = build_tree(bestSets[0], min_sample, min_err)
left = build_tree(bestSets[1], min_sample, min_err)
return node(fea=bestCriteria[0], value=bestCriteria[1],\
right=right, left=left)
else:
return node(results=leaf(data)) #返回当前的类别标签作为最终的类别标签
build_tree函数用于构建CART回归树模型,在构建CART回归树模型的过程中,如果节点中的样本的个数小于或者等于指定的最小的样本数min_sample,则该节点不再划分,函数leaf用于计算当前叶子节点的值;当节点需要划分时,首先计算当前节点的error值在开始构建的过程中,根据每一维特征的取值尝试将样本划分到左右子树中。划分后产生左子树和右子树,此时,计算左右子树的error值,若此时的error值小于最优的error值,则更新最优划分,当该节点划分完成后,继续对其左右子树进行划分:
def leaf(dataSet): '''计算叶节点的值 input:dataSet(list):训练样本 output:np.mean(data[:,-1])(float):均值 ''' data = np.mat(dataSet) return np.mean(data[:,-1])
函数leaf用于计算当前叶子节点的值,计算的方法是使用划分到该叶子节点的所有样本的标签的均值。
CART回归树剪枝
在CART树回归中,当树中的节点对样本一直划分下去时,会出现的最极端的情况是:每一个叶子节点中仅包含一个样本,此时,叶子节点的值即为该样本的标签的值。这种情况极易对训练样本”过拟合”,通过这样的方式训练出来的样本可以对训练样本拟合得很好,但是对于新样本的预测效果将会较差。为了防止构建好的CART树回归模型过拟合,通常需要对CART回归树进行剪枝,剪枝的目的是防止CART回归树生成过多的叶子节点。在剪枝中主要分为:前剪枝和后剪枝。
前剪枝
前剪枝是指在生成CART回归树的过程中对树的深度进行控制,防止生成过多的叶子节点。在build_tree函数中,我们通过参数min_sample和min_err来控制树中的节点是否需要进行更多的划分。通过不断调节这两个参数,来找到一个合适的CART树模型。
后剪枝
后剪枝是指将训练样本分成两个部分,一部分用来训练CART树模型,这部分数据被称为训练数据,另一部分用来对生成的CART树模型进行剪枝,这部分数据被称为验证数据。由上述过程可知,在后剪枝的过程中,通过验证生成好的CART树模型是否在验证数据集上发生了过拟合,如果出现过拟合的现象,则合并一些叶子节点来达到对CART树模型的剪枝。
CART回归树对数据预测
有了以上的理论准备,我们利用上述实现好的函数,构建CART树回归模型。利用CART回归树算法进行求解的过程中,主要包括:①利用训练数据训练CART回归树模型;②利用训练好的CART回归树模型对新数据进行预测。
当训练好CART回归树,需要评估训练好的CART回归树模型时,函数cal_error用于评估训练好的CART回归树模型:
def cal_error(data, tree):
'''评估CART回归树模型
input:data(list):
tree:训练好的CART回归树模型
output:err/m(float):均方误差
'''
m = len(data) #样本的个数
n = len(data[0]) - 1 #样本中特征的个数
err = 0.0
for i in xrange(m):
tmp = []
for j in xrange(n):
tmp.append(data[i][j])
pre = predict(tmp, tree) #对样本计算其预测值
#计算残差
err += (data[i][-1] - pre) * (data[i][-1] - pre)
return err/m
函数cal_error用于评估训练好的CART回归树模型,函数的输入分别为训练数据data和训练好的CART回归树模型tree,在评估CART回归树模型的过程中,利用训练好的CART回归树模型对每一个样本进行预测,函数predict的具体实现如下所示。当预测完成后,利用预测的值和原始的样本的标签计算残差。
def predict(sample, tree):
'''对每一个样本sample进行预测
input:sample(list):样本
tree:训练好的CART回归树模型
output:results(float):预测值
'''
#1、只是树根
if tree.results != None:
return tree.results
else:
#2、有左右子树
val_sample = sample[tree.fea] #fea处的值
branch = None
#2.1、选择右子树
if val_sample >= tree.value:
branch = tree.right
#2.2、选择左子树
else:
branch = tree.left
return predict(sample, branch)
函数predict利用训练好的CART回归树模型tree对样本sample进行预测。在预测的过程中,主要分为如下的情况:
- 若此时只有根结点,则直接返回其值作为最终的预测结果
- 若此时该结点有左右子树,则比较样本sample中在fea索引处的值val_sample和CART回归树模型中在划分处的值value
- 若val_sample大于或等于CART回归树模型中的值value,则选择右子树
- 若val_sample小于CART回归树模型中的值value,则选择左子树
最终对数据的拟合效果如图:
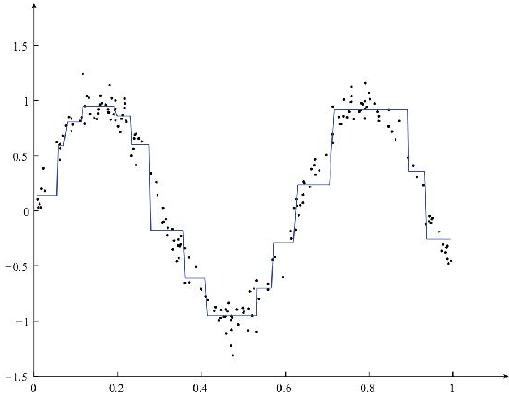 对min_sample和min_err取值进行调整,如图所示:
对min_sample和min_err取值进行调整,如图所示:
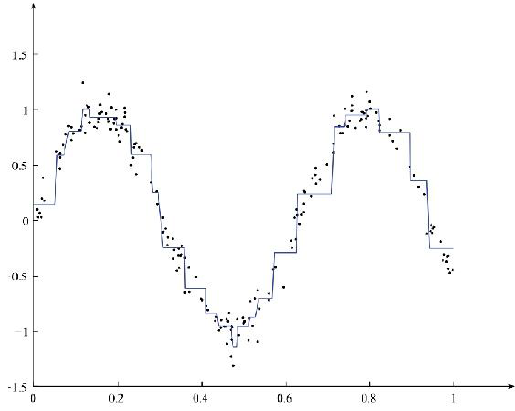
Python中用Scikit-Learn实现决策树
决策树分类
from sklearn import tree
from sklearn.datasets import load_iris
import graphviz
iris = load_iris()
clf = tree.DecisionTreeClassifier(criterion="gini", splitter="best")
clf.fit(iris.data, iris.target)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph.view('iris', 'data')
决策树回归
# -*- coding: utf-8 -*-
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.25, random_state=33)
ss_X = StandardScaler()
ss_y = StandardScaler()
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
# fit_transform与transform都要求操作2D数据,而此时的y_train与y_test都是1D的,因此需要调用reshape(-1,1),例如:[1,2,3]变成[[1],[2],[3]]
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1, 1))
dtr = DecisionTreeRegressor()
dtr.fit(X_train, y_train)
dtr_y_predict = dtr.predict(X_test)
# 使用R-squared、MSE、MAE指标评估
print('R-squared:', dtr.score(X_test, y_test))
print('MSE:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))
print('MAE:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))